Characterizing the dependence of pure-tone frequency difference limens on frequency, duration, and level

Abstract

This study examined the relationship between the difference limen for frequency (DLF) of pure tones and three commonly explored stimulus parameters of frequency, duration, and sensation level. Data from 12 published studies of pure-tone frequency discrimination (a total of 583 DLF measurements across 77 normal-hearing listeners) were analyzed using hierarchical (or “mixed-effects”) generalized linear models. Model parameters were estimated using two approaches (Bayesian and maximum likelihood). A model in which log-transformed DLFs were predicted using a sum of power-law functions plus a random subject- or group-specific term was found to explain a substantial proportion of the variability in the psychophysical data. The results confirmed earlier findings of an inverse-square-root relationship between log-transformed DLFs and duration, and of an inverse relationship between log(DLF) and sensation level. However, they did not confirm earlier suggestions that log(DLF) increases approximately linearly with the square-root of frequency; instead, the relationship between frequency and log(DLF) was best fitted using a power function of frequency with an exponent of about 0.8. These results, and the comprehensive quantitative analysis of pure-tone frequency discrimination on which they are based, provide a new reference for the quantitative evaluation of models of frequency (or pitch) discrimination.

1 INTRODUCTION

A fundamental goal of psychophysics is to formulate mathematical models of the relations between physical variables, such as sound intensity or frequency, and measures of sensation or perception, such as detection and discrimination thresholds. Thresholds for the discrimination of the frequency of pure tones, which are traditionally referred to as “difference limens for frequency” (DLFs), reflect a fundamental limit of the auditory system’s ability to discriminate pure tones based on differences—or changes—in frequency. Frequency is the primary determinant of pitch. Therefore, psychophysical data concerning the ability of human listeners to discriminate frequency provide important constraints for models of pitch perception: models of pitch perception must be able to account for the remarkably small size of DLFs, and for the way in which these thresholds vary as a function of stimulus parameters such as frequency, duration, and level (e.g., Dai et al., 1995; Freyman and Nelson, 1986; Heinz et al., 2001a;b; Micheyl et al., 1998; Moore and Glasberg, 1989; Sek and Moore, 1995; Siebert, 1970). Thus, the formulation of mathematical models that describe DLFs as a function of frequency, duration, and level appears a useful, and important, endeavor (Freyman and Nelson, 1991; Nelson et al., 1983).

Although numerous studies have measured DLFs for different frequencies, tone durations, and/or levels (e.g., Amitay et al., 2006; Dai and Micheyl, 2011; Dai et al., 1995; Delhommeau et al., 2005; Freyman and Nelson, 1986;1991; Hall and Wood, 1984; Harris, 1952; Jesteadt and Bilger, 1974; Jesteadt and Wier, 1977; Jesteadt et al., 1977; Moore, 1973; Moore and Glasberg, 1989; Nelson et al., 1983; Shower and Biddulph, 1931; Wier et al., 1976;1977), to our knowledge, only one study so far has been devoted specifically to formulating a mathematical model of the dependence of DLFs on stimulus parameters in human listeners (Nelson et al., 1983). The authors of this study found that DLFs measured at various frequencies and levels were well fitted by a relatively simple equation, wherein the base-10 logarithm of the DLF (in Hz), is predicted as a linear combination of the square-root of frequency, f (in Hz), and of the reciprocal of the sensation level, s (in dB), plus a constant, as follows:

$${\text{log}}_{10}[d(f,s)]=a\sqrt{f}+{\mathit{\text{bs}}}^{-1}+c$$ (1)

In this equation, d(f,s) denotes the predicted DLF (in Hz).¹ The coefficients, a, b, and c, of this equation were estimated (using a least-squares fitting procedure) for three data sets, including Nelson et al.’s (1983) own data, and the data of two earlier studies (Harris, 1952; Wier et al., 1977). The fits were performed separately for each of the three studies, resulting in three sets of coefficients, a, b, and c. The fits were found to account for a large proportion of the variance in the mean DLFs across frequency and level, as indicated by R² coefficients between 0.92 and 0.99, depending on the dataset to which the fits were applied.

Although Nelson et al.’s (1983) study provided an important step forward in the development of a general equation relating DLFs to various stimulus parameters, the study has some limitations. Firstly, the general equation that was proposed by these authors lacks a term for stimulus duration. As indicated by the results of many studies, duration strongly influences DLFs (Freyman and Nelson, 1986;1987; Liang and Chistovich, 1961; Micheyl et al., 1998; Moore, 1973; Oetinger, 1959; Sekey, 1963), and the effect of duration on DLFs can play an important role in constraining models and theories of pitch (Freyman and Nelson, 1986; Hanekom and Krüger, 2001; Heinz et al., 2001a; Micheyl et al., 1998; Siebert, 1970; Wier et al., 1977). Accordingly, the first aim of the current study was to extend the development of a general equation for DLFs by including duration, in addition to frequency and level.

A second limitation of Nelson et al.’s (1983) general equation stems from the fact that the parameter estimates were based on relatively small datasets, consisting of three studies, each of which included only three listeners. The fits were performed on the mean DLFs across the three listeners, separately for each study. Therefore, each fit is based on only 28 to 36 data points. Although the fits yielded relatively high R² coefficients (0.92 – 0.99), it is important to note that because these fits were performed on the mean DLFs (averaged across listeners), the resulting R² coefficients do not fully take into account an important source of variability in the measurements, relating to inter-individual differences. Accordingly, two additional goals of the current study were to aggregate a relatively large set of previous publications containing individual DLF measurements for a relatively wide range of frequencies, durations, and level, and to explicitly take into account inter-individual differences by including data from individual subjects. To that purpose, we gathered data from 12 studies, representing a total of 583 data points from 77 listeners.

Finally, it is important to note that Nelson et al. (1983) formally tested only two models: one corresponding to equation 1, and one alternative model involving a logarithmic transformation of frequency. They found that the logarithmic transformation of frequency often yielded significantly smaller R² coefficients than the square-root transformation.² However, it remains unclear whether other functional relationships, besides square-root and log, would have provided a more accurate description of the data. Accordingly, in the current study, we evaluated a model involving power-law relationships between the stimulus parameters and the DLFs, which provides a more general description and includes square-root and linear relationships as specific cases.

2 METHODS

2.1 Database

Pure-tone DLF data from 12 published studies were analyzed (Dai and Micheyl, 2011; Dai et al., 1995; Delhommeau et al., 2005; Freyman and Nelson, 1986; Micheyl et al., 1998; Moore, 1973; Moore and Glasberg, 1989; Nelson et al., 1983; Nelson and Stanton, 1982; Sek and Moore, 1995; Wier et al., 1976, 1977). These studies were selected based on the following criteria: First, only studies that measured DLFs using discrete steady tones were included. Studies in which frequency-modulated tones were used were not included because it has been suggested that the detection of frequency modulation involves different underlying mechanisms than the discrimination of differences in frequency between steady pure tones (Moore and Glasberg, 1989; Sek and Moore, 1995). Second, only measurements obtained in the absence of across-trial frequency roving were included. Although the influence of frequency or level roving on DLFs appears to be relatively small, DLFs measured in the presence of roving have generally been found to be larger than DLFs measured in the absence of roving (Dai et al., 1995; Moore and Glasberg, 1989). Third, only data from listeners with normal hearing were included.

Our original intention was to include only individual data; however, it became clear that this would have led to the exclusion of important sources of information on the dependence of DLFs on frequency and level, such as Wier et al.’s (1977) and Nelson et al.’s (1983) studies. The study of Harris (1952), which was analyzed by Nelson et al. (1983), was not included here because, as noted by Nelson et al., this study used an unusual procedure for measuring thresholds, which made it difficult to determine what d' the thresholds correspond to. Moreover, this study used exceptionally long stimuli and inter-tone intervals (1.4 s for each).

2.2 Tasks, procedures, and stimuli

The tasks, procedures, and targeted percent-correct points on the psychometric function for the 12 studies are listed in Table I. All but one of the studies (Moore, 1973) used a computerized, modified adaptive procedure (Levitt, 1971). Moore (1973) used a constant-stimuli procedure, and estimated thresholds corresponding to the 75%-correct point on the psychometric function via interpolation. Eight of the 12 studies, including the study by Moore (1973), used a two-interval two-alternative forced-choice task (2I-2AFC) task. Nelson and Stanton (1982), Nelson et al. (1983), Freyman and Nelson (1986), used a four-interval four-alternative forced-choice (4I-4AFC) task. Delhommeau et al. (2005) used a three-interval, two-alternative forced-choice task (3I-2AFC) task. Ten of the 12 studies targeted the 70.7%-correct point on the psychometric function. One study (Sek and Moore, 1995) targeted the 79.4%-correct point.

Table I.

Tasks, procedures, and targeted percent-correct for the twelve studies included in the analysis. PC: percent-correct at threshold.

Study	Authors	Task	Procedure	PC
M73	Moore (1973)	2I-2AFC	Constant stimuli	75.0
W76	Wier et al. (1976)	2I-2AFC	Adaptive	70.7
W77	Wier et al. (1977)	2I-2AFC	Adaptive	70.7
N82	Nelson & Stanton (1982)	4I-4AFC	Adaptive	70.7
N83	Nelson et al. (1983)	4I-4AFC	Adaptive	70.7
F86	Freyman & Nelson (1986)	4I-4AFC	Adaptive	70.7
M89	Moore & Glasberg (1989)	2I-2AFC	Adaptive	70.7
D95	Dai (1995)	2I-2AFC	Adaptive	70.7
M95	Moore & Sek (1995)	2I-2AFC	Adaptive	79.4
M98	Micheyl et al. (1998)	2I-2AFC	Adaptive	70.7
D05	Delhommeau et al. (2005)	3I-2AFC	Adaptive	70.7
D11	Dai & Micheyl (2011)	2I-2AFC	Adaptive	70.7

The stimuli that were used in these studies were pure tones ranging from 125 to 8500 Hz in frequency and from 5 to 500 ms in duration (measured at the 0-voltage points on the envelope). To account for the fact that different studies used different ramp shapes and ramp durations, the stimulus durations for all studies were re-expressed in terms of “effective durations,” defined here as the duration measured at the half-amplitude points of the envelope. Depending on the study, stimulation levels were specified in dB SL, dB SPL, or in terms of constant loudness. For studies in which stimulation levels were specified in dB SPL, the absolute threshold at the stimulus frequency (or a nearby frequency) was subtracted from the indicated SPL to obtain a value in dB SL. When the listener’s absolute threshold at the signal frequency was not indicated in the original publication, the “reference” absolute-threshold curve—with threshold expressed in terms of minimum audible pressure, as illustrated in Moore (2003)—was used. For the study that used a constant loudness of 60 phons (Moore, 1973), the equal-loudness contour corresponding to 60 phons (digitized from Fig. 4.1 on p. 129 in Moore, 2003) was used to compute the SPLs of the tones for different frequencies, and the resulting SPL values were then converted into dB SL values by subtracting the reference absolute threshold at the considered frequency. The resulting SL values ranged from 5 to 80 dB SL.

2.3 Data acquisition and pre-processing

The DLF data were obtained in one of three ways: by digitizing figures in the source article; by entering values from a table in the source article; or by using the original data, when we had access to them. The DLFs reported in some studies (e.g., Delhommeau et al., 2005) were based on a single “run” of the adaptive procedure (or a single block of trials), whereas for other studies, the reported DLFs were averages of the DLFs measured across multiple runs (or blocks of trials).

To correct for differences in thresholds related to differences in measurement procedures, such as differences in the task or in the targeted point on the psychometric function, the DLFs (in Hz) were divided by the d' value corresponding to the targeted point of the psychometric function (70.7%, 75%, or 79.4%), taking into account the task (2I-2AFC, 3I-2AFC, or 4I-4AFC), so that the resulting (“normalized”) DLFs all corresponded to a d' of 1. The d' values corresponding to 70.7%, 75%, or 79.4% in the 2I-2AFC, 3I-2AFC, or 4I-4AFC task were computed using standard formulas based on the assumption of equal-variance Gaussian distributions of internal noise (Green and Swets, 1966; Macmillan and Creelman, 2005). The division of the DLFs by d' rests on the assumption that d' increases linearly with the frequency difference (in Hz) between the two tones being compared—an assumption that is supported by the results of several studies (Jesteadt and Bilger, 1974; Jesteadt and Sims, 1975; Wier et al., 1976; Turner and Nelson, 1982; Nelson and Freyman, 1986; Dai and Micheyl, 2011). Prior to statistical analysis, the normalized DLFs (in Hz) were transformed into (base-10) logarithmic units. The use of log-transformed DLFs was motivated by two main considerations. First, DLFs are usually measured using a multiplicative, rather than additive, adaptive rule whereby the frequency difference between the tones that the listener must discriminate is usually increased or decreased by a factor, rather than by a constant amount in Hz.³ Second, standard deviations of DLF estimates (in Hz), measured across runs for a given condition and/or a given listener, tend to increase with their mean. The logarithmic transformation corrects for this trend and makes the standard deviations more uniform across different conditions.

2.4 Statistical analyses

2.4.1 Model structure

The relationship between the log-transformed normalized DLFs (i.e., the DLF in Hz corresponding to d' = 1 converted into log₁₀ units) and the stimulus parameters (frequency, duration, and level) was described using generalized-linear models involving a linear combination of power functions. The rationale for using power functions was twofold. Firstly, Nelson et al.’s (1983) model, which involves a square-root relationship between log-transformed DLFs and frequency and an inverse relationship between log-transformed DLFs and level, can be written as a linear combination of power functions with exponents 0.5 and −1. Secondly, power functions provide a simple yet flexible mathematical model for monotonic relationships between physical and sensory variables; they can accommodate both concave and convex relationships—depending on the sign of the exponent—and they include the linear relationship as a specific case—when the exponent equals 1.

Three models were evaluated. Model A was defined by the following equation:

$$E[d_i(f,d,s)]={\mathrm{\beta }}_f{\left(\frac{f}{1000}\right)}^{{\mathrm{\gamma }}_f}+{\mathrm{\beta }}_d{\left(\frac{d}{100}\right)}^{{\mathrm{\gamma }}_d}+{\mathrm{\beta }}_s{\left(\frac{s}{10}\right)}^{{\mathrm{\gamma }}_s}+r_i+\mathrm{\alpha }$$ (2)

In this equation, E[d_i(f, d, s)], denotes the expected value of the log-transformed normalized DLF for frequency, f (in Hz), duration, d (in ms), and sensation level, s (in dB) for “group” i. The word “group” is used here to refer either to a single subject (for studies for which we had access to the individual data) or to a group of subjects (for studies for which we had access only to the mean DLFs across subjects). The coefficients, β_f, β_d, and β_s, and the power-function exponents, γ_f, γ_d, and γ_s, operate on the stimulus variable indicated by the subscript. The term, r_i, is the group-specific term reflecting the difference between α and the mean log-normalized DLF for the i^th group. The value of the index, i, ranged from 1 to 70, so that each of the 67 individuals, two groups of three listeners (Nelson et al., 1983; Wier et al., 1977), and one group of four listeners (Micheyl et al., 1998) in the database had a specific r_i value associated with it. In the regression literature, terms such as r_i in equation 2 are traditionally referred to as “random effects.” They are distinguished from “fixed effects,” which are common to all subjects or groups. Random effects allow the separation of subject- or study-specific variability and of other sources of variance in the data, taking into account the fact that thresholds measured across different stimulus conditions for a given individual or a given study can be generally higher (or lower) than thresholds measured for another listener, or study (Demidenko, 2004). However, our model assumes that the data trends (i.e., variations as a function of stimulus parameters) are the same across groups. The last term in equation 2, α, is the intercept. Thus, the model described by equation 2 is a mixed-effects model, which includes a combination of fixed effects (α, β_f, β_d, and β_s, γ_f, γ_d, and γ_s) and random-effects (r_i). The coefficients, β_f, β_d, and β_s, and the exponents, γ_f, γ_d, and γ_s, were treated as free parameters, i.e., as unknown random variables, the values of which were to be estimated. The purpose of the denominators of 1000, 100, and 10 in equation 2 is to ensure that the quantities in parentheses are commensurate, even though the corresponding variables, f, d, and s are not. For typical values of the variables, f, d, and s, the values of the ratios inside the parentheses had values between 0 and 10, and the coefficients, β_f, β_d, and β_s had similar orders of magnitude; this scaling in the model limited the need for adaptive scaling in the gradient-based and Markov-Chain Monte-Carlo algorithms that were used to estimate the values of these parameters (see below).

Model B was a reduced version of Model A. The two models differed only with respect to whether the exponents, γ_f, and γ_s were treated as random variables (Model A) or as deterministic, i.e., pre-determined and fixed, scalars (Model B). For model B, the exponents, γ_f, and γ_s, were set to −0.5 and −1, respectively, consistent with Nelson et al.’s (1983) equation.

Model C was defined by the following equation:

$$E[d_i(f,d,s)]={\mathrm{\beta }}_f{\left(\frac{f}{1000}\right)}^{{\mathrm{\gamma }}_f}+{\mathrm{\beta }}_d{\left(\frac{d}{100}\right)}^{{\mathrm{\gamma }}_d}+{\mathrm{\beta }}_s{\left(\frac{s}{10}\right)}^{{\mathrm{\gamma }}_s}+{\mathrm{\beta }}_{\mathit{\text{fd}}}{\left(\frac{d}{100}\right)}^{{\mathrm{\gamma }}_{d2}}{\left(\frac{f}{1000}\right)}^{{\mathrm{\gamma }}_{f2}}+r_i+\mathrm{\alpha }.$$ (3)

Note that the only difference between equation 2 and equation 3 relates to the presence of an additional term, β_fd (d / 100)^γ_d2 (f / 1000)^γ_f2, in equation 3. This term was added to model possible interactions in the effects of the two stimulus parameters, d and f, on the log(DLF).

2.4.2 Model evaluation

Model evaluation proceeded according to the following steps. First, estimates of model parameters were obtained using a maximum-likelihood (ML) procedure (Pinheiro and Bates, 1995). The procedure was implemented in Matlab (MathWorks, Natick, MA) using the nlmefit function. The function yields point estimates of the model parameters and 95% confidence intervals on the parameters. One limitation of this approach, however, is that it relies on normality assumptions to compute confidence intervals on the parameter estimates; when this assumption is not met, results obtained using ML methods can be in error. Thus, in addition to the ML approach, we used computational Bayesian methods (Markov-chain-Monte-Carlo and Gibbs sampling) to estimate the probability density function (PDF) of the model parameters given the data—this PDF is traditionally referred to as the “posterior distribution” of the model parameters (see the Appendix for details). One advantage of the Bayesian approach is that it yields credible intervals—also known as “Bayesian confidence intervals”—for the model parameters. Unlike a classical (frequentist) confidence interval, a Bayesian credible interval encapsulates all sources of uncertainty concerning the parameter value (Gelman and Carlin, 2004; Gregory, 2005).

Goodness of fit was quantified using the root-mean-square error (RMSE) between the data and the model predictions. While the RMSE is a simple and intuitive measure of goodness of fit, its usefulness as a model-comparison tool is limited, due to the fact that it does not take into account the number of free parameters in the model—all other things being equal, the RMSE decreases monotonically as the number of free parameters increases, so this measure always favors models that have more free parameters. A better indicator of model superiority, which takes into account the number of free parameters, is the Bayesian information criterion (BIC) (Schwarz, 1978). The BIC for model i is defined as,

$${\mathit{\text{BIC}}}_i=-2\text{ln}[f(\mathbf{D}|{\mathbf{\theta ̂}}_i,M_i)]+k_i\text{ ln}(n),$$ (4)

where f (D | θ̂_i, M_i) denotes the maximum likelihood of the data (D) conditioned on the considered model (M_i), k_i is the number of free parameters in the model, and n is the number of data points. The second term on the right of equation 4 can be understood as a “penalty for complexity”—or “Ockam’s razor”—which penalizes models containing a larger number of free parameters, relative to models containing fewer parameters. The BIC value decreases as the likelihood of the data under the considered model increases, and it increases as the number of free parameters and/or the number of data points increases. Thus, a lower BIC value is indicative of a better model.

Although it is difficult to build intuition for BIC values, such values can easily be transformed into Bayes factors, which are likelihood ratios for one model relative to another. The Bayes factor for model M_i relative to model M_j, BF_i,j, can be approximated as (Kass and Raftery, 1995):

$${\mathit{\text{BF}}}_{i,j}=e^{-\frac{1}{2}({\mathit{\text{BIC}}}_i-{\mathit{\text{BIC}}}_j)}.$$ (5)

Very large or small Bayes factors are usually expressed in decibans (see Jeffreys, 1961; Good, 1979), i.e., as 10log₁₀ (BF_i,j).

Another commonly used measure of goodness-of-fit for hierarchical models is the deviance information criterion (DIC) (Spiegelhalter et al., 2002). One advantage of the DIC over the BIC is that, while the BIC treats all free parameters equivalently (which is questionable when the parameters do not all vary over the same range, or have different prior distributions), the DIC includes an estimation of the effective number of free parameters in the model (Spiegelhalter et al., 2002). The DIC for model i is defined as:

$${\mathit{\text{DIC}}}_i={\mathrm{D̅}}_i+p_{\mathit{\text{Di}}},$$ (6)

where the first term, D̅_i, corresponds to the posterior expectation of the deviance,

$${\mathrm{D̅}}_i=E_{{\mathbf{\theta }}_i|\mathbf{D}}[-2\text{ln }f(\mathbf{D}|{\mathbf{\theta }}_i,M_i)],$$ (7)

and the second term, p_Di, is the “effective number of degrees of freedom,” a measure of model complexity, which is defined as the difference between the posterior mean of the deviance and the deviance evaluated at the posterior mean of the parameters, θ̄_i, as follows.

$$p_{\mathit{\text{Di}}}={\mathrm{D̅}}_i+2\text{ln }f(\mathbf{D}|{\mathbf{\theta ̄}}_i,M_i).$$ (8)

All three model-comparison indices (BIC, Bayes Factors, and DIC) were computed, and all three are reported in the text.

3 RESULTS

3.1 Overview of the data

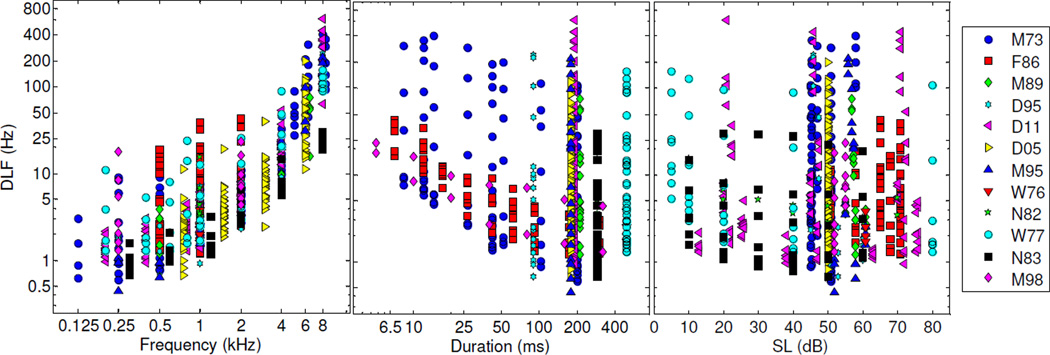
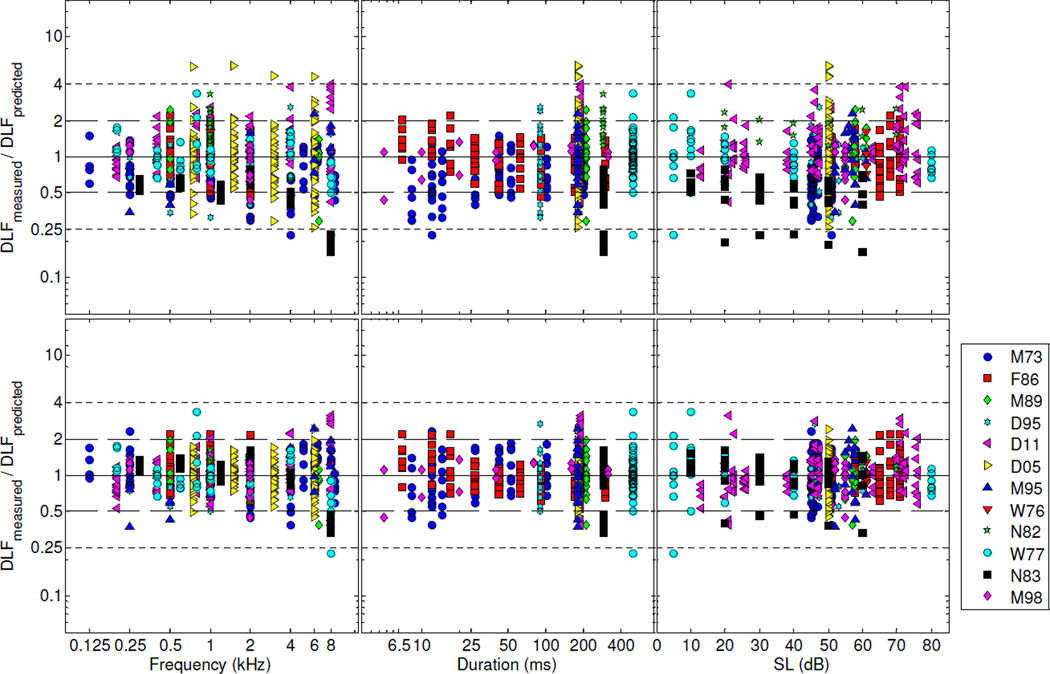
Figure 1 shows the normalized DLFs from all 12 studies as a function of the three stimulus parameters: frequency, duration, and level. As explained in the methods section, these thresholds were scaled so that they all correspond to a d' of 1, regardless of the d' value targeted in the original studies. Each panel in this figure shows the normalized DLFs as a function of one stimulus parameter: frequency, duration, or level. The large dispersion in the data is not surprising because the DLFs are plotted as a function of a single stimulus parameter, with the two other stimulus parameters varying over a wide range. Thus, for instance, the largest DLFs in the left panel, in which DLFs are plotted as a function of frequency, correspond to stimulus conditions involving short durations and/or low SLs—conditions under which DLFs have usually been found to be quite large. The goal of this figure is merely to provide an overall view of the data that were used in the model-based analyses described below; more detailed and less compact visual representations of the data can be found in the original publications.

Figure 1.

Normalized DLFs as a function of frequency, duration, and level. The different studies are indicated by different symbol-color combinations, as shown in the key. Note that this figure shows normalized DLFs, scaled so that they correspond to a d' of 1.

3.2 Model-parameter estimates

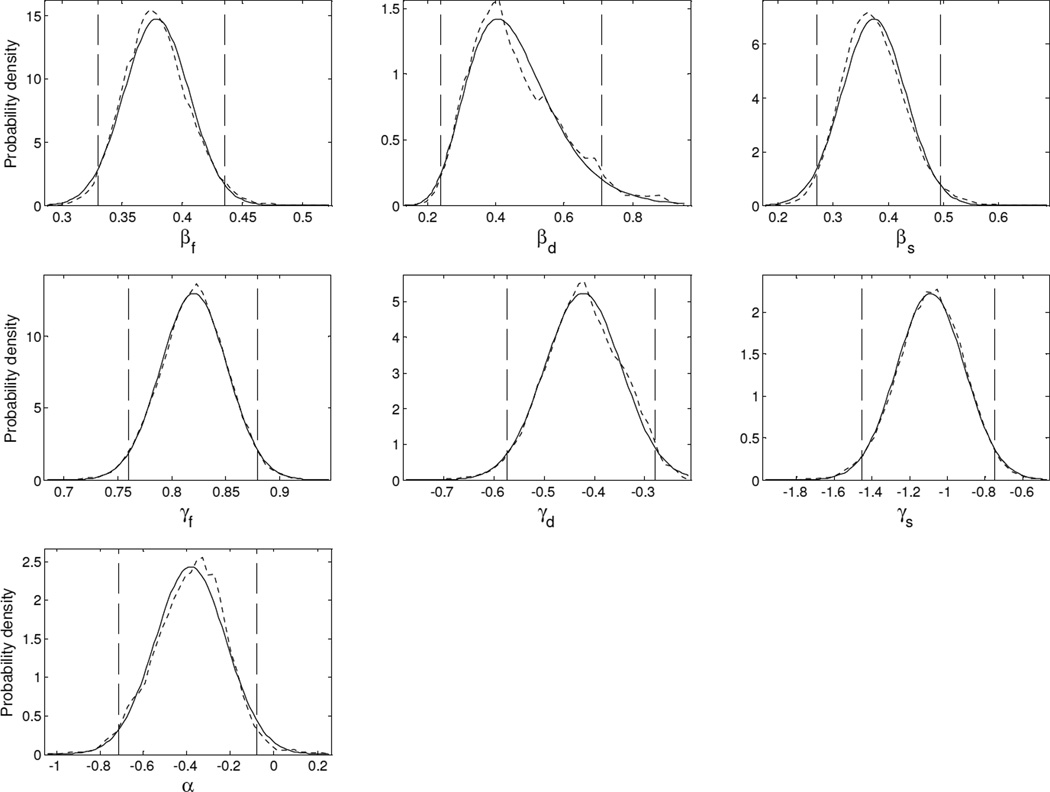
Figure 2 shows the posterior distributions for the parameters of Model A. The parameter is indicated under each panel. Except for parameter β_d, the posterior PDFs (dashed lines) were well approximated using Gaussian functions (solid lines). For parameter β_d, the posterior PDF exhibited positive skew, and a log-normal function (solid line) was found to provide a better fit than an untransformed Gaussian function (not shown). The vertical dashed lines superimposed onto the posterior distributions in Fig. 2 indicate the upper and lower bounds of the 95% credible interval for the considered model parameter. The values of these bounds are listed in Table II, together with other posterior summary statistics (mean, median, and mode). The last three columns in Table II show the ML estimates of the parameters of Model A, with their associated 95% confidence intervals. The ML confidence intervals were usually similar to the Bayesian credible intervals.

Figure 2.

Posterior distributions of the model parameters. Each panel corresponds to one model parameter. The name of the parameter is indicated underneath the x-axis. The dashed lines show the contours of MCMC-sample histograms. The solid lines show maximum-likelihood fits of those histograms using Gaussian or Gamma probability density functions. The vertical dashed lines mark the upper and lower boundaries of the 95% credible interval.

Table II.

Bayesian and maximum-likelihood estimates of the parameters of Model A. The different parameters are listed in the first column. The next five columns show the mean, the mode, the median, and the lower and upper bounds of the central 95% interval of the posterior probability distribution (determined by Bayes theorem and computed using a Markov-Chain Monte Carlo technique) for each parameter. The last three columns show the mode of the likelihood function (i.e., the maximum-likelihood estimate), and the lower and upper bounds of the 95% confidence interval estimated based on the likelihood function, assuming normality. Note that, under the normality assumption, the mean and median of the likelihood function coincide with the mode.

	Bayes mean	Bayes mode	Bayes median	Bayes 2.5%	Bayes 97.5%	ML mode	ML 2.5%	ML 97.5%
γf	0.82	0.83	0.82	0.76	0.88	0.82	0.76	0.88
γd	−0.42	−0.42	−0.42	−0.57	−0.28	−0.48	−0.63	−0.33
γs	−1.09	−1.09	−1.09	−1.46	−0.75	−1.16	−1.53	−0.78
βf	0.38	0.37	0.37	0.33	0.44	0.38	0.32	0.43
βd	0.42	0.40	0.40	0.24	0.71	0.33	0.16	0.50
βs	0.37	0.37	0.37	0.27	0.50	0.36	0.25	0.46
α	−0.38	−0.36	−0.37	−0.37	−0.08	−0.29	−0.47	−0.12

The following observations concerning Fig. 2 and Table II can be made: First, the credible interval for parameter γ_s contains the value −1, which corresponds to an inverse relationship between log-transformed DLFs and sensation level, as in Nelson et al.’s (1983) equation. Second, the credible interval for parameter γ_f does not contain the value 0.5, which corresponds to the square-root relationship between log-transformed DLFs and frequency suggested by Wier et al. (1977) and Nelson et al. (1983). Possible reasons for this outcome are considered in the discussion. Thirdly, the credible interval for parameter γ_d contains the value −0.5, which is consistent with Siebert’s (1970) suggestion of an inverse-square-root relationship between DLFs and duration (in ms)⁴.

3.3 Analysis of model fits and residuals

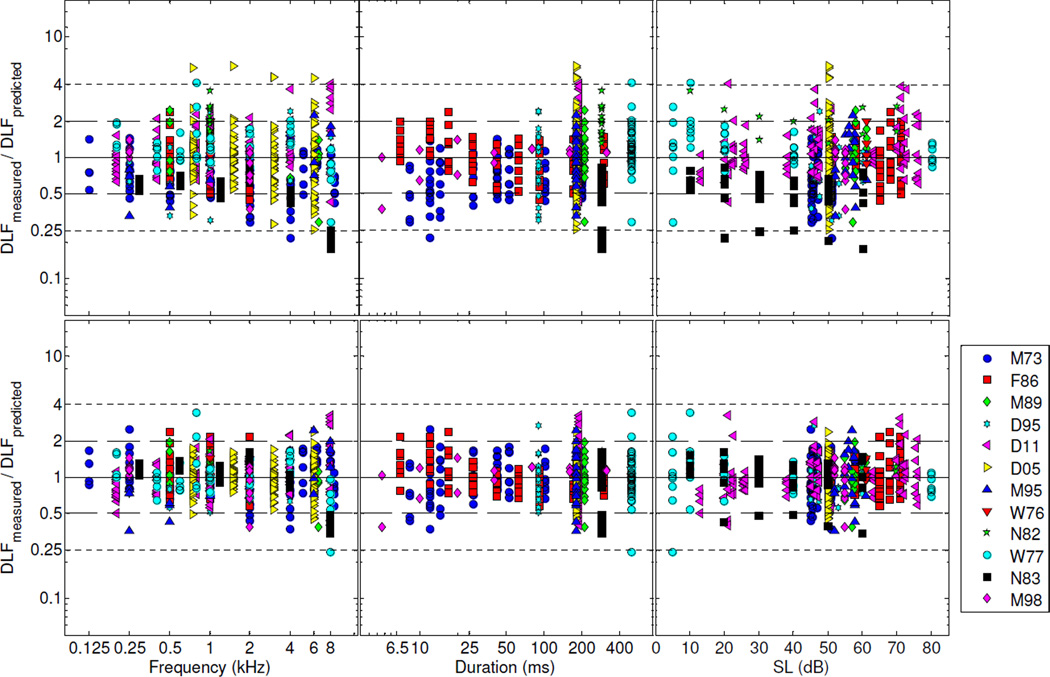
Given that the ML and Bayesian point estimates did not differ markedly from each other, and that the ML point estimates always fell within the corresponding Bayesian credible intervals, the ML estimates were used to compute predicted DLFs. The predictions were obtained by inserting the ML estimates into equation 2, with the random effects set to zero.⁵ The upper row in Fig. 3 shows the residuals between the measured DLFs and the DLFs predicted in this way. These residuals were computed by taking the difference between the log-transformed normalized DLFs (DLF_measured) and the predicted DLFs (DLF_predicted). For plotting purposes, these differences (in log units) were transformed into ratios (i.e., DLF_predicted/ DLF_measured) using the antilog function. They are plotted on a logarithmic scale, so that ratios of, e.g., 2 and 1/2, correspond to symmetric locations around the midline. The midline itself corresponds to a ratio of 1, i.e., no difference between DLF_predicted and DLF_measured. Expressed as a percentage of the mean normalized DLF (in Hz), the RMSE (computed as the antilog of the arithmetic mean of the squared residuals in log units) was equal to 68%.

Figure 3.

Fit residuals for the full model (Model A). Upper row: residuals for predictions obtained using equation 2 with the random effects set to zero. Bottom row: residuals for predictions obtained using equation 2 with the random effects replaced by their ML estimates. The solid line indicates a measured-to-predicted DLF ratio of 1, which corresponds to the situation in which the predicted DLF is exactly equal to the measured DLF. The long- and short-dash lines indicate measured-to-predicted DLF ratios of 2 and 0.5, and 4 and 0.25, respectively.

What proportion of the mean squared error (MSE) can be accounted for by differences in overall sensitivity between listeners? To answer this question, we re-computed the MSE after replacing the random effects (r_i) in equation 2 with their ML estimates. The resulting residuals are plotted in the bottom row of Fig. 3. The resulting RMSE was equal to 42% of the mean normalized DLF in Hz. This value is substantially lower than the RMSE (68%) that was obtained with the random effects set to 0. This indicates that a substantial proportion of the variance in the DLFs can be accounted for by inter-individual differences. In fact, for this model, the results indicate that inter-individual differences in sensitivity account for almost half (46%) of the variance in the DLFs.

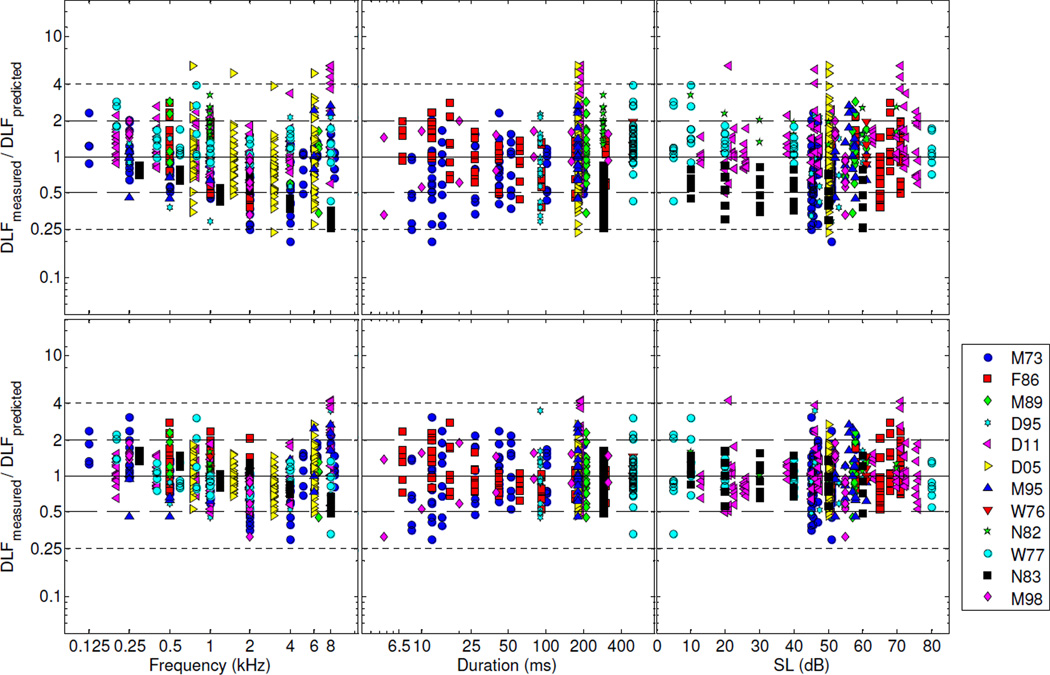
Figure 4 shows the residuals for Model B. As explained above, Model B differed from Model A in that the exponents, γ_f and γ_s, were fixed at 0.5, and −1, respectively, consistent with the model of Nelson et al. (1983). As in Fig. 3, the upper row shows the residuals for predictions obtained with the random effects set to zero, while the bottom row shows the residuals for predictions obtained with the random effects replaced by their ML estimates. Although the overall RMSE for this model (73% of the DLF with the random effects set to 0, and 48% with the random effects replaced by their ML estimates) was not markedly larger than the RMSE for Model A, a downward trend is apparent in the leftmost panels of the two rows, which show the residuals as a function of frequency. This indicates that the square-root function, which was used in Model B, was unable to capture an important aspect of the dependence of DLFs on frequency.

Figure 4.

As Figure 3, except for Model B. For this model, the predictions were computed using equation 2 with the parameters, γ_f and γ_s, fixed at 0.5 and −1, respectively. Upper row: residuals for predictions obtained with the random effects set to zero. Bottom row: residuals for predictions obtained with the random effects replaced by their ML estimates.

3.4 Model comparison: BIC, DIC, and Bayes factors

The superiority of Model A over Model B was confirmed using quantitative measures. The BIC for Model A (BIC_A = −280) was lower than the BIC for Model B (BIC_B = −183). The same conclusion was reached using the DIC. The DIC for model A was equal to −389; the DIC for model B was equal to −269. Lower BIC and DIC values are indicative of a better fit. The Bayes factor for Model A over Model B was equal to 211 decibans. According to Jeffrey’s scale for the interpretation of Bayes factors (Jeffreys, 1961), a Bayes factor greater than 20 decibans provides “decisive” evidence for the considered model over the alternative; thus, according to this criterion, the results of this study provide decisive evidence for Model A over Model B.

Figure 5 shows the fit residuals for Model C. As mentioned above, this model differed from Model A in that it included an additional term to capture interactions in the effects of frequency and duration on the log(DLF). However, the RMSE values obtained using this model (42% with the random effects and 68% with only the fixed effects) were not markedly smaller than those obtained for Model A (48% with the random effects and 73% with only the fixed effects). The difference in BIC between Model C (BIC_C = −266) and Model A (BIC_A = −280) corresponds to a Bayes factor of 30 decibans in favor of Model A.

Figure 5.

As Figure 3, except for Model C. Upper row: residuals for predictions obtained with the random effects set to zero. Bottom row: residuals for predictions obtained with the random effects replaced by their ML estimates.

4 DISCUSSION

4.1 Comparisons with previous studies

Two previous studies examined the dependence of DLFs on frequency across several datasets (Nelson et al., 1983; Wier et al., 1977). Both studies found that this dependence was well described by a linear relationship between the square-root of frequency and the logarithm of the DLF. This conclusion was supported quantitatively by relatively large R² coefficients (typically, 0.8–0.9) for linear fits performed on those coordinates. Wier et al. (1977) considered other combinations of coordinates, including log-log, but they found that the square-root-versus-log coordinates “provided the simplest description of the data” (Wier et al., 1977, p. 179; see also Footnote ² in their article for further information concerning the origin of this transformation).

Our results, based on a considerably larger dataset than used in any single previous study, indicate that the dependence of log-transformed DLFs on frequency is better described by a power function of frequency with an exponent of about 0.8 than by a square-root function of frequency. Moreover, the 95% confidence and credible intervals for this parameter (0.76–0.88) do not contain the value 0.5, indicating that for the datasets analyzed in this study the square-root function does not provide an adequate description of the relationship between the log-transformed DLFs and frequency.

To determine whether the difference between the present findings and those of Nelson et al. (1983) concerning the relationship between FDLs and frequency could be due to the use of different models, we fitted Model A to the data of Nelson et al. (1983). Since we did not have access to the individual data for this study, random effects were not included in the model. Using this model, we found a best-fitting exponent of 0.56, with a 95% confidence interval of 0.41 – 0.70.⁶ This confidence interval encompasses the value, 0.5, which corresponds to a square-root function. This outcome is consistent with Nelson et al.’s (1983) conclusion that the relationship between log(DLFs) and frequency in their data was well captured using a square-root function. A possible explanation for why the relationship between log(DLFs) and frequency in Nelson et al.’s (1983) data is well described by a square-root function, whereas the data from other studies are better described by a power function with an exponent different from 0.5, stems from the observation that the DLFs that these authors measured at 8 kHz are generally lower (better) than those measured in the other studies included in our database—compare the black squares in the left panel of Fig. 1, which show the DLFs measured by Nelson et al. (1983), with the DLFs measured in other studies for the 8-kHz frequency. A similar trend can also be observed for the 4-kHz data and—to a lesser extent—for the 2-kHz data. This difference between the data of Nelson et al. (1983) and those of other studies was noted by Moore and Sek (1995), who suggested that it might be related to Nelson et al.’s use of a four-interval task instead of the more common two-interval task. The presentation of three standard stimuli on every trial and the possibility of responding correctly without necessarily having to identify the direction of the frequency change in the four-interval task—in contrast to the 2I-2AFC task—may have made it easier for the listeners in Nelson et al.’s (1983) study to discriminate frequency changes at high frequencies. Consistent with this interpretation, Moore and Sek (1995) found that, at 8 kHz, DLFs measured using a 2I-2AFC task were consistently larger, by a factor of about 2 on average, than DLFs measured—for the same listeners—using a four-interval task similar to that used by Nelson et al. (1983). The fact that significant differences between DLFs measured using different paradigms remain, even after these thresholds have been “corrected” using SDT principles to account for differences in stimulus designs, suggests that DLFs are affected by factors that are not taken into account in the standard SDT model.

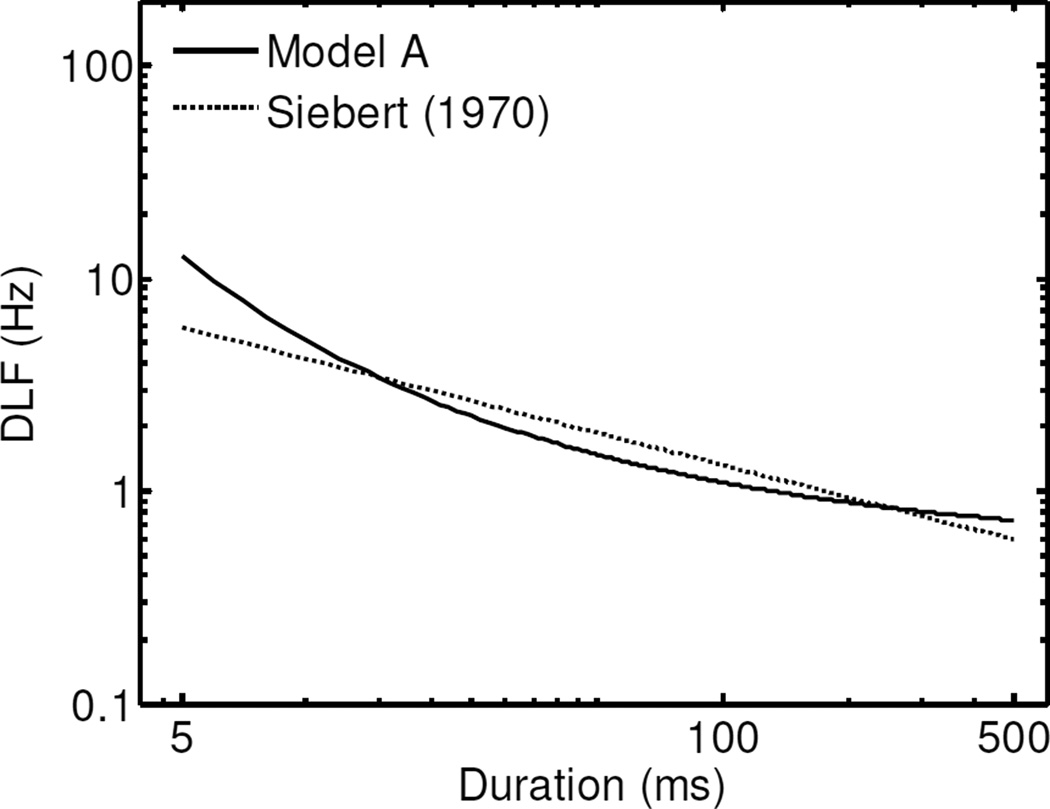
Several studies have measured the dependence of DLFs (in Hz) on tone duration (in ms). A few of these studies have attempted to model this dependence using either a power function (Siebert, 1970) or two-segment lines on log-log coordinates (Freyman and Nelson, 1986; 1987). Based on the psychophysical data of Oetinger (1959) and Liang and Chistovich (1961), Siebert (1970) suggested that DLFs (in Hz) are inversely related to the square-root of duration. However, as noted by Moore (1973), different studies have yielded rather different estimates of the exponent relating duration to the DLF (in Hz), with values ranging from −1.28 to −0.5. In this study, we found a best-fitting exponent of −0.4 for the relationship between duration and the log-transformed DLFs. As illustrated in Fig. 6, over the range of durations considered in this study, DLFs predictions obtained using Model A (with the random effects set to zero) differ somewhat, albeit not markedly, from DLFs predictions using a square-root function of duration, as suggested by Siebert (1970). However, as we discuss in the next section, while the inverse-square-root function provides a simple model of, and good first-approximation to, the effect of duration on DLFs, this simple model does not accurately capture certain aspects of the dependence of DLFs on duration.

Figure 6.

DLF predictions as a function of tone duration for Model A and for Siebert’s (1970) optimal-observer model without knowledge of the stimulus starting phase. The latter predictions follow the reciprocal of the square-root of duration times a constant. The constant was adjusted to minimize the RMSE between the predictions of the two models.

An unexpected outcome of the present study is the finding that Model A, which did not include a term for modeling interaction effects involving frequency and duration, was statistically superior to Model C, which did include such a term. This is surprising because results in the literature indicate that DLFs decrease less rapidly with stimulus duration at high frequencies than at low frequencies (e.g., Freyman and Nelson, 1986; Micheyl et al., 1998). The present finding of a lower BIC for Model A than for Model C suggests that, for the set of data analyzed in the current study, interactions between frequency and duration effects were not sufficiently robust to justify (in a statistical sense) the inclusion of an additional term, and hence additional free parameters, in the model. However, as more data concerning the combined effects of frequency and duration become available, and are included into analyses of the type described here, this conclusion may change.

A few studies have measured DLFs as a function of the stimulus presentation level, or SL (Freyman and Nelson, 1991; Harris, 1952; Nelson et al., 1983; Wier et al., 1977). The results of these studies have shown that DLFs usually decrease (improve) as SL increases from 0 to about 30 dB SL, with little further improvement at higher levels. Nelson et al. (1983) modeled this relationship using an inverse function (1/SL, where SL is expressed in dB), and they found that this model provided a good description of their data and those of two other studies (Harris, 1952; Wier et al., 1977). The results of the present study are also consistent with this conclusion. In fact, the estimated exponent of the power function relating sensation level to log-transformed DLFs was almost exactly equal to −1.

4.2 Implications for models of frequency discrimination

The nature of the mechanisms underlying the perception of frequency is a fundamental question in hearing research. In particular, numerous studies have been devoted to determining whether human listeners’ ability to discriminate small frequency differences depends critically on precise spike-timing information (owing the “phase locking” property of auditory neurons), or whether this ability can be accounted for by models that rely solely on the spatial (or “tonotopic”) distribution of spike-rate (or spike-count) information—which are traditionally referred to as “place” or “rate-place” models (de Cheveigné, 2005). An important test for these models is whether their predictions are consistent with psychophysical data concerning the dependence of DLFs on frequency, duration, and level.

4.2.1 Models of the dependence of DLFs on frequency

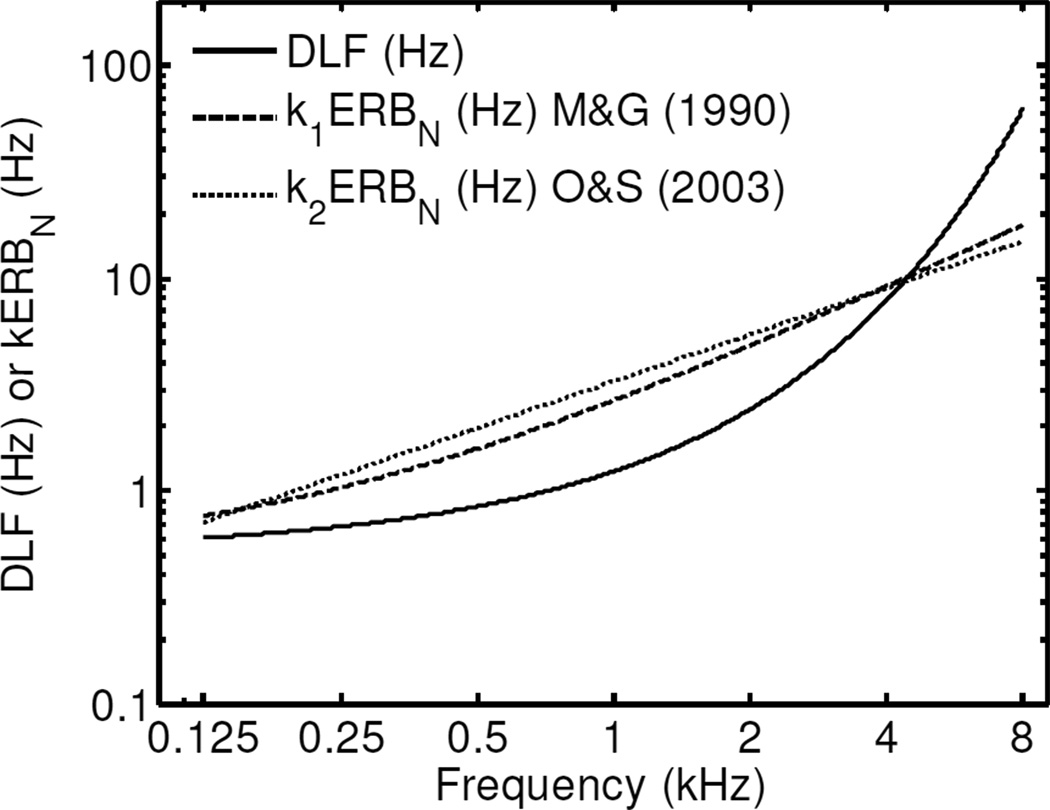
Early attempts to account for the variation of DLFs with frequency were based on the assumption that frequency discrimination is related to frequency selectivity; accordingly, it was suggested that DLFs should be directly related to psychophysical measures of frequency selectivity such as the critical band, or the critical ratio (Fletcher, 1953; Scharf, 1970; Zwicker, 1970). Specifically, Fletcher (1953) and Zwicker (1970) proposed that DLFs should be a constant proportion of the width of the critical band, and they suggested values of 0.05 and 0.037, respectively, for the proportionality constant. Consistent with this suggestion, Wier et al. (1977) found that, for the lowest sensation level tested in their study (5 dB SL), the slope of the best-fitting lines through their log(DLF)-versus-$\sqrt{f}$ data was similar to the slope of the best-fitting line through the critical-band data of Zwicker et al. (1957)—also plotted on log-versus-square-root coordinates; however, at higher levels, the two slopes diverged. Figure 7 illustrates the dependence of DLFs on frequency predicted using Model A (with the random effects set to zero) and, on the same plot, lines corresponding to a constant proportion of the equivalent rectangular bandwidth of auditory filters for normal-hearing listeners (ERB_N). The ERB_N was computed using either the equation provided by Glasberg and Moore (1990), or using the estimates of Oxenham and Shera (2003) based on notched-noise forward masking of low-level tones. In each case, the proportionality constant, k_i, where k₁ denotes the proportionality constant obtained using the ERB_N values computed with Glabserg and Moore’s (1990) estimates, and k₂ denotes the proportionality constant obtained using the ERB_N values computed with Oxenham and Shera’s (2003) equation (which required extrapolation below 1 kHz – the lowest frequency tested in their study), was determined by minimizing the RMSE between log(k_iERB_N) and log(DLF).⁷ It can be seen that DLFs increase with frequency, first less rapidly, then more rapidly than expected if the DLF was a constant proportion of the ERB_N. Thus, it appears that, for the data analyzed in the current study, the dependence of the DLF on frequency is inconsistent with the hypothesis that the DLF is equal to a constant proportion of the ERB_N. This observation does not necessarily imply that it is impossible to account for the variation in DLFs with frequency using a place model. However, it does indicate that frequency discrimination is not related in a simple manner to frequency selectivity as measured using the ERB_N.

Figure 7.

DLF predictions as a function of frequency for Model A versus a constant proportion of the ERB_N. The ERB_N was computed using the equations provided by Glasberg and Moore (1990) and Oxenham and Shera (2003). The proportionality constants, k₁ and k₂, were adjusted to minimize the RMSE between the ERB_N predictions and the predictions of Model A.

One of the first, most rigorous, and most thorough efforts to explain the dependence of DLFs on frequency, duration, and sensation level based on physiological data was made by Siebert (1968;1970); see also the more recent study of Heinz et al. (2001a), who used an updated and more physiologically realistic computational model based on cat auditory-nerve data. Assuming a statistically optimal (maximum-likelihood) observer using all the information contained in the spiking patterns of auditory-nerve fibers—the stochastic behavior of which he approximated as a non-homogeneous Poisson process—Siebert derived an equation for predicting the DLF (in Hz) as a function of frequency (f in Hz), duration (d in s), and stimulus amplitude (a in “units of threshold intensity”; see: Siebert, 1970, p. 727),

$$d_{\mathit{\text{Siebert}}}(f,d,a)\approx {[3\times {10}^6{\mathit{\text{df}}}^{-2}+1.5\times {10}^6{d}^3\text{ ln }a]}^{-\frac{1}{2}},$$ (9)

where the subscript, Siebert, serves to distinguish DLFs predictions obtained using this equation from DLFs predictions obtained using other equations in the text. Note that the expression between brackets on the right-hand side contains two main terms. The first term, 3×10⁶ df⁻², represents the contribution of place cues, disregarding precise spike-timing information. The second term, 1.5×10⁶ d³ ln a, represents the contribution of spike-timing cues, disregarding place information. Two facts are worth noting in this equation. First, in the second term (timing cues), d is raised to the third power and multiplied by ln a, whereas in the first term (rate-place cues), d is divided by f²; thus, the predictions are dominated by timing cues. Secondly, the second term (timing cues) does not include frequency. Thus, Siebert’s (1970) model predicts that, over the range of frequencies where the strength of phase locking is approximately constant, and high, DLFs (in Hz) should not vary as a function of frequency. This is different from the predictions obtained using Nelson et al.’s (1983) model, or the model derived in the current study, both of which predict an increase in DLFs (in Hz) as a function of frequency, even for frequencies below 1 kHz, where the strength of phase-locking (as reflected in the synchronization index or “vector strength” metric) has usually been found to be approximately constant and high (0.8–0.9 on average) in the mammalian species studied to date (Heinz et al., 2001a; Johnson, 1974;1980; Köppl, 1997). However, it should be noted that, over this range of (relatively low) frequencies, the variation in DLFs (in Hz) with frequency is relatively modest. In fact, the rate at which DLFs increase with frequency at these low frequencies is less than 1, so that, when DLFs are expressed as Weber fractions, they are found to decrease with increasing frequency—a trend that is qualitatively consistent with the predictions of Siebert’s model.

The predictions that were obtained by Heinz et al (2001a, Fig. 4a) using their all-information (i.e., timing and place) implementation of Siebert’s optimal-observer model in combination with a physiologically realistic model of the auditory periphery show a slower decrease in DLFs (expressed as Weber fractions) with increasing frequency at low frequencies than predicted by Siebert’s timing model (1970). This suggests that physiological mechanisms that were not included in Siebert’s model, but were included in Heinz et al.’s computational model, contribute to limiting DLFs at low frequencies. However, the decrease in DLFs with increasing frequency between 250 and 500 Hz predicted by Heinz et al.’s (2001a) all-information model is still less steep than that observed in the psychophysical data of Moore (1973). Looking at the leftmost panel of Fig. 1 in the present article, it can be seen that other data sets—specifically, those of Dai and Micheyl (2011), Wier et al. (1977), and Nelson and Freyman (1983) show either a similar, or less marked, increase in DLFs (in Hz) with increasing frequency between 125 and 500 Hz as Moore’s (1973) data. Thus, when re-plotted as Weber fractions, these data would also show a steep decrease in thresholds with increasing frequency over this frequency range. This suggests that additional factors must limit the ability of human observers to take advantage of timing cues at low frequencies. At present, it is unclear what these other factors may be. One possibility is that the presence of multiple peaks per cycle in interspike-interval histograms—a phenomenon often referred to as “peak splitting” (Johnson, 1980; McKinney and Delgutte, 1999; Ruggero and Rich, 1989)—at low frequencies adversely affects the accuracy with which frequency is estimated based on interspike-interval information at these frequencies.

Another important aspect of the psychophysical data, which was observed in all studies in which DLFs have been measured as a function of frequency beyond 1 kHz, and which models of frequency discrimination should be able to predict, is the rapid increase in DLFs with increasing frequency at high frequencies—beyond 1 kHz when DLFs are plotted in Hz on a logarithmic scale, as done here, or 2 kHz when DLFs are plotted as Weber fraction on a logarithmic scale (e.g., Moore, 1973). Heinz et al. (2001a) have shown that this effect could be accounted for using an optimal-observer model similar to that proposed by Siebert, after taking into account the rapid decrease in phase locking with increasing frequency for frequencies higher than 1–2 kHz. If the increase in DLFs at high frequencies is due to the progressive loss of phase locking, and if timing cues become weaker than rate-place cues beyond a certain frequency, one should expect to see a plateau in DLFs beyond some critical frequency where rate-place cues become predominant. Consistent with this, two recent studies have found that DLFs cease to increase markedly with frequency above 8–10 kHz (Moore and Ernst, in press; Oxenham and Micheyl, in press). These data suggest that, at these high frequencies, phase-locking cues may be too weak to be useable, and DLFs are determined by rate-place cues. In the current study, we only analyzed DLFs for frequencies of 8 kHz or less. As additional data concerning the influence of level and duration on DLFs at very high frequencies become available, it will be interesting to include these data into model-based analyses similar to those described here in order to formulate a new equation that researchers can use to predict DLFs over the entire frequency range of human hearing.

4.2.2 Models of the dependence of DLFs on duration

Siebert’s (1970) optimal-observer model, the predictions of which are dominated by the contribution of timing cues, predicts that DLFs should be approximately proportional to the inverse square-root of the duration cubed, which corresponds to an exponent of −3/2 or −1.5. Siebert pointed out that this predicted rate of decay in DLFs with increasing duration was steeper than observed in several psychophysical studies. Indeed, in the present study, the psychophysical data were found to be best fitted by a power-function of duration with an exponent close to −1/2 or 1/2 (see Fig. 5 and Table II). One way to obtain the inverse-square-root relationship between DLFs and duration using Siebert’s model is to assume that only rate-place information is used, which amounts to eliminating the second term between brackets on the right hand side of equation 9. Alternatively, the inverse-square-root relationship can be obtained using a timing-based model that discards absolute timing information, and operates on first-order inter-spike interval information (Siebert, 1977; Goldstein and Srulovicz, 1977).

Despite the good fit of an inverse-square-root law over most of the range of durations, at short durations (< 40 ms), the fit is less convincing (e.g., Fig. 4b of Heinz et al., 2001a). In fact at the shortest durations, the relationship becomes steeper and more similar to that predicted by the optimal-observer models of Siebert (1970) and Heinz et al. (2001a) with timing cues. In terms of fitting procedures, this observation indicates that a more complex model, involving a combination of two power functions, is needed to more accurately capture the dependence of DLFs on duration. The “central-spectrum model” proposed by Srulovicz and Goldstein (1983) was found to provide a “good fit” to the psychophysical data of Liang and Chistovich (1961), Moore (1973), and Ronken (1971). However, this model, which uses a combination of place and timing (interspike-interval) information, is more sophisticated, and less straightforward to implement, than the simple descriptive models considered in the present study.

4.2.3 Models of the dependence of DLFs on level

Heinz et al.’s (2001a) computational study indicates that optimal-observer models operating either on place information alone, or on place-and-time information, can predict a marked decrease in DLFs with increasing sensation level at low sensation levels (from 0 to about 20 dB SL). For higher sensation levels, the predictions of the two models differ: whereas the place-only model of Heinz et al. (2001) and its analytical predecessor (Siebert, 1970) predict that DLFs should either increase or remain flat as the sensation level increases between 20 and 60 dB SL, the all-information (i.e., place-and-time) models predict that DLFs should continue to improve—by a factor of about 2—over this range. The psychophysical data of Wier et al. (1977), which Heinz et al. (2001a) used to illustrate the dependence of DLFs on sensation level (see Fig. 4, panel c, on p. 2294 in Heinz et al., 2001a) are consistent with the latter prediction: the DLFs measured for human listeners using a standard frequency of 1 kHz in that study improved by a factor of about 2 over the range 20–60 dB SL. A similar trend was observed at other test frequencies used in that study, except for the highest (8 kHz). The data of Nelson et al. (1983) also show a decrease in DLFs between 20 and 60 dB SL at most test frequencies between 300 and 8000 Hz (Fig. 2 on p. 2119 in Nelson et al. 1983). The modeling results of Nelson et al. (1983) and those of the present study concur in showing that the dependence of (log-transformed) DLFs on sensation level is well described using a power function with an exponent approximately equal to −1. This function shows a rapid decline in DLFs a low sensation levels and a shallower but continued decline at higher levels, consistent with the predictions of Heinz et al.’s (2001) all-information optimal-observer model.

Wakefield and Nelson (1985) modified the temporal model of frequency discrimination proposed by Goldstein and Srulovicz (1977) to include the dependence of phase locking on intensity. They found that this simple modification was sufficient to correctly account for the dependence of DLFs on sensation level for normal-hearing listeners over a wide frequency range (300–8000 Hz)—although inspection of Fig. 3 in Wakefield and Nelson’s article (1985) indicates that, for the lowest frequency that these authors tested, 300 Hz, the model did not fit the data well. Importantly, Wakefield and Nelson’s (1985) model predicts constant DLFs for sensation levels higher than about 30 dB. Although the psychophysical data (in three normal-hearing listeners) collected by the authors appear to be consistent with this prediction, other data (e.g., Nelson et al., 1983) show some decrease in DLFs with increasing sensation level over the range 20–60 dB. This suggests either that the assumed dependence of phase-locking on intensity in Wakefield and Nelson’s (1985) model is not quite correct or that this model lacks ingredients that would allow it to account for further decreases in DLFs beyond 30 dB SL.

5 CONCLUSIONS

This study analyzed data from 12 published studies of pure-tone frequency discrimination, including 583 DLF measurements from 77 normal-hearing listeners, to derive a quantitative relationship between DLFs and the three major parameters of frequency, duration, and sensation level, using a generalized linear mixed-effects model. The model was defined by a linear combination of three power functions corresponding to the three stimulus parameters. Three versions of the model were evaluated: in the first, most general model (Model A), the linear coefficients and the exponents of the power functions were all treated as free parameters; in the second model (Model B), the exponent of the power-function for frequency was set to 0.5 (corresponding to a square-root relationship between log-transformed DLFs and frequency) while the exponent of the power-function for sensation level was set to −1 (corresponding to an inverse relationship between the log-transformed DLFs and sensation level), as proposed in an earlier study (Nelson et al., 1983); the third model (Model C) was similar to Model A, but included an additional term for modeling interactions in the effects of frequency and duration. Using quantitative model-comparison criteria (BIC, DIC, and Bayes factors), Model A was found to be superior to the other two models. Across a large set of studies, the dependence of (log-transformed) DLFs on frequency was more accurately described by a power function with an exponent of 0.8 than by a power function with an exponent of 0.5 (i.e., a square-root function), and the introduction of an additional term to model interactions in the effects of frequency and duration was not justified statistically. Consistent with Nelson et al. (1983), the exponent of the power function relating sensation level to the log-transformed DLF was found to be close to −1. This function predicts a marked decrease in DLFs over low sensation levels and a shallower but continued decline at higher levels, consistent with the predictions of Heinz et al.’s (2001) all-information (place-and-time) optimal-observer model. Lastly, the dependence of log-transformed DLFs on duration was found to be best described by a power function with an exponent of approximately −0.5, i.e., an inverse square-root relationship. Such a relationship between DLFs and duration is consistent with the predictions of “constrained” optimal-observer models operating either on place information alone, or on first-order inter-spike-interval information (Siebert, 1970; Goldstein and Srulovicz, 1977; Srulovicz and Goldstein, 1983).

ABBREVATIONS

BIC

Bayesian information criterion

dB

decibel

DIC

deviance information criterion

DLF

difference limen for frequency

ERB_N

equivalent-rectangular bandwidth for normal-hearing

PC

percent correct

PDF

probability density function

Hz

Hertz

ML

maximum likelihood

ms

milliseconds

RMSE

root-mean-square error

s

seconds

SL

sensation level

SPL

sound pressure level

2I-2AFC

two-interval, two-alternative, forced-choice

3I-2AFC

three-interval, two-alternative, forced-choice

4I-4AFC

four-interval, four-alternative, forced-choice

APPENDIX

COMPUTATION OF THE POSTERIOR DISTRIBUTIONS OF MODEL PARAMETERS

According to Bayes’ theorem, the distribution of the model parameters given the data is

$$\mathrm{\pi }(\mathbf{\theta }|\mathbf{D},M)=\frac{\mathrm{\pi }(\mathbf{D}|\mathbf{\theta },M)\mathrm{\pi }(\mathbf{\theta })}{\mathrm{\pi }(\mathbf{D})}.$$ (A1)

In this equation, D denotes the data, i.e., the log-transformed normalized DLFs across all studies; θ denotes the vector of parameters (θ = [α₀, r₁,…,r₇₀, β_f, β_d, β_s, γ_f, γ_d, γ_s]^T) for model M; π(θ | D, M) is the posterior, i.e., the PDF of the parameters, given the data; π(D | θ, M) is the likelihood, i.e., the PDF of the data given the parameters; π(θ) is the prior on the parameters, i.e., the PDF of the parameters before data are observed; and π(D) is the evidence, i.e., the marginal PDF of the data.

Under the assumption that fluctuations around the mean for DLFs on a logarithmic scale have a Gaussian distribution—an assumption made by Nelson et al. (1983) and many other investigators—the likelihood function can be written as,

$$\mathrm{\pi }(\mathbf{D}|\mathbf{\theta },M)=\mathrm{\lambda }{\displaystyle \prod _{j=1}^{587}}{e}^{-\frac{1}{2}{\left(\frac{y_j-x_j}{{\mathrm{\sigma }}_{\mathrm{\epsilon }}}\right)}^2},$$ (A2)

where λ is a normalizing constant, y_j denotes the j^th datum in the database, while x_j is the log-normalized predicted DLF computed as,

$$x_j=\mathrm{\alpha }+r_{i(j)}+{\mathrm{\beta }}_f{\left(\frac{f_j}{1000}\right)}^{{\mathrm{\gamma }}_f}+{\mathrm{\beta }}_d{\left(\frac{d_j}{100}\right)}^{{\mathrm{\gamma }}_d}+{\mathrm{\beta }}_s{\left(\frac{s_j}{10}\right)}^{{\mathrm{\gamma }}_s},$$ (A3)

where i(j) denotes the group corresponding to datum j, and f_j, d_j, and s_j denote the stimulus parameters (standard frequency, duration, and level) for the current datum. Equation 4 stems from the assumption that any unexplained variability in the data (including measurement error and any other source of variability that was not accounted for by the model) was distributed normally.⁸ The posterior PDF of the unexplained variance, ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$, was computed along with the posterior PDFs of the other model parameters.

The prior PDFs were selected to reflect weak a priori assumptions on the model parameters. The coefficients, β_f, β_d, and β_s, were assigned independent Gamma(1.1, 0.5) priors. In this article, the gamma probability density function is defined as follows.

$$\mathit{\text{Gamma}}(a,b)=\frac{b^a{x}^{a-1}{e}^{-\mathit{\text{bx}}}}{\mathrm{\Gamma }(a)},$$ (A4)

where Γ(.) denotes the gamma function. The use of a gamma prior enforced a positivity constraint for the coefficients. The exponent, γ_f, and the negatives of the two other exponents, γ_d, and γ_s, were assigned independent Gamma(1.1, 2) priors. The use of Gamma priors for γ_f, −γ_d, and −γ_s is logically consistent with the fact that DLFs increase with frequency, and decrease with both duration and level—a fact that was clear prior to the collection of the data used in the present study. The parameters of these Gamma priors were chosen to yield so-called “vague” priors, i.e., priors having a variance substantially larger than the variance of the corresponding posteriors. The prior density decreased slowly toward large values, making it possible to obtain large posterior estimates for the coefficients and the exponents. It decreased rapidly toward zero, reflecting an assumption that the values of these parameters were likely to be relatively small but unlikely to equal zero. The intercept, α, was assigned a Gaussian(0, 2) prior, and the random effects, r_i, were assigned independent Gaussian(0, 1) priors. The use of a Gaussian prior for the intercept term in generalized linear models is consistent with standard practice in the Bayesian literature (Gelman and Carlin, 2005). The use of independent Gaussian priors for the random effects parameters reflects the assumption that the different subjects were exchangeable a priori, and that the mean DLF measured for a given subject was equally likely a priori to be larger or smaller than the mean across all subjects, and that very large positive or negative deviations from the mean DLF were relatively unlikely (Gelman and Carlin, 2005). Finally, the error variance, ${\mathrm{\sigma }}_{\mathrm{\epsilon }}^2$, was assigned an inverse-Gamma(0.25, 4) prior. The use of inverse-Gamma priors for variance parameters is also very common in the Bayesian literature.

The posterior PDFs of the parameters were estimated using Markov-chain-Monte-Carlo methods (Geman and Geman, 1984; Marin and Robert, 2007). Stochastic and DIC computations were performed using WinBugs (Lunn et al., 2000) with Matbugs (Murphy and Mahdaviani, 2005). Two Markov chains, each 10⁵ samples in length (including 5×10⁴ samples in the burn-in phase), with different starting points, were computed. Convergence and mixing were assessed by visually inspecting trace and autocorrelation plots of the Markov chains and posterior-density plots, and quantitatively, using the Gelman-Rubin R̂ statistic (Gelman and Rubin, 1992). R̂ values were between 1.00 and 1.02, providing further evidence of good convergence. The final 5×10⁴ samples of each chain were pooled to estimate the posterior shape (using the histogram method) and to compute posterior summary statistics (posterior mean, median, mode, and 95% credible intervals). Finally, the posterior samples were used to compute the deviance information criterion, DIC (Spiegelhalter et al., 2002); this criterion was used to compare the two models.