Patterns of variance in stage-structured populations: Evolutionary predictions and ecological implications

Abstract

Variability in population growth rate is thought to have negative consequences for organism fitness. Theory for matrix population models predicts that variance in population growth rate should be the sum of the variance in each matrix entry times the squared sensitivity term for that matrix entry. I analyzed the stage-specific demography of 30 field populations from 17 published studies for pattern between the variance of a demographic term and its contribution to population growth. There were no instances in which a matrix entry both was highly variable and had a large effect on population growth rate; instead, correlations between estimates of temporal variance in a term and contribution to population growth (sensitivity or elasticity) were overwhelmingly negative. In addition, survivorship or growth sensitivities or elasticities always exceeded those of fecundity, implying that the former two terms always contributed more to population growth rate. These results suggest that variable life history stages tend to contribute relatively little to population growth rates because natural selection may alter life histories to minimize stages with both high sensitivity and high variation.

When describing the rate of population growth, there is an increasing emphasis on not only the mean contribution of some trait but also on how variance in that trait contributes to population growth (1–12). Variance in population growth rate has important implications for extinction probabilities (see, e.g., ref. 9) and local coexistence among species (13–14). The important role that variance might have in affecting population growth rate was first explored theoretically in a model that considered the fitness of genotypes that differed in the amount of variance in offspring number (15–17). Gillespie (16) shows that, in the case of two genotypes with equivalent means but differing variance, the genotype with the lower variance will have a higher geometric mean fitness. Thus, the fitness over time will be approximately:

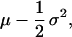1

where μ and σ² are the arithmetic mean and variance in the number of offspring. Thus, in Gillespie’s model, adding variance to offspring number has a net negative effective on the geometric mean although in some instances, variation may be favored (18).

The importance of Eq. 1 to the study of the evolution of life histories was the suggestion that selection should act on both the mean and the variance of offspring number. A tradeoff between the mean and variance of a trait was the basis of the “bet-hedging” literature (8, 17, 19), which suggested that organisms with a higher mean trait related to fitness may not always be favored. A related body of literature has developed around the effects of variability on long-run population growth rate, in which theory and modeling have highlighted the effects of stochastic variation on population growth rate (7, 12) and on the contribution to population growth of a given age class (12) in age-classified population models.

Despite the importance of understanding the relationship among variability, population growth rate, and selection, there are relatively few empirical investigations of how the mean and variance in population traits affect population growth rate (but see refs. 9 and 20) and whether patterns in the relationships support predictions of evolutionary theory. In the Lacey et al. (20) study, the contributions of mean and variance to performance are demonstrated, and both are found to be determinants of fitness in several plant species. Fortunately, there is increasing interest in both basic and applied demography, resulting in a body of data useful for analyzing components of population growth, including variance in demographic traits. Commonly, these demographic data are reported in a matrix model format.

The publication of several texts on matrix model construction and analysis (21, 22) have made matrix models a widespread method of demographic analysis. Matrix models were first constructed for age-structured populations (23, 24) and later modified to include size- and stage-structured populations (25). Perhaps the most appealing characteristics of matrix models are the equivalence between the dominant eigenvalue of the matrix and long term population growth rate (λ) and the capability to describe how each component of the life cycle contributes to λ via elasticity analyses. An elasticity denotes the proportional contribution of each matrix term to λ. Because the elasticity of each matrix entry sums to 1, the contribution of each stage of the life cycle to λ is quantifiable (26, 27). By using these tools, ecologists and evolutionary biologists have explored mathematically the implications and consequences of various alterations to an organisms life cycle. For example, matrix models have been used to estimate the effect of different conservation strategies on the future trajectories of a species (11, 28–30), the effects of harvesting (31–33), the contribution of different life history strategies to population growth (34–36), and how social structure affects population growth rate (37).

Although matrix analyses usually are based on some estimated mean value for transition probabilities, some studies have included variability estimates for those matrix entries— often explicitly sampling temporal and spatial variation and including it in population projections. Variability has been incorporated by systematically or randomly drawing from separate matrices, which include demographic estimates over separate intervals of time or from populations distributed in space (10, 38) or by randomly drawing a value for each matrix element at each time step from estimated distributions for each vital rate (11). However, there are many examples in which spatial or temporal variation in matrix parameters have been estimated but have not been explicitly included in estimates of population growth rate (see, e.g., refs. 39 and 40).

Based on the evolutionary theory summarized above, we might expect that, for organisms in natural populations, natural selection should minimize variance in population growth rate (λ), where population growth rate is approximately equivalent to fitness (sensu 41, 42). Furthermore, in the context of matrix population models, we can estimate the effect of different vital rates on the variance in population growth rate. Based on Caswell (21), a first-order approximation for variance in population growth rate [V(λ)] is:

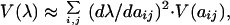2

where ∂λ/∂a_ij is the sensitivity of λ to changes in some matrix entry (a_ij) in row i and column j (21, 43) and V(a_ij) is an estimate of variance in a matrix entry. Thus, variability in the dominant eigenvalue is the sum of each matrix entry multiplied by the square of the sensitivity term. Because an elasticity (e_ij) is simply a proportional change in sensitivity defined as:

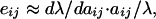3

we can express Eq. 2 in terms of elasticity as

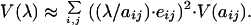4

Because sensitivity or elasticity is a squared term in Eqs. 2 and 4, any changes to it will have a nonlinear effect on the variance in population growth rate, and V(a_ij) will have a constant, linear effect on V(λ). Although the expected relationship between sensitivity and V(a_ij) is not obvious, minimizing variance in population growth rate requires minimizing V(a_ij), sensitivity, or both. Furthermore, if overall variation in life history traits is somehow constrained, then, because V(a_ij) and dλ/da_ij multiply to affect V(λ), negative correlations between sensitivity and V(a_ij) will result in decreased variance in population growth and hence should be favored. Conversely, variance in population growth rate could be increased greatly by simultaneously having life history stages that both were highly variable and contributed greatly to population growth rate.

In this study, I searched for general patterns in life history variation in published demographic studies that used matrix models. Although matrix model entries do not always correspond directly with a life history trait (e.g., variance in the timing of first reproduction is difficult to explore in a matrix model; ref. 44), published matrix models represent a logical starting point to ask whether there are patterns between variability in a demographic term and its contribution to population growth. Thus, among a wide variety of taxa, I first explored whether there was a relationship between temporal variation in demographic terms and the sensitivity or elasticity of those terms. Specifically, I explored whether there were correlates among demographic terms such that variance in population growth rate was minimized. I then used those same studies to search for patterns in how survivorship, growth, and fecundity sensitivity and elasticity terms were ranked among different organisms. This final analysis provided a means of determining whether there are consistent patterns among certain life history groupings and their contribution to population growth.

METHODS

The Relationship Between Life Cycle Variability and Sensitivities.

To examine the relationship between the temporal variance estimate of a demographic stage and its corresponding sensitivity or elasticity, I used 17 published studies in which matrix models were used for demographic analysis, representing 20 species and 30 separate populations of organisms (see Table 1). I searched the literature and used only studies in which calculations of temporal variance in matrix entries (a_ij) were possible given the available data. Thus, there are many matrix population model studies that I did not use because they either did not cover multiple time intervals or did not report the data with enough detail for my analyses. I used the authors’ estimates of sensitivities or elasticities only when they provided an estimate based on the mean matrix entry (29, 51). Otherwise, I estimated sensitivities and elasticities myself based on a mean matrix entry. For example, Nault and Gagnon (55) studied a population of Allium tricoccum, a perennial forest herb, and reported an elasticity estimate for each stage in each of 4 years of the study. I used their published data to produce a matrix of arithmetic mean, a_ij, and calculated sensitivities and elasticities based on those mean values. Although it is not clear how a mean entry should be characterized, theory suggests that the arithmetic average of vital rates determine greatly how sensitive a population will be to variability in those vital rates (5); thus, I used these averages. I estimated temporal variability in two ways: as a variance of the mean [referred to subsequently simply as V(a_ij)] and as a coefficient of variation (CV) where CV = (σ/μ)*100; σ was the SD, and μ was the mean. In this way, I was able to estimate the V(a_ij) and sensitivity elements of Eqs. 2 and 4. Because CV is normalized to the mean a_ij and some a_ij (especially fecundity) could vary over orders of magnitude, I used CV to achieve higher comparability among a_ijterms. The only work for which I estimated matrix entries from a life table was the McFadden et al. (54) study on brook trout. Although Jensen (57) had expressed the McFadden et al. (54) data in matrix form, I repeated the procedure to obtain variance estimates for each matrix entry. I converted the life table data to matrix form by using the methods for a birth-pulse survivorship probability in a postbreeding census (21).

Table 1.

The demographic studies used in Figures 1 and 2

Species	Intervals, n	Length of interval	Model type	Dimension	Reference
*†Ascophyllum nodosum (brown alga)	3	yr	size	5	45
*Fumana procumbens (“perennial plant”)	6	yr	stage	6	46
*†Arisaema triphyllum (Jack-in-the-Pulpit)	2	yr	size	7	47
*†Panax quinquefolium (American Ginseng)	3	yr	size	6	48
§Gopherus agassizii (desert tortoise)	4–11	yr	stage	8	11
*Potentilla anserina (clonal herb)	3	yr	stage	6	49
* Calochortus albus (mariposa lily)	2	yr	size	4	50
*C. obispoensis	2	yr	size	3	50
*C. pulchellus	2	yr	size	4	50
*C. tiburonensis	2	yr	size	3	50
‡Leptogorgia virgulata (soft coral)	23	mo	size	5	51
*Calathea ovandensis (perennial herb)	4	yr	stage	8	40
*Alnus incana spp. rugosa (alder)	3	yr	size	5	52
*Agaricia agaricites (foliaceous stony coral)	2	yr	stage	4	53
*Salvelinus fontinalis (brook trout)	11	yr	age	6	54
*Pedicularis furbishiae (Furbish’s Lousewort)	3	yr	stage	6	38
*Danthonia sericea (bunchgrass)	2	yr	size	6	39
*Allium tricoccum (wild leek)	4	yr	size	15	55
Falco pergrinus anatum (peregrine falcon)	varied	varied	stage	4	29
*Uma inornata (fringe-toed lizard)	7	yr	age	3	56

Studies are listed in alphabetical order by first author.

^*I estimated mean matrix entries and elasticities for these mean matrices myself.

^†Incomplete data. Not all terms had temporal variation terms.

^‡Fecundity divided evenly between size classes.

^§Two different fecundity levels used. yr, year; mo, month.

I estimated the correlation between V(a_ij) and sensitivity of a_ij in all 30 populations. I also estimated the correlation between the CV of a_ij and the elasticity of a_ij for each study separately to see whether terms with proportionality (CV is normalized to the mean, and elasticities are a proportional contribution to λ) would show a relationship similar to that between V(a_ij) and sensitivity. Because V(a_ij) and CV terms are often related to the mean a_ij and there was preliminary evidence that the mean was related to sensitivity and elasticity, I estimated partial correlation coefficients between V(a_ij) and sensitivity or CV and elasticity, holding the mean a_ij constant (58). Each partial correlation coefficient was estimated by using a Spearman’s correlation coefficient among each of the three variables. I then used a test of homogeneity among two or more correlation coefficients to compare among all studies (58), where the quantity −2⋅Σln(p_n) over all n studies is distributed as χ² with the degrees of freedom equivalent to two times the number of correlations used.

A Comparison of Survivorship, Growth, and Reproduction Elasticities.

By using the same demographic studies listed in Table 1, I ranked the sensitivities and elasticities of survivorship (defined as a_ij terms where the organism stayed in the same age, stage, or size class), growth (defined as any transition of growth or shrinkage), and fecundity (defined as terms on the top row of the matrix) for each study. The number of a_ijterms that can comprise each category can differ. For example, there are always more survivorship terms (terms on the main diagonal) than fecundity terms. Thus, I also analyzed whether average survivorship, growth, shrinkage, or fecundity sensitivities and elasticities differed across all studies with ANOVA. There are two potential problems with using aggregate elasticity estimates. The first is that they sum to 1 within a given matrix analysis and thus should not be considered independent data. Sensitivities, however, do not sum to 1; thus, I give the results of both elasticity and sensitivity analyses for comparison. The second problem is that the dimensionality of the matrix can influence the aggregate elasticities of growth, survivorship, and, to a lesser extent, fecundity (59). Matrices of smaller dimension can result in a higher probability that individuals remain in the same class, decreasing the elasticity or sensitivity of growth. However, dimensionality does not appear to change greatly the elasticity estimates for fecundity (59). A final concern about making comparisons among the sensitivities and elasticities of matrix elements is that fecundity entries incorporate both fecundity and survivorship values. Thus, fecundity and adult survivorship entries share some of the same underlying vital rates.

RESULTS

The Relationship Between Life Cycle Variability and Elasticities.

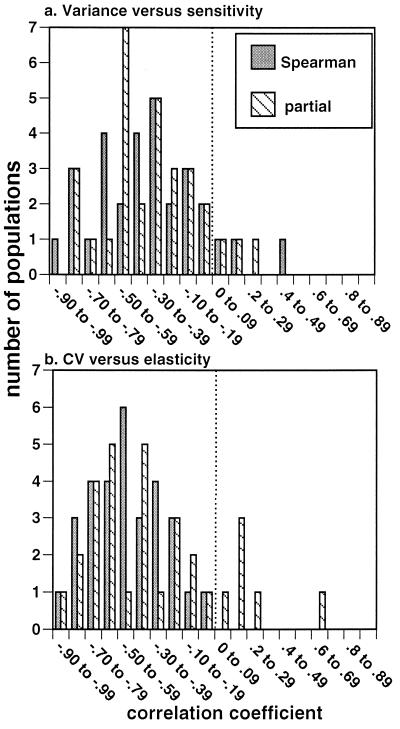
V(a_ij) and sensitivity were correlated significantly negatively in all but 2 of the 30 populations whereas CV and elasticity were correlated significantly negatively in all populations when Spearman’s correlations were used (Fig. 1). These negative correlations remained dominant when partial correlation coefficients were used, with V(a_ij) and sensitivity having negative partial correlation coefficients in 27 of 30 populations (Fig. 1a) whereas CV of a matrix entry and its corresponding elasticity showed negative partial correlation coefficients in 24 of 30 populations (Fig. 1b). An overall significance test on partial correlation coefficients, using the probabilities from each of the negative correlations, rejected the null hypothesis that there was no correlation between V(a_ij) and sensitivity (χ²₆₀ = 145.73, P < 0.001) or CV and elasticity (χ²₆₀ = 194.75, P < 0.001). For the few positive correlations that did exist, I conservatively assigned a P value of 1.0, which meant they contributed 0 to the χ² value. Thus, with either proportional terms (CV, elasticity) or V(a_ij) and sensitivity, the data show a strong negative correlation between variance of a term and its contribution to population growth.

Figure 1.

Spearman and partial correlation coefficients between (a) the variance of each matrix entry and its corresponding sensitivity and (b) CV and elasticity, by using all populations listed in Table 1. The vertical hatched line represents a correlation of 0. An overall significance test on partial correlation coefficients rejected the null hypotheses of no correlation between V(a_ij) and sensitivity (χ²₆₀ = 145.73, P < 0.001) and CV and elasticity (χ²₆₀ = 194.75, P < 0.001).

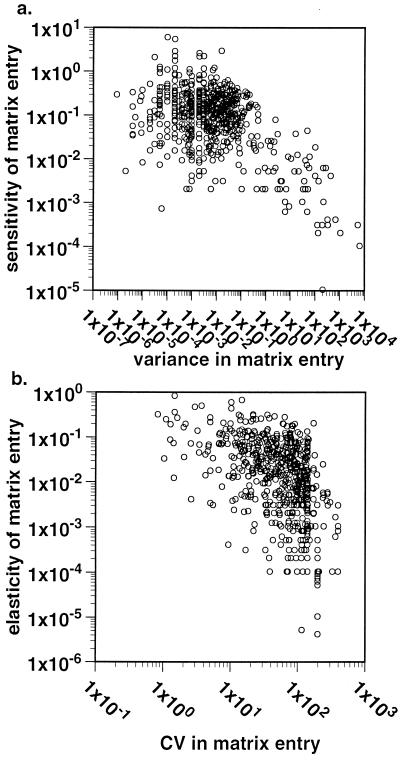
The relationship between V(a_ij) of each demographic estimate and its corresponding sensitivity and between CV and elasticity was generally curvilinear, both for each study separately and for all studies combined. There were never any instances in which V(a_ij) and sensitivity or CV and elasticity were both large for an element; instead, points clustered at high variance and low contribution to population growth rate, low variance and high contribution to population growth rate, or relatively low estimates of both. The data from all studies are plotted on a log scale in Fig. 2.

Figure 2.

A log-log plot of (a) V(a_ij) vs. sensitivity and (b) temporal CV vs. elasticity for each matrix entry in all studies cited in Table 1. There are 660 total entries plotted.

A Comparison of Survivorship, Growth, and Fecundity Elasticities.

There was never any population in which the total fecundity sensitivity or elasticity exceeded that of either survivorship or growth, and there was only one instance in which fecundity elasticity did not rank last (desert tortoises, number 9 in Table 1). All populations but three showed sensitivities ranked as growth > survivorship > fecundity. The exceptions were two instances in which survivorship sensitivities were greater than growth or fecundity (numbers 15 and 18 in Table 1) and one in which fecundity exceeded survivorship but not growth (study number 3).

There were 12 size- or stage-classified populations in which survivorship elasticities were greatest (studies numbered 4, 6, 9, 12–15, 17, 18, 24, 27, and 28 in Table 1), and 11 revealed highest elasticities for growth terms (studies 3, 5, 7, 10, 11, 16, 21, 22, 23, 25, and 26). Although the studies with survivorship ranking highest had a mean dimension of 5.3 and those with growth ranking highest had a mean dimension of 6.1, these differences were not significant statistically (two-sample t test, t = 1.435, P = 0.166). The age-classified models (54, 56) and a study on peregrine falcons (29) all showed higher survivorship sensitivity and elasticity than their fecundity counterparts.

The overall pattern of fecundities showing the lowest sensitivity or elasticity values was retained even when data were analyzed to account for the number of matrix entries contributing to each aggregate sensitivity or elasticity. By using mean sensitivity and elasticity estimates, I found significant differences among both sensitivity and elasticity means [ANOVA: F(2,66) = 22.756, P < 0.001 and F(2, 66) = 29.869, P < 0.001, respectively]. Tukey’s multiple comparison test indicated that sensitivities were ranked as growth > survivorship > fecundity, and elasticities were ranked as survivorship > growth = fecundity.

DISCUSSION

The findings from the studies analyzed here suggest that there is an inverse relationship between variance in a life history trait and its contribution to population growth among many organisms. In other words, stages of the life cycle with the highest variation generally have the lowest effect on population growth rate (λ) (Figs. 1 and 2). These results are robust for a wide variety of taxa that includes marine algae, terrestrial plants, aquatic invertebrates, an aquatic vertebrate, and terrestrial vertebrates (Table 2). These results are also consistent over a wide range of differences in model construction—from matrices of 3–15 dimensions. Although estimates of variance for all of the organisms used in this study must include sampling variance as well as actual variance, one might expect that sampling variance would be higher in survivorship than fecundity because survivorship is often more difficult to estimate than fecundity. Despite this, I found that fecundity terms tended to have the highest variability (and lowest sensitivity and elasticity).

Other published studies of demographic analyses also suggest an inverse relationship between the effect of an entry on population growth rate and its variance. For example, for the spotted owl (Strix occidentalis) models presented by Lande (9) and Thomas et al. (60), the least variable stage of the life cycle (adult survivorship) had the highest elasticity. The only contradiction to this pattern is mentioned in ref. 9. By using Tuljapurker’s (6) methodology for estimating long-run population growth rates, Lande (9) found only a small effect of variation in adult survivorship. Lande suggested that this was because of the longevity (17 years) of the spotted owl; variability would have had a greater effect on a shorter-lived species. Additionally, the amount of variation that was used (CV = 10%) was relatively modest compared with the empirical CV estimates reported here (Fig. 1).

Studies of marine organisms, in which dispersal often can result in high temporal variability in recruitment, also corroborate the patterns shown here. Population growth rate in the brown algae Sargassum siliquosum (O. Fucales) and Laminaria longicruris (O. Laminariales) have low elasticity estimates for fecundity (or recruitment) terms (61). Both of these species are representative of groups that can have high variation in the success of recruitment among years (45, 62). Similarly, in an open population model of marine fishes, Pfister (63) also found that demographic estimates with relatively high variance did not cause a corresponding large amount of variation in population size. In the framework provided by Eq. 2, the results of this study suggest that the effects on variation in population growth rate [V(λ)] by highly variable stages of the life cycle may be dampened by corresponding low sensitivity or elasticity for those entries.

In a recent summary of matrix models from 66 plant species, Silvertown et al. (64) found several interesting patterns relevant to this study. First, elasticities of different parts of the life cycle (survivorship, growth, or fecundity) differed between plants with dissimilar life cycles. Elasticities for fecundity were relatively higher in herbaceous plants whereas survivorship elasticities were relatively higher in woody plants. Similarly, long-lived tropical tree species showed highest elasticities for survivorship terms, and only a short-lived tropical tree species had relatively high elasticities for fecundity terms (65). Additionally, Silvertown et al. (64) found that the intrinsic rate of increase in woody plants was positively correlated with the fecundity elasticity. In general, the fecundity elasticities that they reported were similar to those reported here—fecundity elasticities ranked low relative to growth or survivorship elasticities. When I estimated the combined elasticity for fecundity in their study (defined as both recruitment of seeds and seedlings), it was smaller than growth or survivorship elasticities in 53 of 66 studies (80.3%). These low estimates for fecundity elasticities also have been noted previously (21, 51, 66). Although Silvertown et al.’s (64) use of aggregate elasticity terms to analyze tradeoffs has been criticized (67), aggregate terms have indicated strongly that low fecundity sensitivities and elasticities are ubiquitous in published empirical studies. As noted previously, however, fecundity entries are comprised of both adult survivorship and reproductive vital rates. Because adult survivorship elasticities tend to be relatively high, strictly reproductive terms may have even lower effects on population growth than reported here and in previous studies. Future analyses will certainly benefit from both reporting and analyzing separately the relative contribution of survivorship vs. reproduction to fecundity.

However, by using matrix model simulations, Benton and Grant (12) were able to demonstrate an increasing contribution of fecundity to population growth when they increased the variation in a fecundity term or had fecundity positively covary with survivorship. However, these responses were only found in matrices representing short lives (≤2 years) or where adult survivorship was low (0.20 per year). Although life spans were not always given by the authors, most of the empirical studies used in this study (Table 1) probably represent organisms that live longer than 2 years and have adult survivorship often exceeding 0.20. Indeed, in their simulations of organisms with 6- and 8-year lifespans, Benton and Grant (12) uniformly found that fecundity elasticities were relatively low and relatively resistant to change when either variability in fecundity or covariance with survivorship was added. Although the results reported here show a clear pattern among the variance in a matrix term and its corresponding sensitivity and elasticity, the pattern for how covariation among all matrix entries affect sensitivity and elasticity is an important subject for future study (see, e.g., refs. 7, 37, 68, and 69).

Previous theoretical studies also provide insight into the sensitivity of population growth rate to changes in different demographic terms. Cole (70) and Smith (71) emphasized the importance of the age at first reproduction and the mean generation time to population growth rate. Lewontin (72) and Meats (2) both explored how changes in mortality and fecundity might affect the exponential rate of population increase (r) in the Euler–Lotka equation. Their results depended on the age of maturation and r. When r was relatively high, a given change in fecundity or mortality had equivalent effects (72); however, when r was near zero and mortality was relatively high, a given change in mortality had a greater effect than one in fecundity (2). Boyce (73) considered explicitly the role that demographic variation might have on population growth rate (r) in a matrix model context. He found that increasing variation in the survivorship of young-of-the-year in an age-based 3 × 3 matrix caused the projected population size to decline, eventually to extinction. He attributed this to the concave relationship between r and survivorship; as variation in a matrix entry increased, the arithmetic mean r increasingly deviated from the r expected when there was no variability. Thus, for any matrix entry, the effect variation has on r will be determined by the extent of the concavity of the relationship between r and any a_ij.

The picture that emerges from these theoretical studies is that the relative contribution of changes to, or variance in, a demographic term depends on the population growth rate, the current estimates of mortality and fecundity, the amount of variation that characterizes that matrix entry, and covariance among matrix terms (see also ref. 7). Given these potentially complex relationships between sensitivity or elasticity and variability over a variety of life histories, it is remarkable to see such an identifiable pattern between the two (Fig. 1). Of interest, for the populations used in this study, 14 of 30 (46.7%) have an estimated r (or ln λ) between 0.0 and ±0.1, and an additional 9 (30.0%) are between ±0.1 and ±0.3. Whether these results indicate that most organisms are characterized by life histories in which mortality and survivorship will contribute disproportionately to population growth remains to be seen.

The relationships among sensitivities and demographic variability are essential information if we are to identify the stages of an organism’s life history that are primarily responsible for population fluctuations, a goal for basic and applied science. The results reported here imply that variability in fecundity and early survival, often a focus of ecological research (e.g., refs. 63 and 74–76), may contribute relatively little to explaining why population growth rates vary temporally for certain life histories. Clearly, the relative effects that different life history stages have on population growth need to be evaluated in the context of the entire life cycle, not simply in isolation.

The demographic analyses presented here provide strong support for theoretical models that suggest that variance in population growth rate can be minimized by either (i) decreased sensitivity or elasticity of a demographic term or (ii) decreased variation in that demographic term. No demographic studies showed evidence for demographic terms that both were highly variable and had a large effect on population growth rate (Fig. 1). For the organisms studied here, life histories appeared to be a suite of demographic traits that minimized variation in population growth rate.

ABBREVIATION

CV

coefficient of variation