Finding Seeds for Segmentation Using Statistical Fusion

Abstract

Image labeling is an essential step for quantitative analysis of medical images. Many image labeling algorithms require seed identification in order to initialize segmentation algorithms such as region growing, graph cuts, and the random walker. Seeds are usually placed manually by human raters, which makes these algorithms semi-automatic and can be prohibitive for very large datasets. In this paper an automatic algorithm for placing seeds using multi-atlas registration and statistical fusion is proposed. Atlases containing the centers of mass of a collection of neuroanatomical objects are deformably registered in a training set to determine where these centers of mass go after labels transformed by registration. The biases of these transformations are determined and incorporated in a continuous form of Simultaneous Truth And Performance Level Estimation (STAPLE) fusion, thereby improving the estimates (on average) over a single registration strategy that does not incorporate bias or fusion. We evaluate this technique using real 3D brain MR image atlases and demonstrate its efficacy on correcting the data bias and reducing the fusion error.

1. INTRODUCTION

Image labeling is an important step in automated analysis of medical images. Several segmentation algorithms that can be used for labeling, such as region growing, the random walker^[1], and graph cuts^[2], require the identification of one or more initial seeds. Typically, seeds are manually picked by human raters, which means that these algorithms are not fully-automatic, and the burden of providing human raters to pick seeds on a very large database of images can become prohibitive due to either time or cost reasons. In some cases, multiple raters may be desirable for robustness in face of human error, and this becomes even more costly. It has become increasingly common to use human raters to establish an initial atlas of validated training data from which a fully-automated, multi-atlas algorithm is established to mimic the human raters to carry out the desired task on an otherwise prohibitively large dataset. The statistical fusion of object labels carried over from multiple registrations of a set of labeled atlases has been well explored and is being actively investigated and improved^{[3, 4, 5, 6]}. In this paper, we explore the statistical fusion of seeds that are intended to initialize a segmentation algorithm that would run in the native subject space. At this stage of development, we consider seeds that are defined as object centers of mass, but the basic technique we present can be easily modified to estimate seeds that are optimized for a particular segmentation algorithm or to establish multiple seeds within each object.

2. METHODS

Suppose an atlas of labeled objects in a standardized space (such as affine-registered MNI space) is available. Then a subject image is registered into this standardized space and the centers of mass on each of its objects are desired. A "standard" approach might be to register all objects into the subject space, fuse the labels using (for example) classic discrete Simultaneous Truth And Performance Level Estimation (STAPLE) algorithm^[3], and then recompute the centers of mass. In this work, we are looking for a general approach in which centers of mass that are known in the atlas spaces might be directly fused after registration without requiring a recomputation based on an estimated label fusion.

Therefore, first we deformably register^[7] each atlas from the training set into the subject, establishing a collection of estimates of centers of mass for each object. Before these data can be fused, in correspondence to our previously reported method called MAP-CSTAPLE^[6] where both the continuous STAPLE algorithm (CSTAPLE)^{[4, 5]} and prior information on rater (training atlas) performance (bias and variance) are needed, we still need to establish a prior model of rater performance. So now we only consider the training set having the centers of mass of all labeled objects. Every atlas in it is deformably registered to all other atlases and the transformed centers of mass are compared to the true positions, generating a set of error vectors. Some atlases will perform well on some datasets and not so well on others, and in general each object within each atlas will have an a priori performance^[8] characterized statistically by its bias and variance. With this prior information also incorporated, continuous data fusion is established by MAP-CSTAPLE resulting in reduced error due to the expected bias and variance of each training atlas taken into account.

To explain mathematically, let the subject atlas be denoted as A_t, and R training atlases are denoted as {A₁, A₂, …, A_R} with corresponding labels {I₁(x), I₂(x), …, I_R(x)}. Each label set contains same number of object labels, i.e. the j^th label of atlas A_m is donated with indicator function $I_m^j(\mathit{x})$ where it is 1 when coordinate x belongs to the label and 0 elsewhere. The center of mass of this object label is define as

$${\mathit{c}}_m^j=\frac{\int \mathit{x}·I_m^j(\mathit{x})d\mathit{x}}{\int I_m^j(\mathit{x})d\mathit{x}}$$ (1)

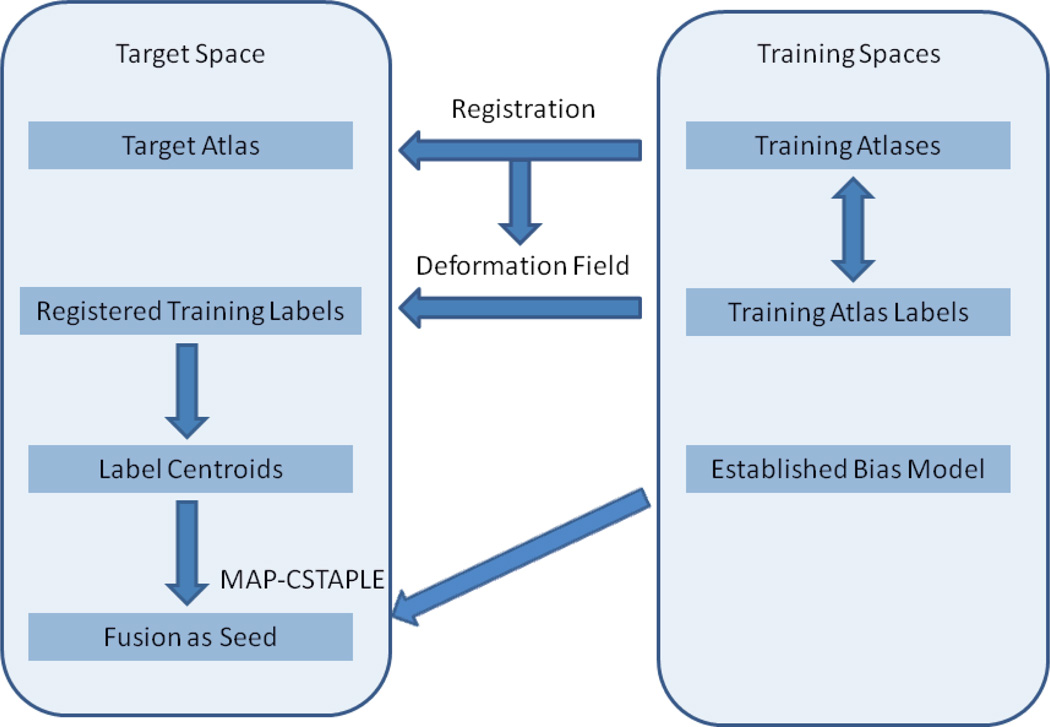
Our approach has the following steps, as illustrated using a flowchart in Figure 1.

1. Register every training atlas to the subject atlas. Deformable registration is required to properly align different atlases. In our experiments we apply FNIRT algorithm^[7] for the registration. The deformation fields from atlas A_m to A_t are calculated and stored as {φ_1t, φ_2t, …, φ_Rt}.

2. Deform the labels of all training atlases with the deformation field, which will result in R registered label sets in the subject space {I_1t(x), I_2t(x), …, I_Rt(x)}, where

   $$I_{\mathit{\text{mt}}}(\mathit{x})=I_m({\phi }_{\mathit{\text{mt}}}^{-1}(\mathit{x}))$$ (2)
3. For every label j, calculate the centers of mass $\{{\mathit{c}}_{1t}^j,{\mathit{c}}_{2t}^j,\dots ,{\mathit{c}}_{\mathit{\text{Rt}}}^j\}$ after labels are transformed by registration, i.e., the centers of mass of {I_1t(x), I_2t(x), …, I_Rt(x)}, by

   $${\mathit{c}}_{\mathit{\text{mt}}}^j=\frac{\int \mathit{x}·I_{\mathit{\text{mt}}}^j(\mathit{x})d\mathit{x}}{\int I_{\mathit{\text{mt}}}^j(\mathit{x})d\mathit{x}}$$ (3)
4. The bias of a center of mass must be learned as prior information to be applied within MAP-CSTAPLE. Both forward and backward registrations are performed on every pair of the training atlases, so that we know the location ${\mathit{c}}_m^j$ of every center of mass j in its own space A_m as well as the location ${\mathit{c}}_{\mathit{\text{mn}}}^j$ in the space of any other training atlas A_n. Under the assumption that the biases of all atlases lie in the same standardized space after registration, the bias ${\mathit{b}}_m^j$ of center of mass j is computed by the equation below.

   $${\mathit{b}}_m^j=\frac{1}{R-1}{\displaystyle \sum _{n\ne m}}({\mathit{c}}_{\mathit{\text{mn}}}^j-{\mathit{c}}_n^j)$$ (4)
5. Now we can apply the MAP-CSTAPLE algorithm as described in our previous report. In contrast to STAPLE, which estimates a fusion of discrete labels as well as rater performance parameters (sensitivity and specificity) simultaneously, CSTAPLE deals with multi-dimensional continuous variables. The labeled point location is usually written in the form of vector ${\mathit{d}}_m^j$, which is the decision of rater m for point j. A fusion of these decisions denoted as t^j is to be found for each point j. And also for each rater m, the performance parameter, i.e., bias μ_m, and variance Σ_m is to be estimated simultaneously. Mathematically, it can be proved that under the same maximum likelihood estimation framework as discrete STAPLE, CSTAPLE yields equal likelihood for arbitrary rater bias parameter μ_m so that bias is indeterminate^[6]. If a rater has a systematic bias, the resulting fusion may not be accurate if this bias is not accounted. Therefore we previously proposed the MAP-CSTAPLE algorithm which utilizes prior information to restrict the rater bias and guide the iterations to converge to a proper bias estimate through a maximum a posteriori estimation framework. The proposed EM iteration^{[9, 10]} equations are

   • E-Step:

     $$\{\begin{array}{c}\hfill {\mathit{A}}^{(n)}={({\displaystyle \sum _{\mathrm{m}}}{{\mathbf{\Sigma }}_m}^{-1(n)})}^{-1}\hfill \\ \hfill {\mathit{t}}^{j(n)}={\mathit{A}}^{(n)}·{\displaystyle \sum _m}{{\mathbf{\Sigma }}_m}^{-1(n)}({\mathit{d}}_m^j-{\mathit{\mu }}_m^{(n)})\hfill \end{array}$$ (5)
   • M-Step:

     $$\{\begin{array}{c}\hfill {\mathit{\mu }}_m^{(n+1)}={(\mathit{I}+\frac{{\mathbf{\Sigma }}_m^{(n+1)}}{J{\mathrm{\sigma }}_{{\mathit{\mu }}_m}^2})}^{-1}(\frac{1}{J}{\displaystyle \sum _j}({\mathit{d}}_m^j-{\mathit{t}}^{j(n)})+\frac{{\mathbf{\Sigma }}_m^{(n+1)}}{J{\mathrm{\sigma }}_{{\mathit{\mu }}_m}^2}{\mathit{\mu }}_{{\mathit{\mu }}_m})\hfill \\ \hfill {\mathit{\Sigma }}_m^{(n+1)}=\frac{1}{J}{\displaystyle \sum _j}[{\mathit{A}}^{(n)}+({\mathit{d}}_m^j-{\mathit{\mu }}_m^{(n+1)}-{\mathit{t}}^{j(n)}){({\mathit{d}}_m^j-{\mathit{\mu }}_m^{(n+1)}-{\mathit{t}}^{j(n)})}^T]\hfill \end{array}$$ (6)

   where μ_μm and ${\sigma }_{{\mathit{\mu }}_m}^2$ are the prior mean and prior variance of bias μ_m, and J is the total number of points. Notice that in this method, the bias of a specific rater is assumed to be unchanged at different points. Comparison against discrete STAPLE shows that this is not always true and might introduce a systematic deviation. Also in our experiments with the real brain label centroid dataset, we have observed that the same rater (registered atlas) has different biases at different label points. Therefore we modified the algorithm to consider spatially-varying bias by assuming different biases at different points, i.e., mathematically, change μ_m to ${\mathit{\mu }}_m^j$. And the new EM iteration equations are

   • E-Step:

     $$\{\begin{array}{c}\hfill {\mathit{A}}^{(n)}={({\displaystyle \sum _{\mathrm{m}}}{{\mathbf{\Sigma }}_m}^{-1(n)})}^{-1}\hfill \\ \hfill {\mathit{t}}^{j(n)}={\mathit{A}}^{(n)}·{\displaystyle \sum _m}{{\mathbf{\Sigma }}_m}^{-1(n)}({\mathit{d}}_m^j-{\mathit{\mu }}_m^{j(n)})\hfill \end{array}$$ (7)
   • M-Step:

     $$\{\begin{array}{c}\hfill {\mathit{\mu }}_m^{j(n+1)}={(\mathit{I}+\frac{{\mathbf{\Sigma }}_m^{(n+1)}}{{({\mathrm{\sigma }}_{{\mathit{\mu }}_m}^j)}^2})}^{-1}({\mathit{d}}_m^j-{\mathit{t}}^{j(n)}+\frac{{\mathbf{\Sigma }}_m^{(n+1)}}{{({\mathrm{\sigma }}_{{\mathit{\mu }}_m}^j)}^2}{\mathit{\mu }}_{{\mathit{\mu }}_m}^j)\hfill \\ \hfill {\mathit{\Sigma }}_m^{(n+1)}=\frac{1}{J}{\displaystyle \sum _j}[{\mathit{A}}^{(n)}+({\mathit{d}}_m^j-{\mathit{\mu }}_m^{(n+1)}-{\mathit{t}}^{j(n)}){({\mathit{d}}_m^j-{\mathit{\mu }}_m^{(n+1)}-{\mathit{t}}^{j(n)})}^T]\hfill \end{array}$$ (8)

Figure 1.

A flowchart for the proposed seed identification technique.

Note that the new bias updating equation avoids the averaging through all the points and now treat each point differently with a specific bias, even for the same rater. Using symbols from previous steps, for any target atlas t, we substitute decision ${\mathit{d}}_m^j\text{ with }{\mathit{c}}_{\mathit{\text{mt}}}^j$ and bias prior mean ${\mathit{\mu }}_{{\mathit{\mu }}_m}^j\text{ with }{\mathit{b}}_m^j$ Also for bias prior variance ${({\mathrm{\sigma }}_{{\mathit{\mu }}_m}^j)}^2$ we use the scalar variance of $({\mathit{c}}_{\mathit{\text{mn}}}^j-{\mathit{c}}_n^j)$ over all targets n. After equations (7) and (8) converge^[11], the estimated fusion t^j(∞) can be used as seed for label point j.

3. RESULTS

The dataset of 148 complete 3D real brain atlases were evaluated in the experiment. On each atlas, 38 labels were identified and validated which segmented the entire brain volume. In correspondence with our model, for any target atlas, the total number of points J was 38. First, 147 of the atlases were used as training dataset to get the bias prior for raters in order to evaluate the one rest subject atlas. We explored the fusion of different rater numbers from 1 to 147. For any fixed rater number, the raters were randomly drawn from the training dataset to be used to calculate the fusion. Every one of the atlases was regarded as the subject atlas with the rest as training. The entire setup was repeated in 50 Monte-Carlos with random raters and random subject atlas. We then computed the mean squared error (MSE) of fusion from the truth for every subject atlas, and got an average MSE of 1.9613±1.0565 voxel². At the same time, we also did the evaluation on each of the same dataset with the fusion technique replaced with normal averaging and MAP-CSTAPLE with zero prior, and got an average MSE of 2.2881±1.0230 voxel² and 2.3126±1.1153 voxel² respectively. The MSE of one subject atlas is shown in Figure 2(d).

Figure 2.

(a) The bias model of one training atlas that has a symmetrical spatial pattern. (b) The MSE of every fusion point from the truth, which demonstrates MAP-CSTAPLE has an ability to reduce the fusion errors with the bias prior model. (c) The number of fusion points close to the truth. (d) The MSE of the fusion of one subject with respect to rater numbers. Training data has 147 atlases.

We also used 50 of the atlases as training data and the remaining 98 atlases as testing data. 50 Monte-Carlos were performed with the same setup as in previous experiment. For fixed training and testing datasets, the fusion on every single subject atlas was also evaluated with MAP-CSTAPLE and normal averaging. The average MSE was 1.6734±1.3962 voxel² for MAP-CSTAPLE and 2.0130±1.4050 voxel² for averaging. Figure 2(c) shows the number of fusion points with respect to distance from the truth. Generally speaking, at a certain distance from the truth (a ball centered at truth with certain radius), MAP-CSTAPLE is more likely to capture points than normal averaging technique.

4. CONCLUSION AND DISCUSSION

In this work we described a new approach to automatically determine seed locations for segmentation algorithms that require initial seeds. The approach was based on the STAPLE framework used for fusion approximation. We designed our model based on a previously proposed method – MAP-CSTAPLE – for continuous vector fusion problems and modified the equations and assumptions to fit the real brain atlas data we are evaluating, i.e., augmented the algorithm to handle the spatially bias-varying case. Experiment results demonstrated improved performance as compared to simple averaging. By using this approach, semi-automatic segmentation algorithms can become fully automatic, and this provides an alternative multi-atlas approach to image labeling over the conventional label fusion approaches.

By directly modifying the bias parameters to spatially vary at different label points, we may have introduced another problem of insufficiency. In particular, since each rater performs only once at each label point, it is difficult to reliably estimate a spatially-varying bias for the rater at that point. In the future, therefore, we will develop and investigate a model that incorporates measurement repetitions.