Acetate-Bridged Platinum(III) Complexes Derived from Cisplatin

Abstract

Oxidation of the acetate-bridged half-lantern platinum(II) complex, cis-[Pt^II(NH₃)₂(µ-OAc)₂Pt^II(NH₃)₂](NO₃)₂, [1](NO₃)₂, with iodobenzene dichloride or bromine generates the halide-capped platinum(III) species, cis-[XPt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)₂X](NO₃)₂, where X is Cl in [2](NO₃)₂, or Br in [3](NO₃)₂, respectively. These three complexes, characterized structurally by X-ray crystallography, feature short (≈ 2.6 Å) Pt–Pt separations, consistent with formation of a formal metal-metal bond upon oxidation. Elongated axial Pt–X distances occur, reflecting the strong trans influence of the metal-metal bond. The three structures are compared to those of other known dinuclear platinum complexes. A combination of ¹H, ¹³C, ¹⁴N, and ¹⁹⁵Pt NMR spectroscopy was used to characterize [1]²⁺–[3]²⁺ in solution. All resonances shift downfield upon oxidation of [1]²⁺ to [2]²⁺ and [3]²⁺. For the platinum(III) complexes, the ¹⁴N and ¹⁹⁵Pt resonances exhibit decreased linewidths by comparison to those of [1]²⁺. Density functional theory (DFT) calculations suggest that the decrease in ¹⁴N linewidth arises from a diminished electric field gradient (EFG) at the ¹⁴N nuclei in the higher valent compounds. The oxidation of [1](NO₃)₂ with the alternative oxidizing agent, bis(trifluoroacetoxy) iodobenzene, affords the novel tetranuclear complex, cis-[(O₂CCF₃)Pt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)(µ-NH₂)]₂(NO₃)₄, [4](NO₃)₄, also characterized structurally by X-ray crystallography. In solution, this complex exists as a mixture of species, the identities of which are proposed.

Introduction

The redox chemistry of late 2^nd and 3^rd row transition metals is dominated by two-electron transformations. Mononuclear compounds of platinum, for example, usually exist in formal oxidation states of 0, +2, or +4. The +3 oxidation state of platinum is much less common, and only a few mononuclear platinum(III) compounds are known.^1–4 The paucity of such compounds may in part be due to the reactive nature of the unpaired electron, which resides in a sterically exposed d_z² orbital. In contrast, platinum(III) compounds with metal-metal bonds are relatively common.^5–7 The unpaired electrons of the platinum(III) units couple to form a metal-metal σ-bond, thus eliminating any radical character and increasing the stability of the platinum(III) centers.

Early interest in dimeric and oligomeric platinum(III) complexes was motivated by the discovery⁸ that such species are a component of the deeply colored class of compounds known as the platinum blues,^9,10 some members of which display anticancer properties.^11,12 Since then, a large array of ligand-bridged dinuclear platinum(III) complexes have been synthesized and characterized,^5,6 as well as several unbridged platinum(III) dimers with unsupported metal-metal bonds.^13–18 In addition to their potential utility as anticancer agents,^19–22 dinuclear platinum(III) complexes have found use as photoluminescent materials^23–25 and catalysts.²⁶

Here, we utilize the previously reported dinuclear platinum(II) complex, cis-[Pt^II(NH₃)₂(µ-OAc)₂Pt^II(NH₃)₂](NO₃)₂, [1](NO₃)₂,²⁷ as a synthon for new platinum(III) species. We present full structural and multinuclear NMR spectroscopic characterization of [1](NO₃)₂ and its two-electron oxidation products, cis-[ClPt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)₂Cl](NO₃)₂, [2](NO₃)₂, and cis-[BrPt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)₂Br](NO₃)₂, [3](NO₃)₂. Electrochemical studies of these complexes are also reported. Lastly, a novel amido-bridged tetranuclear platinum(III) complex, obtained by the treatment of [1](NO₃)₂ with PhI(O₂CCF₃)₂, is reported. Both its solid-state structure and solution properties are described.

Experimental Section

General Methods and Materials

Cisplatin was purchased from Strem Chemicals and used as received. Silver(I) nitrate was obtained from Alfa Aesar, and bromine and bis(trifluoroacetoxy)-iodobenzene were acquired from Sigma Aldrich. Iodobenzene dichloride was prepared by a previously reported method.²⁸ Reactions were carried out under normal atmospheric conditions with no precautions taken to exclude moisture or oxygen.

Physical Measurements

NMR measurements were made on a Bruker DPX-400 spectrometer in the MIT Department of Chemistry Instrumentation Facility. ¹H and ¹³C{¹H} NMR spectra were referenced internally to residual solvent peaks and chemical shifts are expressed relative to tetramethylsilane, SiMe₄ (δ = 0 ppm). ¹⁹⁵Pt{¹H}, ¹⁹F{¹H}, and ¹⁴N{¹H} NMR spectra were referenced externally using standards of K₂PtCl₄ in D₂O (δ = −1628 ppm relative to Na₂PtCl₆), trifluorotoluene (δ = −63.72 ppm relative to CFCl₃), and NH₄Cl in 0.1 M HCl (δ = 0 ppm), respectively. Fourier transform infrared (FTIR) spectra were recorded with a ThermoNicolet Avatar 360 spectrophotometer running the OMNIC software. Samples were prepared as KBr disks. Melting points were measured on a Meltemp apparatus. Electrochemical measurements were carried out utilizing a VersaSTAT3 potentiostat from Princeton Applied Research accompanied by the V3 Studio software. A three-electrode cell was used comprising a glassy carbon (GC) working electrode, a Pt wire auxiliary electrode, and a Ag/AgCl reference electrode. The electrolyte was 0.1 M (Bu₄N)(PF₆) (TBAP) in DMF. Under the experimental conditions described, the reversible ferrocene/ferrocenium redox couple occurred at 0.55–0.56 V versus the reference. Elemental analyses were performed by a commercial analytical laboratory.

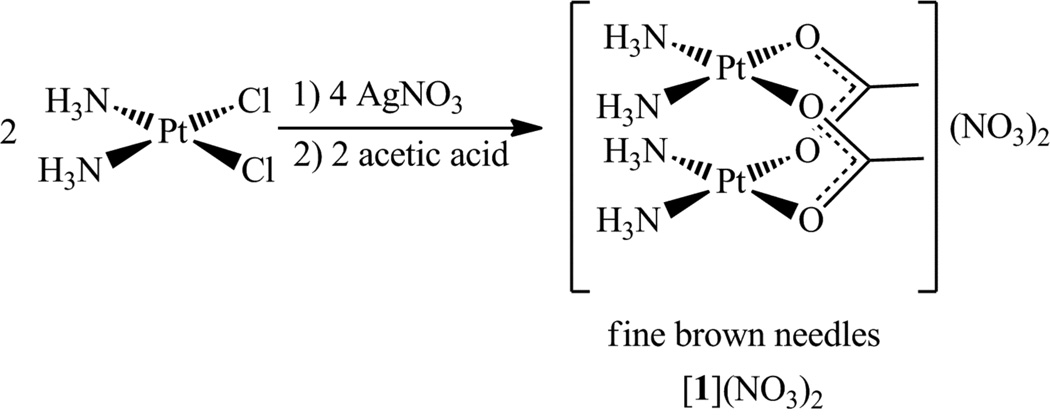
Synthesis of cis-[Pt^II(NH₃)₂(µ-OAc)₂Pt^II(NH₃)₂](NO₃)₂, [1](NO₃)₂

This compound was synthesized as previously reported²⁷ with slight modifications. A suspension of cisplatin (1.00 g, 3.33 mmol) and AgNO₃ (1.10 g, 6.48 mmol) in 15 mL of water was stirred for 16 h in the absence of light at room temperature. The resulting mixture was filtered to remove AgCl. To the filtrate was added 80% acetic acid (0.250 g, 3.33 mmol). Storage of this solution at 4 °C for three days afforded the desired compound as thin brown needles, which were isolated by filtration and washed with 5 mL of diethyl ether. Yield: 151 mg, 13%. Four additional crops could be isolated from the filtrate by continued storage at 4 °C over the course of several weeks. Yield of additional crops: 270 mg, 24%. M.p. 194–200 °C (dec). ¹H NMR (DMF-d₇, 400 MHz): δ 5.07 (br s, 12H), 1.97 (s, 6H). ¹³C{¹H} NMR (DMF-d₇, 100 MHz): δ 185.9, 22.3. ¹⁴N{¹H} NMR (DMF-d₇, 29 MHz): δ 356, −86 (W_1/2 ≈ 300 Hz). ¹⁹⁵Pt{¹H} NMR (DMF-d₇, 86 MHz): δ −1401. IR (KBr, cm⁻¹): 3432 m, 3284 m, 1541 s, 1442 s, 1384 vs, 1303 s, 1042 w, 839 w, 704 w, 536 w. Anal. Calcd. for [1](NO₃)₂, C₄H₁₈N₆O₁₀Pt₂: C, 6.86; H, 2.59; N, 12.00. Found: C, 6.75; N, 2.59; N, 11.84.

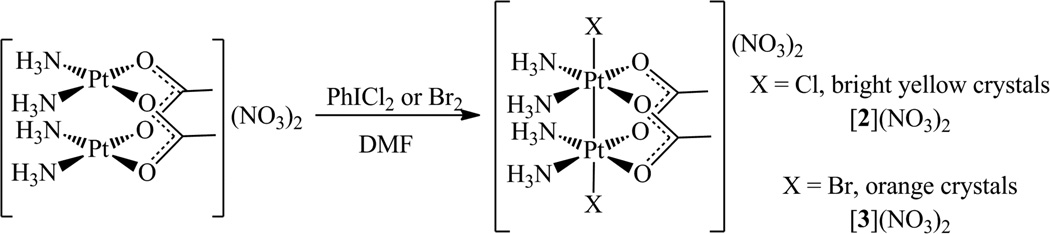
Synthesis of cis-[ClPt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)₂Cl](NO₃)₂·3DMF, [2](NO₃)₂·3DMF

To a brown suspension of [1](NO₃)₂ (100 mg, 0.143 mmol) in 3 mL of DMF was added a solution of PhICl₂ (40 mg, 0.145 mmol) in 1 mL of DMF. The brown suspension became a bright yellow solution immediately upon the addition of PhICl₂. Vapor diffusion of Et₂O into this yellow solution at 4 °C over the course of 16 h afforded bright yellow crystals. The supernatant was decanted, and the crystals were rinsed three times with 2 mL of Et₂O before being dried in vacuo. Yield: 130 mg, 92%. M.p. 101–106 °C (dec). ¹H NMR (DMF-d₇, 400 MHz): δ 6.44 (t, 12H, ¹J_NH = 49 Hz), 2.33 (s, 6H). ¹³C{¹H} NMR (DMF-d₇, 100 MHz): δ 195.2, 22.4. ¹⁴N{¹H} NMR (DMF-d₇, 29 MHz): δ 355, −65 (W_1/2 ≈ 50 Hz). ¹⁹⁵Pt{¹H} NMR (DMF-d₇, 86 MHz): δ −76 (quintet, ¹J_PtN = 226 Hz). IR (KBr, cm⁻¹): 3443 m, 3097 s, 1648 s, 1585 m 1540 m, 1496 w, 1384 vs, 1289 m, 1106 w, 1044 w, 911 w, 722 w, 665 w. Anal. Calcd. for [2](NO₃)₂·3DMF, C₁₃H₃₉Cl₂N₉O₁₃Pt₂: C, 15.76; H, 3.97; N, 12.73. Found: C, 15.65; H, 3.93; N, 12.56.

Synthesis of cis-[BrPt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)₂Br](NO₃)₂·3DMF, [3](NO₃)₂·3DMF

To a brown suspension of [1](NO₃)₂ (58 mg, 0.083mmol) in 2 mL of DMF was added a freshly prepared 1.23 M solution of Br₂ in DMF (75 µL, 0.092 mmol Br₂). The mixture became a dark orange-red solution immediately. Vapor diffusion of Et₂O into the orange-red solution at 4 °C over the course of 16 h afforded bright orange crystals. The supernatant was decanted and the crystals were washed three times with 5 mL of Et₂O before being dried in vacuo. Yield: 80 mg, 89%. M.p. 78–85 °C (dec). ¹H NMR (DMF-d₇, 400 MHz): δ 6.43 (t, 12H, ¹J_NH = 44 Hz), 2.31 (s, 6H). ¹³C{¹H} NMR (DMF-d₇, 100 MHz): δ 196.2, 22.6. ¹⁴N{¹H} NMR (DMF-d₇, 29 MHz): δ 355, −67 (W_1/2 ≈ 45 Hz). ¹⁹⁵Pt{¹H} NMR (DMF-d₇, 86 MHz): δ −216 (quintet, ¹J_PtN = 232 Hz). IR (KBr, cm⁻¹): 3437 w, 3150 m, 1648 s, 1611 m, 1540 w, 1496 w, 1384 vs, 1352 m, 1286 w, 1107 w, 1043 w, 903 w, 720 w, 662 w. By combustion analysis, 3 analyzed as a solvate containing 2.75, rather than 3, DMF molecules per formula unit as observed by X-ray crystallography and ¹H NMR spectroscopy. Presumably, a small fraction of DMF was lost from the lattice under vacuum or during transport of the sample. Anal. Calcd. for [3](NO₃)·2.75DMF, C_12.25H_37.25Br₂N_8.75O_13.75Pt₂: C, 13.66; H, 3.49; N, 11.38. Found: C, 13.85; H, 3.52; N, 11.34.

Synthesis of cis-[(O₂CCF₃)Pt^III(NH₃)₂(µ-OAc)₂Pt^III(NH₃)(µ-NH₂)]₂(NO₃)₄·4DMF, [4](NO₃)₄·4DMF

To a suspension of [1](NO₃)₂ (62 mg, 0.089 mmol) in 1 mL of DMF was added a solution of PhI(O₂CCF₃)₂ (39 mg, 0.091 mmol) in 1 mL of DMF. The mixture, initially a dark red suspension, became a yellow solution after ten minutes at room temperature. Vapor diffusion of Et₂O into this yellow solution afforded yellow-orange crystals after 16 h at room temperature. The supernatant was decanted and the crystals were washed three times with 2 mL of Et₂O before being dried in vacuo. Yield: 68 mg, 40%. M.p. > 180 °C (gradual darkening), 195–202 °C (dec). IR (KBr, cm⁻¹): 3432 br m, 3122 br m, 1651 vs, 1542 m, 1454 s, 1421 s, 1384 vs, 1301 m, 1267 m, 1190 m, 1138 w, 1106 w, 1083 w, 837 vw, 800 vw, 722 w, 666 vw, 521 vw, 470 vw. Anal. Calcd. for [4](NO₃)₄·4DMF, C₂₄H₆₂F₆N₁₆O₂₈Pt₄: C, 15.04; H, 3.26; N, 11.69. Found: C, 14.97; H, 3.10; N, 11.94.

X-Ray Crystallography

Single crystals, mounted in Paratone oil on a cryoloop, were cooled to 100 K under a nitrogen cold-stream. A Bruker APEX CCD X-ray diffractometer controlled by the APEX2 software package²⁹ with a graphite-monochromated Mo Kα radiation source (λ = 0.71073 Å) was used for data collection. Data were integrated with SAINT³⁰ and then corrected for absorption with SADABS.³¹ Space group determination was carried out by analysis of the unit cell parameters and systematic absences in the diffraction pattern using the program XPREP.³² Structures were solved and refined against F² with the SHELXTL-97 software package.^33,34 Non-hydrogen atoms were located on difference Fourier maps. Hydrogen atoms were placed at idealized locations with displacement parameters constrained to be either 1.2 or 1.5 times (for terminal CH₃ or NH₃ groups) the thermal parameter of the atoms to which they were attached. Specific refinement details are provided below, and relevant X-ray crystallographic data collection and refinement parameters are reported in Table 1. X-ray data, in CIF file format, are provided in the Supporting Information.

Table 1.

X-ray Crystallographic Data Collection and Refinement Parameters

	[1](NO3)2·0.5H2O	[2](NO3)2·3DMF	[3](NO3)2·3DMF	[4](NO3)4·4DMF
formula	C4H18N6O10.50Pt2	C13H39Cl2N9O13Pt2	C13H39Br2N9O13Pt2	C24H62F6N16O28Pt4
fw	708.42	990.61	1079.53	1917.26
space group	C2/c	P21/c	P21/c	C2/c
a, Å	19.1794(9)	13.3959(5)	24.2462(12)	35.401(4)
b, Å	15.7804(7)	10.3272(4)	10.5186(5)	13.8473(14)
c, Å	10.8811(5)	25.3699(10)	26.2471(13)	12.8506(13)
β, deg	100.4520(10)	121.7120(10)	113.6230(10)	107.367(2)
V, Å3	3238.6(3)	2985.7(2)	6133.0(5)	6012.3(11)
Z	8	4	8	4
ρcalcd, g·cm−3	2.906	2.204	2.338	2.118
T, °C	−173(2)	−173(2)	−173(2)	−173(2)
µ(Mo Kα), mm−1	17.320	9.610	11.788	9.384
θ range, deg	1.68–30.10	1.79–29.33	1.83–28.92	1.59–25.13
completeness to θ (%)	99.4	99.7	99.6	99.7
total no. of data	35449	61247	124152	45478
no. of unique data	4748	8166	16123	5366
no. of parameters	233	387	755	424
no. of restraints	3	81	126	261
R1a (%)	2.27	3.72	5.55	7.78
R1a, I>2σ (%)	1.82	2.86	3.74	5.36
wR2b (%)	3.83	6.59	7.21	14.86
wR2b, I>2σ (%)	3.70	6.22	6.66	13.61
GOFc	1.036	1.119	1.105	1.071
max, min peaks, e·Å−3	1.320, −1.529	3.643, −1.828	1.673, −1.599	4.849, −1.761

^aR1 = Σ‖F_o| − |F_c‖/Σ|F_o|.

^bwR2 = {Σ[w(F_o² − F_c²)²]/Σ[w(F_o²)²]}^1/2.

^cGOF = {Σ[w(F_o² − F_c²)²]/(n − p)}^1/2 where n is the number of data and p is the number of refined parameters.

Vapor diffusion of Et₂O into a DMF solution of [1](NO₃)₂ afforded a mixture thin yellow needlelike crystals and orange shards. An orange shard was selected for X-ray diffraction analysis, for the yellow needles were too small to afford appreciable diffraction. The asymmetric unit consists of the [1]²⁺ cation, a nitrate anion situated on a general position at full occupancy, a nitrate anion residing on a crystallographic two-fold axis, and a nitrate anion disordered with a water molecule about a crystallographic inversion center. For the nitrate anion disordered about the inversion center, the bond distances and angles were restrained to be similar to those of the non-disordered nitrate anion. The occupancy factors of the disordered nitrate and water atoms were 50:50 as necessitated by the crystallographic inversion center about which they are disordered. The protons of this half occupancy water molecule could not be located on the difference Fourier map and were therefore not included in the final model. The remaining largest electron density peak (1.32 e-Å⁻³) and hole (−1.53 e-Å⁻³) are 0.77 and 0.66 Å from Pt1, respectively.

Yellow crystals of [2](NO₃)₂·3DMF were grown by vapor diffusion of Et₂O directly into the DMF solution of the crude reaction mixture. The asymmetric unit comprises one molecule of [2](NO₃)₂ and three molecules of DMF. One molecule of DMF is disordered over two orientations. The bond lengths and angles of the two disordered components were restrained to be similar to one another, as were the thermal displacement parameters. The site occupancy factors of the disordered components refined to a ratio of 71:29. The remaining largest electron density peak (3.64 e-Å⁻³) and hole (−1.83 e-Å⁻³) are 0.77 and 0.64 Å from Pt2, respectively.

Orange crystals of [3](NO₃)₂·3DMF were grown by vapor diffusion of Et₂O directly into a DMF solution of the crude reaction mixture. The asymmetric unit comprises two molecules of [3](NO₃)₂ and six molecules of DMF. One molecule of DMF is disordered over two positions. The bond lengths and angles of the two disordered components were restrained to be similar to one another as were the thermal displacement parameters. The site occupancy factors of the disordered components were allowed to refine freely and converged at a ratio of 52:48. The central nitrogen atom of one of the nitrate counterions (N9) gave non-positive definite ellipsoids upon anisotropic refinement. Attempts to constrain the ellipsoid parameters to match those of other well-behaved nitrate nitrogen atoms in the structure gave rise to spurious large electron density peaks and holes in the difference Fourier map near these atoms. In the final model, N9 was therefore refined isotropically without restraints or constraints. We hypothesize that difficulty in refining N9 may arise from a small amount of bromide ion at the site of the nitrate counterion, which would lead to the observed contraction of the N9 thermal displacement parameter. The remaining largest electron density peak (1.67 e-Å⁻³) and hole (−1.60 e-Å⁻³) appear at 0.66 Å from Pt4 and 0.63 Å from Pt2, respectively.

Pale yellow crystals of [4](NO₃)₄·4DMF were obtained by vapor diffusion of Et₂O directly into a DMF solution of the crude reaction mixture. Half of the tetranuclear complex cation is related to the other half by a crystallographic inversion center. Also in the asymmetric unit are the two nitrate counterions and two molecules of DMF. One of the DMF molecules is disordered over two orientations. Similarity restraints were used to model this disorder, and the site occupancy factors refined to a ratio of 56:44. The axial trifluoroacetate ligands of [4]⁴⁺ were also disordered. One carbon (C1) and one oxygen (O2) atom were modeled in different orientations using the appropriate similarity restraints. The disordered components refined to site occupancy factors of 52:48. After full anisotropic refinement and placement of the hydrogen atoms, severely disordered residual electron density was still present about a crystallographic inversion center. This disordered electron density was modeled with SQUEEZE as part of the crystallographic program PLATON.³⁵ Two solvent accessible voids of 300 ų with 91 e⁻ were excluded from this model with SQUEEZE. We hypothesize that this electron density corresponds to disordered diethyl ether molecules that are readily lost under reduced pressure. The largest remaining electron density peak (4.85 e-Å⁻³) and hole (−1.76 e-Å⁻³) were locating 1.07 and 0.85 Å from Pt2 and Pt1, respectively.

Computational Studies

Geometries were optimized in the gas phase starting from coordinates obtained by X-ray crystallography. Frequency calculations on optimized geometries were employed to ensure convergence to local minima on the potential energy surface. For [1]²⁺ and [1](NO₃)⁺, geometry optimization required the use of an ultrafine integration grid in order to achieve convergence at a local minimum. All geometry optimization and frequency calculations were carried out using the Gaussian03 software package³⁶ with the hybrid functional, PBE0.³⁷ The LANL2DZ basis set and effective core potential³⁸ were utilized for platinum atoms and the 6–311+G(d,p) basis set³⁹ was used for the other elements. The Cartesian coordinates of all optimized structures are provided in the Supporting Information (SI, Tables S1–S6).

Electric field gradient (EFG) parameters and ¹⁴N NMR chemical shifts were computed with the program ORCA⁴⁰ using optimized geometries obtained from the Gaussian03 calculations. The PBE0 functional was applied for these calculations as well. The all-electron basis set, def2-TZVP(-f), and its corresponding decontracted auxiliary basis set, def2-TZVP/J,⁴¹ were used for all atoms. The zero^th-order regular approximation (ZORA)⁴² was applied to correct for relativistic effects. Solvation effects were modeled with the conductor-like screening model (COSMO)⁴³ for DMF. Isotropic shielding parameters for ¹⁴N nuclei were computed with the IGLO approach,^44,45 as implemented in ORCA. The isotropic shielding of NH₄⁺ was calculated at the same level of theory with simulated solvation in water and was used as a reference to convert other values to ppm.

Results and Discussion

Synthesis

Treatment of the cis-diamminediaquaplatinum(II) cation with one equivalent of acetic acid in water afforded the acetate-bridged dinuclear platinum(II) complex [1]²⁺ (Scheme 1), as previously described.²⁷ At 4 °C the nitrate salt of this compound precipitates from aqueous solution as brown needles. The initial yield of the compound was only 13%. More crops, however, could be isolated from the filtrate, increasing the total yield to 37%. In aqueous solution, a mixture of acetic acid and the cis-diamminediaquaplatinum(II) cation gives rise to multiple species that differ in the binding mode and stoichiometry of the acetate ligand.⁴⁶

Scheme 1.

When a solution of [1](NO₃)₂ in DMF was allowed to react with slightly greater than one equiv of the two-electron oxidizing agents PhICl₂ and Br₂, nitrate salts of the halide-capped platinum(III) dimers, [2]²⁺ and [3]²⁺, respectively, were obtained (Scheme 2). Although partially oxidized chains of [1]²⁺ have previously been isolated following bulk electrolysis,⁴⁷ compounds [2]²⁺ and [3]²⁺ are the first examples of discrete cis-diammineplatinum(III) dinuclear complexes bridged by acetate ligands. Previously employed bridging ligands for dinuclear cis-diammineplatinum(III) complexes are primarily monoanionic N,O donors, including α-pyridonate,^48–52 α-pyrrolidonate,^53–55 pyrimidines,^56–60 and amidates.^61–64 Somewhat analogous carboxylate-bridged dinuclear cis-dimethylplatinum(III) complexes have been reported,^65–68 and carboxylate-bridged cyclometallated diplatinum(III) complexes have also recently been described.^69–71

Scheme 2.

Description of the Structures

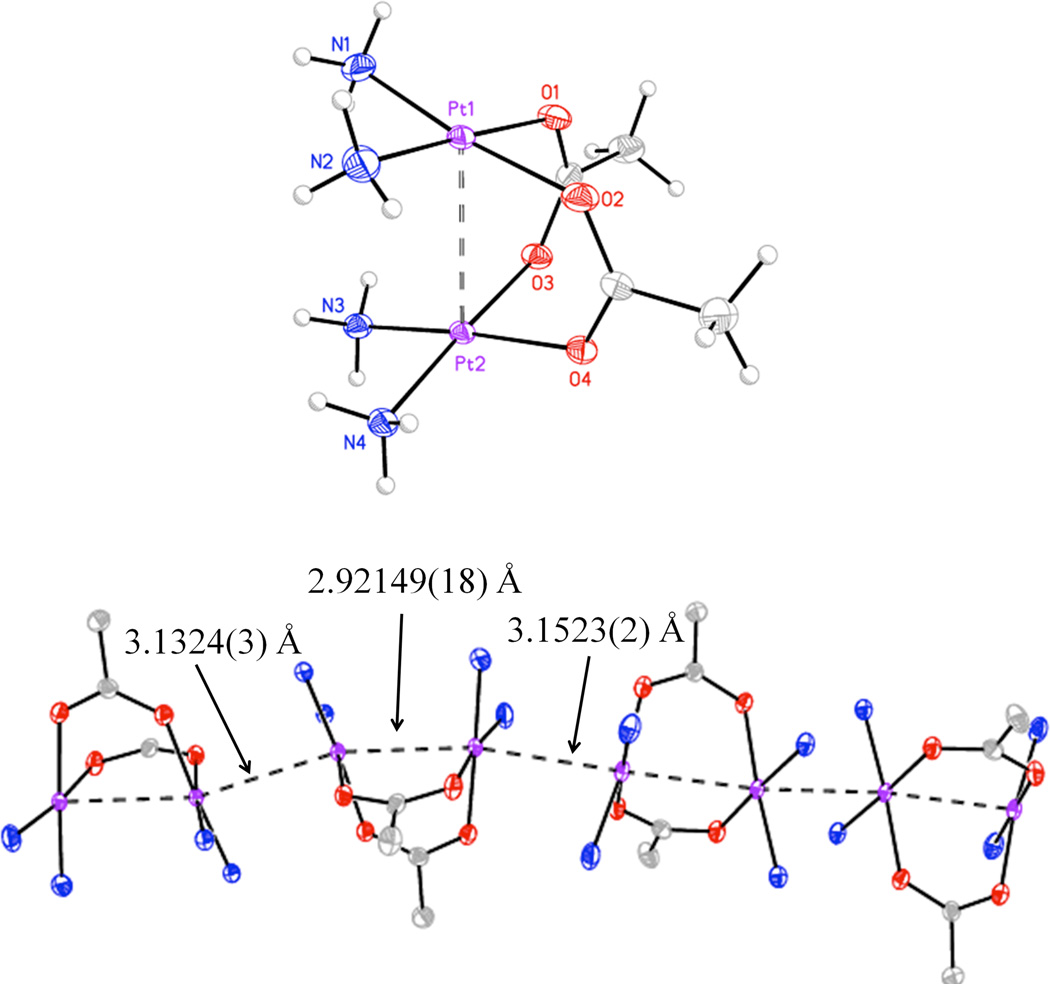
Dinuclear platinum(II) cation [1]²⁺ has previously been structurally characterized as the SiF₆²⁻ salt.²⁷ Here, we obtained crystals of [1]²⁺ as the nitrate salt by vapor diffusion of Et₂O into a DMF solution. Two different polymorphs formed under these conditions, very fine yellow needles, which were too small for X-ray diffraction studies, and larger orange shards, which were selected for analysis by X-ray diffraction. The structure of the orange cation [1]²⁺ is shown in Figure 1, and selected structural features are summarized in Table 2. As expected, the structure is an acetate-bridged dimer. There are two nitrate counterions per platinum(II) dimer, consistent with a Pt(II) oxidation state and indicating the stability of the complex in the presence of oxygen. The distance between Pt1 and Pt2 (atoms labeled in Figure 1) is 2.92149(18) Å. This value is significantly longer than those of dinuclear platinum(III) complexes, which generally range from 2.5–2.7 Å,⁵ indicating the absence of a formal metal-metal bond between two d⁸ metal ions.⁷² The tilt angle (τ) between adjacent platinum coordination planes is 31.9°, and the average torsion angle (ω) about the Pt–Pt vector is 5.5°. These values for [1]²⁺ compare favorably to those in the related α-pyridonate head-to-tail-bridged dinuclear platinum(II) complex, [Pt₂(NH₃)₄(C₅H₄NO)₂](NO₃)₂, which are 2.8981(5) Å and 28.8°, respectively.⁷³ The torsion angle in the α-pyridonate complex is 13.0°.⁷³

Figure 1.

Structure of [1]²⁺ (top). Intermolecular interactions between cations are also depicted (bottom). Thermal ellipsoids are drawn at the 50% probability level.

Table 2.

Relevant Structural Features of [1]²⁺–[3]²⁺ and Related Structures from the Literature

Compound	Pt oxidn state	Pt–Pt dist, Å	Pt–Laxial dist, Å		τ,a deg	ω,b deg	ref
[Pt2(O2CCH3)2(NH3)4](NO3)2, [1](NO3)2	2	2.92149(18)			31.9	5.5	c
[Pt2(O2CCH3)2(NH3)4](SiF6)·4H2O	2	2.9713(8)			36.3	7.2	27
HT-[Pt2(C5H4NO)2(NH3)4](NO3)2·2H2O	2	2.8981(5)			28.8	13.0	77
HH-[Pt2(C4H6NO)2(NH3)4](SO4) ·H2O	2	2.9749 (11)			29.9	4.3	78
[Pt2Cl2(O2CCH3)2(NH3)4](NO3)2·3DMF, [2](NO3)2·3DMF	3	2.5997(2)	2.4321(12)	2.4017(11)	19.3	1.4	c
[Pt2Br2(O2CCH3)2(NH3)4](NO3)2·3DMF, [3](NO3)2·3DMFd	3	2.6004(3) 2.6052(3)	2.5590(7) 2.5597(7)	2.5465(7) 2.5399(7)	18.4 19.6	3.5 2.6	c
HT-[Pt2Cl2(C5H4NO)2(NH3)4](NO3)2	3	2.568(1)	2.444(2)	2.429(4)	19.5	27.4	51
HT-[Pt2Br2(C5H4NO)2(NH3)4](NO3)2·0.5H2O	3	2.582(1)	2.573(1)	2.562(1)	20.5	29.4	51
HH-[Pt2Cl2(C4H6NO)2(NH3)4](SO4) ·2H2O	3	2.6235 (13)	2.410 (5)	2.446 (5)	16.3	0.4	79
HH-[Pt2Br2(C4H6NO)2(NH3)4](NO3)2	3	2.6476 (4)	2.5647 (9)	2.5889 (8)	18.1	1.0	80
[Pt2(C6H7N)2(O2CCF3)2(CH3)4]	3	2.557(1)	2.09(2)	2.17(2)	17.6	22	67
[Pt2(C5H5N)2(O2CCH3)2(CH3)4]	3	2.529(1)	2.200(11)		15.6	24.8	68

^aτ is the tilt angle between adjacent platinum coordination planes.

^bω is the average torsion angle about the Pt–Pt vector.

^cThis work.

^dThe features of both molecules in the asymmetric unit are reported.

As indicated in Figure 1, dimers of [1]²⁺ stack in the crystal lattice to form infinite chains. The Pt–Pt separation between Pt1 and its symmetry equivalent, Pt1A is 3.1523(2) Å, and the corresponding value for the Pt2/Pt2A pair is 3.1324(3) Å. Hydrogen-bonding interactions between oxygen atoms of the bridging acetates and protons of the ammine ligands stabilize the interaction between Pt2 and Pt2A, for which the torsion angle is 180° and the N–O distances are 2.97 and 3.00 Å. At the Pt1–Pt1A interface, the torsion angle is 41.5° and the nearest N–O distance is 3.19 Å, which rules out hydrogen-bonding as a contributor to this interaction. Closed-shell d⁸–d⁸ interactions most likely promote this close contact.^74–76 The structure of the previously reported SiF₆²⁻ salt of [1]²⁺ also includes infinite stacking of platinum(II) dimer cations,²⁷ which rules out crystal packing as an explanation for the phenomenon.

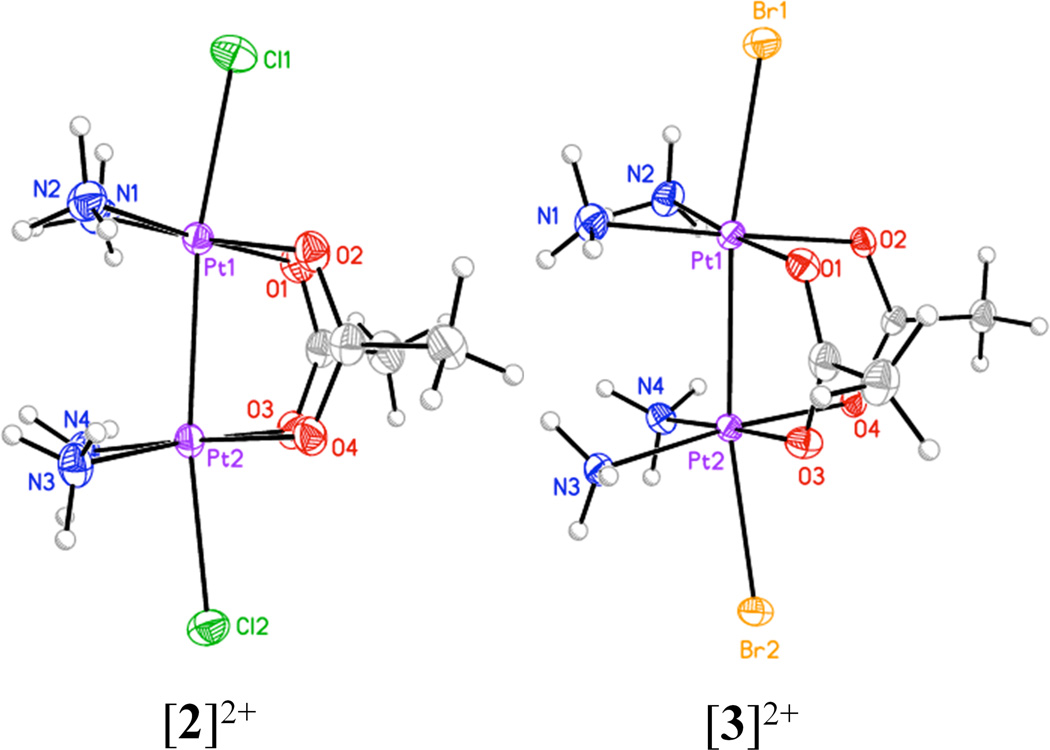
The X-ray crystal structures of [2]²⁺ and [3]²⁺ reveal discrete halide-capped cis-diammineplatinum(III) dimers, with the platinum atoms are bridged by two acetate ligands (Figure 2). Selected structural features of these and related dinuclear platinum complexes are given in Table 2. The two-electron oxidation of [1]²⁺ to generate [2]²⁺ or [3]²⁺ is accompanied by an approximate 0.3 Å shortening of the Pt–Pt distance and a 10° decrease in the tilt angle, signifying removal of two electrons from a strongly metal–metal antibonding orbital (vide infra). The Pt–Pt distance in [2]²⁺ is 2.5997(2) Å. There are two molecules of [3]²⁺ in the asymmetric unit, with Pt–Pt distances of [3]²⁺ 2.6004(3) and 2.6052(3) Å. The small difference in Pt-Pt bond lengths between [2]²⁺ and [3]²⁺ indicates that the axial ligands have a negligible trans influence. This result is similar to that for the head-to-tail α-pyridonate bridged platinum(III) dimers,⁴⁹ where the Pt–Pt bond lengthens by only 0.014(1) Å upon changing axial ligands from chloride to bromide.⁵¹ For similar head-to-head α-pyrrolidonate-bridged dimers, the Pt–Pt bond elongates by 0.024(1) Å when chloride is replaced by bromide.^79,80 For [2]²⁺ and [3]²⁺, the trans influence of the Pt–Pt bond on the axial Pt–ligand bond is clearly noticeable, however. The Pt–Cl bond length in [2]²⁺ are 2.4321(12) and 2.4017(11) Å, > 0.1 Å larger than typical Pt–Cl bond distances in most platinum(II) and platinum(IV) structures. A similar effect occurs in [3]²⁺, where the Pt–Br distances (2.5399–2.5597 Å) are greater than typical 2.45 Å Pt–Br distances in other compounds.

Figure 2.

X-ray crystal structures of the cations [2]²⁺ (left) and [3]²⁺ (right). Only one of the cations in the asymmetric unit of [3]²⁺ is shown. Thermal ellipsoids are drawn at the 50% probability level.

The torsion angles in [1]²⁺–[3]²⁺ are all less than 5.5°, indicating nearly eclipsed geometries. The α-pyridonate-bridged Pt(II) complexes exhibit moderate torsion angles (13.0°), which increase upon oxidation to ~28° (Table 2). The α-pyrrolidonate-bridged platinum complexes, like [1]²⁺–[3]²⁺, remain eclipsed conformations (ω < 5°) irrespective of oxidation state (Table 2). Structurally analogous carboxylate-bridged platinum(III) dimers with cis methyl groups instead of ammines exhibit relatively large torsion angles (22–25°).^67,68 The small torsion angles of [1]²⁺–[3]²⁺ are therefore most likely not a consequence solely of the bridging acetate ligands. Ammine ligands, unlike methyl groups, are capable of hydrogen bonding. Indeed, significant hydrogen-bonding interactions are present in the crystal lattices of [1]²⁺–[3]²⁺ with DMF and nitrate ion. These hydrogen-bonding interactions may also stabilize the eclipsed conformations.

Multinuclear NMR Spectroscopy

Further characterization of [1]²⁺–[3]²⁺ was provided by ¹H, ¹³C, ¹⁴N, and ¹⁹⁵Pt NMR spectroscopy (Table 3). The ¹³C NMR spectra each display two signals for the inequivalent carbon atoms of the bridging acetate ligands. Although the methyl group resonance, which occurs near 22 ppm for [1]²⁺–[3]²⁺, is not affected by the platinum oxidation state, the central carboxylate carbon shifts downfield by approximately 10 ppm, from 185.9 ppm to 195.2 and 196.2 ppm, upon oxidation to [2]²⁺ and [3]²⁺, respectively.

Table 3.

NMR Spectroscopic Data for [1]²⁺–[3]^2+a

	1H		13C	14N	195Pt
compound	δ NH3, ppm	1JNH, Hz	δ CH3CO2−	δ NH3, ppm	δ, ppm	1JNPt, Hz
[1]2+	5.07	n.o.b	185.9	−86	−1401	n.o.b
[2]2+	6.44	49	195.2	−65	−76	226
[3]2+	6.43	44	196.2	−67	−216	232

^aAll spectra were acquired at room temperature in DMF-d₇.

^bNot observed under these experimental conditions.

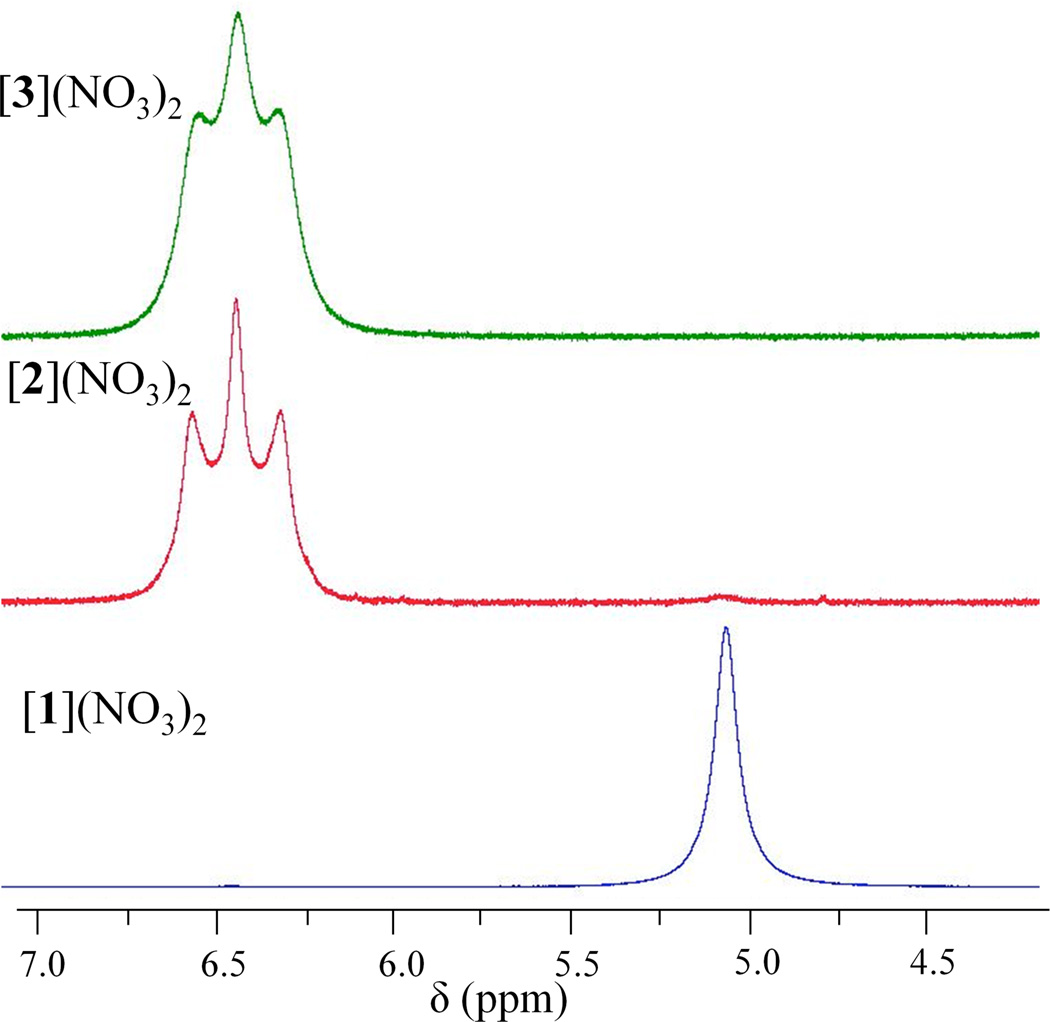
The ¹H NMR spectra of [1]²⁺–[3]²⁺ display sharp singlets for the CH₃ group of the bridging acetate near 2 ppm and broad resonances between 5–7 ppm for the coordinated NH₃ groups. Upon oxidation of [1]²⁺, the methyl group resonance shifts from 1.97 ppm to 2.33 and 2.31 ppm for [2]²⁺ and [3]²⁺, respectively, indicating that the electron-deficient platinum(III) center has an appreciable effect on the electron density at the protons of methyl group. A similar effect is observed for the protons of the NH₃ ligands. The greater deshielding effect of the platinum(III) centers shifts the resonances of these protons from 5.07 in [1]²⁺ to 6.44 ppm in [2]²⁺ and [3]²⁺. Whereas the resonance appears as a broad singlet for [1]²⁺, it is a broadened triplet in [2]²⁺ and [3]²⁺ (Figure 3). The triplet splitting pattern is due to coupling with the quadrupolar ¹⁴N nucleus (I=1, 99.63% natural abundance). Quadrupolar relaxation by the ¹⁴N nucleus broadens the lines and leads to poorly resolved multinuclear coupling. At constant temperature and solvent viscosity, the quadrupolar relaxation rate depends on the asymmetry and magnitude of the electric field gradient (EFG) at the nucleus.⁸¹ Because the solvent and temperature used for all NMR measurements were the same, the ability to resolve ¹H–¹⁴N coupling in [2]²⁺ and [3]²⁺ denotes a significant change in the EFG at the coordinated ammines in the platinum(III) complexes. Values for ¹J_NH of [2]²⁺ and [3]²⁺ are 49 and 44 Hz, respectively, slightly smaller than those observed for cis-diamminedichloroplatinum(IV) complexes bearing axial aromatic carboxylate ligands, which range from 53–54 Hz.⁸²

Figure 3.

NH₃ region of the ¹H NMR spectra of [1]²⁺–[3]²⁺ in DMF-d₇ recorded at room temperature and at a frequency of 400 MHz.

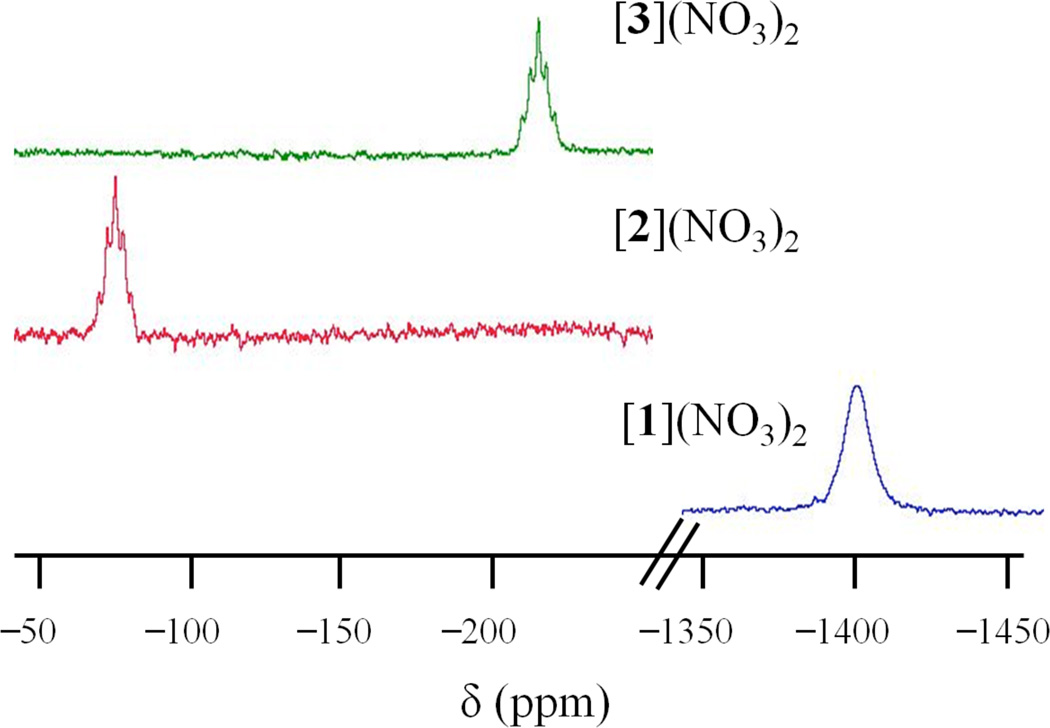
Proton-decoupled ¹⁴N NMR spectra were also recorded. ¹⁴N NMR spectral analyses of platinum complexes have been used to study reactions of cisplatin with components of human blood plasma.⁸³ More recently, this methodology was applied to investigate photoreactive anticancer platinum(IV) azido complexes.^84–87 Figure 4 shows a comparison of the ¹⁴N NMR spectra of [1]²⁺–[3]²⁺ in the NH₃ region. Not shown are sharp signals that appear at 355 ppm, due to the nitrate counterions for all three complexes. The NH₃ signal of [1]²⁺ shifts downfield upon oxidation to form [2]²⁺ and [3]²⁺, from −86 ppm to −65 and −67 ppm, respectively, consistent with the higher oxidation state in the latter complexes. The coordinated ammine ligands in platinum(IV) azido complexes shift even farther downfield, to ~ −40 ppm.^84–87 The ¹⁴N NMR resonance of the coordinated NH₃ group in [1]²⁺ is significantly broader (W_1/2 ≈ 300 Hz) than those of the platinum(III) complexes [2]²⁺ and [3]²⁺ (W_1/2 ≈ 50, 45 Hz). Because quadrupolar relaxation is the dominant relaxation mechanism for ¹⁴N nuclei,⁸⁸ the sharpening of the signal in [2]²⁺ and [3]²⁺ most likely reflects a decrease in the quadrupolar relaxation rate induced by changing the EFG upon oxidation, as discussed above. Shoulders are also present in the NH₃ signal of [2]²⁺ and [3]²⁺. These shoulders are due to coupling to the ¹⁹⁵Pt nucleus (I=1/2), which is 33% abundant.

Figure 4.

¹⁴N{¹H} NMR spectra of [1]²⁺–[3]²⁺ in DMF-d₇ recorded at room temperature and at a frequency of 29 MHz.

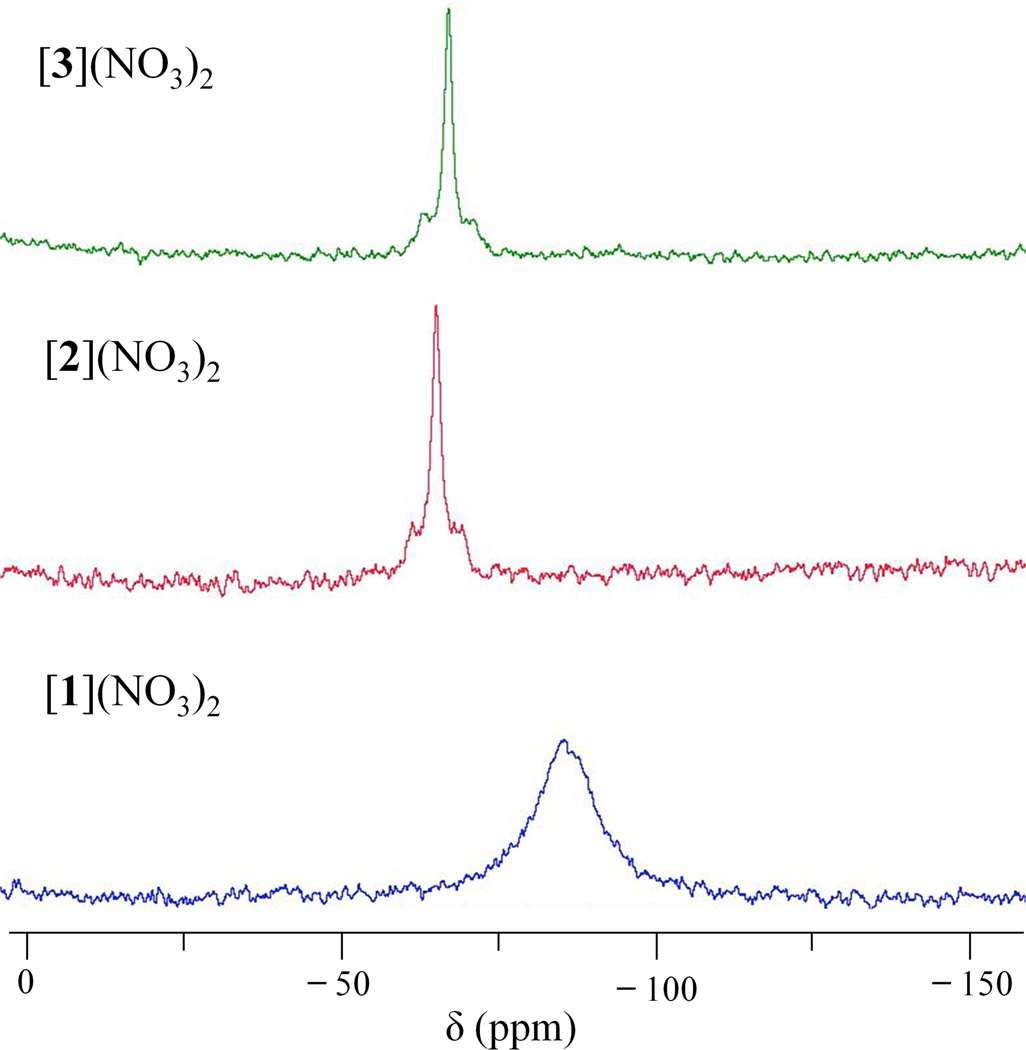
The proton-decoupled ¹⁹⁵Pt NMR spectra of [1]²⁺–[3]²⁺ are shown in Figure 5. The broad peak for [1]²⁺ occurs at −1401 ppm, a value similar to those of other platinum(II) complexes having O₂N₂ coordination environments.⁸⁹ The ¹⁹⁵Pt NMR chemical shifts for [2]²⁺ and [3]²⁺ are −76 and −216 ppm, respectively, within the region expected for a dinuclear platinum(III) complex.⁵² The 140 ppm upfield shift of [3]²⁺ relative to [2]²⁺ is consistent with the empirical observation that softer ligands shift ¹⁹⁵Pt NMR resonances to more negative values.⁹⁰ The signals of [2]²⁺ and [3]²⁺ appear as quintets, which arise from coupling to two equivalent ¹⁴N nuclei. The presence of such ¹⁴N coupling in the spectra of [2]²⁺ and [3]²⁺, but not [1]²⁺, is most likely a consequence of decreased quadrupolar relaxation at the nitrogen nuclei in the latter. Chemical shift anisotropy (CSA) of ¹⁹⁵Pt plays a large role in its relaxation and attendant NMR line width.^91,92 The octahedral coordination geometries of [2]²⁺ and [3]²⁺ produce less CSA than the square-planar geometry of [1]²⁺. Smaller CSAs for [2]²⁺ and [3]²⁺ decrease the line width and are another factor that enables observation of ¹⁴N–¹⁹⁵Pt coupling. The values for ¹J_NPt for [2]²⁺ and [3]²⁺ are 226 and 232 Hz, respectively, larger than that of the platinum(IV) complex cis, cis, trans-[Pt(NH₃)₂Cl₂(OH)₂], 194 Hz,⁹³ and those of several cis-diamminedichloroplatinum(IV) complexes having axial aromatic carboxylate ligands, which range from 172–179 Hz.⁸²

Figure 5.

¹⁹⁵Pt{¹H} NMR spectra of [1]²⁺–[3]²⁺ in DMF-d₇ recorded at room temperature and a frequency of 86 MHz.

Electrochemistry

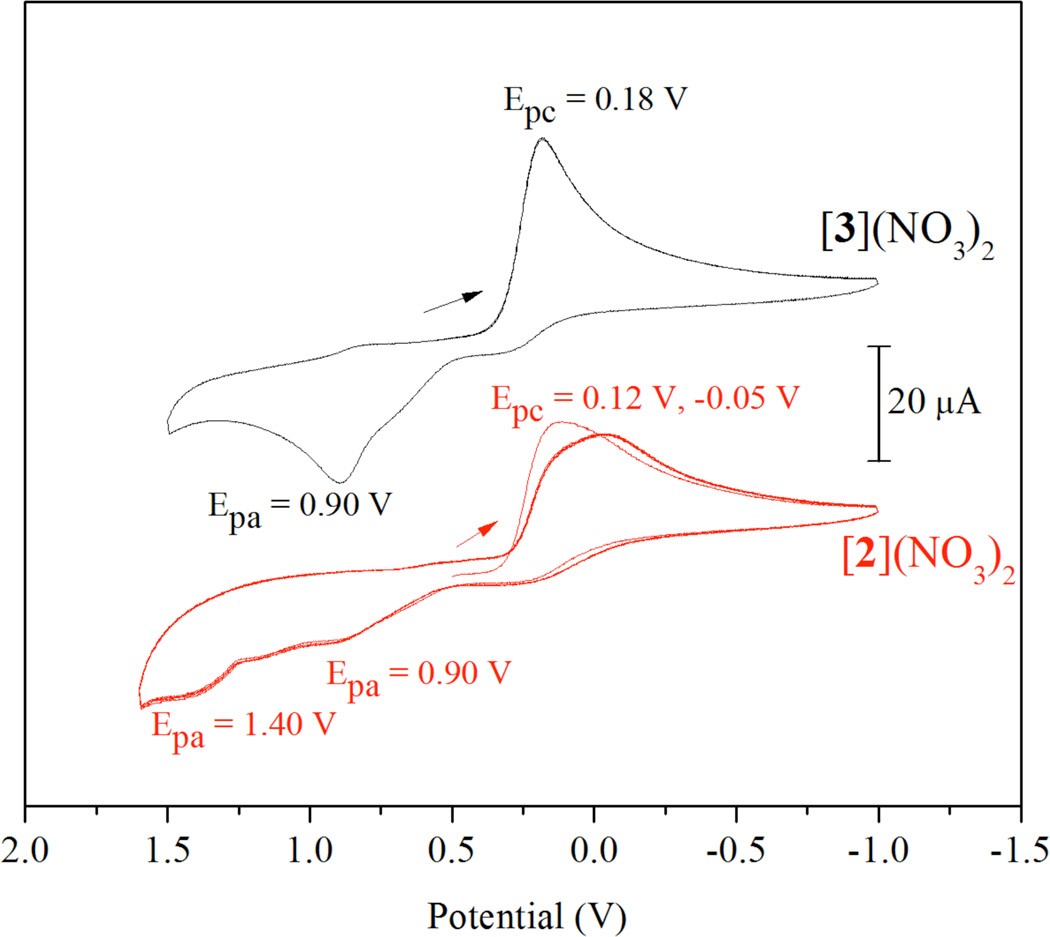
The cyclic voltammogram of [1]²⁺ in DMF with 0.1 M TBAP is shown in Figure S1, SI. An irreversible oxidation is observed at 1.20 V vs Ag/AgCl. The return scan shows a peak at 0.53 V, presumably corresponding to the reduction of the oxidized species obtained on the forward scan. In contrast to the irreversible oxidation observed for [1]²⁺, a number of ligand-bridged dinuclear platinum(II) complexes exhibit reversible oxidations on the CV time scale.^{48,50,94–96} Even at scan rates as low as 10 mV/s and as high as 1000 mV/s and at −20 °C the oxidation of [1]²⁺ remained irreversible.

The cyclic voltammograms of [2]²⁺ and [3]²⁺, obtained under the same conditions, are shown in Figure 6. The initial scan towards negative potential for [2]²⁺ reveals a reduction with a peak potential of 0.12 V. Return scans to positive potentials are marked by weak oxidation features at 0.90 V and 1.40 V. On the second and subsequent cycles, the irreversible reduction peak broadens and shifts slightly negative, to −0.05 V. At −20 °C and at both fast (1000 mV/s) and slow (10 mV/s) scan rates, no reversibility is observed. The initial reduction peak potential of [3]²⁺ is 0.18 V. This peak does not shift after the first cycle or subsequent cycles. The return scan shows an irreversible peak at 0.90 V that is much more pronounced than those observed for [2]²⁺. As with [1]²⁺ and [2]²⁺, no reversibility was observed at −20 °C at different scan rates. It is somewhat surprising that the reduction peak potentials of [2]²⁺ and [3]²⁺ are so similar. The axial halide ligands appear to have little influence on this peak potential. This observation is in contrast to a previous electrochemical study on lantern-type pyrimidine-thiolate bridged platinum(III) dimers, in which complexes bearing axial bromide ligands were reduced at potentials that were 100 mV more positive than analogous complexes with axial chloride ligands.⁹⁷ Also strange is the fact that the return oxidation features are different. Intuitively, it is expected that the reduction products of [2]²⁺ and [3]²⁺ might be [1]²⁺. Because the return oxidation does not occur at 1.20 V, as observed in the CV of [1]²⁺, it appears that different reduction products are being formed for [2]²⁺ and [3]²⁺.

Figure 6.

Cyclic voltammograms of of [2](NO₃)₂ (bottom in red) and [3](NO₃)₂ (top in black) in DMF with 0.1 M (Bu₄N)(PF₆) obtained at a scan rate of 100 mV/s. The arrows mark the initial potential and scan direction. Potentials are referenced to Ag/AgCl.

To test this hypothesis, we reduced [2]²⁺ and [3]²⁺ chemically and followed the reactions by ¹H NMR spectroscopy. Reduction with Zn powder produced the platinum(II) dimer [1]²⁺ as the major product (Figures S2 and S3, SI). In contrast, the use of SnCl₂·2H₂O as the reducing agent resulted in the release of the NH₃ ligands as ammonium ions, as evidenced by the presence of a sharp 1:1:1 triplet centered at 7.68 ppm (Figure S4 and S5, SI). These results demonstrate that the reduction products of [2]²⁺ and [3]²⁺ depend on the nature of the reducing agent and suggest that the electrochemical reduction within the diffusion layer of the electrode could reduce [2]²⁺ and [3]²⁺ to species other than [1]²⁺.

DFT Calculations

The geometries of [1]²⁺–[3]²⁺ were optimized in the gas phase using the hybrid functional PBE0 and the 6–311+G(d,p) basis set for atoms other than platinum. The LANL2DZ basis set and effective core potential were used for the platinum atoms. Table 4 compares structural features of the calculated and experimentally determined geometries. At this level of theory, the Pt–Pt interactions are poorly modeled. This shortcoming is manifested in computed Pt–Pt distances and tilt angles that are significantly greater than the experimental ones. For the platinum(III) species, the Pt–Pt separation is overestimated by 0.10–0.14 Å, whereas for [1]²⁺ this distance exceeds experimental values by 0.64 Å. The larger discrepancy between the computed and experimental Pt–Pt distance for Pt(II) is consistent with a recent observation that standard hybrid DFT functionals have difficulty in modeling weak d⁸–d⁸ interactions between Pt(II) centers.⁹⁸ Otherwise, the computed platinum-ligand distances agree well with experimental values. Notably, the trans influence of the metal-metal bond in [2]²⁺ and [3]²⁺ is recapitulated, as revealed by the long computed platinum-halide distances.

Table 4.

Comparison of Selected Structural Features of [1]²⁺–[3]²⁺ Determined Experimentally by X-ray Diffraction and Calculated by DFT^a

	[1]2+exp	[1]2+calc	[1](NO3)+calc	[2]2+exp	[2]2+calc	[2](NO3)+calc	[3]2+exp	[3]2+calc	[3](NO3)+calc
Pt–Pt	2.921	3.561	3.138	2.600	2.705	2.660	2.603	2.743	2.686
Pt–X				2.427	2.444	2.445	2.552	2.587	2.584
Pt–Oacetate	2.046	2.035	2.052	2.031	2.032	2.048	2.028	2.033	2.050
Pt–Nammine	2.024	2.056	2.045	2.024	2.070	2.042	2.022	2.070	2.044
τb	31.9	70.11	42.5	19.3	32.8	23.7	19.0	33.2	24.0
ωc	5.5	0.1	1.9	1.4	11.8	1.8	3.1	11.8	1.6

^aExperimental values reported are the averages of chemically equivalent distances or angles found in the asymmetric unit of the X-ray structure.

^bTilt angle between adjacent platinum coordination planes in the binuclear unit.

^cAverage twist or torsion angle about the Pt–Pt vector.

Because the crystal structures of [1]²⁺–[3]²⁺ indicate significant hydrogen-bonding between the coordinated ammine ligands and the solvent or counterions, additional geometry optimizations were carried out, at the same level of theory, in which a nitrate counterion was explicitly added as a hydrogen-bond partner for the ammines. Images of the resulting geometries and their coordinates are given in the Supporting Information (Figures S6–S8, SI). The addition of the nitrate counterion leads to optimized geometries in which the Pt–Pt distances are significantly shorter. For [2]²⁺ and [3]²⁺ the Pt–Pt distances in these optimized ion pairs are only overestimated by 0.06 and 0.08 Å, respectively. The Pt–Pt separation in the nitrate adduct of [1]²⁺ exceeds experimental values by 0.22 Å. Although still quite large, this result marks a significant improvement over that computed for the free ion [1]²⁺ (0.64 Å). The presence of the nitrate ion had little effect on the other platinum-ligand bond distances.

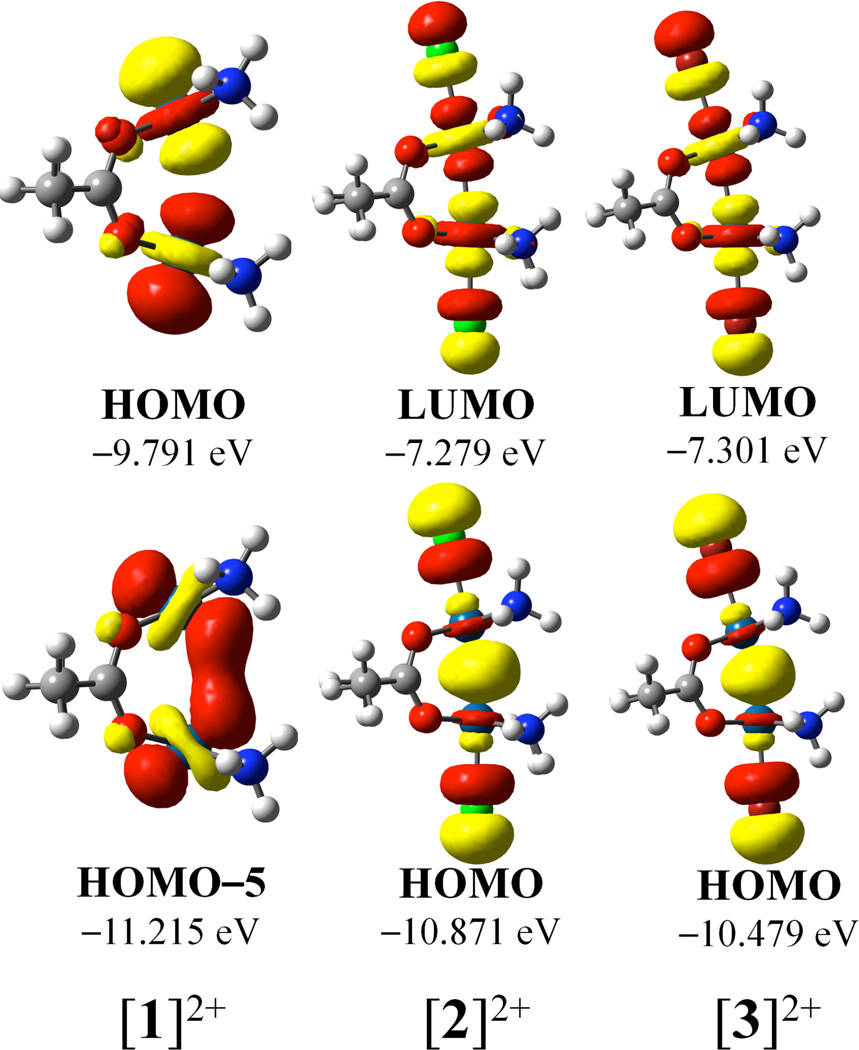
Molecular orbitals relevant to the Pt–Pt bonding interactions of the dimers are shown in Figure 7. The molecular orbitals of the free ions and the nitrate ion pairs of [1]²⁺–[3]²⁺ were qualitatively similar. Because the optimized geometries of the nitrate ion pairs are closer to the experimental ones than to those of the isolated cations, the molecular orbitals of the ion pairs are shown. The HOMO and LUMO of [2]²⁺ and [3]²⁺ are σ and σ* orbitals derived from the symmetric and antisymmetric combination of the d_z² orbitals of the platinum centers. The HOMOs of [2]²⁺ and [3]²⁺ signify the formal Pt–Pt single bond. Furthermore, the HOMOs are antibonding with respect to the axial ligands, thus giving rise to the long Pt–X axial bond lengths. For [1]²⁺, which is reduced by two electrons relative to [2]²⁺ and [3]²⁺, the HOMO is the σ* orbital. Population of this strongly Pt–Pt antibonding molecular orbital in [1]²⁺ is consistent with the large Pt–Pt atomic separation and absence a formal metal-metal bond. The symmetric combination of the d_z² orbitals is found lower in energy as the HOMO-5.

Figure 7.

Relevant frontier molecular orbitals of [1]²⁺–[3]²⁺, optimized as the ion pair with a single nitrate counterion. The nitrate ions included in the calculation are omitted for clarity. Isovalues are drawn at 0.04.

DFT calculations were further employed to understand the NMR spectral properties of [1]²⁺–[3]²⁺. Nitrogen-14 NMR chemical shifts and EFG parameters of the nitrogen-14 nuclei were computed for the optimized geometries of the nitrate ion pair and are collected in Table 5. The computed ¹⁴N NMR chemical shifts of the associated nitrate counterions range from 357.0 to 360.0 ppm, in excellent agreement with the experimentally measured chemical shift of 355 ppm. Calculated values for the coordinated ammine ligands are approximately 50 ppm farther downfield from experimentally measured values. Given that the known window for nitrogen-14 NMR chemical shifts in diamagnetic compounds spans a region of 1100 ppm,⁸⁸ this seemingly large 50 ppm deviation represents only a 4.5% absolute error. Importantly, the calculation successfully predicts the downfield shift of the ¹⁴N resonance observed upon the oxidation of [1]²⁺ to [2]²⁺ or [3]²⁺.

Table 5.

DFT Computed Isotropic ¹⁴N NMR Chemical Shifts and EFG Parameters for the Coordinated Ammine Ligands^a

	14N δcalc, ppm	NQCC, MHz	η	$\left(1+\frac{{\eta }^2}{3}\right)•{\left(\text{NQCC}\right)}^2$
[1](NO3)+	−29.8	−0.858	0.450	1.05
[2](NO3)+	−17.2	−0.400	0.493	0.173
[3](NO3)+	−19.0	−0.394	0.585	0.173

^aThe reported values are averages of those calculated for the four distinct ammine ligands.

The quadrupolar relaxation rate of a ¹⁴N nucleus determines its observed spectral line-width (W_1/2). The line-width is, therefore, proportional to η, the asymmetry of the EFG at the nucleus, the nuclear quadrupole coupling constant (NQCC), a measure of the magnitude of the EFG at the nucleus, and τ_q, the correlation of the molecule in solution, according to eq 1. The EFG parameters, η, and the NQCC can be readily calculated with DFT methods. The values computed for the ¹⁴N atoms of the

$$W_{1/2}\propto (1+\frac{{\eta }^2}{3})•{(\text{NQCC})}^2•{\tau }_{\mathrm{q}}$$ (1)

coordinated ammine ligands are listed in Table 5. The asymmetry at the EFG (η) of ammine ligands is similar for all three complexes. The NQCC of [1](NO₃)⁺, however, is more than twice as large as the corresponding values for [2](NO₃)⁺ and [3](NO₃)⁺, and therefore the more important contributor to the large observed W_1/2 of [1]²⁺. If the correlation times are assumed to be equal for the three complexes, the ratio of ¹⁴N NMR line-widths can be calculated from eq. 1, using the computed values for η and the NQCC. This calculation predicts that, for the platinum(III) complexes, the line widths are equal, whereas the same signal for platinum(II) complex is broader by a factor of six. This value is in perfect agreement with experimental observations; the W_1/2 value for [1]²⁺ (≈ 300 Hz) is close to six times greater than those of [2]²⁺ or [3]²⁺, which are 50 and 45 Hz, respectively.

Synthesis and Characterization of the Tetranuclear Complex [4](NO₃)₄

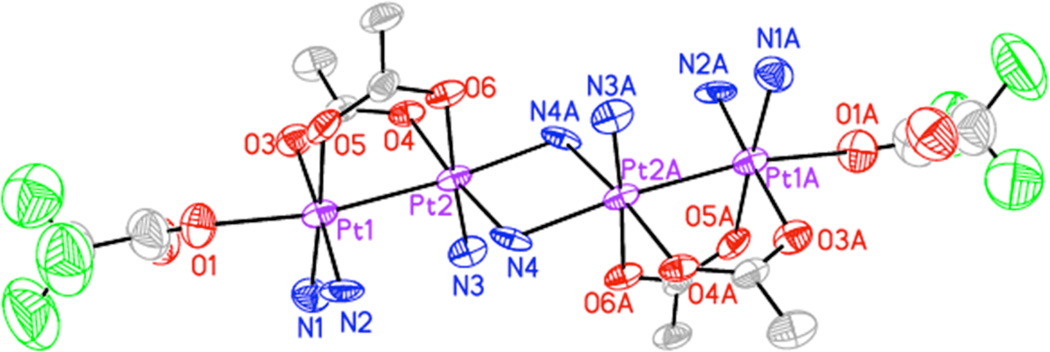
Treatment of [1](NO₃)₂ in DMF with a slight excess of the hypervalent iodine reagent PhI(O₂CCF₃)₂, followed by crystallization via vapor diffusion of Et₂O, afforded an apparently homogeneous crop of yellow-orange crystalline material. Analysis by X-ray diffraction revealed the compound to be the amido-bridged tetranuclear platinum compound [4](NO₃)₄, illustrated in Figure 8 and Scheme 3, the interatomic distances and angles of which are summarized in Table 6.

Figure 8.

X-ray crystal structure of [4]⁴⁺. Ellipsoids are drawn at the 50% probability levels. Unlabelled grey and green ellipsoids correspond to carbon and fluorine atoms, respectively. Hydrogen atoms and the minor component of disorder in the trifluoroacetate group have been omitted for clarity.

Scheme 3.

Table 6.

Selected Structural Features of [4]^{2+ a}

Pt1–Pt2	2.5561(7)	Pt1–O5	2.021(8)	Pt2–O4	2.057(7)	Pt2–N4	2.002(9)	τb	18.1
Pt1–O1	2.210(9)	Pt1–N1	2.011(10)	Pt2–O6	2.037(7)	Pt2–N4A	2.136(10)	ωc	1.5
Pt1–O3	2.043(8)	Pt1–N2	2.006(9)	Pt2–N3	2.028(9)	Pt2–Pt2A	3.1470(10)

^aAtoms are labeled as indicated in Figure 8. Numbers in parentheses are estimated standard deviations in the last significant figures. Interatomic distances are reported in Å.

^bτ, the tilt angle in degrees between the coordination planes of Pt1 and Pt2.

^cω, the average torsion angle in degrees about the Pt1–Pt2 vector.

Two acetate-bridged diplatinum(III) units are connected by two bridging amido ligands to form the observed tetranuclear complex. A crystallographic inversion center relates the amido-bridged dimers. The amido groups could alternatively be assigned as hydroxo ions because the X-ray scattering power of nitrogen and oxygen are similar. Reasonable and similar thermal displacement parameters were obtained from isotropic refinements using either assignment, with insignificant changes in refinement statistics or geometry as shown in Table S7, SI. We therefore studied the crystal packing to make the assignment. Both H atoms of the proposed bridging amido ligands act as hydrogen bond donors to a nitrate counterion and a DMF molecule in the crystal lattice (Table S8, SI) A hydroxide bridge would hydrogen bond as a donor on one side and an acceptor on the other. Therefore our assignment of the bridging atoms as amido groups is most likely correct. The coordination sphere of the inner two platinum centers (Pt2 and Pt2A) is derived from two oxygen atoms of bridging acetate ligands in equatorial positions, a nitrogen atom from an ammine ligand in an equatorial position, and two amido ligands, one in an equatorial position and one in the axial position. The bridging amido ligand that is coordinated in the axial position is significantly elongated relative to that in the equatorial position [2.002(9) versus 2.136(10) Å]. This elongation of the axial ligand is due to the strong trans influence of the Pt–Pt bond [Pt1–Pt2, 2.5561(7) Å]. The outer two platinum atoms are coordinated to trifluoroacetate ligands in the axial position. The Pt–O bond is 2.210(9) Å. This value is significantly longer than those typically observed Pt–TFA bonds in Pt(II) and Pt(IV) compounds, ~ 2.0 Å.^99–101 The significant elongation of this bond may be due to the additive trans influence^102,103 of the metal-metal bond and the amido ligand. Longer Pt–TFA bonds of around 2.3 Å have been observed in multinuclear complexes with strong thallium–platinum bonds.¹⁰⁴ The [4]⁴⁺ structure is analogous to those of the α-pyrrolidonate/amido-bridged tetranuclear platinum(III) complex, HH-[(NO₃)(NH₃)₂-Pt^III(C₄H₆NO)₂Pt^III(NH₃)(µ-NH₂)]₂(NO₃)₄.¹⁰⁵ The difference between this complex and [4]⁴⁺ is the presence of acetate rather than α-pyrrolidonate as bridging ligands and trifluoroacetate instead of nitrate axial ligands for the outer platinum atoms. In a subsequently described analog the α-pyrrolidonate ligands are oriented in a head-to-tail fashion.⁵⁴ The central bridging ligands were assigned as hydroxo rather than amido.⁵⁴ Analysis of the CIF file deposited in the CSD of the head-to-tail structure indicates that the bridging ligand donates two hydrogen bonds with nitrate counterions, suggesting that these ligands are incorrectly assigned as hydroxo rather than amido.

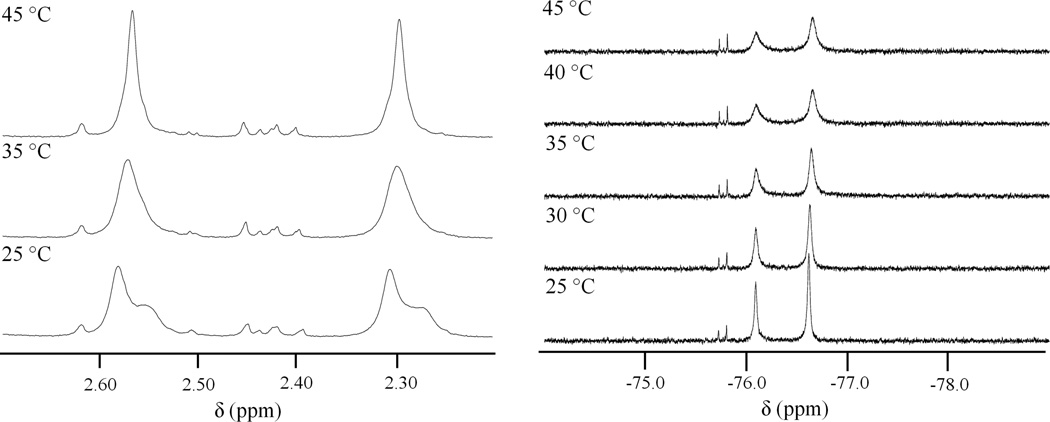
The ¹H and ¹⁹F NMR spectra of [4]⁴⁺ indicate complex solution behavior. Broad ill-defined peaks occur between 5.5 and 7.5 ppm in the ¹H NMR spectrum of [4]⁴⁺ in DMF-d₇ at 25 °C (Figure S9, SI). These features most likely correspond to protons from the ammine and bridging amido ligands. The proton chemical shifts of µ-NH₂ ligands in platinum(II) complexes range from −1 to 3 ppm depending on the solvent and nature of the peripheral ligands.^106–109 In platinum(IV) complexes, the protons of these groups resonate farther downfield, between 4.5 and 5.5 ppm.^110,111 Based on the chemical shifts observed for the µ-NH₂ ligands in [4]⁴⁺, it appears that the metal-metal bonded diplatinum(III) centers produce deshielding similar that in the more electron-deficient platinum(IV) centers. The CH₃ resonances of the two inequivalent bridging acetate ligands appear at 2.58 and 2.30 ppm. Notably, these peaks display shoulders at 2.54 and 2.27 ppm. Also present in the CH₃ region are several small peaks between 2.45 and 2.30 ppm that integrate to one tenth of the area of those of the major CH₃ resonances. The minor peaks are present consistently in solutions of crystalline material obtained from different syntheses. The ¹⁹F NMR spectrum of [4]⁴⁺ at 25 °C similarly displays two major peaks, at −76.09 and −76.62 ppm, and two minor ones at −75.72 and −75.80 ppm. The two major peaks integrate to a ratio of 1 to 1.4, whereas the minor peaks integrate to ratios of 0.04 and 0.06, respectively. At 45 °C, the two major CH₃ resonances coalesce into sharp singlets, losing the shoulders observed at room temperature (Figure 9). The NH region of the ¹H NMR spectrum also displays subtle changes at higher temperatures (Figure S10, SI). The major peaks in the ¹⁹F NMR spectrum at 45 °C are significantly broadened (Figure 10), suggesting interconversion between two species. Upon returning the temperature to 25 °C, the peaks in the ¹H NMR spectrum display shoulders again and the peaks in the ¹⁹F NMR spectrum return as sharp singlets, indicating the process to be reversible. At temperatures greater than 65 °C, the two ¹⁹F peaks coalesce completely (Figure S11, SI). At these higher temperatures there is significant decomposition of the starting material, however, as evidenced by a number of new species in the ¹H NMR spectrum upon returning to 25 °C.

Figure 9.

Variable-temperature ¹H (left) and ¹⁹F (right) NMR spectra of [4]⁴⁺ in DMF-d₇.

Figure 10.

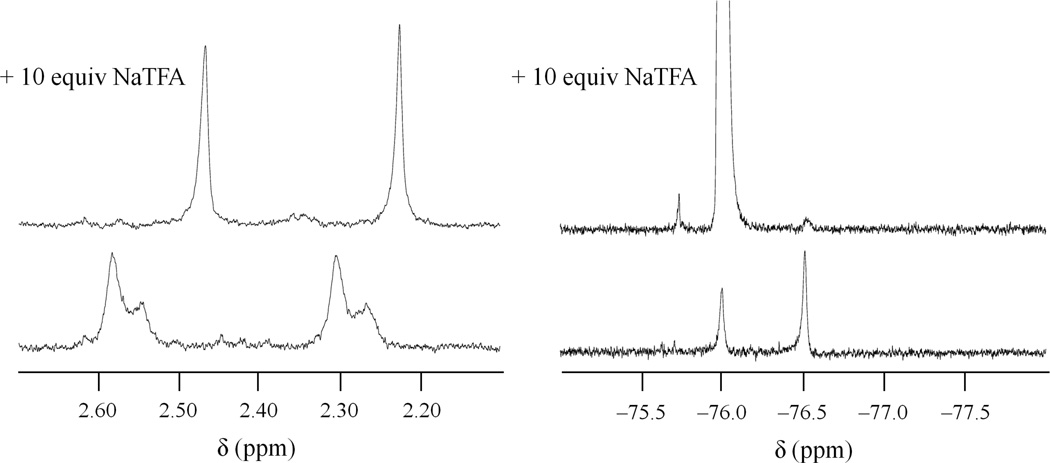
¹H (left) and ¹⁹F (right) NMR spectra of [4]⁴⁺ before (bottom) and after (top) the addition of 10 equiv NaTFA in DMF-d₇.

The ¹⁹F NMR signal of NaTFA appears at −76.00 ppm in DMF-d₇. Therefore, the peak observed at −76.09 ppm might arise from the TFA ion in solution. The addition of 10 equiv of NaTFA to solution of [4]⁴⁺ results in coalescence and a slight upfield shift of the CH₃ signals in the ¹H spectra, and the corresponding ¹⁹F NMR spectra displays a change in the intensities of the peaks (Figure 10). The peak near −76 ppm increases dramatically due to the presence of excess TFA ion, and the minor peak −75.80 ppm increases as well. These data suggest that the axial TFA ligands are labile and that solution the complex exists as a mixture of different species bearing different axial ligands. Because the addition of 40 equiv of NaNO₃ produces no significant changes in either the ¹H or ¹⁹F NMR spectra (Figure S12, SI), it is most likely DMF that competes with TFA for axial coordination to the tetranuclear platinum ion.

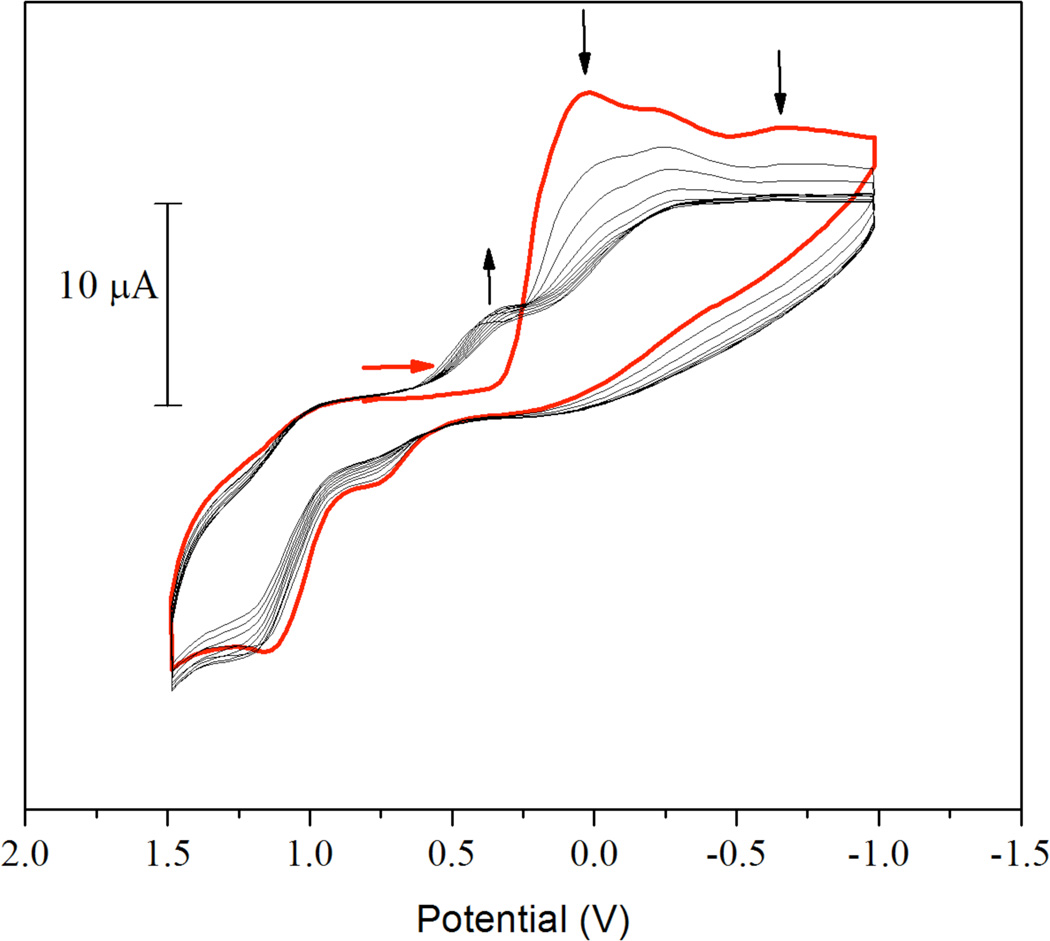
The electrochemistry of [4](NO₃)₄ in DMF was investigated by cyclic voltammetry at a glassy carbon working electrode with 0.1 M (Bu₄N)(PF₆) as supporting electrolyte. Cyclic voltammograms of [4](NO₃)₄ are highly dependent on the polishing state of the electrode. With thorough polishing between scans, fairly reproducible voltammograms were obtained, as shown in Figure 11. The voltammogram evolved over the course of multiple scan cycles, however, as indicated by the arrows of Figure 11. The initial scan shows an irreversible reduction comprising several broad peaks that occur at an onset potential of near 0.4 V and a peak potential of approximately 30 mV. The presence of what appear to be multiple peaks may reflect the presence of multiple species of [4]⁴⁺ in solution or sequential reduction of individual platinum centers. After the initial reduction of [4]⁴⁺, an irreversible oxidation feature appears near 1.2 V. Subsequent cycles lead to the growth of a reduction feature near 0.5 V and decay of the initial reduction feature at 30 mV. The oxidation feature at 1.2 V and the reduction at 0.5 V are consistent with those of the platinum(II) dimer [1]²⁺ and suggest that [1]²⁺ an electrochemical reduction product of [4]⁴⁺. The consistent decrease in peak current upon multiple cycles and the need for stringent electrode polishing between experiments indicates that other reduction products may be adsorbed to or deposited on the electrode surface.

Figure 11.

Cyclic voltammogram of [4](NO₃)₄ in DMF with 0.1 M (Bu₄N)(PF₆) as supporting electrolyte. The potential is reported relative to Ag/AgCl and the voltammogram was obtained at a scan rate of 100 mV/s. The red arrow indicates the starting potential and initial scan direction. The bold red trace is the first scan cycle. Following scans are in black. Changes in current as the potential is cycled are indicated by black arrows.

Summary and Conclusions

The oxidative reactivity of the acetate-bridged cis-diammineplatinum(II) complex [1]²⁺ has been explored. Treatment of [1](NO₃)₂ with halogen-based oxidants affords the first discrete diacetate-bridged cis-diammineplatinum(III) complexes, [2](NO₃)₂ and [3](NO₃)₂. Complexes [1]²⁺–[3]²⁺ were fully characterized by multinuclear NMR spectroscopy, X-ray crystallography, electrochemical methods, and DFT calculations. A novel tetranuclear amido-bridged platinum(III) species, [4]⁴⁺, was also characterized structurally by X-ray crystallography and in solution by NMR spectroscopy. The complexes represent new additions to the growing family of dinuclear platinum(III) complexes derived from cisplatin.