Power of Automated Algorithms for Combining Time Line Follow Back and Urine Drug Screening Test Results in Stimulant-Abuse Clinical Trials

Abstract

Background

In clinical trials of treatment for stimulant abuse, researchers commonly record both Time-Line Follow-Back (TLFB) self reports and urine drug screen (UDS) results.

Objectives

Compare the power of self report, qualitative (use vs. no-use) UDS assessment, and various algorithms to generate self-report-UDS composite measures to detect treatment differences via t-test in simulated clinical trial data.

Methods

We performed Monte Carlo simulations patterned in part on real data to model self-report reliability, UDS errors, dropout, informatively missing UDS reports, incomplete adherence to a urine donation schedule, temporal correlation of drug use, number of days in the study period, number of patients per arm, and distribution of drug-use probabilities. Investigated algorithms include Maximum Likelihood and Bayesian estimates, self-report alone, UDS alone, and several simple modifications of self-report (referred to here as ELCON algorithms) which eliminate perceived contradictions between it and UDS.

Results

Among algorithms investigated, simple ELCON algorithms gave rise to the most powerful t-tests to detect mean group differences in stimulant drug use.

Conclusions

Further investigation is needed to determine if simple, naïve procedures such as the ELCON algorithms are optimal for comparing clinical study treatment arms. But researchers who currently require an automated algorithm in scenarios similar to those simulated for combining TLFB and UDS to test group differences in stimulant use should consider one of the ELCON algorithms.

Scientific Significance

This analysis continues a line of inquiry which could determine how best to measure outpatient stimulant use in clinical trials ^1,2,3.

Introduction

Time Line Follow Back (TLFB) ^4,5 is an instrument for obtaining participant self-reports using specially trained interviewers. TLFB uses various interviewing techniques, including anchoring, in which the participant’s recall of important days such as birthdays is used to help recall drug use. The participant may or may not be asked to keep a daily substance use diary to aid recall. In this paper, we focus on TLFB as applied to clinical trials for stimulant use.

With urine drug screens (UDS), recent substance use is assessed by measuring the concentration of either the substance or one of its metabolites in periodically submitted urine samples. For example, recent cocaine use is commonly assessed by measuring the concentration of the cocaine metabolite, benzoylecgonine (BE) in submitted urine samples. UDS values may be assessed quantitatively or as qualitative yes /no indicators of recent substance use. This paper explores only qualitative UDS assessments¹.

One way to use UDS values and TLFB in tandem is to notify participants when their self-report conflicts with UDS assessment, allowing them to amend their self report. While potentially improving the accuracy of self reports, this practice could sour the rapport between participant and interviewer. Damaged rapport might adversely affect accuracy of the self-report, or even cause the participant to drop out of the study. Too, this notification algorithm loses information concerning conflicts between UDS and self reports that could indicate participant reliability². Also, introducing notification into TLFB requires interviewers to manually interpret UDS results on short notice, which can be error-fraught.

In practice, TLFB and UDS are often collected independently and later combined in various manners into a single composite measure, although sometimes they are also used separately. This paper statistically investigates various algorithms for composite indices in the context of a simulated clinical trial to test differences between two arms in stimulant drug use. We statistically investigate the use of UDS alone, the use of TLFB self reports alone, and the use of various algorithms that combine UDS and self reports into a single use index.

Methods

The basic approach is: (1) Simulate many realistic replicates of data sets from stimulant drug trials, where each data set is composed of time series depicting drug use, self-report, and urine drug screens from each of the many participants in the two arms of the trial; (2) For each participant in a data set, apply each algorithm to generate from the self-report and UDS time series a set of drug-use indexes, one for each algorithm; (3) For each algorithm, in each data set, apply Student’s t test to the indexes to test the difference between the participants in the two arms with respect to the number of days of use. Thus, each data set generates one t-test for each algorithm; and (4) Identify which algorithms most often give rise to significant (p < 0.05) t-tests when there is in fact a treatment effect.

The data sets simulate drug use, self-report, and UDS using parameters derived from two 12-week real trials ^10,11 in which cocaine was tracked using TLFB and BE in urine.

Basic Simulation Model

For each day being tracked, a participant randomly and independently chooses to either use or not use a given substance. Later, the participant randomly reports having used or not used on that day. A participant’s daily choices of use or abstinence and subsequent self report occur with the following probabilities:

• p is the probability that the participant will use on any particular day

• L is the probability that the participant will report no use for a particular day, given that he or she actually did use on that day

• M is the probability that the participant will report use for a particular day, given that he or she actually did not use on that day

Urine samples are periodically collected. In the basic simulation model, we assume the qualitative UDS value from a given urine sample is an error-free indicator of substance use during a specific window immediately before the sample is taken. If substance use did not occur on any of the days in the window, the UDS will be negative, and if substance use occurred on one or more of those days, the UDS will be positive.

Modifications of basic simulation model

To generate more realistic data, we modified the basic simulation model in several ways:

1. In some scenarios, we made the participant’s decision to use drugs on a particular day dependent on whether he or she used drugs the previous day. Here, we generated drug use-decisions with a Markov chain such that the probability of drug use on a randomly-selected day was controlled at p, but the correlation between drug use on adjacent days was 0.5 instead of 0. For these “high correlation” scenarios, the participant’s drug use and non-use occur in runs that are on average twice as long as in the “no correlation” scenarios.

2. It seemed unrealistic to suppose that all participants in, say, the low-drug use arm have exactly the same probability of drug use. Rather, some participants in a given arm might be heavy drug users relative to others in that arm, who would be relatively light drug users. So, rather than making p be constant in an arm, we independently drew for each participant the drug use probability p from a distribution. The mean and variance of the distribution differed between arms as detailed in the footnote to Table 3. We used two different types of distribution: the Beta distribution and the “spike” distribution. In the latter, real-world data suggest a proportion of participants had drug use probabilities of 1, while the remainder had drug use probabilities uniformly distributed on (0,1).

3. All scenarios had dropout, and some also had informatively missing urine collection data,^12,13,14 in which participants were more likely to skip urine donation if they had just used drug. Some urine collection schedules were regular, while others were irregular, based on real data.

4. The Basic Simulation Model assumes that a UDS is an infallible indicator of what happened during a preceding 3-day time window, and other algorithms also use this time window (Table 1 and “Automated Algorithms for Combining TLFB and UDS” below). We felt that it would be unrealistic to present these algorithms with simulated data that actually obeyed this constraint. BE concentration in urine is roughly an exponentially declining function of time since dose, with values of the rate constants having means and variances fitted from a sample of 10 individuals in reference (7). This means that the most important determinant of urine concentration is time since last use. The variances are presumably due to differences among patients, and to measurement error, which we assume is small. The means and variances, considered in conjunction with the concentration expression in reference (7) and using a normal assumption, translate into a probability that a given dose, when tested T time-units later, will result in a positive UDS. We used these probabilities in our simulation to determine whether a particular UDS was to be positive, based on the number of days since last use. Our estimates of the probabilities of positivity for days 1-9 previous to the urine sample are (1.0, 0.91, 0.73, 0.55, 0.39, 0.22, 0.07, 0.01, 0.0).

Table 3.

Simulated power of algorithms for NPAT participants per arm when NPAT is chosen so power of TRUTH is approximately 0.9, D = 30, and NumUDS = 3. For meanings of parameters, see footnote of table. Highlighted cells denote algorithms that are among the best attainable.

Dist	E1	E2	S	L	Corr	info	npat	Truth	Ideal	Elcon	UDS	Self	MLE	Bayes	Elcon2
beta	0.46	0.38	0.01	0.3	0	0	35	.91	.74	.63	.31	.64	.32	.41	.65
						0.5	35	.91	.69	.62	.27	.63	.28	.40	.64
					0.5	0	86	.90	.83	.78	.60	.77	.58	.70	.80
						0.5	86	.89	.81	.78	.54	.78	.55	.70	.79
				0.5	0	0	35	.91	.64	.44	.31	.43	.32	.37	.49
						0.5	35	.91	.55	.42	.27	.42	.26	.36	.47
					0.5	0	86	.90	.77	.68	.60	.63	.58	.68	.71
						0.5	86	.90	.71	.64	.53	.62	.51	.63	.69
			0.10	0.3	0	0	66	.90	.81	.74	.47	.75	.46	.57	.76
						0.5	66	.90	.79	.74	.43	.75	.42	.57	.76
					0.5	0	117	.91	.85	.82	.69	.81	.65	.75	.83
						0.5	117	.90	.83	.81	.62	.81	.60	.73	.82
				0.5	0	0	66	.91	.75	.60	.47	.58	.47	.56	.64
						0.5	66	.90	.68	.58	.41	.58	.38	.52	.63
					0.5	0	117	.90	.80	.74	.69	.69	.67	.76	.77
						0.5	117	.90	.77	.71	.61	.69	.60	.71	.75
	0.54	0.62	0.01	0.3	0	0	35	.91	.65	.56	.17	.58	.20	.29	.58
						0.5	35	.91	.62	.57	.16	.58	.17	.32	.58
					0.5	0	86	.90	.79	.75	.43	.75	.49	.61	.76
						0.5	86	.90	.77	.74	.40	.74	.47	.60	.75
				0.5	0	0	35	.91	.50	.35	.17	.37	.24	.24	.39
						0.5	35	.91	.43	.35	.16	.36	.19	.26	.38
					0.5	0	86	.90	.68	.59	.43	.59	.47	.58	.62
						0.5	86	.90	.65	.57	.40	.57	.43	.57	.61
			0.10	0.3	0	0	66	.90	.75	.70	.26	.72	.34	.46	.71
						0.5	66	.91	.73	.70	.24	.72	.26	.45	.72
					0.5	0	117	.91	.82	.78	.51	.79	.58	.70	.80
						0.5	117	.91	.81	.79	.49	.79	.51	.67	.80
				0.5	0	0	66	.90	.64	.50	.25	.52	.36	.41	.54
						0.5	66	.90	.57	.49	.23	.52	.30	.40	.53
					0.5	0	117	.90	.74	.65	.51	.64	.56	.64	.68
						0.5	117	.91	.72	.66	.49	.65	.52	.64	.69
spike	0.74	0.58	0.32	0.3	0	0	94	.90	.85	.85	.40	.87	.59	.72	.85
						0.5	94	.90	.86	.86	.47	.87	.58	.76	.86
					0.5	0	94	.89	.84	.83	.58	.85	.74	.78	.83
						0.5	94	.89	.84	.83	.64	.84	.76	.82	.84
				0.5	0	0	94	.91	.79	.78	.41	.81	.64	.63	.79
						0.5	94	.91	.79	.79	.46	.81	.62	.70	.80
					0.5	0	94	.88	.79	.76	.56	.79	.76	.73	.78
						0.5	94	.88	.79	.78	.63	.79	.75	.79	.79

The parameters illustrated in this table have the following meanings:

• DIST: Each participant in each data set draws an observation p from this distribution of probability of drug use. Values are Beta and Spike.
• (E1, E2): Means of p in arms 1 and 2. Beta means of (0.46, 0.38) were suggested by real data. For Beta distribution, values are (0.46, 0.38) or (0.54, 0.62). For Spike distribution, (0.74, 0.48)
• S: Standard deviation of p in both arms. For Beta distribution, values are 0.01 or 0.10. For Spike distribution, 0.32.
• L: Probability of reporting no drug use on a day, given there was drug use on that day. (L,M) = (0.3, 0.05) suggested by real data. Values are 0.3 or 0.5
• M: Probability of reporting drug use on a day, given there was no use on that day. M=0.05
• NumUDS: Number of urine donations per week. Values are 1 (M), 2 (M,Th), or 3 (M,W,F; but see text).
• Corr: Serial correlation in a participant‘s daily decision to use drugs. Values are 0 or 0.5
• D: Number of days in the study period. Values are 30 or 90.
• NPAT: Number of participants per arm. For Figure 1, values are 25, 35, 45, or 55. For Tables 3 and 4, NPAT was chosen to yield power of 0.9 for the Truth algorithm, and is reported in the table.
• INFO: The probability that a given participant skips a urine donation, given the UDS would be positive. Values are 0 or 0.5

Table 1.

Automated Algorithms for Combining TLFB and UDS

Name	Description /Comments	Index of drug use
	Unattainable algorithms
TRUTH	This presumably provides an upper bound on the power one could expect from any attainable algorithm.	Proportion of truly positive days.
IDEAL*	Participant is “notified” inside computer when a self report conflicts with a UDS. Once notified, the simulated participant tells the truth about all the drug use days within the UDS window. These true values are used to correct the self-report.	Proportion of positive days in corrected self-report.
	Attainable algorithms
SELF	Ignores UDS	Proportion of positive days in self report.
UDS	Ignores self-report	Proportion of positive UDS reports
ELCON	Starting from the beginning of the study period and proceeding to the end, the self-report is compared to the UDS. If a window** is found in which the UDS is positive and all self-reports are negative, the self-report for the last day in the window is modified from negative to positive, in an attempt to eliminate perceived contradiction between self-report and UDS. If any self-reports in a window are positive, or if the corresponding UDS is negative, the self-reports are left unchanged.	Proportion of positive days in modified self-report.
ELCON2	As in ELCON, but in addition also modifying positive self reports from positive to negative when they are contained in the window of a negative UDS.	Proportion of positive days in modified self-report.
MLE	Maximum likelihood estimate of p obtained under model explained in the section “Basic TLFB model”. In this algorithm, estimates are obtained for the triplet (p, L, M) [or equivalently (p, PPV, NPV***)], but the estimates for L and M are ignored. The derivation of this approach is available at the URL XXXXXXXXXXX.	Maximum likelihood estimate of probability of drug use p.
BAYES	Uses same likelihood function as MLE, and imposes a uniform prior distribution on NPV*, and a Beta prior with mean close to 1 on PPV, as suggested by real data. The derivation of this approach is available at the URL XXXXXXXXXXX.	Mean of posterior distribution of probability of drug use p.

^*IDEAL is a less powerful than TRUTH, mostly because self-reports can be inaccurate and still fail to contradict a UDS, thus not lead to a notification. IDEAL presumably is at least as accurate as similar real-world methods that incorporate UDS-based notification of the participant.

^**All other things being equal, the probability that a UDS is positive is roughly an exponentially descending function of the time since last dose (3), so that a positive UDS suggests recent use, as opposed to use in the remote past. The window very roughly approximates this elementary notion. The trailing edge of the window is day -1 because urines are presumably mostly donated during the day, so only a part of day 0 is available for use to occur in.

^***PPV = positive predictive value, the probability that, on a particular day, the participant truly used, given that the self-report was positive. NPV = negative predictive value, the probability that, on a particular day, the participant truly did not use, given that the self-report was negative. PPV and NPV are completely determined by (p,L,M).

Simulation scenarios

We generated the simulation scenarios by choosing values for the simulation parameters indicated in the footnote to Table 3. When there were 3 urine donations per week, the donations were intended for Monday, Wednesday, and Friday, but not all participants adhered to this schedule every week. Instead, we used a distribution of visits observed in real data, in which the most common visit schedule (37%) was MWF, but other somewhat different schedules were also present.

Data from one of us suggest that about 83% of participants in a cohort provide about 12 weeks of study data, while the remainder have days of last contact uniformly distributed between 1 and 84. Roughly speaking, we used this dropout distribution for our simulations of 90-day study periods. For simulations of 30-day periods, we assumed that those 30 days were the last of an 84-day period. This implies that about 92% of those entering the 30-day period finish, with the remainder having dropout days uniformly distributed over the 30-day period.

Automated algorithms for combining TLFB and UDS

We investigated the power of the t-test when drug-use indexes were generated for each participant by each of the algorithms shown in Table 1. Algorithms are either attainable or unattainable. An unattainable algorithm is one that requires knowledge of true drug use, hence cannot be performed in real life. Unattainable algorithms can serve only as benchmarks against which to measure attainable algorithms. Several attainable algorithms (ELCON, ELCON2, MLE, BAYES) use the concept of a “UDS Window” (see Table 1) For each urine donation, counting the day of donation as day 0, the UDS window assumed by the algorithm extends from day -3 to day -1. For example, if urine was donated on Friday (0), the window extends from the previous Tuesday (-3) to the previous Thursday (-1).

Results

Figure 1 shows the power of the t-test when the p-value distributions in the two arms are Beta with means of 0.46 and 0.38, respectively, and standard deviation of 0.01, and there is no correlation between adjacent days in the decision to use drugs. Urine donations are intended for MWF, L = 0.30, and M = 0.05. Power is shown here for all tested algorithms when the sample sizes are 25, 35, 45, and 55 participants per arm and the study period is 30 days. UDS data are uninformatively missing. Except for MLE and BAYES, the power estimates are based on 10,000 iterations. For MLE and BAYES, which are much more computer-intensive than the other algorithms, the power estimates are based on 1,000 iterations.

Figure 1.

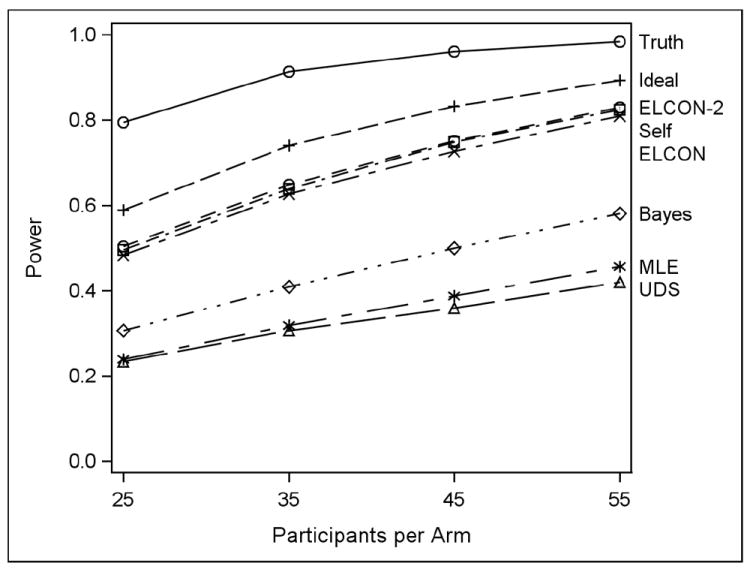
Simulated power of 9 algorithms used in conjunction with t-test when the drug useprobabilities in each arm have beta distributions with expected value (0.46, 0.38) and standard deviation 0.01, drug-use decisions on adjacent days are independent, L = 0.3, M = 0.05, there are 30 days in the study period, urine donations are intended for MWF, UDS data are uninformatively missing, and sample sizes are 25, 35, 45, or 55 participants per arm.

It is expected for the non-attainable algorithms TRUTH and IDEAL to have the best power. In this scenario, the ELCON, ELCON2, and SELF algorithms appear the best attainable choices. Recall that ELCON algorithms eliminate contradiction between self-report and UDS, while SELF ignores UDS. The other algorithms are worse. Note that there is very little crossing-over of power curves in Figure 1. This is true of the other scenarios as well.

Table 2 shows for each algorithm the simulated probability that the nominal p-value is less than 0.05 when the null hypothesis of equality between arms is true. Shown are two scenarios, both with uncorrelated data over 90 days: one with (distribution, expected value, std, sample size) = (Beta, 0.46, 0.01, 55) in both arms and with (Spike, 0.74, 0.32, 90). Test size is appropriate for both distributions.

Table 2.

Simulated Test Size at alpha = 0.05 for scenarios described in text

	Distribution
Algorithm	Beta	Spike
TRUTH	.048	.051
IDEAL	.048	.050
ELCON	.048	.048
UDS	.040	.049
SELF	.047	.048
MLE	.055	.050
BAYES	.054	.051
ELCON2	.047	.050

Table 3 displays power (i.e. the simulated probability that the nominal p-value is significant when the null hypothesis is false) at alpha = 0.05 when the length of the study period is 30 days and there are 3 UDS per week. Here, we control the number of participants per arm NPAT so the power of TRUTH is about 0.9, and show the simulated power of the other algorithms for the same sample size. In each row, the most powerful attainable algorithm is highlighted, as well as all other algorithms that are “among the best”, i.e. having power within 5 percentage points of the most powerful algorithm. Recall that TRUTH and IDEAL are not attainable. For example, in the first row, the best attainable algorithm is ELCON2, with a power of 0.65. ELCON and SELF have power within 5 percentage points of 0.65, so they are also highlighted.

Like Figure 1, Table 3 suggests that the two ELCON algorithms are preferable to the others. SELF is also often among the best, except for beta cases in which the lying rate (L) is comparatively high and the drug-use rates (E1, E2) are comparatively low. Tables for 90-day study periods, and for 1 and 2 UDS per week, are available at the URL XXXXXXXX, but not shown here. Instead, we summarize them in Table 4, where there is an icon for every attainable algorithm and every scenario. The icon is an array with 3 rows and 2 columns. The columns stand for study periods of (30, 90) days, and the rows stand for (1,2,3) UDS per week. Cell (i, j) in the icon is blacked in for a particular algorithm under a particular scenario when that algorithm is among the best for that scenario when there are i UDS per week and the study period is j days long. For example, in the first row of Table 4, cell (3,1) is blacked in for algorithms ELCON, ELCON2, and SELF because those algorithms are the only ones highlighted in row 1 of Table 3. Note that Table 3 compares algorithms within a scenario, but is not ideal to show power of a single algorithm across multiple scenarios (for which see detailed tables at URL XXXXXXXX).

Table 4.

Icons summarizing attainable-algorithm power results for D = (30,90) and NumUDS = (1,2,3). For meanings of parameters, see footnote to Table 3. For explanation of graphical icons, see text.

Dist	E1	E2	S	L	Corr	info	Elcon	UDS	Self	MLE	Bayes	Elcon2
beta	0.46	0.38	0.01	0.3	0	0
						0.5
					0.5	0
						0.5
				0.5	0	0
						0.5
					0.5	0
						0.5
			0.10	0.3	0	0
						0.5
					0.5	0
						0.5
				0.5	0	0
						0.5
					0.5	0
						0.5
	0.54	0.62	0.01	0.3	0	0
						0.5
					0.5	0
						0.5
				0.5	0	0
						0.5
					0.5	0
						0.5
			0.10	0.3	0	0
						0.5
					0.5	0
						0.5
				0.5	0	0
						0.5
					0.5	0
						0.5
spike	0.74	0.58	0.32	0.3	0	0
						0.5
					0.5	0
						0.5
				0.5	0	0
						0.5
					0.5	0
						0.5

Tables 3 and 4 suggest that, over the range of scenarios investigated, the two ELCON algorithms are generally preferable to the others, although SELF performs reliably provided the lying rate is not too high. We also investigated variants of the ELCON algorithm (not shown), in which, when a UDS was positive but all self-report days in the window were negative, either 2 or 3 self-report days were modified to positive instead of just 1. In general, these variants did not perform as well as ELCON. Similarly, in our initial investigation of BAYES (not shown), we imposed uniform priors on (PPV, NPV). However, we found that power improved somewhat when PPV received a Beta prior with mean close to 1. This is the BAYES method whose performance we document here.

Discussion

In our simulations, the primitive and naïve ELCON algorithms outperformed more sophisticated and statistically sounder methods. We have attempted to describe the limitations of our investigations below. But if a clinical trialist who wishes to choose now from among the algorithms simulated here feels that our simulations are realistic and his or her parametric values are close to ours, then judging by how often algorithms are among the best over the scenarios simulated, the two ELCON algorithms generally recommend themselves over other alternatives investigated on the basis of their simplicity and power.

For a statistician, a surprising aspect of these results is that MLE did not do as well as algorithms that seem ad hoc. Likelihood theory is well established, and maximum likelihood estimators are known to have a variety of favorable attributes, such as consistency, being asymptotically unbiased and Normal, and so on. A possible explanation for the poor performance is that the likelihood model does not exactly fit the data (as will doubtless always be true in real life). For example, both MLE and BAYES assume an error-free UDS with a 3-day window, but this was not how UDS errors were simulated. But the UDS explanation does not suffice, since both MLE and BAYES had relatively poor performance in other simulations (not shown) in which the simulated UDS was error-free as described. It seems more likely that the culprit is the fact that MLE must simultaneously estimate not only the probability of drug use p, but also two other nuisance probabilities L and M (or, more precisely, related probabilities PPV and NPV). BAYES in part gets around this by imposing priors on PPV and NPV, and in consequence does somewhat better; it has “integrated out” the nuisance parameters. However, it still does not do better than the two ELCON algorithms, which edit the self-report when it contradicts the UDS. The MLE and BAYES algorithms are much more complicated to calculate than other algorithms.

IDEAL is better than the realizable algorithms. Does this argue that one should abandon automated algorithms in favor of an actual notification TLFB? A real life notification may not be as accurate as the idealized notification, because participants may not tell the truth when notified. It is not known how much better IDEAL is than a real-life notification TLFB. In addition, the real-life notification TLFB has disadvantages mentioned earlier.

The objective of the paper is to discover the best algorithm to compare means. This is not the same as discovering the most accurate descriptor of drug use. For example, it could be that algorithms other than the two ELCON algorithms are less biased, but that the biases in the two groups under study largely cancel each other out in the t-test. A drug counselor might prefer an unbiased algorithm, while a clinical trialist might prefer a biased algorithm with a smaller variance, as long as the bias affects both treatment conditions equally. UDS is unbiased for the probability of drug use in the UDS window when data are uninformatively missing, but is not powerful as other algorithms in this simulation.

A reviewer observes that it is probably rare for UDS to be performed 3 times per week in clinical practice; once per month may be more realistic. So it is reassuring that self-report alone did as well as it did. If these simulations reflect real life, it is probably untrue that self-report is worthless, even in a research context.

When interpreting the results of the current study, it is important to keep in mind its limitations. Our assumptions concerning the probability of positive UDS as a function of time since last dose are at least oversimplified; the relationship between actual substance use and UDS indications is almost always imperfect and complex. The simulated participants in this study behave with temporal consistency with respect to both substance use and honesty while real-world participants may not. We ignored that, unlike those dependent on opioids, stimulant users have mild withdrawal symptoms, and may sometimes more easily refrain from use just before a urine test. We did not explore the full range of parameters (like p, L, and M) that could be plausible in real-world data. Although we did simulate informatively missing UDS, we did not explore algorithms that attempted to adjust for it.