Detection of rapidly exchanging compounds using on-resonance frequency labeled exchange (FLEX) transfer

Abstract

Frequency-labeled exchange (FLEX) transfer is a promising MRI technique for labeling and detecting exchanging protons of low concentration solutes through the water signal. Early FLEX studies have used off-resonance excitation-based labeling schemes which are well suited to study rapidly exchanging protons or molecules far from the water resonance (e.g., water in paramagnetic contrast agents) or slowly exchanging protons close to the water resonance (e.g., some amide protons). However off-resonance labeling is not efficient for rapidly exchanging protons close to water. Here we show that a new FLEX labeling scheme with excitation pulses applied on the water resonance gives much higher exchange contrast for rapidly exchanging protons resonating close to the water resonance frequency. This labeling scheme is particularly suited for studying rapidly exchanging hydroxyl, amine and imino protons in diamagnetic CEST agents.

Introduction

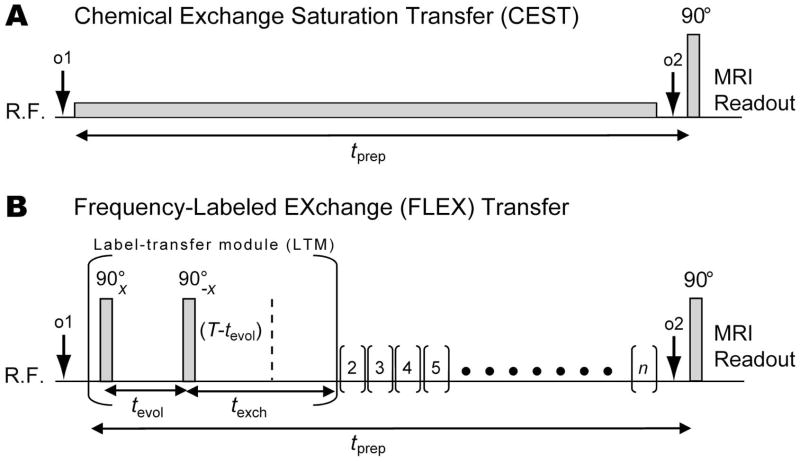
Frequency-labeled exchange (FLEX) transfer is a new magnetization transfer (MT) based technique for detecting low concentration solutes that contain exchanging protons or molecules [1–3]. Analogous to chemical exchange saturation transfer (CEST) [2,4–7], FLEX labels the magnetization of these exchangeable protons and, after transfer of this label, detects it indirectly through the water signal with enhanced sensitivity. In contrast to CEST, which employs RF saturation for magnetic labeling (Figure 1A), FLEX uses a series of excitation pulses and chemical shift evolution (Figure 1B). This enables labeling in a timeframe on the order of microseconds (duration of RF excitation pulses plus evolution period) instead of waiting for the RF irradiation to reach at least a partial saturation steady state, as is the requirement for CEST. FLEX therefore is especially advantageous to study rapidly exchanging protons or molecules [3]. Additional advantages of this technique include (i) multiple exchanging compounds can be labeled simultaneously, (ii) different MT mechanisms can be separated using time domain analysis (e.g., exchanging protons can be distinguished from protons of semi-solid macromolecules in tissue), and (iii) exchange rate filtering is possible by varying timing parameters in the pulse sequence. Consequently, FLEX imaging is a potentially powerful technique for studying low concentration solutes containing moieties with high exchange rates in vitro and in vivo.

Figure 1.

CEST and FLEX pulse sequences for detecting exchanging solute protons indirectly via the water signal. (A) Conventional CEST: Protons are labeled through continuous saturation and concurrently exchange into the water pool thus transferring the saturation label. In the FLEX sequence (B), exchangeable protons are labeled using a series of n label transfer modules (LTMs) with each LTM (represented by parentheses) containing periods for chemical shift evolution of transverse magnetization (t_evol) and exchange transfer of longitudinal magnetization (t_exch). The t_evol is varied for a number of different acquisitions, here using a constant time (T) approach, to encode the chemical shift evolution of magnetization excited by the first 90°_x RF pulse. After evolution as a function of the frequency difference between the resonance frequency of the exchangeable protons and the offset frequency of the RF pulse (o1), part of the magnetization is returned to the longitudinal plane using a 90°_−x RF pulse. This labeled magnetization is transferred to the water pool during t_exch. Each LTM is repeated n times to enhance the effect.

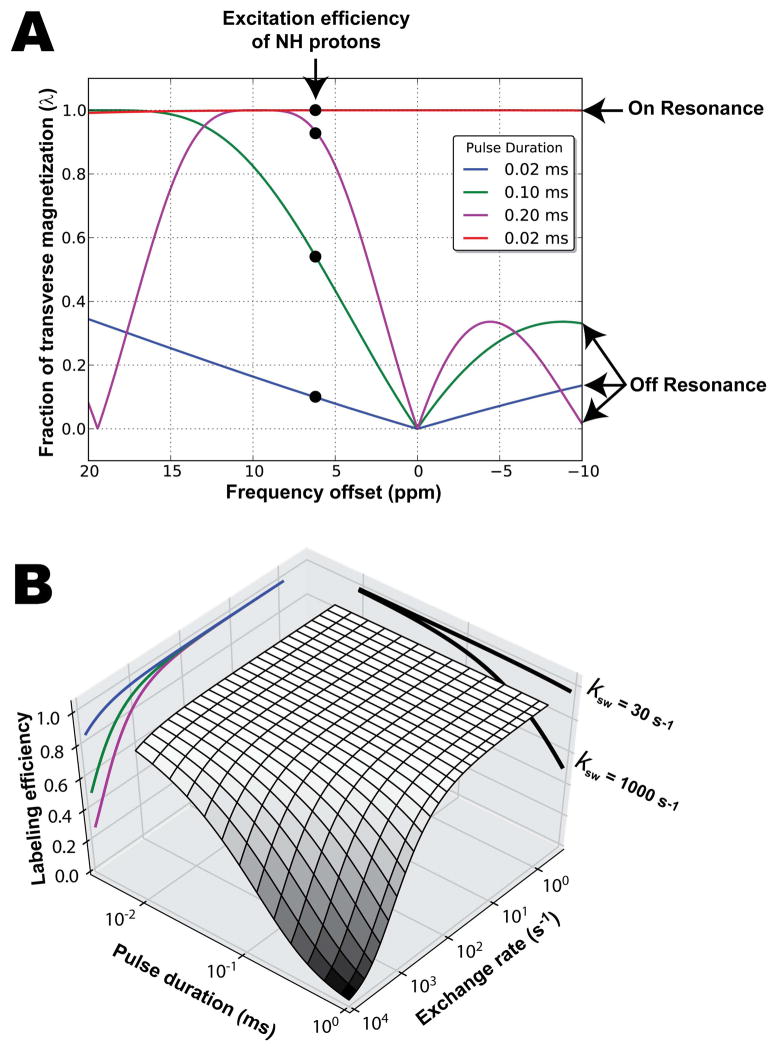
As with any method, FLEX also has some potential disadvantages. Using a train of excitation pulses for labeling can lead to experimental complications if a significant fraction of the bulk water pool is also excited. Similar to direct saturation in CEST, this would lead to sensitivity loss. In addition, in phantom experiments performed on high-Q probes, radiation damping may occur. Consequently, the early FLEX studies [1,3] have used frequency-selective labeling pulses designed to minimize water excitation whilst maximizing excitation efficiency at the solute resonance frequencies. This selectivity has been accomplished by applying the labeling pulses far away from the water resonance frequency and allowing off-resonance effects of the RF pulse (e.g., variations in phase, amplitude, rotation angle) [8] to null the bulk water signal. Such selective excitation approaches work well for paraCEST agents [6,7,9–11] where very short excitation pulses can be placed far off-resonance from the water peak whilst maintaining high excitation efficiency at the solute protons of interest that are also far off-resonance. However for diaCEST agents [12,13] or endogenous compounds [14–18], which are much closer to the water resonance frequency, applying very short pulses far off-resonance results in low excitation efficiency at the resonance frequencies of interest (< 10 ppm). Consequently, pulses need to be lengthened to allow placement close to the resonance frequency of the solute protons of interest whilst still nulling at the water resonance frequency (see Figure 2A). These longer labeling pulses still allow efficient detection of slowly exchanging protons (e.g., amide protons of mobile proteins and peptides). However, they have reduced efficiency for more rapidly exchanging protons (e.g., imino, amine or hydroxyl protons), since a large fraction of protons can already exchange during the labeling period consisting of two of such RF pulses (see Figure 2A). Here we present a new method for conducting FLEX experiments for rapidly exchanging protons near the water resonance frequency. We apply short (broad-band) FLEX labeling pulses directly at the water resonance frequency and show that rapidly exchanging compounds with resonances close to the water frequency can be detected with high sensitivity, despite the fact that all of the water protons are excited too.

Figure 2.

(A) Excitation profiles for FLEX labeling pulses applied at several off-resonance frequencies (blue, green, magenta curves) and on-resonance (red curve). The selectivity profiles of the off-resonance pulse pairs vary as a function of pulse duration and, in order to null the water signal, the different pulse durations have different offset frequencies (o1). These different offset frequencies lead to different efficiency of excitation for the exchangeable protons, e.g. the imino protons indicated here. The use of a short non-selective excitation pulse (red line) is shown to give much higher λ, but also excites water, which may cause complications (ignored in this plot). (B) On-resonance labeling efficiency for different pulse durations and exchange rates. Example slices taken through the surface plot are projected onto the vertical planes (i.e., curves for k_sw = 30 and 1000 s⁻¹ shown on the labeling efficiency/pulse duration plane and curves for pulse duration = 0.02, 0.1, and 0.2 ms shown in blue, green, and magenta respectively plotted on the labeling efficiency/exchange rate plane).

Theory

In contrast to saturation transfer, which leads to a decrease in the water signal, FLEX modulates the water signal intensity depending on the resonance frequencies of the exchangeable groups by encoding the chemical shift evolution of exchanging protons within so-called label transfer modules (LTMs, represented by parentheses in Figure 1B). Each LTM consists of (i) a selective 90_x RF pulse which excites protons over a range of frequencies (ii) a delay (t_evol) during which excited protons undergo chemical shift evolution, (iii) a selective 90_−x RF pulse which flips the magnetization back to the longitudinal axis, and (iv) another delay (t_exch) which allows time for the labeled protons to exchange into the bulk water pool. Each acquisition contains a preparation time consisting of a number of LTMs (n) to allow sensitivity enhancement by repeatedly exchanging frequency labeled protons with unlabeled protons from the large water pool.

The magnitude of the FLEX contrast for each exchangeable proton can be described by the proton transfer ratio (PTR_s) [1,2]:

$${\text{PTR}}_{\text{s}}=x_{\text{s}}·{\lambda }_{\text{s}}·\left(1-e^{-k_{\text{sw}}·t_{\text{exch}}}\right)·\sum _{i=1}^n{e}^{[-1+(i-1)/n]·t_{\text{prep}}/T_{\text{1w}}}$$ (1)

where s is a labeled solute proton, x_s the fractional solute proton concentration, λ_s the excitation efficiency of the pair of selective labeling pulses at the solute resonance, k_sw the exchange rate with water, and T_1w the longitudinal relaxation time constant for water. By performing a series of acquisitions at different evolution times, the intensity of the exchangeable-proton originated water signal (I_w,ex), which includes contributions from labeled protons at multiple resonances, is [1,2]:

$$I_{\text{w},\text{ex}}=\sum _{\text{s}}{\text{PTR}}_{\text{s}}·e^{-(k_{\text{sw}}+1/T_{2\text{s}}^{\ast })·t_{\text{evol}}}·cos(\mathrm{\Delta }{\omega }_{\text{s},\text{o1}}·t_{\text{evol}}+{\phi }_{\text{s}})$$ (2a)

where T_2s^* the effective transverse relaxation time constant of the solute proton, Δω_s,o1 is the chemical shift difference between the labeled proton and the offset frequency of the labeling pulse (o1), and φ_s is phase of the modulation. From Eq. 2a, we can see that the FLEX time domain signal modulates with the superposition of frequencies from the components (s), each having a frequency determined by Δω_s,o1 and decay rate proportional to k_sw + 1/T_2s* of the exchangeable proton pool. In FLEX-MRI, the resulting water signal as a function of evolution time will be a convolution of the modulations of all participating exchangeable protons. The magnitude depends on the concentration of the solute and generally is a few percent or more of the large water signal detected in MRI.

The situation becomes a bit more complicated when there is simultaneous excitation of some water protons. In zero order, the latter can be approximated by adding a term:

$$I_{\text{w},\text{sew}}=I_{\text{sew}}·e^{-(1/T_{2\text{sew}}^{\ast })·t_{\text{evol}}}·cos(\mathrm{\Delta }{\omega }_{\text{sew},\text{o}1}·t_{\text{evol}}+{\phi }_{\text{sew}}),$$ (2b)

in which “sew” indicates spuriously excited water (sew) protons. For off-resonance FLEX MRI, I_w,sew generally is a relatively small contribution (a few percent) on the order of magnitude of the FLEX signal. It is known from previous off-resonance FLEX experiments [1,3] that $T_{2\text{sew}}^{\ast }$ is long relative to the evolution time, leading mainly to a signal modulation and no decay for this component, allowing its simple deconvolution from the total water and exchangeable proton signals based on the knowledge of its frequency offset during FLEX excitation. However, excitation of too much water signal will cause the convolved FLEX signal to modulate in a non-sinusoidal fashion.

For excitation pulses applied on the water resonance (on-resonance FLEX MRI), the situation is more complicated because a large water magnetization is present during t_evol. This can result in radiation damping and, in a series of RF pulses, the occurrence of a complex series of multiple echoes. In theory, the formation of a complex series of echoes should be limited because the 90_x – 90_−x LTM pulse design should work as a jump-return sequence for spins that are exactly on resonance. Consequently, the on-resonance spins should all be flipped back because the large water resonance should not evolve. Unfortunately, in vivo and especially in our phantom setup of multiple tubes with air in between, there are spatial field differences so the water magnetization in many areas will be slightly off-resonance and therefore evolve. When a large number of RF pulses is used, multiple types of water echoes can be generated by the train of 90° excitation pulses [19–22]. These multiple echoes result in a water magnetization steady state, which can vary depending on t_evol. This will cause a water signal decay that is not trivial to describe, but can be determined experimentally and subsequently deconvolved from the FLEX signal of interest. Notice that even though this decay appears to be a T₂* decay, it is not. The large water signal decay is not an issue for off-resonance FLEX because the water protons are barely excited by the FLEX labeling pulses.

Materials and Methods

Thymidine solutions were prepared by dissolving thymidine (purchased from Sigma, catalogue no. T1895) to a concentration of 20 mM in PBS. This solution was placed in seven separate 5 mm NMR tubes, with the pH in each tube titrated to: 4.3, 5.3, 6.2, 6.9, 7.2, 7.5, and 8.1 to generate a different exchange rate for the imino protons. Separate solutions of 20 mM myo-Inositol (Sigma, catalogue no. I5125) and creatine (Sigma, catalogue no. C0780) were also prepared in a similar fashion. The myo-Inositol was titrated to pH 6.4 and 7.3 while the creatine pH was titrated to pH 7.3.

FLEX and CEST MRI data were acquired on a horizontal bore 11.7 T Bruker Biospec pre-clinical MRI system equipped with a 23 mm transceiver coil at 20 °C. FLEX experiments were conducted using “rectangular” off-resonance excitation pulses (duration: 0.2 ms, amplitude: 29 μT) and “rectangular” excitation pulses applied on the water resonance (duration: 0.02 ms, amplitude: 294 μT). For experiments on the thymidine solutions, the FLEX time domain signal was generated by varying t_evol from 0.0 to 1.5 ms in steps of 0.03 ms (dwell time); o1 was set to 9.7 ppm for off-resonance FLEX and 0 ppm (o1=o2) for on-resonance FLEX. Other FLEX parameters were n = 1500 LTMs and t_exch = 2 ms. For FLEX experiments on myo-inosotol and creatine, on-resonance FLEX experiments were performed by varying t_evol from 0.0 to 5.0 ms in steps of 0.1 ms, LTMs = 300, t_exch = 10 ms. Imaging parameters for all experiments were a single-shot fast spin-echo (FSE) MRI readout consisting of a 32 × 32 acquisition matrix, FOV = 17 mm × 22 mm, slice thickness = 0.5 mm, TE = 4 ms, and TR = 8 s. To test for radiation damping, experiments were run with and without bipolar gradients during t_evol (at 1–4 ms) and t_exch [1,3]. There was no difference in FLEX signal between these experiments and, therefore, we did not apply any gradients during the exchange and evolution times for thymidine experiments,. For the experiments with longer evolution and exchange periods on myo-inositol and creatine, gradients (10 mT m⁻¹) were placed in the exchange period to reduce any possible radiation damping [1,3].

Exchange rates were quantified with the saturation power dependent CEST approach (QUESP) and Bloch equation fitting [23], using a 6 s saturation pulse with B₁ field strengths of 1, 3, 5, 7, and 9 μT. B₀ field inhomogeneities in the CEST experiments were corrected for using a water saturation shift referencing (WASSR) [24].

PTR and k_sw were quantified from FLEX experiments by fitting Eq. 2a to the experimental data using the L-BFGS-B algorithm [25]. For off-resonance FLEX experiments, the number of pools in each fit was the number of exchangeable proton resonances plus one to account for water protons inadvertently excited by the FLEX labeling pulses and another with a zero frequency component to account for the baseline. Consequently, for thymidine data, we used a 5-pool model to account for hydroxyl resonances at 1.0 and 1.4 ppm with respect to the water resonance, an imino NH proton at 6 ppm, and two additional pools for water and the baseline. For on-resonance FLEX experiments, the decay of the solute FLEX signal (k_sw + 1/T_2s^*) is convolved with the decay of the detected bulk water magnetization as a function of t_evol (see Theory section). Consequently, estimating k_sw directly from the decay of the FLEX signal will lead to an overestimation of k_sw. Therefore for on-resonance experiments, before estimating k_sw, we deconvolved the decay of water from the decay of the solute pool (k_sw + 1/T_2s^*) using a two-step fitting procedure. The initial step involves fitting Eq. 2a to the on-resonance experimental data (using the same number of pools as off-resonance data but without the water pool). The zero frequency component of this fit is used to normalize out the bulk water decay. The normalized data are subsequently re-fit to Eq. 2a (using the same parameters as in the initial step) and k_sw of the solute determined from the decay of the FLEX signal. Consequently, for on-resonance FLEX data from thymidine, we used a four-pool fit. For on-resonance data from creatine and myo-inositol, we used a two-pool model to account for a single exchangeable proton resonance (at 1.9 ppm and 1.3 ppm respectively) and a zero frequency component. The modulation frequency for each component in Eq. 2a was constrained to correspond to the chemical shift frequency of each proton with respect to o1. Constraining the fits minimized uncertainties in our fitting results, however it is not an inherent requirement for the FLEX method.

All simulations and experimental data were processed using Python, Scipy, and Numpy (www.python.org, scipy.org, and numpy.scipy.org, respectively) using code written in-house.

Results and Discussion

The effect of varying the solution pH on the exchange rate of the imino NH proton of thymidine, as measured using the QUESP method is shown in Table 1. The exchange rate ranged from 0.30 × 10³ s⁻¹ for pH 4.3 up to 10 × 10³ s⁻¹ at pH 8.1.

Table 1.

Exchange rates of the thymidine imino NH protons as determined from QUESP (using Bloch equation fitting), off-resonance FLEX, and on-resonance FLEX experiments.

pH		4.3	5.3	6.2	6.9	7.2	7.5	8.1
ksw/103 (s−1)	QUESP	0.30	0.50	1.1	2.7	4.0	5.7	10
	Off-res. FLEX	0.70	1.1	1.4	2.5	2.8	2.4	1.3
	On-res. FLEX	0.30	1.0	1.5	3.0	3.8	5.5	9.8

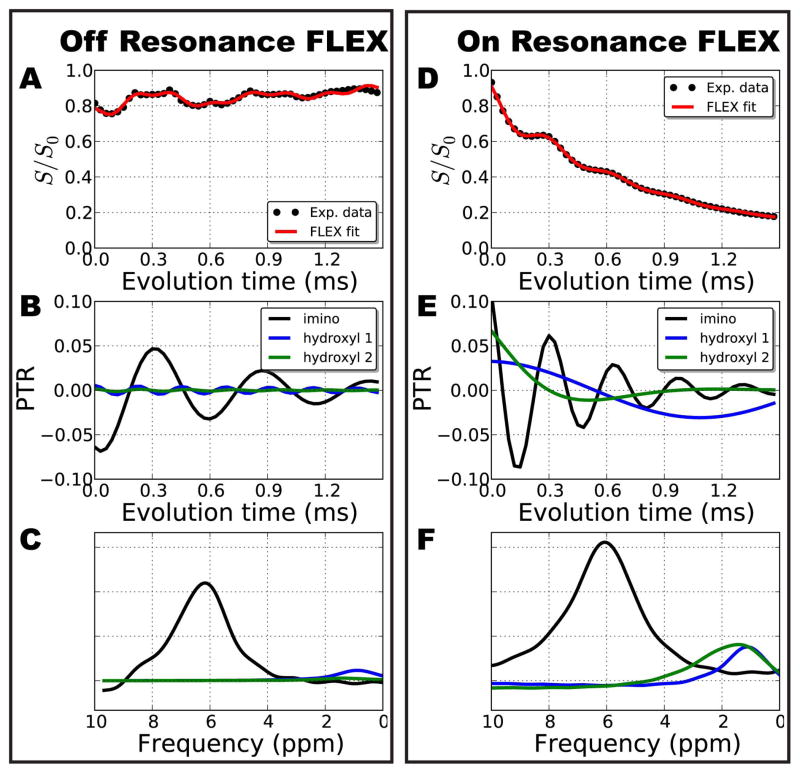
The results from on- and off-resonance FLEX experiments on the thymidine solution at pH 6.2 are shown in Figure 3. For off-resonance FLEX experiments (Figures 3A–C), the experimental data shows a modulating signal that clearly exhibits multiple components. Fitting Eqs. 2a + 2b with a constant baseline to the experimental data, we measured PTR values of 1%, 0%, and 7% for the hydroxyl proton at 1.0 ppm, hydroxyl proton at 1.4 ppm (Table 2), and imino proton at 6.2 ppm, respectively. The FLEX time domain signal from the hydroxyl pools (shown in Figure 3B) had very little signal while the component assigned to the imino NH proton represents a 7.7 M effect (7% of the total water signal) or sensitivity enhancement by a factor of 400. The decay rate of the imino NH modulation in Figure 3B gives k_sw = 1.4 × 10³ s⁻¹ when neglecting 1/T_2s^* (assuming k_sw ≫ 1/T_2s^*). The peaks corresponding to the each of the solute pools can also be visualized in the frequency domain after Fourier transformation of the FLEX signal (Figure 3C). The experimental data from on-resonance FLEX experiments (Figure 3D) shows a clear modulation convolved with an exponential decay. From the FLEX fit, we determined FLEX PTR values of 10%, 12%, and 9% to resonance frequencies of 1.0 ppm, 1.4 ppm, and 6.0 ppm respectively. The components attributed to each solute pool are shown in Figure 3E and their corresponding spectral peaks in Figure 3F.

Figure 3.

Comparison of the data processing steps between off–resonance and on resonance FLEX for the pH 6.2 solution of thymidine. For off-resonance excitation the water signal intensity modulates around S/S₀ ~ 0.8 as a function of t_evol (A). The fitted components (Eq. 1) corresponding to the imino NH protons, hydroxyl protons at 1.0 ppm, and hydroxyl protons at 1.4 ppm of thymidine is shown in B. (C) A FLEX spectrum obtained by Fourier transforming the FLEX time domain signals in B. (D) The signal for on resonance FLEX experiments modulates about an exponential decay due to significant additional echoes generated by the train of labeling pulses. (E) Deconvolved FLEX time domain signal from the three solute pools; (F) corresponding resonance frequencies. Notice that the modulation frequencies shown in B and E differ because of the different Δω_s,o1, for the two experiments, but that the same resonance frequency results in the final spectrum referenced to the water resonance frequency (C and F). FLEX fit parameters are in Table 2.

Table 2.

Fitting parameters for off-resonance and on-resonance FLEX MRI for the data in Figure 3.

	off-resonance (red line in A)				on-resonance (red line in D)
Baseline offset	1.0				0.0
s	PTR	ksw+1/T2* (s−1)	Δωs,o1 (ppm)	φ (radians)	PTR	ksw+1/T2* (s−1)	Δωs,o1 (ppm)	φ (radians)
H2O	0.02	100	9.8	0.3
OH1.0 ppm	0.01	530	8.8	0.1	0.10	260	0.9	5.7
OH1.4 ppm	0.00	1000	8.2	0.2	0.12	2340	1.4	0.1
NH	0.07	1370	3.6	2.6	0.09	3064	6.0	0.2
baseline	0.20	30	−0.2	3.3	0.69	500	0.0	0.1

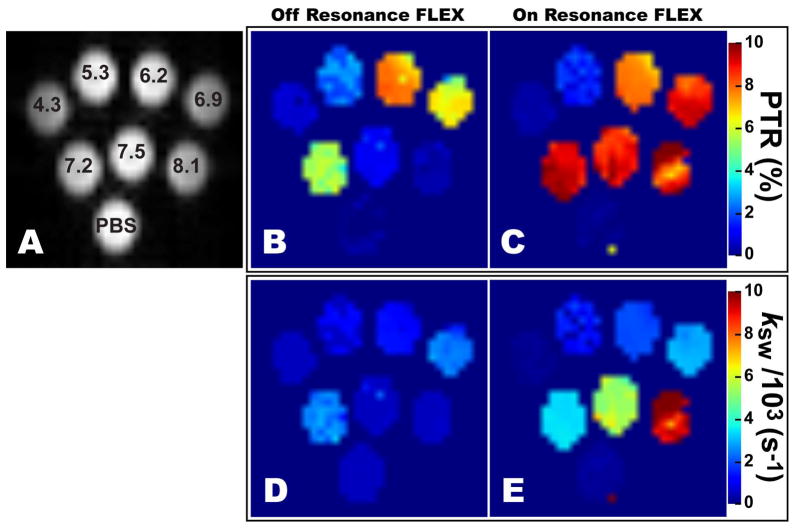
Maps of PTR and k_sw obtained from off- and on-resonance FLEX experiments on thymidine are shown in Figure 4. The off-resonance results initially show PTR increasing with pH, followed by a reduction for pH > 6.2. An increased PTR with increasing pH is expected based on an increased exchange rate leading to a larger fraction of labeled protons exchanging to the water pool during t_exch. However above pH 6.2, despite the increased exchange rate, this is no longer the case for off-resonance FLEX. The reason is that, because of the longer RF pulses, a substantial fraction of solute protons already exchanges during the FLEX labeling period, thus reducing the labeling efficiency and, consequently, the PTR. In comparison, the PTR map obtained from on-resonance FLEX experiments (Figure 4C) shows increasing PTR until the pH 6.9 solution, after which PTR stays about constant for higher pH solutions. Again the increase in PTR from pH 4.3 to 6.9 is due to a larger fraction of labeled protons exchanging to water during t_exch. At pH 6.9 and above, the imino NH protons are exchanging fast enough (k_sw ≥ 2.5×10³ s⁻¹) that the label transfer process reaches a steady state and consequently the PTR stays constant. It is important to note that the FLEX contrast was filtered towards faster exchanging agents using a t_exch = 2 ms. Using a longer t_exch would weight the FLEX contrast towards slowly exchanging protons since they would have more time to transfer their label into the water pool. On-resonance FLEX does not suffer from a reduction in PTR at the higher pH range since the RF pulses during the labeling period are much shorter, which minimizes exchange losses.

Figure 4.

Tube arrangement (A) and FLEX maps (B–E) of PBS and thymidine solutions at different pH. The FLEX maps were created by fitting Eq. 1 to off-resonance (B,D) and on-resonance (C,E) FLEX experiments and plotting the PTR (B,C) and exchange rate (D,E) of the thymidine imino proton in each voxel. The off-resonance FLEX experiments show signal loss and erroneous exchange rates at higher pH values due to exchange losses during the labeling period.

Comparing the exchange rates determined using off- and on-resonance FLEX with QUESP rates in Table 1 and Figure 4D–E, we can see that both FLEX methods generally overestimate k_sw for the low pH tubes but this trend diverges for the higher pH tubes, showing underestimated rates for off-resonance and values comparable to QUESP for on-resonance. The overestimation of slower k_sw values by both FLEX methods is attributed to the short t_exch used in the thymidine experiments that was weighted towards faster exchanging agents. Due to the short t_exch, slowly exchanging solute protons do not have enough time to exchange into the bulk water pool before the next LTM. This violates the assumption used to derive Eqs. 1 and 2a, that unlabeled solute protons are present at the beginning of each LTM. Consequently, slowly exchanging solute protons are re-labeled which reduces the effect. This is easily corrected for by increasing t_exch but here, as previously stated, we are interested in the rapidly exchanging agents.

To demonstrate the capability of on-resonance FLEX MRI to detect exchangeable protons much closer to the water resonance (relative to the imino NH proton of thymidine), FLEX data for creatine and myo-inositol is shown in Figure 5 and Table 3. The results show clear modulations corresponding to the resonance of the NH₂ protons of creatine (~2 ppm in Figure 5A–C) and OH protons in myo-inositol (~1.3 ppm in Figure 5D–I). Myo-inositol was measured at both high and low pH to highlight corresponding changes in the FLEX signal in the raw data (see Figure 5D) and its applicability to detect rapidly exchanging protons close to the water resonance (Figure 5G–I). Note that we used longer evolution periods for creatine and myo-inositol phantoms compared to thymidine. This was to increase the spectral resolution of the FLEX peaks for these resonances that were closer to water. A longer t_exch was also used for these slower exchanging protons. The hydroxyl protons of thymidine were not a good candidate to demonstrate the on-resonance FLEX technique since their separate resonances coalesce into a single peak at higher pH.

Figure 5.

On-resonance FLEX data from creatine at pH 7.3 (A–C), myo-inositol at pH 6.4 (D–F), and myo-inositol at pH 7.3. The experimental data in B, D and G show modulations corresponding to the evolution frequency of the exchangeable protons in creatine (B) and myo-inositol (D,G). The myo-inositol modulation at high pH (G) decays much faster than at low pH (D) due to the increased exchange rate. The fitted frequency components are shown in B, E, and H; and their corresponding spectral peaks in C, F, and I. FLEX fit parameters are in Table 3.

Table 3.

Fitting parameters for on-resonance FLEX MRI for the data in Figure 5.

	creatine				myo-inositol pH 6.4				myo-inositol pH 7.3
baseline offset	0.1				0.1				0.1
s	PTR	ksw+1/T2* (s−1)	Δωs,o1 (ppm)	φ (radians)	PTR	ksw+1/T2* (s−1)	Δωs,o1 (ppm)	φ (radians)	PTR	ksw+1/T2* (s−1)	Δωs,o1 (ppm)	φ (radians)
NH2/OH	0.10	1110	2.1	5.3	0.17	1510	1.3	5.9	0.09	2470	1.3	0.0
baseline	0.83	375	0.2	1.9	0.79	401	0.2	1.9	0.91	540	0.1	0.1

Despite the increased sensitivity to rapidly exchanging protons, the on-resonance FLEX technique will not always be the most appropriate technique for detecting exchanging protons. Figure 2 shows that off-resonance FLEX still offers high PTR if (i) labeling pulses can be placed close enough to the resonance of interest to achieve a higher excitation efficiency, and (ii) being short enough, relative to the exchange rate, to achieve high labeling efficiency (e.g., paraCEST agents). On-resonance FLEX becomes more suitable when either of these two conditions cannot be met. Another potential limitation for on-resonance FLEX is the requirement to sample enough data points in the indirect FLEX dimension to achieve adequate spectral resolution. This might be challenging for very rapidly exchanging agents with rapid signal decay (e.g., protons with resonances <1 ppm from water with k_sw > 10⁴ s⁻¹).

For cases where on-resonance FLEX is deemed appropriate, the train of FLEX labeling pulses on the water resonance produces a large evolving magnetization which can result in additional MR effects that need be considered carefully. The most significant is a fast signal decay of the measured bulk water signal with increasing t_evol, and the convolution of this decay with the solute decays due to k_sw+1/T_2s^*. We tentatively attribute the rapid signal decay to spatial field differences in our phantom setup of multiple tubes with air in between leading to water magnetization in many areas being slightly off-resonance and causing the magnetization to evolve. When a large number of RF pulses is used, multiple types of water echoes can be generated by the train of 90° excitation pulses [19–22] leading to a water magnetization steady state which varies with t_evol. A theoretical analysis of this multi-echo situation is beyond the scope of this communication, which is to show the benefits of the new on-resonance FLEX technique. Fortunately, this water signal decay can be determined experimentally and subsequently deconvolved from the FLEX signal of interest.

Conclusion

On-resonance FLEX transfer labeling enabled the use of much shorter excitation pulses, making the approach more suitable for the study of rapidly exchanging protons near the water resonance. We showed that protons with exchange rates up to 10,000 s⁻¹ (well into the intermediate exchange regime) could be detected with high sensitivity using this new FLEX approach.