Using Generalized Additive Modeling to Empirically Identify Thresholds within the ITERS in Relation to Toddlers’ Cognitive Development

Abstract

Research linking high-quality child care programs and children’s cognitive development has contributed to the growing popularity of child care quality benchmarking efforts such as quality rating and improvement systems (QRIS). Consequently, there has been an increased interest in and need for approaches to identifying thresholds, or cut-points, in the child care quality measures used in these benchmarking efforts that differentiate between different levels of children’s cognitive functioning. To date, research has provided little guidance to policymakers as to where these thresholds should be set. Using the Early Childhood Longitudinal Study, Birth Cohort (ECLS-B) data set, this study explores the use of generalized additive modeling (GAM) as a method of identifying thresholds on the Infant/Toddler Environment Rating Scale (ITERS) in relation to toddlers’ performance on the mental development subscale of the Bayley Scales of Infant Development (the Bayley Mental Development Scale Short Form–Research Edition, or BMDSF-R). Our findings suggest that simple linear models do not always correctly depict the relationships between ITERS scores and BMDSF-R scores and that GAM-derived thresholds were more effective at differentiating among children’s performance levels on the BMDSF-R. Additionally, our findings suggest that there is a minimum threshold on the ITERS that must be exceeded before significant improvements in children’s cognitive development can be expected. There may also be a ceiling threshold on the ITERS, such that beyond a certain level, only marginal increases in children’s BMDSF-R scores are observed.

Over the past several decades, evidence has mounted about the importance of high-quality infant/toddler child care to children’s positive development (Shonkoff & Phillips, 2000). Experimental studies, such as the Carolina Abecedarian Project, have found that toddlers from low-income families who were enrolled in early education programs that provided stimulating, structured environments showed improved subsequent intellectual development, academic achievement, and social skills through 12 years of age. Participation in the programs also increased their likelihood of economic independence during adulthood (Campbell & Ramey, 1994; Campbell, Ramey, Pungello, Sparling, & Miller-Johnson, 2002). While effects appear more modest than in demonstration programs, higher structural and process quality indicators in less intensive, typically occurring infant/toddler child care have also been associated with better cognitive and language skills in young children (Burchinal, Roberts, Nabors, & Bryant, 1996), especially for those with social-risk factors (Loeb, Fuller, Kagan, & Carrol, 2004). Several studies have also reported on the enduring effects of high-quality infant/toddler care through the elementary years (Broberg, Wessels, Lamb, & Hwang, 1997; Field, 1991). The plethora of evidence attesting to the positive association between child care quality and children’s cognitive and language outcomes led Vandell and Wolfe (2000) to conclude that there is strong economic justification for investing public funds in improving the quality of non-parental child care.

Consequently, states across the country have attempted to improve child care by implementing a number of quality improvement initiatives. Many of these initiatives hinge on assessments of classroom quality. These assessments are often used to direct professional development efforts as well as to incentivize staff to offer higher-quality services. For example, many initiatives have set thresholds or cut-points on classroom quality measures that are used to award different levels of funding to classrooms or bonuses to teaching staff. Thresholds can also be used to allow or restrict a classroom access to additional services and funding streams. In many cases, classroom assessments are included in a state’s quality rating and improvement system (QRIS), whereby thresholds set on assessments are used as one measure among several to assign a program a “star” or “quality rating” that is often made public to assist families in selecting better care (Schaack, Tarrant, Boller, & Tout, 2012). These types of quality initiatives and policy strategies are undertaken under the untested assumption that as classrooms improve their scores on quality measures to meet higher thresholds, corresponding improvements to children’s development and school readiness skills will follow. Given the considerable financial investments that states are making in these types of quality initiatives and in QRIS in particular, combined with their potential high stakes, setting empirically defensible thresholds on quality measures that can differentiate between levels of child functioning is an important consideration for states.

One of the most frequently used classroom assessments in quality benchmarking and improvement initiatives is the Infant/Toddler Environment Rating Scale (ITERS; Harms, Clifford & Cryer, 1990). Among the 26 states with QRIS in operation, all but one includes the ITERS (Tout et al., 2010). Although the ITERS is widely used in child care research, other than the ITERS developers’ recommendations, the extant research literature provides little guidance to policymakers as to where thresholds on the ITERS should be set (Zellman & Perlman, 2008). In part, this lack of threshold guidance may stem from the field’s heavy reliance on linear methods, which have produced a body of research largely indicating that the better the classroom quality, as measured by the ITERS, the better the child’s cognitive outcomes (Burchinal et al., 1996; Loeb et. al., 2004; Field, 1991; Vandell, 2004). While it is reasonable to assume that a higher rating on the ITERS is associated with better cognitive outcomes in young children, it is also reasonable to expect that there may be a point at which the relationship between quality on the ITERS and children’s outcomes levels off. Alternatively, there may be a point along the quality continuum that must be reached before children’s cognitive and language outcomes start to improve. In other words, the relationships between developmental outcomes and quality may be non-linear, or perhaps linear only within certain ranges.

Potential Thresholds on the ITERS

Our hypotheses regarding where thresholds on the ITERS may exist are informed by various theories about children’s development that are reflected in the construction of the ITERS. For example, constructivist theories of learning contend that conceptual development occurs as a result of children’s active exploration and manipulation of their environments (Piaget, 1952). As infants and toddlers explore their worlds, including the materials available in classrooms, they are provided with opportunities to perceptually discriminate small differences and general similarities among objects and begin to build categorical knowledge. In addition, attachment theory (e.g., Bowlby, 1969) contends that when children receive responsive care, it instills them with basic trust and security in their caregivers, which is necessary for children to explore their environments and learn (Howes & Ritchie, 2002).

The ITERS is constructed as a global measure of classroom quality incorporating both structural and process elements, including physical setting, health, safety, play materials, scheduling of time, curriculum, and caregiver-child interactions, among other aspects of quality (Perlman, Zellman, & Le, 2004). Although there are some items at the lower end of the scale that focus on ensuring that children experience positive child-teacher interactions for some part of the day, the majority of items clustered at the low and mid-range of the ITERS focus on ensuring that the daily schedule and physical environment are structured in a manner that allows children adequate time and access to a variety of learning materials (Moore, 1994). Therefore, one can hypothesize that there may exist a first threshold in the mid-range of the ITERS that ensures that children have adequate time and access to a variety of learning materials, and are cared for by teachers who are positive and responsive enough that the children can use their teachers as a secure base for exploration. It is likely that such a threshold may need to be reached before a relationship between ITERS scores and children’s cognitive development can be observed.

To some extent, social constructivist theories of learning and development (Vygotsky, 1978) are also reflected in the ITERS. These theories contend that social interaction is at the heart of the learning process. Teachers of very young children typically serve as children’s primary social partners. Effective teachers then work within individual children’s zones of proximal development to scaffold their experiences; they help young children attend to the environment and differentiate elements of it to assist in building categorical knowledge. Items clustered at the higher end of the ITERS tend to reflect these theories and focus more on teacher behaviors toward children (Moore, 1994), particularly with regard to using language to promote concept knowledge. Thus, one can also hypothesize that there may be a second threshold at the upper end of the scale, where items focus on teachers’ active engagement with individual children and the use of materials to purposefully facilitate children’s development. It also may be that, through these interactions, children have extended opportunities to hear and practice language. However, because the ITERS relies more heavily on structural quality to assess learning opportunities than on specific care and instructional practices that may be more strongly related to cognitive development (Cassidy et al., 2005), there may also be a leveling-off effect, where beyond a certain threshold, higher scores on the ITERS will no longer be related to better cognitive development.

Previous Studies on Non-Linear Relationships Between Quality and Outcomes

Several recent studies have examined whether there are non-linear relationships between child care quality and children’s outcomes, and they provide a possible means of exploring thresholds in quality indicators. NICHD Early Childa Care Research Network and Duncan (2003a) included both linear and quadratic terms in regression models that examined the relationship between child care quality indicators (including group size, child-staff ratio, caregiver education, and scores on the Observational Record of the Caregiver Environment) and children’s cognitive development and academic achievement. They did not find evidence of nonlinearity in their analysis. However, in a follow-up study of the long-term effects of child care on academic outcomes, risk-taking, impulsivity, and externalizing behaviors at age 15, Vandell and colleagues (2010) found significant non-linear associations between child care quality variables (measured when children were between one month and four years old) and children’s subsequent outcomes (when they were 15 years old). Burchinal, Kainz, and Cai (2010) used data from the National Center for Early Learning and the Development study of pre-kindergarten and the Family and Child Experiences Survey 1997 to examine whether the relationships between quality and child outcomes were linear or curvilinear. Using linear and quadratic terms, they found some evidence of a curvilinear relationship, such that children’s outcomes started to improve only when quality reached a certain level. In other words, relationships between quality and language and reading outcomes were stronger within higher-quality ranges.

Using piecewise regression, Burchinal, Vandergrift, Pianta, and Mashburn (2010) identified thresholds that suggested non-linear relationships between a measure of preschool process quality, the Classroom Assessment Scoring System (CLASS; see Pianta, La Paro, & Hamre, 2004), and children’s academic, language, and social skills. Using the CLASS developers’ recommendations and an empirical distribution to identify meaningful splits in the data, they explored three possible thresholds on the instructional quality dimension of the seven-point CLASS: (1) 2.5–7.0, which corresponded to the upper quartile of the sample distribution; (2) 3.0–7.0, which corresponded to the developers’ definition of medium to high quality; and (3) 3.25–7.0, which corresponded to the upper 15th percentile. On the emotional climate dimension, they explored cut-points at 5.0–7.0, which represented the developers’ definition for high quality, and 6.0–7.0, which defined the upper quartile. They found evidence of threshold effects for both instructional quality and emotional climate, such that instructional quality was more strongly related to expressive language, reading, and math skills in moderate- to high-quality classrooms than in low-quality classrooms, and emotional climate was more positively predictive of social competence and more negatively predictive of behavioral problems in high-quality classrooms than in low- to moderate-quality classrooms.

These studies suggest that non-linear statistical methods can indeed be useful for estimating threshold impacts in child care quality variables. However, there are several important caveats to the previous research. First, it might not always be easy to specify the non-linear functional form that best fits the data. For example, if the relationship between quality and child outcomes does not follow a quadratic association but takes some other form, then the use of quadratic models might not fit the data well. Likewise, the use of piecewise regression requires the prior identification of cut-points in the data, but it is not always clear where to split a piecewise regression. Although it is intuitively appealing to use the sample distribution to determine these splits, that approach can lead to the adoption of a myriad of potential cut-points. For example, policymakers might want to adopt cut-points at key percentiles, but there are arguably several key percentiles, such as the median, upper and lower tenth, quarter, and third of the distributions. Moreover, it is unclear why effective thresholds would be more likely to occur at key percentiles than at other points on the distribution. Finally, focusing only on the developers’ definitions for what constitutes low, medium, or high quality could ignore the existence of other thresholds that may be better at discriminating among children’s outcomes.

Using General Additive Models to Identify Thresholds

Generalized additive modeling (GAM; Hastie & Tibshirani, 1990) offers a non-linear method for identifying thresholds that address some of the limitations noted above. GAM allows for threshold identification by estimating the relationship between a quality measure and children’s outcomes without making any assumptions about whether the nature of that relationship is linear, quadratic, or polynomial with a known power. Instead, it empirically determines the relationship between a quality measure and outcomes based on the data, without the analyst needing to specify the form of that relationship. Furthermore, the identification of thresholds under GAM is not independent of outcomes; rather, it is informed by the relationships between quality measures and outcomes, thereby facilitating the identification of cut-points within the quality variables that can distinguish between poorer and better outcomes.

The purpose of this exploratory study was to demonstrate the potential utility of GAM in identifying thresholds on the ITERS in relation to children’s cognitive development, as measured by the Bayley Mental Development Scale Short Form–Research Edition (BMDSF-R; Bayley, 1993). We selected the ITERS because it is one of the most commonly used measures of classroom quality in state QRIS (Tout et al., 2010), its ratings have been shown to correlate with children’s cognitive and language development (Burchinal et al., 1996), and it includes developer-recommended thresholds that can serve as a basis for comparison with the GAM-derived thresholds. We chose the BMDSF-R measure because it has been shown to be among the strongest predictors of preschool children’s cognitive and language skills (DiLalla et al., 1990) and because it taps into developmental outcomes that are of interest to policymakers. To facilitate in-depth analysis and interpretation, we limit our study to the BMDSF-R scores.

Overall, this study (1) compares the relationships between ITERS scores and children’s BMDSF-R scores under traditional linear models and under GAM, (2) uses GAM to identify thresholds on the ITERS with respect to children’s cognitive and language development, and (3) examines whether GAM-derived thresholds and developer-recommended thresholds differentiate in a dissimilar way among children’s levels of cognitive and language development.

METHOD

Sample

The data used for this study were drawn from the Early Childhood Longitudinal Study, Birth Cohort (ECLS-B). The ECLS-B collected information on multiple indicators of children’s development and on children’s home experiences starting at birth through the first five years of life. It also collected information pertaining to children’s child care experiences beginning at age two for a subset of children.

The ECLS-B used a clustered frame sampling design of registered births, in which counties (or groups of adjacent counties) served as the primary sampling unit. Approximately 14,000 infants born to mothers over the age of 15 in 2001 were eligible to participate.¹ The ECLS-B researchers used home addresses on birth certificates to stratify the sample and to contact mothers to obtain consent for study participation. Of the 14,000 eligible infants, approximately 10,700 children participated in the study. The ECLS-B researchers collected the first wave of data on children and their home experiences at approximately nine months of age, then gathered follow-up data when the children turned two. When the children were two years old, the researchers identified those who attended out-of-home child care for at least 10 hours per week and asked their child care providers to participate in the study. The team then randomly selected approximately 1,400 of the 4,800 children in non-parental care for an in-depth observational study of their child care arrangement. Of these children, approximately 600 attended child care centers. These 600 children represent the analytic sample used for this study.

Measures

The ECLS-B team collected data through a variety of methods, including computer-assisted personal interviews with families and child care directors; self-administered questionnaires to families, teachers, and directors; and direct observation of children and the child care classroom.

Classroom quality: The Infant/Toddler Environment Rating Scale

The ECLS-B data collection team used the ITERS to assess the global quality of toddler child care classrooms. The ITERS consists of 41 items, organized into seven subscales: Furnishings and Display for Children, Personal Care Routines, Listening and Talking, Learning Activities, Interaction, Program Structure, and Adult Needs. The ECLS-B researchers decided that six items on the ITERS—two items pertaining to health and safety policies and four items pertaining to adult needs—were too distal to children’s development or redundant with information collected elsewhere and thus omitted these items, thereby reducing the ITERS to 35 items and six subscales. The ECLS-B team scored each item on a 1–7 Likert scale, with 1 representing poor quality and 7 representing excellent quality, then averaged these item scores to yield an overall ITERS score of 1–7. The average ITERS score in the full ECLS-B data was 4.24 points, with a standard deviation of 0.99 points, and a range from 1.63 to 6.76 points. The ECLS-B researchers reported that the ITERS had high internal consistency; with a Cronbach’s alpha value of 0.86 for the total score (Nord, Edwards, Andreassen, Green & Wallner-Allen, 2006).

Program, classroom, and staff characteristics

During the ITERS observation, the ECLS-B researchers also recorded the number of children and teachers in each of the sample children’s classrooms. They recorded three to six counts during different types of activities (e.g., free play, group activity) and used these counts to calculate average child-staff ratios and group sizes. In addition, the ECLS-B researchers conducted extensive telephone interviews and surveys with directors and teachers to yield information about staff educational backgrounds, including whether the directors/teachers held a bachelor’s degree, whether they had earned a degree in early childhood education or a related field, and their years of experience caring for young children. Directors also provided information about whether the center had any type of accreditation (e.g., local, state, or National Association for the Education of Young Children accreditation) and whether the study child’s classroom received Early Head Start funding.²

Child and family characteristics

When participating children were nine months and again when they were two years old, the ECLS-B researchers conducted interviews with parents (usually mothers) that yielded information related to the child’s age, gender, ethnicity, primary language spoken at home, and number of weekly hours the child attended child care. They also gathered information about parents’ education level, occupation, and income, and this information was summarized in a five-category socioeconomic composite measure of family social standing (see Duncan, 1961, for more information about the socioeconomic composite).

Cognitive development

To assess cognitive and language development, trained ECLS-B researchers administered the BMDSF-R (Bayley, 1993) mental development subscale to children at nine months and two years of age. The BMDSF-R for two-year-olds is a 33-item measure (it is 31 items at nine months), shortened from the original Bayley Scales of Infant Development, Second Edition (BSID-II) (Bayley, 1993). Items were chosen for ease of administration and robust psychometric properties, and the reduced measure was shown to retain the sound psychometric properties of the longer instrument (Andreassen & Fletcher, 2006). The BMDSF-R scale included items designed to assess early communication skills, expressive vocabulary, receptive vocabulary, listening comprehension, abstract thinking, and early problem-solving skills. The assessment presented children with a variety of tasks, such as naming pictures, demonstrating verbal comprehension, discriminating objects and pictures, comparing sizes of objects, and matching colors (Nord et al., 2006). The average BMDSF-R score for two-year-olds in the full ECLS-B sample was125.53 points, with a standard deviation of 10.99 points, and a range from 92.35 to 174.14 points.

Analytic Approach

Most studies that have examined relationships between children’s outcomes and child care quality measures have used linear regression models of the following form:

$${\mathit{Outcome}}_i=\mu +{\alpha }_1{X}_{1i}+\dots +{\alpha }_p{X}_{pi}+\beta {\mathit{Quality}}_i+{\epsilon }_i,$$

where for child i, Outcome_i represents the outcome, Quality_i denotes the vector of child care quality and characteristics, X_pi (k = 1,2,…,p) indicates the child-level covariates, and ε_i is a random error, commonly assumed to be normally distributed with mean 0 and constant variance. The main parameters of interest in these linear regression models are the fitted coefficients, β, that represent the predicted effects of various quality indicators (in this case, ITERS scores) on the outcomes of interest (in this case, BMDSF-R scores). Similar to Vandell et al. (2010), when we use causal language to describe the parameter β and the relationship between the ITERS and BMDSF-R, it is for heuristic purposes. Thus, terminology such as “effect,” “influence,” “impact,” or “contribution” is used to convey predictive or associative relationships, not necessarily causal relationships.

This study departs from this traditional linear model and adopts a non-parametric GAM model, which allows for more flexible modeling because the relationship between the outcome (BMDSF-R scores) and the independent variable (ITERS scores) is not necessarily assumed to be linear or known. GAM instead uses an equation of the following form:

$${\mathit{Outcome}}_i=\mu +f_1(X_{1i})+\dots +f_p(X_{pi})+g({\mathit{Quality}}_i)+{\epsilon }_i,$$

where f₁, …, f_p and g represent unknown, non-linear functions that are estimated non-parametrically, thus allowing the chosen model to better fit the data than a linear regression model and allowing for the identification of thresholds if they exist.

The non-parametric function g(Quality_i) also provides a better approximation of the effect of the quality indicator on the outcome than does βQuality_i from the linear regression model, because the non-parametric function does not assume that the effect of quality on outcomes is necessarily constant. For example, with linear regression, a one-unit increase in ITERS scores from 1.0 to 2.0 is assumed to have the same effect on BMDSF-R scores as a one-unit increase in ITERS scores from 5.0 to 6.0. However, GAM allows for non-linear estimates of effects in which an increase in an ITERS score from 1.0 to 2.0 could produce an increase in BMDSF-R scores, while an ITERS increase from 5.0 to 6.0 could have a different effect, for example, hypothetically resulting in no increase in the BMDSF-R scores. In this way, GAM facilitates the identification of “leveling-off” effects.

When using GAM to identify thresholds, we plot the raw values of the ITERS scores against the “smoothed” values from g(Quality_i). The smoothing parameters used for the estimation of g(Quality_i) are chosen by the generalized cross-validation method proposed by Wahba (1990), which entails using a subset of the sample to estimate a smoothing parameter, then using the remaining sample to determine whether the chosen parameter is optimal. The resulting GAM graph of raw values against the “smoothed” values provides a point-by-point estimate of the effect of each of the continuous levels of the ITERS on BMDSF-R scores. When the GAM graphs displays positive slopes, this denotes increasingly stronger effects of ITERS scores on BMDSF-R scores, whereas when the GAM graphs displays negative slopes, it denotes decreasing (i.e., weaker) effects. Thus, if there is a minimum threshold on the ITERS that must be exceeded before significant effects on cognitive and language development can be observed, it is expected that there will be flat or negative slopes in the GAM graph, followed by a sharp positive slope, denoting a surge in effect. Similarly, if there is a threshold indicating diminishing returns such that improvements in ITERS scores beyond this threshold are associated with only marginal gains in BMDSF-R scores, it is expected that there will be flat or negative slopes in the GAM plot in that ITERS range.

Independent variables

To account for child and family factors associated with child care quality and children’s cognitive outcomes (Burchinal, Peisner-Feinberg, Bryant, & Clifford, 2000; Lamb, 1998; Phillips, McCartney, & Scarr, 1987), we included gender, ethnicity, age (in months), hours enrolled in the center, whether the child’s primary language was English, and the child’s family socioeconomic status (a composite score clustered into five levels) in our models. In addition, we included the child’s prior BMDSF-R scores collected at nine months of age. Our models also controlled for several classroom- and center-level variables that are commonly included as part of states’ QRIS (Zellman & Perlman, 2008; Tout, Zaslow, Halle, & Forry, 2009). These variables included group size, staff-child ratio, whether the teacher or director had a bachelor’s degree, whether the teacher or director had a degree in early childhood education or a related field, teachers’ and directors’ years of experience, and whether the center was for-profit or accredited by a national, state, or local organization. For each analysis, we adjusted the standard errors using the Huber-White method to account for the complex sampling design.

RESULTS

Sample Characteristics

The sample composition was approximately 51% boys and 49% girls, with most children around two years of age at the time of assessment. With respect to socioeconomic status, the sample of children was almost evenly split among very low, low, medium, high, and very high composite scores. Forty-six percent of the sample was white, 28% African-American, and all the other racial/ethnic groups (i.e., Hispanic/Latino, Asian, and other) formed the remaining 17% of the sample. During the two-year-old assessment administration, children’s scores on the BMDSF-R scale ranged from 92.61 to 157.98 points, with an average score of 128.57 points and a standard deviation of approximately 11.02 points.

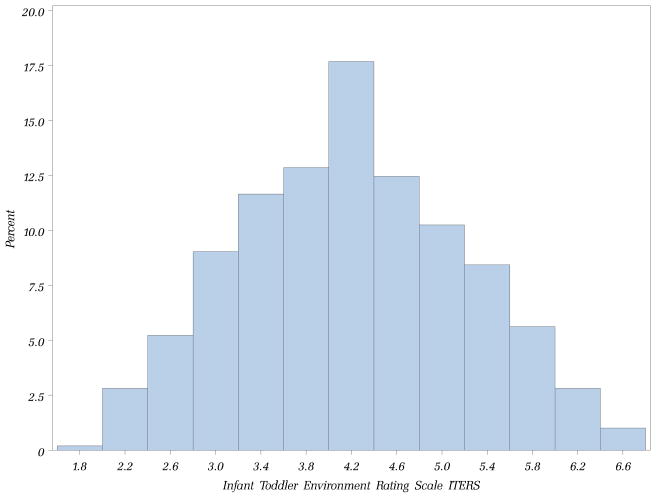
Toddlers spent on average 35 hours per week in center-based child care in an average classroom group size of nine children, with an average child-staff ratio of five to one. About 46% of the centers that children attended were for-profit; 32% were accredited by local, state, or national organizations; and 1% of classrooms were funded by Early Head Start. Due to the small sample of Early Head Start programs, this variable was dropped from the modeling. Directors had an average of six years of experience, with 54% holding at least a bachelor’s degree and 50% holding at least an associate’s degree in early childhood education or a related field. Teachers had an average of nine years of experience, but only 13% held at least a bachelor’s degree and 20% reported having at least an associate’s degree in early childhood education or related field. ITERS scores in the analytic sample varied from 1.82 to 6.76 points, with an average score of 4.19 points and a standard deviation of one point. As shown in Figure 1, the distribution was approximately normally distributed. This average score was about a point below what is commonly considered good quality, but it is similar to the average classroom quality observed in the United States (Helburn, 1995).

Figure 1.

Histogram of ITERS Quality

The initial sample of approximately 600 children decreased to approximately 500 children due to missing responses, mostly on the directors’ and teachers’ interviews. When comparing the sample used in the analysis to the sample of children who were not included in the analysis due to missing responses, only one significant difference emerged--the children included in the analytic sample were, on average, almost half a month younger than the children excluded from the analytic sample. This difference, while of little practical significance, was statistically significant because there was very little variability in the ages when children were assessed. Overall, we concluded that there was little difference between the missing and non-missing sample, suggesting that little chance of bias was introduced into the analysis through missing data.

Comparing the Relationship of ITERS Scores to BMDSF-R Scores Under the Traditional Linear and GAM Models

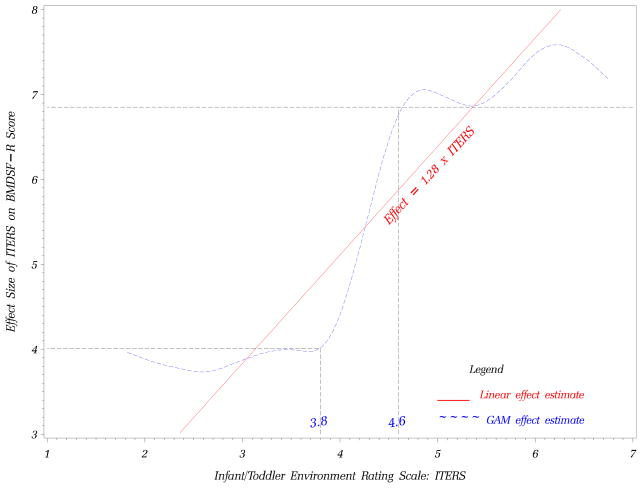
Figure 2 provides a graphical representation of the relationship between ITERS scores and BMDSF-R scores under the traditional linear model (indicated by the straight solid line) and under the GAM model (indicated by the dashed curve). The traditional linear model estimated the effect of classroom quality on children’s cognitive development as the average of the GAM model, such that for every unit increase on the ITERS, there was an expected increase of 1.28 points on the BMDSF-R, assuming all other variables remained constant. Figure 2 illustrates that the traditional linear approach did not provide as accurate a point-by-point estimate of the effect on BMDSF-R scores as the GAM analysis. Namely, the linear model underestimated the impact of quality on BMDSF-R scores for classrooms scoring below 3.0 and for classrooms scoring between 4.2 and 5.3. Within the range of 3.0 and 4.2, however, the linear model overestimated the impact of quality on BMDSF-R scores. The traditional linear model also suggested that improvements in ITERS scores from 5.0 to 5.8 were associated with improvements in BMDSF-R scores. In contrast, the GAM analysis did not support such an inference but instead indicated that an ITERS score of 5.0 had comparable effects on BMDSF-R performance as an ITERS score of 5.8.

Figure 2.

Plots of Predicted Effect Sizes under the Traditional Linear Regression and GAM

Note.

The GAM analysis used a smoothing spline with degrees of freedom DF = 5.

Using GAM to Identify Thresholds

Although the GAM analysis does not directly identify which specific cut-point(s) discriminate among different levels of BMDSF-R scores, it does delineate the ranges at which those cut-points are likely to exist. For example, the GAM plot showed a positive slope starting at an ITERS score of approximately 2.5, which suggests that the impact of quality on BMDSF-R scores began to increase at an ITERS score of 2.5. While it may be intuitively appealing to adopt a threshold of 2.5 on the ITERS, the graph also showed that an ITERS score of 2.5 was a global minimum (i.e., the value with the lowest predicted impact on the graph) and that the impact of quality on the BMDSF-R score at an ITERS score of 2.5 was relatively weak and not different from levels on the ITERS between 1.7 and 3.8. Based on the graph, we can establish a potentially more defensible cut-point for the ITERS at 3.8, where the estimated impact for all ITERS scores below that threshold was estimated to be similar to or slightly weaker than the expected impact for an ITERS score of 3.8. Put another way, up to a score of 3.8, the ITERS had a predicted contribution of no larger than four points on BMDSF-R scores; however, beyond a score of 3.8, the ITERS showed increasingly stronger effects. Thus, 3.8 represents a cut-point on the ITERS that can potentially distinguish between weaker and stronger effects on children’s BMDSF-R scores.

Similar reasoning can be applied to identify an upper threshold. While a score of 4.8 on the ITERS indicated a relatively strong impact on cognitive development, it was also a local maximum (i.e., the impact of the ITERS on BMDSF-R scores increases up to the local maximum, then decreases from that point), and there were slight declines in the influence of classroom quality on BMDSF-R scores between the range of 4.8 and 5.3 on the ITERS. Instead, a potentially more meaningful cut-point on the ITERS can be found at 4.6, where the model predicted that classes that met or exceeded this threshold would show relatively strong effects of approximately 6.8 points or higher on BMDSF-R scores.

We can potentially establish a final threshold on the ITERS at 5.4, where the graph indicated sharply increasing effects of quality on BMDSF-R scores. However, when we conducted additional statistical analyses to determine the feasibility of a cut-point at 5.4 (see below for the discussion), the results did not support a significant threshold.

Adopting the visually observed thresholds at 3.8 and 4.6 on the ITERS, we then classified children into three groups. The first, the “GAM Poor Quality” group, consisted of children in classrooms with scores less than or equal to 3.8, where the GAM analysis indicated that the effect of ITERS scores up to 3.8 was constant and relatively weak. The second group, “GAM Transitional Quality,” included the children in classrooms with scores greater than 3.8 but less than or equal to 4.6. Within this range, the effects of classroom quality on BMDSF-R scores were linearly increasing and more pronounced than for the previous group but weaker than those observed in the next group. The final group, the “GAM Good Quality,” consisted of children in classrooms with ITERS scores above 4.6. Within this range, the model predicted the influence of the ITERS on BMDSF-R scores to be relatively strong. Thirty-five percent of children were in the GAM Poor Quality group, 31% were in the GAM Transitional Quality group, and 33% were in the GAM Good Quality group.

For analytical comparison, we also classified children into three quality groups corresponding to the ITERS-developers’ recommended cut-points (Harms, Clifford, & Cryer, 1990). The “Developer Poor Quality” group included children in classrooms with ITERS scores less than or equal to 3.0, the “Developer Transitional Quality” group included children in classrooms with ITERS scores greater than 3.0 but less than or equal to 5.0, and the “Developer Good Quality” group included children in classrooms with ITERS scores greater than 5.0. Thirteen percent of children were in the Developer Poor Quality group, 64% were in the Developer Transitional Quality group, and 23% were in the Developer Good Quality group.

Using Piecewise Regression to Validate the Selection Thresholds

Because GAM requires investigators’ judgments as to where the thresholds should be established, it is important to examine the validity of the visually chosen thresholds through other statistical methods. Thus, we examined the validity of the GAM-derived and developer-recommended thresholds in two ways, the first of which was the group slope method. For the group slope model, we used a piecewise regression to determine whether the identified thresholds represented meaningful splits in the data. If the thresholds were meaningful, the relationship between ITERS scores and BMDSF-R scores would be expected to vary across the different regions defined by the thresholds. For example, if there were two thresholds denoted as T₁ and T₂, and T₁ was the lower threshold and T₂ was the upper threshold, there would be three potential regions where the ITERS slopes could vary: (1) between 1 (the lowest score on the ITERS) and T₁; (2) between T₁ and T₂; and (3) between T₂ and 7 (the highest score on the ITERS). We used an F-test of nested linear models to determine whether the piecewise regression model was a better fit to the data than the traditional linear model.

Table 1 compares the traditional linear regression model to the two piecewise regression models, the first of which used the developer-recommended thresholds and the second of which used the GAM-observed thresholds.³ As Table 1 shows, the traditional linear model indicated that the ITERS was a significant predictor of BMDSF-R scores, with a one-point improvement on the ITERS associated with a 1.28-point (effect size = 0.12) increase in children’s BMDSF-R scores. In a similar vein, the piecewise regression model for the developers’ recommended cut-points suggested that the ITERS was a significant predictor of BMDSF-R scores in the Developer Transitional Quality group, in which a one-point improvement on the ITERS was associated with a 1.87-point (effect size = 0.12) increase in children’s BMDSF-R scores. However, the ITERS was not significantly associated with BMDSF-R scores in the Developer Poor Quality and the Developer Good Quality groups. Furthermore, an F-test for nested models indicated that the piecewise regression model using the developer-recommended thresholds was comparable to the traditional linear model with respect to model fit (F-statistic = 0.81, n.s.).

Table 1.

Regression Coefficients for the ITERS under the Traditional Linear and Piecewise Regression Models

Parameter	Traditional Linear Model		Piecewise Regression Models
			Developer’s Thresholds		GAM Thresholds
	R2 = 0.28, AIC = 3646.6		T1 = 3.0, T2=5.0		T1 = 3.8, T2 = 4.6
			R2 = 0.28, AIC = 3,649.7		R2 = 0.29, AIC = 3,645.9
	Est.	Std. Err.	Est.	Std. Err.	Est.	Std. Err.
BMDSF-R mental score (9 months)	0.25 **	0.04	0.25 **	0.04	0.25 **	0.04
Black	−4.24 **	1.14	−4.24 **	1.15	−4.32 **	1.16
Other race/ethnicity	−1.14	1.17	−1.16	1.15	−1.27	1.11
Male	−1.40	0.90	−1.45	0.89	−1.46	0.88
Child’s age (months)	1.34 **	0.37	1.34 **	0.37	1.33 **	0.38
Weekly hours in care	0.00	0.05	0.00	0.05	−0.01	0.05
Primary language is English	1.32	2.15	1.32	2.15	1.43	2.22
Low to median socioeconomic composite	0.84	1.69	0.81	1.70	0.74	1.70
Median socioeconomic composite	2.28	1.58	2.41	1.55	2.42	1.58
Median to high socioeconomic composite	5.25 **	1.43	5.35 **	1.42	5.40 **	1.45
Highest socioeconomic composite	7.46 **	1.69	7.54 **	1.70	7.65 **	1.74
Group size	0.01	0.13	−0.01	0.13	−0.03	0.13
Child-staff ratio	0.02	0.25	0.04	0.26	0.07	0.27
Teachers with ECE degree	−0.41	1.21	−0.33	1.21	−0.28	1.21
Teachers’ years of experience	−0.02	0.06	−0.03	0.06	−0.03	0.06
Teachers with bachelor’s degree	0.61	1.46	0.54	1.44	0.60	1.41
Director with ECE degree	−1.03	1.07	−0.95	1.06	−0.96	1.04
Director’s years of experience	−0.03	0.07	−0.03	0.07	−0.03	0.07
Director with bachelor’s degree	−0.60	0.79	−0.60	0.80	−0.63	0.80
For-profit center	0.23	0.96	0.30	0.96	0.30	0.96
Accredited center	2.93 **	0.94	2.90 **	0.94	2.80 **	0.93
ITERS (traditional model slope)	1.28 *	0.49
ITERS slope:
Poor Quality group: 1 ≤ ITERS ≤ T1			−0.96	2.36	−0.64	1.31
Transitional Quality group: T1 < ITERS ≤ T2			1.87 *	0.72	5.05 **	1.63
Good Quality group: T2 < ITERS ≤ 7			0.29	1.31	−0.30	0.94

Notes.

ECE = early childhood education.

T₁ is the lower threshold and T₂ is the upper threshold, which varies by the method used to select the thresholds.

AIC denotes the Akaike Information Criteria for model comparison.

^*p < .05,

^**p < 0.01.

In contrast, when we conducted a statistical test comparing the traditional linear model with the piecewise regression model that used the GAM-derived thresholds to split the data, the results suggested that the piecewise model with the GAM-derived thresholds was a better fit to the data than the linear model (F-statistic = 3.64, p-value < 0.05). The piecewise regression results also indicated that the relationships between ITERS scores and BMDSF-R scores were not the same in the three groups. The ITERS was not significantly related to BMDSF-R scores in the GAM Poor Quality group, but the ITERS was significantly related to BMDSF-R scores in the GAM Transitional Quality group. In that group, a one-point increase on the ITERS was associated with a 5.05-point (effect size = 0.14) increase in BMDSF-R scores. In the GAM Good Quality group, there was again no relationship between the ITERS and BMDSF-R scores.

Because the GAM plot suggested the possibility of a threshold at an ITERS score of 5.4, we conducted a sensitivity analysis using a piecewise linear regression with an additional threshold at 5.4. The results estimated a slope for ITERS beyond 5.4 at β = 2.09 (effect size = 0.04), but it was not statistically significant, suggesting that the ITERS impact in the range from 4.6 to 5.4 was similar to the impact beyond 5.4. Furthermore, the F-test confirmed that an additional threshold was not supported at 5.4.

Overall, the pattern of findings for the piecewise regression mirrored the results of the GAM analyses. The piecewise regression results supported the existence of a threshold at 3.8, which appeared to be the cut-point that must be exceeded before the effects of quality, as measured by the ITERS, can be observed on BMDSF-R scores. Between the ITERS range of 3.8 and 4.6, there was a strong relationship between ITERS scores and BMDSF-R scores. However, improving ITERS scores beyond 4.6 (i.e., between the range of 4.6 and 7) was not associated with significant improvements on the BMDSF-R scores. Although the GAM plot suggested the possibility of improvements beyond an ITERS score of 4.6 (at around 5.4), the piecewise regression results indicated that the increases in BMDSF-R scores were not large enough to show a significant impact on BMDSF-R scores.

Using Linear Models with Quality Groups to Explore the Validity Thresholds

As a second means to evaluate the validity and feasibility of the GAM and developers’ thresholds, we used a group category model. With this approach, we conducted a linear model analysis in which we replaced the ITERS scores for the quality group indicators defined by the thresholds from the GAM-derived analyses and from the developers’ recommendations. Significant differences in performance among the different quality-level groups would provide validity support for the selection of the chosen thresholds. That is, if the thresholds were meaningful, we would expect children in the GAM (or Developer) Poor Quality group to perform significantly worse on the BMSDF-R than children in the GAM (or Developer) Transitional Quality and GAM (or Developer) Good Quality groups.

As shown in Table 2, there were no significant differences in BMDSF-R scores among the three groups using the developers’ conceptualization for thresholds. However, when we applied the GAM-derived thresholds, the GAM Good Quality group showed significantly better BMDSF-R scores than the GAM Poor Quality group (i.e., 2.66 more points, p-value < 0.05). It is worth noting, however, that this improvement in BMDSF-R scores by 2.66 points for the GAM Good Quality group is equivalent to an effect size of 0.10, while the non-significant improvement in the Developer Good Quality group is equivalent to an effect size of 0.08.Thus, although there were differences in their statistical significance, the two effect sizes were practically similar. Both of these effect sizes can be considered modest as the commonly used recommendations of Cohen (1988) suggests that effect sizes around 0.10 be regarded as modest.

Table 2.

Regression Coefficients for Different Quality Groups Using the Developers’ and GAM-Derived Thresholds

Parameter	Developers’ Thresholds		GAM Thresholds
	T1 = 3.0, T2 = 5.0		T1 = 3.8, T2 = 4.6
	R2 = 0.27, AIC = 3,653.2		R2 = 0.28, AIC = 3,649.5
	Est.	Std. Err.	Est.	Std. Err.
ITERS:
Poor Quality group: 1 ≤ ITERS ≤ T1 (comparison)
Transitional Quality group: T1 < ITERS ≤ T2	1.35	1.23	0.48	1.07
Good Quality group: T2 < ITERS ≤ 7	2.79	1.40	2.66 *	1.09

Notes.

These models controlled for all the covariates used in Table 1.

T₁ is the lower threshold and T₂ is the upper threshold, which varies by the method used to select the thresholds.

AIC denotes the Akaike Information Criteria for model comparison.

^*p < .05.

^**p < 0.01.

Comparing GAM-derived thresholds to the developers’ thresholds

To compare the performance of the developer-recommended and GAM-derived threshold models, we used the Akaike Information Criterion (AIC; Akaike, 1974) and the Davidson-MacKinnon J-test (Davidson & MacKinnon, 2002) for non-nested models. AIC measures the relative goodness of fit of a statistical model and estimates relative support for the model. It provides a comparison of model fit between two models, such that the model with the smaller AIC value describes the data better. However, because AIC cannot provide a classical test statistic for non-nested models, the J-test represents an alternative test for model comparison. The J-test method uses “double testing” to determine whether one model (e.g., GAM thresholds) contains additional explanatory information not captured by another model (e.g., developer thresholds) by including the fitted values of the second model in the set of regressors in the first model. If the first model best fits the data, then the fitted values of the second model should not provide any additional improvements in model fit over and beyond the first model. The test is then repeated “in reverse,” with the fitted values of the first model included in the set of regressors in the second model so as to determine the robustness of the results.

There was almost a four-point drop in the AIC value from the developer to the GAM thresholds group model, suggesting that the GAM thresholds model fit the data better than the developer thresholds model. The J-tests also suggested that, after fitting the regression model that included the ITERS groups defined by the GAM analysis, the inclusion of the developer-recommended thresholds did not add any additional information (J-test = −0.06, n.s.). In contrast, we obtained a significant improvement in model fit when we added the GAM-derived threshold groups to the regression model that included the groups defined by the developers’ thresholds (J-test = 1.19, p-value < 0.05). These findings suggested that at least for this sample, the GAM-derived thresholds had better discriminating power than the developers’ recommended thresholds with respect to the BMDSF-R scores.

Conducting Sensitivity Analysis on the ITERS Subscales

An important issue to examine is the mechanisms by which the ITERS may influence children’s cognitive development. Thus, we examined the relationships between BMDSF-R scores and the ITERS subscales to determine whether the thresholds observed on the total ITERS score were consistent across the different subscales or whether particular subscales were driving the results (see Appendix A for descriptive statistics, Cronbach’s alpha coefficients, and intercorrelations among the subscales). Table 3 provides the regression coefficients for each of the subscales under the traditional linear model. Because the ITERS is a linear combination of all the subscales, this analysis is equivalent to the traditional linear model in Table 1, except that we are able to isolate the different effects each subscale has on the outcome. As shown in Table 3, only the Interactions subscale was significantly related to BMDSF-R scores.⁴

Appendix A.

Descriptive Statistics, Cronbach Alphas, and Intercorrelations for the ITERS Subscales

Subscales	Mean	Std. Err.	Alpha	Correlation Between Subscales
				(1)	(2)	(3)	(4)	(5)
(1) Furnishings and display	4.48	1.15	0.81	—
(2) Personal care routines	2.95	1.23	0.76	0.48	—
(3) Listening and talking	4.91	1.73	0.86	0.43	0.37	—
(4) Learning activities	4.28	1.09	0.77	0.62	0.50	0.62	—
(5) Interactions	5.08	1.59	0.86	0.37	0.52	0.60	0.52	—
(6) Program structure	4.70	1.59	0.80	0.51	0.48	0.56	0.56	0.72

Table 3.

Regression Coefficients for the ITERS Subscales Under Different Model Specifications

Model	Subscale predictor	Model
		Est.	Std. Err.
Traditional linear model for ITERS subscales: R2 = 0.29	Furnishings and display	0.52	0.51
	Personal care routines	−0.29	0.41
	Listening and talking	0.05	0.34
	Learning activities	0.48	0.59
	Interactions	1.21 **	0.43
	Program structure	−0.57	0.52
Piecewise Regression model R2 = 0.29	Interactions subscale: slope estimates in quality groups
	Lower-quality group: 1 ≤ ITERS ≤ 4.2	0.63	0.67
	Upper-quality group: 4.2 < ITERS ≤ 7	1.55 **	0.53
Group Category Regression model R2 = 0.30	Interactions subscale: Lower-quality as comparison group
	Lower-quality group: 1 ≤ Interactions ≤ 4.2	NA	NA
	Upper-quality group: 4.2 < Interactions ≤ 7	5.13 **	1.60

Notes.

These models controlled for all the covariates used in Table 1.

We conducted piecewise regression and group category regression analyses only on the Interactions subscale because this was the only subscale that was significantly related to the ITERS under the traditional linear model.

^*p < .05.

^**p < 0.01.

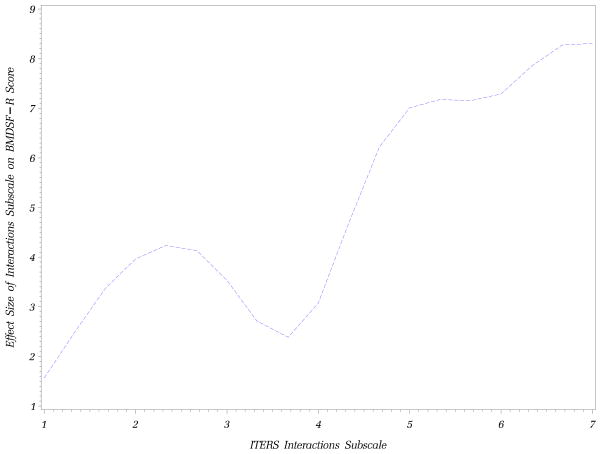
We then conducted GAM on the Interactions subscale (see Appendix B for the GAM plot). Using a reasoning process similar to that used to identify the upper threshold on the total ITERS score; we identified a potential threshold of 4.2 on the Interactions subscale. We adopted this 4.2 score as a cut-point to define a Lower Interactions Quality group and an Upper Interactions Quality group, then used piecewise regression and group category regression to determine whether the slopes differed between the two groups, and whether there were mean differences in BMDSF-R scores (see Table 3 for the regression results). As shown in Table 3, there was evidence for the validity of a threshold at 4.2 on the Interactions subscale. Namely, there were significant differences in BMDSF-R scores, with the Upper Interactions Quality group scoring more than five points higher than the Lower Interactions Quality group. In addition, the relationship between BMSDSF-R scores and interactions differed between the two groups, such that there was no relationship between interaction quality and BMDSF-R performance for the Lower Interactions Quality group, but there was a significantly positive relationship for the Upper Interactions Quality group. Thus, 4.2 represents a minimum level of quality that must be exceeded before the Interactions subscale begins to shown significant relationships to BMDSF-R scores. In addition, there was no statistical evidence of a leveling off effect, as the relationship between BMDSF-R scores and the Interactions subscale continued to be positive, even at the upper end of the Interactions subscale.

Appendix B.

Plot of Predicted Effect Sizes under the GAM Model for the Interactions Subscale

DISCUSSION

The growing prominence of high-stakes child care quality initiatives, such as QRIS and other quality benchmarking efforts, has created an immediate need for research to help states establish defensible thresholds on classroom quality measures—thresholds that meaningfully differentiate among categories of care associated with different levels of children’s cognitive development. To date, thresholds have largely been informed by expert opinions and theoretical expectations (Zellman & Perlman, 2008). This study suggests that GAM may be a useful tool for informing these efforts by identifying cut-points on quality measures that distinguish ranges on the scale that are most strongly associated with children’s developmental outcomes.

In particular, this study found that the overall ITERS could be constructed in such a way as to yield two distinct thresholds associated with different levels of toddler’s cognitive functioning. The first threshold occurred at approximately 3.8, and represents the point on the ITERS quality continuum that must be exceeded before positive relationships to toddlers’ cognitive development can be observed. Classrooms that have achieved a score of at least 3.8—a score between the developer’s definition of mediocre and good quality—have typically met specific criteria on the ITERS, indicating that they structure their days and environments in a manner that offers toddlers adequate learning materials and access to these materials for at least some of the day. Children in these classrooms also experience mostly positive interactions with their teachers, and such interactions may enable children to actively explore their environments and take advantage of these learning materials.

The second threshold was observed at approximately 4.6 on the ITERS, where the GAM plot showed strong impacts of classroom quality on BMDSF-R scores. This may reflect the fact that constructs measured on the ITERS at a score of 4.6 and beyond tend to focus more on teacher and classroom processes (Moore, 1994), such that children have access to learning materials for most of the day and teachers are frequently engaged with children via materials and everyday routines. Not surprisingly then, as shown by the group category analysis, toddlers in classrooms with ITERS scores that exceeded 4.6 (i.e., the GAM Good Quality group) showed higher BMDSF-R scores than the GAM Poor Quality group. While these effects were modest, with effect size improvements in BMDSF-R scores ranging from 0.11 to 0.14, they were also consistent with the effect sizes found in other studies that examined the effect of child care quality on toddler’s BMDSF-R scores (e.g. NICHD Early Child Care Research Network and Duncan, 2003b; Sylva et al. 2011).

This study also suggests that, with respect to the total ITERS score, the greatest improvements in children’s cognitive and language development would likely occur by helping classrooms improve their quality to scores in the range of 3.8 and 4.6 on the ITERS. Classrooms with ITERS scores between 1 and 3.7 had a comparable and weak association to cognitive and language development; thus, policies aiming to improve quality to levels that affect children’s cognitive and language development may need to incentivize classrooms to surpass an ITERS score of 3.8. Between scores of 4.6 and 7.0, improvements in the ITERS might not lead to marked differences in children’s cognitive and language development, at least for toddlers. However, the leveling-off effect should not be used as a reason to discontinue efforts to improve a child’s learning environment once the classroom environment surpasses the 4.6 threshold. Instead, the results of this study may suggest the limited utility of the ITERS in measuring the types of teacher-child interactions that are more strongly related to cognitive and language development. Namely, as a measure of global process quality, the ITERS may not be sufficiently sensitive in capturing care and instructional practices, such as caregiving responsiveness and effective instructional techniques that have been shown to be important predictors of toddler’s cognitive development (Katz & Chard, 2000).

Indeed, the subscale analysis lent support to the notion that the leveling-off effect on the total ITERS score may be an artifact of the construction of the ITERS, which places greater emphasis on structural quality than on specific care and instructional practices. Of the six administered subscales, the Interactions subscale is arguably the most process-oriented and notably, the only subscale that showed a significant relationship to BMDSF-R scores. A GAM plot of the Interactions subscale showed roughly the same pattern as the overall ITERS, such that the strongest relationships between quality and BMDSF-R performance occurred in the quality score range of approximately four to five points. However, unlike the overall ITERS, the Interactions subscale did not show diminishing returns at the upper end of the quality scale. This suggests that the leveling-off effect observed on the overall ITERS may be attributable to the greater focus on structural quality than on process quality by the remaining subscales. This finding also suggests that positive and responsive teacher interactions are a key mechanism by which children learn and develop.

It is important to emphasize that the thresholds identified in this study should not be interpreted as definitive. Had we examined different developmental outcomes or different age or socioeconomic groups, it is likely that different thresholds would have emerged. For example, given that the lower end of the ITERS focuses on health and safety practices, had we chosen to examine children’s health outcomes, it is likely that we may have identified lower thresholds than those identified for cognitive outcomes. In a similar vein, if we had chosen to examine children’s social development, it is possible that higher thresholds may have emerged because, unlike cognitive development, which may be influenced to some extent by the physical learning environment, social development is largely dependent on interactional processes between children and their caregivers (Bowlby, 1969; DeMulder, Denham, & Mitchell-Copeland, 1997), which are measured at the higher end of the ITERS (Moore, 1994).

This study also only examined thresholds related to differences in toddlers’ cognitive development. Infant development—even more so than toddler development—unfolds within the context of caregiving relationships (Shonkoff & Phillips, 2000); in contrast to toddlers, the physical learning environment is not as crucial for infants’ cognitive development as the affective learning environment. To help organize perceptual and sensory input, infants, more so than toddlers, rely on their caregivers to access their environment and to create experiences that build on one another. Consequently, thresholds on the ITERS that differentiate between infants’ levels of cognitive development may be higher than those found in this study of toddlers. Such findings may suggest the need for different QRIS rating criteria for infant and toddler classrooms.

It is also important to note that child care quality has been found to contribute more to the development of lower-income children than to their more advantaged counterparts (Burchinal et al., 2000), which may mean that lower thresholds on the ITERS may be found for higher-risk samples of children than for more affluent samples of children. Thus, it will be very important to replicate these findings with diverse populations of children, providers, and programs. On a related note, it is possible that using a strictly empirical approach, such as GAM, can result in a model that overfits the data. That is, the quality thresholds that we identified may be limited to the particular data at hand, but different analytic samples could yield slightly different cut-points. Additionally, our study may reflect self-selection effects. Although we controlled for children’s BMDSF-R performance at nine months—a covariate that is likely to be related to unobserved self-selection covariates that are also related to the outcome—the nine-month measure assesses different types of skills and knowledge than the two-year measure, so it is unknown whether the observed differential associations are attributable to selection biases. Although the inclusion of BMDSF-R scores at nine months mitigates the potential bias resulting from unmeasured self-selection characteristics, future research should nonetheless explore the robustness of the quality thresholds across different populations, particularly in a randomized context.

Potential differences in thresholds across outcome measures and populations of children may limit the utility of GAM as a method to help inform cut-points on quality measures. While it would be ideal to identify a single threshold that would exist across all outcomes, all age groups, or all income levels, it might be unrealistic to expect uniformity in the cut-points and similar strengths of associations. Consequently, even if GAM could be used to identify statistically meaningful thresholds, state-level policymakers will have to weigh all the empirical thresholds and their goals for children to create effective policies.

There are also other limitations to using GAM in policy contexts. Because GAM requires visual inspection, there can be differences in the interpretations of the GAM plots. While cut-points identified by visual inspection should be validated empirically through other means (such as piecewise regression or linear models using quality groups defined by the GAM-derived thresholds), there is still the possibility that the GAM graphs will support different but equally viable alternative thresholds. While these thresholds may lead to slightly different quality classifications or reimbursements for centers, it is essential to recognize that any cut-points will introduce artificial variation between centers that are on the cusp of two different levels.

Furthermore, while GAM may be able to empirically identify meaningful thresholds, it does not obviate the need for policymakers to consider other practical issues when setting thresholds, such as those relating to comparability. For example, if there were strong linear relationships between ITERS scores and outcomes in a specific range of ITERS scores defined by observed thresholds (i.e., the slope is particularly steep within the defined quality range), children with scores at the lower end of that range (delimited by the thresholds) may score significantly worse than children with quality scores at the upper end of the range. In this particular case, adopting thresholds at these two points may result in combining or labeling of two or more groups of children who are qualitatively very different. Instead, policymakers may wish to adopt additional thresholds at a different point (e.g., a mid-range point) than would be suggested by the GAM analysis. These types of considerations underscore the complexity of setting quality thresholds in policy contexts that go beyond empirical considerations alone.

As states continue to develop and implement QRIS and other early childhood education accountability systems, there is an increased need for research that assists policymakers in setting meaningful benchmarks of quality and in directing public dollars effectively. GAM appears to be a promising method to inform these efforts. However, further research is needed to replicate these findings, to explore thresholds related to other developmental domains, and to determine whether those thresholds apply for various groups of children and early childhood education programs.