Abstract
Since the invention of cancer radiotherapy, its primary goal has been to maximize lethal radiation doses to the tumor volume while keeping the dose to surrounding healthy tissues at zero. Sadly, conventional radiation sources (γ or X rays, electrons) used for decades, including multiple or modulated beams, inevitably deposit the majority of their dose in front or behind the tumor, thus damaging healthy tissue and causing secondary cancers years after treatment. Even the most recent pioneering advances in costly proton or carbon ion therapies can not completely avoid dose buildup in front of the tumor volume. Here we show that this ultimate goal of radiotherapy is yet within our reach: Using intense ultra-short infrared laser pulses we can now deposit a very large energy dose at unprecedented microscopic dose rates (up to 1011 Gy/s) deep inside an adjustable, well-controlled macroscopic volume, without any dose deposit in front or behind the target volume. Our infrared laser pulses produce high density avalanches of low energy electrons via laser filamentation, a phenomenon that results in a spatial energy density and temporal dose rate that both exceed by orders of magnitude any values previously reported even for the most intense clinical radiotherapy systems. Moreover, we show that (i) the type of final damage and its mechanisms in aqueous media, at the molecular and biomolecular level, is comparable to that of conventional ionizing radiation, and (ii) at the tumor tissue level in an animal cancer model, the laser irradiation method shows clear therapeutic benefits.
Keywords: biophotonic, femtosecond laser, radiobiology, radiation sciences
Radiation therapy is the most widely used modern cancer treatment and continues to play an irreplaceable role in the management of a vast array of potentially curable malignancies (1). Many of the most recent advances in conventional radiation therapy have derived from innovations, and technology and engineering developments, of three-dimensional computer imaging techniques (2). These advances have led to sophisticated radiation therapy methods such as intensity-modulated radiation therapy (IMRT) (3) and many others. As with all advances in radiation therapy, the final goal of these technology improvements is to deliver the highest possible energy dose to the tumor volume while sparing surrounding normal tissues. This is the most important challenge to modern radiotherapy because all high-energy photons or electrons used in the clinic result in a dominant entrance dose in front of the tumor and a nonnegligible exit dose behind it (Fig. 1D) (4). Proton and heavy ion beams (mainly carbon beams) have a much more desirable dose deposition patterns for the individual particle trajectories (5). However, even here the entrance dose in healthy tissue of the actual therapeutic many-particle beams used on patients is about 20–70% of the dose in the “spread out Bragg peak” placed in the tumor volume (Fig. 1D) (5). While such results are certainly an improvement on radiation therapy using X or γ rays, the very high costs of proton or carbon ion beam irradiation facilities, however, drastically limits their widespread clinical availability (6). The unwanted irradiation of healthy tissue surrounding tumors may not only lead to secondary cancers in young patients (3), but it more importantly constrains clinicians to optimize radiation doses according to the overall tolerance of the healthy tissue rather than giving a therapeutic high dose allowing the elimination of all cancer cells. Moreover, irradiating healthy tissue near tumors promotes invasion and migration of cancer cells, leading to metastasis. Thus, it is the utmost challenge to develop a novel irradiation method, or source, with much more advantageous dose distribution properties that allow us to avoid damage to healthy tissue surrounding the malignant tumors. Such improvement to radiation therapy has, as its ultimate goal, to deposit the highest possible dose of spatially concentrated energy density (so far only from ionizing radiation), at the highest possible temporal dose rate (mainly to overload the tumor’s cellular repair mechanisms), exclusively to the tumor volume, while leaving the surrounding healthy tissue in a pristine and undamaged state as the so-called “dream beam” (Fig. 1D). Moreover, the dose delivered to a specific volume inside the medium, or organism, must be controllable in both space and time to cover the entire range of tumor extent or response to such energy depositions.
Fig. 1.
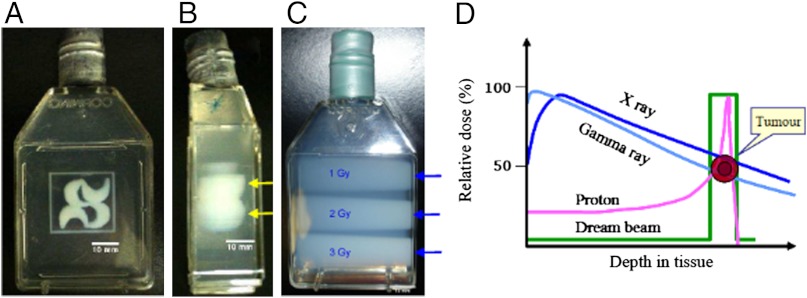
Photographs of containers filled with optically transparent radiologically tissue-equivalent polymer gel dosimeter and irradiated with fs laser pulses (approximately 400 μm × 400 μm) to draw the logo of Université de Sherbrooke (A) top view and (B) side view. The entrance dose was effectively zero up to a certain depth, which in B was wave modulated (yellow arrows) by changing the laser pulse duration (input beam from the right of the container) to show depth control of the zero dose region before the target volume in which filamentation occurs. The length of the filamentation tracks—i.e., their end—is controlled in part by the physical geometry of the optics (e.g., lenses) as well as the energy (intensity) per laser pulse at a given pulse width, ceteris paribus, for laser pulse energies above filamentation threshold and below dielectric breakdown (10, 11). In C, the polymer gel was irradiated with X-rays (150 kVp) from a clinical X-ray therapy system (Therapax HF150T) at 1, 2, and 3 Gy and clearly shows that the deposited dose is maximum upon “tissue entry” (blue arrows). D is a comparison of depth-dose distributions of various conventional radiation modalities related to radiation therapy.
While numerous biomedical applications of ultra-fast lasers have been established (7), they are not used for radiotherapy of tumors that reside macroscopic distances inside human tissue. This is of interest, because, e.g., many of the modern, long wavelength high power lasers can deliver high energy density pulses (i.e., doses and dose rates), which in principle surpass any clinical radiation sources. Thus, some of the fundamental questions that arise naturally from this fact are (i) Can lasers, non-linear optics, and near visible photons (IR, visible) be used to somehow generate a true radio-therapeutic effect, not upon entry in the tissue, but a macroscopic distance within a tissue? and (ii) Can IR lasers in particular, which emit non-ionizing radiation, replace ionizing radiation (viz radioactive materials) in some cancer treatments? In other words: Can nonlinear energy deposition of laser light be adapted to circumvent the main fundamental problem of dose distribution upon tissue entry that persistently plagues modern radiation therapy using ionizing radiation. Nonlinear energy deposition can occur during the propagation of a powerful femtosecond laser pulse in a medium such as water, when the intensity of the light is sufficiently high so that its electromagnetic field will strongly perturb and change the optical properties of the medium. Some phenomena related to nonlinear laser interaction are already used in cancer treatments—e.g., two-photon photodynamic therapy (8, 9).
Here, we propose that the main problem of radiotherapy (i.e., the undesirable dose distribution upon tissue entry) can be solved by a nonlinear photonic process called filamentation (10, 11). This process is related to the self-focusing of an intense laser pulse, induced by the Kerr effect, counterbalanced by defocusing induced by subsequent laser-plasma interactions. The Kerr effect is characterized by a nonlinear change in the refractive index of a medium (e.g., water), which varies proportionately with the square of the electric field strength. Applied to intense laser pulses with Gaussian intensity profiles, this local, nonlinear change of refractive index acts as a convex lens and results in intense self-focusing of the laser beam along its propagation axis. Thus, after some propagation distance, the laser intensity becomes so high that it overcomes the thresholds for both multi-photon ionization and the tunnel effect, creating free electrons. Especially in a medium with a density close to water, these first events of ionization are followed by the inverse Bremsstrahlung effect (10, 11), in which the free electrons are accelerated in the laser’s strong field until they reach the ionization threshold of water molecules, thus producing further free electrons, with low kinetic energies below the ionization threshold. As a result, this high-density avalanche of low-energy free electrons (up to 1018 electrons/cm3) generates a local plasma (12). The interaction of the laser light with the highly defocusing environment created by this plasma will now diverge the laser beam, such that the resulting decrease in light intensity will arrest the process of plasma generation, thus allowing the laser pulse to undergo self-focusing again at a slightly different position along the lase pulse propagation axis. This dynamic equilibrium between Kerr-effect self-focusing and plasma-induced defocusing continues as long as the laser pulse intensity, which slowly decreases due to such energy transfers to the medium, is sufficiently high to allow the appearance of such nonlinear processes such as the Kerr effect. The two counterbalanced processes keep the filament core intensity almost constant below the optical breakdown threshold, yielding a self-regulated generation of spatially homogenous low-density plasma spots along the laser-beam propagation axis. This kind of plasma makes it possible to produce a high rate of ionizations in the heart of such filaments, while minimizing thermo-mechanical effects related to “hot” high-density plasmas (bubble formation, shock wave emission and transient cavitation due to optical breakdown) (13–16). These ionizing properties of laser induced filamentation are thus proposed here to give rise to changes in the medium that are equivalent to conventional ionizing radiation used in radiotherapy. Indeed, conventional high energy ionizing radiation, such as X or γ rays, generates radicals, ions, and secondary electrons as it travels through biological systems. The majority of secondary electrons generated are low energy electrons (LEEs) with energies below 20 eV (5 × 104 electrons per MeV) (17), which in themselves are genotoxic (18). In living tissue, the interaction of conventional ionizing radiation with water leads to the production of highly reactive and unstable free radicals, or reactive oxygen species (ROS), and is responsible for a large part of the deleterious effects of radiation because these radicals and ROS react with the cellular DNA, thereby producing mutations and cell death. As we show here, IR laser-pulse-induced filamentation produces the same reactive species as the radiolysis of water by ionizing radiation (see below). Furthermore, the potential usefulness of low-density plasma generation for radiobiological purposes has already been highlighted (13, 19–21). More importantly, as we show here, the filamentation process has the advantage of allowing large energy depositions, not upon entry in the medium but deep inside a well-controlled macroscopic volume, because the depth at which filamentation begins and ends within a material is regulated by the laser pulse parameters (duration, energy, and focus geometry) that are controlled by the operator. Thus, we propose IR-laser-induced filamentation as a unique tool for radiotherapeutic applications with a zero dose upon entry into the irradiated medium.
Here, as in all applications of nonlinear photonics processes in biomedical fields, the future challenge remains the propagation of femtosecond laser pulses in the light scattering inhomogeneous human tissue (22, 23). Given some promising recent breakthroughs (24–29), our future work will focus on gaining a detailed understanding of laser-tissue interactions before we can apply laser filamentation in clinical radiotherapy of human cancers to avoid either under-treatment of tumor tissue or damage to healthy tissue.
Results and Discussion
Dosimetry of Filamentation.
We report that filamentation, produced by intense, ultra-short infrared laser pulses (pulse duration was 100 fs; pulse energy was 0.3 mJ/pulse; repetition rate was 1 kHz; the central wavelength was 800 nm) can be used to produce a high density of chemical reactions induced by free electrons and ROS through low-density plasma generation. This yields a dose deposit with a high rate at a macroscopic distance inside a well-controlled macroscopic volume. As seen in Fig. 1 A and B, the most striking feature of our dose deposition profile is the complete absence of an entrance dose (meaning no damage to healthy tissue in front of the tumor), a characteristic that still eludes conventional radiation sources used for cancer therapy, as clearly seen in Fig. 1C. The objective of our contribution here is to demonstrate (i) the radiation-chemical and radiobiological equivalence of IR laser filamentation to ionizing radiation in liquid or tissue equivalent liquid media, and (ii) the potential curative utility of femtosecond laser irradiation in an animal breast cancer model.
Firstly, the macroscopic dose rate of the laser induced filamentation process was determined by two different chemical dosimeters (see SI Text); secondly, the spatial dose distribution, and hence the microscopic energy density and dose rate, of the laser-induced filamentation process was captured by an optically transparent polymer gel dosimeter and visualized by magnetic resonance imaging (MRI) (see SI Text). Using this radiologically tissue-equivalent, three-dimensional gel dosimeter (30), our results clearly show that changing the laser irradiation parameters such as pulse duration enables us to precisely control the distance in the tissue equivalent medium over which the entrance dose is zero (Fig. 1B).
Using the chemical Fricke and the ceric-cerous dosimeters we find that the dose rate by laser filamentation is extremely high along the actual filamentation tracks. Ceric-cerous dosimeters are used for high intensity radiation, because the yield of ceric ions is independent of O2 concentration and of dose rate (31, 32). Here, the dose absorbed in our macroscopic chemical dosimeter volume (2 ml) varies linearly with irradiation time for femtosecond laser filamentation and for γ-irradiation using a standard 137Cs source (see SI Text). The macroscopic dose rates of the laser filaments and γ-irradiation in the 2-ml volume are 7.8 ± 0.1 and 0.20 ± 0.01 Gy/s, respectively (see SI Text). For comparison, the dose rate achieved by clinical proton beam sources (at 60 MeV) is 2.8 Gy/s (33). These results show that laser filamentation can deposit a dose with a high rate in a very local track within the macroscopic sample volume. In addition, the chemical yield of these types of radiation dosimeters results from reactions of water radiolysis products with metal ions (Fe2+ and Ce4+) in aqueous solutions (31, 32). Thus, our results also show that the IR laser pulse induced filamentation process generates the same type of radical water radiolysis species than conventional ionizing radiations.
The spatial morphology of the energy-deposition process by laser induced filamentation was evaluated at the microscopic and macroscopic level using a clinically validated tissue-equivalent polymer gel-dosimeter and magnetic resonance imaging (MRI) (Fig. 1 and Fig. S1) (see SI Text); the gels are three-dimensional (34, 35) and the tissue equivalent radiation dosimeters (36) used here are used widely in clinical applications. The gel dosimeter is based on radiation-induced polymerization of two monomer species, which is initiated by free radicals derived from water radiolysis (37). The amount of polymerization produced in the dosimeter is directly related to the absorbed radiation dose (i.e., energy deposited). The spatial distribution of the polymer influences the spatial MRI properties of the dosimeter gel. The formation of polymer also alters the initial optical transparency of the dosimeter, and this is directly visible to the human eye. Here, the dosimeter sample cells were imaged by MRI as described elsewhere (38). The diameters of filamentation tracks produced here for the MRI micro-dosimetry measurements are estimated to be approximately 300–400 μm. We note that because the Gaussian intensity profile of the laser beam is not smooth, any small fluctuation in intensity on the beam profile will lead to local self-focusing so long as the local power is higher than the critical power for self-focusing. This results in bunching of multiple filaments with a total cross-section diameter around 300 micrometer and around 10 micrometer for each individual filament (Fig. S2)dissolved oxygen at high absorbed dose, which agrees with previous studies of filamentation in aqueous solutions (12, 24). Using the measured macroscopic dose rate of 7.8 Gy/s, discussed above, and the MRI measurements of the multiple filamentation track’s dimensions, we find that the actual linear ionization density (39) within the filaments varies from 7.1 × 1010 to 1.3 × 1011 ionizations/μm, while the effective dose rate equals approximately 4.9 × 1011 Gy/s (see SI Text). These values surpass those of even the most intense conventional clinical radiation sources to date. Fig. 1 A and B shows photographs of a large polymer gel dosimeter irradiated with laser filamentation. Here, changing the pulse duration leads to changes in the starting point of filaments as shown in Fig. 1B. In case of conventional X-ray irradiation in Fig. 1C, where a clinical irradiator was used, the absorbed dose decrease as a function of depth in the gel dosimeter, from a maximum delivered dose that occurs upon entry into the tissue equivalent medium. Thus, unlike conventional ionizing radiation, such as clinical X-rays, the femtosecond IR-laser-pulse filamentation process is capable to generate a zero entrance dose, while allowing precise control over the depth and volume shape in which the dose is deposited in the macroscopic medium at the high microscopic dose rates described here.
Laser Filamentation Effect on Biological Systems.
Clearly, the laser-induced filamentation process, as observed here in chemical and tissue equivalent clinically validated dosimeters, is able to induce similar or identical chemical processes or polymerizations (all related to formation of free radicals) as conventional ionizing radiation; yet, a key question is if the type of genotoxic damage, induced in DNA or its components, by IR-laser-induced filamentation is the same as that of conventional ionizing radiation. Here, we use the nucleoside thymidine and double stranded plasmid DNA as benchmarks to answer this question.
Biological compound damage.
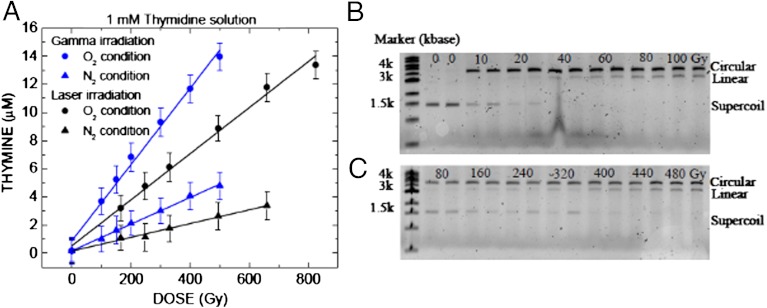
Thymidine decomposition resulting from γ-irradiation and laser filamentation is shown here both in the absence and the presence of oxygen (Fig. 2A). The pathway of decomposition of thymidine in solution by γ-radiation involves the generation of an •OH radical and its addition to the 5,6-double bond of thymine or H-atom abstraction from the 2-deoxyribose moiety. The resulting carbon-centered radicals of thymidine lead to a large number of stable modifications (40). In view of the very similar profiles of products observed here by HPLC-UV of samples exposed in solution to γ radiation and laser filamentation, the mechanism of formation of products involves •OH radicals in both cases. Thymine is a well-known benchmark product of thymidine decomposition by γ-radiation, which arises from initial abstraction of H-atoms from the 2-deoxyribose moiety by •OH radicals generated in the solution (40). The greater release of thymine in oxygenated solution (approximately three times) compared to that in deoxygenated solution (Fig. 2A) may be attributed to the addition of oxygen to carbon centred radicals at the 2-deoxyribose moiety leading to more efficient cleavage into thymine. Again, the similarities of thymine release and the effect of oxygen on the decomposition of thymidine in both clinical γ-irradiation and IR laser filamentation experiments demonstrate here that •OH radicals are also the damage inducing species in laser filamentation. However, other damage pathways to DNA components, such those mediated by LEEs (41) are also possible.
Fig. 2.
DNA damage induced by 137Cs gamma radiation, and laser filamentation at 800 nm: (A) a graph of the release of thymine (glycosidic bond cleavage) from the irradiation of thymidine in solution versus absorbed dose. Agarose gel electropholysis separating supercoiled plasmid DNA damage (circular and linear DNA conformations correspond to single and double strand breaks) using (B) gamma irradiation and (C) IR femtosecond laser pulse filamentation. The absorbed macroscopic doses to the 2 ml target solution are given in Gy, and the two lanes in (B) after the marker are unirradiated controls.
DNA damage.
Supercoiled, double-stranded plasmid DNA [pGEM 3Zf(-)], was used to compare the genotoxicity of laser filamentation and γ radiation in aqueous solution. Our results in Fig. 2 B and C clearly show that the damage to double stranded DNA, as indicated by the production of single stand breaks (SSBs, circular form) and double stand breaks (DSBs, linear form) by IR laser induced filamentation is identical to that induced by conventional γ-irradiation; moreover, in both cases this involves the formation of free radical species in the solution, including scavengeable solvated electrons in aqueous solutions (42). Here, filamentation also generates a high-density avalanche of LEEs (approximately 1018 cm-3) by inverse Bremsstrahlung and multiphoton ionization processes in the aqueous solution (10–12). These LEEs, similar to those formed along conventional radiation tracks, have approximately 10-nm range in water (43) and damage DNA even at subionization energies (18). Regardless of their formation mechanism, LEEs will also fragment surrounding molecules, yielding radicals, including ROS (31, 44–46), which may attack DNA and lead to SSB and DSB (19–21, 42) that are accepted benchmarks for genotoxic radiation effects.
Animal tumor model.
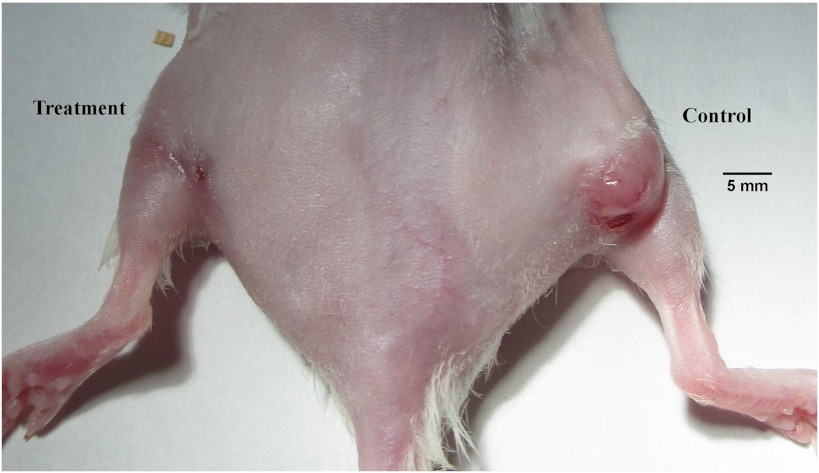
To test the therapeutic curative potential of this fs IR laser irradiation technique, we have begun to study its effects on a well-known and validated subcutaneous animal tumor model. Tumors were grown in female Balb/c mice by subcutaneous injection of mouse mammary carcinoma cells (MC7-L1) in both legs, irradiating only one. Our preliminary results 23 days after treatment show that (i) tumor involution is clearly observed in the treated leg, and (ii) while the untreated tumor volume increased on average by 1,500% (± 160%), the average reduction in treated tumor volume is at least 50% (± 44%). Most encouragingly, in one out of three cases the tumor was completely eradicated as shown in Fig. 3. This is likely be due to the fact that the geometric spacing of the five targeted irradiation spots on each tumor was not identical for each mouse, such that tighter spacing could lead to better tumor control. A higher power laser, allowing multiple beam grid-pattern and thus simultaneous irradiation with multiple filaments at constant spacing will remedy this. This improvement will yield a better cover of tumors during laser irradiation combined with a better control and stability of the filamentation generation (47). We currently believe that the local plasma induced by the laser pulses trigged a massive necrosis. The ensuing cascade of inflammatory cytokines then diffuses from the path of the laser beam leading to a volume of cell death larger than the diameter of the laser beam. Our results support that irradiation of a tumor at five points leads to a complete regression of a tumor with a diameter of 6–8 mm. In any case, our results suggest that the fs IR laser irradiation method used here has a definite curative effect on tumor tissue and warrants intensive study due to its vast potential to greatly improve cancer therapy.
Fig. 3.
Femtosecond IR (800 nm) laser pulse treatment (left leg) of a MC7-L1 mouse mammary carcinoma tumor compared to control (right leg) 23 days after laser irradiation. MC7-L1 cells were injected into the right and left thighs of female Balb/c mice. The right side tumor was used as control. Three to four weeks later, mice bearing tumors with a diameter of 3–5 mm were irradiated by femtosecond IR laser pulses. The best laser treatment result here was obtained by irradiating five separate spots (100–300 μm diameter, separated by approximately 1–1.5 mm, with four spots forming a square and one center spot) on the tumors, with 10-min irradiation times for each spot; the laser irradiation and dosimetry conditions were identical to those used for filamentation during chemical dosimetry (see SI Text).
Conclusion
We have presented evidence that the radiation-chemical and radiobiological mechanisms and outcomes of fs IR laser induced filamentation, even in tissue equivalent dosimetric media, seem equivalent to conventional ionizing radiation. Moreover, we have shown here that this conceptually unique approach to cancer therapy, using high-power fs infrared laser pulse filamentation (48) in macroscopic targets, may bring us a step closer to an ideal beam for radiation therapy in that it maximizes the energy dose inside the tumor volume, while keeping the (entrance) dose to healthy tissue zero. In other words, it seems possible to effectively “beam in” radiotherapeutic energy, at a high density, into a well-controlled volume, leaving the surrounding medium untouched. Our studies on DNA molecular models and animal tumor models are still underway, particularly regarding the efficiency with which laser filamentation might occur in opaque scattering media such as living tissue, which remains unanswered (24), as well as possible side effects in healthy pigmented tissue due to one-photon absorption of the laser light (49); however, the use of adaptive optimization by a spatial light modulator could partly compensate for the scattering of light in actual opaque tissue (25–28). While the adaptability of the method described here to very deep seated tumors is not yet clear, we are currently testing specially adapted hollow fiber optic methods to bring the radiotherapeutic pulsed IR laser beam physically closer to specific deep-seated target volumes.
Materials and Methods
Laser Irradiation.
The laser irradiation setup used here for all the experiments in aqueous solutions is shown in Fig. S3 (see SI Text). Sample solutions were irradiated by femtosecond Ti-sapphire laser beams with the following properties: Pulse duration was 100 fs; pulse energy was 0.3 mJ/pulse; repetition rate was 1 kHz; the central wavelength was 800 nm; and the cross-section radius at the 1/e2 level of the beam profile was 7 mm. The laser beam was focused by a 30-cm focal length plano-convex lens into the sample container (quartz cuvette, 1 × 1 × 5 cm3). The sample cell was located approximately 24 cm from the focal lens.
For a 30-cm focal length convex lens, the cross-section radius after the lens of a Gaussian laser pulse (wz) is:
where w0 is the waist at the geometrical focus, z is the distance related to the focus position, and zr is the Rayleigh length. So, with these irradiation parameters, we can confirm theoretically the occurrence of the filamentation process in the cuvette by evaluating the starting point of filaments in water (50). If one takes into account that we approximate our incident beam by a Gaussian parallel beam with a radius at the 1/e2 level of the beam profile equals to w(z), it will self-focus in the cuvette after the empirical distance zf:
where k is the wave member, P is the laser pulse peak power and Pc the critical power threshold of self-focusing (4.2 MW in water). Here, however, P exceeds Pc by three orders of magnitude, so that the collapse distance of our intense laser beams in a bulk Kerr medium no longer scales as 1/P1/2 but scales as 1/P (51). Thus, we estimated zf close to 2.5 mm in the cuvette. Furthermore, the value of wz inside the quartz cuvette is composed between 7.3 × 10-2 cm and 6.1 × 10-2 cm. For a 3.5-GW laser pulse, the intensity inside the sample container due to the geometrical focus reaches values between 2.1 × 1011 W·cm-2 and 3 × 1011 W·cm-2. According to (50), the optical breakdown threshold of water for our laser pulses is close to 5.6 × 1012 W·cm-2. Thus, our irradiation parameters avoid in theory the generation of hot high-density plasmas in aqueous solutions. During our experiments, we visualized a beautiful super-continuum white light generation on a screen oriented perpendicular to the laser propagation axis placed behind the quartz cuvette, which is a feature of all filamentation phenomena (50). However, we did not detect visual indications of optical breakdown, such as bubble formation observed elsewhere (13). Therefore, we conclude that we are essentially in the filamentation regime, well below the conditions for optical breakdown.
Gamma and X-ray Irradiation.
The samples were irradiated to a maximum of 300 Gy at 25 °C with 137Cs γ-rays (0.662 MeV) in a Gammacell (Elan 3000, Atomic Energy of Canada Limited). The dose rate for 137Cs gamma irradiation was 0.20 ± 0.01 Gy/s, as determined by Fricke dosimetry. In some cases gels where irradiated with a clinical X-ray therapy system (Therapax HF150T), at 1, 2, and 3 Gy, to demonstrate typical entrance dose of clinical X-rays.
Chemical Radiation Dosimeters.
We used 1 mM of ammonium ferrous sulfate hexahydrate (≥99.99% Sigma), 0.4 M H2SO4 (98%, Sigma) in saturated oxygen condition, the so-called “super Fricke” dosimeter (32). The concentration of Fe3+ was measured by UV spectrophotometer at 304 nm (where its molar extinction coefficient ε = 2196 ± 5 M-1 cm-1) (52). Typically, the production of ferric ions is most sensitive to the radical species produced in the radiolysis of water. Under low linear energy transfer (LET) irradiation conditions, G(Fe3+) is equal to 15.6 ± 0.3 molecules/100 eV (32). However, the yield of ferric ions was found to decrease with increasing dose rate above 108 Gy/s (32) and was appreciably dependent on the initial concentrations of dissolved oxygen at high absorbed dose (> 500 Gy) (32). Because here the microscopic dose rate within the filament volume can exceed such dose rates, a ceric sulfate dosimeter is used here as well (Fig. S4).
The ceric sulfate dosimeter has been recommended as a chemical dosimeter for high dose rate radiations (31). The principle of the dosimeter is reduction of Ce4+ to Ce3+ by radiolysis processes that do not consume oxygen. Here, we used 1 mM cerium (III) sulfate (≥99.99%, Sigma) and 0.25 mM, ammonium cerium (IV) sulfate dihydrate (> 99%, Sigma) in 0.4 M H2SO4 (98%, Sigma) (32). The concentration of ceric ions was measured by UV spectrophotometer at 320 nm (where ε = 5,610 ± 7 M-1 cm-1) (53). At high dose rate (> 1010 Gy/s), the yield of ceric depends on yield of H2O2 which was 1.4 molecules/100 eV (31).
Polymer Gel Dosimeter.
The dosimeter gels were prepared with acrylamide (AA) and N,N’-methylenebisacrylamide (BIS) (99 + %, electrophoresis grade, Aldrich), each at 3% w/w dissolved in gelatin (300 bloom, Aldrich) at 5% w/w, and water (de-ionized). The monomers (AA and BIS) were dissolved in an aqueous gelatin matrix. In the manufacture process, gelatin was added to water at room temperature and left to soak for 10 min. The solution was then heated and maintained at a temperature of 45 °C. AA and BIS were successively added and magnetically stirred for typically 15 min until complete dissolution. The gels were prepared under a controlled N2 atmosphere inside a glove box (38). The solution was poured into glass cell (diameter 2 cm × length 5 cm) as shown in SI Text, Fig. S1A. For the plastic container as shown in Fig. 1 A–C, the gel was prepared in the glove box with the same recipe but 5 mM of alkaline tetrakis (hydroxymethyl) phophonium chloride (THPC) (80%, Aldrich) as an oxygen scavenger.
Thymidine Decomposition.
The biochemical reagents used in the experiment were the nucleoside thymidine (> 99%, Sigma), a component of cellular DNA, and de-ionized water. A 1-mM thymidine solution was prepared; 2 ml was poured into a bubble forming anaerobic cell (1 × 1 × 5 cm3, NSG). The sample cell was purged with nitrogen or oxygen for 15 min immediately before irradiation. The samples were irradiated by conventional gamma radiation and laser filamentation. These samples were analyzed by high-performance liquid chromatography (HPLC) with ultraviolet (UV) detection.
Plasmid DNA Damage.
pGEM-3Zf(-) plasmid DNA (3,197 bp, Promega) was extracted form Escherichia coli DH5α and purified with the QIAfilter Plasmid Giga Kit (Qiagen). Agarose gel electropholysis was used to show that 96% of DNA was initially in the supercoiled form, 3% was in the concatemeric form and 1% was in the circular form. The DNA was dissolved in de-ionized water. The concentration of DNA was measured by its UV absorption at 260 nm, assuming a molar extinction of 7,120 mol-1 cm-1 at pH 7.0 (54). The amount of DNA in each sample that was used for irradiation was 200 ng/mL. The samples were irradiated by conventional gamma radiation and laser filamentation and analyzed by standard gel electrophoresis.
MC7-L1 Tumors Implanted in Balb/c Mice and Laser Irradiation.
The experimental protocol was approved by the institutional ethical committee and complied with the regulations of the Canadian Council on Animal Care. The mouse mammary carcinoma cell line MC7-L1 was generously provided by Dr. Alfredo A. Molinolo of the Instituto de Biologia y Medicina Experimental, Concejo Nacional de Investigaciones Cientificas y Técnicas en Facultad de Medicina, Universidad de Buenos Aires, Buenos Aires, Argentina (55). The MC7-L1 cells were grown in minimal essential medium (MEM) supplemented with 10% fetal bovine serum (FBS) (Gibco), 1 mM sodium pyruvate, 2 U/mL penicillin G, 2 μg/mL streptomycin, and 250 ng/mL amphotericin B. The MC7-L1 cells (106) were subcutaneously injected in both thighs of female Balb/c mice six weeks old. Three to four weeks later, mice bearing tumors with a diameter of 3–5 mm were put under anaesthesia (ketamine/xylazine) and irradiated in one tumor (thigh) only by femtosecond laser pulses, such that the unirradiated tumor (thigh) acted as a control. The laser treatment was performed by irradiating five spots on a tumor and the irradiation time was 10 min each spot. The tumor volume was calculated using the equation, L in mm × W in mm × H in mm × 0.5, for measured values of L, W, and H at specific days after the irradiation day.
Supplementary Material
ACKNOWLEDGMENTS.
Funding for this research was provided by the Canadian Institutes of Health Research, the Canadian Institute for Photonics Innovations of Canada, and the Banque National-Centre de Recherche Clinique of the Centre Hospitalier Universitaire de Sherbrooke. R.M. acknowledges a scholarship from the Ministry of Science and Technology of the Royal Thai Government and Applied Radiation and Isotope Department, Faculty of Science, Kasetsart University, Bangkok, Thailand. M.A.H., J.R.W., J.-P.J.-G., and M.L. acknowledge funding from the Natural Science and Engineering Research Council of Canada. D.H., M.A.H., J.R.W., M.L., B.P., and J.-P.J.-G. are members of the Fonds de Recherche Santé Québec (FRSQ)-funded Centre de Recherche Clinique Étienne-Le Bel.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. T.O. is a guest editor invited by the Editorial Board.
See Author Summary on page 15086 (volume 109, number 38).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1116286109/-/DCSupplemental.
References
- 1.IAEA TECDOC-1537. The Role of PET/CT in Radiation Treatment Planning for Cancer Patient Treatment. Vienna: IAEA; 2008. [Google Scholar]
- 2.Intensity Modulated Radiation Therapy Collaborative Working Group. Intensity-modulated radiotherapy: Current status and issues of interest. Int J Radiat Oncol Biol Phys. 2001;51:880–914. doi: 10.1016/s0360-3016(01)01749-7. [DOI] [PubMed] [Google Scholar]
- 3.Hall EJ, Phill D. Intensity-modulated radiation therapy, protons, and the risk of second cancers. Int J Radiat Oncol Biol Phys. 2006;65:1–7. doi: 10.1016/j.ijrobp.2006.01.027. [DOI] [PubMed] [Google Scholar]
- 4.Suit H, et al. Proton beams to replace photon beams in radical dose treatments. Acta Oncol. 2003;42:800–808. doi: 10.1080/02841860310017676. [DOI] [PubMed] [Google Scholar]
- 5.Glimelius B, et al. Potential gains using high-energy protons for therapy of malignant tumors. Acta Oncol. 1999;38:137–145. doi: 10.1080/028418699431537. [DOI] [PubMed] [Google Scholar]
- 6.Goitein M, Jermann M. The relative costs of proton and x-ray radiation therapy. Clin Oncol. 2003;15:S37–S50. doi: 10.1053/clon.2002.0174. [DOI] [PubMed] [Google Scholar]
- 7.Chung SH, Mazur E. Surgical applications of femtosecond lasers. J Biophotonics. 2009;10:557–572. doi: 10.1002/jbio.200910053. [DOI] [PubMed] [Google Scholar]
- 8.Wilson BC, Patterson MS. The physics, biophysics and technology of photodynamic therapy. Phys Med Biol. 2008;53:R61–R109. doi: 10.1088/0031-9155/53/9/R01. [DOI] [PubMed] [Google Scholar]
- 9.Ogawa K, Kobuke Y. Recent advances in two-photon photodynamic therapy. Anti Cancer Agents Med Chem. 2008;8:269–279. doi: 10.2174/187152008783961860. [DOI] [PubMed] [Google Scholar]
- 10.Chin SL, et al. The propagation of powerful femtosecond laser pulses in optical media: Physics, applications, and new challenges. Can J Phys. 2005;83:863–905. [Google Scholar]
- 11.Couairon A, Mysyrowicz A. Femtosecond filamentation in transparent media. Phys Rep. 2007;441:47–189. [Google Scholar]
- 12.Minardi S, et al. Time-resolved refractive index and absorption mapping of light-plasma filaments in water. Opt Lett. 2008;31:86–88. doi: 10.1364/ol.33.000086. [DOI] [PubMed] [Google Scholar]
- 13.Vogel A, Noack J, Huttma NG, Paltauf G. Mechanisms of femtosecond laser nanosurgery of cells and tissues. Appl Phys B. 2005;81:1015–1047. [Google Scholar]
- 14.Hallo L, et al. Laser-matter structuration of optical and biological materials. Appl Surf Sci. 2012;258:9263–9269. [Google Scholar]
- 15.Noack J, Hammer DX, Noojin GD, Rockwell BA, Vogel A. Influence of pulse duration on mechanical effects after laser-induced breakdown in water. J Appl Phys. 1998;83:7488–7495. [Google Scholar]
- 16.Vogel A, et al. Energy balance of optical breakdown in water at nanosecond to femtosecond time scales. Appl Phys B. 1999;68:271–280. [Google Scholar]
- 17.Cobut V, et al. Monte Carlo simulation of fast electron and proton tracks in liquid water I: Physical and physiochemical aspect. Radiat Phys Chem. 1998;51:229–243. [Google Scholar]
- 18.Boudaïffa B, Cloutier P, Hunting D, Huels MA, Sanche L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science. 2000;287:1658–1660. doi: 10.1126/science.287.5458.1658. [DOI] [PubMed] [Google Scholar]
- 19.Shafirovich V, et al. Multiphoton near-infrared femtosecond laser pulse-induce DNA damage with and without the photosensitizer proflavine. Photochem Photobiol. 1999;68:265–274. doi: 10.1562/0031-8655(1999)069<0265:mniflp>2.3.co;2. [DOI] [PubMed] [Google Scholar]
- 20.Tirlapur UK, König K, Peuckert C, Krieg R, Halbhuber K-J. Femtosecond near-infrared laser pulses elicit generation of reactive oxygen species in mammalian cells leading to apoptosis-like death. Exp Cell Res. 2001;263:88–97. doi: 10.1006/excr.2000.5082. [DOI] [PubMed] [Google Scholar]
- 21.Botchway SW, Reynolds P, Parker AW, O’Neill P. Use of near infrared femtosecond lasers as sub-micron radiation microbeam for cell DNA damage and repair studies. Mutat Res. 2010;704:38–44. doi: 10.1016/j.mrrev.2010.01.003. [DOI] [PubMed] [Google Scholar]
- 22.Cheong WF, Prahl SA, Welch AJ. A review of the optical properties of biological tissues. IEEE J Quantum Electron. 1990;26:2166–2185. [Google Scholar]
- 23.Kim A, Wilson BC. Measurement of ex-vivo and in vivo tissue optical properties. In: Welch AJ, van Gemert MJC, editors. Optical Thermal Response of Laser-Irradiated Tissue. New York: Springer; 2011. [Google Scholar]
- 24.Jukna V, et al. Filamentation of ultrashort light pulses in a liquid scattering medium. Appl Phys B. 2009;94:175–179. [Google Scholar]
- 25.Katz O, Small E, Bromberg Y, Silberberg Y. Focusing and compression of ultra-short pulses through scattering media. Nat Photon. 2011;5:372–377. [Google Scholar]
- 26.Dela Cruz JM, Pastirk I, Comstock M, Lozovoy VV, Dantus M. Use of coherent control methods through scattering biological tissue to achieve functional imaging. Proc N atl Acad Sci USA. 2004;49:16996–17001. doi: 10.1073/pnas.0407733101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vellekoop IM, Mosk AP. Focusing coherent light through opaque strongly scattering media. Opt Lett. 2007;32:2309–2311. doi: 10.1364/ol.32.002309. [DOI] [PubMed] [Google Scholar]
- 28.Vellekoop IM, Lagendijk A, Mosk AP. Exploiting disorder for perfect focusing. Nat Photon. 2010;4:320–322. [Google Scholar]
- 29.McCabe DJ, et al. Spatio-temporal focusing of an ultrafast pulse through a multiply scattering medium. Nat commun. 2011;2:447. doi: 10.1038/ncomms1434. [DOI] [PubMed] [Google Scholar]
- 30.Baldock C, et al. Polymer gel dosimetry. Phys Med Biol. 2010;55:R1–R63. doi: 10.1088/0031-9155/55/5/R01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ferradini C, Pucheault J. Biology of Ionizing Radiation Action “Biologie de l’Action des Rayonnements Ionisants”. Paris: Masson; 1983. pp. 75–77. [Google Scholar]
- 32.Spinks JWT, Woods RJ. An Introduction to Radiation Chemistry. New York: Wiley; 1990. [Google Scholar]
- 33.Goitein M, Abrams M, Rowell D, Pollari H, Wiles J. Multi-dimensional treatment planning: II. Beam’s eye-view, back projection, and projection through CT sections. Int J Radiat Oncol Biol Phys. 1983;9:789–797. doi: 10.1016/0360-3016(83)90003-2. [DOI] [PubMed] [Google Scholar]
- 34.Maryanski MJ, Gore JC, Kennan RP, Schulz RJ. NMR relaxation enhancement in gels polymerized and cross-linked by ionizing radiation: A new approach to 3D dosimetry by MRI. Magn Reson Imaging. 1993;11:253–258. doi: 10.1016/0730-725x(93)90030-h. [DOI] [PubMed] [Google Scholar]
- 35.Baldock C, et al. Experimental procedure for the manufacture and calibration pf polyacrylamide gel (PAG) for magnetic resonance imaging (MRI) radiation dosimetry. Phys Med Biol. 1998;43:695–702. doi: 10.1088/0031-9155/43/3/019. [DOI] [PubMed] [Google Scholar]
- 36.Venning AJ, Nitschke KN, Keall PJ, Baldock C. Radiological properties of normoxic polymer gel dosimeters. Med Phys. 2005;32:1047–53. doi: 10.1118/1.1881812. [DOI] [PubMed] [Google Scholar]
- 37.Lepage M, Whittaker AK, Rintoul L, Bäck SÅJ, Baldock C. The relationship between radiation-induced chemical processes and transverse relaxation times in polymer gel dosimeters. Phys Med Biol. 2001;46:1061–1074. doi: 10.1088/0031-9155/46/4/311. [DOI] [PubMed] [Google Scholar]
- 38.Meesat R, Jay-Gerin J-P, Khalil A, Lepage M. Evaluation of the dose enhancement of iodinated compounds by polyacrylamide gel dosimetry. Phys Med Biol. 2009;54:5909–5917. doi: 10.1088/0031-9155/54/19/016. [DOI] [PubMed] [Google Scholar]
- 39.Kudryashov YB. Radiation Biophysics (ionization radiation) In: Lomanov MF, editor. New York: Nova Science Publications; 2008. pp. 1–7. [Google Scholar]
- 40.Cadet J, Douki T, Gasparutto D, Ravanat J-L, Wagner JR. In: Radical and Radical Ion Reactivity in Nucleic Acid Chemistry. Greenberg MM, editor. Hoboken, NJ: Wiley; 2010. pp. 69–98. [Google Scholar]
- 41.Li Z, Zheng Y, Cloutier P, Sanche L, Wagner JR. Low energy electron induced DNA damage: Effects of terminal phosphate and base moieties on the distribution of damage. J Am Chem Soc. 2008;130:5612–5613. doi: 10.1021/ja077601b. [DOI] [PubMed] [Google Scholar]
- 42.D’Souza JS, Dharmadhikari JA, Dharmadhikari AK, Rao BJ, Mathur D. Effect of intense, ultrashort laser pulses on dna plasmids in their native state: Strand breakages induced by in situ electrons and radicals. Phys Rev Lett. 2011;106:118101. doi: 10.1103/PhysRevLett.106.118101. [DOI] [PubMed] [Google Scholar]
- 43.Meesungnoen J, Jay-Gerin J-P, Filali-Mouhim A, Mankhetkorn S. Low-energy electron penetration range in liquid water. Radiat Res. 2002;158:657–660. doi: 10.1667/0033-7587(2002)158[0657:leepri]2.0.co;2. [DOI] [PubMed] [Google Scholar]
-
44.Meesungnoen J, Jay-Gerin J-P. High-LET radiolysis of liquid water with
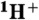 ,
, 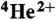 ,
, 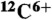 , and
, and  ions: Effects of multiple ionization. J Phys Chem A. 2005;109:6406–6419. doi: 10.1021/jp058037z. [DOI] [PubMed] [Google Scholar]
ions: Effects of multiple ionization. J Phys Chem A. 2005;109:6406–6419. doi: 10.1021/jp058037z. [DOI] [PubMed] [Google Scholar] - 45.Chin SL, Lagacé S. Generation of H2, O2, and H2O2 from water by the use of intense femtosecond laser pulses and the possibility of laser sterilization. Appl Opt. 1996;35:907–911. doi: 10.1364/AO.35.000907. [DOI] [PubMed] [Google Scholar]
- 46.Sanche L. In: Radical and Radical Ion in Nucleic Acid Chemistry. Greenberg MM, editor. Hoboken, NJ: Wiley; 2010. pp. 239–294. [Google Scholar]
- 47.Schroeder H, Liu J, Chin SL. From random to controlled small-scale filamentation in water. Opt Express. 2004;12:4768–4774. doi: 10.1364/opex.12.004768. [DOI] [PubMed] [Google Scholar]
- 48.Houde D, Meesat R, Allard J-F, Brastaviceanu T. Method of generating low-energy secondary electrons for applications in biological sciences, radiochemistry, and chemistry of polymers and physics of radiotherapy. U.S. Provisional Patent Application No 61/313,553, (2010), PCT Patent Application PCT/WO 2011/109907 A1. 2011.
- 49.Master BR, et al. Mitigating thermal mechanical damage potential during two-photon dermal imaging. J Biomed Opt. 2004;9:1265–1270. doi: 10.1117/1.1806135. [DOI] [PubMed] [Google Scholar]
- 50.Liu W, et al. Femtosecond laser pulse filamentation versus optical breakdown in H2O. Appl Phys B. 2003;76:215–229. [Google Scholar]
- 51.Fibich G, et al. Self-focusing distance of very high power laser pulses. Opt Express. 2005;13:5897–5903. doi: 10.1364/opex.13.005897. [DOI] [PubMed] [Google Scholar]
- 52.Buxton GV, Stuart CR. Re-evaluation of the thiocyanate dosimeter for pulse radiolysis. J Chem Soc Faraday Trans. 1995;91:279–281. [Google Scholar]
- 53.Matthews RW. Effect of solute concentration and temperature on the ceric-cerous dosimeter. Radiat Res. 1973;55:242–255. [PubMed] [Google Scholar]
- 54.Zheng Y, Sanche L. Gold nanoparticles enhance DNA damage induced by anti-cancer drugs and radiation. Radiat Res. 2009;172:114–119. doi: 10.1667/RR1689.1. [DOI] [PubMed] [Google Scholar]
- 55.Lanari C, et al. Five novel hormone-responsive cell lines derived from murine mammary ductal carcinomas: In vivo and in vitro effects of estrogens and progestins. Cancer Res. 2001;61:293–302. [PubMed] [Google Scholar]