Quantifying selection in high-throughput Immunoglobulin sequencing data sets

Abstract

High-throughput immunoglobulin sequencing promises new insights into the somatic hypermutation and antigen-driven selection processes that underlie B-cell affinity maturation and adaptive immunity. The ability to estimate positive and negative selection from these sequence data has broad applications not only for understanding the immune response to pathogens, but is also critical to determining the role of somatic hypermutation in autoimmunity and B-cell cancers. Here, we develop a statistical framework for Bayesian estimation of Antigen-driven SELectIoN (BASELINe) based on the analysis of somatic mutation patterns. Our approach represents a fundamental advance over previous methods by shifting the problem from one of simply detecting selection to one of quantifying selection. Along with providing a more intuitive means to assess and visualize selection, our approach allows, for the first time, comparative analysis between groups of sequences derived from different germline V(D)J segments. Application of this approach to next-generation sequencing data demonstrates different selection pressures for memory cells of different isotypes. This framework can easily be adapted to analyze other types of DNA mutation patterns resulting from a mutator that displays hot/cold-spots, substitution preference or other intrinsic biases.

INTRODUCTION

Large-scale characterization of B-cell immunoglobulin (Ig) repertoires is now feasible in humans, as well as model systems through the applications of next-generation sequencing approaches (1–3). During the course of an immune response, B cells that initially bind antigen with low affinity through their Ig receptor are modified by cycles of somatic hypermutation (SHM) and affinity-dependent selection to produce high-affinity memory and plasma cells. This affinity maturation is a critical component of T-cell dependent adaptive immune responses, helps guard against rapidly mutating pathogens and underlies the basis for many vaccines (4). Characterizing this mutation and selection process can provide insights into the basic biology that underlies physiological and pathological adaptive immune responses (5,6), and may further serve as diagnostic or prognostic markers (7,1). However, analyzing selection in these large datasets, which can contain millions of sequences, presents fundamental challenges requiring the development of new techniques.

Existing computational methods to detect selection work by comparing the observed frequency of replacement (i.e. non-synonymous) mutations (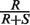) to the expected frequency 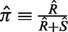with R being the number of replacement mutations and S being the number of silent (i.e. synonymous) mutations. The expectations are calculated based on an underlying targeting model to account for SHM hot/cold-spots and nucleotide substitution bias (8). This is critical since these intrinsic biases alone can give the illusive appearance of selection (9,10). An increased frequency of replacements indicates positive selection, whereas decreased frequencies indicate negative selection. Since the framework region (FWR) provides the structural backbone of the receptor, while contact residues for antigen mainly reside in the complementary determining regions (CDRs), one generally expects to find negative selection in the FWRs and positive selection in the CDRs. The statistical significance is determined by a binomial test (5). In this setup, R + S, R and 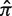are the number of trials (N), number of successes (x) and probability of success (p) for the binomial process, respectively. Several variations of this statistical test have been proposed using somewhat different definitions for these parameters [see (5,8,10–12) and Table 1 in (13)]. We previously developed the Focused-Z test to detect selection with improved specificity and allow for grouping sequences with different baseline probabilities of replacement (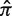) (13). Regardless of the particular approach, it is not possible to use the P-value from these statistical tests to compare the extent of selection between experimental groups since lower P-values are not equivalent to stronger selection strengths (see for example Supplementary Figure S1). In addition, results are not easily interpretable when analyzing more than a handful of sequences. There are several reasons why selection strengths can differ. For example, positive selection will increase over time as multiple mutations with subtle effects on affinity become fixed in the population. Second, a more highly competitive environment (e.g. with limited survival niches) should produce increased selection strengths. Finally, the observed selection strength can be impacted by alterations in the balance of positive and negative selection. Here we derive a new approach for Bayesian estimation of Antigen-driven SELectIoN (BASELINe) in Ig sequecnes. BASELINe provides a more intuitive means to analyze selection by shifting the problem from one of detecting selection to one of quantifying selection. By operating in log-odds ratio space, the approach also allows, for the first time, comparative analysis between groups of sequences derived from different germline V(D)J segments. An online implementation of our method for BASELINe along with R source code, is available at: http://clip.med.yale.edu/baseline.

MATERIALS AND METHODS

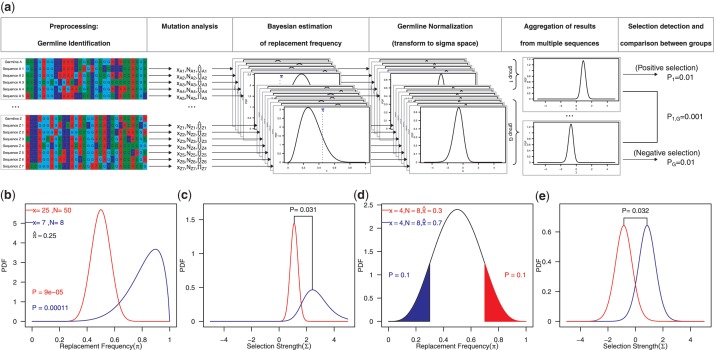
The workflow begins with a set of Ig sequences along with their associated germlines, which can be determined using available approaches (for example: 14,15). These data are then analyzed in five steps (Figure 1), which we briefly outline below, and then further expand in subsequent sections:

1. Mutation analysis: point mutations are identified in each sequence and grouped by location (CDR or FWR) and type (R or S) resulting in four categories (R_CDR, R_FWR, S_CDR, S_FWR). The expected number of mutations for each category (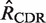,,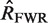 ,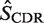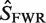) is then calculated based on an underlying targeting model as described previously (13).

2. Bayesian estimation of replacement frequency (π): a posterior probability distribution function (PDF) is calculated for π using a binomial likelihood function and a β prior. The hyperparameters for the β distribution are optimized to estimate selection strength through a numerical approach (see further Figures 2 and 3).

3. Germline normalization: the posterior distributions for the replacement frequency (π) are not directly comparable between sequences. High values for one sequence may be low for another, as the expected frequency (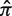) varies depending on the germline segments (Figure 1). For that reason, the well-known concept of log-odds ratios is applied to transform the PDF of π into 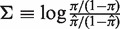, which is referred to below as the selection strength. This normalization step allows for direct comparison between sequences with different baseline expected replacement frequencies ().

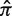4. Aggregation of results from multiple sequences: a single PDF for the selection strength is obtained from a group of multiple independent sequences (e.g. collected following a defined treatment). This is accomplished through a fast numerical convolution technique we have developed for this purpose.

5. Selection detection and comparison between groups: a numerical integration approach is used to identify differences between selection strength PDFs, allowing for the statistical detection of positive and negative selection and the comparison between two independent sequences or groups of sequences.

Figure 1.

BASELINe. (a) Summary of the basic work flow. (b and d) Posterior distributions for the frequency of replacement mutations (π) for hypothetical sequences with the indicated number of replacement (x) and total mutations (N). The shaded area indicates the fraction of the distribution that exceeds the expected frequency (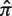). (c and e) The posterior distributions that result after transforming to the Σ-space quantifying selection strength for the same sequences in [b] and [d] respectively.

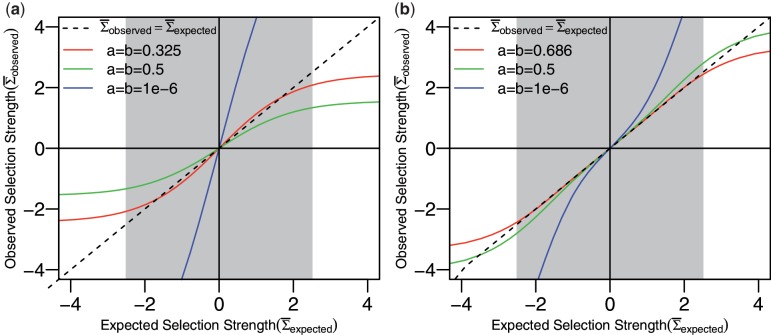
Figure 2.

Fitting the hyperparameters of the β prior. The observed and expected selection strengths are compared for different choices of the hyperparameters for the β prior for (a) N = 1 and (b) N = 10. In both cases .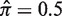

Figure 3.

The interval of optimal estimation depends on 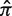. The hyperparameters for the Bayesian prior were estimated for each value of N (N = 10 here) at 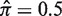by fitting within the shaded region (b). Although the hyperparameters remain fixed, the interval of optimal estimation (shaded) will shift for different values of 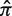[0.25 in (a) and 0.75 in (c)].

Mutation analysis

The first step in BASELINe involves the analysis of each sequence to: (i) identify the occurrence of point mutations, and (ii) estimate the expected number of mutations. These observed and expected numbers are calculated separately for each mutation type (R and S) and region (CDR and FWR). Mutations within the same codon are considered independently and the germline context is used to determine the mutation type. The observed numbers are used to define the number of trials (N) and the number of successes (x) in the Binomial formulation, whereas the expected numbers define the Binomial probability of success (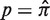). The precise definition of these relationships depends on the statistical formulation being used as defined in Table 1 from (13) . For example, when testing for selection in the CDR using the focused test formulation (used throughout this article), we define x as the number of observed replacement mutations in the CDR (R_CDR), N = R_CDR + S_CDR + S_FWR and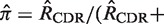 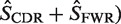. When calculating the expectations, we use Equation (1) (13). We derived this formula to fully account for the effects of microsequence specificity (16) and also to introduce the well-characterized substitution bias of somatic hypermutation (17,18). For example, the expected number of R mutations in the CDR (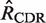) is the sum of the product of two factors: (1) the relative probability that a point mutation will fall in the CDR, and (2) the probability that the base substitution results in an amino acid replacement:

(1)

where i is summed over all positions (excluding gaps and N's) in the region (i.e. CDR or FWR) and b over all possible nucleotides ({A, C, T, G}). In this equation 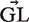is a vector containing the nucleic content of each position in the germline sequence, 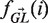is the mutability index for position i in germline 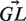, M_a→b is the relative rate in which nucleotide a mutates to b (while M_a→a = 0) and 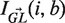is an indicator function that is 1 in cases where a mutation in position i from GL[i] to b results in a replacement mutation and 0 otherwise. As explained in (8), 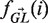is calculated by averaging over the relative mutabilities of the three trinucleotide motifs that include the nucleotide GL[i]. In the present implementation of BASELINe, the relative mutatbilities of each trinucleotide are taken from previous studies (16) which calculate these for mouse and human separately and M_a→b is taken from (17). It is important to note that BASELINe could take into account any mutability and substitution matrix: in the case where new studies will come up with more accurate models for somatic hypermutation targeting, the available code could be easily adapted to use them.

Bayesian estimation of replacement frequency (π)

Following the mutation analysis step, BASELINe utilizes the observed point mutation pattern along with Bayesian statistics to estimate the posterior distribution for the replacement frequency (P(π|x)) in each sequence, according to:

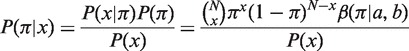(2)

where P(x) is the marginal probability of x and can be thought of as a normalization factor. P(x|π) is a Binomial likelihood function and P(π) is a prior distribution. We chose a β prior (β(π|a, b)) as it forms a conjugate pair with the Binomial likelihood (i.e. using a β prior implies a β posterior).

Germline normalization

In order to allow for the comparison between sequences, we use a log-odds ratio formulation and normalize π using its expected value to arrive at an estimate of selection strength: 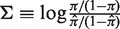. Using this formula, positive (negative) values of Σ arise when the estimated replacement-to-silent frequency is higher (lower) than expected, indicating positive (negative) selection. This is why we refer to Σ as the selection strength.

The PDF for Σ is derived by the following transformation:

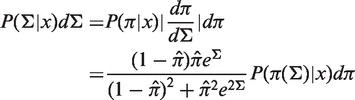(3)

where

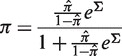(4)

and P(π(Σ)|x)dπ is the β posterior PDF from Equation (2).

Aggregation of results from multiple sequences

While the selection strengths predicted by BASELINe perform well on average, the estimates for individual sequences can be highly variable, especially when the number of mutations is small. Experimentally, many data sets include a mix of sequences with and without detectable selection (12,19) making interpretation difficult. Therefore, we included in BASELINe a method for aggregating results from multiple sequences to provide a single result. The selection strength PDFs for any two independent sequences [P₁(Σ₁) and P₂(Σ₂)] can be combined using standard numerical convolution to derive the PDF for the sum (Σ₁ + Σ₂) by the following formula:

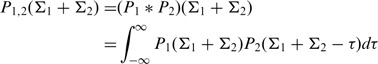(5)

Since convolution is an associative operation (the order of more than two consecutive operations does not affect the result), extending this technique to G sequences is straight forward:

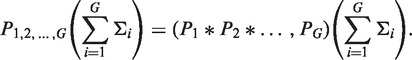(6)

This equation can be implemented directly by carrying out G sequential convolution steps from Equation (5) to arrive at a single PDF estimating the selection strength acting on the G independent sequences. Although numerical convolution is a well-studied problem with highly efficient implementations, these approaches scale poorly when the number of sequences (G) is large, such as for high-throughput sequencing data. The problem is that Σ is a continuous variable, whose PDF is sampled at a finite number of points (S), and each convolution step adds more points to the estimated PDF. The complexity of this approach is 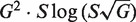where S is the number of sampling points in the PDFs and G is the number of sequences to combine, leading to unrealisitic computation times for many current data sets. Thus, we developed the following approach to group the posterior PDFs obtained from a large number of individual sequences:

1. First, we recognized that convolution can be carried out efficiently for groups composed of an integer power of two (2ⁿ) sequences. This is done by: (i) dividing the group into pairs and performing a convolution between each pair (resulting in 2ⁿ⁻¹ PDFs in 2S + 1 points), (ii) sampling the resulting PDFs in S points, and then (iii) repeating these steps until a single PDF is obtained.

2. Any arbitrary G sequences can be divided into distinct powers of 2: 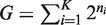, where n_i are integers and n₁ < n₂ < .. < n_K. For each group i, we calculate a single PDF using the method described in item 1 above for powers of two. These PDFs are then combined serially (i = 1 … K) using a weighted convolution, with weights that are equal to 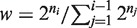for the i-th added group. Weighting is implemented by interpolating the next PDF to be included in the convolution at S·w points. Following the convolution, the PDF is again sampled in S points. Having w greater than 1 ensures that we do not lose information in the sampling stage.

3. It can still be the case that some of the weights are very large [O(G)] leading to long computation times for the convolution step. For example, if G = 1025 and S = 4000 (our default value) the approach above will produce a weight of 1024, requiring a convolution between PDFs with 4000 and 4000·1024 points. To overcome this obstacle, we do not divide G into distinct powers of 2. Rather, we divide G into as many groups of size 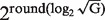as possible, and up to one larger group that may not be a power of 2. Sequences in this larger group are handled as described in item 2 producing a single PDF. The remaining groups that are an integer power of 2 are first combined individually as described in item 1, and then the resulting PDFs are combined using weighted convolution as described in item 2. Finally, these two PDFs are combined using weighted convolution with the weight of the larger group adjusted appropriately for the number of sequences it contains.

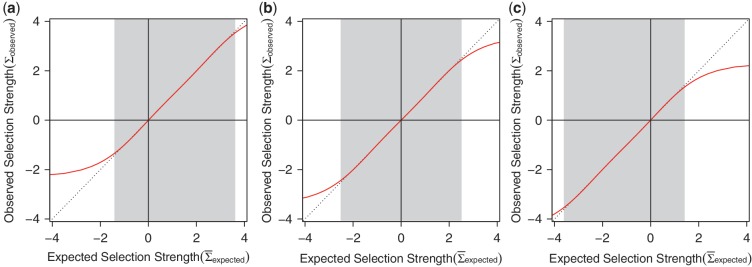
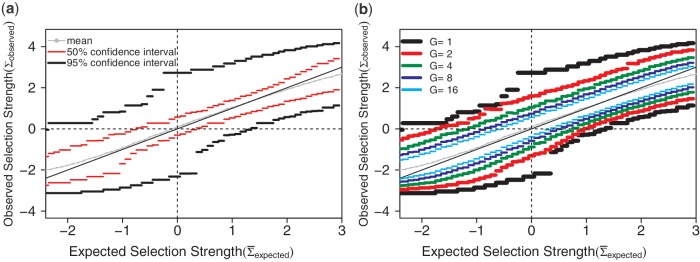
This approach decreases the complexity of sequence aggregation by more than a factor of G, greatly facilitating the analysis of large data set. The ability to efficiently aggregate results from multiple sequences dramatically increases the statistical power of BASELINe by improving the confidence of the mean estimated selection strength (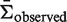, see Figure 4b and Supplementary Figure S4b).

Figure 4.

Simulation-based validation of BASELINe. Ten thousand mutated sequences were generated using a sequence-based simulation starting from the IGHV3-23 germline segment. The mean estimated selection strength obtained by BASELINe was recorded for each sequence. (a) The mean of these values along with the 50 and 95% confidence intervals. (b) Tighter 95% confidence intervals are obtained by aggregating data from groups of G = 1,2,4,8 or 16 sequences.

Selection detection and comparison between groups

Aggregation provides a single estimate of the selection strength PDF for a group of sequences. Similar to previous methods for detecting selection, BASELINe can use this PDF to supply a single P-value for detecting the presence of positive (or negative) selection. This is done by calculating the area under the curve of the selection strength PDF which has positive (or negative) values. However, a different method is needed for comparing two groups, since calculating two P-values for the deviations from the null hypothesis (i.e. no selection) for two different groups is not the same as calculating a P-value for the equivalence of both groups (20). The ability to compare these PDFs across different groups enables important biological question to be addressed. For example, we could compare selection between (i) wild-type and knockout mouse strains showing defects in germinal center formation, (ii) vaccination responses that succeed or fail to generate protective antibody titers, or (iii) autoimmune responses with matched healthy controls. To answer these questions, we compare the two posterior selection strength PDFs (P₁ and P₂) using numerical integration to obtain a (one-sided) P-value. Specifically, we calculate the probability that x₁, which is a random variable drawn from P₁, is larger than x₂ (drawn from P₂). The resulting P-value for testing the alternate hypothesis that the selection strength in the group producing P₁ is larger than that for P₂ is:

(7)

where Θ(x) is the Heaviside step function equals to 0 when x < 0, 1 when x > 0 and 1/2 when x = 0.

RESULTS

Quantifying selection pressure (with a Bayesian estimate of π or Σ), rather than simply detecting its presence (with a single P-value from a binomial test), opens up new possibilities for analysis. The P-values that result from previous methods do not provide knowledge about how selection is altered under different experimental conditions because lower P-values do not necessarily imply stronger selection. For example, the two hypothetical Ig sequences in Figure 1 b and c were derived from the same germline and thus have the same expected replacement frequency (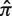 = 0.25), but the pattern of accumulated mutations is different. Even though the P-value from a binomial-based test of sequence A (plotted in red) is smaller than that for sequence B (plotted in blue), the full posterior PDF reveals stronger selection in sequence B. In this case, the replacement frequencies for these sequences can be directly compared, since the expected replacement frequency is the same for both. This is often the case for experiments using transgenic mice. However, with next-generation sequencing approaches, a mix of sequences from different germlines is often obtained so that replacement frequency estimates are not comparable, even when the overall number of mutations is equivalent. For example, the two hypothetical Ig sequences in Figure 1 d and e have the same pattern of mutations (x = 4, N = 8), but were derived from non-identical germlines and thus have different underlying expectations (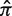). While the PDF of the replacement frequency is the same for both sequences, comparing the selection strength, as we propose, clearly shows that the sequences are subject to different selection pressures.

Fitting the hyperparameters of the Bayesian prior

As described in ‘Materials and Methods’ section, the Bayesian estimation of replacement frequency utilizes a β prior [Equation (2)]. The beta prior has two parameters (hyperparameters) a and b, which yield a beta posterior with parameters a + x and b + N − x. In principal, many different criteria can be used to fit the hyperparameters using features of the posterior distribution. Here, we applied two constraints to estimate a and b. First, we require that a = b < 1, which has been shown to give credential intervals close to the confidence intervals obtained by frequency methods (21). Second, we fit the hyperparameters in such a way that the mean of the posterior distribution for selection strength (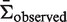) at 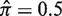will be as close as possible to the actual selection strength (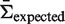) for 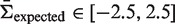. This is accomplished through a least-squares minimization procedure, in which 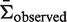is a weighted average of the means of the posterior PDFs for x = 0 … N, and the weights are given by the corresponding binomial probabilities [Bin(x, N, π), where π is calculated from 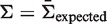using Equation (4)]. Since the hyperparameters depend on the total number of mutations (N), our fitting approach provides advantages over choosing a fixed value (Figure 2). Fitting the hyperparameters is done separately for each value of N to obtain a(N) (Supplementary Figure S3). The advantage of requiring a = b is seen in Figure 3: once the parameters are chosen (a = b = 0.686 in this case, N = 10), then changing the expected frequency of replacement mutations (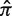) does not alter the quality of the fit. However, the values of Σ associated with the fitted region will depend on 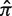. If the actual 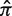is smaller (larger) than 0.5 we will gain accuracy for positive (negative) values of Σ but underestimate negative (positive) selection pressures. Thus, our approach is conservative. Outside the region used for fitting ( 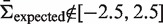for 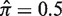) the proposed approach will underestimate the actual selection pressure, which means BASELINe is also conservative in the limits of large and small selection strengths.

Simulation-based validation

We validated BASELINe using a stochastic simulation approach. The advantage of using simulated data is that the underlying biological parameters controlling mutation and selection are all known precisely, and can be set to explore a wide range of biological conditions. We first sought to validate BASELINe using mutation data simulated by a generic binomial process. In this case, mutations are generated directly by applying the Binomial distribution to determine the number of replacement mutations (x) for a fixed number of total mutations (N). In each simulation x is drawn from a Binomial probability with parameters N and π_expected, where π_expected is defined by Equation (4) and 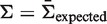. For each 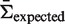, 10 000 simulations were run and the resulting mutation pattern was used as input to BASELINe in order to estimate the selection strength PDF. By taking the mean of each PDF, we calculated the average selection strength for each 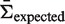(Supplementary Figure S4a). The actual biological processes of somatic hypermutation and selection do not precisely conform to a binomial process. To account for these features, we further tested BASELINe using data from a sequence-based simulation (R source code is available through the BASELINe website). In this case, mutations are introduced into actual Ig sequences in a way that allows different selection strengths in CDR (Σ_CDR) and FWR (Σ_FWR). The simulation is initiated with a single IMGT formatted Ig V germline sequence. Mutations are introduced one-by-one along the entire length of the sequence (excluding gaps) in two steps. First, the position is chosen stochastically based on the microsequence specificity of each nucleotide to account for hot/cold-spots (16). Second, the particular substitution is probabilistically determined accounting for transition bias (17). Selection is implemented by specifying selection strengths independently for CDR (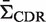) and FWR (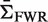). These selection strengths are translated into R frequencies (π) for each region (CDR and FWR) according to Equation (4). For each region, we then uniformly alter the probability of all possible R mutations in order to achieve the specified R frequency. For example, Σ_CDR values of − 1, 0 and 1 yield synthetic data with negative, neutral and positive selection in the CDR, respectively. To validate BASELINe, we simulated sequences with strong negative selection in the FWR (Σ_FWR = −1) and varied the extent of positive selection in the CDR (Σ_CDR). BASELINe was used to quantify the selection strength in the CDR. By comparing expected and observed selection strengths, one can see that the approach yields tight estimates and, as designed, is conservative at the strongest selection strengths for both positive and negative selection (Figure 4a).

Example applications

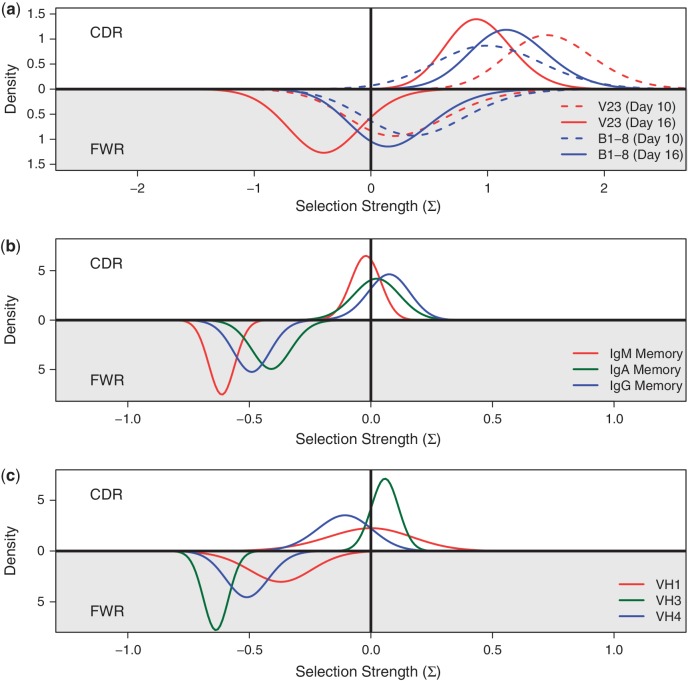
To illustrate the types of insights that can be gained, we analyzed two sets of experimental data. The first data set comes from a study comparing B-cell affinity maturation in IgH transgenic mice where the heavy chain receptor is fixed to encode moderate (B1 − 8) or very low (V23) affinity antibodies when paired with an endogenous λ1 light chain. These data are described in (19). Briefly, sequences from each of 166 B-cell clones were collected through microdissection of splenic Germinal Centers at days 10 and 16 post-immunization with nitrophenyl. Clonality of the sequences was determined as described in (8). Since mutation is restricted to the λ light chain, this provides an ideal system to study antigen-driven selection where all the selection pressure rests solely on the variable domain of the λ light chain. The sequences were grouped by mouse genotype and day post-immunization. The results of applying BASELINe to the entire Ig sequence, spanning the V and J regions, clearly show positive selection in the CDR for both genotypes. Most importantly, we can now compare the selection strengths in these two mice. Looking at Figure 5a, we do not observe significantly different selection strengths between these mice, suggesting that the selection process can operate independently of the germline receptor affinity.

Figure 5.

Applications of BASELINe to estimate selection strength from real data. (a) Posterior probability distributions for Ig sequences from two mice strains with moderate (B1-8) or low (V23) initial affinity for the immunizing antigen at different days post-immunization (10 and 16) (19). (b and c) Posterior probability distributions for different memory cell subsets (b) or the three most frequent IGHV families (c) for data in (2). The top half of each plot shows the estimated selection strength in the CDR, whereas the bottom part provides an estimate for FWR.

The second data set comes from a next-generation sequencing study of the Ig heavy chain repertoire from the blood of three healthy individuals. These data are described in (2). Briefly, five B cell types (transitional, naïve, IgM memory, IgA memory and IgG memory) were sorted from peripheral blood mononuclear cell (PBMCs) of three healthy adults. High-throughput sequencing of these cells was carried out to generate 3577 Ig heavy chain sequences after filtering for quality and picking one sequence to represent each clone (2). We additionally removed sequences that were identified as non-functional, or had more than 50 point mutations according to IMGT High V-Quest (14), resulting in a dataset containing 880 sequences from memory cells. These sequences were grouped by individual, cell type and IGHV germline segment family for analysis of the V and J regions [the D segment and surrounding N and P additions were excluded due to uncertainty in the germline assignment (15)]. Figure 5b shows that all memory isotypes are subject to significant negative selection in the FWR, but the selection strength is stronger in IgM compared with IgG and IgA memory cells (although the difference is only significant for IgA, P = 0.02). Weaker negative selection for IgG and IgA could reflect a higher starting affinity for these cells (allowing them to be more tolerant of affinity-decreasing mutations), or positive selection for some mutations in the FWR region. While the latter hypothesis is supported by the observation that these isotypes show a trend towards increased selection strengths in the CDR, we did not detect statistically significant differences in the CDR selection strength PDFs for any of the memory cell isotypes. Taken together, this pattern suggests that IgM memory cells are formed earlier in the germinal center reaction. Wu et al. (2) were able to identify significant differences in the repertoire composition of IgM and class-switched memory cells. The ability to combine data from different germline segments allows us to extend these observations by showing that the differences in selection strength that we observe for the isotypes are driven by variation in selection strengths of each germline family, with IGHV3 contributing much of the CDR positive selection observed in IgM and IgA memory cells (Figure 5c and Supplementary Figure S6).

DISCUSSION

We have developed BASELINe, a Bayesian framework for quantifying immune selection that can be applied to large-scale B-cell Ig sequence data sets. When combined with the dramatic improvements being made in high-throughput sequencing, BASELINe opens exciting possibilities for the future analysis of B-cell repertoires. Since new data sets are likely to include orders of magnitude increases in the number of sequences, we have developed an optimized code implementing BASELINe. Benchmarking results indicate that 10 000 sequences can be analyzed in 4 min on a single 1.73 GHz processor (Supplementary Figure S8), which means a complete human repertoire analysis is feasible.

The framework developed here is quite general, and can easily be extended. First, selection strength can be defined based on patterns other than the replacement frequency. For example, it has been suggested that selection impacts the frequency of non-conservative mutations (i.e. those that change the amino acid property) even beyond the number of replacement mutations (22). This could be implemented simply by changing the definition of which nucleotide exchanges constitute replacement mutations.

Second, BASELINe can be adapted to other biological questions. At its core, our method quantifies the deviation from the expectation of repeated independent binomial variables, each of which has a different probability of success. This allows a wide range of problems to be addressed by re-defining replacement and silent mutations as arbitrary sets of positions/substitutions. As one such example, the framework can be used to quantify strand-bias for AID, which targets cytosines (C) for mutation. This is done by re-defining all mutations at C to be replacements and all mutations at guanine to be silent. In this formulation, positive selection indicates a coding-strand bias, whereas negative selection would indicate a non-coding-strand bias. Existing methods for testing strand-bias are limited since they do not account for the full range of hot/cold-spots and variation across germline segments (18,23,24).

In summary, we have developed a framework for analyzing arbitrary DNA mutation patterns in the context of a mutator that displays intrinsic biases (i.e. hot/cold-spots and substitution preference). This approach was implemented for Bayesian estimation of Antigen-driven SELectIoN (BASELINe) in large-scale immunoglobulin sequence datasets, which are becoming increasingly common with the advent of next-generation sequencing. In the future, the approach may also be extended to take advantage of the information that exists in sequence abundance distributions within each clone to assess selection strength from all available sequences (25). Looking beyond the analysis of immune selection, the basic framework underlying BASELINe might be adapted to quantify selection acting on viral sequences. BASELINe is available at: http://clip.med.yale.edu/baseline.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–8.

FUNDING

National Institutes of Health (NIH) [R03AI092379-01 to S.H.K.]; Yale University Biomedical High Performance Computing Center (NIH) [RR19895]. Funding for open access charge: NIH [R03AI092379-01].

Conflict of interest statement. None declared.