Abstract
Pharmacokinetic modeling of dynamic contrast enhanced (DCE)-MRI data provides measures of the extracellular volume fraction (ve) and the volume transfer constant (Ktrans) in a given tissue. These parameter estimates may be biased, however, by confounding issues such as contrast agent and tissue water dynamics, or assumptions of vascularization and perfusion made by the commonly used model. In contrast to MRI, radiotracer imaging with SPECT is insensitive to water dynamics. A quantitative dual-isotope SPECT technique was developed to obtain an estimate of ve in a rat glioma model for comparison to the corresponding estimates obtained using DCE-MRI with a vascular input function (VIF) and reference region model (RR). Both DCE-MRI methods produced consistently larger estimates of ve in comparison to the SPECT estimates, and several experimental sources were postulated to contribute to these differences.
Keywords: MRI, dynamic contrast, DCE, tumor, pharmacokinetic modeling, SPECT, radionuclide, diffusion
Introduction
Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) is a technique often employed to characterize the microvascular environment in tumor tissues (1,2). This quantitative imaging technique provides a measure of the volume transfer constant (Ktrans) and the volume fraction of extracellular-extravascular tissue space (ve) via tracer kinetic modeling of an MRI contrast agent (CA), typically Gd-DTPA. The most commonly used DCE metric is Ktrans, which reports on perfusion, but accurate measure of ve may also be of clinical importance in assessing tumor type and response to treatment. For example, it has been shown that the relative size of ve can help distinguish between gliomas, meningiomas, and metastases (1) in brain tumors. The pharmacokinetic modeling necessary for DCE-MRI reduces a complex tissue micro-environment into a relatively simple compartmental model (3), which has known limitations (4–7). Also, parameter estimation is sensitive to the sometimes difficult to acquire vascular input function (VIF) (8–10) or the more easily acquired reference region (RR) signal (11–12). Given the array of potential sources of error in DCE-MRI, the interpretation of fitted model parameters as physical characteristics of tissue remains a question.
One of the DCE-MRI model parameters, ve, can potentially be measured directly with single photon emission computed tomography (SPECT). To this end, a dual-isotope SPECT approach was developed and implemented on rats to obtain estimates of ve that did not require dynamic tracer modeling, assumptions about water dynamics, or a VIF or RR signals. In a orthotopic rat glioma tumor model, these SPECT estimates of ve were compared with estimates derived from DCE-MRI using both the VIF and RR approaches, with the objective of elucidating some of the sources of error in the DCE-MRI.
Methods
Approximately two weeks prior to imaging, female Sprague-Dawley rats (n=8, 234–270g) were anesthetized, given analgesic, and inoculated with C6 glioma cells (1×105 cells) via stereotaxic injection. Two jugular catheters were placed in each rat, up to 24 hours before imaging. One catheter was used for CA injection while the other was used for blood sampling. Each rat was anesthetized using ≈ 2% isoflurane in oxygen for all surgical and imaging procedures. For MR imaging procedures body temperature was maintained near 37° C by a flow of warm air directed over the animal. Respiration was monitored using a pneumatic pillow placed on the side of the animal near the abdomen. Rats were imaged using a DCE-MRI protocol and were allowed to recover after the scan. Dual-isotope SPECT measurements were performed the following day, within 24 hours of the completion of the DCE-MRI measurements. Prior to SPECT, a bi-lateral nephrectomy was performed to prevent washout of the radiotracer, as was required for analysis of the SPECT data. The animals were anesthetized before the nephrectomy and remained anesthetized throughout SPECT imaging and euthanasia by overdose of isoflurane. All procedures were approved by Vanderbilt University’s institutional animal care and use committee.
DCE-MRI
MRI was performed on a 9.4T horizontal-bore magnet (Agilent, Santa Clara, CA). The animal’s head was positioned in a 38 mm diameter Litz quadrature coil (Doty Scientific, Columbia, SC) and was secured by a bite bar apparatus that also served to deliver the anesthetic gas. Scout images were collected to identify a 2 mm thick imaging slice through the center of the brain tumor and a second slice in the neck containing the major vessels feeding the brain.
Prior to DCE-MRI, an inversion-recovery snapshot experiment—TR = 12 s, TI (inversion time) = 0.250-11 s, 2 averaged excitations, 128 × 128 samples, 32 mm × 32 mm FOV—was used to generate data to produce a pre-contrast R1 (longitudinal relaxation rate = 1/T1) map, R10. A three parameter fit to these data was used to estimate R1 in the presence of imperfect inversion. The DCE-MRI protocol employed a standard spoiled gradient-echo (SPGE) sequence—TR = 10 ms, TE = 2.1 ms, flip angle (α) = 15°, 96×96 samples, and 2 averaged excitations—over the prescribed slices. Approximately 40 images were collected before a 200 µl bolus of Gd-DTPA (0.05 mmol/kg) was delivered over 5 s via the jugular catheter. After injection of the contrast agent, dynamic images were collected for 20 minutes (~2s per image) and were reconstructed to 128 × 128 samples to match the spatial resolution of the R10 map. Following the completion of the DCE-MRI experiment, a 3D SPGE—TR = 20 ms, TE = 2.1 ms, α = 20°, 128 × 128 × 64 samples, 32 × 32 × 32 mm3 slab—was acquired to provide a reference for image registration between MRI and SPECT images.
Bi-lateral Nephrectomy
Under anesthesia, two parallel incisions, one on each side, were made on the lower back of the rat. Using a swab, the kidneys were exposed and 3-0 silk sutures were slipped around each kidney and tightened around the renal pedicles, preventing clearance through the kidney. The kidneys were returned to their original position and the incisions were sutured shut. The total time for the procedure was approximately 20 minutes.
SPECT
Radionuclide imaging was performed on a NanoSPECT/CT (Bioscan, Washington DC, USA) with image reconstruction carried out using HiSPECT in the corresponding InVivoScope software. Under anesthesia, an extracellular radiotracer, 111In-DTPA (~19 MBq), was injected first, followed by a saline flush, and allowed to equilibrate for approximately 30 minutes (longer than the known wash-in time for Gd-DTPA). An intravascular tracer, 99mTc-RBCs (Ultratag®) (~130 MBq), was then injected. The higher activity of 99mTc compared with 111In was used to minimize scatter of 111In emitted photons into the 99mTc energy window. After injection of the second tracer, images were collected (48 projections (helical SPECT), 40 s per projection, reconstructed volume = 67 × 67 × 35 mm3). Three energy windows (width=18%) were set about the 99mTc and 111In photopeaks (140 keV and 171/245 keV, respectively), and projection data were recorded independently for each energy window using a 9-pinhole aperture collimator (pinhole diameter = 2.0 mm) on each of four detector heads. After collecting the brain images a blood sample (500 µL) was obtained from the unused jugular catheter and imaged with the previously described dual-isotope protocol. An X-ray CT scan was also collected for registration purposes (imaging dimensions same as SPECT). All SPECT images were reconstructed with 0.4 × 0.4 × 0.4 mm3 voxels to match the CT image.
To test the dual-isotope SPECT method, 99mTc and 111In solutions were prepared across a range of concentrations, and activities of each were measured in a gamma counter. These solutions were then used to make five mixed-isotope imaging phantoms (500 µL) with activity ratios (i.e. A99mTc / A111In) similar to those expected in the blood samples. The dual-isotope SPECT protocol was used to measure activity of each isotope in each imaging phantom, and the results were compared to the gamma counter derived measures from single isotope samples.
Data Analysis
SPECT-MRI Registration
All MR and SPECT/CT imaging data were imported into MATLAB (Mathworks, Natick, MA) for processing. Prior to any quantitative analysis, the CT data were registered to the 3D SPGE data set using a rigid registration algorithm. All SPECT data were subsequently registered to the MR-space as the SPECT images were implicitly co-registered to the CT scan. This process allowed co-registration of the single slice dynamic data (from the brain tumor) to the SPECT images.
DCE-MRI
The R10 map was used to identify a tumor region of interest (ROI) within which an R1 tissue time course, R1t(t), was determined for each voxel using:
| [1] |
where S0 was defined as
| [2] |
S− was the measured SPGE signal intensity prior to contrast agent injection, and S(t) was the measured signal intensity at a time t after contrast injection. Similarly, from a 5–10 voxel ROI in the linguofacial artery in the neck an image derived VIF was defined as R1b(t). The concentration of CA in the plasma space (Cp) was then determined using an assumption of fast water exchange across red blood cell membranes,
| [3] |
where the hematocrit (h) was 0.46, r1 (the relaxivity of Gd-DTPA at 9.4T) was assumed to be 3.8 mM−1s−1 (13,14), and the pre-contrast R1 of blood was assumed to be R10b = 0.435 s−1 (15,16).
Ktrans, ve, and vp (plasma volume fraction) were then estimated by fitting Cp(t) and R1t(t), with Eqs. [4] and [5] (5):
| [4] |
and
| [5] |
In these equations, Ct(t) is the concentration of the CA in tumor tissue as represented by the extended Tofts model (3). Subsequently, in this paper, Ktrans and ve estimates from this VIF-based analysis are defined as and ve,VIF, respectively. Non-linear fitting, here and below, used the default settings of the lsqcurvefit function in MATLAB R2011a (Natick, MA) with fitted parameters (Ktrans, ve and vp) constrained to non-negative values.
In addition to analysis using the VIF, the dynamic data were also analyzed using a RR model (11). In the RR analysis, a reference tissue ROI was selected in the temporal muscle surrounding the skull. Two parameters, Ktrans,t and ve,t, were then estimated by fitting the R1 dynamic time course from each tumor voxel and the RR with
| [6] |
where subscripts t and ref indicate tumor and reference regions, R=Ktrans,t/Ktrans,ref, and Ktrans,ref = 0.05 min−1 and ve,ref = 0.11 were set from literature values (8,11). Subsequently, in this paper, Ktrans,t and ve,t estimates from this RR-based analysis are defined as and ve,RR, respectively.
SPECT
The nephrectomy procedure allowed the extracellular radiotracer to reach equilibrium in the vascular and the extracellular-extravascular space such that
| [7] |
The concentrations of tracers in the blood sample were determined from the SPECT image of the blood sample as
| [8] |
| [9] |
where Vblood was the known volume of the blood sample and A was the measured activity of the specified radiotracer (in MBq) from the entire sample in the SPECT image. Similarly, the activity in the tumor tissue was described by
| [10] |
| [11] |
where VIV and VECEV are the volumes of the intravascular space and extracellular extravascular space, respectively, in the tumor tissue. Given the measured activities in a given tumor voxel and tracer concentrations in the blood from Eqs. [8] and [9], Eqs. [7], [10] and [11] were solved to calculate VIV and VECEV. From here, ve was estimated voxel by voxel as
| [12] |
where Vtissue was the known SPECT voxel volume. Subsequently, in this paper, ve estimates from the SPECT measurements are defined as ve,SP.
Results
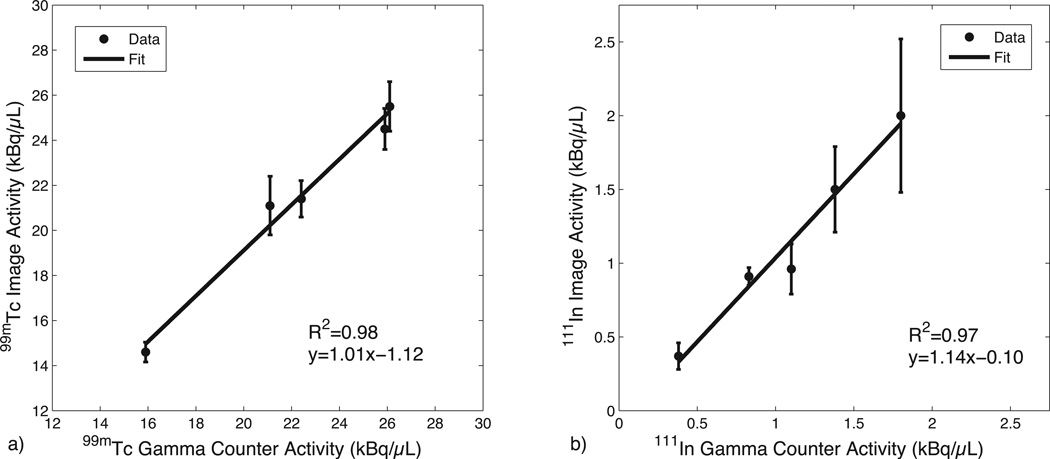
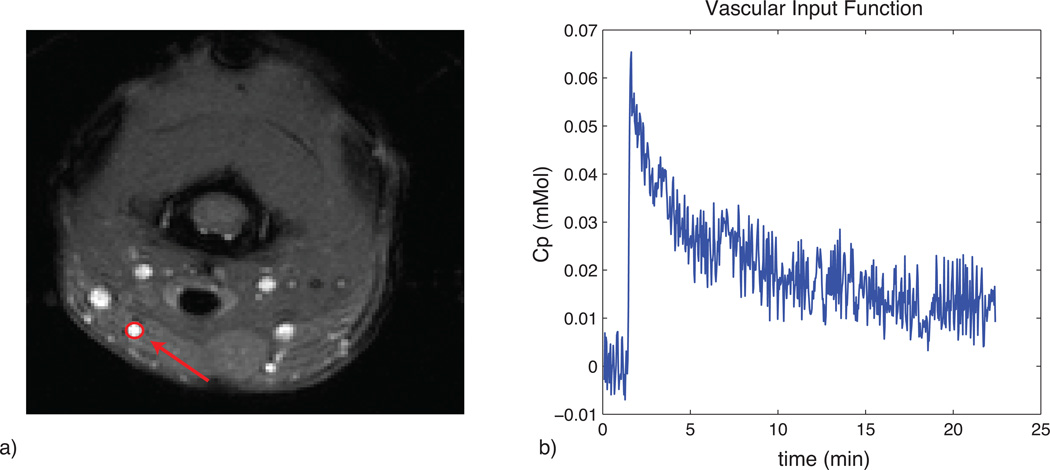
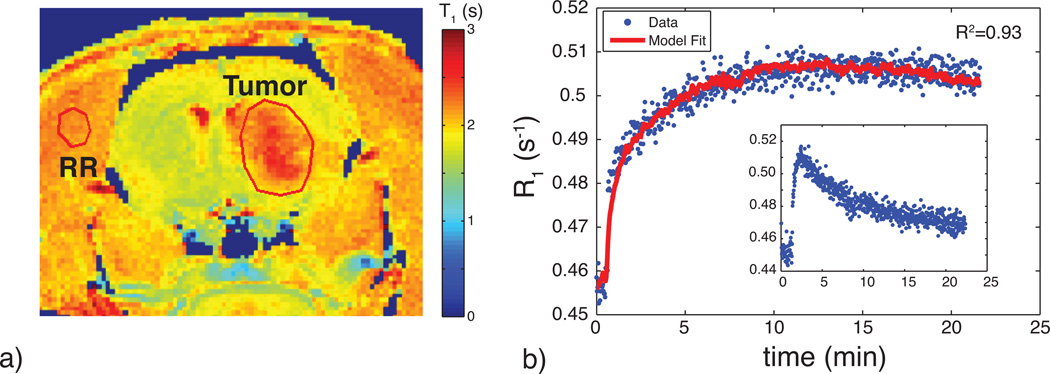
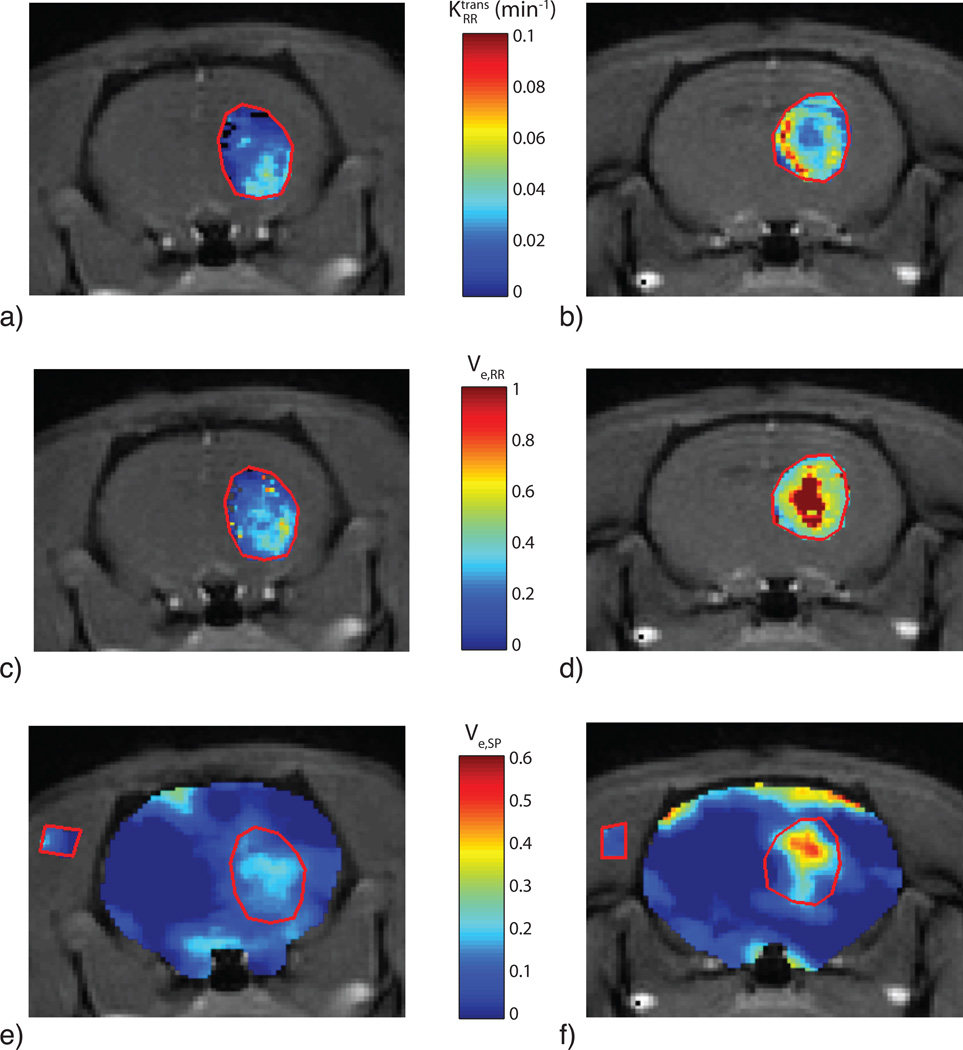
Figure 1 shows the results of the phantom SPECT measurements, demonstrating good accuracy of the dual-isotope SPECT protocol across a wide range of activities. Figure 2a shows an example of the MRI slice used to visualize and select an ROI for the VIF; a typical VIF is shown in Fig. 2b. Figure 3 shows a typical tumor ROI as manually selected on a pre-contrast T1 map (Fig. 3a) and a corresponding example voxel dynamic R1 time course along with the fit to the RR model (Fig. 3b). Figure 3a also shows a reference region (skeletal muscle) ROI and the inset in Fig. 3b shows its R1 time course, which was used for the DCE-MRI RR model fitting. All DCE-MRI fitting showed qualitatively good fits and quantitative estimates of parameter uncertainties that were much less than the spatial and inter-animal variations in model parameters. Figure 4 shows results of the parametric maps from the RR model fitting and the dual-isotope SPECT analysis from two example rats (left and right). On the left, the tumor is relatively uniformly perfused (Ktrans, Fig 4a) with moderate estimates of ve (DCE-MRI, Fig 4c; SPECT, Fig 4e). In contrast, on the right, the tumor exhibits more heterogeneous maps of Ktrans (4b), ve,RR (4d), and ve,SP (4f). In this case, although the colorbar indicates a maximum ve,RR = 1, in the tumor core some voxels exhibited ve > 1 (sometimes >> 1), indicating a breakdown of the model for accurately describing the DCE data. In order to avoid extreme outliers, only voxels exhibiting ve < 2 and Ktrans < 0.5 min−1 were included in subsequent analysis. This restriction resulted in discarding 2 - 30% (range, across animals) of tumor voxels from VIF analysis and 0.5 – 8% of tumor voxels from RR analysis.
Fig. 1.
Mixed isotope phantom validation for activity measurement with the dual-isotope protocol. a) 99mTc activity measures per volume from the SPECT image and gamma counter. b) 111In activity measures per volume from the SPECT image and gamma counter. Error bars were determined from the standard deviation across voxels in the SPECT images, and the uncertainties in the gamma counter derived measures were smaller than the marker size. Linear regression analysis also shown.
Fig. 2.
a) Example of ROI placement for the VIF in the linguofacial artery. ROIs contained between 5 – 10 voxels. b) Example VIF time-course (in [CA]) recorded over an approximately 20 minute time period. Note the rapid rise and washout of the CA.
Fig. 3.
a) An example T10 map showing the location of the manually defined brain tumor ROI and reference tissue ROI in the temporal muscle. Note the elevated T1 times in the tumor region. b) Corresponding R1 time course including RR model fit. The RR model shows a good fit to the dynamic data. The inset displays the dynamic time course of the reference tissue used for RR modeling.
Fig. 4.
Parametric maps from RR model fitting and co-registered SPECT/MR images for two different rats (one per column). (a,b) maps, (c,d) ve,RR maps, and (e,f) ve,SP maps. Note the pseudocolor scale for ve is maximum at 1, apparent in the central region of the tumor in frame d). The SPECT maps in e) and f) display the tumor ROI as well as a ROI in the muscle. The apparent discrepancy between spatial location of of high ve,RR and high ve,SP might reflect limitation in the MRI-SPECT registration.
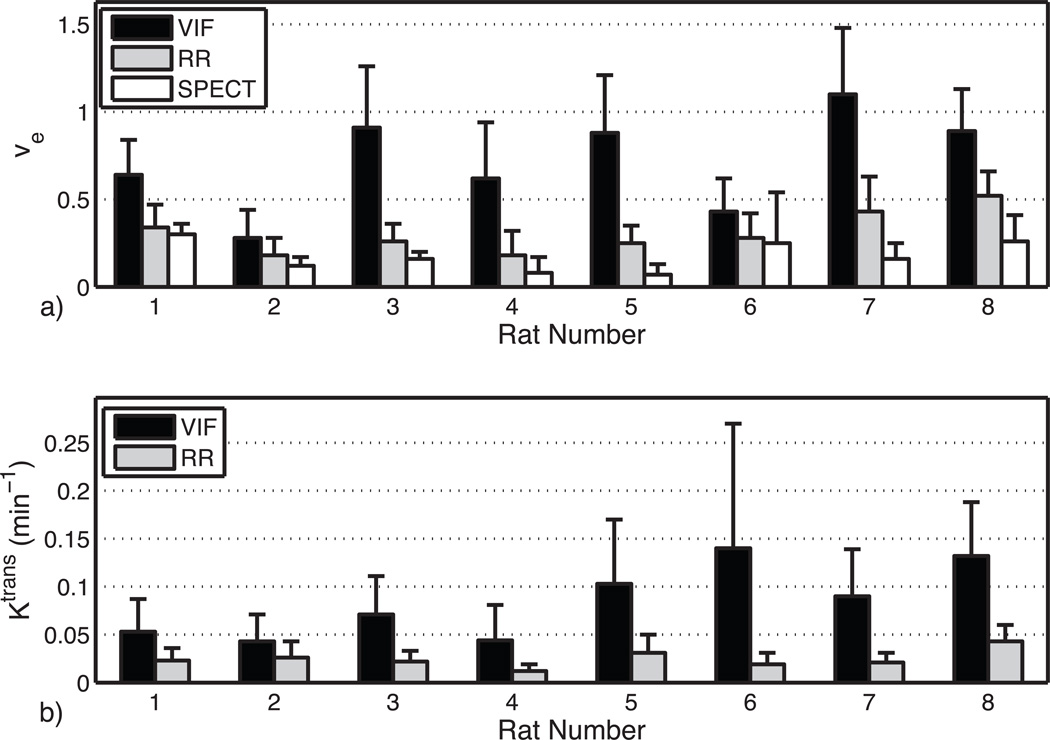
Figure 5 shows the tumor ROI mean ± standard deviation (SD) of estimates of ve (top) and Ktrans (bottom) from both DCE-MRI methods and SPECT (for ve only) for all eight animals. In general, the ve estimates from the VIF analysis exceeded those of the RR analysis, and both DCE-MRI analyses of ve were higher than those found in the dual-isotope SPECT. Computed voxel-by-voxel from the tumor ROIs in all eight animals, ve,VIF - ve,SP = 0.57 (±0.01 standard error (SE)), and the difference was significant (t-test, p<0.0001) in all eight animals. Similarly, across all tumor ROI voxels, ve,RR - ve,SP =0.14 (±0.005 SE), and the difference was significant (t-test, p<0.01) in 7 of 8 animals. Comparing the DCE-MRI analysis techniques, ve,VIF - ve,RR =0.43 (±0.008 SE), and again, the difference was significant (t-test, p<0.0001) in all eight animals.
Fig. 5.
a) Comparison of ve for VIF, RR, and SPECT analysis for each animal studied. b) Comparison of Ktrans for VIF and RR analysis. Solid bars represent mean values while error bars represent the standard deviations. Note that error bars are somewhat underestimated because outlier voxels exhibiting ve > 2 or Ktrans > 0.5 min−1 were not included in analysis.
Although there was no comparable measure for Ktrans from the SPECT data, it is worth noting that across all eight animals (Fig. 5b). Also, although not shown in Fig. 5, a similar overestimation of blood volume fraction by VIF analysis of DCE-MRI (range across animals of mean = 0.04–0.18 and of SD = 0.03–0.15) compared with SPECT measures (range across animals of mean = 0.019–0.036 and of SD = 0.005–0.011) was found. Note, however, that constraining vp to a priori values similar to those found by SPECT had little effect on the fitted values of ve by DCE-MRI.
Discussion
To the authors’ knowledge, this is the first account of an in vivo radionuclide measure of the extracellular-extravascular volume fraction; although previous such measures have been made ex vivo via whole tissue gamma counting or autoradiography (17,18). While the radionuclide imaging used in this study is not practical for routine pre-clinical use because it involves surgical intervention to allow tracer equilibration, it is insensitive to water dynamics and does not require a vascular input function. Regarding surgical effects on parameter estimates, two previous studies showed no significant changes in plasma space or tissue water content of normal rat brain over the time, post-nephrectomy, during which the current measurements were recorded (19,20). Phantom tests (see Fig. 1) demonstrated the accuracy of this dual-energy SPECT method for measuring concentrations of 99mTc-RBCs and 111In-DTPA, and the in vivo results demonstrate a reasonable correspondence of both ve (0.10 ± 0.04) from skeletal muscle (17,18, 21) and blood volume (0.03 ± 0.01) in tumors to literature values (22). Thus, although no independent validation of the in vivo SPECT measurements from tumor have been made, we interpret the observed differences in SPECT and MRI measures of ve (Fig. 5) to predominantly reflect an overestimation of ve from DCE-MRI.
The explanation for why DCE-MRI overestimated ve is not entirely clear, but is apparent that DCE analysis using a VIF resulted in a much greater overestimation than did analysis using the reference region. Averaging of the vascular signal over space with non-vascular signal or over time during the peak of the VIF will result in a diminished VIF and, in turn, an increased estimate of ve (8, 23). However, in this study, the VIF was acquired at relatively high spatial and temporal resolutions, so these factors are unlikely to explain the differences between ve,VIF and ve,RR. The VIF amplitude may also be reduced by T2* effects, but again, in this study, with TE = 2.1 ms and peak Cp ~0.2 mM, a relaxivity of ~10 s−1/mM results in < 1 % signal reduction. A third potential source of error in the VIF is due to the inflow effect on the T1-weighting image contrast, which has been studied in detail recently (24, 25) and an earlier study showed roughly the same scale of ve overestimation when inflow effects were not avoided (26).
Inflowing blood which did not experience the previous RF excitation pulses is not T1-weighted and results in an overestimation of S0 (Eq. [2]) and an underestimation of the change in S(t) (Eq [1]). Both of these factors diminish the VIF and, in turn, result in an overestimation of ve. In the context of the present study, an arterial blood velocity of 5 cm/s (27) dictates that ≈¼ of the blood in a 2 mm imaging slice is replaced with inflowing blood every TR (10 ms). Crudely then, one can consider the blood signal to be 75% from magnetization at steady state and 25% from magnetization at equilibrium. Then, given R10b = 0.435 s−1 and α = 15°, Eq. [2] will overestimate S0,blood by ≈3× and, for a peak Cp ~0.2 mM, the net effect is to overestimate ve by ≈2×. This model of inflow agrees well with the observations (not shown) that S0,blood ≈ 3 × S0,muscle and roughly with the observations of ve,VIF compared with ve,RR (Fig. 5), thereby suggesting that inflow is the dominant source of discrepancy between the VIF and RR results in this study. The simplest strategy to avoid inflow effects on the VIF is to use a 3D acquisition protocol, but this is difficult in rodents due to the high temporal sampling requirements of the VIF (28). Various other strategies to minimize the inflow effect include: deriving the VIF from small vessels with slowly flowing blood and/or vessels lying in the imaging plane (29); through appropriate RF preparation of out of slice magnetization (26, 30); or through the use of a reference tissue for calibration of the AIF (22,29). Alternatively, the reference region method can be used to avoid the VIF altogether.
The reference region analysis provided values of ve,RR that were closer to but still consistently larger than ve,SP (Fig. 5). The DCE model used in this study assumed fast exchange of water between intra- and extra-cellular tissue spaces, which may not be a valid assumption, particularly with the introduction of extra-cellular contrast agent (4). However, in the case where fast exchange is not valid, the effect on the DCE analysis is to underestimate not overestimate ve, so while water exchange may be affecting the DCE analysis it does not explain the observations here. In addition to water dynamics, CA dynamics may also affect DCE parameter estimation. Pellerin et al. postulated that in tumors CA diffuses from well-vascularized regions to adjacent poorly perfused regions over the time-course of a DCE experiment (7). To account for the slow arrival of CA to poorly perfused tissues, the Tofts model assigns very low (non-zero) values to Ktrans and overestimates of ve (7,31). If this phenomenon were contributing to overestimates of ve,RR, the greatest effect would be expected in necrotic tumor regions, which is consistent with previous DCE observations of large ve in necrotic tissue by Donahue et al. (17). Indeed, the central tumor voxels of rats 7 and 8 exhibited a large ve,SP (e.g., Fig. 4f) perhaps indicating a necrotic core, and the DCE analysis showed low Ktrans and ve,RR > 1 from the same voxels. (Of course, slow arrival of 111In-DTPA to necrotic regions could also result in a reduced value of ve,SP, although more time was allowed for tracer distribution in the SPECT studies.) Also, Sourbron and Buckley recently demonstrated that DCE analysis with the Tofts model is sensitive to variations in vascularization and perfusion, independent of CA diffusion between voxels (6). Their analysis shows that in intermediate-to-highly vascularized tissues or tissues that are poorly perfused, ve may be overestimated by DCE-MRI, which may explain the observations here of ve,RR > ve,SP in non-necrotic tumor regions.
The interpretation that DCE-MRI may overestimate ve might also explain previous studies that have found, surprisingly, only weak to moderate correlations between ve and the apparent diffusion coefficient (ADC) of water (32–34) in tumors. While DCE-MRI measures of ve in tumors has been found to shrink in response to treatment (35, 36), water ADC has been shown to increase in response to treatment (36). Perhaps this apparent inconsistency reflects a change in the state of tumor vascularization or perfusion with treatment that results in a more accurate measure of ve. In this case, the observed ve from DCE-MRI may go down in response to treatment simply because it is less overestimated, while in fact the extracellular volume fraction goes up, resulting in an increased water ADC. Regardless of the exact source of error in measures of ve, the wide range of ve values observed in this study indicates that one should be cautious about an absolute quantitative, physical interpretation of ve particularly if an in-flow sensitive VIF is used.
Acknowledgements
The authors thank Zou Yue for performing the animal surgeries and Don Nolting, Ron Baldwin, Noor Tantawy, and Clare Osborne for help with radiotracer labeling and SPECT imaging. The authors also thank Mary Loveless and Jennifer Whisenant for informative discussions.
Grant Sponsor: EB001744, CA138599
Abbreviations Used
- DCE
dynamic contrast enhanced
- ve
extracellular-extravascular volume fraction
- Ktrans
volume transfer constant
- VIF
vascular input function
- RR
reference region
- CA
contrast agent
- SPECT
single photon emission computed tomography
- TI
inversion time
- SPGE
spoiled gradient-echo
- Gd-DTPA
gadopentate dimeglumine
- 111In-DTPA
indium 111 labeled diethylene triamine pentaacetic acid
- 99mTc-RBCs
technecium 99 metastable labeled red blood cells
- CT
computed tomogrphy
- vp
plasma volume fraction
- ADC
apparent diffusion coefficient
References
- 1.Ludeman L, Grieger W, Wurm R, Wust P, Zimmer C. Quantitative measurement of leakage volume and permeability in gliomas, meningiomas and brain metastases with dynamic contrast-enhanced MRI. Magn Reson Imag. 2005;23:833–841. doi: 10.1016/j.mri.2005.06.007. [DOI] [PubMed] [Google Scholar]
- 2.Harrer JU, Parker GJM, Haroon HA, Buckley DL, Embelton K, Roberts C, Baleriaux D, Jackson A. Comparative study of methods for determining vascular permeability and blood volume in human gliomas. J Magn Reson Imag. 2004;20:748–757. doi: 10.1002/jmri.20182. [DOI] [PubMed] [Google Scholar]
- 3.Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J Magn Reson Imag. 1997;7:91–101. doi: 10.1002/jmri.1880070113. [DOI] [PubMed] [Google Scholar]
- 4.Yankeelov TE, Rooney WD, Li X, Springer CS. Variation of the relaxographic "shutter-speed" for transcytolemmal water exchange affects the CR bolus-tracking curves shape. Magn Reson Med. 2003;50:1151–1169. doi: 10.1002/mrm.10624. [DOI] [PubMed] [Google Scholar]
- 5.Landis CS, Li X, Telang FW, Coderre JA, Micca PL, Rooney WD, Latour LL, Vetek G, Palyka I, Springer CS. Determination of the MRI contrast agent concentration time course in vivo following bolus injection: effect of equilibrium transcytolemmal water exchange. Magn Reson Med. 2000;44:563–574. doi: 10.1002/1522-2594(200010)44:4<563::aid-mrm10>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 6.Sourbron SP, Buckley DL. On the scope and interpretation of the Tofts models for DCE-MRI. Magn Reson Med. 2011;66(3):735–745. doi: 10.1002/mrm.22861. [DOI] [PubMed] [Google Scholar]
- 7.Pellerin M, Yankeelov TE, Lepage M. Incorporating contrast agent diffusion into the analysis of DCE-MRI data. Magn Reson Med. 2007;58:1124–1134. doi: 10.1002/mrm.21400. [DOI] [PubMed] [Google Scholar]
- 8.Cheng HLM. Investigation and optimization of parameter accuracy in dynamic contrast enhanced MRI. J Magn Reson Imag. 2008;28:736–743. doi: 10.1002/jmri.21489. [DOI] [PubMed] [Google Scholar]
- 9.Pickup S, Zhou R, Glickson J. MRI estimation of the arterial input function in mice. Acad Radiol. 2003;10:963–968. doi: 10.1016/s1076-6332(03)00291-5. [DOI] [PubMed] [Google Scholar]
- 10.Zhou R, Pickup S, Yankeelov, Springer CS, Glickson JD. Simultaneous measurement of arterial input function and tumor pharmacokinetics in mice by dynamic contrast enhanced imaging: Effects of transcytolemmal water exchange. Magn Reson Med. 2004;52:248–257. doi: 10.1002/mrm.20143. [DOI] [PubMed] [Google Scholar]
- 11.Yankeelov TE, Luci JL, Lepage M, Li R, Debusk L, Lin PC, Price R, Gore JC. Quantitative pharmacokinetic analysis of DCE-MRI data without an arterial input function: a reference region model. Magn Reson Imag. 2005;23:519–529. doi: 10.1016/j.mri.2005.02.013. [DOI] [PubMed] [Google Scholar]
- 12.Yankeelov TE, Cron GO, Addison CL, Wallace JC, Wilkins RC, Pappas BA, Santyr GE, Gore JC. Comparison of a reference region model with direct measurements of an AIF in the analysis of DCE-MRI data. Magn Reson Med. 2007;57:353–361. doi: 10.1002/mrm.21131. [DOI] [PubMed] [Google Scholar]
- 13.Donahue KM, Burstein D, Manning WJ, Gray ML. Studies of Gd-DTP relaxivity and proton exchange rate in tissue. Magn Reson Med. 1994;32:66–76. doi: 10.1002/mrm.1910320110. [DOI] [PubMed] [Google Scholar]
- 14.Rodriguez E, Roig A, Molins A, Arus C, Qunitero MR, Cabanas ME, Cerdan S, Lopez-Larrubia P, Sanfeliu C. In vitro characterization of an Fe8 cluster as a potential MRI contrast agent. NMR Biomed. 2005;18:300–307. doi: 10.1002/nbm.959. [DOI] [PubMed] [Google Scholar]
- 15.Dobre MC, Uğurbil K, Marjanska M. Determination of blood longitudinal relaxation time (T1) at high magnetic field strengths. Magn Reson Imag. 2007;25(5):733–735. doi: 10.1016/j.mri.2006.10.020. [DOI] [PubMed] [Google Scholar]
- 16.Tsekos NV, Zhang F, Merkle H, Nagayama M, Ladecola C, Kim S. Quantitative measurements of cerebral blood flow in rats using the FAIR technique: Correlation with previous lodoantipyrine autoradiographic studies. Magn Reson Med. 1998;34(4):564–573. doi: 10.1002/mrm.1910390409. [DOI] [PubMed] [Google Scholar]
- 17.Donahue KM, Weisskoff RM, Parmelee DJ, Callahan RJ, Wilkinson RA, Mandeville JB, Rosen BR. Dynamic Gd-DTPA enhanced MRI measurements of tissue cell volume fraction. Magn Reson Med. 1995;34:423–432. doi: 10.1002/mrm.1910340320. [DOI] [PubMed] [Google Scholar]
- 18.Dedieu V, Finat-Duclos F, Renou JP, Joffre F, Vincensini D. In vivo tissue extracellular volume fraction measurement by dynamic spin-lattice MRI relaxometry: application to the characterization of muscle fiber types. Investigative Radiology. 1999;34(3):185–189. doi: 10.1097/00004424-199903000-00005. [DOI] [PubMed] [Google Scholar]
- 19.Gregory TR, Wallis CJ, Printz MP. Regional changes in rat brain angiotensinogen following bilateral nephrectomy. Hypertension. 1982;4:827–838. doi: 10.1161/01.hyp.4.6.827. [DOI] [PubMed] [Google Scholar]
- 20.Galons JP, Trouard T, Gmitro AF, Lien YH. Hemodialysis increases apparent diffusion coefficient of brain water in nephrectomized rats measured by isotropic diffusion-weighted magnetic resonance imaging. J Clin Invest. 1996;98(3):750–755. doi: 10.1172/JCI118847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Landis CS, Li X, Telang FW, Molina PE, Palyka I, Vetek G, Springer CS., Jr Equilibrium transcytolemmal water-exchange kinetics in skeletal muscle in vivo. Magn Reson Med. 1999;42:467–478. doi: 10.1002/(sici)1522-2594(199909)42:3<467::aid-mrm9>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 22.Li X, Rooney WD, Varallyay CG, Gahramanov S, Muldoon LL, Goodman JA, Tagge IJ, Selzer AH, Pike MM, Neuwelt EA, Springer CS. Dynamic-contrast-enhanced-MRI with extravasating contrast reagent: rat cerebral glioma blood volume determination. J Magn Reson. 2010;206:190–199. doi: 10.1016/j.jmr.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Henderson E, Rutt BK, Lee TY. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magn Reson Imag. 1998;16(9):1057–1073. doi: 10.1016/s0730-725x(98)00130-1. [DOI] [PubMed] [Google Scholar]
- 24.Roberts C, Little R, Watson Y, Zhao S, Buckley DL, Parker GJM. The effect of blood inflow and B1-field inhomogeneity on measurement of the arterial input function in axial 3D spoiled gradient echo dynamic contrast-enhanced MRI. Magn Reson Med. 2011;65(1):108–119. doi: 10.1002/mrm.22593. [DOI] [PubMed] [Google Scholar]
- 25.Garpebring A, Wirestam R, Östlund N, Karlsson M. Effects of inflow and radiofrequency spoiling on the arterial input function in dynamic contrast-enhanced MRI: A combined phantom and simulation study. Magn Reson Med. 2011;65(6):1670–1679. doi: 10.1002/mrm.22760. [DOI] [PubMed] [Google Scholar]
- 26.McIntyre DJ, Ludwig C, Pasan A, Grifffiths JR. A method for interleaved acquisition of a vascular input function for dynamic contrast-enhanced MRI in experimental rat tumours. NMR Biomed. 2004;17:132–143. doi: 10.1002/nbm.868. [DOI] [PubMed] [Google Scholar]
- 27.Kreis D, Schulz D, Stein M, Preuss M, Nestler U. Assessment of parameters influencing the blood flow velocities in cerebral arteries of the rat using ultrasonographic examination. Neurol Res. 2011;33(4):389–395. doi: 10.1179/1743132810Y.0000000010. [DOI] [PubMed] [Google Scholar]
- 28.Heisen M, Fan X, Buurman J, van Riel NAW, Karczmar GS, Romeny B. The influence of temporal resolution in determining pharmacokinetic parameters from DCE-MRI data. Magn Reson Med. 2010;63:811–816. doi: 10.1002/mrm.22171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fan X, Haney CR, Mustafi D, Yang C, Zamora M, Markiewicz EJ, Karczmar GS. Use of a reference tissue and blood vessel to measure the arterial input function in MRI. Magn Reson Med. 2010;64:1821–1826. doi: 10.1002/mrm.22551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ragan DK, Bankson JA. Suppression of vascular enhancement artifacts through the use of a multiband, selectively spoiled radiofrequency excitation pulse. J Magn Reson Imaging. 2011;33:1256–1261. doi: 10.1002/jmri.22523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Barnes SL, Gore JC, Yankeelov TE. Proc. 19th Mtg. ISMRM. Montreal, QU, CA: 2011. Modeling the effect of diffusion on the assessment of Ktrans and ve in DCE-MRI. Abstract. [Google Scholar]
- 32.Mills SJ, Soh C, Rose CJ, Cheung S, Zhao S, Parker GJM, Jackson A. Candidate biomarkers of extravascular extracellular space: a direct comparison of apparent diffusion coefficient and dynamic contrast-enhanced MR imaging-derived measurement of the volume of the extravascular extracellular space in glioblastoma multiforme. Am J Neuroradiol. 2010;31:549–553. doi: 10.3174/ajnr.A1844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Loveless ME, Lawson D, Collins M, Reimer C, Huszar D, Halliday J, Waterton JC, Gore JC, Yankeelov TE. Proc. 19th Mtg. ISMRM. Montreal, QU, CA: 2011. Correlation of quantitative tissue characteristics from DCE-MRI, DW-MRI and histology in murine tumors. Abstract. [Google Scholar]
- 34.Arlinghaus LR, Li X, Rahman AR, Welch EB, Xu L, Gore JC, Yankeelov TE. On the relationship between the apparent diffusion coefficient and extravascular extracellular volume fraction in human breast cancer. Magn Reson Imag. 2011;29:630–638. doi: 10.1016/j.mri.2011.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wedham SB, Low SA, Yang SX, Chow CK, Choyke P, Danforth D, Hewitt SM, Berman A, Steinberg SM, Liewehr DJ, Plehn J, Doshi A, Thomasson D, McCarthy N, Koeppen H, Sherman M, Zujewski J, Camphausen K, Chen H, Swain SM. Antiangiogenic and antitumor effects of bevacizumab in patients with inflammatory and locally advanced breast cancer. J Clin Oncol. 2006;24:769–777. doi: 10.1200/JCO.2005.03.4645. [DOI] [PubMed] [Google Scholar]
- 36.Yankeelov TE, Lepage M, Chakravarthy A, Broome EE, Niermann KJ, Kelley MC, Meszoely I, Mayer IA, Herman CR, McManus K, Price RR, Gore JC. Integration of quantitative DCE-MRI and ADC mapping to monitor treatment response in human breast cancer: initial results. Magn Reson Imag. 2007;25:1–13. doi: 10.1016/j.mri.2006.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]