ATP binding and cross-bridge detachment steps during full Ca²⁺ activation: comparison of myofibril and muscle fibre mechanics by sinusoidal analysis

Abstract

Single myofibrils 50–60 μm in length and 2–3 μm in diameter were isolated from rabbit psoas muscle fibres, and cross-bridge kinetics were studied by small perturbations of the length (∼0.2%) over a range of 15 frequencies (1–250 Hz). The experiments were performed at 15°C in the presence of 0.05–10 mm MgATP, 8 mm phosphate (P_i), 200 mm ionic strength with KAc (acetate), pCa 4.35–4.65, and pH 7.0. Two exponential processes, B and C, were resolved in tension transients. Their apparent rate constants (2πb and 2πc) increased as the [MgATP] was raised from 0.05 mm to 1 mm, and then reached saturation at [MgATP] ≥ 1. Given that these rate constants were similar (c/b∼1.7) at [P_i]≥ 4 mm, they were combined to achieve an accurate estimate of the kinetic constants: their sum and product were analysed as functions of [MgATP]. These analyses yielded K₁= 2.91 ± 0.31 mm⁻¹, k₂= 288 ± 36 s⁻¹, and k₋₂= 10 ± 21 s⁻¹ (±95% confidence limit, n= 13 preparations), based on the cross-bridge model: AM+ATP ↔ (step 1) AM.ATP ↔ (step 2) A+M.ATP, where K₁ is the ATP association constant (step 1), k₂ is the rate constant of the cross-bridge detachment (step 2), and k₋₂ is the rate constant of its reversal step. These kinetic constants are respectively comparable to those observed in single fibres from rabbit psoas (K₁= 2.35 ± 0.31 mm⁻¹, k₂= 243 ± 22 s⁻¹, and k₋₂= 6 ± 14 s⁻¹; n= 8 preparations) when analysed by the same methods and under the same experimental conditions. These values are respectively not significantly different from those obtained in myofibrils, indicating that the same kinetic constants can be deduced from myofibril and muscle fibre studies, in terms of ATP binding and cross-bridge detachments steps. The fact that K₁ in myofibrils is 1.2 times that in fibres (P≍ 0.05) may be explained by a small concentration gradient of ATP, ADP and/or P_i in single fibres.

Key points

• Sinusoidal length change was employed to study the single myofibril mechanics during full Ca²⁺ activation for the first time, and the tension time course results were compared with those of single muscle fibres.

• With myofibrils, the rate constants of exponential processes (tension transients) B and C were very close to each other at 8 mm phosphate, indicating that they could not be analysed independently. Thus, the sum and the product of the two rate constants were fitted to a cross-bridge model.

• The results demonstrate that the association constant of MgATP to cross-bridge is K₁= 2.91 mm⁻¹, and the rate constants of the cross-bridge detachment step are k₂= 288 s⁻¹ and k₋₂= 10 s⁻¹. These values compare to those for fibres: K₁= 2.35 mm⁻¹, k₂= 243 s⁻¹, and k₋₂= 6 s⁻¹, which are respectively not significantly different from myofibril values.

• With inspection of video records, we did not observe any local shortening, wave propagation, or sarcomere inhomogeneity along myofibrils during isometric contraction or while applying sinusoidal length oscillations, indicating the integrity of the analysis method and the data acquired.

Introduction

A new era in biology often commences when a new method is invented. When skinned fibres (Natori, 1954) and glycerinated fibres (Szent-Györgyi, 1949) were first explored, a significant barrier to understanding chemomechanical energy transduction by the contractile machinery was raised. These preparations have made it possible to measure force, which is a distinct advantage in studying the mechanisms of contraction. The ability to probe the effects of small ions and ligands directly on the cross-bridge interaction and concomitant force generation provided many new insights into the molecular mechanisms of contraction.

The single muscle fibres, however, have had some limitations. These preparations are still quite large, with a diameter in the range of 50–100 μm, which creates a concentration gradient across the cross-section of the preparation, thereby introducing imperfections in measurements (Cooke & Pate, 1985; Selivanov et al. 2007). In the mid 1980s, small fibres and split fibres (Sugi et al. 1983) were used to circumvent this problem. More recently, small bundles of myofibrils were used (Bartoo et al. 1993). Tesi et al. (1999) used single myofibrils, which are subcellular structures with a diameter in the range of 2–3 μm. In spite of the fact that single myofibrils are simpler preparations than single fibres, they still retain all essential features of contraction, and offer the advantage that there is little diffusion barrier between ‘interior’ and ‘exterior’ of the preparation. These investigators found that the K_m of the Michaelis–Menten kinetics was half of that observed in muscle fibres; they suggested that the concentration gradient of ATP was a cause of this difference. The introduction of a technique for rapidly (∼10 ms) switching the solution has since made it possible to use the single myofibril preparation to study the kinetics of Ca²⁺ activation, force redevelopment after quick length release/restretch, and relaxation (Stehle et al. 2002a; Tesi et al. 2002b). Single myofibril preparations are also advantageous in that the appearance of each sarcomere can be studied in detail by video microscopy (Telley et al. 2006; Pavlov et al. 2009).

Sinusoidal analysis has been used to study the cross-bridge mechanisms of force generation in muscle fibres (Pringle, 1967; Kawai & Brandt, 1980), and also the kinetic constants of the elementary steps of the cross-bridge cycle (Kawai & Halvorson, 1991). Here we use this method with single myofibrils for the first time, applying very small changes in length (amplitude: 0.125–0.25%) to Ca²⁺-activated myofibrils during the plateau of tension, and recording the resulting tension transients. Previously, this combination was thought not possible: the small size of the signal from myofibrils was thought to make it difficult to obtain detectable signals in response to small length changes. With improved optical coupling of an atomic force cantilever and its detection apparatus, we have been able to measure forces as small as 10–20 nN. The application of sinusoidal analysis is a useful tool because even when mechanical perturbation of the contractile apparatus is minimal, the choice of a particular frequency can enable the experimenter to make the length oscillation resonate to an elementary step of the cross-bridge cycle. Thus, the signal output from this step is maximized. Moreover, the ability to average signal from many sinusoidal cycles minimizes the effects of noise.

Here we report on a study of the effects of MgATP on cross-bridge kinetics, in single myofibrils vs. single muscle fibres. Tension transients were induced by small changes in sinusoidal length at varying frequencies, and the resulting exponential processes in tension were analysed in terms of a cross-bridge model. By studying the kinetics of the transients and the effects of [MgATP], we were able to identify and characterize intermediate states of the cross-bridge cycle, and to compare the results between myofibrils and muscle fibres. We found that the MgATP association constant was slightly larger (1.2×, P≍ 0.05) in myofibrils than in muscle fibres, confirming the presence of a slight concentration gradient of ATP in fibres. Nevertheless, the rate constants of subsequent cross-bridge detachment steps did not differ significantly between these preparations. It was also evident that the measured rate constants of two fast exponential processes were very close in myofibrils, though this was not the case in muscle fibres.

Methods

Myofibril preparations

This part of experiments was carried out at University of Köln (Cologne), Germany. All animal studies were conducted in accordance with institutional guidelines and approved by Animal Research Committee at University of Köln. Freshly dissected rabbit psoas muscle fibre bundles were tied to a wooden stick and incubated first in Na-skinning solution (for compositions, see under Solutions) for 1–2 h, and then in K-skinning solution for >1 h, both in the presence of protease inhibitors (500 μm AEBSF (4-(2-Aminoethyl) benzenesulfonyl fluoride hydrochloride), 10 μm leupeptin, 10 μm antipain, 5 mg ml⁻¹ aprotinin)) and 2 mm dithiothreitol (DTT), at 0–4°C. Muscle fibre bundles were stored in K-skinning solution mixed with 50% (v/v) glycerol at −20°C, without freezing. Single myofibrils were freshly prepared (at 0°C) on the day of the experiment. A small segment was removed from a stored fibre bundle, washed twice in ice-cold relaxing solution, chemically skinned using 0.5% (v/v) Triton X-100, washed again, and homogenized using a T8 Ultra-Turax tissue homogenizer (IKA Works, Staufen, Germany) at 25,000 rpm for 5–7 s. The myofibril suspension was filtered through a 22 μm polypropylene mesh to remove large and/or aggregated myofibrils. A small volume of myofibril suspension was transferred to a temperature-controlled experimental bath filled with relaxing solution, and allowed to sediment for ∼1 h. Selected single myofibrils or thin bundles (2–4 myofibrils) were mounted horizontally between a needle connected to the length driver, and the tip of the force transducer.

The sarcomere length (SL) of the preparation was adjusted to 2.7 μm using a video monitor (Fig. 1A). Upon force generation, the SL became ∼2.5 μm (Fig. 1B), a length that is advantageous in rabbit psoas; it is at the peak of the length–tension diagram based on filament lengths (Higuchi et al. 1995), and sarcomere shortening in myofibrils is most homogeneous at SL = 2.0–2.6 μm (Bartoo et al. 1993). The diameter and length of the myofibrils were determined from the video screen. Such preparations develop ∼0.5 μN of force with our activating solutions. The condition of the preparation was monitored at 90× magnification (Olympus, IX70); when any irregularities occurred, the preparation was discarded. At both the beginning and end of the experiment, the myofibril preparation was tested with the 10S activating solution, and reproducibility of the data was examined. Data from any preparation that exhibited ≤80% force were not used for subsequent analysis. The details of the psoas myofibril preparation were previously described (Knight & Trinick, 1982; Bartoo et al. 1993; Colomo et al. 1997; Stehle et al. 2002b; Rassier et al. 2003).

Figure 1. Images of myofibrils during the following steps: relaxation (A), isometric contraction in standard activating solution (B), isometric contraction with oscillation at 84 Hz (C), isometric contraction with oscillation at 30 Hz (D), and relaxation (E).

The amplitude of oscillation was 0.12%L₀. Because of the flow of the solution (top to bottom), the myofibrils are bent in A and E; the myofibrils are not bent in B, C and D, because of the active tension development. The scale bar in A corresponds to 10 μm. Sarcomere length (SL) was: A, 2.70 ± 0.02 μm (mean ± SEM of n= 20 sarcomeres); B, 2.57 ± 0.04 μm (n= 19); C, 2.53 ± 0.06 μm (n= 19); D, 2.48 ± 0.05 μm (n= 19); E, 2.63 ± 0.03 μm (n= 20).

Experimental apparatus to study myofibril mechanics

The experimental apparatus was built on an Olympus IX70 inverted microscope and was described previously (Stehle et al. 2002a; Stehle et al. 2002b). Briefly, a rectangular myofibril chamber (5 ml volume) was placed on the centre of the microscope stage; it consists of an aluminum block with a glass cover slip at the bottom for microscopy, and a glass window at one side through which the laser beam passes and to detect force. The temperature of the chamber was regulated to 15°C by circulating water from a temperature-controlled bath. Two micromanipulators were attached to the base of the microscope. Each was invested with coarse and fine controls in three directions. One micromanipulator on the left held a piezoactuator (P-821.20, Physik Instruments, Karlsruhe, Germany) which served as the length driver, and its moving end was connected to a stiff microtool (a tungsten needle). The micromanipulator on the right held a cantilever (Nanosensors, Wetzlar-Blankenfeld, Germany) used for atomic force microscopy. The beam of a 4 mW laser diode (660 nm) was focused onto the cantilever at 20 μm spot size, and the position of the reflected light was sensed as the difference in two currents of a double photodiode detector. When a myofibril developed force, it deflected the cantilever, deflected the pass of the reflected light, and hence the position of the light falling onto the detector. This signal was used as the force after proper calibration. The compliance of the cantilever was 0.25–0.5 N⁻¹ m, and its own resonance frequency was above 60 kHz (Stehle et al. 2002a). The myofibrils were glued to these moving parts using a 1:3 mixture of silicone glue (3140 RTV Coating, Dow-Corning, Midland, MI, USA) and 2% nitrocellulose dissolved in amylacetate (Stehle et al. 2002a). The length of a typical myofibril preparation was 50–60 μm, and the diameter was 2–3 μm.

A series of syringes containing experimental solutions were suspended ∼0.3 m above the experimental chamber, and one of the solutions was injected through chromatography tubing (250 μm ID) mounted in a perfusion pipette, which opens in front (∼0.5 mm away) of the myofibrils using the gravitational force. In this apparatus, solution flows past the myofibrils at a rate of ∼0.05 m s⁻¹ (Tesi et al. 2002a). Different solutions were injected by operating a series of solution switches, the outputs of which were merged into two chromatography tubes. These were channeled into openings of a θ capillary (TGC150-15, Clark Electromedical Instruments, Reading, UK), and solutions were switched by quickly shifting the capillary using a piezoactuator (P289.40, Physik Instruments) as described previously (Colomo et al. 1998; Poggesi et al. 2005). The detailed experimental method can be found in a previous publication (Stehle et al. 2002a).

Muscle fibre experiments

This part of the experiments was carried out at the University of Iowa. All animal studies were conducted in accordance with institutional guidelines. The University of Iowa has an Animal Welfare Assurance (A-3021-01) on file with the Office of Laboratory Animal Welfare, National Institutes of Health. Bundles of rabbit psoas fibres were prepared as described (Zhao et al. 1996), and stored at −20°C in the storage solution. On the day of an experiment, single fibres were dissected and mounted to the experimental apparatus. One end of the preparation was glued (using nail polish) to the moving end of a length driver made of two loud speakers as described previously (Kawai & Brandt, 1980). The other end was similarly glued to the tip of a Güth-type force transducer (Scientific Instruments, Heidelberg, Germany). The length of the preparation was 3–4 mm, and the diameter was 60–100 μm. SL was adjusted to 2.5 μm by optical diffraction, using a He–Ne laser at a wavelength of 632.8 nm. The solution was changed by drainage with a 1 ml pipette, and new solution was added using a 500 μl pipette. The detailed experimental method can be found in a previous publication (Kawai & Brandt, 1980).

Solutions

The Na-skinning solution contained (mm): 10 H₄EGTA, 7 Na₂H₂ATP, 2 MgAc₂·4H₂O, 118 NaAc, 48 NaOH, and 10 MOPS. The K-skinning solution contained (mm): 10 H₄EGTA, 7 Na₂H₂ATP, 2 MgAc₂·4H₂O, 118 KAc, 48 KOH, and 10 morpholinopropane sulphonic acid (MOPS). The standard (10S) activating solution contained (mm): 6 K₂CaEGTA, 12.1 Na₂H₂ATP, 11.5 MgAc₂·4H₂O, 15 Na₂CP, 4 KH₂PO₄, 4 K₂HPO₄, 1 NaAc, 45 KAc, and 10 MOPS; the pCa of this solution was 4.65, and [MgATP²⁻] was 10 mm. The 0.05S activating solution contained (mm): 6 K₂CaEGTA, 0.062 Na₂H₂ATP, 1.74 MgAc₂·4H₂O, 15 Na₂CP, 4 KH₂PO₄, 4 K₂HPO₄, 25 NaAc, 86 KAc, and 10 MOPS; the pCa of this solution was 4.35, and [MgATP²⁻] was 0.05 mm. An intermediate activating solution was an appropriate mixture of 10S and 0.05S solutions. For fibre experiments, creatine kinase (CK) was added at 320 unit ml⁻¹; CK was not used for myofibril experiments. The relaxing solution contained (mm): 6 K₂H₂EGTA, 7 Na₂H₂ATP, 2 MgAc₂·4H₂O, 4 KH₂PO₄, 4 K₂HPO₄, 41 NaAc, 71 KAc, and 10 MOPS. The rigor solution contained (mm): 4 KH₂PO₄, 4 K₂HPO₄, 55 NaAc, 122 KAc, and 10 MOPS. In the Ca²⁺ activating, rigor, and relaxing solutions, [Na⁺] was 55 mm, [Mg²⁺] was 1 mm, total phosphate (P_i) was 8 mm, ionic strength was 200 mm, and pH was adjusted to 7.00 using KOH. All experiments were performed at 15°C.

Sinusoidal analysis

During a plateau of tension, the length of the preparations was oscillated with small amplitude sine waves in the range 0.25–250 Hz for fibres, and 1–250 Hz for myofibrils. These frequency ranges correspond to 0.64–640 ms for fibres, and 0.64–160 ms for myofibrils in time domain analysis. The amplitude of the oscillations was 0.125–0.25%L₀, which corresponds to ±0.8–1.6 nm at the cross-bridge level with 50% series compliance. At this point, both tension and length time courses were recorded (Fig. 2). The complex modulus (written as Y(f)) is defined as the ratio of the stress change to the strain change expressed in the frequency (f) domain, and is represented by complex numbers. Their real component (= Re(Y(f))) is referred to as the elastic modulus, and their imaginary component (= Im(Y(f))) as the viscous modulus. In both myofibrils and muscle fibres, the complex modulus was fitted to eqn (1) which represents three ‘exponential processes’ (Kawai & Brandt, 1980):

Figure 2. Simultaneous recordings of length (A) and force (B) over time for a myofibril preparation.

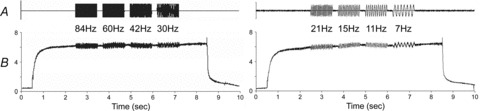
Two consecutive standard activations of the same preparation. The amplitude of the length oscillation was 0.19%L₀; frequencies are indicated. At 0.5 s, the relaxing solution was replaced with activating solution, and at 8.5 s the activating solution was replaced with the relaxing solution. Active isometric tension corresponds to 191 kPa. Length and force data were digitalized every 1 ms.

Process A B C

(1)

where . a, b, and c are the characteristic frequencies (a < b < c) of processes A, B and C, respectively, and A, B and C are their respective magnitudes (amplitudes).

The exponential processes in eqn (1) are referred to as such because their expression within the time domain takes the form of exponential functions Aexp(–2πat), etc., where t is time. Consequently, 2πa, 2πb and 2πc are their respective rate constants, and correspond to the rate constants of phases 4, 3 and 2 of the tension transients that follow a step-length change (Heinl et al. 1974; Huxley, 1974). H is a constant, and Y_∞=Y(∞) =H+A−B+C refers to the elastic modulus during activation, which is often called ‘stiffness’ in muscle mechanics literature. Y_∞ corresponds to phase 1 of step analysis. An earlier paper reporting on step analysis of intact frog semitendinosus fibres proposed that phase 2 reflects the ‘force generation step’ (Huxley & Simmons, 1971). However, our later sinusoidal analyses of skinned rabbit psoas fibres demonstrated that process C (phase 2) represents the ATP binding and cross-bridge detachment steps, because the process C was ATP sensitive (Kawai, 1978) but P_i insensitive (Kawai, 1986; see also Kawai & Halvorson, 1989, 1991). The complex modulus data from myofibrils and muscle fibres were corrected using the complex modulus of rigor preparations, to eliminate artifacts arising from different frequency response of tension transducers as reported previously in Kawai & Brandt (1980).

Analysis of the results from sinusoidal length perturbation experiments

The results of sinusoidal analysis were interpreted in the context of the following cross-bridge model:

where A is actin, and M is myosin. MgATP (ATP) binds to AM with the association constant K₁, and actin subsequently detaches from myosin at the rate constant k₂. The rate constant of its reversal step is k₋₂. Because the apparent rate constants 2πb and 2πc are close in myofibrils, their sums and products were calculated, and their [MgATP] dependence was fitted to eqns (2) and (3):

(2)

(3)

where S=[MgATP], D=[MgADP], K₀ is the association constant of MgADP, K₁ is the association constant of MgATP, and k₂ and k₋₂ are the rate constants of the cross-bridge detachment step.

Because K₀∼2.8 mm⁻¹ (Kawai & Halvorson, 1989) and D∼0.02 mm in skinned fibres in the presence of CP/CK, K₀D≍ 0.056 x226A;1, and hence K₀D can be dropped from eqns (2) and (3). The ADP dissociation step takes place to the left of Scheme 1 (see Kawai & Halvorson, 1989). Equations (2) and (3) were derived as eqns (14) and (15) in Kawai & Halvorson (1991), and assuming the cross-bridge model described in Scheme 1. w and z are determined by subsequent reaction(s) that would give rise to exponential process B, but are simply unknown terms for the purpose of this report. Note that eqns (2) and (3) are very similar in their formulation and have the common K₁, which is the reciprocal of [MgATP] at the half-saturation point. Other than K₁, eqn (2) is linear with the unknown terms K₁k₂ and (k₋₂+w), and eqn (3) is linear with wK₁k₂ and z. K₁ was chosen to minimize the sum of squared deviations of eqns (2) and (3) simultaneously, by weighting two equations equally. For the chosen K₁, the unknown terms were determined using the usual linear regression, from which k₂, w, and k₋₂ were calculated. This method was previously employed to characterize elementary steps of the cross-bridge cycle in ferret papillary muscles (Kawai et al. 1993).

Results

Single myofibrils were mounted to the experimental apparatus in the relaxing solution. The solution flow caused the myofibril to curve under these conditions (Fig. 1A). At this stage, the average sarcomere length (SL) was adjusted to 2.70 μm. Thus, in Fig. 1A, the mean ± SEM of the 20 visible sarcomeres was SL = 2.70 ± 0.02 μm (± SEM). The solution was then rapidly replaced (in 20 ms) with activating solution, whereupon the isometric tension developed (Fig. 1B). The myofibrils became taut and the SL shortened by 5% to 2.57 ± 0.04 μm (n= 19) because of tension development (Fig. 1B). When the tension reached a plateau, myofibril length was oscillated at varying frequencies, and changes in both tension and length were recorded at a rate of 0.1–1 ms (Fig. 2). Notably, visual inspection during Ca²⁺ activation failed to reveal any local shortening, wave propagation, or sarcomere inhomogeneity along the myofibrils (Fig. 1B–D; also see video image in supplementary file). SL was 2.53 ± 0.06 μm (n= 19) in Fig. 1C, and 2.48 ± 0.05 μm (n= 19) in Fig. 1D. The preparation was subsequently relaxed (Fig. 1E), and the appearance of the sarcomere did not change (compare to Fig. 1A). SL at this point was 2.63 ± 0.03 μm (n= 20). The same activation protocol was repeated, and myofibrils were subjected to sinusoidal length oscillations at a different set of frequencies (Fig. 2). The amount of shortening during activation varied depending on the preparation, ranging from 5 to 18% and averaging 12 ± 2% (n= 8). An advantage of using myofibrils vs. muscle fibres is that individual sarcomeres can be visualized, such that their length can be analysed statistically.

Figure 3 plots isometric tension and elastic modulus as functions of [MgATP]. Depending on [MgATP], pCa was between 4.35 and 4.65. Figure 3A shows data from single myofibrils, and Fig. 3B shows data from single muscle fibres. In fibres, tension was greatest at lowest [MgATP] (0.05 mm), whereas in myofibrils the error bars were generally larger and no clear peaks were visible. Both myofibrils and fibres developed comparable amounts of tension. However, the elastic modulus during activation was 1.5× greater in fibres than in myofibrils. Their values at 1 mm MgATP are summarized in Table 1.

Figure 3. Tension (left ordinate, open squares) and elastic modulus (Y_∞, stiffness) (right ordinate, open circles) during activation of single myofibrils (A), and single muscle fibres (B).

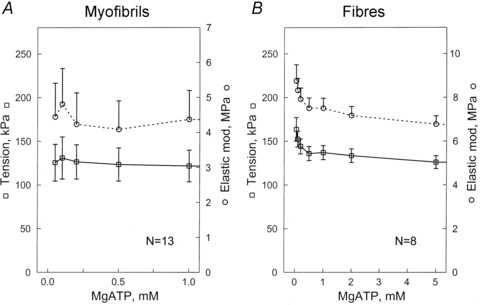
Both are plotted as a function of the [MgATP]. Experiments were carried out at pCa 4.35–4.65 in the presence of 8 mm P_i, and at 200 mm ionic strength and pH 7.00. Error bars represent the SEM for 13 experiments in A, and for 8 experiments in B.

Table 1.

Comparison of cross-bridge kinetics

	Myofibrils	Muscle fibres	Units
Tension	122 ± 18	137 ± 8	kPa
2πa	1.5 ± 0.3	3.3 ± 0.2	s−1
2πb	98 ± 7	53 ± 4	s−1
2πc	166 ± 15	201 ± 12	s−1
A	3.6 ± 0.7	4.7 ± 0.5	MPa
B	9.3 ± 2.0	7.1 ± 0.8	MPa
C	10.1 ± 2.1	8.0 ± 0.8	MPa
Y∞	4.4 ± 0.8	7.5 ± 0.5	MPa
Rigor stiffness	5.1 ± 0.9	7.6 ± 0.5	MPa
Number of experiments	12	7

Data are means ± SEM. These parameters were measured in 1S activating solution (pCa 4.40, 1 mm MgATP, 1 mm Mg²⁺, 8 mm P_i, 200 mm ionic strength).

Figure 4 represents Nyquist plots of myofibrils (Fig. 4A) and fibres (Fig. 4B), at 1 mm MgATP. In these plots, the viscous modulus is plotted against the elastic modulus, with the frequency as the intervening parameter. The advantage of this plot is that each exponential process is represented by a semicircle with its centre on the abscissa. In both preparations, three exponential processes are evident as three contiguous semicircles, on which eqn (1) is based. These are called exponential processes A, B, and C in the order of increasing speed (Kawai & Brandt, 1980). The continuous curves are calculated based on best-fit to eqn (1). In both preparations, the viscous modulus is negative in the middle frequency range (3–11 Hz), because of the presence of process B, which takes the negative term in eqn (1).

Figure 4. Comparison of Nyquist plots for single myofibrils (A), and single muscle fibres (B), during maximal activation with 1S solution (1 mm MgATP, 8 mm P_i).

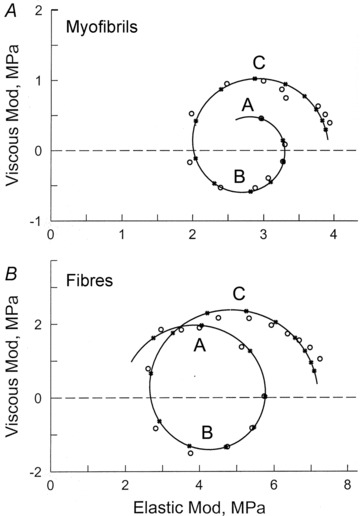
Data points (x25CB;) represent the average for 13 experiments in A, and for 8 experiments in B. The continuous curves were established based on best-fit to eqn (1). Frequency is the intervening parameter, and is represented by a data point (x25CB;) and its calculated value (•). Frequencies used in A are 1, 2, 3.2, 5, 7, 11, 15, 21, 30, 42, 60, 84, 120, 170 and 250 Hz (clockwise direction). Frequencies in B are 0.25, 0.5, 1, 2, 3.2, 5, 7.5, 11, 17, 25, 35, 50, 70, 100, 135, 187 and 250 Hz. Some of the frequencies are different to avoid an interference from the power line (50 Hz in Germany, 60 Hz in USA). Processes A, B and C are marked. These are represented by individual semicircles. In the case of the myofibril experiments at low frequencies, floating objects interfered with the optical path of the laser beam and thereby introduced noise; thus, experiments at 0.25–0.5 Hz were not included for myofibrils.

Figure 5 plots the complex modulus data as the function of frequency for six different [MgATP], ranging from 0.05–10 mm. Figure 5A and B plots the elastic modulus, and Fig. 5C and D plots the viscous modulus. The data are compared between myofibrils (Fig. 5A and C) and muscle fibres (Fig. 5B and D), and curves represent the best fit to eqn (1). This figure demonstrates that the trends are similar for the two types of preparations, and that the complex modulus Y(f) is typical of that for fast-twitch skeletal muscle fibres (Galler et al. 2005). We found that in myofibrils, 2πa= 1.5 s⁻¹, 2πb= 98 s⁻¹ and 2πc= 166 s⁻¹ when MgATP is 1 mm (Table 1). In muscle fibres 2πa= 3.3 s⁻¹, 2πb= 53 s⁻¹ and 2πc= 201 s⁻¹ (Table 1). Process B has the negative sign in eqn (1), because at around frequency b, the viscous modulus has a negative value (Fig. 5C and D), and the elastic modulus has a local minimum at 7–20 Hz (Fig. 5A and B). At approximately frequency b, oscillatory work (Pringle, 1967) is generated on the forcing apparatus (length driver).

Figure 5. Plot of complex modulus Y(f) as function of frequency.

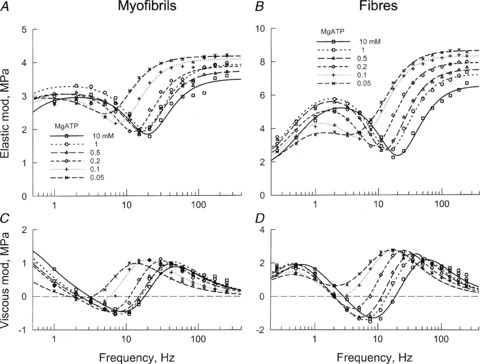
A and B plot the elastic modulus (real part of Y(f)), and C and D the viscous modulus (imaginary part of Y(f)). A and C are for single myofibrils (average of 13 records), and B and D for single muscle fibres (average of 8 records). The data are shown at 6 different MgATP concentrations, as indicated. Continuous curves are best-fit results to eqn (1).

When the [MgATP] was increased from 0.05 to 10 mm, both 2πb and 2πc increased from 0.05 to 0.5 mm; each was saturated at 1–10 mm. The [MgATP] dependence of these rate constants are plotted in Fig. 6A (for myofibrils) and Fig. 6B (for muscle fibres). These observations are consistent with the three-state cross-bridge model depicted in Scheme 1, as proposed based on data from skinned fibres (Kawai & Halvorson, 1989), myofibril suspensions (Herrmann et al. 1992; Stehle et al. 2000; Candau & Kawai, 2011), and isolated proteins (Bagshaw et al. 1974). This scheme is common to account for the data shown in Fig. 6A and B.

Figure 6. The apparent rate constants 2πb and 2πc (in A and B) and their magnitudes (in C and D), plotted as functions of [MgATP].

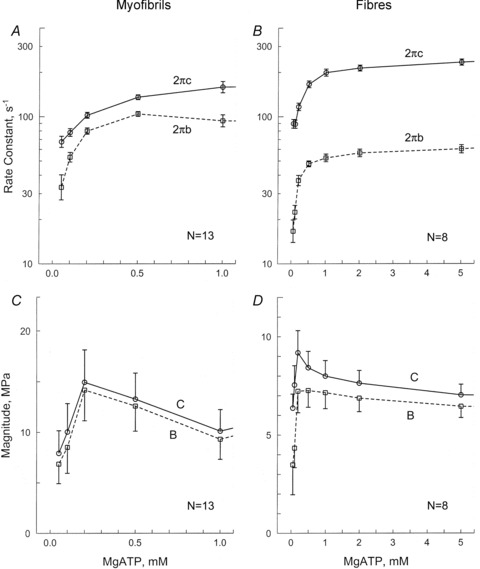
A and C are for single myofibrils (average of 13 records), and B and D for single muscle fibres (average of 8 records). Error bars represent SEM.

The data represented in Fig. 6A are striking in that 2πb and 2πc for myofibrils are very close (2 πc/2 πb ≍ 1.7 under some conditions) (Fig. 6A). This was not the case for muscle fibres, where 2πc/2πb≍ 4–5 (Fig. 6B). In both preparations, the magnitudes of B and C increased at 0.05 mm≤[MgATP]≤ 0.2 mm, and then decreased again for [MgATP]≥ 0.2 mm (Fig. 6C and D). Both also had a peak at 0.2 mm[MgATP] (Fig. 6C and D). Notably, in myofibrils, processes B and C compensate for each other near this peak and assume large values because (i) they are of opposite sign in eqn (1), and (ii) their individual values B and C far exceed Y_∞ shown in Fig. 3A. This is apparently not the case in single fibres, however, where B and C (Fig. 6D) are comparable to Y_∞ (Fig. 3B). This is also seen in Table 1. As a consequence in myofibrils, the magnitudes of B and C appear to be almost in parallel (Fig. 6C). These observations indicate that processes B and C cannot be separated in myofibrils; hence they should be combined and considered together, as shown in eqns (2) and (3).

The sums and the products of 2πb and 2πc in myofibrils are plotted in Fig. 7A and C, respectively, and those for muscle fibres are shown in Fig. 7B and D, respectively. The fitted results are shown as continuous curves. As these plots demonstrate, the data fit to eqns (2) and (3) reasonably well, indicating that eqns (2) and (3) are good representations and justify Scheme 1 for the cross-bridge model. From these fittings, we obtained the following values: in myofibrils, K₁= 2.91 ± 0.31 mm⁻¹, k₂= 288 ± 36 s⁻¹, and k₋₂= 10 ± 21 s⁻¹ (±95% confidence limit, n= 13 preparations); in muscle fibres, K₁= 2.35 ± 0.31 mm⁻¹, k₂= 243 ± 22 s⁻¹, and k₋₂= 6 ± 14 s⁻¹ (n= 8 preparations). Thus, it can be concluded that K₁ is slightly larger (P≍ 0.05) in myofibrils than in muscle fibres, but that k₂ and k₋₂ respectively do not differ significantly between myofibrils and muscle fibres (summarized in Table 2, along with kinetic constants of elementary steps of fibres deduced by assuming that 2πb and 2πc are well separated). With this approximation, the two methods of evaluating the kinetic constants yield similar results for K₁ (slight differences), and no difference for k₂. However, the new method yields a small rate constant for the reversal step (k₋₂; indistinguishable from 0), whereas the old method yields a finite k₋₂. For the purposes of comparison, K₁k₂ is also listed in Table 1.

Figure 7.

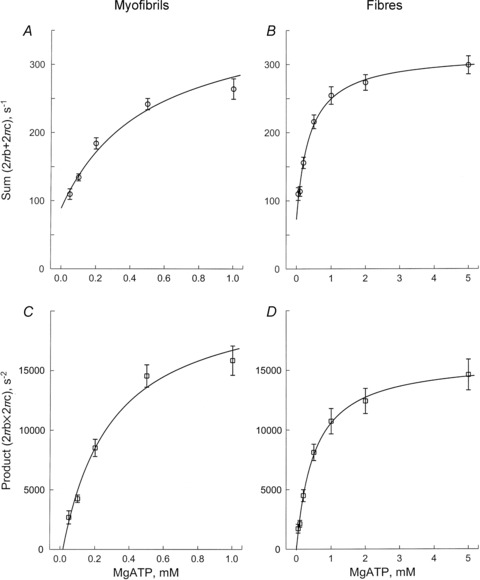
The sum (A and B) and the product (C and D) of the apparent rate constants 2πb and 2πc, plotted as functions of [MgATP] for single myofibrils (A and C, average of 13 records), and for single muscle fibres (B and D, average of 8 records)

Table 2.

Comparison of elementary steps

	Myofibrils (*)	Fibres (*)	Fibres (**)	Units
K1	2.91 ± 0.31	2.35 ± 0.31	1.69 ± 0.19	mm−1
k2	288 ± 36	243 ± 22	200 ± 18	s−1
k−2	10 ± 21	6 ± 14	70 ± 11	s−1
K1k2	838 ± 138	571 ± 91	338 ± 49	mm−1s−1
Ndf	150	120	60

These parameters were measured in the presence of 8 mm P_i. ±95% confidence limits are shown. For K₁k₂, errors were propagated. N_df= degree of freedom. *Sum and product (eqns (2) and (3)) were used to deduce the kinetic constants; **eqn (16) of Kawai & Halvorson (1991) was used to deduce the kinetic constants.

While isometric tension was comparable between myofibrils and muscle fibres, stiffness during activation (Y_∞) and stiffness after rigor induction was 1.5–1.7× larger in muscle fibres than in myofibrils (Table 1). It is possible that the attachment of the myofibrils to the measuring apparatus is not as solid as in the case of muscle fibres.

Discussion

The main purpose of our investigation was to perform sinusoidal analysis on single myofibrils and muscle fibres under the identical experimental conditions, and to compare the mechanical data obtained for differences in cross-bridge kinetics. An additional reason for carrying out this comparison was to establish whether the large diameter of muscle fibres (60–100 μm) leads to the formation of a concentration gradient of ligands across their cross-sections, as previously suggested (Cooke & Pate, 1985; Tesi et al. 1999; Selivanov et al. 2007), and whether results (in particular with respect to the ATP dissociation constant, K₁) are more reliable when myofibrils rather than muscle fibres are analysed. Our results demonstrate that K₁ is slightly larger (1.2 ± 0.2 times with error propagation, P≍ 0.05) in myofibrils than in fibres, consistent with the existence of a slight concentration gradient across fibres. At the same time, we found that the rate constants of the cross-bridge detachment step (k₂ and k₋₂) do not differ significantly between myofibrils and muscle fibres (Table 2). One advantage of analysing myofibrils is that because individual sarcomeres (and half-sarcomeres) can be visualized as in Fig. 1, their behaviours can be detected (Telley et al. 2006).

By measuring the unloaded shortening velocity of myofibrils using the slack test at varying [MgATP], and deriving the K_m from the Michaelis–Menten kinetics of the velocity, Tesi et al. (1999) showed that the K_m of myofibrils was about half of that of muscle fibres (at 5°C), as measured elsewhere (Cooke & Bialek, 1979; Cooke & Pate, 1985; Regnier et al. 1998). These authors suggested that this difference was caused by the concentration gradients of ATP and ADP, which form during ATP hydrolysis in the fibres. When k₋₂≍ 0, Scheme 1 is a typical Michaelis–Menten kinetics (Kawai, 1979), and K_m and K₁ are related by eqn (4):

(4)

Consequently, K_m and K₁ are approximately reciprocally related, and our results can be related to those of Tesi et al. (1999). k₁ is the rate constant of a diffusion-limited collision-complex formation and very first (>10,000 m⁻¹s⁻¹), hence the step 1 is approximated by an equilibrium in Scheme 1. K₁ is expected to be load sensitive, and 1/K₁ decreases when the tension is reduced, as shown by plotting tension against K₁ (Fig. 12 of Zhao et al. (1996)) and by analysis of cross-linked myofibrilar suspensions using a stopped-flow method (Table 2 of Candau & Kawai (2011)). This would explain the discrepancy between the low K_m (120 μm) found by Tesi et al. for active unloaded shortening, and the high 1/K₁ (about 340 μm from Table 2) found in this report under the isometric contraction. The difference between fibres and myofibrils was less (1.2×) in our case than in the study of Tesi et al. (1999) (2×).

The slack test also depends on multiple cross-bridges cycles (section 19 of Kawai & Halvorson (2007)); hence more ATP is hydrolysed during unloaded shortening than under isometric conditions (He et al. 1998). We measured elementary steps 1 and 2 independently of the rest of the cross-bridge cycle at near-isometric conditions. Hence the ATP usage must have been less than that of shortening fibres/myofibrils, to account for the quantitative difference in results. The difference in temperature (15°C in our study versus 5°C in other studies) is not an issue here, because if we were to carry out experiments at a lower temperature, the difference between myofibrils and muscle fibres would be between 1.0 (no difference) and 1.2 (current observation at 15°C), because the ATP hydrolysis rate is less at the lower temperature (Zhao & Kawai, 1994).

As is evident here, the concentration of ATP need not be changed quickly such as tried by Goldman et al. (1984) in order to induce the transient that enables the deduction of the kinetic constants surrounding the ATP binding step (Scheme 1). Instead, with our approach, the ATP concentration was kept constant while the tension transient was induced by sinusoidal length changes, and the ATP concentration was changed while transient tension measurements were not carried out. Because the preparation was already under tension when the sinusoidal analysis was carried out, series compliance elements (Huxley et al. 1994; Wakabayashi et al. 1994; Higuchi et al. 1995) were stretched to their full extent, and no further change in their over all length was expected. In our experiments, the length change was kept very small. The typical amplitude was 0.2%, which corresponds to 2.5 nm/half-sarcomere (=1.25 μm × 0.2%) when the sarcomere length was 2.5 μm (skeletal myofibrils). Because of the presence of series compliance, perhaps only one-half (∼1.3 nm) of this change was applied to each cross-bridge under our standard activating conditions. It is essential that this value is kept much smaller than the myosin step size (∼5.3 nm), so that transients associated with the elementary steps of the cross-bridge cycle can be resolved.

While we found no significant differences in the kinetic constants of step 2 between myofibrils and fibres, the apparent rate constants 2πb and 2πc were much more close to one another in myofibrils (Fig. 6A) than in muscle fibres (Fig. 6B). This implies that the rate constant of an additional step immediately to the right of those depicted in Scheme 1 is similar to k₂. This step could be: the ATP cleavage step; the step at which actin is attached to myosin; or the force generation step. The closeness in the rate constants 2πb and 2πc apparently does not hold true for muscle fibres (Fig. 6B). Because of their closeness in myofibrils (Fig. 6A), the approximations we used for 2πb and 2πc (eqns (16) and (17) of Kawai & Halvorson (1991)) could not be used. However, equations in the absence of such approximation (eqns (14) and (15) of Kawai & Halvorson (1991)) are still valid, and they are reproduced here as eqns (2) and (3). The important commonality of these equations is K₁, which is the reciprocal of [MgATP] at the half-saturation point in both sum and product. Thus, the data were simultaneously fitted to two equations to find the kinetic constants of steps 1 and 2. To avoid any discrepancies related to methodology, we used the same method to characterize the kinetic constants of muscle fibres. The question of why myofibrils and muscle fibres differ in terms of the closeness in rate constants 2πb and 2πc remains unclear and requires further study. The ADP dissociation step precedes step 1 (i.e. occurs to the left of Scheme 1), and influences both rate constants 2πb and 2πc, as shown in eqns (2) and (3).

Isometric tension was comparable between myofibrils and muscle fibres (122–137 kPa, Table 1). However, this value is at the lower end of those reported in various studies (Dantzig et al. 1992; Coupland et al. 2001; Ranatunga et al. 2010). This can be explained by the fact that we used 8 mm P_i and 200 mm ionic strength, whereas other studies scarcely added P_i to the activating solutions (which made the actual [P_i] 0.6–0.8 mm (Kawai & Halvorson, 1991; Dantzig et al. 1992) owing to contaminating P_i in ATP and CP, and liberated P_i as a result of ATP hydrolysis), and ionic strength was lower (150–180 mm). It has been shown that an increase in [P_i] from 0 to 8 mm leads to an 1.5–2× decrease in psoas fibre tension at 5–30°C (Cooke & Pate, 1985; Kawai, 1986; Coupland et al. 2001) and to a decrease of ∼3× in psoas myofibril tension at 5°C (Tesi et al. 2000); the decrease was larger at a lower temperature (Coupland et al. 2001). An increase in ionic strength from 150 to 200 mm results in a ∼1.2× decrease in tension (Kawai et al. 1990). In addition, an increase in temperature from 15°C to 30°C leads to a tension increase of 1.5–2× in psoas fibres (Zhao & Kawai, 1994; Ranatunga, 1996; Coupland et al. 2001; Bershitsky & Tsaturyan, 2002). The physiological [P_i] in active human calf muscles (mixture of fast and slow twitch fibres) was reported to be 4–6 mm (Roth et al. 1989), ∼13 mm in human gastrocnemius muscles (Russ et al. 2002), 4–9 mm in active cardiomyocytes (Opie et al. 1971), and ionic strength 215 mm (Godt & Maughan, 1988). In contrast, [P_i] of resting mammalian type IIA and IIB muscle fibres was reported to be 0.8 mm, and that of type I and IIX (IID) fibres to be 6 mm at 20°C (Kushmerick et al. 1992); and 3–4 mm in human gastrocnemius muscles (Russ et al. 2002). The solution conditions we used have the advantage that they avoid inducing high active tension that could lead to deterioration of preparations.

In summary, our study demonstrates that sinusoidal analysis can be applied to myofibril preparations to produce signals sufficient for characterizing the elementary steps of the cross-bridge cycle. We have also shown that the elementary steps surrounding ATP binding to cross-bridges and the subsequent rapid dissociation of cross-bridges do not differ much when the measurements are carried out in myofibrils or muscle fibres under the current experimental conditions.

Glossary

SL

sarcomere length

Author contributions

This project was designed by MK and RS; experimental apparatus on single myofibrils was constructed by RS, BI, and GP; experimental apparatus on single muscle fibres was constructed by MK; computer programs were written by MK and RS; experiments on myofibrils were carried out by BI and RS; experiments on fibres were carried out by LW; data analyses were carried out by BI, LW, and MK; results were discussed by all authors; the manuscript was written by MK and corrected by all authors.

Supplementary material

video image in supplementary file