Abstract
Introduction
Progression of intervertebral disc (IVD) herniation does not occur exclusively in a linear manner through the anulus fibrosus (AF), but can migrate circumferentially due to localized AF delamination. Consequently, resistance to delamination is an important factor in determining risk of herniation progression. The inter-lamellar matrix located between the AF layers is responsible for resisting this delamination; however, its mechanical properties are largely unknown. This study aimed to determine the mechanical properties of the inter-lamellar matrix in human AF samples via a peel test.
Materials and methods
Seventeen human IVDs (degeneration grades of 2–3) were obtained from six lumbar spines. From these 17 discs, 53 tissue samples were obtained from the superficial and deep regions of the anterior and posterior AF. Samples were dissected into a ‘T’ configuration to facilitate a T-peel test (or 180-degree peel test) by initiating delamination between the two middle AF layers.
Results
Peel strength was found to be 33 % higher in tissues obtained from the superficial AF region as compared with the deep region (p = 0.047).
Conclusion
This finding may indicate a higher resistance to delamination in the superficial AF, and as a result, delamination and herniation progression may occur more readily in the deeper layers of the AF.
Keywords: Spine, Anulus fibrosus, Lamellae, Biomechanics, Disc herniation
Introduction
The intervertebral disc (IVD) is a uniquely designed structure capable of supporting load while allowing flexibility of the spine. Of particular interest in the IVD is the multi-layered, collagenous ringed-structure, the anulus fibrosus (AF), which surrounds the proteoglycan-rich, more gelatinous nucleus pulposus (NP). The AF is responsible for constraining the NP within the boundaries of the IVD. The inner layers of the AF contain a large proportion of round chondrocyte-like cells that synthesize primarily type II collagen, and the outer layers of the AF contain elongated fibroblast-like cells that synthesize primarily type I collagen fibers [1–4]. In addition to differing collagen fiber types, previous studies have also documented variations in stiffness [5, 6] and strength [7] as a consequence of these location differences (inner versus outer layers) as well as a result of varying strain rate [8]. However, repetitive stress and strain on the IVD can result in failure of the AF, often resulting in delamination of the layers. Further, in the healthy AF, the layers are well adhered to one another to create a ply-like structure. This adhesion is provided by the inter-lamellar matrix. This matrix provides strength and resistance to delamination and is comprised of various proteins including type VI collagen [9, 10], proteoglycans [11], and elastin [12]. This is of great importance as it has been suggested that delamination of the AF is a possible precursor to IVD herniation [13]; a common and often debilitating injury to the IVD. Further, delamination can occur as a result of mechanical stimulus such as spinal twisting [14] or as a result of degeneration and hydration loss which naturally occur with age [15, 16]. Given that delamination is a common mode of AF failure, which can lead to the progression of IVD herniation, it is important to have a good understanding of the mechanical properties of the adhesive matrix between the AF layers.
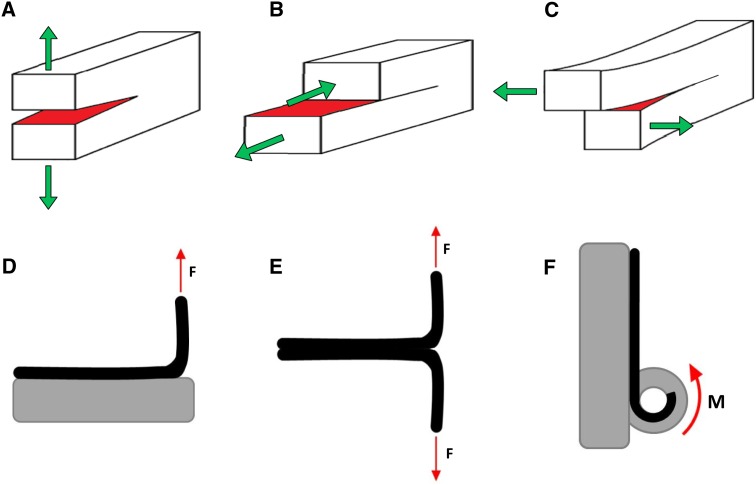
Material fracture is characterized by local separation or crack progression in a material as a result of excessive stress [17, 18]. The fracture properties of a material can be determined via three different modes of crack propagation (Fig. 1a–c). Mode I crack propagation, also referred to as the opening mode, occurs when tensile stress is applied normal to the plane of the crack progression. Mode II, also referred to as the sliding shear mode, occurs when tensile stress is applied in opposing directions parallel to the plane of the crack, but perpendicular to the crack front. Mode III, also referred to as tear or twist shear mode, occurs when tensile stress is applied in opposing directions both parallel to the plane of the crack as well as the crack front. These three modes, even in isotropic elastic material, can yield different fracture properties as they reflect distinct ways in which the microstructure of a material resists failure [18]. Therefore, it is important to identify the fracture properties during a mode of failure that is akin to how the material is loaded in real life scenarios.
Fig. 1.
Modes of crack or fracture propagation. a Mode I occurs when tensile stress is applied normal to the plane of the crack progression. b Mode II occurs when tensile stress is applied in opposing directions parallel to the plane of the crack, but perpendicular to the crack front. c Model III occurs when tensile stress is applied in opposing directions both parallel to the plane of the crack as well as the crack front. d–f Peel test configurations. d 90-degree peel test; e 180-degree peel test, also referred to as the T-peel test; f climbing drum peel test
Given that the anulus is a soft laminate tissue, an appropriate test for determining the mechanical properties of the inter-lamellar matrix is the peel test. The peel test can be performed in many configurations (Fig. 1d–f). Each configuration has its advantages depending on the materials tested. The 90-degree, 180-degree and climbing drum are all useful when one of the materials is solid (for example bone). However, if both materials that are adhered together are soft, such as the case when two anular layers are adhered together by the inter-lamellar matrix, the T-peel test (also called the 180-degree test) is most appropriate [19].
Peel tests have been extensively used in material engineering, as well as in various biological applications such as wound dressings [recently 20–22], dental prostheses adhesion [recently 23–25], and biological tissue adhesion (fetal membrane adhesion [26]; cartilage [27, 28]; and tissue repair adhesion [29, 30]). Generally, peel adhesion strength is expressed in the units N/mm, which is the force (N) required to peel the two materials apart normalized by the width (mm) of the adhesive surface. By expressing the peel strength in this manner, the amount of material adhered together is accounted for, as a material with relatively larger width would require relatively more force to separate. In the previously mentioned studies, peel strength, when documented, ranged in the order of <1 N/mm up to almost 10 N/mm. Adhesive strength can also be expressed in the units J/m2, which are the same units as fracture energy, the energy required to propagate fracture (or peeling apart in the case of a peel test) for a given area of adhesion. However, fracture energy is a relatively difficult property to determine accurately due to energy dissipation other than due to fracture; therefore, peel strength can be used as a practical measure.
This paper examines the use of a T-peel test for determining the mechanical behavior of the inter-lamellar matrix of the AF. The purpose of the paper is twofold: (1) To examine regional differences in the properties of the AF inter-lamellar matrix (anterior, posterior, superficial, deep) obtained from human lumbar IVDs; (2) to determine if displacement rate alters the mechanical properties of the inter-lamellar matrix.
Methods
Six human lumbar spines (mean age 58.2 ± 4.0 years) were obtained a maximum of 2 days post-mortem from an organ bank. Lumbar spines were frozen at −20 °C until used for mechanical testing. Each lumbar spine was allowed to come to room temperature and then subsequently MR imaged (3 T on GE Signa HDx, fast spin echo, no fat suppression, TR = 2,000 ms, TE = 70 ms, FOV = 18–20 cm, matrix = 320 × 256). Magnetic resonance images were used to grade the level of degeneration of each IVD [31]. Three independent individuals (two orthopedic researchers and one radiologic researcher) graded the IVDs. Only IVDs that were graded as two or three (with agreement across the three graders) of a maximum grade of five were used in the current study.
Tissue dissection
Thawed lumbar spines were cut transversely through the vertebral body into individual spinal units (intact IVD). Spinal units were obtained from the following vertebral levels: T12/L1, L1/2, L2/3, L3/4, L4/5, and L5/S1. For each vertebral level, 2–3 IVDs were obtained from different donors yielding a total of 17 IVDs. IVDs were carefully dissected from the endplates to ensure no cartilage remained on the dissected disc.
Each disc was further dissected into four tissue samples from the anterior and posterior regions of the disc, yielding a maximum of four tissue samples from each disc. In certain cases, obtaining a viable tissue sample from all four regions was not possible. Specifically, a maximum of 68 tissue samples was possible from the 17 IVDs (17 IVDs multiplied by four tissue samples); however, only 53 viable tissue samples were obtained: 28 from the anterior region (of which 15 were obtained from the superficial layers and 13 from the deep layers) and 25 from the posterior region (of which 15 were obtained from the superficial layers and ten from the deep layers) (Fig. 2a). Each tissue sample contained approximately eight adjacent AF lamellae and had the approximate dimensions of 5 mm in width and 30 mm in length.
Fig. 2.
a Multi-layered anulus fibrosus (AF) samples were dissected from intervertebral discs from superficial and deep regions of both the anterior and posterior AF. b Tissue samples were dissected into a “T” formation in order to facilitate the T-peel test (or 180-degree) configuration. Each anular tab consisted or approximately four AF layers. c Tissue bond width was measured for each tissue sample
Delamination was initiated in each tissue sample by peeling apart the two adjacent lamellae in the approximate middle of the tissue sample (Fig. 2b, c). This delamination created a “T” shaped tissue sample. This configuration facilitated a T- or (180-degree) peel test similar to those used to determine the mechanical properties of adhesive materials. Dissected “T” samples were soaked in 10 % PBS for a maximum of 1 h prior to mechanical testing. Preliminary testing of tissue samples was conducted prior to and following PBS soaking with negligible differences in test data (tests conducted on the same tissue sample).
Mechanical testing
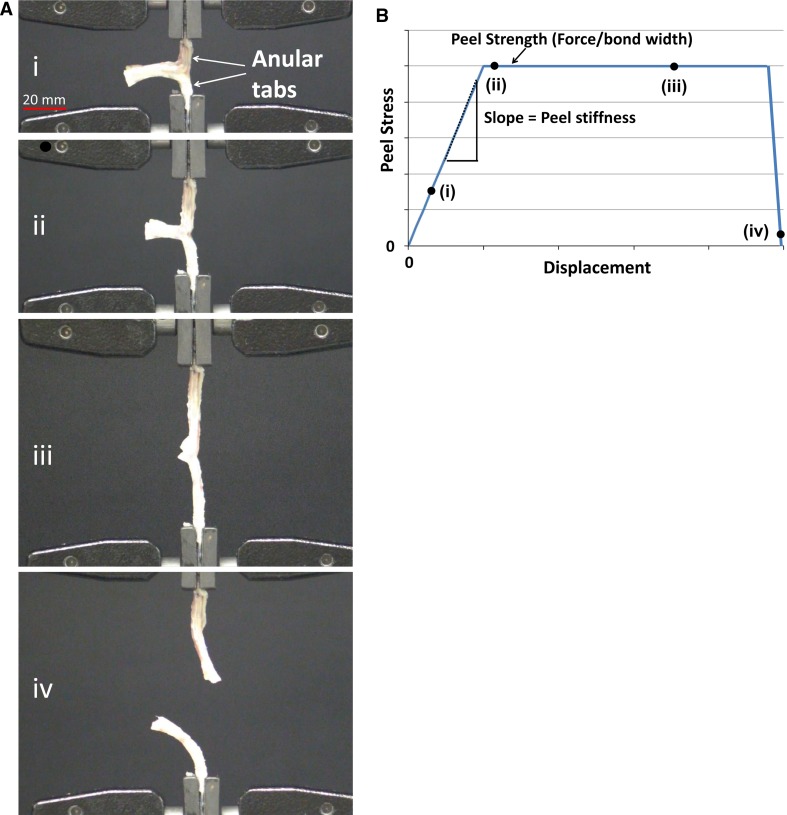
Tissue samples were clamped (pneumatic side action grips, 2712-041, Instron, Norwood, MA, USA) in a material testing apparatus (5565A, Instron) to facilitate a T-peel test. Tension was applied until tissues were taut, but care was taken to ensure delamination had not progressed at this point. Delamination subsequently progressed by displacing the clamps (Fig. 3a) at a rate of 0.5 and 5.0 mm/sec. These particular values were chosen to represent physiologically slow and fast, or traumatic, delamination of the anulus. Each tissue sample was tested at both displacement rates in which the order presented was randomized.
Fig. 3.
a Tissues were clamped at the tabs and tested in the T-peel test configuration at both 0.5 and 5.0 mm/sec displacement rates. The four images (i, ii, iii, iv) show progression of the peel test until complete separation of the tissue (iv); b example of the generic shape of a peel test stress–displacement curve. Peel stress is determined by normalising the force measured by the width of the tissue sample. Note the plateau in stress (referred to as peel strength); at this stage the tissue is peeling (corresponding to frames a (ii) and a (iii)). When the tissue has completed separating (frame a (iv)), the stress would drop to zero. Examples of where each image (i–iv) could fall on the curve are indicated by black dots. The variables of interest from this curve were peel stiffness (slope of linear increasing curve) and peel strength (average over plateau region)
Generally, during a peel test of an adhesive material, the force–displacement curve displays increasing force with increasing displacement, followed by a “levelling off” or plateau in force as displacement continues to increase (Fig. 3b). A region of increasing force reflects increasing load and stress within the sample, whereas the plateau region reflects steady peeling or separation of the two materials. The parameters describing these phenomena were (1) slope of linear region of the curve (stiffness, units (N/mm)/mm or N/mm2); (2) peel strength (peel stress, force averaged over the plateau region, normalized to tissue sample width, units N/mm) (Figs. 2c and 3b). Stiffness is expressed in units of N/mm2 because it is calculated as the slope of the stress (N/mm)–displacement (mm) curve.
Statistics
Peel stiffness and peel strength were compared statistically using a 3-way repeated measures ANOVA with the following factors: location (anterior versus posterior); depth (superficial versus deep); and rate (0.5 versus 5.0 mm/s). Statistical significance was set at p < 0.05. Tukey’s post-hoc tests were used to examine any significant findings.
Results
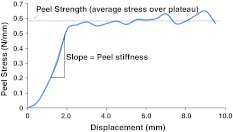
The stress–displacement curve for the peel tests showed the expected increase in peel stress with increasing displacement followed by a plateau in the peel stress (referred to as peel strength; Fig. 4). This plateau confirmed delamination, or peeling, between the lamellae.
Fig. 4.
Example of T-peel test stress–displacement curve. Peel force has been normalized to unit bonded width (referred to as peel stress). Variables of interest included the average peel strength (the plateau region) and the peel stiffness (slope of the increasing linear region of the curve)
Effect of depth and location
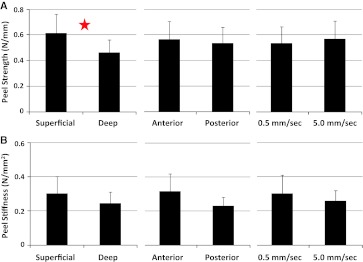
Tissues obtained from the superficial region of the AF exhibited a higher peel strength as compared with samples obtained from the deep region (p = 0.047). Specifically, peel strength was approximately 33 % greater in the superficial region (Fig. 5a). No significant difference in peel stiffness was observed between the superficial and deep tissue samples (p = 0.272) (Fig. 5b).
Fig. 5.
a Average peel strength as a function of depth (superficial versus deep), as a function of location (anterior versus posterior), and as a function of displacement rate. Star denotes significance (p = 0.047 for deep versus superficial). b Average peel stiffness as a function of depth (superficial versus deep), as a function of location (anterior versus posterior), and as a function of displacement rate. Error bars represent standard error
In terms of tissue location (anterior versus posterior), no significant differences were observed in the peel strength values (p = 0.909; Fig. 5a), or the stiffness values (p = 0.102) (Fig. 5b).
Effect of displacement rate
Two displacement rates were examined, 0.5 and 5.0 mm/s. No significant differences were observed between these rates for both peel strength (p = 0.903) and peel stiffness (p = 0.543) (Fig. 5a, b).
Interactions
No significant 2- or 3-way interactions were observed for peel strength (p values ranged from 0.055 to 0.660) or peel stiffness (p values ranged from 0.409 to 0.737). The p value of 0.055 for peel strength was observed for the interaction between location and depth such that the significant difference between the peel strength values in the superficial region versus deep region was more pronounced in the anterior AF as compared with the posterior AF.
Discussion
The AF of the IVD is a unique structure with multiple collagenous layers adhered together to allow for both strength and flexibility, while simultaneously assisting in maintaining the NP within the boundaries of the AF. This study examined the mechanical properties of the adhesive matrix between the layers of the AF, termed the inter-lamellar matrix, obtained from human lumbar IVDs using a T-peel test. The most notable finding was significantly greater peel strength in the superficial AF as compared with the deep AF. Specifically, the inter-lamellar matrix in the superficial region was found to be 33 % stronger than the matrix in the deep region.
Previous studies have examined IVD regional variations in the mechanical properties of the AF. Superficial layers of the AF tend to be stiffer [5, 6] and have higher tensile failure strength [7] when compared with deep layers. Further, the shear modulus of the anulus is higher in the superficial region as compared with the deep region [32]. Therefore, based on these previous studies it is not surprising that the current study also observed mechanical differences in the inter-lamellar matrix as a function of depth. The inter-lamellar matrix is a particularly important structure in the AF because, similar to other composite materials, the AF is stronger as a result of the adhesion of adjacent lamellae, when compared with the strength of individual lamellae in isolation [10, 11, 33]. One potential source of this increased peel strength in the outer layers is interaction between the lamellae. Specifically the presence of trans-lamellar bridges [9, 10, 34, 35] may provide resistance against delamination in the outer AF. Melrose et al. [9] noted greater bridging in the mid to outer anulus with little to no bridging in the inner layer of ovine IVDs. Perhaps similar structures are evident in the human IVD providing greater resistance to delamination in the outer AF. Further, increased toughness (or failure energy) has also been observed in the outer AF in tissue samples that ultimately failed via slipping, or delamination, of layers relative to each other [36], which also supports the findings of the currently study. Given the finding of greater resistance to delamination in the superficial region, it is reasonable to conclude that the deep region of the AF will likely delaminate prior to the superficial region when exposed to similar loading and deformation patterns. However, similar loading and deformation across the AF is unlikely in vivo. Rather, the outer layers of the AF are more likely to be exposed to greater deformation due to their greater distance from the center of the rotation of the disc which is generally within the nucleus [37]. It is therefore probable that the higher peel strength, and therefore resistance to delamination, in the outer layers is because these layers are exposed to greater deformation during spine loading.
When the IVD is under compression, the NP pressurizes, which deforms the AF (generally bulging outward). This deformation results in both shear and tensile strain of the layers of the AF as well as the inter-lamellar matrix. Specifically, the matrix is subject to shear strain when the layers attempt to slide with respect to one another and tensile strain when these layers resist separation or delamination. The peel test used in this study aimed to mimic the tensile strain experienced by the inter-lamellar matrix when resisting delamination, which most closely resembles mode I fracture propagation (Fig. 1a).
Previous studies have aimed to determine the mechanical properties of the inter-lamellar matrix. Most recently, Gregory and colleagues [38] examined the inter-lamellar matrix of porcine cervical discs via a novel lap test. In this configuration, the properties of the inter-lamellar matrix were ascertained. High shear stress at the ends of the bonded lamellae existed with a mean peak strength of 0.3 N/mm in this configuration. Fujita and colleagues [32] also examined the inter-lamellar matrix of 3 × 3 × 3 mm anular cubes from human IVDs. These authors applied shear to these cubes along the same plane as the lamellar layers. This configuration, however, was only capable of determining the mechanical shear properties of multiple anular layers rather than the isolated inter-lamellar matrix. The current study employed the peel test to isolate the inter-lamellar matrix for a number of reasons. First, the inter-lamellar matrix acts not only as a biological adhesive in the AF by keeping the layers bound to prevent migration of the nucleus during herniation, but by also allowing some movement between the layers during spinal motion and IVD loading. Second, a T- or 180-degree peel test was chosen as both adherents, the AF tabs, are considered flexible: a necessity for the T-peel test [19]. Third, when choosing an appropriate testing method, it is important to consider a test that mimics how the tissue is loaded and fails in vivo. In the case of the AF, delamination is frequently observed, especially in the case of degeneration [15, 16].
It has been previously documented that herniation progression is not necessarily linear, but rather migrates circumferentially through the AF [39], and that a certain degree of anular delamination must exist for herniation to progress [13]. It appears that migration of the NP propagates this delamination by placing localized stresses on the inter-lamellar matrix that act to further pry open the layers (similar to the mechanism of the T-peel test) and subsequently allow the NP to occupy the fissure that has formed between lamellae. For these reasons, the peel test, and specifically the T-peel test, was considered a representative mode of loading and failure of the inter-lamellar matrix, and thus appropriate for determining the mechanical properties of the matrix.
The study was limited by a number of factors. First, the human cadaveric tissue obtained for this study was fresh-frozen. However, all lumbar spines were obtained at approximately the same time post-mortem and were all immediately frozen at −20 °C until thawed for mechanical testing. Second, it is possible that slight deformation in the anular tabs occurred during the peel tests. However, tissues were dissected in a manner such that each tab consisted of a minimum of four lamellae to help make the tabs much stiffer than the inter-lamellar matrix and ensuring that deformation, and ultimately failure, occurred within the matrix. Video imaging of all tissue tests assisted in confirming this assumption.
Conclusion
The AF is a multi-layered structure at risk of delamination, especially as degeneration progresses, and is thought to precede IVD herniation progression. The adhesive layers between the lamellae resist this delamination. The current study observed lower peel strength, and thus lower resistance to delamination, in the deep layers of human AF as compared with the superficial layers. As a result, the deep layers of the AF may be at an increased risk of delamination and herniation progression. A complete understanding of the properties of the inter-lamellar matrix is important to understand the risk of injury to the IVD. Further, it is important to study how these properties change as a result of various exposures and IVD damage/degeneration to ascertain any additional risk of injury to the IVD.
Acknowledgments
The authors wish to acknowledge NIH for funding (NIH P01AR48152). Diane Gregory was further supported by a NSERC postdoctoral fellowship and the ISSLS McNab-Larocca fellowship for this research.
Conflict of interest
None.
References
- 1.Bruehlmann SB, Rattner JB, Matyas JR, Duncan NA. Regional variations in the cellular matrix of the annulus fibrosus of the intervertebral disc. J Anat. 2002;201:159–171. doi: 10.1046/j.1469-7580.2002.00080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Errington RJ, Puustjarvi K, White IRF, Roberts S, Urban JP. Characterisation of cytoplasm-filled processes in cells of the intervertebral disc. J Anat. 1998;192:369–378. doi: 10.1046/j.1469-7580.1998.19230369.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eyre DR, Muir H. Type-1 and type-2 collagens in intervertebral-disk: interchanging radial distributions in annulus fibrosus. Biochem J. 1976;157:267–270. doi: 10.1042/bj1570267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hayes AJ, Benjamin M, Ralphs JR. Extracellular matrix in development of the intervertebral disc. Matrix Biol. 2001;20:107–121. doi: 10.1016/S0945-053X(01)00125-1. [DOI] [PubMed] [Google Scholar]
- 5.Ebara S, Iatridis JC, Setton LA, Foster RJ, Mow VC, Weidenbaum M. Tensile properties of nondegenerate human lumbar anulus fibrosus. Spine. 1996;21:452–461. doi: 10.1097/00007632-199602150-00009. [DOI] [PubMed] [Google Scholar]
- 6.Holzapfel GA, Schulze-Bauer CAJ, Feigl G, Regitnig P. Single lamellar mechanics of the human lumbar anulus fibrosus. Biomech Model Mechanobiol. 2005;3:125–140. doi: 10.1007/s10237-004-0053-8. [DOI] [PubMed] [Google Scholar]
- 7.Skaggs DL, Weidenbaum M, Iatridis JC, Ratcliffe A, Mow VC. Regional variation in tensile properties and biochemical-composition of the human lumbar anulus fibrosus. Spine. 1994;19:1310–1319. doi: 10.1097/00007632-199406000-00002. [DOI] [PubMed] [Google Scholar]
- 8.Kasra M, Parnianpour M, Shirazi Adl A, Wang JL, Grynpas MD. Effect of strain rate on tensile properties of sheep disc annulus fibrosus. Technol Healthc. 2004;12:333–342. [PubMed] [Google Scholar]
- 9.Melrose J, Smith SM, Appleyard RC, Little CB. Aggrecan, versican and type VI collagen are components of annulus trans-lamellar cross-bridges in the intervertebral disc. Eur Spine J. 2008;17:314–324. doi: 10.1007/s00586-007-0538-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schollum ML, Robertson PA, Broom ND. ISSLS prize winner: microstructure and mechanical disruption of the lumbar disc annulus part I: a microscopic investigation of the trans-lamellar bridging network. Spine. 2008;33:2702–2710. doi: 10.1097/BRS.0b013e31817bb92c. [DOI] [PubMed] [Google Scholar]
- 11.Adams MA, Green TP. Tensile properties of the annulus fibrosus. I. The contribution of fibre–matrix interactions to tensile stiffness and strength. Eur Spine J. 1993;2:203–208. doi: 10.1007/BF00299447. [DOI] [PubMed] [Google Scholar]
- 12.Yu J, Fairbank JCT, Roberts S, Urban JPG. The elastic fiber network of the anulus fibrosus of the normal and scoliotic human intervertebral disc. Spine. 2005;30:1815–1820. doi: 10.1097/01.brs.0000173899.97415.5b. [DOI] [PubMed] [Google Scholar]
- 13.Adams MA, Hutton WC. Gradual disc prolapse. Spine. 1985;10:524–531. doi: 10.1097/00007632-198507000-00006. [DOI] [PubMed] [Google Scholar]
- 14.Marshall LW, McGill SM. The role of axial torque in disc herniation. Clin Biomech. 2009;25:6–9. doi: 10.1016/j.clinbiomech.2009.09.003. [DOI] [PubMed] [Google Scholar]
- 15.Adams MA, Roughley PJ. What is intervertebral disc degeneration, and what causes it? Spine. 2006;31:2151–2161. doi: 10.1097/01.brs.0000231761.73859.2c. [DOI] [PubMed] [Google Scholar]
- 16.Vernon-Roberts B, Fazzalari NL, Manthey BA. Pathogenesis of tears of the anulus investigated by multiple-level transaxial analysis. Spine. 1997;22:2641–2646. doi: 10.1097/00007632-199711150-00012. [DOI] [PubMed] [Google Scholar]
- 17.Ahsan T, Sah RL. Biomechanics of integrative cartilage repair. Osteoarthr Cartil. 1999;7:29–40. doi: 10.1053/joca.1998.0160. [DOI] [PubMed] [Google Scholar]
- 18.Anderson T. Fracture mechanics: fundamentals and applications. 2nd. Boca Raton: CRC Press; 1995. [Google Scholar]
- 19.Standard test method for peel resistance of adhesives (T-Peel Test) West Conshohocken: ASTM International; 2008. [Google Scholar]
- 20.Taghizadeh SM, Soroushnia A, Mohamadnia F. Preparation and in vitro evaluation of a new fentanyl patch based on functional and non-functional pressure sensitive adhesives. AAPS PharmSciTech. 2010;11:278–284. doi: 10.1208/s12249-009-9366-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Renvoise J, Burlot D, Marin G, Derail C. Adherence performances of pressure sensitive adhesives on a model viscoelastic synthetic film: a tool for the understanding of adhesion on the human skin. Int J Pharm. 2009;368:83–88. doi: 10.1016/j.ijpharm.2008.09.056. [DOI] [PubMed] [Google Scholar]
- 22.Dykes PJ, Heggie R. The link between the peel force of adhesive dressings and subjective discomfort in volunteer subjects. J Wound Care. 2003;12:260–262. doi: 10.12968/jowc.2003.12.7.26567. [DOI] [PubMed] [Google Scholar]
- 23.Hatamleh MM, Watts DC. Bonding of maxillofacial silicone elastomers to an acrylic substrate. Dent Mater. 2010;26:387–395. doi: 10.1016/j.dental.2010.01.001. [DOI] [PubMed] [Google Scholar]
- 24.Tanimoto Y, Saeki H, Kimoto S, Nishiwaki T, Nishiyama N. Evaluation of adhesive properties of three resilient denture liners by the modified peel test method. Acta Biomater. 2009;5:764–769. doi: 10.1016/j.actbio.2008.08.021. [DOI] [PubMed] [Google Scholar]
- 25.Machado AL, Breeding LC, Puckett AD. Effect of microwave disinfection on the hardness and adhesion of two resilient liners. J Prosthet Dent. 2005;94:183–189. doi: 10.1016/j.prosdent.2005.04.017. [DOI] [PubMed] [Google Scholar]
- 26.Kumar D, Novince R, Strohl A, Mercer BM, Mansour JM, Moore RM, Moore JJ. A new methodology to measure strength of adherence of the fetal membrane components, amnion and the choriodecidua. Placenta. 2009;30:560–563. doi: 10.1016/j.placenta.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Scotti C, Wirz D, Wolf F, Dirk J, Schaefer DJ, Burgin V, Daniels AU, Valderrabano V, Candrian C, Jakob M, Martin I, Barbero A. Engineering human cell-based, functionally integrated osteochondral grafts by biological bonding of engineered cartilage tissues to bony scaffolds. Biomaterials. 2010;31:2252–2259. doi: 10.1016/j.biomaterials.2009.11.110. [DOI] [PubMed] [Google Scholar]
- 28.Englert C, Greiner G, Berner A, Hammer J. T-peel test for the analysis of articular cartilage integration. Stud Health Technol Inform. 2008;133:95–102. [PubMed] [Google Scholar]
- 29.Miyamoto K, Masuda K, Inoue N, Okuma M, Muehleman C, An HS. Anti-adhesion properties of a thrombin-based hemostatic gelatin in a canine laminectomy model: a biomechanical, biochemical, and histologic study. Spine. 2006;31:E91–E97. doi: 10.1097/01.brs.0000199902.80607.ce. [DOI] [PubMed] [Google Scholar]
- 30.Sonoda M, Harwood FL, Amiel ME, Moriya H, Temple M, Chang DG, Lottman LM, Sah RL, Amiel D. The effects of hyaluronan on tissue healing after meniscus injury and repair in a rabbit model. Am J Sports Med. 2000;28:90–97. doi: 10.1177/03635465000280012801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pfirrmann CWA, Metxdorf A, Zanetti M, Hodler J, Boos N. Magnetic resonance classification of lumbar intervertebral disc degeneration. Spine. 2001;26:1873–1878. doi: 10.1097/00007632-200109010-00011. [DOI] [PubMed] [Google Scholar]
- 32.Fujita Y, Wagner DR, Biviji AA, Duncan NA, Lotz JC. Anisotropic shear behaviour of the annulus fibrosus: effect of harvest site and tissue prestrain. Med Eng Phys. 2000;22:349–357. doi: 10.1016/S1350-4533(00)00053-9. [DOI] [PubMed] [Google Scholar]
- 33.Elliott DM, Setton LA. Anisotropic and inhomogeneous tensile behaviour of the human annulus fibrosus: experimental measurement and material model predictions. J Biomech Eng. 2001;123:256–263. doi: 10.1115/1.1374202. [DOI] [PubMed] [Google Scholar]
- 34.Schollum ML, Appleyard RC, Little CB, Melrose J. A detailed microscopic examination of alterations in normal anular structure induced by mechanical destabilization in an ovine model of disc degeneration. Spine. 2010;35:1965–1973. doi: 10.1097/BRS.0b013e3181e0f085. [DOI] [PubMed] [Google Scholar]
- 35.Schollum ML, Robertson PA, Broom ND. A microstructural investigation of intervertebral disc lamellar connectivity: detailed analysis of the trans-lamellar bridges. J Anat. 2009;214:805–816. doi: 10.1111/j.1469-7580.2009.01076.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Skrzypiec D, Tarala M, Pollintine P, Dolan P, Adams MA. When are intervertebral discs stronger than their adjacent vertebrae? Spine. 2007;32:2455–2461. doi: 10.1097/BRS.0b013e3181573b87. [DOI] [PubMed] [Google Scholar]
- 37.Adams M, Bogduk N, Burton K, Dolan P. The biomechanics of back pain. Toronto: Elsevier Ltd; 2006. [Google Scholar]
- 38.Gregory DE, Veldhuis JH, Horst C, Brodland GW, Callaghan JP. Novel lap test determines the mechanics of delamination between annular lamellae of the intervertebral disc. J Biomech. 2011;44:97–102. doi: 10.1016/j.jbiomech.2010.08.031. [DOI] [PubMed] [Google Scholar]
- 39.Tampier C, Drake JD, Callaghan JP, McGill SM. Progressive disc herniation: an investigation of the mechanism using radiological, histochemical, and microscopic dissection techniques on a porcine model. Spine. 2007;32:2869–2874. doi: 10.1097/BRS.0b013e31815b64f5. [DOI] [PubMed] [Google Scholar]