The Spiking Component of Oscillatory Extracellular Potentials in the Rat Hippocampus

Abstract

When monitoring neural activity using intracranial electrical recordings, researchers typically consider the signals to have two primary components: fast action potentials (APs) from neurons near the electrode, and the slower local field potential (LFP), thought to be dominated by postsynaptic currents integrated over a larger volume of tissue. In general, a decrease in signal power with increasing frequency is observed for most brain rhythms. The 100–200 Hz oscillations in the rat hippocampus, including “fast gamma” or “epsilon” oscillations and sharp wave-ripples (SPW-Rs), are one exception, showing an increase in power with frequency within this band. We have used detailed biophysical modeling to investigate the composition of extracellular potentials during fast oscillations in rat CA1. We find that postsynaptic currents exhibit a decreasing ability to generate large-amplitude oscillatory signals at high frequencies, whereas phase-modulated spiking shows the opposite trend. Our estimates indicate that APs and postsynaptic currents contribute similar proportions of the power contained in 140–200 Hz ripples, and the two combined generate a signal that closely resembles in vivo SPW-Rs. Much of the AP-generated signal originates from neurons further than 100 μm from the recording site, consistent with ripples appearing similarly strong regardless of whether or not they contain recognizable APs. Additionally, substantial power can be generated in the 90–150 Hz epsilon band by the APs of rhythmically firing pyramidal neurons. Thus, high-frequency LFPs may generally contain signatures of local cell assembly activation.

Introduction

Oscillations in extracellular electrical recordings within neural tissue are thought to reflect coordinated network activity, although their functional role and the physiology underlying their emergence remain enigmatic (Buzsáki, 2006). The extracellular signal contains ∼40–500 μV spikes (<1 ms wide) from the action potentials (APs) of nearby neurons (Gold et al., 2006), as well as slower features that are more widespread across the cortex and range from tens to thousands of microvolts. The precise origins of the latter components, collectively referred to as the local field potential (LFP), are still poorly understood (Logothetis, 2003; Einevoll et al., 2010; Buzsáki et al., 2012), but postsynaptic currents are typically presumed to be the dominant source of LFP fluctuations (Mitzdorf, 1985). As a result, researchers often filter their recordings in an attempt to separate synaptic input (<300 Hz) from spiking output (>500 Hz) of the neuronal population around the electrode. Other contributors have been proposed (Buzsáki et al., 2012), but experimental decomposition of LFPs is rarely feasible because transmembrane currents over several hundred micrometers are integrated into the signals (Katzner et al., 2009; Lindén et al., 2011).

Observing the LFP and its relationship with neuronal firing is a common method of identifying network oscillations. In general, as oscillation frequency increases, signal power tends to decrease (Buzsáki and Draguhn, 2004). An exception is found in the 100–200 Hz band in the rat hippocampus, in which power and frequency are positively correlated for 90–150 Hz epsilon (often referred to as “fast gamma”) (Sullivan et al., 2011; Belluscio et al., 2012) and 140–200 Hz sharp wave-ripple (SPW-R) oscillations (Csicsvari et al., 1999b; Sullivan et al., 2011). There are two general aspects of such oscillatory phenomena to be explained: the mechanisms for coordinating network activity and the current sources generating the measured signal. Several of the former have been proposed for SPW-Rs (Ylinen et al., 1995; Traub and Bibbig, 2000; Brunel and Wang, 2003; Maier et al., 2011), with the common theme that rippling in CA1 emerges as the network responds to the excitatory impulse from CA3 that makes up the sharp wave (Buzsáki, 1986). Dramatic increases in the firing of pyramidal cells and some types of interneurons are observed during SPW-Rs, with spikes phase-locked to the ripple field (Buzsáki et al., 1992; Csicsvari et al., 1999a; Klausberger et al., 2003, 2004). Although nearby APs will contribute features to ripple waveforms (Buzsáki, 1986; Reichinnek et al., 2010), perisomatic inhibitory currents in pyramidal cells were thought to generate most of the ripple signal (Ylinen et al., 1995). However, several recent studies report evidence of spike “contamination” of LFP oscillations (Ray et al., 2008a; Quilichini et al., 2010; Ray and Maunsell, 2011; Zanos et al., 2011; Belluscio et al., 2012). Utilizing detailed biophysical models of neuronal populations of the hippocampus, as well as previously reported in vitro measurements of the LFP contributions from individual interneurons (Glickfeld et al., 2009; Bazelot et al., 2010), we show that spiking neuron populations can generate a substantial proportion of the power above 100 Hz in the local extracellular field.

Materials and Methods

Neuron models.

Neurons were compartmental models based on reconstructed cells from the rat hippocampus and simulated in NEURON (Carnevale and Hines, 2006). Pyramidal cells throughout the population were based on a single neuron from rat CA1 that was patched, stained, and reconstructed by Henze et al. (2000), and modeled by Gold et al. (2006, 2007) to recreate extracellular action potential (EAP) waveforms (cell D151a; available for download at http://senselab.med.yale.edu/modeldb/ShowModel.asp?model=84589). The model neuron has the following basic dimensions: soma surface area, 559 μm²; total dendrite length, 10,155 μm; vertical (stratum oriens to stratum lacunosum-moleculare) dendritic arbor height, 677 μm. In addition to the passive properties of the membrane (membrane resistance R_m = 15 kΩ cm²; membrane capacitance C_m = 1 μF cm²; intracellular resistivity R_i = 70 Ω cm), the model incorporates 12 types of ion channels, including Na⁺, K⁺, Ca²⁺, Ca²⁺-dependent K⁺, and dendritic hyperpolarization-activated I_h currents. The model had a resting membrane potential at the soma of −65 mV. A total of 512 compartments and a 0.01 ms time step were used for the simulations.

The dentate gyrus basket cell model of Nörenberg et al. (2010) and Hu et al. (2010) was adopted and modified for estimating the extracellular potentials generated by AP currents in the CA1 interneuron population during fast oscillations. Its membrane incorporates nonuniform passive resistance, I_h currents, and Na⁺ and K⁺ channels that confer the fast-spiking behavior typical of these interneurons (Wang and Buzsáki, 1996). The model includes an extensive unmyelinated axon, which was morphed to remain within a flat disk around the CA1 pyramidal layer (see below). The model neuron has soma surface area of 883 μm², total dendrite length of 3756 μm, vertical (stratum oriens to stratum lacunosum-moleculare) dendritic arbor height of 419 μm, and total axon length of 17,461 μm. Its initial membrane properties (R_m,soma = 6.4 kΩ cm²; R_{m,prox. dend.} = 6.4 kΩ cm²; R_{m,dist. dend.} = 12.7 kΩ cm²; R_m,axon = 325.4 kΩ cm²; C_m = 1.06 μF cm²; R_i = 137 Ω cm) were originally determined by fitting to in vitro measurements of basket cell responses to current injection (Hu et al., 2010; Nörenberg et al., 2010), resulting in axon R_m values almost 2 orders of magnitude greater than the somatic R_m, and a low Na⁺ channel density in the distal axon (30 mS cm⁻², compared with 200 mS cm⁻² in the soma and 600 mS cm⁻² in the proximal axon). However, these parameter fits would have been affected by the myelination that is present on portions of basket cell axons (Freund and Buzsáki, 1996). In an attempt to obtain an upper bound on the axon contribution to EAPs by allowing strong AP propagation through the entire axonal arbor, we changed the axon R_m to that of the soma, kept the high Na⁺ channel density of the proximal axon, and we set the Na⁺ channel density in the distal axon to the somatic value. The model had a resting membrane potential at the soma of −66.3 mV. Basket cell simulations were performed using 2935 compartments and a 0.001 ms time step. The extensive axon and fast channel kinetics necessitated a shorter time step than the pyramidal cell model.

Synaptic inputs were modeled as transient conductance changes with a double exponential time profile g(t) = G₀[exp(−t/τ_decay) − exp(−t/τ_rise)] in series with a reversal potential E_syn, which had a value of 0 mV for excitatory synapses (Jonas et al., 1993) and −75 mV for inhibitory (Buhl et al., 1995). To isolate the AP currents, spikes were elicited by randomly placed synapses on the dendrites (in a volley of 50 excitatory and 50 inhibitory synapses for the pyramidal cell, but only 15 excitatory synapses and no inhibition for the basket cell) in 50 trials. Each trial was then repeated with a passive soma and axon and the same synaptic input, which failed to elicit an AP. The membrane currents of the “suppressed-AP” case were subtracted from those of the spiking case, and the remaining membrane currents from 2 ms before to 5 ms after the somatic V_m passed above −10 mV were saved and averaged across all trials to remove effects of the specific synapse distribution. These “average AP currents,” cleansed of any direct synaptic contributions, were then used to calculate the extracellular potentials within each spiking population. We confirmed that suppressing APs in a spiking population (see above) and adding in these average AP currents at the same times and locations as spikes in the fully active population introduced negligible differences in the extracellular potentials.

In simulations of synaptically generated LFPs within pyramidal cell populations, active ion channels were removed from the entire membrane to prevent spike generation at any point in the cell. Synapses were then distributed randomly throughout certain dendritic regions, with inhibitory synapses restricted to the soma and dendritic compartments ≤100 μm from the soma, and excitatory synapses in the apical dendrites 100–350 μm away from the soma, in the region of stratum radiatum Schaffer collateral input. The precise kinetics of synapse conductances are notoriously difficult to measure due to cable filtering, but for fast excitatory (e.g., AMPA receptor-mediated) and inhibitory (GABA_A receptor-mediated) synapses, estimates for τ_rise and τ_decay (defined above) range from 0.1–1 and 2–10 ms, respectively (Hestrin et al., 1990; Jonas et al., 1993; Maccaferri et al., 2000; Glickfeld et al., 2009; Bazelot et al., 2010). We set τ_rise to 0.1 ms and tested τ_decay values from 1 to 7 ms. Two hundred excitatory and 200 inhibitory synapses were activated every 50 ms, with individual peak synapse conductances of G₀ = 0.3 nS.

Calculating extracellular potentials.

We approximated the extracellular medium as a uniform, isotropic, ohmic conductor with resistivity ρ = 333 Ω cm (López-Aguado et al., 2001; Logothetis et al., 2007; Goto et al., 2010; Anastassiou et al., 2011; but see Bédard et al., 2010). The extracellular potential, V_e, at a particular location within a population of cells is simply the linear superposition of the contributions from all compartments of all cells (10⁵–10⁶ total in the population simulations), with the contribution of each compartment being proportional to its net transmembrane current and inversely proportional to its distance from the electrode (see Fig. 1A). We treated compartments as line sources of current (Holt and Koch, 1999; Gold et al., 2006). Using Ohm's law in a cylindrical coordinate system,

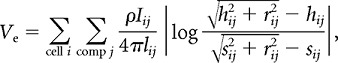where I is transmembrane current (positive value indicates current exiting the membrane), l is compartment length, r is the perpendicular distance from the electrode to a line through the compartment, h is longitudinal distance along this line from the electrode to one end of the compartment, and s = l + h is longitudinal distance to the other end of the compartment. These calculations were performed in MATLAB using the results of the NEURON simulations.

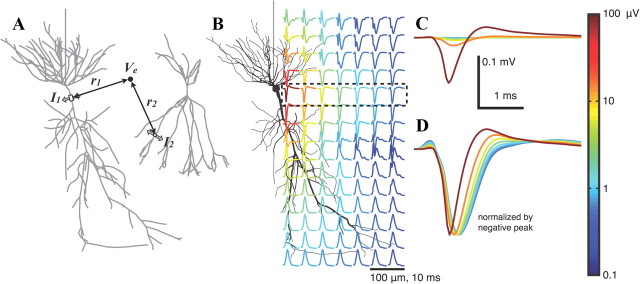
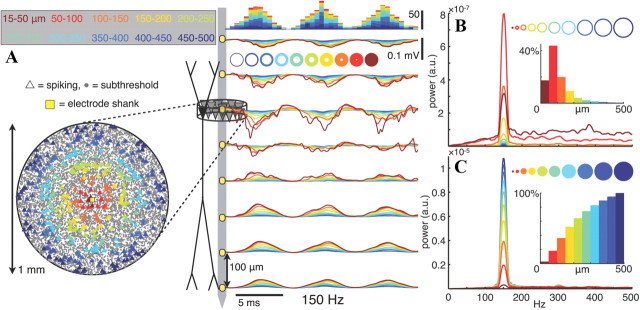
Figure 1.

Average extracellular action potential (EAP) of the pyramidal cell model. A, Illustration of V_e calculation in a population through the superposition of contributions from all compartments in all cells. Individual compartment contributions are primarily determined by their transmembrane currents and distances from the electrode (see Materials and Methods). B, Location dependence of the EAP for the pyramidal cell model. The peak-to-peak voltage range is indicated by the color of each trace. Subthreshold currents have been removed (see Materials and Methods), and each EAP waveform is an average over 25 points at a fixed radius from the apical axis (the vertical direction here) to remove the dependence on the precise dendritic geometry. EAPs are calculated at the location of the start of each trace. C, EAPs within the cell body layer (B, dashed box) with voltages drawn to scale. EAP amplitude decreases rapidly with distance. The largest EAP is calculated 20 μm from the soma center, and then at 50 μm intervals. D, Same traces as in C, but normalized by the negative peak.

Population activity.

For the pyramidal cell population, we used a single morphology and one set of membrane parameters, and likewise for the basket cell population. Cells were oriented with the apical axis along the stratum oriens to stratum radiatum direction, with random rotations about this axis, and somata were randomly placed within the cell body layers for the respective cell types. The centers of pyramidal cell somata were located within a disk 40 μm thick and 1 mm in diameter at a density of 3 × 10⁵ per cm³ (Boss et al., 1987; Aika et al., 1994) (9416 sites), and the basket cell soma centers were within an 80-μm-thick disk (Freund and Buzsáki, 1996) of the same diameter at a density of 7.5 × 10³ per cm³, resulting in 471 sites (5% of pyramidal cell number; 2.5% of the density) (Olbrich and Braak, 1985; Aika et al., 1994; Freund and Buzsáki, 1996). This basket cell population approximates interneurons known to be active during SPW-Rs (Klausberger et al., 2003, 2004). Cell bodies were excluded from a 15 μm radius volume around the electrode shank. Because the cell position refers to the location of the center of its soma, which had a maximum diameter of 11.5 μm for the pyramidal cell and 12 μm for the basket cell, soma surfaces could therefore approach within 9 μm of the “virtual electrode.”

The dendritic arbor of each pyramidal neuron in the rat hippocampus (which typically has a total of ∼30,000 synaptic contacts; Megías et al., 2001) constantly receives input from numerous afferents, but independently simulating all 9416 neurons in our population would have prohibited us from effectively exploring the large parameter space available for the spatiotemporal patterns of synaptic input. Instead, similar to our technique for constructing a population of spiking neurons, we simulated 50 passive pyramidal neurons receiving similar synaptic input patterns (see above, Neuron models). The resulting membrane currents in each compartment were averaged across these 50 trials to obtain the “average subthreshold cell,” which was then used to calculate the contribution from constituent cells in the population. The contributions from all cells within 100 μm of the electrode shank were calculated; outside of this radius, the potentials from 20% of the cells were scaled up by a factor of 5 and added to the potentials from those of the inner cells. This estimation method resulted in <5% error when compared with tests in which each cell was separately simulated and included in the calculation of the population potentials, but reduced simulation time by nearly 2 orders of magnitude.

By using average subthreshold and AP currents in cells with synaptic currents removed, we effectively decoupled spike and synapse currents within the population and could estimate their contributions separately. When simulating AP-generated potentials from rhythmically firing cell populations, the spiking neurons were randomly chosen from the population, with an independent set each oscillation period. Spike times were pulled from a periodic probability density function (pdf) that consisted of repeating Gaussians (exp[−t²/2σ²]). Unless otherwise noted (see Fig. 3), we set σ to one-fifth of the cycle period. This pdf was also used to generate synapse activation times for simulations of synaptically generated LFPs (see Fig. 10). Additional spiking from cells that are poorly modulated within an oscillation does not impart substantial power at frequencies <500 Hz on average (see Fig. 2, black curves, which are barely visible in C because they remain below 2.2 × 10⁻⁷).

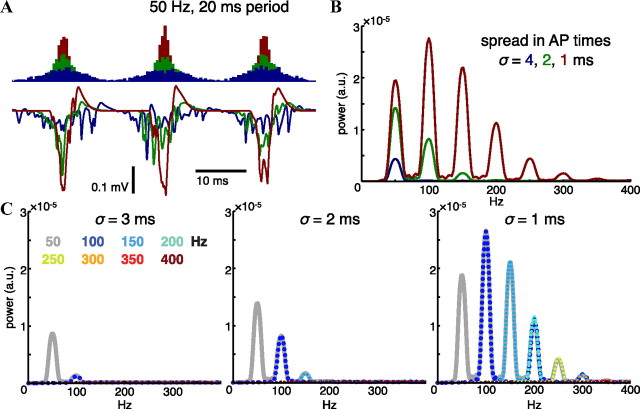
Figure 3.

Effect of additional synchrony at slower oscillation frequencies. A, Spike histograms and the resulting stratum pyramidale extracellular potentials for three different widths of the Gaussian-shaped bursts of spiking in the population [σ = 1 ms (red), 2 ms (green), 4 ms (blue)] during a 50 Hz rhythm. At low σ (high synchrony), the extracellular potentials essentially consist of periodically reoccurring population spikes. B, The 25 trial averages of the FFT spectra of the extracellular potentials in A. Narrower population bursts increase power at both the rhythm frequency and its harmonics, with the power at the harmonics exceeding that at the rhythm frequency for very synchronous spiking. C, Average power spectra for 50–400 Hz rhythms in which the repeating Gaussian-shaped population bursts have widths of σ = 3, 2, 1 ms, independent of the oscillation. Six percent of the population fires each 10 ms with spike times modulated within the periodic probability density function. Faster rhythms therefore have these spikes separated into more bursts and, consequently, have fewer spikes per burst.

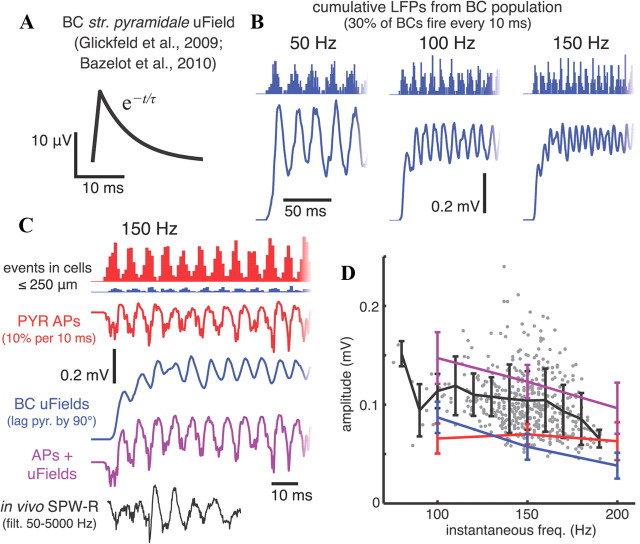
Figure 10.

APs and IPSCs contribute similar amounts of power to 100–200 Hz SPW-R LFPs. A, uField in stratum pyramidale from a single basket cell (BC) spike, modeled after uFields measured by Glickfeld et al. (2009) and Bazelot et al. (2010). B, Cumulative LFPs in a rhythmically firing basket cell population when the uField in A is added at the time of each spike for basket cells within 250 μm of the electrode contribute uFields; 30% of the population spikes each 10 ms. Histograms above the LFP curves indicate spike times. C, Comparison of simulated LFPs from pyramidal cell EAPs (red) during a 150 Hz population rhythm with 10% spiking each 10 ms (as in Fig. 6), basket cell uFields (blue), the two combined (magenta) with the basket cell spiking rhythm lagging the pyramidal cell rhythm by 90° (Sullivan et al., 2011), and a 50–5000 Hz bandpass filtered SPW-R recorded in vivo (black). The histogram shows all events occurring in cells within 250 μm from the electrode; the potentials include pyramidal cell EAPs from all cells within 500 μm and basket cell uFields from all cells within 250 μm of the electrode (see Materials and Methods and Results). D, Comparison of amplitudes for in vivo and simulated ripples. The gray dots show instantaneous amplitudes and frequencies of individual troughs within in vivo fast oscillation events between 50 and 210 Hz (see Materials and Methods), the black line marks the mean (±SD) trough amplitudes in 10 Hz bins of these in vivo ripple waves, and colored lines (same colors as in C) indicate mean (±SD) trough amplitudes during simulated ripples in populations oscillating at 100, 150, and 200 Hz.

Figure 2.

Extracellular signatures of phase-modulated spiking in a pyramidal cell population. A, Illustration of the model. The 9416 pyramidal cells were randomly distributed with their soma centers in a 40-μm-thick circular disk with 1 mm diameter. V_e values were calculated along a virtual electrode shank oriented along the central axes of the disk. Layer abbreviations: o, Stratum oriens; p, stratum pyramidale; r, stratum radiatum; lm, stratum lacunosum-moleculare. B, Extracellular potentials in stratum pyramidale arising from AP currents in randomly and rhythmically spiking populations with varying modulation frequency and three different average firing rates (2, 4, 6% per 10 ms). Histograms of APs are shown above the corresponding voltage traces. C, Averaged FFT power spectra over 25 trials for V_e in stratum pyramidale. Spectra are shown for each case from B and for two additional frequencies (250 and 350 Hz). Note that the unmodulated spiking spectra (grayscale in B) are not visible because the maximum value in the most active case shown is 2.2 × 10⁻⁷. Power spectral densities (psds) throughout this manuscript were estimated using the multitaper method with a time-bandwidth product of 4 and an 8192-point FFT (Percival and Walden, 1993), so the arbitrary psd units (a.u.) are consistent in all figures.

IPSCs from unitary field potentials.

To estimate the contribution of IPSCs elicited by firing basket cells to LFPs, we summed up the stratum pyramidale “unitary field potentials” (uFields) arising from individual CA1 basket cells measured by Glickfeld et al. (2009). Spike times for basket cells were pulled from the periodic Gaussian pdf described above, and a positive uField was added at each “spike” to the total V_e with the following characteristics: 15.8 μV amplitude, linear rise with 1.2 ms 10–90% rise time, exponential decay with 6.6 ms time constant (Glickfeld et al., 2009) (see Fig. 10A). Bazelot et al. (2010) measured similar uFields from basket cells in CA3, and they found that the uFields could be detected in stratum pyramidale across a total distance of ∼1000 μm on average, although their amplitudes typically decreased by >50% within 250–300 μm from the locations at which they were maximal. The same uField was therefore added for each basket cell spike within a 500-μm-diameter disk around the electrode, regardless of the exact location of the cell.

Experimental procedures.

In vivo CA1 recordings from a male Long–Evans rat with a chronically implanted multielectrode array were used for direct comparison with simulation results. All experimental data presented here are from eight channels from one shank of a silicon multielectrode array within dorsal CA1 during one recording session while the animal slept in its home cage. Surgery, recording methods, and experimental procedures were described by Montgomery et al. (2008).

Data analysis.

Filters were implemented using bandpass Butterworth IIR filters, designed using fdatool in MATLAB, with ≥60 dB stopband attenuation. The filters were applied in both the forward and reverse directions to remove phase distortions. For some portions of the LFP analysis of in vivo recordings, electrode signals were downsampled to 1250 Hz. Current source densities (CSDs) were calculated using the 1-D second spatial derivative of the depth-recorded LFPs (Nicholson and Freeman, 1975). In the sleep session analyzed here, theta epochs were detected using the ratio of power in the theta band (5–11 Hz) to delta band (1–4 Hz) of the LFP (Mizuseki et al., 2009). Nontheta epochs during sleep sessions were considered slow wave sleep (SWS). All data presented here are from SWS.

To detect SPW-R events in in vivo recordings, we followed a procedure based on Sullivan et al. (2011). In brief, the LFP signal was bandpass filtered from 140 to 210 Hz, rectified, smoothed with three-sample boxcar kernel, and z-score normalized. Portions of the resulting signal were marked as candidate events if their amplitude was >2 SDs above the mean. Event peaks were extracted by taking the maxima of the 140–210 Hz pyramidal layer CSD and enforcing a minimum separation between event peaks of 50 ms. One hundred millisecond segments of the wideband LFP signal around these event peaks were then analyzed further using the multitaper FFT in the MATLAB signal processing toolbox. FFT power spectra were z-score normalized by the mean and SD of power at each frequency in 20,000 randomly chosen 100 ms windows throughout the SWS epochs during the recording session. Candidate events with spectral peaks >3 SD above the mean that were between 140 and 210 Hz were classified as ripples.

The duration of ripple events and the frequency and amplitude of individual waves within a single ripple vary in vivo, but the amplitude and frequency of our simulated ripples are approximately constant. To perform a fair comparison, we also estimated the instantaneous frequency and amplitude of individual troughs in the 50–210 Hz bandpass-filtered signal (the pass band was widened from the SPW-R detection procedure above to prevent attenuation of ∼100 Hz oscillations). The frequency of the trough was defined as the inverse of the time interval between the peaks flanking it, and its amplitude was defined as the absolute value of the trough minimum of the filtered signal. Only troughs with flanking peaks that were within oscillatory events (defined as intervals during which the 1.4 ms boxcar average of the absolute value of the 50–210 Hz bandpass filtered signal remained above 1 SD and has at least one peak >2 SDs) (Csicsvari et al., 1999b) were included.

Power spectra presented for simulated extracellular potentials were first calculated using 100 ms time windows of the raw signal, and the spectra were then averaged over 25 trials.

Results

Spiking contribution to the LFP

To reliably estimate the spike content of extracellular recordings using our theoretical framework, it is necessary to simulate accurate spike waveforms. The model by Gold et al. (2006, 2007) was developed for this purpose, emulating intracellular and extracellular action potentials based on simultaneous in vivo intracellular and extracellular recordings of rat CA1 pyramidal cell APs (Henze et al., 2000) based on appropriate distribution of transmembrane currents. Figure 1 shows the spatial variation of EAPs produced by the pyramidal cell model with membrane biophysics governed by parameter set A of Gold et al. (2007). Before calculating the extracellular potential V_e, subthreshold membrane currents were subtracted (see Materials and Methods), and the remaining membrane currents were averaged over 50 trials. To visualize EAP trends that were less dependent on details of the dendritic morphology, each plotted waveform is an average of 25 EAPs on a ring around the apical axis (Fig. 1B, top to bottom), with the radius and vertical position indicated by the starting point of each trace. The amplitudes of EAPs decrease with distance from the soma (Fig. 1C), and they widen (Fig. 1D) due to both the decreasing dominance of the strong Na⁺ currents at the soma and axon hillock (Gold et al., 2006), as well as intrinsic low-pass filtering of currents by the cell membrane, which leads to smaller current dipoles for high-frequency components (Mitzdorf, 1985; Pettersen and Einevoll, 2008).

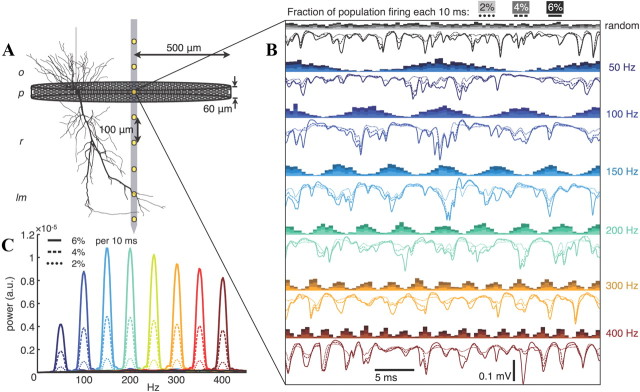
Using these average AP currents, we calculated the extracellular potentials due to spiking within a population of pyramidal cells arranged to resemble those in the dorsal CA1 region of the rat hippocampus (Fig. 2A) (see Materials and Methods). We computed V_e during firing that was either random or synchronized by a rhythm of frequency f, with f ranging from 50 to 400 Hz (Fig. 2B). In the rhythmic cases, spike times were modulated by a periodic Gaussian pdf, with the SD of spike times in each group of APs given by σ = 0.2/f. Because f and σ were inversely related, higher frequency rhythms more effectively synchronized spiking within the population, resulting in more EAP overlap and greater signal power. We quantified this trend using the averaged FFT of 100 ms segments of V_e over 25 trials (Fig. 2C). Oscillation power peaked between 150 and 200 Hz, and then slowly decreased with further increases in frequency, because fewer APs occurred within each period. In these simulations, 2, 4, or 6% of the population fired each 10 ms, which is within the physiological range estimated for fast oscillations of the rat hippocampus during SWS by Csicsvari et al. (1999a,b, 2000).

The power–frequency relationship depends crucially on the relationship between σ and f. Our choice of the σ = 0.2/f spread in each Gaussian-shaped packet of spikes in the population results in an approximately sinusoidal shape of the spiking pdf with a nearly full depth of modulation. Lower depths of modulation (e.g., 0.3/f) may be treated as a combination of a fully modulated set of events superimposed on a baseline of unmodulated activity (i.e., random events with constant probability), and the effective “baseline” spikes add inconsistent power at frequencies <500 Hz that averages out over multiple events (Fig. 2B,C, black traces). Firing phase histograms constructed from many fast LFP oscillations recorded in vivo do not appear to show population bursts that are substantially narrower than the period of oscillation in the normal hippocampus (Ylinen et al., 1995; Csicsvari et al., 1999b, 2003; Colgin et al., 2009; Sullivan et al., 2011). If tighter phase coupling was present, it led to increases in the power at both the oscillation frequency as well as at its harmonics in our simulations. For example, decreasing σ from 4 to 2 ms in the 50 Hz case approximately tripled the power of the 50 Hz LFP oscillations, but also caused a peak at 100 Hz to emerge in the spectrum that was around one-half the power of the 50 Hz component (Fig. 3A,B). Further decreasing σ to 1 ms caused the power of the 100 Hz harmonic to become greater than the 50 Hz peak, due to a more prominent positive repolarization phase (Fig. 3A). Firing rates during normal oscillations near 50 Hz are not as high as during the faster ripple oscillations, however, and the number of cells effectively modulated by medium to slow gamma rhythms is substantially less than for epsilon frequency rhythms (Belluscio et al., 2012). These considerations are instead most relevant during spike-and-wave discharges and “fast ripples” of the epileptic state (Bragin et al., 1999; Blumenfeld, 2005; Foffani et al., 2007; Staley, 2007).

If σ is independent of f, then rhythms with frequencies less than ∼0.2/σ will have substantial power in their harmonics, with the power of these harmonics determined by σ. This is illustrated for σ = 3, 2, and 1 ms in Figure 3C. The average signal power during rhythms faster than that which was most powerful for a given σ dropped off quickly in our scheme (we kept the average firing rate of the population constant while varying the frequency of the rhythm that modulates spike timing), because faster rhythms have fewer spikes clustered into each population burst. Additionally, once f went above ∼0.2/σ neighboring burst events overlapped and the depth of modulation of firing rapidly fell off. The peak power was between 150 and 200 Hz in the σ = 0.2/f case (Fig. 2C) because that range was where the optimal balance was achieved between synchrony and spike count in each population burst.

When the pyramidal cell population was in an active state and the firing rhythm was synchronized over several hundred micrometers, much of the field potential amplitude could be attributed to cells too far away for their APs to be recognized as such (Buzsáki, 2004). Figure 4 illustrates this with an eight-electrode shank in the center of a 1-mm-diameter population in which spike times are modulated by a 150 Hz rhythm. In Figure 4A, the extracellular potentials are decomposed by cell distance from the electrode in 50 μm steps in an outside-in manner. That is, cells with somata in a particular 50-μm-wide ring have their EAPs added to the signal generated by all the cells further away. The firing of cells >100 μm from the electrodes produced a smooth 150 Hz V_e that was at least one-half of the amplitude of most peaks in the cumulative potential, with more proximal EAPs adding larger but narrower spikes on top of this signal at the pyramidal layer, but adding little to the signal in the dendritic layers. In terms of oscillatory power (Fig. 4B), spikes from the few cells near the electrode created a wideband spectrum, although with a consistent peak at 150 Hz (which is why this peak dominates the 25 trial average spectrum in Fig. 4B). The most power coming from an individual ring was for cells 50–100 μm from the electrode; this range had the most effective combination of spike count and EAP amplitude. On average, the signal originating from cells 100–150 μm away was as powerful as that from cells closer than 50 μm (Fig. 4B), and adding the contribution from all cells >100 μm to the signal from cells <100 μm increased the signal power fivefold (Fig. 4C).

Figure 4.

EAPs from groups of distant neurons can contribute substantially to fast LFP oscillations. A, Extracellular potentials (right) along the stratum oriens–stratum radiatum axis in a rhythmically bursting population with ∼6% of the population firing each 10 ms. Spike bursts recur periodically at 150 Hz and have a Gaussian shape with σ = 1.3 ms (i.e., one-fifth of the oscillation period). The locations of neurons that spike during one 6.7 ms period are indicated by triangles in a top-down view of the pyramidal layer (left), with colors indicating the 50-μm-wide ring from which the spikes originate. V_e traces are colored correspondingly, with contributions from each ring of cells adding cumulatively from the outside in. Stacked histograms above the potential traces show spike times. B, C, Averaged power spectra of the stratum pyramidale V_e from each individual ring (B) and for the inside-out cumulative potentials indicated by the colored disks (C). The insets indicate the proportions of the total V_e 150 Hz power generated by each ring- or disk-shaped subpopulation (i.e., the peak values of the power spectra, normalized by the power at 150 Hz in the full population). Note that the contributions of the rings in B to the cumulative spectra in C do not sum linearly because we are displaying spectral power, which is proportional to the square of the amplitude.

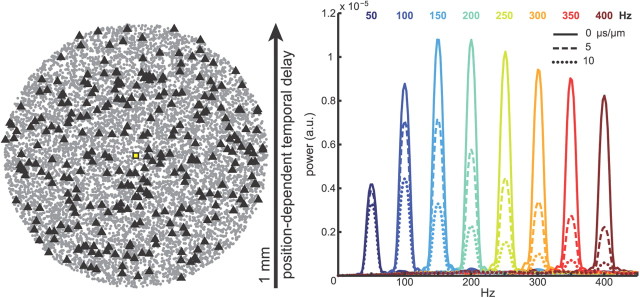
These results depended on a high degree of synchrony across space in the rhythm driving the population firing. Substantial phase coherence of LFP oscillations is often present over distances >1 mm in both the transverse and longitudinal directions within the CA1 pyramidal layer during SPW-Rs occurring in SWS (Ylinen et al., 1995; Sullivan et al., 2011), with the amplitude and spatial coherence of the ripple positively correlated (Csicsvari et al., 2000). Phase delays and decoherence within CA1 have been reported for theta and gamma band oscillations (Bragin et al., 1995; Lubenov and Siapas, 2009), but we are not aware of detailed analyses of the spatial profile of fast oscillation phase synchrony within CA1 stratum pyramidale during theta activity. If population synchrony is related to oscillation frequency, with slower oscillations exhibiting a greater spread in spike timing, then the temporal delays associated with activity propagating at a finite speed through the hippocampus (Lubenov and Siapas, 2009) will affect high-frequency rhythms more than those at lower frequencies, because a given temporal delay in activity between two locations will correspond to a larger phase delay for the faster oscillation. For example, temporal delays of 10 μs/μm along one direction (e.g., if spiking activity is locked to the local theta phase, which propagates along the septotemporal axis at approximately this speed) (Lubenov and Siapas, 2009) resulted in an average spectral power at the oscillation frequency that was approximately one-half of the power in the case with no delays for a population undergoing 100 Hz oscillations, and the ratio was approximately one-quarter for 200 Hz oscillations (Fig. 5). Thus, there may be a close link between high-frequency power and temporal coordination of firing across space, with a more synchronized population able to generate stronger oscillations in the LFP (Csicsvari et al., 2000; Ray et al., 2008b).

Figure 5.

Effect of spatial synchrony on oscillatory potentials. Left, Locations of CA1 pyramidal cell somata within a 1-mm-diameter disk. The triangles show the location of cells spiking within a 5 ms interval (3% of the population). The temporal offsets of the periodic probability density function that modulates spike timing are shifted in a position-dependent manner along one dimension within the cell body layer, similar to the case in which activity propagates along one direction in CA1 (Lubenov and Siapas, 2009). Right, Average power spectra of V_e in stratum pyramidale over 25 trials with pyramidal neurons undergoing rhythmic firing, as in Figure 2, with varying levels of spatial synchrony. Color indicates the frequency of the firing rhythm, and line type indicates the time delay per unit distance of the oscillating spike probability function. Solid lines, 0 μs/μm (no delays); dashed lines, 5 μs/μm; dotted lines, 10 μs/μm.

Comparison with in vivo recordings

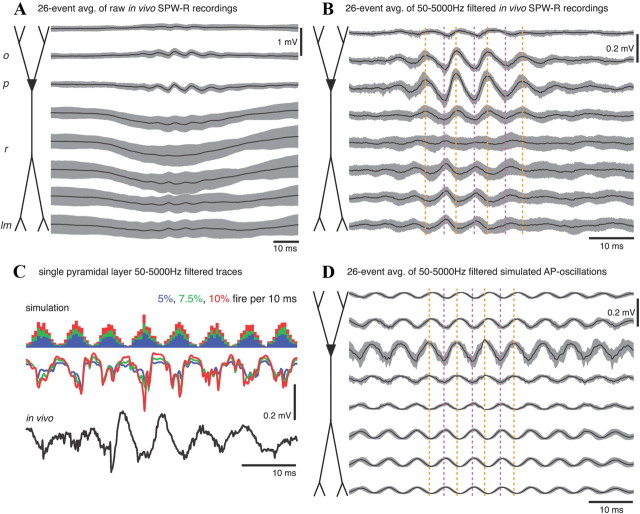
We analyzed recordings from linear electrode arrays in the rat hippocampus during SWS (Montgomery et al., 2008). SPW-Rs were detected in dorsal CA1 during SWS epochs from a single sleep session (see Materials and Methods), and events with a dominant ripple frequency between 140 and 160 Hz were extracted for comparison to V_e within a simulated pyramidal cell population exhibiting a 150 Hz firing rhythm (Fig. 6). During in vivo SPW-R events, APs in a large portion of pyramidal cells and some inhibitory interneuron types (e.g., basket cells and bistratified cells) (Klausberger et al., 2003, 2004) are phase-locked to the field ripple, with pyramidal cell firing centered at the ripple trough (recorded in stratum pyramidale) and interneurons lagging ∼1–2 ms (Sullivan et al., 2011). Of the oscillatory events that met our SPW-R detection criteria (Materials and Methods), 26 had dominant frequencies between 140 and 160 Hz. Averaging the wideband signal during these events (Fig. 6A) showed that, overall, they indeed occurred during negative deflections in the stratum radiatum LFP, reflecting excitatory “sharp wave” input from CA3 (Ylinen et al., 1995). The oscillatory characteristics of this input were highly variable, however, in contrast to the consistent perisomatic ripple. Applying a bandpass filter from 50 to 5000 Hz before averaging removed the slower SPW LFP deflection and revealed weaker ripple-frequency oscillations in stratum radiatum with the opposite phase of the stratum pyramidale potentials (Fig. 6B), reflecting what are most likely passive return currents in the dendrites from a perisomatic drive. We simulated similar depth profiles for rhythmic population firing at the same frequencies as these 26 in vivo ripples, then applied the same filter and averaged the resulting potentials (Fig. 6D). The amplitude and phase profiles of the simulated averages were very similar to those of the in vivo recordings (Fig. 6B), and individual in silico voltage traces were characteristically similar to the in vivo ripples (Fig. 6C). More quantitative comparisons of these AP-generated potentials to both in vivo recordings and simulations of synaptically generated LFPs are described below (see Fig. 10).

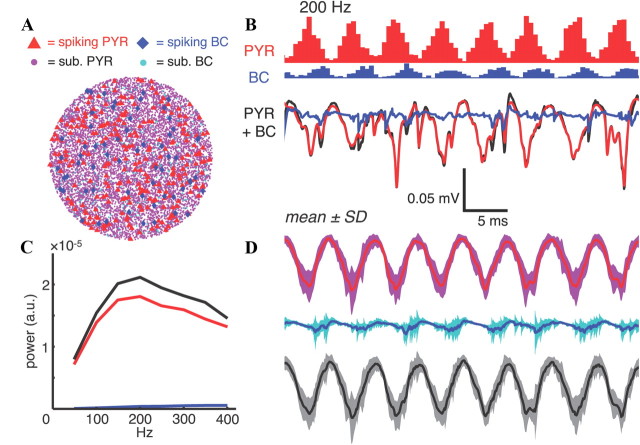
Figure 6.

Simulated AP-generated ripples are characteristically similar to in vivo ripples. A, Ripple-triggered average of wideband in vivo depth recordings (100 μm electrode spacing) during 26 SPW-Rs with a dominant frequency between 140 and 160 Hz. Note the large variability in the SPW field potentials in the apical dendritic region, consistent with the ripple oscillation being generated locally, rather than driven by a coherent CA3 oscillation (Csicsvari et al., 2000). B, Fifty to 5000 Hz bandpass filter applied before averaging the ripple events in A. The ripple is strongest in the pyramidal layer (Ylinen et al., 1995), with a phase reversal 150–200 μm below (in stratum radiatum). The dashed vertical lines are visual aids for phase alignment. C, Comparison of single representative stratum pyramidale voltage traces for simulated ripples consisting only of EAPs from a pyramidal cell population in which 5% (blue), 7.5% (green), or 10% (red) of the cells fire each 10 ms (spike histograms shown above voltage traces) and filtered in vivo ripple events (black). The firing probabilities are modulated by the same probability function as in Figures 2 and 4. D, The 26 trial average of simulated EAP-generated ripples with frequencies set to the dominant frequencies measured during the in vivo ripple events of A and B.

Interneuron AP contributions to field potentials

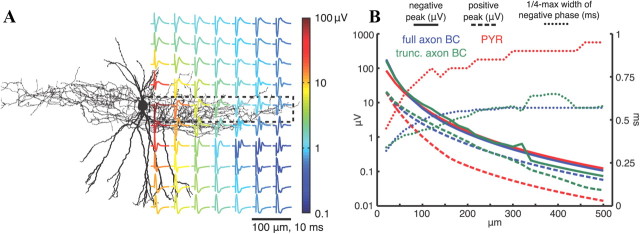
Some interneuron types, specifically basket and bistratified cells (Klausberger et al., 2003, 2004), substantially increase their firing during SPW-Rs, with spike times modulated by the ripple. While these cells make up <5% of the cell population in CA1 (Olbrich and Braak, 1985; Aika et al., 1994; Freund and Buzsáki, 1996), their average firing rates during SPW-Rs can be three to four times greater (Csicsvari et al., 1999a, 2000). To estimate the contribution of their EAPs to SPW-Rs and other fast oscillations, we used the dentate gyrus basket cell model of Nörenberg et al. (2010) and Hu et al. (2010). While the model was not specifically tuned to reproduce basket cell EAPs, the qualitative features of the EAP shape and amplitude (Fig. 7A) are similar to those reported by Henze et al. (2000) for a CA1 basket cell that was 50–100 μm from two neighboring shanks of a multielectrode array. Their EAP amplitude is similar to pyramidal cell EAPs, but the basket cell EAPs were significantly narrower (Fig. 7B), consistent with experimental observations (Barthó et al., 2004). A previous modeling study saw little effect of axon fibers beyond the initial segment on EAPs (Gold et al., 2006), but that was for pyramidal cells with myelinated axons that project out of the local region. The situation could plausibly be different with a dense arbor of unmyelinated axon fibers and terminals, as with local interneurons. However, we saw only minor effects on the average EAP profile (Fig. 7B) for basket cells with and without an extensive, active axon (see Materials and Methods).

Figure 7.

Spatiotemporal characteristics of basket cell EAPs. A, Location dependence of EAPs for the single basket cell model with peak-to-peak voltage range indicated by the color of each trace. As in Figure 1, subthreshold currents have been removed, and each trace is an average over 25 points at a fixed radius around the vertical dendritic axis. B, EAP amplitude and width versus distance for the cell models: blue, pyramidal cell (PYR); purple, basket cell (BC); orange, basket cell with axon truncated at 68 μm. The amplitude of the negative (solid lines) and positive (dashed lines) peaks correspond to the left axis, and the width of the negative phase (dotted lines) corresponds to the right axis.

We simulated V_e signatures of spiking in a combined population of 471 basket cells and 9416 pyramidal cells. The basket cell somata were positioned in a disk of the same radius as the pyramidal cells (0.5 mm), but approximately twice as thick (100 μm); this population was intended to account for both the basket and bistratified cells that are active during SPW-Rs. We allowed 40% of the basket cells and 8% of the pyramidal cells to fire each 10 ms. With the number of basket cells being 5% of the number of pyramidal cells, but five times more active, the total number of basket cell APs was one-quarter the total number of pyramidal cell APs. These values are similar to the activity levels reported in Csicsvari et al. (1999a, 2000) during SPW-Rs, although they actually overestimate the proportion of spikes estimated to originate from basket cells. Spike times in both populations were again clustered in population bursts with σ = 0.2/f (Csicsvari et al., 1999a), and the preferred spike phase for basket cells was delayed by 90° from pyramidal cell firing (Sullivan et al., 2011). The lower numbers of basket cell spikes and their narrower width resulted in a substantially smaller contribution to the combined population potentials than the pyramidal cell spikes. Figure 8, B and D, shows the case of a 200 Hz rhythm, and the results for 50–400 Hz are summarized in Figure 8C. The average power over 25 trials at the oscillation frequency of the extracellular potentials generated by spiking basket cells was <5%, even at 400 Hz. The more visible increases in power when this was added to the pyramid AP-generated potentials (Fig. 8C) are due to the (V_e^PYR× V_e^BC) product term contributing to the power measure when the (V_e^PYR + V_e^BC) signal amplitude was squared.

Figure 8.

Basket cell EAPs contributed little to simulated ripple LFPs. A, Locations of pyramidal cell (PYR) and basket cell (BC) somata within stratum pyramidale in a 1-mm-diameter simulated population. The small circles represent subthreshold cells, and the larger triangles and diamonds represent cells spiking within one 5 ms period. B, Spiking histograms and extracellular potentials from populations of pyramidal cells (red) and basket cells (blue) during 200 Hz rhythmic spiking with all synaptic driving currents removed, as well as the extracellular potential when both signals are combined (black). Here, basket cells are less numerous (5% of pyramids) but have five times higher average firing rates than pyramidal cells. Peak basket cell firing lags that of pyramidal cells by 90° (1.25 ms at 200 Hz) (Sullivan et al., 2011). C, Spectral peaks of 25-trial-average FFTs of stratum pyramidale potentials from the separate (color) and combined (black) populations during rhythms from 50 to 400 Hz. D, Mean ± SD for the potentials in B over 25 trials.

Consistent with their small effect on average single cell EAPs, axons in the basket cell population contributed little to the LFP oscillation. For the 200 Hz oscillations in Figure 7, the root-mean-square error of the pyramidal layer V_e with the truncated axon (compared with the population with the full axon) was 2.7 μV, resulting in an average power at 200 Hz that was ∼8% less for the population with truncated axons.

Synaptic currents during fast oscillations

In the AP-generated extracellular potentials described above, the increase in power with increasing frequency (up to ∼150 Hz) is due to the narrow EAPs overlapping more as the faster rhythms more effectively synchronize spikes. This is in contrast to the behavior expected for signals generated by slower postsynaptic currents with similar temporal synchrony. The postsynaptic conductance change resulting from synapse activation has a quick rise, but its decay is much slower than an AP, with exponential decay time constants between 2 and 10 ms in hippocampal pyramidal cells (Hestrin et al., 1990; Jonas et al., 1993; Maccaferri et al., 2000). The slower this decay, the greater the attenuation of the high-frequency component of the total synaptic current.

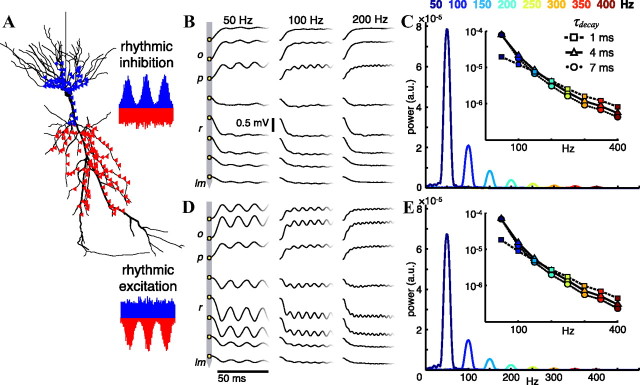
We explored the frequency dependence of V_e in a population receiving layer-specific oscillatory synaptic input (Fig. 9A). The initiation times for the rhythmically modulated synapses were determined by the same pdf as the APs in Figures 2, 4, 6, and 8. The potentials shown are for synapses with τ_decay of 4 ms (Materials and Methods), but similar results were obtained when τ_decay was varied from 1 to 7 ms (Fig. 9C,E, insets). In one scheme, constant excitation impinged on the apical Schaffer collateral dendritic region along with rhythmic inhibition at perisomatic basket and bistratified cell target domains (Sik et al., 1995; Megías et al., 2001) (Fig. 9B,C), similar to the input pattern thought to be important for rippling LFPs in CA1 during SPW-Rs (Buzsáki et al., 1992; Csicsvari et al., 2000). Next, the opposite pattern was used—rhythmic apical excitation and constant perisomatic inhibition (Fig. 9D,E), analogous to oscillating input from CA3 (or entorhinal cortex, although entorhinal input is even more distal) (Andersen et al., 2007) during tonic inhibition. The ability of such synaptic inputs to generate oscillatory signals at the rhythm frequency rapidly decreases as the oscillation frequency increases, which is illustrated qualitatively in Figure 9, B and D, and quantitatively in Figure 9, C and E. Also noteworthy are the differences in the depth profile of the oscillating signals between the two schemes shown. Apical excitation generated larger amplitude fluctuations in the extracellular potentials in the dendritic layers, with a distinct phase reversal just proximal to the somatic layer, similar to gamma frequency LFPs in CA1 following lesions to the entorhinal cortex (Bragin et al., 1995). In contrast, rhythmic perisomatic inhibition produced a relatively strong oscillation in the pyramidal layer potential, but extended weakly into the dendritic layers. There were two primary causes of this: (1) differences in the strength and geometry of the current dipoles produced by synaptic input distributed around the soma versus apical input, and (2) an inhibitory synapse reversal potential E_rev,inh that is closer to the subthreshold V_m than the excitatory E_rev,exc. When either (1) rhythmic excitation is instead placed perisomatically with constant inhibition in the apical dendrites, or (2) E_rev,inh is set to −130 mV (the same voltage difference from the −65 mV resting potential of the membrane as the 0 mV E_rev,exc), the dendritic layer V_e did start to oscillate, but both alternatives produced substantially weaker oscillations than the case of a strong apical rhythmic drive (data not shown).

Figure 9.

Simulation of extracellular potentials from synaptic input oscillations in a passive pyramidal cell population. A, 200 apical excitatory and 200 perisomatic inhibitory synapses are triggered each 50 ms, with the initiation times for one type (B, C, inhibitory; D, E, excitatory) modulated within a periodic Gaussian probability density function for f = 50–400 Hz in 50 Hz steps with SDs σ = 0.2/f, similar to the firing profiles in the rhythmically spiking population simulations. Synapses of the opposing type are activated with a constant probability. Both synapse types have τ_decay = 4 ms (see Materials and Methods). B, D, Example V_e traces for the 50, 100, and 200 Hz cases. C, E, Power spectra of stratum pyramidale V_e. Insets show the peak power values on a log scale for each oscillation frequency with τ_decay of the oscillating synapses varied from 1 to 7 ms.

Combining APs and IPSCs

Our neuronal population simulation methods allow us to explore the effects of the spatiotemporal distribution, reversal potentials, and kinetics of synaptic currents on extracellular potentials. Unfortunately, the large number of parameters and the lack of precise experimental validation of many of them make a reliable quantification of synaptic contributions to fast LFPs impractical. To perform more trustworthy quantitative comparisons between synaptically generated field potentials and both our simulated AP-generated potentials and in vivo recordings, we took advantage of measurements reported by Glickfeld et al. (2009) and Bazelot et al. (2010). They performed intracellular and extracellular recordings in hippocampal slices and characterized the extracellular uFields following individual inhibitory interneurons APs. These deflections in the extracellular potential presumably reflect the summed IPSCs elicited in the numerous neurons contacted by the axons of the interneurons. The uFields were visible over several hundred micrometers, but their amplitude decayed with distance, with amplitudes reduced by >50% at electrodes 250–300 μm from the site with the largest uField (Bazelot et al., 2010). We therefore constructed an interneuron population with the same parameters as before, but only included cells within 250 μm of the electrode, to estimate the combined field potentials when 30% of the population fired every 10 ms (Csicsvari et al., 2000). We added the average CA1 basket cell stratum pyramidale uField (Fig. 10A; 15.8 μV amplitude, linear rise with 1.2 ms 10–90% rise time, exponential decay with 6.6 ms time constant) (Glickfeld et al., 2009) to the total stratum pyramidale V_e at the time of each basket cell spike. Spike times were modulated by a periodic Gaussian pdf (σ = 0.2/f) at different frequencies f.

As in the simulations of compartmental models receiving synaptic input, the amplitude of the oscillatory component of the resulting LFP decreased with increasing frequency (Fig. 10B). In this case, however, there were fewer critical parameters to determine because we started with experimentally characterized basket cell uFields. We therefore used these simulations to estimate the contributions of both IPSCs and pyramidal cell AP currents to oscillations in the cumulative LFP and compared them to in vivo ripples. The amplitude and frequency of the V_e oscillation is not constant during SPW-Rs, however, in contrast with the more consistent simulated potentials generated by our simulations, so fixed time window FFT measurements of oscillation power would not produce a fair comparison. We instead measured instantaneous frequencies and amplitudes of individual waves within detected ripples (see Materials and Methods) and compared these with simulated ripples. With 10% of the pyramidal cell population firing and 30% of the basket cell population producing uFields each 10 ms (Csicsvari et al., 2000), the waveform characteristics, ripple amplitudes, and frequency–amplitude relationship of in vivo ripples with dominant frequencies between 140 and 160 Hz were very well reproduced by the combined AP-generated and IPSC-generated ripples (Fig. 10C,D). The contributions of the two components were similar over the 100–200 Hz frequency range, with APs remaining similarly powerful (Fig. 2), but IPSC-generated power decreasing with increasing frequency. In these simulations, the basket cell firing rhythm underlying the IPSC-generated ripples (i.e., the summed uFields) lagged the pyramidal cell rhythm by 90° (Sullivan et al., 2011). Experimental estimates of the average phase lag are between 60 and 100° for gamma, epsilon, and ripple oscillations in CA1 (Csicsvari et al., 2003; Sullivan et al., 2011). The combined ripple amplitudes were reduced by 10–13 and 40–47% for 0 and 180° phase lags, respectively, and the oscillation amplitude of each component of the simulated LFPs was proportional to the size of the active population (data not shown).

Discussion

Given the observed relationship between spike synchrony and oscillation frequency during hippocampal fast oscillations (Csicsvari et al., 1999b; Sullivan at al., 2011), the increase in oscillation power at frequencies >80 Hz is likely to involve more substantial contributions from local AP currents to the measured LFP signal. The details of our findings rest on accurate reproduction of the spatiotemporal profiles of AP membrane currents, for which the CA1 pyramidal cell model of Gold et al. (2006, 2007) was developed. The EAP amplitudes from our model (cell D151a) (Gold et al., 2007) are on the low end of the spectrum reported by Henze et al. (2000). Our population model may therefore underestimate stratum pyramidale signal amplitudes. Furthermore, the model of Gold et al. was not designed to accurately recreate slower Ca²⁺ spikes (Schiller et al., 1997; Kamondi et al., 1998), spike afterpotentials (afterhyperpolarization, or AHP, being the most prominent) (Gustafsson and Wigström, 1981; Storm, 1987, 1989), and intrinsic membrane oscillations (Leung and Yim, 1991; Leung and Yu, 1998), all of which may affect LFPs.

While our simulations indicate that APs in basket cells, even with their dense local constellation of axon terminals, contribute much less to slower components of the extracellular potential than pyramidal cells, further experimental dissection or more focused axon modeling are needed to demonstrate this more definitively.

Most of the simulations presented here have event timing modulated in an approximately sinusoidal fashion, resulting from the 0.2/f width of each Gaussian-shaped burst. The signal power contributed by AP currents depends on the relationship between synchrony and rhythm frequency (Fig. 3). We kept the σ = 0.2/f relationship for spike synchronization consistent across frequencies because of the high degree of phasic modulation of spikes within fast hippocampal oscillations (Csicsvari et al., 1999a,b, 2000; Sullivan et al., 2011; but see Colgin et al., 2009). The neuronal networks of the brain do often display an excitation–frequency–synchrony relationship in which stronger excitatory driving force leads to faster oscillations (Whittington et al., 1995; Csicsvari et al., 1999b; Sullivan et al., 2011), with inhibition being effective at gating spike times (Whittington et al., 1995; Hasenstaub et al., 2005; Cardin et al., 2009).

The 100–200 Hz oscillations in the hippocampus during SWS exhibit a high degree of phase coherence across CA1 (Ylinen et al., 1995; Csicsvari et al., 2000; Sullivan et al., 2011), as required for AP currents to contribute a substantial portion of the LFP signal. If similar coherence characteristics of fast oscillations that occur during theta states are found, it could indicate that these network patterns share common mechanisms of generation, which would have implications for our understanding of how these oscillations may assume their hypothesized role in interregional coupling in the behaving animal (Colgin et al., 2009). More detailed analyses and perturbations of network activity throughout the hippocampal–entorhinal circuit during these brain states are still needed to better appreciate how these regions are interacting.

The contribution of fast spikes to slower LFP signals additionally relies upon a large number of active, synchronous neurons. Our firing rates and synchrony parameters were motivated by the estimates of Csicsvari et al. (1999a,b, 2000), which were based on units classified as putative pyramidal cells and interneurons, but how representative such units are of the CA1 neuron population remains an open question. While a significant fraction of CA1 pyramidal cells may be inactive during exploration, many of the “silent cells” are active during SWS (Thompson and Best, 1989).

We found that summed synaptic and AP currents are both capable of generating oscillatory extracellular potentials, and our results suggest that there is an opportunity for a transition from synaptic to spike-related currents as the dominant current generator of oscillatory potentials near 100–150 Hz. This is consistent with widespread experimental observations of a high correlation between spiking activity and power in LFP bands faster than 90 Hz, and with principal cell firing consistently centered on the oscillation trough in the cell body layer (Csicsvari et al., 1999a,b, 2000; Canolty et al., 2006; Le Van Quyen et al., 2008, 2010; Ray et al., 2008a,b; Colgin et al., 2009; Bragin et al., 2011; Jackson et al., 2011; Ray and Maunsell, 2011; Sullivan et al., 2011; Belluscio et al., 2012). A specific LFP pattern near this transition point is the SPW-R complex of the hippocampal CA1 region (Buzsáki et al., 1992). These events coincide with dramatic increases in excitation and synchrony within the pyramidal cell population, more so than the interneuron population (Csicsvari et al., 1999a), and our simulated AP-generated ripples reproduce several features of the SPW-R waveform and depth profile. A large AP component of ripple fields provides a parsimonious explanation of a number of observations reported in the investigations by Csicsvari et al. (1999a,b, 2000): (1) a much stronger correlation between ripple amplitude and pyramidal cell firing rates than interneuron firing rates (Csicsvari et al., 1999b); (2) the summed activity of CA1 pyramidal cells better predicted ripple features than interneuron and CA3 pyramidal cell activity (Csicsvari et al., 1999a, 2000); (3) the discharge probability curve of pyramidal cells matched the ripple power curve much more precisely than the discharge probabilities of the two classes of recorded interneurons (Csicsvari et al., 1999a); (4) ripple amplitude was correlated with the spatial coherence of pyramidal cell firing, but not with the spatial coherence of interneuron firing (Csicsvari et al., 2000); (5) oscillation amplitude was larger for higher frequencies (Csicsvari et al., 1999b).

These results do not resolve questions concerning the mechanisms of synchronization, however. Indeed, they are consistent with any mechanism that properly synchronizes pyramidal cell firing [e.g., rhythmic inhibition (Ylinen et al., 1995); recurrent excitation (Maier et al., 2011); electrical synapses (Draguhn et al., 1998); ephaptic coupling (Holt and Koch, 1999; Anastassiou et al., 2011)]. Optogenetic and pharmacogenetic manipulation of neuronal activity offers the possibility of testing these mechanisms and our hypotheses in vivo by selectively silencing either pyramidal cells or parvalbumin-expressing interneurons in CA1, though the network response to SPW input with either of these cell types inactivated is unknown. We have also not addressed the shape of the SPW-R envelope. It presumably reflects the SPW synaptic excitation, inhibitory synaptic currents, AP and AHP currents, active dendritic currents such as Ca²⁺ spikes, and passive return currents from all of these.

Network and field patterns at frequencies >80 Hz have been linked to several aspects of cognition, learning, memory, and cross-regional coupling (Chrobak and Buzsáki, 1996; Canolty et al., 2006; Colgin et al., 2009; Jacobs and Kahana, 2009; Carr et al., 2011). At the same time, several authors have noted the likelihood that filtered LFPs at these frequencies are “contaminated” by local spiking activity (Ray and Maunsell, 2011; Zanos et al., 2011), and our results indicate that much of the spiking component cannot be removed by subtraction of spikes from the nearby units (Zanos et al., 2011; Belluscio et al., 2012). Thus, it is worth highlighting ways to mitigate this ambiguity in the source of these signals. First, if AP currents dominate an oscillatory signal, the negative spikes created by strong inward Na⁺ currents at the soma during APs should appear at the troughs of the signal in the cell body layer. If perisomatic inhibition is the primary current generating the LFP, we might also expect cells receiving this inhibition to fire near the troughs (i.e., the inhibitory current minima). However, time delays between minimal inhibitory current and depolarization of the membrane past threshold may correspond to significant phase difference at high frequencies. Indeed, in the network model of Taxidis et al. (2012), pyramidal cell spikes during SPW-Rs occurred ∼90° after the trough of inhibitory synaptic current, and we have seen similar delays in preliminary simulations of synaptically driven SPW-Rs with the model of Gold et al. (2007). Second, depth recordings and current source density analyses (Nicholson and Freeman, 1975; Pettersen et al., 2006) can locate the signal source layers in laminated structures, and the depth profiles of synaptic currents and AP currents can differ substantially (Figs. 6, 9). Passive return currents during processes with concentrated active driving currents should cause a phase reversal somewhere along the somatodendritic axis; knowledge of the location and spread of synaptic contacts along this axis should provide clues about which processes are generating the field fluctuations. Third, phase synchrony of rhythmic spiking over several hundred micrometers within the somatic layer is important for the summation of AP currents from many distant cells to generate a smooth LFP oscillation waveform.

It may be that fast oscillations primarily reflect a highly excited network, with local inhibitory interneurons synchronizing themselves and effectively gating principal neuron firing within narrow time windows (Whittington et al., 1995; Hasenstaub et al., 2005). Complicating this picture, excitatory input from an afferent region undergoing fast oscillations may also generate such fast LFP signals, as well as push the local network into its own fast oscillation state. Simultaneous multisite recordings along the somatodendritic axis and within the cell body layers of several connected brain regions are therefore important for the dissection of network interactions during fast oscillations.