Abstract
The goal of this paper is to examine the evaluation of interfacial stresses using a standard, finite difference based, immersed boundary method (IMBM). This calculation is not trivial for two fundamental reasons. First, the immersed boundary is represented by a localized boundary force which is distributed to the underlying fluid grid by a discretized delta function. Second, this discretized delta function is used to impose a spatially averaged no-slip condition at the immersed boundary. These approximations can cause errors in interpolating stresses near the immersed boundary.
To identify suitable methods for evaluating stresses, we investigate three model flow problems at very low Reynolds numbers. We compare the results of the immersed boundary calculations to those achieved by the boundary element method (BEM). The stress on an immersed boundary may be calculated either by direct evaluation of the fluid stress (FS) tensor or, for the stress jump, by direct evaluation of the locally distributed boundary force (wall stress or WS). Our first model problem is Poiseuille channel flow. Using an analytical solution of the immersed boundary formulation in this simple case, we demonstrate that FS calculations should be evaluated at a distance of approximately one grid spacing inward from the immersed boundary. For a curved immersed boundary we present a procedure for selecting representative interfacial fluid stresses using the concepts from the Poiseuille flow test problem. For the final two model problems, steady state flow over a bump in a channel and unsteady peristaltic pumping, we present an ’exclusion filtering’ technique for accurately measuring stresses. Using this technique, these studies show that the immersed boundary method can provide reliable approximations to interfacial stresses.
Keywords: Immersed boundary, interfacial stress
1. Introduction
Fluid dynamical stresses are important in the regulation of many physiological phenomenon. For example, the growth of atheroscrolatic plaques in small veins occurs in the presence of a low and oscillatory wall shear stress (Ku et. al.) [17]. A second example is the function of epithelial cells, which line the pulmonary airways - here potentially damaging normal and shear stresses can arise in the reopening of airways during artificial ventilation of premature neonates (Gaver et. al. [13]). A characteristic feature of modeling these fluid-structure interaction problems is that the boundary motion is coupled to the motion of the fluid. A numerical method which is designed for handling these complex problems is the immersed boundary method [22, 23, 20]. The essence of the immersed boundary method (IMBM) is to represent boundaries by local forces in the Navier-Stokes equations, which are then solved computationally on a regular grid. This eliminates the need to re-grid after every time step for time dependent geometries, and it allows the exploitation of the superior performance of fluid solvers on regular grids. A critical feature of the IMBM is the use of an approximate Dirac delta function to communicate between the fluid domain and the immersed boundary. In the discretization of the governing equations, this discrete delta function spreads Lagrangian boundary forces onto an Eulerian fluid grid, and interpolates Eulerian fluid velocities onto the Lagrangian boundary.
The immersed boundary method has been used for decades to simulate intriguing and complex systems in biological fluid dynamics, spanning a wide range of Reynolds numbers (e.g. [1, 4, 7, 8, 9, 14, 24]. Throughout these works the immersed boundary method has successfully modeled the large-scale motion of the fluid and the elastic behavior of the solid, and in many cases, solutions have been validated against experimental, analytical and other computational results. However, with the exception of the brief excursion in Arthurs et. al. [1], the issue of how accurately the immersed boundary method can predict the stresses at elastic interfaces remains largely unexplored. The evaluation of interfacial stresses within the immersed boundary method is complicated by two factors: first the interface is represented by a smeared force; second, an immersed boundary imposes a spatially averaged no-slip boundary condition as discussed in detail in §4.2.
Our goal is to determine how to evaluate interfacial stresses accurately using the immersed boundary method. Our approach here is to compare interfacial stresses calculated using the immersed boundary method with results available from other techniques for a set of representative problems. In this paper, we limit ourselves to the investigation of low Reynolds number flows so that we can compare our results to those provided by a clearly independent technique – the Boundary Element Method (BEM), due to Ladyzhenskaya [18]. The boundary element method offers a ‘gold standard’ for calculating interfacial stresses, to compare with immersed boundary calculations, and has been applied to many different problems (for example, Pozrikidis [26]). The boundary element method proceeds by reducing the n-dimensional Stokes flow equations to a n – 1 dimensional boundary integral, in terms of boundary stresses and velocities; it is therefore suited to interfacial stress evaluation. Furthermore, it is only necessary to discretize the solution domain boundary. However, the boundary element method assumes that the flow is inertia-free.
In §2 we describe the formulation of the immersed boundary method and the numerical implementation using a discrete delta function. In §3 we examine the stress balance on an immersed boundary; this shows two possible methods for stress evaluation - one method using flow-field information, and another using boundary information. In §4 we consider stress evaluation on a straight wall using Poiseuille flow as an example. This motivates our subsequent algorithm for stress evaluation on curved boundaries, as described in §5. In the next two sections, we compare the IMBM fluid stress for two low-Reynolds number test flows with zero-Reynolds number boundary element solutions. First, in §6, we compare the stresses for the steady-state flow over a bump in a channel; Gaver & Kute [12] have computed BEM solutions for this flow. Second, in §7, we compare the stresses for the peristaltic pumping of a fluid. These test problems do not illustrate the best or most efficient use of the immersed boundary method. However, these caricature problems do provide useful insight into stress evaluations at interfaces in non-zero Reynolds number, fluid-structure interaction simulations, where the positions of the immersed boundaries are not prescribed, but result from the coupled system.
2. The Immersed Boundary Method
2.1. A fluid-structure interaction problem
Consider the motion of an immersed elastic boundary X(s, t), which is parameterized by s over the range , through a viscous incompressible Newtonian fluid. Let the immersed boundary exert a force density per unit length f(s, t) on the fluid. The equations of motion governing the fluid-structure interaction are:
| (1) |
| (2) |
| (3) |
| (4) |
where u is the fluid velocity, x = (x, y) is a two-dimensional Cartesian coordinate system, ρ is the fluid density, p(x, t) is pressure, and μ is the fluid viscosity. Here, the force density F exerted by the immersed boundary on the fluid assumes the boundary is the source of a continuous distribution of Dirac delta point forces f(s, t)δ(x – X(s, t)). The incompressible Navier-Stokes equations (2-3) describe the response of the fluid to the force exerted by the immersed boundary and any imposed driving-force density FD. The no-slip condition is imposed by advecting the immersed boundary at the local Eulerian fluid velocity (4).
The force f may be due to elastic restoring forces, bending forces or other constitutive properties of the boundary. For the problems tackled herein, the ideal position of the boundary will be specified and may be time-dependent. In these examples we impose forces due to stiff ’tether’ springs that connect the immersed boundaries to prescribed spatial locations:
| (5) |
where X* (s, t) is the ideal location of the immersed boundary, and A is the spring constant. We choose this stiffness constant to be very large (A ≫ 1) so that the immersed boundary deviates little from the ideal position.
2.2. Numerical implementation: The Immersed Boundary Method
Here we present the standard finite difference implementation of an immersed boundary method, where the fluid domain is discretized by a uniform, rectangular periodic grid with fluid quantities such as pressure and velocity defined at grid points. We remark that there are many methodologies employing an immersed boundary framework, where the fluid equations are solved using a variety of treatments, including finite element methods [31] and grid free particle methods [6]. In the standard formulation, the immersed boundary is represented by a finite collection of discrete Lagrangian points , where the superscript n is the time step and the subscript k is the particle number. These immersed boundary points, in general, do not coincide with fluid grid points. Therefore we distribute the local boundary force to neighboring grid-points using a discrete approximation to the Dirac delta function. Herein, we use the discrete delta function as in Peskin [22]:
| (6) |
Note that the support of the spreading is proportional to the grid spacing h.
The algorithm for the numerical solution of this coupled system may be summarized as follows: at the beginning of the time step n, we have the fluid velocity field un and the locations of the immersed boundary points . In order to update these values:
calculate the elastic force using (5);
spread the elastic force to determine the force-density Fn using (1);
solve the Navier-Stokes equations (2-3) for the Eulerian flow field un+1 and pn+1;
interpolate using the Eulerian velocity field to each immersed boundary point, and advect each Lagrangian point using (4), to obtain .
For the solution of the Navier-Stokes equations in step (3), we use the projection method of Chorin [5] with periodic boundary conditions, which is second-order in space and first-order in time. Herein we use the modified divergence operator, which enhances volume conservation (Peskin & Printz [25]). Since the explicit IMBM algorithm is modular, another fluid solver with higher-order accuracy may be easily substituted; for example Bell et al [2], Lai & Peskin [19], or Griffith et al. [15]. Nevertheless, our goal here is to examine how accurately the IMBM can be used to calculate interfacial stresses at boundaries using a fluid-solver that was traditionally adopted by the immersed boundary community. We expect the results to only improve as the accuracy of the fluid solver increases.
The discrete delta function given above is used to communicate force information from the immersed boundary to the grid (step 2), and to interpolate the fluid velocity to the immersed boundary (step 4). In two-dimensions, the force density acting on an immersed boundary is distributed over 16 neighbouring grid points. Likewise, the fluid velocity at an immersed boundary point is interpolated from the same 16 grid points. The particular delta function used herein (6) was introduced by Peskin [22]; however, some higher-order discrete delta functions are given by Beyer & LeVeque [3]. As mentioned above, the spreading of the boundary force strongly influences the stress calculation near immersed boundaries. Below in §3 we identify two approaches for calculating these stresses. In §4 we use a simple model problem to illustrate the application of these techniques, and describe an algorithm for the accurate prediction of stresses on the boundaries.
3. Calculation of fluid dynamical stress
3.1. The interfacial stress balance
The tangential and normal stress balances on the immersed boundary have previously been derived by Peskin & Printz [25]; we extend their result to include the effect of a driving-force density. We integrate the governing equations using an arbitrary control volume Ω(t) surrounding the immersed boundary with outward normal n and arclength dl. If the driving force density is to reproduce the effect of an isotropic pressure we must restrict FD = ∇ · (αI), where α is a scalar quantity, i.e. we assume there is no deviatoric contribution as found in σ. Combining (1) into (2) and integrating over Ω(t) and applying the divergence theorem, we obtain
| (7) |
Now take the limit as the region Ω(t) collapses to form an infinitesimally thin strip surrounding the immersed boundary. It can be shown that
| (8) |
| (9) |
where t is the anti-clockwise tangential vector, σ = –pI + μ(∇u + (∇u)T) and [ ] denotes the jump in a quantity across the immersed boundary. The factor |∂X/∂s| accounts for the interfacial stretching.
Equations (8-9) motivate two fundamental methods for calculating the jump in stress across the immersed boundary. The left-hand-side involves evaluation of fluid velocity gradients and pressures at each side of the interface. The right-hand-side involves the evaluation of force densities on the interface. We term these methods of evaluation the fluid-stress (FS)-calculation and the wall-stress (WS)-calculation respectively.
3.1.1. Calculating fluid stress using wall stress f (WS)
Equations (8-9) demonstrate the wall stress is equivalent to the jump in fluid stress across the immersed boundary. We can evaluate the force density along the immersed boundary to directly calculate this jump in stress. In the special case where the fluid stress on one side is zero, the jump in wall stress is equivalent to the fluid stress on the other side.
3.1.2. Calculating fluid stress using stress tensor σ (FS)
Let XEk be the point where the fluid stress is evaluated for wall particle k, which may not coincide with the boundary point Xk. To calculate the fluid stress (FS) of wall particle k, we use the values of pressure and velocity available at grid locations surrounding the evaluation point XEk. We employ finite differences to calculate derivatives of velocities at these grid points with central differences used for x-derivatives (since boundaries in our examples will lie mostly in the x-direction), and one-sided differences for y-derivatives, because this uses information in the interior of the flow . We then interpolate the velocity gradients and pressures using bicubic interpolation [27] to obtain their values at the evaluation point XEk, from which we calculate the fluid stress tensor σ at XEk.
Because the immersed boundary method represents the immersed boundary as a mollified singular force distribution, the fluid stress calculated at the boundary (XEk = Xk) may be significantly affected by the nature of the discrete delta function. In the next section, through analytical and computational investigations, we examine the effect that representing a boundary by a locally spread force has on the evaluation of the fluid stress (FS).
4. Poiseuille flow: an example of stress evaluation on a straight boundary
In order to begin our investigation, we focus on the very simple problem of Poiseuille flow in a channel. Here we examine carefully the implications of the distributed boundary forces on determining the near-wall velocities and stresses. As such, we will study an analytical solution of the immersed boundary problem, with a continuous smoothed delta function layer of force at the wall, equivalent to that used in the numerical implementation (1-4). We will also compute the numerical solution to this problem using IMBM and compare the results. The analysis sheds light on the fundamental approximations used in the immersed boundary method, and their implications on flow-field behavior near the boundaries, and will motivate our stress-evaluation procedure.
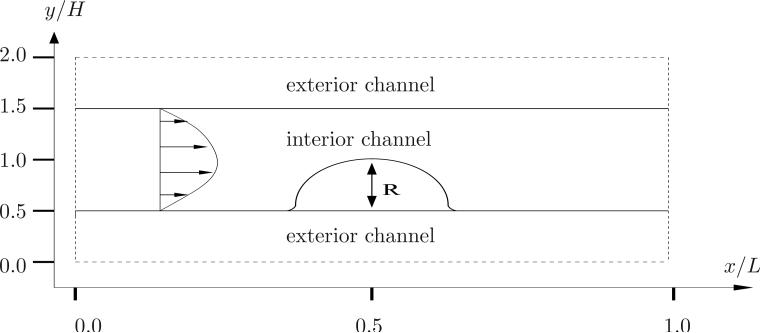
To simulate Poiseuille flow, we introduce two immersed boundaries parallel to the x-axis at y = H/2 and y = 3H/2 within the rectangular domain that is L × 2H, as shown by setting R = 0 in Figure 1. The immersed boundaries run the entire length L = 2H of the fluid domain. Herein, we refer to H/2 < y < 3H/2 as the interior (or inner) channel, and 0 ≤ y < H/2 and 3H/2 < y < 2H as the exterior channel. Periodic boundary conditions will be imposed on the fluid domain. Because of this, we do not impose a pressure drop ΔP, but we specify an equivalent body force to drive the flow. This driving-force density FD(x) = (ΔP/L, 0) is always applied within the interior channel. We examine two options for the driving-force density applied to the exterior channel: one-way flow where no driving-force is applied (FD = 0), or same-way flow where the same driving-force is applied throughout the fluid domain, both interior and exterior to the channel.
Figure 1.
A schematic of the computational domain (bounded by the dashed lines) used by the immersed boundary method, for computing the left-to-right pressure-driven viscous flow through a channel of length L and height H (solid lines). In §4, we study Poiseuille flow where R = 0, however in §6 , we assume R > 0.
4.1. Analytical solution of model problem
Although we will perform computations for both the same-way and one-way flows, our analytical model problem will be restricted to the case of same-way flow, where the driving force FD(x) = (ΔP/L, 0) is applied throughout the fluid domain.
In this model problem, we assume that a constant force density f, the immersed boundary force, is distributed in a layer surrounding the channel boundaries. Also, a spatially averaged no-slip boundary condition will be applied as in the immersed boundary computational algorithm. The force distribution and velocity interpolation will both use the approximation to the two-dimensional delta function (2.3), which has a support width of 2h in each coordinate direction.
We partition the velocity field u = (u(y), 0) into two regions: an interior flow ua(y) for H/2+2h ≤ y ≤ 3H/2–2h and a near-boundary flow ub(y) for 3H/2 – 2h < y ≤ 3H/2 + 2h. In this analytical model problem (as well as in our implementation of IMBM), we impose the periodic boundary condition u(y) = u(y + 2H), but due to the symmetry of this specific problem, we also have u(y) = u(y + H). The immersed boundary force (1), Navier-Stokes equations (2) and incompressibility condition (3), with FD = ΔP/L and dp/dx = 0, reduce to the system of ordinary differential equations:
| (10) |
We impose a symmetry condition dua/dy = 0 at the channel center y = H. Matching conditions between the interior and near-wall flows are also imposed such that ua(3H/2 – 2h) = ub(3H/2 – 2h) and dua/dy = dub/dy at y = 3H/2 – 2h. In addition, the spatially-averaged no-slip condition (4) is given by:
| (11) |
This analytical solution is the limit of the numerical solution under grid refinement with a fixed-width delta-function support of 2h in each direction. Solving (10,11) for ua(y), ub(y) and f while assuming H > 2h > 0 gives:
| (12) |
| (13) |
| (14) |
Observe that the force f exerted by the immersed boundary (14) in the analytical solution is identical to the stress jump across the interface predicted by Poiseuille flow, which can be found from a macroscopic momentum balance. Most interestingly, we note that f is independent of h so that reducing the physical width of the delta function (4h) does not change the WS.
The expression for the velocity at the center of the channel is given by
| (15) |
and the velocity at the edge of the channel is given by
| (16) |
These equations (15–16) demonstrate that for h → 0 the classical Poiseuille flow and a traditional point-wise no-slip boundary condition are recovered. However, for h ≠ 0 a slip velocity exists due to the no-slip condition being satisfied in only an average sense through (4).
We now have an analytical solution to the model problem that represents the IMBM formulation, and will examine the stress behaviour imposed near the wall from this solution.
4.2. Comparison of Analytical and Numerical solutions
In all examples below in this section and §6, we choose H = 0.1m; L = 0.8m; Δp/L = –105kg · m–2 · s–2; μ = 25kg · m–1 · s–1; ρ = 1kg · m–2.
The immersed boundary equations (1 - 4) were time-stepped from a motionless initial condition to a steady state for same-way flow using a 256 × 64 grid. The ideal locations of the immersed boundary walls are at y = H/2 and y = 3H/2 and extend the length of the computational domain. The stiff tether spring constant was chosen to be A = 109kg · m–3 · s–2 .
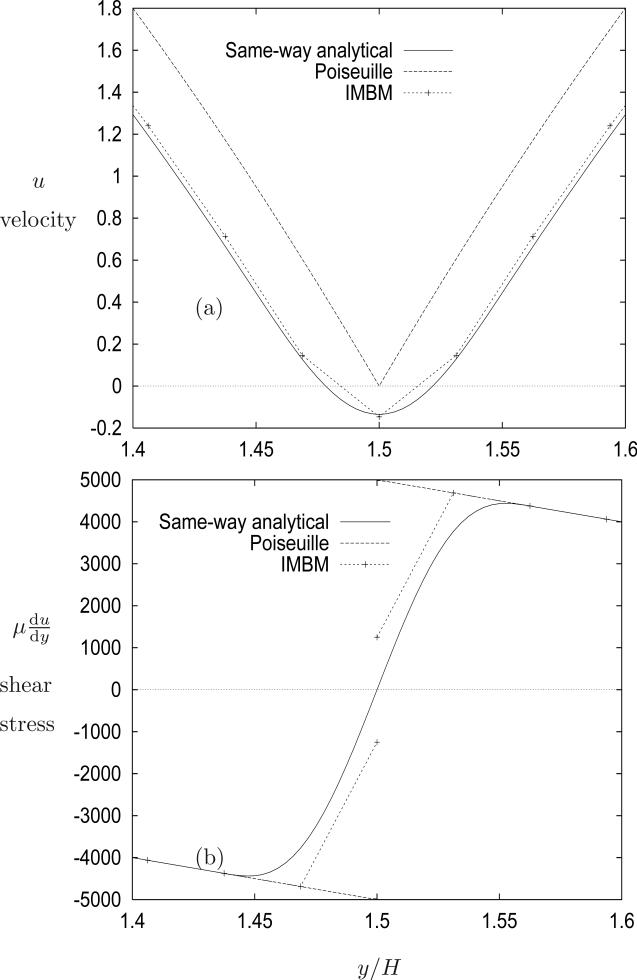
In Figure 2, we show the velocity and shear stress profiles obtained near the boundary at y = 3H/2. This figure shows data from classic Poiseuille flow, the analytical solution (12 – 13), as well as the computational solution. The IMBM solution approximates the analytical solution, where the velocity and jump in stress across the interface at y = 3H/2 are smoothed in comparison to the Poiseuille flow solution. Here we see the implication of the no-slip boundary condition being applied in an averaged sense using equation (4). This results in a reverse flow in the vicinity of the interface.
Figure 2.
The near-boundary u-velocity (m · s–1 ) and shear stress (kg · m–1 · s–2 ) profiles for the same-way flow. The analytical solution is compared with classical Poiseuille flow and the IMBM solution. The position of grid points in the immersed boundary solution is indicated. H = 1/10 and h = H/32.
The shear stress calculations are shown in Figure 2b. Classic Poiseuille flow shows a linear profile, with a discontinuity at the interface. The discontinuous behavior is smoothed by the force spreading that is imposed by the distributed delta-function used in the analytical model problem. At the interface the smoothed solution estimates a zero shear stress. Even if one uses a one-sided difference to compute the shear-stress at the wall using the analytical solution, the shear stress is which is independent of h. The correct shear stress for Poiseuille flow is τ = –5000 kg · m–1 · s–2 . This shows that even under grid refinement FS calculations taken precisely at the interface cannot accurately determine the stress. In Figure 2b, we see that the same-way analytical shear stress is much closer to the Poiseuille shear stress an O(h) away from the wall; i.e. at y/H=1.53125. This motivates our procedure for stress calculation in the IMBM computations given in the remainder of this paper.
In table 1 we show the shear stress computed with IMBM using fluid-stress (FS) and wall-stress (WS) algorithms for both the same-way and one-way flows at different grid resolutions. For the (FS) evaluations, one-sided differences are used to calculate velocity gradients at fluid grid points, where the stencil resides entirely within the interior channel. Interpolating these velocity gradients at the exact wall point locations XEk = Xk gives poor stress values as discussed above. Notice that with the same-way flow, grid-refinement does not improve the prediction of shear stress at the immersed boundary, and gives a value of τ = –1250 kg · m–1 · s–2 an approximation to the prediction of τ = –1013 kg · m–1 · s–2 above. Alternatively, we find that if we interpolate the velocity gradients and pressures at virtual points a distance h inward from the channel wall points XEk = Xk – hnk, the agreement to Poiseuille flow stress is vastly improved. Here nk is the unit normal pointing out of the interior channel. In comparison, Arthurs et al. [1] evaluated fluid stresses two grid points inwardly normal at XEk = Xk – 2hnk.
Table 1.
A comparison of shear stress (kg · m–1 · s–2 ) for one-way and same-way flows, calculated by the IMBM FS and WS using three different grid sizes.
| Grid points | Fluid shear stress t · σ · n | Wall stress f · t/|∂X/∂s | ||||
|---|---|---|---|---|---|---|
| X | X – nh | |||||
| Same-way | One-way | Same-way | One-way | Same-way | One-way | |
| Poiseuille | -5000 | -10000 | -5000 | |||
| 1024 × 256 | -1249.99 | -3110.34 | -4921.87 | -4921.86 | -10000.00 | -5039.06 |
| 512 × 128 | -1249.82 | -3095.69 | -4843.01 | -4843.74 | -10000.00 | -5078.13 |
| 256 × 64 | -1249.99 | -3066.40 | -4687.50 | -4687.49 | -10000.00 | -5156.25 |
The FS was calculated using backwards differencing. The analytical result (Poiseuille) is also given. The fluid shear stress (FS) is evaluated for both flows on the wall at X and one grid point inwardly normal at X – nh.
As described above, an alternative measure of the jump in stress at the immersed boundary interface is given by the wall stress (WS). Calculations involving (WS) rely solely upon the configuration of the Lagrangian immersed boundary and the force density defined on that boundary. There is no need to interpolate fluid quantities from the grid. An important observation is that this information only gives the jump in stress across the boundary. Table 1 shows the computed values for both the same-way and one-way flows, in comparison to the Poiseuille flow. The same-way flow exerts equivalent stresses on each side of the channel wall, and hence the jump in stress is twice that expected for Poiseuille flow. For one-way flow, a slight overestimate of the jump in wall stress occurs because the immersed boundary wall forces also drive a weak reverse flow in the exterior channel due to the averaged no-slip condition.
5. Evaluation of stresses on curved boundaries
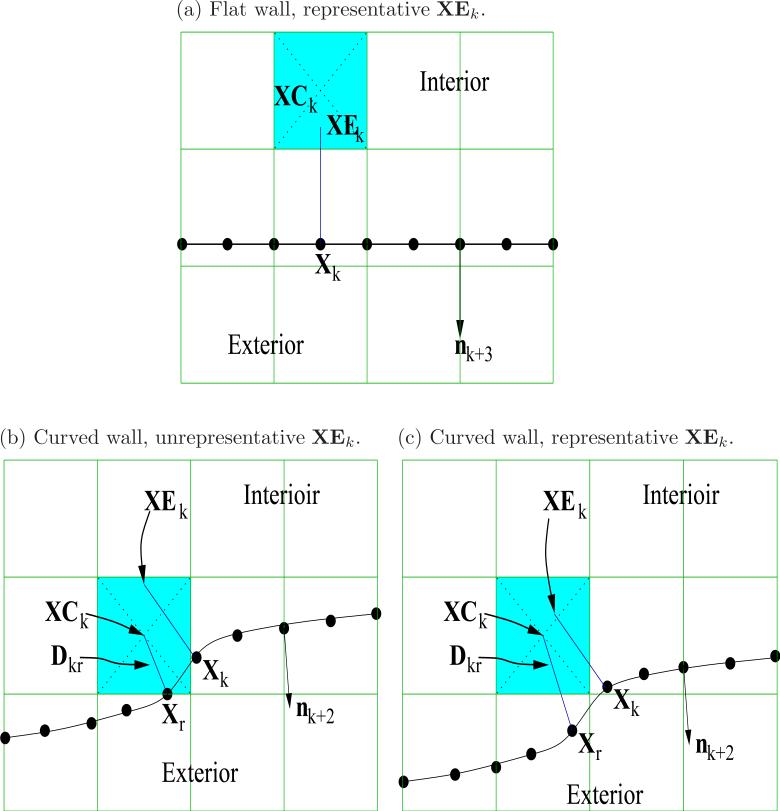
In the previous section we demonstrated that evaluating the fluid stress one fluid grid-point inwardly-normal from a straight wall, at XEk = Xk – hnk, produced a consistent and representative result. The stress was representative because the interpolation box (which defines the four fluid-grid stress-values used for interpolating) was not directly influenced by the flow on the opposite side of the boundary, as illustrated in Figure 3(a). For an arbitrarily curved immersed boundary, which can transect fluid cells, the four fluid-grid stress-values used for the interpolation may either be on different sides of the immersed boundary or be unrepresentative of the flow on the chosen side if they are too close to the immersed boundary. To elucidate this idea examine Figure 3(b,c).
Figure 3.
Illustration of three cases where interpolation one grid-point inwardly normal from the wall point k, for a two-dimensional problem, produces a stress representative of the interior fluid flow (a,c) and where the stress is unrepresentative (b). The shaded area is the interpolation box, which has center XCk, it contains the evaluation point XEk = Xk – hnk of wall particle k, where h is the fluid grid spacing and nk is the outward normal vector of the k’th particle. Dkr is the distance between the center of the interpolation box surrounding evaluation point XEk and nearest wall particle r (shown only in b and c).
In case (b) the interpolation box surrounding the evaluation point XEk overlaps the immersed boundary, hence one of the interpolation box grid points is in the exterior flow. Consequently the stress interpolation is significantly influenced by the exterior flow and therefore unrepresentative of the interior flow. Conversely for case (c) in Figure 3, the interpolation box resides entirely on one side of the boundary and sufficiently far from the immersed boundary that the stress evaluated at XEk will be almost entirely representative of the interior flow. Therefore to recover a stress which represent the physics of the interior flow, we must exclude the unrepresentative stresses. We undertake this ‘exclusion filtering’ for each wall particle based on the minimum distance between the center of the interpolation box XCk and the immersed boundary, this is given by
| (17) |
where Dkr is the distance between the center of the interpolation box for particle k and wall particle r on the same immersed boundary, as shown in Figure 3. num is the total number of particles in the immersed boundary. A sufficient condition for an interpolation box not to overlap an immersed boundary is √2h < M Dk ≤ 3h/2. Physically, M Dk is a measure of how much the interpolation box has been influenced by the force spreading. For M Dk close to 3h/2, the influence is minimized.
Our exclusion principle is based on three criteria for accepting interpolated results as physically representative of the interior flow:
if M Dk is at a local maximum, the interpolation box is locally at its furthest possible distance from the immersed boundary and therefore under the least influence from the locally distributed force;
if M Dk and M Dk+1 are identical for consecutive wall points, accept both values. This keeps all points which are on a straight line parallel with one of the orthogonal axis used by the fluid solver (x or y axis).
if the interpolation box has been used previously for the evaluation of an interfacial stress, we reject the stress. This keeps the resolution equivalent to the finite-difference fluid solver.
A comparison of representative and unrepresentative stresses is shown in §7 justifying the necessity of this exclusion filtering. In the next two sections we apply the above procedures to two test problems.
6. Flow over a bump on a channel wall
This test problem is the steady-state pressure-driven flow of a fluid of viscosity μ and density ρ through a channel with a bump on the lower wall (see Figure 1). Boundary element solutions were previously reported by Gaver & Kute [12], hereinafter referred to as GK. The exact bump geometry used by GK consists of a semi-circle, radius 9R/10, centered at (L/2, H/2 + R/10) with two quarter-circle fillets, each radius R/10, centered at (L/2 ± R, H/2 + R/10); to leading-order, the bump behaves like a semi-circle of radius R. The purpose of the fillets in their work was to ensure the domain had a continuous normal vector. They solved the zero Reynolds number Stokes equations
| (1) |
with no-slip and no-penetration conditions on the upper and lower (including the bump) walls u(x, y = ywall) = 0. A pressure drop was imposed across the ends of the channel by setting p(0, y) = ΔP and p(L, y) = 0.
Using the immersed boundary method, the channel walls (and bump), shown in Figure 1, are forced to behave rigidly by choosing A = 109kg · m–3 · s–2 and X* = (x, y = ywall). The immersed boundaries consist of three parts (two parallel walls and the bump with fillets, as shown in Figure 1). This combination of walls prevented the driving force-density (described above) acting inside the bump from generating a fluid flow in the exterior channel. Here we use the equivalent one-way forcing, as in §4, FD(x) = (FD, 0). There is negligible flow in the exterior channel and inside the bump at high resolution (512 × 128); therefore the jump in fluid stress is virtually identical to the wall stress. The channel length was set to be L = 0.8m. A Reynolds number based on the channel height and Poiseuille centerline velocity U = ΔpH2/8μL is Re = ρΔH3/8μ2L = 0.02. Therefore, inertial effects are small and the immersed boundary solutions may be compared with the Re = 0 BEM solutions found by GK. This was justified by repeating the calculation with a reduced Reynolds number. In our simulations the time step is chosen using Δt = 4ρh2/25μ s. Criteria governing the time step size in IMBM calculations are discussed in Stockie & Wetton [29]. Despite choosing very small time steps it was not possible to completely eliminate high-frequency small-scale instabilities in the wall behaviour. It was necessary to smooth the wall stresses in the post-processing stage using nearest neighbour averaging to remove this noise. We remark that in these test problems, rigid walls are modeled using very stiff tether springs and this, in turn, makes the problems numerically stiff. We expect that these small-scale instabilities will be less prevalent in simulations where the immersed boundary is elastic and flexible.
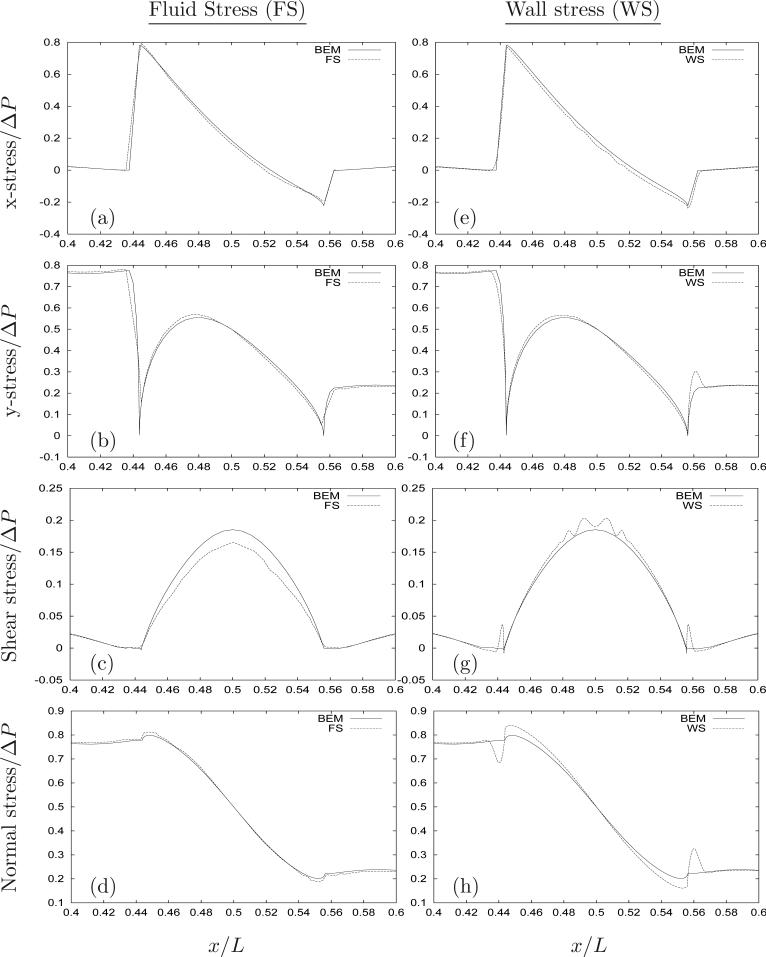
In Figure 4, for R/H = 1/2, we compare the immersed boundary FS (left column) and WS (right column) with boundary element results for the: x-stress (x̂ · σ · n); y-stress (ŷ · σ · n); shear stress (t · σ · n); and normal stress (n · σ · n). In general, there is good agreement between FS and BEM calculations for x- and y-stresses, and the shear stress. Away from the bump there is excellent agreement between the immersed boundary FS and WS, and the boundary element stress. WS calculations show local oscillations where the bump joins the wall at x = L/2 ± R as seen in Figures 4f-h. The relative magnitudes of these oscillations decreased by half when the flat section of immersed boundary between x = L/2 – R and x = L/2 + R was removed. However, this section of wall was necessary to prevent the one-way driving force density from creating a circulation inside the bump. Without this section, however, the entrained recirculation modifies WS throughout the bump by introducing a fluid stress inside the bump.
Figure 4.
Comparison of dimensionless fluid stresses on the lower channel wall for R/H = 1/2 and H/L = 1/8 computed using the immersed boundary fluid stress (FS) and the immersed boundary wall stress (WS). The solid line in each figure is the BEM solution. For the IMBM, a 512 × 128 grid with one-way flow was used, with the FS evaluated one grid-point inwardly normal from the wall at X – nh.
Close to the top of the bump, the WS in Figure 4g shows spatial oscillations. These oscillations occur where the fluid velocity has reached steady-state but the wall particles continue to diverge slightly from their steady-state displacements. This induces noise that may be due to a combination of numerical stiffness from large spring constants and explicit time-stepping of the wall-particle positions. This might be remedied by using a semi-implicit or fully-implicit implementation of the immersed boundary method, as described by: Tu & Peskin [30], Fauci & Fogelson [10], Stockie & Wetton [29], and more recently by Newren et al. [21].
An additional explanation of the oscillations in the WS computation of stresses may come from the following observation. Suppose we can write the immersed boundary force f(s, t) = f0(s, t) + f1(s, t) where f0(s, t) is the physically realistic component and f1(s, t) is an unsteady perturbation (not necessarily small). Then,
| (2) |
Any unsteady perturbation f1(s, t) which satisfies the constraint
| (3) |
will also give rise to the spread force field. Functions f1 that are highly oscillatory (with period less than 2h) may be found that satisfy this constraint. The lack of uniqueness in f shows that computing stresses using the WS technique should first filter out these unphysical, oscillatory forces. This will be the focus of future analysis. Nevertheless, as Figure 4 shows, the general behavior of WS is in good agreement with FS and BEM calculations.
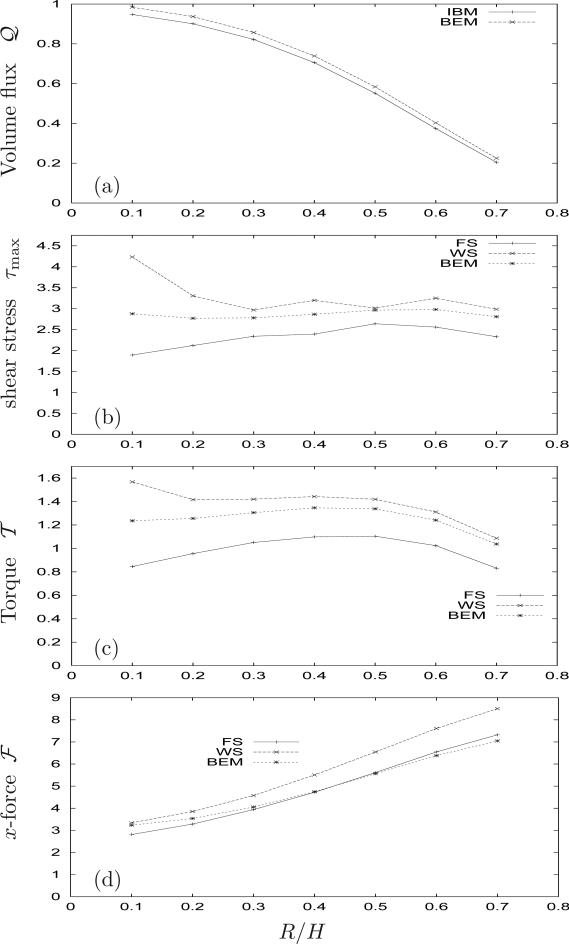
Above, we have identified the small-scale behavior of this system. We now assess the large-scale responses induced by the flow. We examine the non-dimensional fluid-exerted x-component of force and fluid-exerted torque on the bump, and volume flux and maximum shear stress, defined by GK, respectively as
where Γ(x(s), y(s)) is the immersed boundary and Max returns the maximum value.
In table 3, the evaluation of x-force , torque and maximum shear stress τmax on the bump using FS and WS is compared, under grid refinement, with BEM results. This table shows that in all cases WS > BEM > FS calculations. Note that in all cases the maximum WS predictions for maximum shear stress occurred at the top of the bump. The shear stress at the wall predicted by WS exceeds that predicted by FS and BEM because WS represents the jump in shear stress. A small retrograde recirculation appears within the bump due to the spread force, which induces the increase in WS. The volume flux using IMBM is also lower than expected, which correlates with the reduction in FS. This reduced arises because the spreading of the immersed boundary forces ‘thickens’ the boundaries and actually simulates a narrower channel.
In Figure 5 we assess the accuracy of the IMBM predictions of volume flux, maximum shear stress, torque and x-force in comparison to the BEM over a range of R/H. Figure 5a shows that the IMBM volume flux is always smaller than the BEM value. Figures 5(b-d) show that, in general the WS estimate is always greater than the FS estimate, while for the maximum shear stress and torque we again find the boundary element result is intermediate.
Figure 5.
Comparisons of four quantities: x-force, torque, maximum shear stress and volume flux using the IMBM and BEM, in non-dimensional units. For (b-d) the IMBM has two results obtained by using the fluid stresses (FS) and the wall stress (WS). The calculations were performed on a 512 × 128 grid with H/L = 1/8. The fluid stress was evaluated one grid-point inwardly normal from the wall at X – nh.
7. Peristaltic pumping flow
The last test problem is the peristaltic pumping of a viscous fluid by two moving walls. Solutions using the immersed boundary method were previously presented by Fauci [9]. However, fluid dynamical stresses on the moving walls were not calculated. Here we compare the fluid dynamical stresses calculated by the immersed boundary method with those computed by the boundary element method. The boundary element formulation makes use of the fact that for a symmetric peristaltic channel, a steady-state formulation may be obtained by moving to the wave frame of reference. The immersed boundary solutions were computed by prescribing the motion of the top and bottom walls using
| (7.1a) |
| (7.1b) |
where the wave amplitude is Φ; wavelength λ; and wave speed c = ωλ/2π. Here we do not impose a driving-pressure gradient so FD = 0. Again we use stiff ’tether’ springs to prescribe the motion of the immersed boundary channel walls. Now, the positions of the ideal points which the immersed boundary points are tethered to are functions of time as in Equation (5).
We choose the same parameters used by Fauci [9]: spring constant A = 104 kg · m–3 · s–2 ; kinematic viscosity μ = 0.01 kg · m–1 · s–1 ; mean channel width H/2 = 0.1 m; channel length L = 0.2 m; wave speed c = 0.08 m · s–1; wave amplitude Φ = 0.008 m; and wavelength of peristaltic wave λ = L. A Reynolds number (defined in Shapiroet al. [28]) for this flow is given by Re = cH2/4νλ = 1.0. To ensure that Reynolds-number effects were sufficiently small the calculations were repeated with Re = 0.5. The results presented in this section were computed on a 256 × 256 grid with time step Δt = 0.16Δx2.
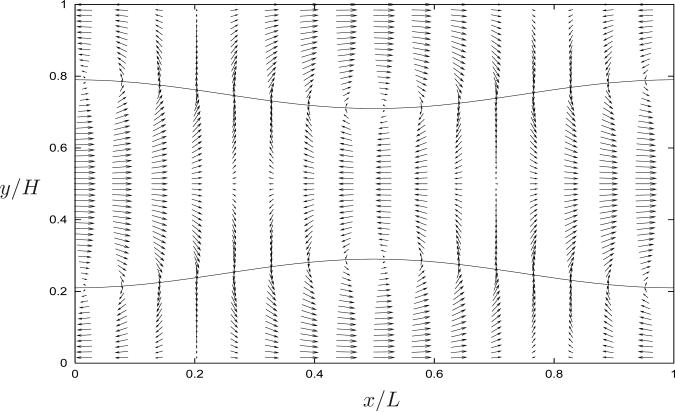
Unlike the prior test problems, the boundary drives the motion and there are comparable strength fluid flows on both sides, as illustrated in Figure 6. Because the flow is periodic in all directions, peristaltic pumping occurs in both the interior and exterior. Finally, because the amplitude of the boundary wave is small, we shall only compare the shear and normal stresses, the x- and y-stresses are respectively very similar.
Figure 6.
A velocity vector field, in the laboratory frame of reference, of a peristaltic pumping flow generated using the IMBM at t = 7.5s, after two complete cycles. The computational domain is periodic in both orthogonal directions.
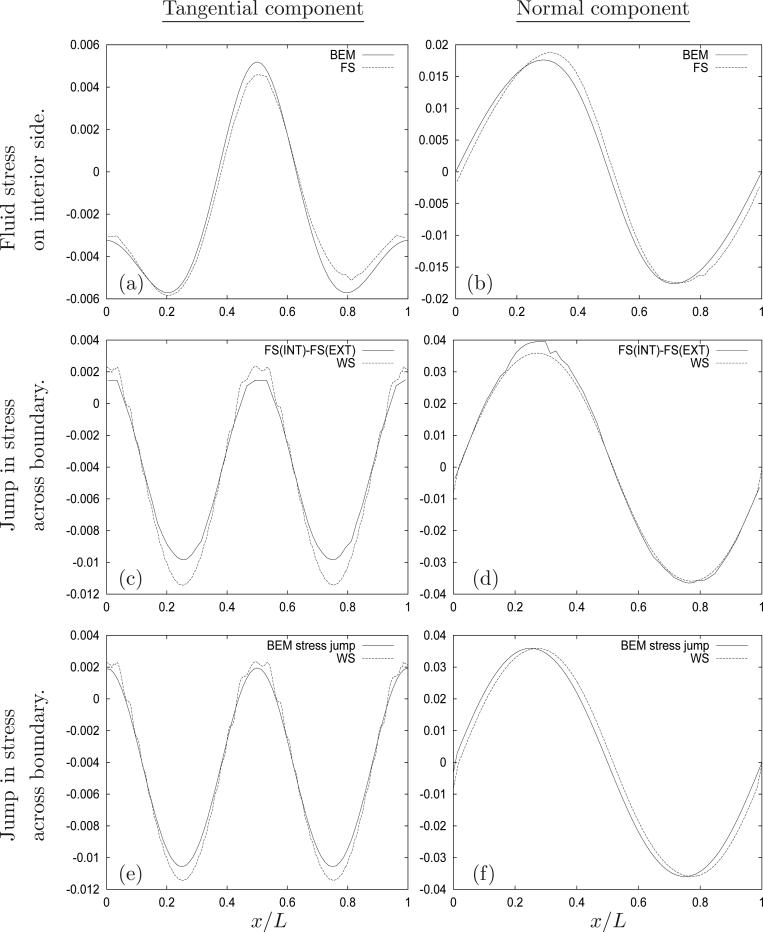
In Figure 7a,b the tangential and normal fluid stresses (FS) for the interior side of the bottom wall are shown to be in good agreement with the BEM predictions. In Figure 7c,d the jump in FS across the immersed boundary is compared to WS (this is a consistency check of 8-9). Figure 7e demonstrates that the WS overestimates the BEM prediction of the jump in shear stress across the interface. This overestimation was also observed in the problems studied in §4 and §6. Figure 7f compares the WS and BEM predictions of the normal stress jump.
Figure 7.
A comparison for each of the two orthogonol components of stress (kg · m–1 · s–2 ) calculated using the IBM at t = 7.5s (after two complete cycles) with results from the BEM on the lower boundary. In (a,b) the fluid stress evaluated on the interior side of the immersed boundary is compared with the BEM prediction. In (c,d) the IMBM prediction of fluid stress jump across the wall is compared with the WS prediction. In (e,f) the BEM prediction of the fluid stress jump is compared with the WS. The IMBM results were computed using a 256 × 256 grid.
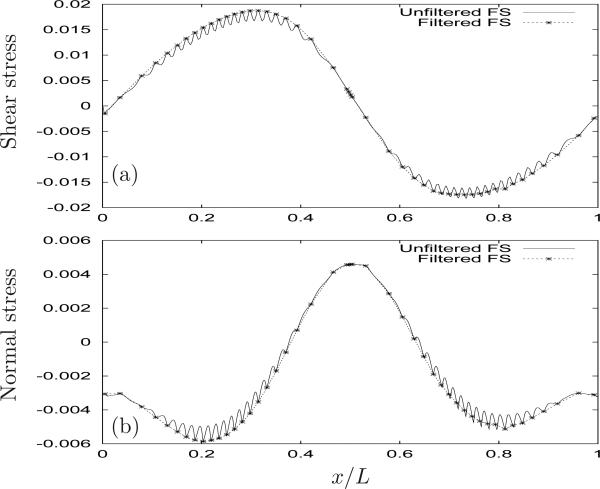
Figure 8 illustrates the effect of exclusion-filtering. The normal stress (a) and shear stress (b) on the top side of the bottom wall are shown for all wall points (unfiltered) and for the filtered points. In both cases exclusion-filtering retains the dominant features of the stress but discards the high frequency oscillations. The wavelength of the oscillations was observed to be proportional to the fluid grid size.
Figure 8.
For the peristaltic flow fluid stresses (kg · m–1 · s–2 ), FS calculation, shown in figure 7, we demonstrate the effect of exclusion filtering.
8. Discussion
While the evaluation of interfacial stresses in immersed boundary calculations is conceptually simple, we have demonstrated that good results are not achieved by direct interpolation of the fluid stress tensor to immersed boundary locations. This is because:
the point forces that represent the immersed boundary are distributed to the underlying fluid solver grid, which ‘smears’ the representation of the wall, and modifies the flow-field that is local to the wall;
the immersed boundary velocity is calculated using the discretized delta function to perform a weighted average of the local flow field in the vicinity of the wall.
To investigate the importance of these two effects, we first examined simple Poiseuille channel flow. We demonstrate with both analytical and numerical solutions of the immersed boundary formulation that with only internal driving forces, the discretized delta function induces a weak external flow. In addition, the weighted-average velocity near the wall satisfies the no-slip condition, while the velocity precisely at the wall location only satisfies the classical no-slip condition as the fluid grid spacing becomes infinitesimal. We furthermore show that the discrete delta function causes the jump in the shear stress across the boundary to be smoothed. Using the results of this model problem, we demonstrate that accurate predictions of the stresses at the boundary can be calculated using the fluid stress tensor (FS) information approximately one grid point inward of the boundary to negate the smoothing of the stress-field near the boundary. Furthermore, if the external stress field is insignificant, then the wall stress (WS) information can be derived simply from forces imposed by the wall.
To identify appropriate protocols for calculating stresses on more complex problems, we examined two additional test problems with curved boundaries - channel flow over an immersed semi-circular bump, and peristaltic pumping. Here we calculated the interfacial stresses using the immersed boundary method and compared the results to those from the boundary element method. While the WS technique was the simplest method for finding stresses, it can only be used when external flows were insignificant, since it provides the ’jump’ in stress across the boundary, and does exhibit unphysical oscillations. Future work will address the filtering out of small scale forces that are unresolved at the scale of the discretized delta function, as discussed previously in §6.
We confirmed that the calculation of interfacial stress by direct evaluation of the fluid stress tensor (FS) one grid point inward of the boundary produces good results. However, post-processing is necessary for this procedure. First, an exclusion filter is implemented to decide which immersed boundary points yield a representative stress. Then for these representative immersed boundary particles, the stress tensor is calculated one grid point inwardly normal using bicubic interpolation, as described in §3.
In conclusion, we have demonstrated by use of these simple test problems that interfacial stresses may be evaluated as part of an immersed boundary simulation. We hope that these test problems provide insight, and a good starting point, towards a complete robust methodology for computing interfacial stresses in fully 3D immersed boundary simulations that capture fluid-structure interactions. This will be of vital importance in the modeling and understanding of physiological systems, where the spatial distributions of stresses are central to the system's response.
Table 2.
For steady-state flow over a bump with R/H = 1/2, we compare FS and WS calculations of the x-force, torque and maximum shear stress under grid refinement with BEM predictions (all in non-dimensional variables). Also shown is the volume flux in comparison to the BEM prediction. In the FS calculations the stress tensor is evaluated at X – nh.
| Grid points | Max Shear stress (τmax) | ||||||
|---|---|---|---|---|---|---|---|
| FS | WS | FS | WS | FS | WS | ||
| BEM | 5.563 | 1.338 | 0.584 | 2.964 | |||
| 512 × 128 | 5.617 | 6.546 | 1.045 | 1.419 | 0.554 | 2.639 | 3.013 |
| 256 × 64 | 5.722 | 6.653 | 0.993 | 1.519 | 0.523 | 2.376 | 3.192 |
| 128 × 32 | 5.817 | 6.877 | 0.801 | 1.723 | 0.458 | 1.951 | 3.819 |
Acknowledgments
The authors would like to thank Dr. Ricardo Cortez for fruitful discussions. A portion of this work was performed when H.A.R. Williams was a postdoctoral researcher at Tulane University.
Contributor Information
Harvey A. R. Williams, Perforating Research Schlumberger, 14910 Airline Road, Rosharon, TX 77583, USA
Lisa J. Fauci, Department of Mathematics Tulane University, New Orleans, LA 70118, USA fauci@tulane.edu
Donald P. Gaver, III, Department of Biomedical Engineering Tulane University, New Orleans, LA 70118, USA.
REFERENCES
- 1.Arthurs KM, Moore LC, Peskin CS, Pitman EB, Layton HE. Modeling arteriolar flow and mass transport using the immersed boundary method. J. Comp. Phys. 1998;147:402–440. [Google Scholar]
- 2.Bell JB, Colella P, Glatz HM. A second-order projection method for the incompressible Navier-Stokes equations. J. Comp. Phys. 1989;85:257–283. [Google Scholar]
- 3.Beyer RP, LeVeque RJ. Analysis of a one-dimensional model for the immersed boundary method. SIAM J. Numer. Anal. 1992;29:332–364. [Google Scholar]
- 4.Bottino DC. Modeling viscoelastic networks and cell deformation in the context of the immersed boundary method. J. Comp. Phys. 1998;147:86–113. [Google Scholar]
- 5.Chorin AJ. Numerical solution of the Navier-Stokes equations. Math. Comp. 1968;22:745–762. [Google Scholar]
- 6.Cortez R, Fauci L, Medovikov A. The method of regularized stokeslets in three dimensions: analysis, validation, and application to helical swimming. Phys. Fluids. 2005;17:031504. [Google Scholar]
- 7.Dillon R, Fauci L, Fogelson A, Gaver DP. Modeling biofilm processes using the immersed boundary method. J. Comp. Phys. 1996;129:57–73. [Google Scholar]
- 8.Eggleton CD, Popel AS. Large deformation of red blood cell ghosts in a simple shear flow. Phys. Fluids. 1998;10:1834–1845. doi: 10.1063/1.869703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fauci L. Peristaltic pumping of solid particles. Computers and Fluids. 1992;21:583–598. [Google Scholar]
- 10.Fauci L, Fogelson A. Truncated newton methods and the modeling of complex immersed elastic structures. Comm. Pure Appl. Math. 1993;46:787–818. [Google Scholar]
- 11.Fogelson A. A mathematical model and numerical method for studying platelet adhesion and aggregation during blood clotting. J. Comp. Phys. 1984;56:111–134. [Google Scholar]
- 12.Gaver DP, Kute SM. A theoretical model study of the influence of fluid stresses on a cell adhering to a microchannel wall. Biophys. J. 1998;75:721–733. doi: 10.1016/S0006-3495(98)77562-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gaver DP, Halpern D, Jensen OE, Grotberg JB. The steady motion of a semi-infinite bubble through a flexible-walled channel. J. Fluid Mech. 1996;319:25–65. [Google Scholar]
- 14.Goldstein D, Handler R, Sirovich L. Direct numerical simulation of turbulent flow over a modeled riblet covered surface. J. Fluid Mech. 1995;302:333–376. [Google Scholar]
- 15.Griffith BE, Hornung RD, McQueen DM, Peskin CS. An adaptive, formally second order accurate version of the immersed boundary method. J. Comp. Phys. 2007;223:10–49. [Google Scholar]
- 16.Haj-Hariri H, Shi Q. Thermocapillary motion of deformable drops at finite Reynolds and Marangoni numbers. Phys. Fluids. 1997;9:845–855. [Google Scholar]
- 17.Ku DN, Giddens DP, Zairns CK, Glagov S. Pulsatile flow and atherosclerosis in the human carotid bifurcation: positive correlation between plaque location and low and oscillating shear stress. Arteriosclerosis. 1985;5:293–302. doi: 10.1161/01.atv.5.3.293. [DOI] [PubMed] [Google Scholar]
- 18.Ladyzhenskaya OA. The mathematical theory of viscous incompressible flow. Gordon & Breach; New York: 1969. [Google Scholar]
- 19.Lai MC, Peskin CS. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. J. Comp. Phys. 2000;160:705–719. [Google Scholar]
- 20.Mittal R, Iaccarino G. Immersed boundary methods. Ann. Rev. Fluid Mech. 2005;37:239. [Google Scholar]
- 21.Newren EP, Fogelson AL, Guy RD, Kirby RM. Unconditionally stable discretizations of the immersed boundary equations. J. Comp. Phys. 2007;222:702–719. [Google Scholar]
- 22.Peskin CS. Numerical analysis of blood flow in the heart. J. Comp. Phys. 1977;25:220–252. [Google Scholar]
- 23.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479. [Google Scholar]
- 24.Peskin CS, McQueen DM. A three-dimensional computational method for blood-flow in the heart .1. Immersed elastic fibers in a viscous incompressible fluid. J. Comp. Phys. 1989;81:372–405. [Google Scholar]
- 25.Peskin CS, Printz BF. Improved volume conservation in the computation of flows with immersed elastic boundaries. J. Comp. Phys. 1993;105:33–46. [Google Scholar]
- 26.Pozrikidis C. Boundary Integral and Singularity Methods for Linearized Viscous Flows. Cambridge University Press; Cambridge: 1992. [Google Scholar]
- 27.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in Fortran - The Art of Scientific Computing. 2nd Edition Cambridge University Press; Cambridge: 1992. [Google Scholar]
- 28.Shapiro AH, Jaffrin MY, Weinberg SL. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969;37:799–825. [Google Scholar]
- 29.Stockie JM, Wetton BR. Analysis of stiffness in the immersed boundary method and implications for time-stepping schemes. J. Comp. Phys. 1999;154:41–64. [Google Scholar]
- 30.Tu C, Peskin CS. Stability and instability in the computation of flows with moving immersed boundaries: a comparison of three methods. SIAM J. Sci. Stat. Comp. 1992;13:1361–1376. [Google Scholar]
- 31.Zhang L, Gerstenberger A, Wang X, Liu WK. Immersed finite element method. Comp. Methods in Appl. Mech. and Engr. 2004;193:2051–2067. [Google Scholar]