Abstract
Studying the spatial pattern and interspecific associations of plant species may provide valuable insights into processes and mechanisms that maintain species coexistence. Point pattern analysis was used to analyze the spatial distribution patterns of twenty dominant tree species, their interspecific spatial associations and changes across life stages in a 20-ha permanent plot of seasonal tropical rainforest in Xishuangbanna, China, to test mechanisms maintaining species coexistence. Torus-translation tests were used to quantify positive or negative associations of the species to topographic habitats. The results showed: (1) fourteen of the twenty tree species were negatively (or positively) associated with one or two of the topographic variables, which evidences that the niche contributes to the spatial pattern of these species. (2) Most saplings of the study species showed a significantly clumped distribution at small scales (0–10 m) which was lost at larger scales (10–30 m). (3) The degree of spatial clumping deceases from saplings, to poles, to adults indicates that density-dependent mortality of the offspring is ubiquitous in species. (4) It is notable that a high number of positive small-scale interactions were found among the twenty species. For saplings, 42.6% of all combinations of species pairs showed positive associations at neighborhood scales up to five meters, but only 38.4% were negative. For poles and adults, positive associations at these distances still made up 45.5% and 29.5%, respectively. In conclusion, there is considerable evidence for the presence of positive interactions among the tree species, which suggests that species herd protection may occur in our plot. In addition, niche assembly and limited dispersal (likely) contribute to the spatial patterns of tree species in the tropical seasonal rain forest in Xishuangbanna, China.
Introduction
Numerous mechanisms have been proposed to explain coexistence of tree species in tropical forests on local scales [1]–[2]. One of the most prominent hypotheses is the Janzen–Connell hypothesis that states that distance- or density-dependent mortality due to predation or host-specific pests should promote less aggregated and more mingled spatial distributions of species [3]–[4]. Condit et al. [5] suggested that the role of density-dependence may only be important among those species with the highest population densities. Later research showed that density-dependence was very common in some tropical forests 6–8. An extension of the Janzen–Connell hypothesis, the species herd protection hypothesis, suggests that heterospecifc neighbors can promote coexistence by thwarting the transmission of biotic plant pests [7], [9]. According to the species-herd protection hypothesis, heterospecific crowding may be of general benefit for the survival of recently established seedlings because fewer encounters between a host and its species-specific pests and pathogens would occur [9]–[10].
The Janzen–Connell and the species herd protection hypotheses make specific predictions on the spatial placement of individuals of different species. First, the spatial pattern of individual species should become with progressing life stage less aggregated because high density clumps of a given species are more prone to predation or host-specific pests. A similar pattern is expected due to self thinning [11]. However, the mechanism of the herd protection hypothesis may additionally create or maintain positive spatial associations among species despite the expected effect of interspecific competition. Thus, we expect for progressing life stages that the species patterns should become less aggregated and the occurrence of positive associations among species should increase (or be maintained). One possibility to explore if observed spatial placement of trees is compatible with this hypothesis is to use techniques of spatial point pattern analysis [12]–[14].
The dipterocarp tropical seasonal rain forest is one the most important vegetation types in southwest China and harbors biodiversity that is important both for global and national species richness in China. The 20-ha Xishuangbanna forest dynamics plot was established in 2007 in this vegetation type to test theories and hypotheses related to biodiversity maintenance. For example, of special interest is to find evidence (direct or indirect) of Janzen-Connell effects (or species herd protection), niche assembly or dispersal limitation [8]. Here we focus on the Janzen-Connell and species herd protection hypotheses and conduct a detailed spatial point pattern analysis of the dominant tree species in this forest. Studying the factors that structure the spatial pattern and relationship of the dominant species is of interest because they determine to a large extend the light climate in the forest and play a major role in structuring the lower layers of the forest. Because of their large size, tree species are also expected to exert positive or negative interactions to other tree species or plants at lower layers. For example, it is believed that the emergent tree species Parashorea chinensis wang hsie at Xishuangbanna could facilitate the survival of other plants by building up a humid microenvironment favorable in the dry season [15]. However, Kohyama [16] demonstrated for a warm-temperate rainforest that one-sided competition for light (i.e., light is intercepted mainly by larger trees and smaller trees have limited access to light) plays a key role in spatial pattern formation of trees. Whether these species promote or hamper each other to reach the light in the top layer remains an open question.
In this paper we used point pattern analysis to analyze the spatial species distributions, interspecific species associations and their change across life stages among the twenty dominant species of the Xishuangbanna forest dynamics plot. Our specific objectives were to explore if Janzen-Connell effects or species herd protection are potential mechanisms for structuring the species patterns in our study site. To this end, we formulate two non exclusive guiding hypotheses: (1) the univariate spatial pattern of the twenty dominant species should become more regular with increasing life stage and (2) the bivariate (interspecific) spatial patterns of the twenty dominant species should show positive association at small scales and all life stages. Finding evidence for hypothesis (1) would suggest operation of Janzen-Connell effects while evidence for (2) would agree with the species herd protection hypothesis and generally facilitation among different species.
Methods
Study site
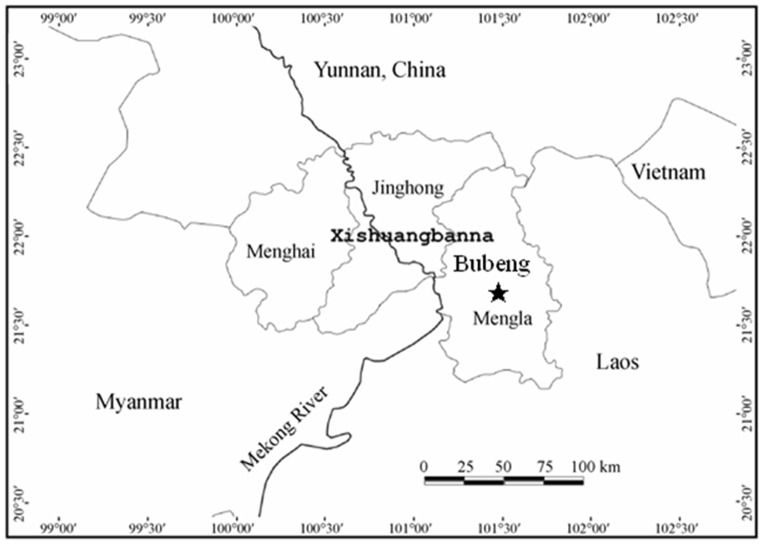
The study site was located in the Xishuangbanna National Nature Reserve in south-western China (101°34′E, 21°36′N) (Fig. 1). It borders Myanmar in the southwest and Laos in the southeast, and has mountainous topography, with mountain ridges running in a north–south direction, decreasing in elevation southward. The uplift of the Himalayas leads to the penetration of warm and moist tropical air mass from the Indian Ocean to Xishuangbanna in the summer, and forms a barrier preventing cold air mass from the north reaching the region in the winter, allowing for the existence of tropical seasonal rain forest in its altitudinal and latitudinal northern limits. The region is dominated by a typical monsoon climate with an alternation between a dry season and a rainy season. As recorded by a weather station 14 km away from the study site, the mean annual temperature is 21.0°C, and the mean annual precipitation is 1532 mm, of which approximately 80% occurs between May and October. The dry season is from November to April [17]. Under these climatic conditions, the tropical seasonal rain forest grows in the lowlands, valleys and hills that have a good water supply [15], [18]–[19].
Figure 1. Location (marked with “★”) of the 20-ha plot in a tropical seasonal rainforest of China.
Data collection
A 20-ha permanent forest plot was established in the Xishuangbanna National Nature Reserve in 2007 following the field protocol of the Center for Tropical Forest Science [20]–[23]. The plot is rectangular in shape and measures 400 m (north-south) by 500 m (east-west). The elevation of the plot ranges from 709 m to 869 m above sea level; the highest elevation occurs in the north-west corner of the plot. Three perennial creeks run through the plot and join together in the south-eastern corner of the plot. The forest occurs mainly on laterite and lateritic red soils with pH values ranging from 4.5–5.5.
All trees (≥1 cm in diameter at breast height, DBH) were mapped and tagged with unique numbers. Tree diameters were measured 1.3 m from the ground. All stems were identified to species. The top tree layer with very uneven crown canopy reaches 30–60 m high and has a coverage of about 30%. As an emergent tree, the single dominant species Parashorea chinensis is the tallest tree, with crown branches near the top and its semi-orbicular crown soars high. Other top tree species such as Sloanea tomentosa (Benth.) Rehd. et Wils, Pometia tomentosa (Bl.) Teysm. et Binn, Semecarpus reticulata Lecte, Barringtonia pendula (Griff.) Kurz usually occupy a space of 30–45 m high above the continuous crown canopy of the second tree layer and under the crown of Parashorea chinensis. The second tree layer reaches up to 18–30 m high. Garcinia cowa predominates in this layer and other representative species are Ficus langkokensis Drake, Knema furfuracea (Hook.f. & Thomson) Warb., Cinnamomum bejolghota (Buch.-Ham.) Sweet, Castanopsis echidnocarpa Hook.f. & Thoms. ex Miq., The third tree layer is 6–20 m high and can be roughly divided into two sub-layers. The upper sub-layer occupies the 10–20 m high space and has as common species Baccaurea ramiflora Lour., Dichapetalum genonioides (Roxb.) Engl., Castanopsis hystrix Miq., Castanopsis indica (Roxb.) Miq., The lower sub-layer is 6–10 m high. The species Pittosporopsis kerrii Craib predominates and other common species are Phoebe lanceolata (Nees) Nees, Mezzettiopsis creaghii Ridl., Leea compactiflora Kurz, Saprosma ternata, , Nephelium chryseum Bl. [18], [24].
Relative density (FD), relative dominance (RA, using basal area) and relative frequency (RF) were calculated for each species in order to estimate the importance value (IV) [24]. We selected the top twenty tree species with the greatest importance values for our analysis. And these species comprised more than 60% of the total individuals (95,498) of trees ≥1.0 cm DBH (see Table 1).
Table 1. Species properties.
| Rank | Species | Code | Family | Life type | Fruit type | Dispersal model | No. of individuals | Percentage (%) | No. of sapling | No. of poles | No. of adults | Habitat association |
| 1 | Parashorea chinesis | PARACH | Dipterocarpaceae | Emergent | Samara | Wind, Gravity | 7919 | 8.3 | 6492 | 1276 | 151 | High plateau−;Gap− |
| 2 | Sloanea tomentosa | SLOATO | Elaeocarpaceae | Upper canopy | Capsule | Ballistic | 502 | 0.5 | 222 | 196 | 84 | N |
| 3 | Pometia tomentosa | POMETO | Sapindaceae | Upper canopy | Drupe | Animal | 480 | 0.5 | 274 | 147 | 59 | Low-slope+; High-plateau− |
| 4 | Semecarpus reticulata | SEMERE | Anacardiaceae | Upper canopy | Drupe | Animal | 619 | 0.6 | 354 | 234 | 31 | High-plateau− |
| 5 | Barringtonia pendula | BARRPE | Lecythidaceae | Upper canopy | Drupe | Gravity | 573 | 0.6 | 314 | 234 | 25 | N |
| 6 | Garcinia cowa | GARCCO | Guttiferae | Lower canopy | Drupe | Animal, Gravity | 4333 | 4.5 | 2795 | 1448 | 90 | High-plateau+; Low-slope− |
| 7 | Knema furfuracea | KNEMFU | Myristicaceae | Lower canopy | Drupe | Animal | 3160 | 3.3 | 2543 | 578 | 39 | Gap+ |
| 8 | Ficus langkokensis | FICULA | Moraceae | Lower canopy | Sycarp | Animal | 1337 | 1.4 | 761 | 537 | 39 | N |
| 9 | Cinnamomum bejolghota | CINNBE | Lauraceae | Lower canopy | Berry | Animal | 1337 | 1.4 | 938 | 376 | 23 | N |
| 10 | Castanopsis echidnocarpa | CASTEC | Fagaceae | Lower canopy | Nut | Animal, Gravity | 881 | 0.9 | 291 | 518 | 72 | High-plateau+; Low-slope− |
| 11 | Castanopsis hystrix | CASTHY | Fagaceae | Lower canopy | Nut | Animal, Gravity | 244 | 0.3 | 32 | 146 | 66 | High-plateau+; Low-slope− |
| 12 | Castanopsis indica | CASTIN | Fagaceae | Lower canopy | Nut | Animal, Gravity | 351 | 0.4 | 166 | 132 | 53 | Valley+; High-plateau− |
| 13 | Baccaurea ramiflora | BACCRA | Euphorbiaceae | Understory | Berry | Animal | 3212 | 3.4 | 1814 | 1365 | 33 | N |
| 14 | Pittosporopsis kerrii | PITTKE | Icacinaceae | Treelet | Drupe | Animal | 20918 | 21.9 | 16439 | 4453 | 26 | low-slope−; high-plateau+ |
| 15 | Mezzettiopsis creaghii | MEZZCR | Annonaceae | Treelet | Berry | Animal | 3300 | 3.5 | 1744 | 1514 | 42 | Valley+; High-plateau− |
| 16 | Nephelium chryseum | NEPHCH | Sapindaceae | Treelet | Drupe | Animal | 1098 | 1.1 | 713 | 343 | 42 | high-slope+ |
| 16 | Phoebe lanceolata | PHOELA | Lauraceae | Treelet | Drupe | Animal | 2409 | 2.5 | 895 | 1496 | 18 | Low-slope−; High-plateau+ |
| 17 | Saprosma ternata | SAPRTE | Rubiaceae | Treelet | Drupe | Animal | 2698 | 2.8 | 2332 | 345 | 21 | Low-slope+; High-plateau− |
| 19 | Dichapetalum gelonioides | DICHGE | Dichapetalaceae | Treelet | Drupe | Animal | 1222 | 1.3 | 704 | 473 | 45 | High plateau− |
| 20 | Leea compactiflora | LEEACO | Vitaceae | Treelet | Berry | Animal | 1051 | 1.1 | 974 | 64 | 13 | N |
| Total | 57644 | 60.4 |
Topographical types include valley (slope<27.1°; elevation<764.87 m), low-slope (slope>27.1°; elevation<764.87 m), high-slope (slope≥27.1°, elevation≥764.87 m, convexity>0), high-gully (slope≥27.1°, elevation≥764.87 m, convexity<0), high-plateau (slope<27.1°, elevation≥764.87 m, convexity>0) and gap (with a total open area greater than 200 m2). “+” indicates positive correlation; “−” indicates negative correlation; “N” indicates neutral correlation.
Data analysis
In order to investigate the species distribution patterns and how the species associations change across life stages, individuals of these species were classified into three life stages: saplings (1 to 5 cm DBH), poles (5 to D950.1 cm DBH) and adults (>D950.1 cm DBH). Here, D950.1 is the 95th percentile of diameter of all trees ≧0.1×Dmax, and Dmax is the diameter of the thickest tree 8,24,25,26. For treelets (maximum DBH no more than 20 cm), individuals between 1 and 3 cm in diameter were classified as saplings, and poles included stem diameters between 3 and D950.1 cm. These divisions roughly correspond to trees that are located in the understory, midstory, and the canopy of the forest [27].
Positive and negative associations of species with habitats were determined by torus-translation tests. The tests assess the similarity between the spatial structure of each focal species population and each habitat [28]. Habitats of the plot were identified by three physical parameters ( i.e., elevation, slope and convexity) in each of the 20×20 m quadrats. We divided the habitat into six types, namely: valley (slope<27.1°; elevation<764.87 m), low-slope (slope>27.1°; elevation<764.87 m), high-slope (slope≥27.1°, elevation≥764.87 m, convexity>0), high-gully (slope≥27.1°, elevation≥764.87 m, convexity<0), high-plateau (slope<27.1°, elevation≥764.87 m, convexity>0) and gap. Here we defined a gap as such if it has a total open area greater than 200 m2. For the tests of association, each simulated map was overlaid by the true distribution of trees. Evaluation of all randomly seeded maps (n = 1000) and all torus-translated maps (n = 4999) gave frequency distributions of relative-density estimates for each species in each of the six principal habitats, one set of distributions for the randomized habitats tests and one set for the torus-translation tests, respectively.
Spatial pattern analysis
We used the pair-correlation function [12], [29] as summary statistic to quantify the spatial structure of the uni- and bivariate patterns. The pair correlation function g 11(r) for univariate patterns of a given life stage of a species 1 can be defined based on the neighborhood density O 11(r) = λ1 g 11(r) which is the mean density of trees of species 1 within rings with radius r and width dr centered in the trees of species 1 [12] where λ1 is the intensity ( = number of species 1 trees in the plot/area of the plot). The pair correlation function is therefore the ratio of the observed mean density of trees in the rings to the expected mean density of trees in the rings. The pair correlation function is especially suitable for exploratory analysis because it isolates specific distance classes [12]–[14], [29]. The pair correlation function for bivariate patterns (i.e., composed of species 1 and species 2 trees) follows intuitively, the quantity g 12(r) is the ratio of the observed mean density of species 2 trees in the rings around species 1 trees to the expected mean density of species 2 trees in these rings [12]. The corresponding neighborhood density function yields O 12(r) = λ2 g 12(r).
The univariate pair correlation function g 11(r) can be used to find out if the distribution of a species is random, aggregated, or regular; and at which distances r these patterns occur. Under the null model of complete spatial randomness (CSR), where the points are independently and randomly distributed over the entire plot, the pair correlation function yields g 11(r) = 1, under aggregation g 11(r)>1, and under regularity g 11(r)<1 [12]. However, this assessment is more complicated in case of environmental heterogeneity [30]. If the pattern contains areas with low point density, the local neighborhood density is larger than the expected density under CSR. As a consequence, spurious aggregation appears which may also obscure an existing small-scale regularity (i.e., virtual aggregation; [30]).
One approach to account for possible first-order effects resulting from larger-scale environmental heterogeneity is to use the heterogeneous Poisson process as null model [12], [31]. This null model is able to approximately factor out the effects of heterogeneity by displacing the points of the pattern only within local neighborhoods of radius h. As a consequence, it maintains the observed large-scale structure but removes potential non-random local spatial structures at distances r below h [31]. This allows for an assessment of potential (conditional second-order) interactions among points if they occur at scales which are smaller than the scales at which the environment varies (i.e., a separation of scales [32]). The occurrence of any point in a heterogeneous Poisson point process is independent of that of others, but the points are distributed in accordance with an intensity function λ(x, y) that varies with location (x ,y) [12], [29], [30]. We used non-parametric kernel estimate of the intensity function based on the Epanechnikov kernel [12], [30] with a bandwidth of h = 30 m and a spatial resolution of 2 m.
We used the bivariate (cross) pair correlation function g 12(r) to study the bivariate species-species associations. Again, first-order effects (habitat preference) may confound conditional second-order effects (direct plant-plant interactions) [30]. To reveal significant conditional second-order interaction we approximately factored out first-order effects by using the heterogeneous Poisson null model described above and randomized the locations of the trees of the second species, but we kept the locations of the trees of the first species fixed [30]. The intensity function was therefore constructed based on the pattern of the second species. A bandwidth of h = 30 m and a spatial resolution of 2 m were also selected for all bivariate analyses. To avoid edge effects, edge correction of Donnelly [33], available for rectangular windows only, was used in the analysis. Note that we assessed the g21-functions also for each species combination because we cannot assume that interactions between species would be symmetric [30].
We used a Monte-Carlo approach to test for significant departures from the null models. Each of the 199 simulations of a point process underlying the null model generates a summary statistic; and simulation envelopes with α≈0.05 were calculated from the 5th highest and lowest values of the 199 simulations [29]. Significant departure from the null model occurred at distance r if the test statistic was outside the simulation envelopes. This approach allowed us to assess scale effects and to determine the type of significant effect. Thus, the univariate analysis indicated aggregation if the observed g 11(r) was above the simulation envelopes and regularity if it was below. Conversely, the bivariate analysis indicated a positive interaction if the observed g 12(r) was above the simulation envelopes and a negative interaction if it was below. However, to avoid spurious rejection of the null model due to simultaneous inference (i.e., we conducted for each distance r one test) we used a goodness-of-fit (GoF) to test for overall departures from the null model for a predefined distance interval [34]. In our study, we selected a distance interval of 0–30 m to assess overall departures from the null model. Significant deviations from the null model were only considered as such if the observed p value of the GoF test was smaller than 0.05. All analyses were performed using the Programita software [12].
Results
Species distributions and topographic habitats
Distribution maps of the twenty tree species across three life stages are shown in Fig. S2. These maps show that trees are not uniformly distributed across the plot: some species are found in the gullies whereas others are found on the slope. The maps suggest that these twenty species have distribution patterns which are related to topography, especially for P. chinensis (Fig. S2a), C. echidnocarpa (Fig. S2j), P. kerrii (Fig. S2n), M. creaghii (Fig. S2o or Fig. 2e). Indeed, torus-translation tests [28] revealed that fourteen of the twenty species showed significant associations with at least one habitat type (Table 1). For example, P. chinensis (Fig. S2a) was negatively associated with the high-plateau and gaps; i.e., there were fewer individuals on the high-plateau or in gaps than expected. P. tomentosa (Fig. S2c) and S. ternate (Fig. S2r) were positively associated with low-slope, but negatively associated with high-slope and high-plateau, and S. reticulata (Fig. S2d), C. indica (Fig. S2l), were negatively associated with high-plateau. However, the test showed that there were no significant associations between the topographic habitats and the distributions of six species such as S. tomentos (Fig. S2b), B. pendula (Fig. S2e), F. langkokensis (Fig. S2h), C. bejolghota (Fig. S2i), B. ramiflora (Fig. S2l) and L. compactiflora (Fig. S2t).
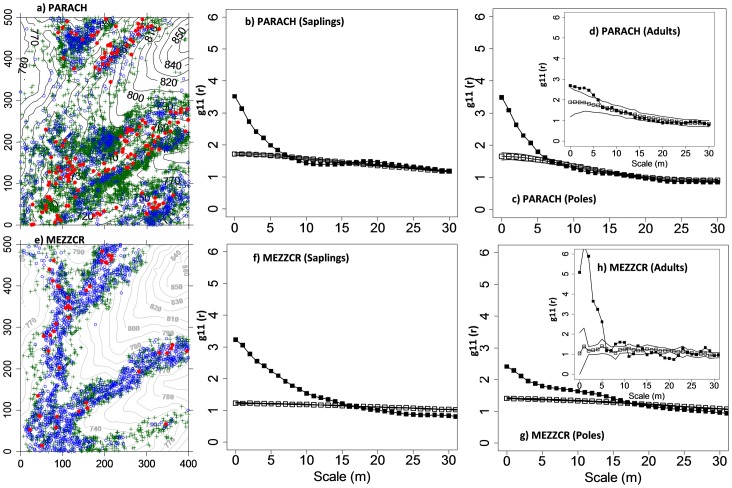
Figure 2. Examples of distribution maps and univariate patterns.
Shown are the univariate g11 pair-correlation functions of the data in dependence on scale r (solid squares), and the expected g11(r) function under the heterogeneous Poisson null model (open squares) and the Monte Carlo simulation envelopes (solid lines) of the null models. Monte Carlo confidence was constructed at approximately 95% confidence level (199 simulations). See Table 1 for species codes. Green cross: saplings, blue open circle: poles, red solid circle: adults.
Species distribution patterns among life stages
Spatial pattern of each life stage of the twenty dominant tree species in the 20 ha plot were analyzed with the univariate pair correlation function. The saplings of all study species showed a strong small-scale aggregation at distances up to 10 m, whereas they followed at larger scales (10–30 m) mostly the heterogeneous Poisson null model (Fig. S3). Our results confirm the existence of separation of scales. Because the heterogeneous Poisson process conditions on the spatial structure for scales larger than 30 m, it is only able to indicate significant effects at scales smaller than 30 m. However, we found a strong additional signal of small-scale aggregation which disappears well below 30 m (mostly within 5 or 10 m). The regularity of P. tomentosa (Fig. S3c3) and S. reticulata (Fig. S3d3) is an artifact of the null model that appears if strongly localized aggregation appears. For poles, the spatial range and the intensity of small-scale aggregation declined compared to the saplings. For adults, though most species display a significant aggregation patterns at the adult stage (figure S3), the degree of spatial clumping deceases from saplings, to poles, to adults (Fig. S3). The loss of the strong clumping observed for juveniles with increasing life stage indicates density-dependent effects and is in agreement with our first guiding hypothesis.
Species associations
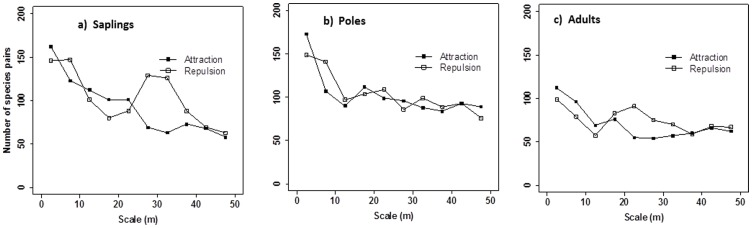
Species associations among the twenty species across life stages were analyzed for scales 0–50 m by using bivariate analyses. In total there were 380 species combinations possible for each class of life stage; i.e., a total of 1140 species pairs were analyzed in this paper. For saplings, 162 (42.6%) of the 380 possible species pairs showed a significant and positive association at small neighborhoods below 5 m, but 146 species pairs (38.4%) showed negative associations at scales 0–5 m. The remaining 72 pairs (18.9%) showed no associations at scales 0–5 m. For poles and adults, positive small-scale associations occurred between 173 pairs (45.5%) and 112 pairs (29.5%), respectively; and 39.2% and 26.1% of the pairs showed negative associations. When comparing the development of the small scale-associations for increasing life stages we made the interesting observation that the number of significant association is higher for poles than for sapling but much lower for adult trees. This is indicated by an increase in the values of the pair correlation function at smaller distances that means that the relative neighborhood density increased.
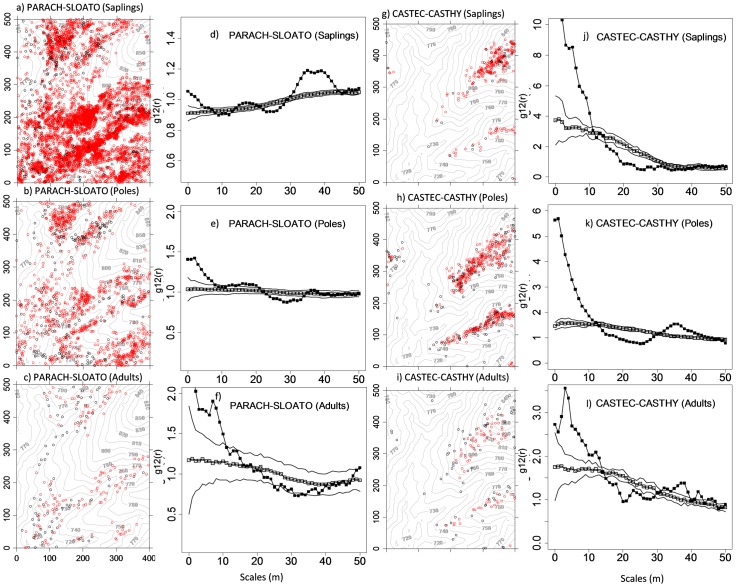
Generally, the larger scale (>5 m) associations of all three life-stages did not show very strong evidence of species interactions. Figure 3 shows some examples of these bivariate analyses across life stages and all bivariate analyses can be found in Table S1. The strongly heterogeneous “banded” pattern of the species P. chinensis creates somewhat erratic pair correlation functions for bivariate patterns (e.g., Fig. 3d–f), but the important message here is the positive small-scale association at distances below 10 m. This indicates that individuals of the species S. tomentosa are more frequently located within neighborhoods of P. chinensis than expected by their overall distribution pattern (i.e., the intensity function). In order to investigate the change of the species associations across life stages, we plotted the number of species pairs against scales across three life stages (Fig. 4). We found for all three life stages a high proportion of positive small-scale (i.e., <10 m) associations. (Fig. 4). Surprisingly, this pattern was largely independent of life stage. However, the large-scale (i.e., >20 m) effects result mostly from the highly heterogeneous pattern of the species P. chinensis which showed a type of banded distribution pattern which creates the positive or negative larger scale association (e.g., Figs. 3d,e).
Figure 3. Examples of species associations in bivariate patterns.
Shown are the bivariate g12 pair-correlation functions of the data in dependence on scale r (solid squares), the expected g12(r) function under the heterogeneous Poisson null model (open squares) and the simulation envelopes (solid lines) of the Monte Carlo simulations of the null model. Monte Carlo confidence was constructed at approximately 95% confidence level (199 simulations). See Table 1 for species codes. Red open circle is the first species, and black solid circle is the second species.
Figure 4. Number of significant attraction and repulsion for all species at the three life stages at scales 0–50 m.
a) saplings, b) poles, c) adults.
Discussion
In this study we investigated how the univariate and bivariate spatial patterns of twenty dominant tree species changed in a tropical seasonal rain forest with life stage. We found strong small-scale aggregation of saplings, and for all life stages a high proportion of positive interspecific small-scale associations. Especially the positive association among the adult trees is somewhat surprising because one would expect that this pattern should disappear due to competition when trees grow to adult size. Thus we have the interesting situation to observe clear self thinning (i.e., loss of the small-scale aggregation with increasing size), but at the same time maintenance of the positive associations among some species. This pattern is compatible with simultaneous action of negative density dependence and a herd protection mechanism and/or facilitative interactions which favor survival of trees with more heterospecific neighbors. In the following we discuss our results in more detail.
Sapling clustering
The twenty dominant species had a large number of juveniles which showed small-scale aggregation and were mostly located close to the adults (Fig. S2). Aggregated spatial distributions are commonly observed in naturally regenerating forests [35]–[36]. The present study provides evidence of clumping for the dominant twenty species in a dipterocarp forest in China. However, the degree of aggregation varied with species, life stages, and spatial scale. Aggregated distributions may result for example from limited seed dispersal [37], animal mediated clump dispersal [38], or habitat heterogeneity [39]–[41]. The topography of our site was very diverse, with an elevation ranging from 709 to 869 m above sea level and three perennial creeks that joined together in the south-eastern corner of the plot. Fourteen of the studied species showed a distribution pattern related to topography. This is confirmed by the species habitat (torus translation) test. However, the positive or negative associations to the topographic habitats are more likely to cause larger-scale aggregation which was approximately factored out by the heterogeneous Poisson null model. Thus, other factors may be responsible for the strong small-scale clustering of saplings. For example, we found especially strong small-scale clustering for saplings of the two species P. chinensis and S. reticulate (Fig. S2). Although P. chinensis produces winged seeds, the seeds are relatively heavy. Hence, P. chinensis is wind- and gravity-dispersed and as a consequence, nearly 60–70% of the seeds fall within a circle of 1–8 m near the conspecific adults [42] thereby causing the strongly aggregated distribution pattern at small scales. The species S. tomentosa produce capsules and when the fruits are ripe, seeds are launched upwards and dispersed ballistically with limited dispersal distance. The species P. tomentosa, S. reticulata produce drupes and are dispersed by animals. The species of C. echidnocarpa, C. hystrix and C. indica produce nuts and are dispersed by Rattus tanezumi, but the distance dispersed by Rattus is no more than 10 m [43]. This phenomenon is interesting because animal dispersal is known to be the most efficient dispersal mode in tropical forest [44]. However, both species B. pendula (with a mass about 220 g) and G. cowa (with a mass more than 70 g) have large seeds and are dispersed by gravity [45]. For G. cowa, there is the highest density of seedlings within a circle of 5–7 m near the conspecific adults [46]. Thus, for these tree species limited seed dispersal is likely to be responsible for the observed aggregated distribution pattern at small scales.
The spatial patterns of our study species lost their strong clumping from the transition from juveniles to adults and approached random patterns as found in previous studies [35], [47]. This indicates that density-dependent mortality of the offspring is ubiquitous in our plot [8]. However, self-thinning especially in tropical forests does not need to lead to regular distributions of tree species, but just random patterns may emerge [48]. Overall, our results on univariate species patterns of trees agree with our first hypothesis and support the presence of Janzen-Connell effects.
Positive species associations
To investigate our second guiding hypothesis on species herd protection, we analyzed potential species interactions among twenty dominant species across three life stages. In order to disentangle the effect of species interactions (second-order effects) and environment (first-order effects) on the species association, we used heterogeneous Poisson null models, accounting for possible environmental heterogeneity, to reveal significant bivariate second-order interactions (repulsion, attraction). Our study revealed marked findings. One of the most interesting results is that second-order effects were strong; overall, 81% of all species pairs showed significant second-order effects (plant-plant interactions). Another interesting result is that positive associations between species made up a high proportion at small neighbourhoods of up to five meters. Interestingly, the highest proportion (45.5%) of positive associations occurred in the poles stage but it declined only to 29.5% in adults. The positive species interaction in the immediate neighbourhood of the youngest life-stage is compatible with the presence of species herd protection. With its emphasis on biotic interactions, this hypothesis is an extension of the classical Janzen-Connell hypothesis and states that increased heterospecific crowding results in fewer encounters between a host and its species-specific pests and pathogens. Thus, survival should increase with the density of heterospecifics, even if conspecific density remains constant [7], [49]. This hypothesis has been proposed to explain, for example, the high tree species diversity on Barro Colorado Island [6]. In addition, species interaction did likely not depend on phylogeny or taxonomy, for example C. echidnocarpa was positively associated with C. hystrix at scale 0–10 m (Fig. 3j-i), however C. hystrix was negatively associated with C. indica at scale 0–5m (Table S1), though these three species belong to the same genus. Only in 72 pairings of saplings showed no significant effects at small scales (0–5 m).
Somewhat unexpectedly we also observed positive associations between adult species. Given the larger size of adults and the observed (univariate) self thinning one would expect rather independence or negative interspecific associations. One explanation for the observed positive associations is that this pattern is still a signal from the species herd protection imprinted during earlier life stages. An alternative, non exclusive explanation is that the positive association could also be the result of facilitation. For example, P. chinensis is a big-statured species of the dipterocarpaceae with a huge umbrella crown which can grow up to 60 m in height. In the tropical seasonal rain forest of Xishuangbanna, the large trees of P. chinensis usually dominate the emergent layer and build up a relatively humid microenvironment favorable to the life of plants, especially in the dry season [15]. In other words, P. chinensis can facilitate the survival of other plants. We found that the associations among P. chinensis adults and adults of three other upper canopy species in our plot showed significant attraction (second-order effects) at small scales 0–5 m.
Previous research of tropical tree species associations were carried out in a Sri Lankan Dipterocarp forest, and the results showed that only 5% of common tree species pairs showed significant second-order effects (species interactions) [30]. However, in tropical seasonal rain forest in Xishuangbanna, 80% of the species pairs showed significant second-order effects (including both positive and negative association) at small scale 0–5 m. Although we do not know why there is such a big difference between the two dipterocarp forest, at least we can infer that mechanisms of tree species coexistence in dipterocarp tropical seasonal rainforest of China are totally different from dipterocarp tropical forest in Sri Lankan.
In conclusion, our results show that the degree of spatial clumping in the twenty dominant species decreases from saplings, to poles, to adults. The reduction of spatial aggregation with life stages is indirect evidence of Janzen–Connell spacing effects. Species distribution maps and the torus translation test indicate some presence of habitat associations and niche assembly. The positive spatial associations among the tree species at small spatial scales suggest operation of species herd protection but may also be indicative of facilitative interactions. Overall, these results suggest that Janzen–Connell spacing effects, habitat association, limited dispersal and species herd protection may contribute to shape the spatial patterns of the tree species in the tropical rainforest in Xishuangbanban, southwest China.
Supporting Information
Habitat of the 20-ha permanent plot of tropical seasonal rain forest in China. Valley: slope<27.1°, elevation<764.87 m; Low-slope: slope>27.1°, elevation<764.87 m; High-slope: slope≥27.1°, elevation≥764.87 m, convexity>0; High-gully: slope≥27.1°, elevation≥764.87 m, convexity<0; High-plateau: slope<27.1°, elevation≥764.87 m, convexity>0; Gap: with a total open area greater than 200 m2.
(TIF)
Distribution maps of the twenty dominant species across life stages in the 20-ha plot of tropical seasonal rainforest. See Table 1 for species codes. Green cross: saplings, blue open circle: poles, red solid circle: adults.
(TIF)
Univariate patterns of the twenty dominant species across life stages in the 20-ha plot of tropical seasonal rainforest. Shown are the univariate g11 pair-correlation functions of the data in dependence on scale r (solid squares), and the expected g11(r) function under the heterogeneous Poisson null model (open squares) and the Monte Carlo simulation envelopes (solid lines) of the null models. Monte Carlo confidence was constructed at approximately 95% confidence level (199 simulations). See Table 1 for species codes.
(TIF)
Spatial associations of twenty dominant species across life stages in 20-ha permanent plot of tropical seasonal rain forest in China. The bivariate statistic of the pair-correlation function was used to analyze the spatial associations among five canopy species under the heterogeneous Poison null model. “p” stands for positive association, “r” stands for no spatial association (randomness), and “n”for negative association. Monte Carlo simulation envelopes were constructed at the approximate 95% confidence level. See Table 1 for species codes.
(DOC)
Acknowledgments
We are grateful to Prof. Fangliang He for proving learning opportunity in Canada and other helps. We are also grateful to all of the field workers who contributed to the tree species census of the 20-ha plot.
Funding Statement
This project was supported by a grant from the National Science Foundation of China (31061160188-03) and a grant from the National Science & Technology Pillar Program of China (2008BAC39B02). SG was supported by the Environmental Research Center Advanced Grant “SpatioDiversity” (grant number 233066) to TW. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Wright SJ (2002) Plant diversity in tropical forests: a review of mechanisms of species coexistence. Oecologia 130: 1–14. [DOI] [PubMed] [Google Scholar]
- 2. Volkov I, Banavar JR, He FL, Hubbell SP, Maritan A (2005) Density dependence explains tree species abundance and diversity in tropical forests. Nature 438: 658–661. [DOI] [PubMed] [Google Scholar]
- 3. Janzen DH (1970) Herbivores and the number of tree species in tropical forests. Am Nat 104: 501–528. [Google Scholar]
- 4.Connell JH (1971) On the role of natural enemies in preventing competitive exclusion in some marine animals and in rain forest trees. In: Dynamics of Populations (eds Boer PJD & Gradwell GR). PUDOC, Wageningen, pp. 298–312. [Google Scholar]
- 5. Condit R, Hubbell SP, Foster RB (1994) Density dependence in two understroy tree species in a neotropical forest. Ecology 75 (3) 671–680. [Google Scholar]
- 6. Wills C, Condit R, Foster RB, Hubbell SP (1997) Strong density- and diversity-related effects helps to maintain species diversity in a neotropical forest. P Natl Acad Sci USA 49: 1252–1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Peters HA (2003) Neighbour-regulated mortality: the influence of positive and negative density dependence on tree populations in species-rich tropical forests. Ecol Lett 6: 757–765. [Google Scholar]
- 8. Lan GY, Zhu H, Cao M, Hu YH, Wang H, et al. (2009) Spatial dispersion patterns of trees in a tropical rainforest in Xishuangbanna, southwest China. Ecol Res 24: 1117–1124. [Google Scholar]
- 9. Wills C, Green DR (1995) A genetic herd-immunity model for the maintenance of MHC polymorphism. Immunol Rev 143: 263–292. [DOI] [PubMed] [Google Scholar]
- 10. Comita LS, Hubbell SP (2009) Local neighbourhood and species' shade tolerance influence survival in a diverse seedling bank. Ecology 90: 328–334. [DOI] [PubMed] [Google Scholar]
- 11. Getzin S, Dean C, He F, Trofymow JA, Wiegand K, et al. (2006) Spatial patterns and competition of tree species in a Douglas-fir chronosequence on Vancouver Island. Ecography 29: 671–682. [Google Scholar]
- 12. Wiegand T, Moloney KA (2004) Rings, circles, and null-models for point pattern analysis in ecology. Oikos 104: 209–229. [Google Scholar]
- 13. Perry GLW, Miller BP, Enright NJ (2006) A comparison of methods for the statistical analysis of spatial point patterns in plant ecology. Plant Ecol 187: 59–82. [Google Scholar]
- 14. Law R, Illian J, Burslem DFRP, Gratzer G, Gunatilleke CVS, et al. (2009) Ecological information from spatial patterns of plants: insights from point process theory. J Ecol 97: 616–628. [Google Scholar]
- 15. Cao M, Zhang J (1997) Tree species diversity of tropical forest vegetation in Xishuangbanna, SW China. Biodivers Conserv 6: 995–1006. [Google Scholar]
- 16. Kohyama T (1993) Size-structured tree populations in gap dynamics forest: the forest architecture hypothesis for the stable coexistence of species. J Ecol 81: 131–143. [Google Scholar]
- 17. Zhang JH, Cao M (1995) Tropical forest vegetation of Xishuangbanna, SW China and its secondary changes, with special reference to some problems in local nature conservation. Biol Conserv 73: 229–238. [Google Scholar]
- 18. Zhu H (2006) Forest vegetation of Xishuangbanna, south China. For Stud China 8: 1–27. [Google Scholar]
- 19. Zhu H, Cao M, Hu H (2006) Geological history, flora, and vegetation of Xishuangbanna, southern Yunnan, China. Biotropica 38: 310–317. [Google Scholar]
- 20. Condit R, Hubbell SP, Foster RB (1992) Recruitment near conspecific adults and the maintenance of tree and shrub diversity in a neotropical forest. Am Nat 140: 261–286. [DOI] [PubMed] [Google Scholar]
- 21. Condit R (1995) Research in large, long –term tropical forest plot. Trends Ecol Evol 10 (1) 18–22. [DOI] [PubMed] [Google Scholar]
- 22. Condit R, Hubbell SP, Foster RB (1996) Changes in tree species abundance in a neotropical forest: impact of climate change. J Trop Ecol 12: 231–256. [Google Scholar]
- 23.Condit R (1998) Tropical forest census plots: Methods and results from Barro Colorado Island, Panama and a Comparion with other plot, Springer-Verlag and R.G. Landes Company. pp: 17–19. [Google Scholar]
- 24. Lan GY, Zhu H, Cao M (2012) Tree species diversity of a 20-ha plot in a tropical seasonal rainforest in Xishuangbanna, southwest China. J For Res online [Google Scholar]
- 25. King DA, Davies SJ, Noor NSM (2006) Life and mortality are related to adult tree size in a Malaysian mixed dipterocarp forest. For Ecol Manage 206: 152–158. [Google Scholar]
- 26. Lan GY, Hu YH, Zhu H, Cao M (2011) Topography related spatial distribution of dominant tree species in a tropical seasonal rain forest in China. For Ecol Manage 262: 1507–1503. [Google Scholar]
- 27. Bunyavejchewina S, LaFrankieb JV, Bakerc PJ, Kanzakid M, Ashtone PS, et al. (2003) Spatial distribution patterns of the dominant canopy dipterocarp species in a seasonal dry evergreen forest in western Thailand. For Ecol Manage 175: 87–101. [Google Scholar]
- 28. Harms KE, Condit R, Hubbell SP, Foster RB (2001) Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. J Eco 89: 947–959. [Google Scholar]
- 29.Stoyan D, Stoyan H (1994) Fractals, random shapes and point fields. Wiley, Chichester. [Google Scholar]
- 30. Wiegand T, Gunatilleke S, Gunatilleke N (2007a) Species associations in a heterogeneous Sri Lankan dipterocarp forest. Am Nat 170: E77–E95. [DOI] [PubMed] [Google Scholar]
- 31. Wang XG, Wiegand T, Hao Z, Li BH, Ye J, et al. (2010) Species associations in an old-growth temperate forest in north-eastern China. J Ecol 98: 674–686. [Google Scholar]
- 32. Wang ZG, Ye WH, Cao HL, Huang ZL, Lian JY, et al. (2009) Species-topography association in a species-rich subtropical forest of China. Basic Appl Ecol 10: 648–655. [Google Scholar]
- 33.Donnelly KP (1978) Simulations to determine the variance and edge effect of total nearest neighbourhood distance, In Simulation methods in archeology, Cambridge: Cambridge University Press. pp: 91–95 [Google Scholar]
- 34. Loosmore NB, Ford ED (2006) Statistical inference using the G or K point pattern spatial statistics. Ecology 87: 1925–1931. [DOI] [PubMed] [Google Scholar]
- 35. He F, Legendre P, LaFrankie JV (1997) Distribution patterns of tree species in a Malaysia tropical forest. J Veg Sci 8: 105–114. [Google Scholar]
- 36. Condit R, Ashton PS, Baker P, Bunyavejchewin S, Gunatilleke S, et al. (2000) Spatial Patterns in the Distribution of tropical tree Species. Science 288: 1114–1118. [DOI] [PubMed] [Google Scholar]
- 37. Grubb PJ (1977) Maintenance of species-richness in plant communities: the importance of the regeneration niche. Biological Reviews of the Cambridge [Google Scholar]
- 38. Wiegand T, Huth A, Martínez I (2009) Recruitment in tropical tree species:Revealing complex spatial patterns. Am Nat 174: E106–E140. [DOI] [PubMed] [Google Scholar]
- 39. Harms KE, Wright SJ, Calderon O, Hernandez A, Herre EA (2000) Pervasive density-dependent recruitment enhances seedling diversity in a tropical forest. Nature 404: 493–495. [DOI] [PubMed] [Google Scholar]
- 40. Getzin S, Wiegand T, Wiegand K, He F (2008) Heterogeneity influences spatial patterns and demographics in forest stands. J Ecol 96: 807–820. [Google Scholar]
- 41. Queenborough SA, Burslem D, Garwood NC, Valencia R (2007) Habitat niche partitioning by 16 species of Myristicaceae in Amazonian Ecuador. Plant Ecol 192: 193–207. [Google Scholar]
- 42. Yin SH, Shuai JG (1990) Study on fruiting behaviour seeding establishment and population age classes of Shorea wantianshuea. Acta Botanica Yunnanic 12 (1) 415–420. [Google Scholar]
- 43.Liu JX (2008) Predation and dispersal of Castanopsis nuts by rodents and yellow chest rat (Rattus tanezumi) storage strategy in Xishuangbanna, Qupu normal university. Master thesis, 1–40 (In Chinese with English abstract). [Google Scholar]
- 44. Seidler TG, Plotkin JB (2006) Seed dispersal and spatial pattern in tropical trees. PLoS Biol 4: 2132–2137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Yang XF, Tang Y, Cao M (2010) Diaspore Traits of 145 Tree Species from a Tropical Seasonal Rain forest in Xishuangbanna,SW China. Acta Botanica Yunnanic 32: 367–377 (in Chinese with English abstract). [Google Scholar]
- 46. Liu Y, Chen J, Bai ZL, Deng XB, Zhang L (2002) Seed dispersal, seed predation, and seedling spatial pattern of Garcinia cowa (Guttiferae). J Plant Ecol 26 (4) 427–434 (In Chinese with English abstract).. [Google Scholar]
- 47. Wiegand T, Gunatilleke S, Gunatilleke N, Okuda T (2007b) Analyzing the spatial structure of a Sri Lankan tree species with multiple scales of clustering. Ecology 88: 3088–3102. [DOI] [PubMed] [Google Scholar]
- 48. Getzin S, Worbes M, Wiegand T, Wiegand K (2011) Size dominance regulates tree spacing more than competition within height classes in tropical Cameroon. J Trop Ecol 27: 93–102. [Google Scholar]
- 49. Comita LS, Condit R, Hubbell SP (2007) Developmental changes in habitat associations of tropical trees. J Ecol 95: 482–492. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Habitat of the 20-ha permanent plot of tropical seasonal rain forest in China. Valley: slope<27.1°, elevation<764.87 m; Low-slope: slope>27.1°, elevation<764.87 m; High-slope: slope≥27.1°, elevation≥764.87 m, convexity>0; High-gully: slope≥27.1°, elevation≥764.87 m, convexity<0; High-plateau: slope<27.1°, elevation≥764.87 m, convexity>0; Gap: with a total open area greater than 200 m2.
(TIF)
Distribution maps of the twenty dominant species across life stages in the 20-ha plot of tropical seasonal rainforest. See Table 1 for species codes. Green cross: saplings, blue open circle: poles, red solid circle: adults.
(TIF)
Univariate patterns of the twenty dominant species across life stages in the 20-ha plot of tropical seasonal rainforest. Shown are the univariate g11 pair-correlation functions of the data in dependence on scale r (solid squares), and the expected g11(r) function under the heterogeneous Poisson null model (open squares) and the Monte Carlo simulation envelopes (solid lines) of the null models. Monte Carlo confidence was constructed at approximately 95% confidence level (199 simulations). See Table 1 for species codes.
(TIF)
Spatial associations of twenty dominant species across life stages in 20-ha permanent plot of tropical seasonal rain forest in China. The bivariate statistic of the pair-correlation function was used to analyze the spatial associations among five canopy species under the heterogeneous Poison null model. “p” stands for positive association, “r” stands for no spatial association (randomness), and “n”for negative association. Monte Carlo simulation envelopes were constructed at the approximate 95% confidence level. See Table 1 for species codes.
(DOC)