Cross-imaging system comparison of backscatter coefficient estimates from a tissue-mimicking material

Abstract

A key step toward implementing quantitative ultrasound techniques in a clinical setting is demonstrating that parameters such as the ultrasonic backscatter coefficient (BSC) can be accurately estimated independent of the clinical imaging system used. In previous studies, agreement in BSC estimates for well characterized phantoms was demonstrated across different laboratory systems. The goal of this study was to compare the BSC estimates of a tissue mimicking sample measured using four clinical scanners, each providing RF echo data in the 1-15 MHz frequency range. The sample was previously described and characterized with single-element transducer systems. Using a reference phantom for analysis, excellent quantitative agreement was observed across the four array-based imaging systems for BSC estimates. Additionally, the estimates from data acquired with the clinical systems agreed with theoretical predictions and with estimates from laboratory measurements using single-element transducers.

INTRODUCTION

Conventional B-mode ultrasound scanning provides primarily qualitative images that depict soft tissue interfaces and internal organ scatterers. Echo signal amplitudes, represented by image brightness, are related to tissue backscatter levels, but the signals detected from a given depth also depend on tissue transmission properties, operator settings, and system-dependent factors such as the transducer geometry, center frequency and bandwidth as well as time-gain compensation (TGC).

We are developing and validating quantitative ultrasound (QUS) imaging methods that derive attenuation and backscatter coefficients (BSCs) from tissues. The methods are based on analysis of radio frequency (RF) echo signals from the region of interest (ROI) and use scans of reference media to account for the system-dependent factors listed above.

QUS has demonstrated potential for detecting diffuse disease and diagnosing focal lesions. For example, spectral analysis of backscattered echo signals has been used to differentiate benign from malignant masses in the eye,1 lymph nodes,2, 3 and liver.4 A scatterer size estimator derived using QUS was successfully applied to kidneys to estimate glomerular and arteriole sizes.5 “Effective scatterer sizes” estimated from the backscatter coefficient provided data to differentiate rat mammary fibroadenomas from 4T1 mouse carcinomas.6

Because the BSC and its dependence on ultrasound frequency are fundamental to many types of QUS imaging, it is important to demonstrate system and operator independence of BSC estimations for its effective and widespread use. To this end, several inter-laboratory studies have been conducted using different experimental apparatuses to estimate BSCs.7, 8, 9 These studies have enabled researchers to uncover sources of errors in measurements that, once eliminated, resulted in inter-laboratory agreement among BSC estimates on identical samples.8, 9

The studies by Wear et al.,7 Anderson et al.,8 and King et al.9 focused on laboratory-based systems, measurement, and data processing techniques. However, to apply QUS in a clinical setting, it is necessary to also demonstrate system and operator independence of BSC estimates using array-based ultrasound imaging systems. Normalizing data using echo signals from planar reflectors, as performed in the preceding studies,7, 8, 9 is complicated in clinical machines because of dynamic focusing of the received beam and use of internal TGC. These systems generally exhibit greater variability in transducer geometry and beamforming functions than simple, single-element transducer systems, and this makes calculation of pulse-echo beam properties as used for BSC data reduction more challenging.

The goal of this study was to assess the accuracy of BSC estimates from data acquired by four clinical ultrasound systems equipped with research interfaces. Data reduction was accomplished using a reference phantom technique in which system dependencies of echo signals are removed by computing depth-dependent ratios of echo signal power spectra from the sample to that from a calibrated reference phantom.10 RF echo data were acquired from a sample used previously to verify performance accuracy of laboratory BSC measurement systems.8 BSC estimates from data acquired by the different clinical imaging systems were compared with these laboratory measurements as well as with results from a theoretical model.

METHODS

Tissue-mimicking phantom

A tissue-mimicking phantom consisting of 41-μm-diameter glass spheres in an agar gel background was used in this study. The spheres had a narrow distribution of diameters (41 ± 2 μm). The sample was cylindrically shaped (2.5-cm-thick, 7.5-cm-diameter) with two circular transmission windows made of 25-μm-thick Saran film^® (Dow Chemical, Midland, MI). The construction process of the sample was described by Madsen et al.11

The acoustic properties of the phantom, measured at 22 °C are presented in Table TABLE I.. Sound speed and attenuation coefficients were estimated using a through-transmission and insertion-loss technique with single-element transducers.7 The backscatter coefficients were measured using a broadband reference reflector method12 with focused single-element transducers. The single-element transducers used to evaluate the properties of the phantom spanned 2.25–10 MHz. In addition, theoretical backscatter coefficients for the phantom were computed using the theory of Faran13 that describes the scattering function and subsequently the BSC for the glass beads. Faran’s theory describes the scattering of sound waves by isotropic spheres and cylinders in a fluid medium. The theory takes into account shear waves as well as compressional waves. In our studies, we used the first 25 terms of the far-field asymptotic solution for spherical scatterers in the Faran model,13 [Eq. (31) with the corrections to Eq. (30) noted by Hickling14]. Input parameters for the calculation include the mass density and sound speed of the background gel as well as the mass density, sound speed, Poisson’s ratio, diameter distribution, and concentration (number of scatterers per unit volume) of the glass sphere scatterers. The values used for the glass beads sample are presented in Table TABLE I..

TABLE I.

Composition and properties of the tissue-mimicking sample used for imaging system BSC estimates.

Number density (g/l)	4.07
Bead type	Borosilicate
Sphere diameter range (μm)	39–43
Sound speed of spheres (m/s)	5572
Poisson’s ratio of spheres	0.210
Mass density of spheres (g/ml)	2.38
Background material	2% agar in water, n-propanol
Density of sample (g/ml)	1.00
Sound speed of sample (m/s)	1539
Slope of attenuation coefficient (dB/cm-MHz)	0.1

A linear function of frequency was fit to the estimated attenuation coefficients versus frequency as previous results have shown this to be valid for this sample.8

Fit parameters are also presented in Table TABLE I.. The backscatter measurements will be presented in Sec. 3 along with BSC estimates from the clinical imaging systems and the theoretical predictions.

Reference phantom

A reference phantom technique10 was employed for BSC estimation to account for imaging system effects on RF echo signals derived from clinical scanners. The reference phantom was made with 6.4 g of 5–43 μm-diameter glass beads evenly distributed in a 1600 cc gel background. The background material was a gelatin emulsion containing 70% safflower oil.15 The top of the reference phantom was covered with a 25-μm-thick Saran Wrap^®. The acoustic properties of the reference phantom were measured using single-element transducers and a narrow-band substitution method7 on test samples manufactured at the same time as the reference phantom. The sound speed was 1492 m/s at 2.5 MHz. Measured attenuation coefficients at frequencies from 2 to 10 MHz were fit to a power law function of frequency, yielding α(f)(dB/cm) = 0.256 f^1.366, where f is the frequency in megahertz.

Ultrasound imaging systems

Four clinical systems from three institutions, each providing RF echo data through a research interface, were used to image the tissue-mimicking sample. The four clinical systems were an Ultrasonix RP (Ultrasonix Medical, Richmond, BC, Canada); a Siemens Acuson S2000 (Siemens Medical Solutions USA, Malvern, PA); a Zonare Z.one (ZONARE Medical Systems, Mountain View, CA); and a VisualSonics Vevo2100 (VisualSonics, Toronto, Ontario, Canada). For each system, the individual transducers used and the selected bandwidths for BSC estimation are summarized in Table TABLE II.. Also shown in the table are the data acquisition digitization rates employed by the systems. (Note, the VisualSonics data are baseband quadrature components of the RF signal.)

TABLE II.

Summary of clinical imaging systems and the respective frequency bandwidths utilized in the analysis of RF data.

System	Transducer	Nominal center frequency (MHz)	Used bandwidth (MHz)	Bandwidth cutoff criterion	Sampling frequency (MHz)
UltraSonix RP	L9-4/38	5	3–7	−6 dB	40
	L14-5/38	7.5	3.9−8.4	−6 dB
Siemens Acuson S2000	18L6	10	4−10	15 dB higher than noise floor	40
Zonare Z.one	L8-3	7	3.1−6.6	−17dB to −21dB	50
	L14-5sp	10	4.7−10.3	−13dB to −20dB
VisualSonics Vevo2100	MS200	15	8.5−13.5	−6 dB	40

Data collection and analysis

Each system was used to image the sample and acquire two to five frames of RF echo data, where a frame consists of signals from all acoustic scan lines used to form a single B-mode image. An elevational translation or rotation of the transducer was applied between each frame to obtain statistically independent echo signals. These data were acquired with the array transducer placed in contact with the sample (see Fig. 1). RF echo data were also obtained from the reference phantom described in the preceding text, using the same transducer, transmit focus, and other equipment settings employed for the sample.

Figure 1.

(Color online) Data collection set-up. The sample was scanned first and the reference was imaged under the same system settings used for the sample.

BSCs were estimated as a function of frequency using the reference phantom technique10 applied to the RF echoes from each system. For all data, periodograms computed from RF data along individual acoustic scan lines were calculated by applying a time-gating window (2-4 mm long, see Table TABLE III.) and computing the squared magnitude of the Fourier transform. Periodograms computed within each analysis window were averaged to compute an echo signal power spectrum. The same processes were applied to the reference phantom RF data. Assuming that multiple scattering can be ignored, which is valid for the sparse scatterer concentration of the phantom,11 and that differences in acoustic beam diffraction between the sample and the reference are negligible, the ratio of the echo signal power spectra (S) from the sample to that from the reference phantom can be written as:

$$\frac{S_{\mathit{s}\mathit{a}\mathit{m}}(f,z)}{S_{\mathit{r}\mathit{e}\mathit{f}}(f,z)}=\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)\exp \{-4{\alpha }_{\mathit{s}\mathit{a}\mathit{m}}(f)z\}}{{\sigma }_{\mathit{r}\mathit{e}\mathit{f}}(f)\exp \{-4{\alpha }_{\mathit{r}\mathit{e}\mathit{f}}(f)z\}},$$ (1)

where $\sigma (f)$ and $\alpha (f)$ are the backscatter and attenuation coefficients, respectively. f is the frequency and z is the depth of the analysis region. The subscripts sam and ref represent the sample and the reference phantom, respectively. Then the backscatter coefficient of the sample is estimated using:

$${\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)=\frac{S_{\mathit{s}\mathit{a}\mathit{m}}(f,z)}{S_{\mathit{r}\mathit{e}\mathit{f}}(f,z)}\times {\sigma }_{\mathit{r}\mathit{e}\mathit{f}}(f)\exp \{4({\alpha }_{\mathit{s}\mathit{a}\mathit{m}}(f)-{\alpha }_{\mathit{r}\mathit{e}\mathit{f}}(f))z\}.$$ (2)

For each system, selection of the ROI in the sample, the duration of the analysis window for power spectrum estimates, and any spatial overlap in the analysis windows was done independently by the individual lab groups. The analysis parameters used for data from each ultrasound system are summarized in Table TABLE III.. The BSC estimates obtained from each analysis window over the ROI were spatially averaged, yielding the sample BSC vs frequency.

TABLE III.

Summary of parameters for BSC estimation. (λ_cf: wave length calculated by the center frequency of RF echoes).

	UltraSonix RP	Siemens Acuson S2000	Zonare Z.one	VisualSonics Vevo2100
Tapering function	Hann window	Hann window	Rectangular window	Hann window
Spectral window size (axial × lateral)	15 λcf × 15 λcf	4 mm × 4 mm	L8-3:2.4 mm × 0.8 mm	15 λcf × 15 λcf
		(31 adjacent beamlines)	L14-5sp: 2.35 mm × 0.53 mm
Spectral window overlap (axial × lateral)	75% × 75%	75% × 75%	99% × 99%	75% × 75%

To analyze variations among these estimates, two quantities were defined and calculated for each transducer used in the experiment:

(1) Bias with respect to the Faran results (B_Faran): This is defined as the relative error of σ_sam with respect to the prediction from Faran theory (σ_Faran). This is expressed as

$$B_{\mathit{F}\mathit{a}\mathit{r}\mathit{a}\mathit{n}}(f)=10\times {\log }_{10}\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_{\mathit{F}\mathit{a}\mathit{r}\mathit{a}\mathit{n}}(f)},$$ (3)

where f is the discrete frequency over the frequency range. The mean and variance of B_Faran(f) within each transducer’s bandwidth is presented in Sec. 3.

(2) Effective scatter diameter (ESD)16: This was estimated through the minimization of the squared difference between the logarithms of BSC estimates using a given transducer (σ_sam), and a scatterer size-dependent theoretical model (σ_T) (in this case using Faran’s theory with the same scatterer concentration as the sample’s), and updating the scatterer diameter assumed for σ_T at each iteration of the minimization procedure. This fit was done over each transducer’s available bandwidth.17 Thus the effective scatter size estimate ($\widehat{d}$) is obtained by,

$$\widehat{d}=\arg \min \frac{1}{N}{{\displaystyle \sum _{f=f_1}^{f_N}\left[10\log \left\{\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_T(f;d)}\right\}-\overline{10\log \left\{\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_T(f;d)}\right\}}\right]}}^2,$$ (4)

where

$$\overline{10\log \left\{\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_T(f;d)}\right\}}=\frac{1}{N}{\displaystyle \sum _{f=f_1}^{f_N}10\log \left\{\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_T(f;d)}\right\},}$$ (5)

and N is the number of discrete frequencies in the analysis bandwidth. d is the effective scatterer diameter, and diameter search ranges used were 10–70 μm.

Once an effective scatterer diameter was estimated using Eq. 4, the goodness of fit, the distance between σ_T calculated by assuming this estimated diameter and the estimated σ_sam was quantified as the mean squared error, $MSE({\sigma }_{\mathit{s}\mathit{a}\mathit{m}},\widehat{d})$. Here the average value was obtained over each available bandwidth using:

$$MSE({\sigma }_{\mathit{s}\mathit{a}\mathit{m}},\widehat{d})=\frac{1}{N}{{\displaystyle \sum _{f=f_1}^{f_N}\left[10\log \left\{\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_T(f;\widehat{d})}\right\}-\overline{10\log \left\{\frac{{\sigma }_{\mathit{s}\mathit{a}\mathit{m}}(f)}{{\sigma }_T(f;\widehat{d})}\right\}}\right]}}^2.$$ (6)

RESULTS AND DISCUSSION

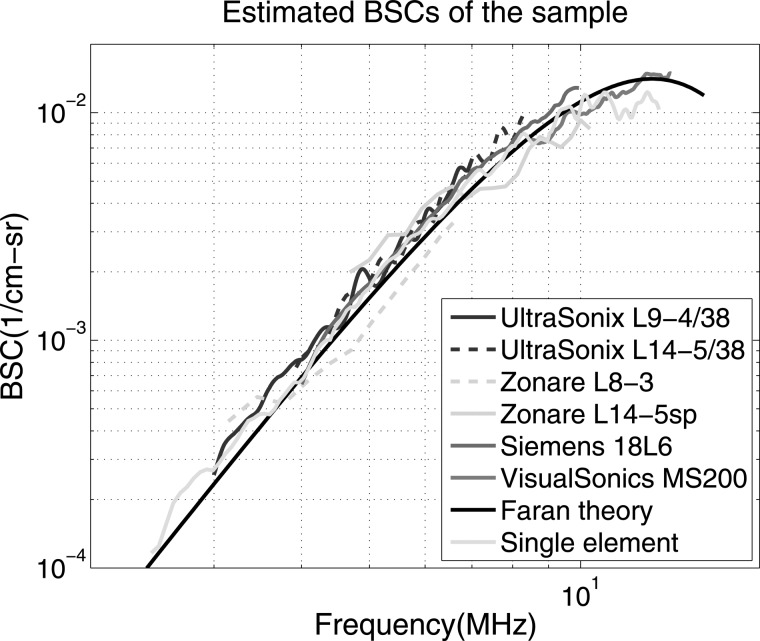
The estimated BSC results for all four ultrasound imaging systems are displayed in Fig. 2. Also shown on this graph are the BSC predictions using Faran’s theory13 and the results of measurements from the laboratory system. The laboratory results are from combined measurements using four single-element transducers as previously presented.8

Figure 2.

(Color online) Backscatter coefficients vs. frequency estimates using each of the clinical ultrasound systems. Results are presented for two transducers for both the UltraSonix and the Zonare scanners. Also shown are lab measurements employing single-element transducers. The solid black curve is computed using the theory of Faran.

From Fig. 2, it can be observed that BSC estimates from all systems are in very good agreement with values from Faran’s theory as well as the laboratory measurements. Most of the transducers exhibited considerable overlap in the frequency ranges employed, and all the transducer results allowed a direct visual magnitude comparison of BSC estimates.

Assuming that the theoretical prediction is correct, the bias with respect to the Faran value (B_Faran) is presented in Table TABLE IV.. The mean values of B_Faran varied from −0.42 to 0.86 dB, which, interestingly, were better than or at least comparable to the results reported in the previous inter-laboratory studies.7, 8, 9

TABLE IV.

B_Faran, or the difference between measured BSC’ and Faran predictions determined over the available frequency range for each system. Shown are mean values of B_Faran as well as one standard deviation for each system.

System	Mean error (dB)	Standard deviation (dB)
UltraSonix L9-4/38	0.86	0.35
UltraSonix L14-5/38	0.84	0.31
Zonare L8-3	−0.42	1.05
Zonare L14-5sp	−0.01	1.24
Siemens 18L6	0.58	0.17
VisualSonics MS200	−0.29	0.31
Single element	−0.02	0.67

The variances of B_Faran also varied among systems, and the one-standard deviation values of B_Faran from all systems were within 1.3 dB. Considering both bias and variance, the BSC estimates from all the imaging systems were within about 1.5 dB from the predicted values. This indicates that with some of these systems we can reliably detect backscatter differences of less than 2 dB (bias plus 3 standard deviations).

Possible causes of the discrepancy between the system estimates and theoretical values are factors such as undetected reverberations in the sample due to its short axial distance (reverb echoes were not observed, however, on B-mode images), minor localized differences in number density of scatterers, and the presence of a small difference between the speed of sound in the reference phantom and the sample, which was ignored. Nam et al.18 have shown that errors in accounting for system dependent factors, using power spectra ratios of sample to reference phantom data, can occur even with small (2%) differences in sound speed between a sample and the reference, depending on the focusing characteristics.

To assess the agreement in frequency dependence of BSC estimates, the effective scatterer diameters were estimated using Eq. 4. The results, along with the mean squared error values computed using Eq. 6 are summarized in Table TABLE V.. The estimated effective scatterer diameters from the UltraSonix L9-4/38 and the Siemens 18L6 were identical to the effective scatterer diameter estimated from the Faran theory using the known glass bead diameter distribution, although their mean squared errors were a little higher than the theory’s. The highest effective scatterer diameter error was observed in the Zonare L8-3 result. This could be caused by the relatively small bandwidth of the data for this transducer (3.1 − 6.6 MHz) and the fact that the frequencies available fall into a low range for the value of “ka” (product of the wave number and scatter radius, ka = 0.42 for 42-μm-diameter scatterers at 4.9 MHz). It has been reported that effective scatterer diameter estimation is highly ill-conditioned for ka < 0.5, below which scatterers exhibit Rayleigh behavior.19 Excluding that result, the effective scatterer diameter estimates agreed with the expected value within 13 μm.

TABLE V.

Estimated effective scatterer diameters (ESDs) from backscatter coefficients obtained by different ultrasound systems. Also shown are the mean square errors (MSE) for each estimate with respect to the Faran theory model, assuming the estimated single ESD. (*ESD for Faran was estimated assuming a single diameter from the Faran BSC prediction obtained by measured size distribution).

System	ESD ($\widehat{d}$, μm)	MSE (dB)
Faran* (single diameter)	42	0.002
UltraSonix L9-4/38	42	0.121
UltraSonix L14-5/38	39	0.090
Zonare L8-3	62	0.670
Zonare L14-5sp	55	0.399
Siemens 18L6	42	0.030
VisualSonics MS200	39	0.037
Single element	46	0.115

One of the reasons why the BSC estimates for this sample exhibited higher accuracy (including laboratory result) than those for samples utilized in previous inter-laboratory studies7, 8, 9 could be its narrow scatterer size distribution (41 ± 2 μm). The narrow size range reduces the uncertainty of the theoretical predictions (for a given number of bead sizes measured to characterize the distribution) to which the measured BSCs were compared.

It should be pointed out that echo data for each acoustic scan line derived from the clinical systems are formed by combining signals from many array elements of a transducer. Clinical data are acquired after TGC, are subject to any effects of transmit focusing, and are formed using dynamic receive focusing. Considering the challenges in accounting for these signal processing effects on data from clinical systems, the agreement among the BSC estimates shown in Fig. 2 is very encouraging.

CONCLUSION

BSC estimates of a tissue-mimicking sample, derived using four array-based ultrasound imaging systems, agreed to within 1.5 dB over the 3 − 13.5 MHz frequency range. The clinical system results were consistent with Faran’s scattering theory both in frequency dependence and scattering magnitude; they also were in agreement with laboratory measurements using single element transducers. These joint experimental results demonstrate that BSC can be estimated accurately with clinical imaging systems using a reference phantom data analysis technique. The findings illustrate the strong potential to translate QUS imaging from the laboratory to clinical settings.