Models of cylindrical bubble pulsation

Abstract

Three models are considered for describing the dynamics of a pulsating cylindrical bubble. A linear solution is derived for a cylindrical bubble in an infinite compressible liquid. The solution accounts for losses due to viscosity, heat conduction, and acoustic radiation. It reveals that radiation is the dominant loss mechanism, and that it is 22 times greater than for a spherical bubble of the same radius. The predicted resonance frequency provides a basis of comparison for limiting forms of other models. The second model considered is a commonly used equation in Rayleigh-Plesset form that requires an incompressible liquid to be finite in extent in order for bubble pulsation to occur. The radial extent of the liquid becomes a fitting parameter, and it is found that considerably different values of the parameter are required for modeling inertial motion versus acoustical oscillations. The third model was developed by V. K. Kedrinskii [Hydrodynamics of Explosion (Springer, New York, 2005), pp. 23–26] in the form of the Gilmore equation for compressible liquids of infinite extent. While the correct resonance frequency and loss factor are not recovered from this model in the linear approximation, it provides reasonable agreement with observations of inertial motion.

INTRODUCTION

A series of recent papers reports experiments on the dynamics of bubbles that are generated in narrow planar channels and grow to sizes that are considerably greater than the widths of the channels.1, 2, 3, 4, 5, 6 The flow of liquid surrounding the bubbles becomes approximately two-dimensional, and therefore the bubbles may be considered to be cylindrical in shape.

Ohl et al., motivated by applications to microfluidic devices, investigated the dynamics of both single1, 2, 3 and pairs4 of cylindrical bubbles generated by lasers. Growth-decay cycles were compared with theory for cylindrical bubbles in an incompressible liquid.1, 2 For single bubbles, an equation of Rayleigh-Plesset form that had been obtained previously by others7, 8, 9, 10 was used. The equation possesses a logarithmic singularity for an infinite incompressible liquid that is associated with infinite inertial load on the bubble wall, and the model therefore requires the radial extent of the liquid to be finite. The authors derived dynamical equations for pulsation and translation of a pair of coupled bubbles, also for an incompressible liquid and likewise requiring the liquid to be finite in extent. In comparisons of theory and experiment,1, 2, 4 the finite radial extent of the liquid required by the models was taken to be a fitting parameter that was determined empirically.

In experiments performed by Zhong et al.5, 6 on pairs of coupled bubbles in a channel, which were motivated by application to cell membrane poration, the lasers were phased to generate the second bubble near the time the first bubble reached its maximum radius. The anti-phase excitation caused the bubbles to form jets that were directed away from one other during collapse. This is in contrast to simultaneous generation of a pair of bubbles, in which case the jets are directed toward one other.

In each of these experiments1, 2, 3, 4, 5, 6 the bubbles are initially spherical (or hemispherical) in shape and, following subsequent inertial growth, become cylindrical only after their diameter exceeds the width of the channel (see Fig. 1). However, even small pulsations of a spherical bubble in a planar channel exhibit dynamics associated with cylindrical bubbles. The same logarithmic singularity appears in the dynamical equation for spherical bubble pulsation between infinite parallel rigid surfaces.11 This can be understood by using the method of images to satisfy the boundary conditions on the surfaces, which creates an infinite line array of spherical bubbles that radiates as a cylindrical source in an unbounded liquid.

Figure 1.

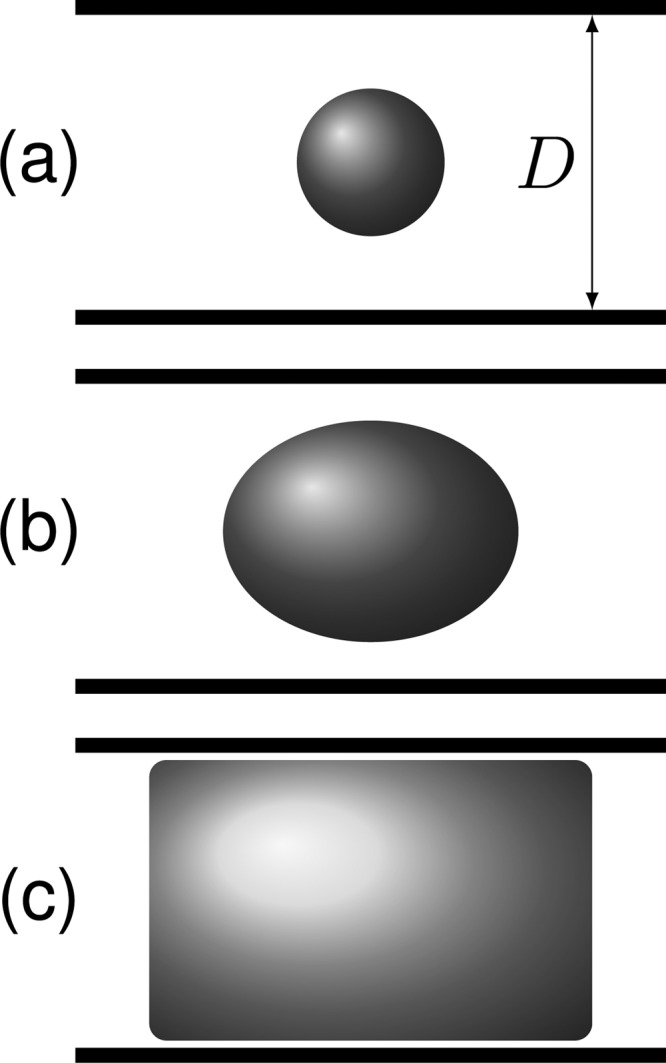
Expansion of an initially spherical bubble in a narrow channel, becoming cylindrical at maximum volume.

Alternatively, cylindrical bubbles are driven ultrasonically near resonance to induce acoustic streaming in microfluidic channels for performing mixing of fluids12 and sorting of microparticles.13 The bubble is formed by trapping gas in a slot, with the gas protruding into the channel forming the cylindrical interface with the liquid. In applications such as these there is interest in predicting the resonance frequency.12

A common approach to modeling the dynamics of cylindrical bubbles formed in rigid channels is to acknowledge that the channels are finite in length and assume they open into free space, because then the inertial load of an incompressible liquid is finite and can be approximated analytically for simple geometries; see especially Leighton14 and the references therein. For the effect of liquid compressibility to be negligible, channel length must be small compared with the acoustic length scale, which for harmonic motion is the wavelength in the liquid. Consider, for example, experiments reported recently by Sankin et al.5 in which bubbles were generated by laser in a channel of width 25 μm covering a rectangular area with dimensions 10 mm × 25 mm that determine the characteristic length of the channel. The bubbles grew to a diameter of approximately 50 μm, such that they were cylindrical in shape, and the flow around them was predominantly two dimensional, for much of their growth-collapse cycles. The duration of the growth and collapse was approximately 10 μs, during which time sound in water propagates 15 mm. This acoustic length scale is comparable to the channel length scale, and therefore in this case one should not assume a priori that the effect of liquid compressibility on the bubble dynamics is insignificant.

The purpose of this paper is to discuss effects of liquid compressibility in the context of cylindrical bubble dynamics, and thus to shed light on the manner in which existing models of cylindrical bubble dynamics are restricted in their domain of validity because of liquid compressibility. To initiate this discussion we begin in Sec. 2 with a derivation of the linear solution for cylindrical bubble pulsations in a compressible liquid. This solution is complete insofar as all three loss mechanisms are taken into account: acoustic radiation, viscosity, and heat conduction. The solution is compared with the corresponding result for a spherical bubble in a rigid channel to show how, in a compressible liquid, spherical bubble dynamics transition to cylindrical bubble dynamics as channel width is decreased. In Secs. 3, 4 the solution is compared with existing models of cylindrical bubble dynamics.

The most widely used model of cylindrical bubble dynamics is of Rayleigh-Plesset form, and this model is considered in Sec. 3. Previous approaches to estimating the aforementioned fitting parameter in this model—the radial extent of incompressible liquid—have focused on modeling inertial growth and collapse;1, 2, 4, 10, 15, 16, 17 see especially the discussion by Kedrinskii.10 It is shown in Sec. 3 by comparison with the solution in Sec. 2 that the radius found experimentally to be most appropriate for modeling inertial motion is smaller by at least an order of magnitude than the radius required to obtain the correct dynamical response for small pulsations of a cylindrical bubble. In particular, we find that the inertial load on an oscillating bubble in a compressible liquid is equivalent to that imposed by an incompressible liquid extending outward from the bubble to a distance on the order of one fifth of the acoustic wavelength. Section 3 concludes with the development of a model for the maximum volume achieved following inertial growth of a bubble in a channel, and which shows that the maximum volume is practically independent of the geometry of the channel.

In Sec. 4, a model in the form of the Gilmore equation that was developed by Kedrinskii10 for a cylindrical bubble in a compressible liquid is compared in the limiting case of small oscillations with the linear solution in Sec. 2.

Only the radial pulsation (monopole) mode is forbidden for a cylindrical bubble in an unbounded incompressible liquid. Because all higher surface modes of the bubble wall motion (dipole, quadrupole, etc.) conserve volume, they can oscillate freely even when the incompressible liquid is presumed infinite in extent. The focus of the present paper is exclusively on the monopole mode. Consideration of higher modes will be reported elsewhere.

LINEAR THEORY

A solution is derived in the linear approximation for the frequency response of a cylindrical bubble in a compressible liquid. Viscosity of the liquid surrounding the bubble and thermal conductivity of the gas inside the bubble are taken into account. An external acoustic pressure $p_{\text{ac}}(t)=p_0{e}^{-i\omega t}$ is applied uniformly to the bubble, where ω is angular frequency, resulting in the scattering of a cylindrical acoustic wave in the liquid. The pressure balance at the wall of a cylindrical bubble with equilibrium radius R₀ is expressed as

$$P_0+P_{\sigma }+p_0{e}^{-i\omega t}+p_{\text{sc}}=P_g\text{at}r=R_0,$$ (1)

where $P_0$ is atmospheric pressure, $P_{\sigma }$ is the Laplace pressure due to surface tension, p_sc is the pressure exerted on the bubble by the scattered acoustic wave, $P_g$ is the gas pressure inside the bubble, and r is the radial coordinate.

The pressures $P_{\sigma }$ and particularly $p_{\text{sc}}$ are calculated in Sec. 2A, $P_g$ in Sec. 2B. The solution for the frequency response is presented in Sec. 3C, where the natural frequency and loss factors are determined and compared with those for a spherical bubble.

Pressure in the liquid

The pressure increase due to surface tension at the cylindrical interface forming the wall of a bubble with radius R is

$$P_{\sigma }=\frac{\sigma }{R},$$ (2)

where σ is the surface tension. With the bubble radius expressed as

$$R(t)=R_0+R_{\omega }{e}^{-i\omega t},$$ (3)

where $R_0$ is the equilibrium radius and $R_{\omega }$ the complex amplitude of the oscillation, linearization of Eq. 2 yields

$$P_{\sigma }=\frac{\sigma }{R_0}-\frac{\sigma }{R_0^2}{R}_{\omega }{e}^{-i\omega t}.$$ (4)

The solution for an outgoing, axisymmetric cylindrical wave is

$$\psi =A{H}_0^{(1)}(\tilde{k}r)e^{-i\omega t},$$ (5)

where $H_0^{(1)}$ is the Hankel function of the first kind, of order zero, and A is an arbitrary constant. The liquid is assumed to be viscous, but not heat conducting, for which the complex wave number $\tilde{k}$ is determined by

$${\tilde{k}}^2=\frac{\rho {\omega }^2}{\tilde{K}+(4/3)\tilde{\mu }},$$ (6)

where $\tilde{K}$ and $\tilde{\mu }$ are complex bulk and shear moduli, respectively, the imaginary parts of which account for losses through the bulk (ζ) and shear (η) viscosity coefficients:

$$\tilde{K}=K-i\omega \zeta ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\tilde{\mu }=-\mathrm{i}\omega \eta .$$ (7)

The real part of $\tilde{\mu }$, which is the shear modulus μ, is zero for the liquid and therefore does not appear. Equations 6, 7 follow from recognition that the compressional wave speed in an inviscid elastic medium is ${[(K+\frac{4}{3}\mu )/\rho ]}^{1/2}$, and that the stress tensor for a viscoelastic medium, for time dependence $e^{-i\omega t}$, is18

$${\sigma }_{\mathit{i}\mathit{j}}=\tilde{K}{\varepsilon }_{\mathit{k}\mathit{k}}{\delta }_{\mathit{i}\mathit{j}}+2\tilde{\mu }({\varepsilon }_{\mathit{i}\mathit{j}}-\frac{1}{3}{\varepsilon }_{\mathit{k}\mathit{k}}{\delta }_{\mathit{i}\mathit{j}}),$$ (8)

where ${\varepsilon }_{\mathit{i}\mathit{j}}$ is the linearized strain tensor and ${\delta }_{\mathit{i}\mathit{j}}$ the Kronecker delta. Expansion of Eq. 6 yields, to leading order in the loss coefficients, the classical complex wave number for a viscous fluid;19

$$\tilde{k}=\frac{\omega }{c_0}+i\frac{{\omega }^2}{2{\rho }_0{c}_0^3}\left(\frac{4}{3}\eta +\zeta \right),$$ (9)

where $c_0={(K/{\rho }_0)}^{1/2}$ is the small-signal sound speed in the liquid and ${\rho }_0$ the equilibrium density.

The function ψ can be any scalar wave variable, such as acoustic pressure. Here it is convenient to regard it as displacement potential, and thus the radial particle displacement in the liquid is

$$u_r=\frac{\partial \psi }{\partial r}=-A\tilde{k}{H}_1^{(1)}(\tilde{k}r)e^{-i\omega t}.$$ (10)

The radial displacement of the bubble wall is given by $u_r$ evaluated at $r=R_0$:

$$R_{\omega }=-A\tilde{k}{H}_1^{(1)}(\tilde{k}{R}_0).$$ (11)

The pressure p_sc exerted by the liquid on the bubble wall is the negative of the radial stress at the bubble wall. From Eq. 8, the radial component of the stress tensor in the liquid is

$${\sigma }_{\mathit{r}\mathit{r}}=\left(\tilde{K}-\frac{2}{3}\tilde{\mu }\right)\left(\frac{\partial u_r}{\partial r}+\frac{u_r}{r}\right)+2\tilde{\mu }\frac{\partial u_r}{\partial r}.$$ (12)

The terms in u_r within the parentheses in Eq. 12 equal ${\nabla }^2\psi$ and can be replaced by $-{\tilde{k}}^2\psi$. Then with Eq. 10 substituted in the last term of Eq. 12, and noting that $\left(d/dz\right)H_1^{(1)}\left(z\right)=H_0^{(1)}-z^{-1}{H}_1^{(1)}$, Eq. 12 can be evaluated at the bubble wall to obtain

$${({\sigma }_{\mathit{r}\mathit{r}})}_{r=R_0}=-\left[{\rho }_0{\omega }^2{H}_0^{(1)}(\tilde{k}{R}_0)+\frac{2i\omega \eta \tilde{k}}{R_0}{H}_1^{(1)}(\tilde{k}{R}_0)\right]A{e}^{-i\omega t}.$$ (13)

Division of Eq. 13 by Eq. 11 and setting $p_{\text{sc}}=-{({\sigma }_{\mathit{r}\mathit{r}})}_{r=R_0}$ yields the scattered pressure in the liquid at the bubble wall in terms of the oscillation of the bubble wall:

$$p_{\text{sc}}=-\left[\frac{{\rho }_0{\omega }^2}{\tilde{k}}\frac{H_0^{(1)}(\tilde{k}{R}_0)}{H_1^{(1)}(\tilde{k}{R}_0)}+\frac{2i\omega \eta }{R_0}\right]R_{\omega }{e}^{-i\omega t}.$$ (14)

Pressure in the gas

It remains to evaluate P_g in Eq. 1. An ideal gas is assumed inside the bubble. The equation of state for an ideal gas typically expresses the pressure as a function of either density and temperature, $P_g=P_g({\rho }_g,T)$, or density and specific entropy, $P_g=P_g({\rho }_g,s)$:

$$\begin{array}{ccc}\frac{P_g}{P_{g0}}=\frac{{\rho }_{g}T}{{\rho }_{g0}{T}_0},\hfill & \hspace{0.17em}\hfill & \frac{P_g}{P_{g0}}={\left(\frac{{\rho }_g}{{\rho }_{g0}}\right)}^{\gamma }\hspace{0.17em}{e}^{(s-s_0)/c_v},\hfill \end{array}$$ (15)

where subscript 0 designates ambient value, and $\gamma =c_p/c_v$ is the ratio of specific heats at constant pressure $(c_p)$ and volume $(c_v)$. The equilibrium gas pressure is

$$P_{g0}=P_0+\frac{\sigma }{R_0},$$ (16)

as required to satisfy Eq. 1 in the absence of sound. Combining the state equations to eliminate density and then linearizing yields

$$\frac{s^{\prime }}{c_v}=\gamma \frac{T^{\prime }}{T_0}-(\gamma -1)\frac{{P^{\prime }}_g}{P_{g0}},$$ (17)

where primes designate perturbations about the ambient values, e.g., $s=s_0+s^{\prime }$.

The linear relation between entropy and temperature is

$${\rho }_{g0}{T}_0\frac{\partial s^{\prime }}{\partial t}={\kappa }_{\text{th}}{\nabla }^2{T}^{\prime },$$ (18)

where ${\kappa }_{\text{th}}$ is the thermal conductivity. Substitution of Eq. 17 in 18 yields

$$\frac{\partial T^{\prime }}{\partial t}=\chi {\nabla }^2{T}^{\prime }+\frac{\gamma -1}{\gamma }\frac{T_0}{P_{g0}}\frac{d{P^{\prime }}_g}{\mathit{d}\mathit{t}},$$ (19)

where $\chi ={\kappa }_{\text{th}}/{\rho }_{g0}{c}_p$ is the thermometric conductivity. Whereas the temperature of the gas $T^{\prime }\left(r,t\right)$ depends on r, it has been assumed that the pressure ${P^{\prime }}_g(t)$ does not because the acoustic wavelength in the gas is assumed large in comparison with the size of the bubble. In contrast, the thermal diffusion length in air, for example at 1 MHz, is on the order of microns. For time dependence $e^{-i\omega t}$ Eq. 19 becomes

$$T^{\prime }(r)=-\frac{\chi }{i\omega }{\nabla }^2{T}^{\prime }+\frac{\gamma -1}{\gamma }\frac{T_0}{P_{g0}}{P^{\prime }}_g.$$ (20)

Equation 20 is solved for $T^{\prime }$ as a function of ${P^{\prime }}_g$, after which the first of Eqs. 15 is used to calculate the change in volume resulting from the change in pressure.

The general solution of Eq. 20 that is finite at the origin is

$$T^{\prime }=B{J}_0(\beta r)e^{-i\omega t}+\frac{\gamma -1}{\gamma }\frac{T_0}{P_{g0}}{P^{\prime }}_g,$$ (21)

where

$$\beta =\sqrt{\frac{i\omega }{\chi }}=\frac{1+i}{l_{\text{th}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{l}_{\text{th}}=\sqrt{\frac{2\chi }{\omega }},$$ (22)

and $l_{\text{th}}$ is identified as the acoustic thermal boundary layer thickness. The constant B is determined by the boundary condition at the bubble wall. With the thermal conductivity of the liquid much higher than that of the gas the temperature at the bubble wall may be taken to be the equilibrium value T₀, such that $T^{\prime }=0$ at $r=R_0$. The coefficient B thus defined yields

$$\frac{T^{\prime }(r,t)}{T_0}=\left(1-\frac{J_0(\beta r)}{J_0(\beta R_0)}\right)\frac{\gamma -1}{\gamma }\frac{{P^{\prime }}_g(t)}{P_{g0}}.$$ (23)

Linearization of the first of Eqs. 15, after the density ratio ${\rho }_g/{\rho }_{g0}$ is replaced by the bubble volume ratio $V_0/V$, gives

$$\frac{V^{\prime }}{V_0}=\frac{T^{\prime }}{T_0}-\frac{{P^{\prime }}_g}{P_{g0}}.$$ (24)

Since Eq. 23 provides the temperature only within an infinitesimally thin cylindrical ring of radius r, Eq. 24 applies only to that particular ring. Thus let the equilibrium volume of that ring be $d{V}_0=2\pi rhdr$, where h is a reference axial length for the bubble, and therefore the equilibrium volume of the entire bubble is $V_0=\pi R_0^{2}h$. With $d{V}^{\prime }$ representing the change in shell volume due to changes in pressure and temperature Eq. 24 becomes, following substitution of Eq. 23, and with $d{V}^{\prime }/d{V}_0$ replacing $V^{\prime }/V_0$,

$$\frac{d{V}^{\prime }}{2\pi hr\hspace{0.17em}\hspace{0.17em}dr}=-\left[1+(\gamma -1)\frac{J_0(\beta r)}{J_0(\beta R_0)}\right]\frac{{P^{\prime }}_g(t)}{\gamma P_{g0}},$$ (25)

integration of which yields

$$\frac{V^{\prime }}{V_0}=-\left[1+(\gamma -1){\displaystyle {\int }_0^{R_0}\frac{J_0(\beta r)}{J_0(\beta R_0)}\frac{2\pi hr\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}dr}{\pi R_0^{2}h}}\right]\frac{{P^{\prime }}_g}{\gamma P_{g0}}$$ (26)

$$=-\frac{{P^{\prime }}_g}{\kappa P_{g0}}.$$ (27)

The quantity

$$\kappa =\frac{\gamma }{1+(\gamma -1)\Lambda (\beta R_0)}$$ (28)

introduced in Eq. 27, where

$$\Lambda (\beta R_0)=\frac{2J_1(\beta R_0)}{\beta R_0{J}_0(\beta R_0)}$$ (29)

$$\to \hspace{0.17em}1\text{as}{R}_0/l_{\text{th}}\to 0$$

$$\to \hspace{0.17em}0\text{as}{R}_0/l_{\text{th}}\to \infty ,$$

functions as a polytropic index for the gas inside the bubble and depends only on $R_0/l_{\text{th}}$. As shown in Fig. 2 for $\gamma =1.4$, in the limit $R_0/l_{\text{th}}\to 0$ the index approaches the value $\kappa =1$ for an isothermal process, and in the limit $R_0/l_{\text{th}}\to \infty$ it increases monotonically toward the value $\kappa =\gamma$ for an isentropic process. Although the magnitude of κ is plotted in Fig. 2, the curve is virtually indistinguishable from a plot of the real part, as the imaginary part is small.

Figure 2.

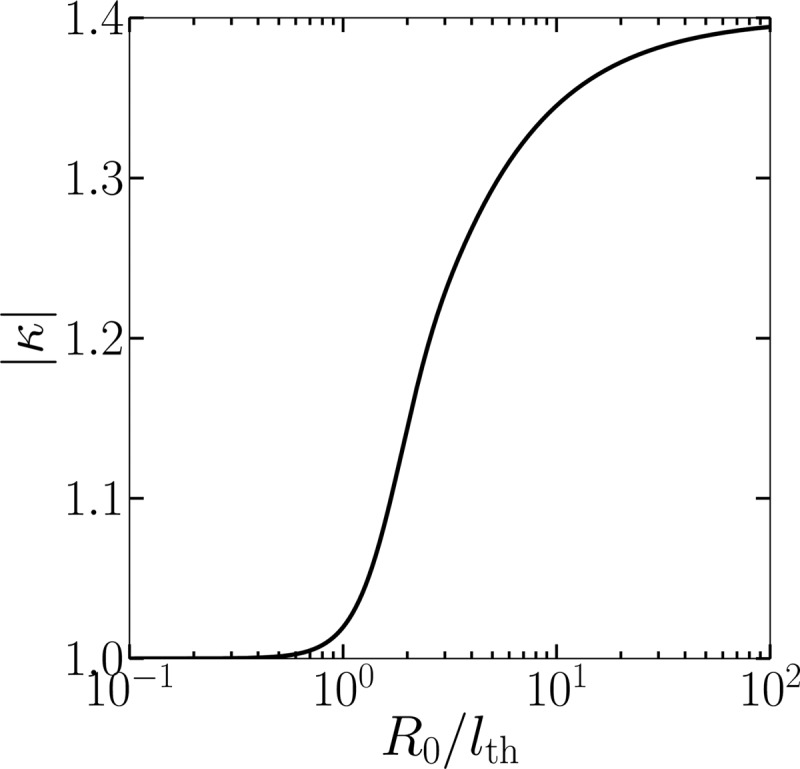
Magnitude of the effective polytropic index for a cylindrical bubble. The real part of κ is virtually indistinguishable from the magnitude.

Since $V\left(t\right)\propto R^2\left(t\right)$ linearization yields $V^{\prime }/V_0=2R_{\omega }{e}^{-i\omega t}/R_0$, and from Eq. 27

$$\frac{{P^{\prime }}_g}{P_{g0}}=-2\kappa \frac{R_{\omega }{e}^{-i\omega t}}{R_0}.$$ (30)

The right-hand side of Eq. 1 thus becomes

$$P_g=P_{g0}+{P^{\prime }}_g(t)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=P_0+\frac{\sigma }{R_0}-2\kappa \left(P_0+\frac{\sigma }{R_0}\right)\frac{R_{\omega }{e}^{-i\omega t}}{R_0}.$$ (31)

Natural frequency and loss factors

Substitution of Eqs. 4, 14 and 31 in Eq. 1 provides the frequency response of the bubble wall to the applied sound pressure:

$$R_{\omega }={\left[\frac{{\rho }_0{\omega }^2}{\tilde{k}}\frac{H_0^{(1)}(\tilde{k}{R}_0)}{H_1^{(1)}(\tilde{k}{R}_0)}-\frac{2\kappa P_0}{R_0}-\frac{(2\kappa -1)\sigma }{R_0^2}+\frac{2i\omega \eta }{R_0}\right]}^{-1}\hspace{0.17em}\hspace{0.17em}{p}_0.$$ (32)

Since the bubble is assumed small in comparison with a wavelength in the liquid we have $\left|\tilde{k}{R}_0\right|\ll 1$, and therefore the Hankel functions can be expanded in powers of $\tilde{k}{R}_0$ to obtain, at leading order,

$$\frac{H_0^{(1)}(\tilde{k}{R}_0)}{H_1^{(1)}(\tilde{k}{R}_0)}=\tilde{k}{R}_0\left(\ln \frac{2}{\tilde{k}{R}_0}-{\gamma }_E+i\frac{\pi }{2}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|\tilde{k}{R}_0\right|\ll 1,$$ (33)

where ${\gamma }_E=0.577\dots$ is Euler’s constant. Equation 32 thus becomes

$$R_{\omega }={\left[{\rho }_0{\omega }^2\hspace{0.17em}{R}_0\hspace{0.17em}\left(\ln \frac{2}{\tilde{k}{R}_0}-{\gamma }_E+i\frac{\pi }{2}\right)-\frac{2\kappa P_0}{R_0}-\frac{(2\kappa -1)\sigma }{R_0^2}+\frac{2i\omega \eta }{R_0}\right]}^{-1}{p}_0.$$ (34)

In the limit $c_0\to \infty$, for which $\tilde{k}\to 0$, the logarithm becomes infinite, and thus $R_{\omega }\to 0$, which is consistent with the transition to an unbounded incompressible liquid, in which volume changes are prohibited.

The Minnaert frequency of a spherical bubble is the natural frequency in the absence of viscosity, surface tension, and heat conduction. Under these conditions ($\eta =\sigma =0$, $\kappa =\gamma$), setting the term in brackets on the right-hand side of Eq. 34 to zero and letting k₀R₀ designate the root of this equation yields

$${(k_0{R}_0)}^2\left(\ln \frac{2}{k_0{R}_0}-{\gamma }_E+i\frac{\pi }{2}\right)=2\frac{\gamma P_0}{{\rho }_0{c}_0^2},$$ (35)

where $\gamma P_0/{\rho }_0{c}_0^2$ is the ratio of the bulk modulus of the gas to that of the liquid. For an air bubble in water this ratio is taken to be 6.4 × 10⁻⁵, in which case the root is

$$k_0{R}_0=0.00467-i0.000718,$$ (36)

where the real part determines the natural frequency and the imaginary part is due to radiation damping. Had the asymptotic approximation in Eq. 33 not been used, the root obtained agrees with Eq. 36 to the accuracy shown.

Unlike for a spherical bubble, a finite undamped natural frequency does not exist for a cylindrical bubble in an unbounded incompressible liquid because the oscillations cannot exist without radiation. Thus define $k_0={\tilde{\omega }}_0/c_0$, where ${\tilde{\omega }}_0={\omega }_0(1-i{\delta }_{\text{rad}}/2)$ is a complex angular frequency, $f_0={\omega }_0/2\pi$ the damped natural frequency, and ${\delta }_{\text{rad}}$ the radiation loss factor, defined such that its reciprocal is the quality factor. Then from Eq. 36

$$R_0{f}_0=1.10\mathrm{m}/\mathrm{s},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\delta }_{\text{rad}}=\mathrm{0.308.}$$ (37)

The corresponding quantities for a spherical air bubble in water are20$R_0{f}_0={(3\gamma P_0/{\rho }_0)}^{1/2}/2\pi =3.26\mathrm{m}/\mathrm{s}$ and ${\delta }_{\text{rad}}=k_0{R}_0=0.014$. For the same radius, a cylindrical bubble thus pulsates at one third the natural frequency, and with 22 times the radiation damping, of a spherical bubble.

An equation that is formally equivalent to Eq. 35 was obtained by Ostrovskii21 for the natural frequency and radiation damping of an empty cylindrical cavity in an elastic medium. There the natural frequency was defined as the solution of only the real part of Eq. 35. The solution of Eq. 35 in the absence of the imaginary term is k₀R₀ = 0.00485, quite close to the real part of Eq. 36.

To obtain the loss factors for heat conduction $({\delta }_{\text{th}})$ and viscosity $({\delta }_{\text{vis}})$ the effect of radiation loss must be removed from Eq. 34, which is accomplished by removing the imaginary term $i\pi /2$. The total loss factor is then expressed as

$${\delta }_{\text{tot}}={\delta }_{\text{rad}}+{\delta }_{\text{th}}+{\delta }_{\text{vis}}.$$ (38)

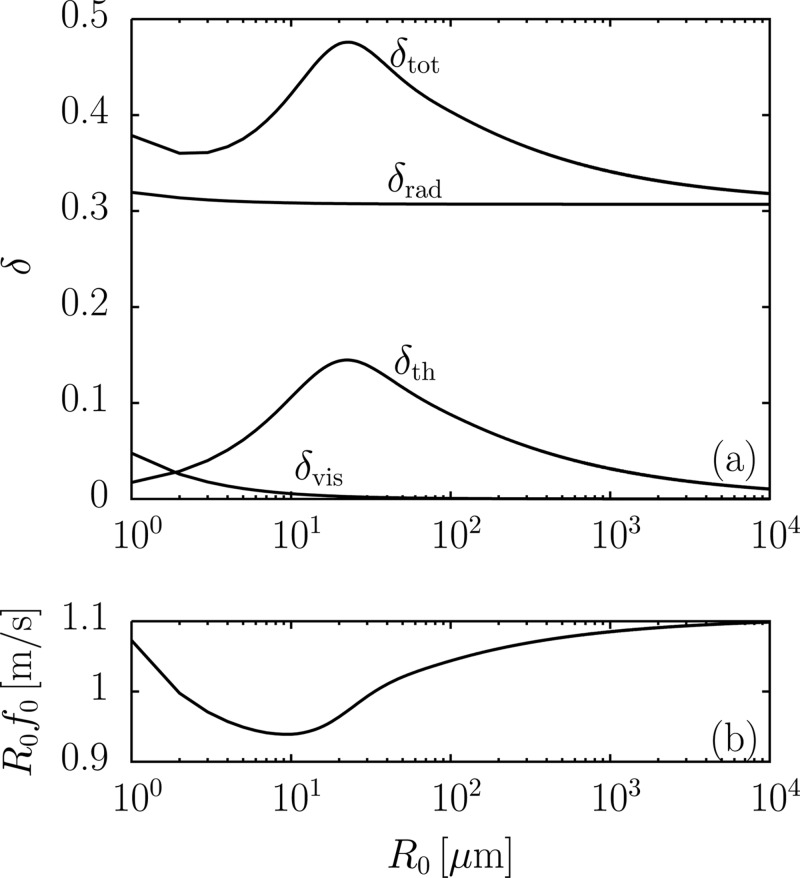
All four quantities are plotted in Fig. 3a with surface tension taken into account. It is seen that acoustic radiation is the dominant loss mechanism over the entire range of radii shown. In contrast, radiation is the dominant loss mechanism for spherical bubbles only for radii greater than approximately 3 mm, whereas heat conduction dominates between 3 μm and 3 mm, and below 3 μm viscosity dominates (see Fig. 3.20 of Leighton20).

Figure 3.

(a) Loss factors and (b) resonance frequency for a cylindrical bubble.

Shown in Fig. 3b is the quantity $R_0{f}_0$ as a function of bubble radius when all effects in Eq. 34 are retained. The value $R_0{f}_0=1.10\mathrm{m}/\mathrm{s}$ in Eq. 37 is achieved only for bubble radii sufficiently large that thermal effects are negligible. The minimum value $R_0{f}_0=0.94\mathrm{m}/\mathrm{s}$ at $R_0\simeq 10\mu \mathrm{m}$ coincides approximately with the maximum value of ${\delta }_{\text{th}}$ in Fig. 3a, which marks the transition from an adiabatic to an isothermal process as R₀ is decreased. Because of surface tension, $R_0{f}_0$ increases without bound as $R_0\to 0$.

Finally, for sufficiently narrow channels formed by rigid parallel walls the dynamics of a spherical bubble may be expected to resemble cylindrical bubble dynamics. The extent to which this occurs may be assessed by comparing Eq. 35 with the corresponding result obtained by Cui et al.11 for a spherical bubble of radius $R_{\text{sph}}$ centered in a compressible liquid between rigid parallel walls separated by distance D [obtained from their Eq. 11 for $\left|k_0{R}_{\text{sph}}\right|\ll 1$]:

$${(k_0{R}_{\text{sph}})}^2\left(2\frac{R_{\text{sph}}}{D}\ln \frac{R_{\text{sph}}/D}{k_0{R}_{\text{sph}}}+1+i\pi \frac{R_{\text{sph}}}{D}\right)=3\frac{\gamma P_0}{{\rho }_0{c}_0^2}.$$ (39)

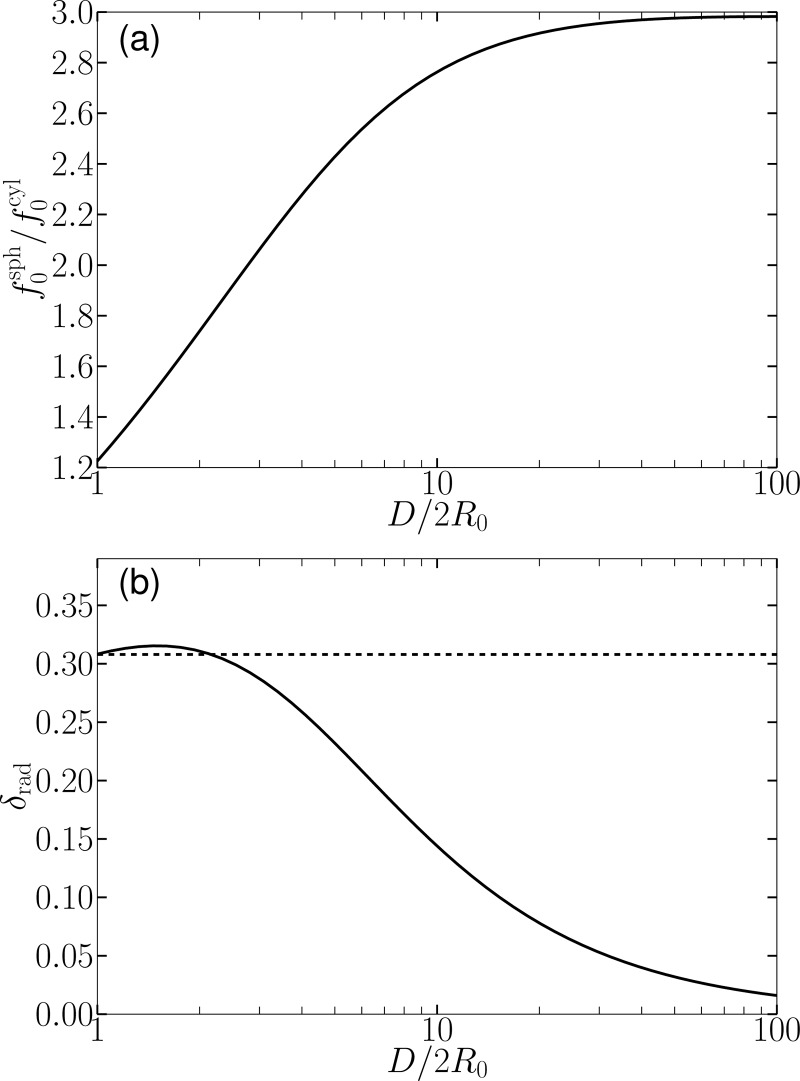
Note that Eqs. 35, 39 exhibit the same functional dependence on k₀, and therefore on natural frequency and radiation damping. For $D\gtrsim 100R_{\text{sph}}$ the solution of Eq. 39 for the natural frequency agrees with that for a spherical bubble in a free field. While a restriction on Eq. 39 is that channel width is less than one wavelength, $D<\lambda$, the solution for the radiation damping obtained from a more general equation,11 valid for arbitrarily wide channels, equals the free-field result for $D\gtrsim 10\lambda$.

Solutions of Eqs. 35, 39 are most easily compared when the spherical bubble has the same radius as the cylindrical bubble, $R_{\text{sph}}=R_0$, because in this case both the ratio of the natural frequencies $f_0^{\text{sph}}/f_0^{\text{cyl}}$ and the radiation loss factor ${\delta }_{\text{rad}}$ depend only on $D/R_0$. These quantities are plotted in Fig. 4 as a function of $D/2R_0$, where $D/2R_0=1$ marks the point where the channel width equals the bubble diameter. Figure 4a shows that $f_0^{\text{sph}}/f_0^{\text{cyl}}$ is within 10% of its free field value of 2.96 for $D/2R_0\gtrsim 10$. As channel width is reduced $f_0^{\text{sph}}/f_0^{\text{cyl}}$ decreases toward unity, indicating the transition to cylindrical bubble dynamics. This transition is also revealed by the plot of the radiation loss factor for the spherical bubble (solid line) in Fig. 4b, which shows that the value of ${\delta }_{\text{rad}}$ is approximately the same as for a cylindrical bubble (dashed line) for $D/2R_0\lesssim 3$. Even for $D/2R_0=10$ the loss factor is an order of magnitude larger than its value of 0.014 in a free field.

Figure 4.

(a) Natural frequency and (b) radiation loss factor (solid line) for a spherical bubble in a rigid channel, compared as a function of channel width with the corresponding quantities for a cylindrical bubble with the same radius [dashed line in (b)].

INCOMPRESSIBLE LIQUID THEORY

The equation of Rayleigh-Plesset form that applies to a cylindrical bubble in an incompressible liquid is now considered. It can be derived using Lagrange’s equation:

$$\frac{d}{\mathit{d}\mathit{t}}\left(\frac{\partial L}{\partial \dot{R}}\right)-\frac{\partial L}{\partial R}=0,$$ (40)

where $L=K-U$, K, and U are taken to be the Lagrangian, kinetic energy, and potential energy of the system, respectively.

The bubble is assumed to be constrained by parallel plates and thus have finite axial length D as depicted in Fig. 1c. The kinetic energy of the gas inside the bubble may be ignored, and the kinetic energy of the liquid is

$$K=\frac{1}{2}{\rho }_{0}D{\displaystyle {\int }_R^{\infty }{v}^{2}2\pi r\hspace{0.17em}dr=\pi {\rho }_{0}D{R}^2{\dot{R}}^2}{\displaystyle {\int }_R^{\infty }\frac{\mathit{d}\mathit{r}}{r},}$$ (41)

where the relation $v=(R/r)\dot{R}$ for the radial velocity in the liquid was taken into account. The integral does not converge, reflecting the infinite inertia of the radial flow due to the incompressibility of the unbounded liquid. For the bubble to pulsate, as predicted by linear theory for a compressible liquid, the inertial load of the liquid on the bubble wall must be finite. This is accomplished by arbitrarily limiting the radial extent of the incompressible liquid to a finite distance r₀ that permits Eq. 41 to be evaluated:

$$K=\pi {\rho }_{0}D{R}^2{\dot{R}}^2\ln \frac{r_0}{R}.$$ (42)

It may be expected that for large bubble oscillations, this approximation of the inertial load on the bubble may require r₀ to depend on R.

Since U depends on R but not $\dot{R}$, the potential energy appears only in the second term in Eq. 40, as $dU/dR$. We thus consider the change in potential energy as the bubble expands incrementally by amount dV, where the bubble volume is $V=\pi R^{2}D$ and thus $dV=2\pi DRdR$. As the bubble expands, the work done on the liquid by the gas $(P_g)$ and vapor $(P_v)$ pressures inside the bubble, and by the pressure at infinity $(P_{\infty })$, is $dW=\left(P_g+P_v-P_{\infty }\right)dV$. Because the liquid is incompressible the potential energy U_p associated with pressure is reduced by an amount equal to this work, and so $d{U}_p=-2\pi D\left(P_g+P_v-P_{\infty }\right)R\hspace{0.17em}dR$.

At the same time, expansion of the bubble increases the potential energy associated with surface tension. To determine this quantity we consider the situation shown in Fig. 1c where the upper and lower planar surfaces of the cylindrical bubble are separated from the channel walls by a thin liquid layer. The energy $U_{\sigma }$ associated with surface tension equals σ times the area of the cylinder, $U_{\sigma }=\sigma (2\pi RD+2\pi R^2)$, the differential of which is $d{U}_{\sigma }=2\pi \sigma \left(D+2R\right)dR$. Setting $dU=d{U}_p+d{U}_{\sigma }$ one obtains

$$\frac{\mathit{d}\mathit{U}}{\mathit{d}\mathit{R}}=-2\pi RD(P_g+P_v-P_{\infty })+2\pi \sigma (D+2R).$$ (43)

At equilibrium, for which $dU/dR=0$, $P_g=P_{g0}$, and $P_{\infty }=P_0$, Eq. 43 can be solved for the equilibrium gas pressure:

$$P_{g0}=P_0+\frac{\sigma }{R_0}+\frac{2\sigma }{D}-P_v.$$ (44)

Substituting Eqs. 42, 43 in Eq. 40, with $P_g=P_{g0}{(R_0/R)}^{2_{\gamma }}$, yields

$$(R\ddot{R}+{\dot{R}}^2)\ln \frac{r_0}{R}-\frac{1}{2}{\dot{R}}^2=\frac{P_L-P_{\infty }}{{\rho }_0},$$ (45)

where

$$P_L=\left(P_0+\frac{\sigma }{R_0}+\frac{2\sigma }{D}-P_v\right){\left(\frac{R_0}{R}\right)}^{2\gamma }-\frac{\sigma }{R}-\frac{2\sigma }{D}+P_v.$$ (46)

An imposed acoustic pressure $p_{\text{ac}}$ is taken into account through $P_{\infty }$:

$$P_{\infty }=P_0+p_{\text{ac}}(t).$$ (47)

From the form of Eq. 45, $P_L$ is recognized as the pressure in the liquid next to the bubble wall.20 Thus, viscosity can be taken into account by adding to $P_L$ the pressure $P_{\eta }$ that viscous stress exerts on the bubble wall [recall Eq. 12]:

$$P_{\eta }=-2\eta {\frac{\partial v}{\partial r}|}_{r=R}=2\eta \frac{\dot{R}}{R}.$$ (48)

Without the terms that account for surface tension and viscosity, Eq. 45 is the most commonly used model of cylindrical bubble dynamics.

Harmonic oscillations

In addition to the infinite inertial load for an unbounded incompressible liquid, as shown in Sec. 2C a deficiency of Eq. 45 is that, except for bubbles with radii less than 1 μm, radiation and thermal losses dominate viscous losses, with radiation being the most important loss mechanism, at least for small bubble pulsations. Comparison of Eq. 34 with the linear approximation of Eq. 45 provides insight into how incompressible-flow theory might be adjusted to approximate the effects of finite inertial load and radiation loss.

Linearization of Eq. 45 after ignoring viscosity and surface tension yields, for $p_{\text{ac}}=p_0{e}^{-i\omega t}$,

$$\left({\omega }^2\ln \frac{r_0}{R_0}-\frac{2\gamma P_0}{{\rho }_0{R}_0^2}\right)R_{\omega }^I=\frac{p_0}{{\rho }_0{R}_0},$$ (49)

where the superscript I denotes incompressible liquid. The natural frequency according to this result, obtained by setting the left-hand side to zero, may be expressed as

$$R_0{f}_0=\frac{1}{2\pi }\sqrt{\frac{2\gamma P_0}{{\rho }_0\ln (r_0/R_0)}}.$$ (50)

The natural frequency predicted by linear theory for a compressible liquid is obtained with this equation by setting R₀f₀ equal to its value in Eq. 37 and solving for r₀, which yields

$$r_0/R_0\sim 350.$$ (51)

As discussed in Sec. 3B, this value of $r_0/R_0$ obtained for harmonic oscillations is an order of magnitude larger than the corresponding values determined empirically by matching Eq. 45 to observations of bubble collapse.

A more general assessment of the inertial load is provided by comparing Eq. 49 with the corresponding form of Eq. 34:

$$\left[{\omega }^2\left(\ln \frac{2}{k{R}_0}-{\gamma }_E+i\frac{\pi }{2}\right)-\frac{2\gamma P_0}{{\rho }_0{R}_0^2}\right]R_{\omega }^C=\frac{p_0}{{\rho }_0{R}_0},$$ (52)

where $k=\omega /c_0$, and the superscript C denotes compressible liquid. Equating the real parts of Eqs. 49, 52 yields $r_0=2/(e^{{\gamma }_E}k)$, or

$$r_0/\lambda \sim \mathrm{0.18.}$$ (53)

The radial extent of incompressible liquid required to simulate the inertial load of a compressible liquid on a pulsating cylindrical bubble is thus on the order of one fifth of a wavelength.

The imaginary term in Eq. 52, which is associated with radiation loss, may be interpreted as a pressure

$$p_{\text{rad}}=-i\frac{\pi }{2}{\rho }_0{\omega }^2{R}_0{R}_{\omega }^I{e}^{-i\omega t}$$ (54)

acting on the bubble. Alternatively, comparison of Eqs. 34, 52 reveals that radiation loss at frequency ω equals the increase in viscous loss that would be achieved by augmenting the viscosity coefficient by an amount ${\eta }^{\prime }=\frac{\pi }{4}{\rho }_0\omega R_0^2$.

Collapse time

During most of the collapse phase following rapid inertial growth of a bubble, the interior of the bubble may be modeled as a vacuum. If surface tension and viscosity are also ignored then $P_L=0$, and the bubble is referred to as a Rayleigh cavity.22 The work done (per unit length) by pressure $P_0$ moving the bubble wall away from an initial (maximum) radius $R_M$ is $\pi \left({\mathit{\text{R}}}_M^2-R^2\right)P_0$. The bubble wall velocity is zero at the start of the collapse phase, and therefore the work equals the kinetic energy in the liquid. If the kinetic energy is assumed to be given by Eq. 42, then the following expression is obtained for the bubble wall velocity:

$${\dot{R}}^2=\frac{P_0}{{\rho }_0}\frac{R_M^2/R^2-1}{\ln (r_0/R)}.$$ (55)

The collapse time $T_c$ is ${\displaystyle {\int }_{R_M}^0\mathit{d}\mathit{R}}/\dot{R}$ and can be expressed as

$$T_c=\Gamma R_M\sqrt{{\rho }_0/P_0},$$ (56)

where

$$\Gamma ={\displaystyle {\int }_0^1{\left(\ln \frac{r_0/R_M}{x}\right)}^{1/2}\frac{x\hspace{0.17em}dx}{\sqrt{1-x^2}}.}$$ (57)

The Rayleigh collapse time for a spherical bubble is given by Eq. 56 with $\Gamma =0.915$.23

The dependence of Γ on $r_0/R_M$ is shown in Fig. 5. Kedrinskii10 showed that measurements of pulsation periods (time for both growth and collapse) for cylindrical bubbles in open water with maximum radii on the order of 10 cm were in good agreement with estimates based on Eq. 45 with $r_0/R_M\sim 10$, for which $\Gamma \sim 1.6$. The collapse time is thus longer than for a spherical bubble with the same initial radius, which is consistent with the prediction in Sec. 2C that cylindrical bubbles have lower natural frequencies. In experiments performed in narrow planar channels, Ohl et al.1, 2 found that the collapse phase of laser-generated bubbles achieving maximum radii of approximately 50 μm was also well described by Eq. 45 with $r_0/R_M$ of order 10. This experimental agreement with Eq. 45 thus spans three orders of magnitude in bubble size.

Figure 5.

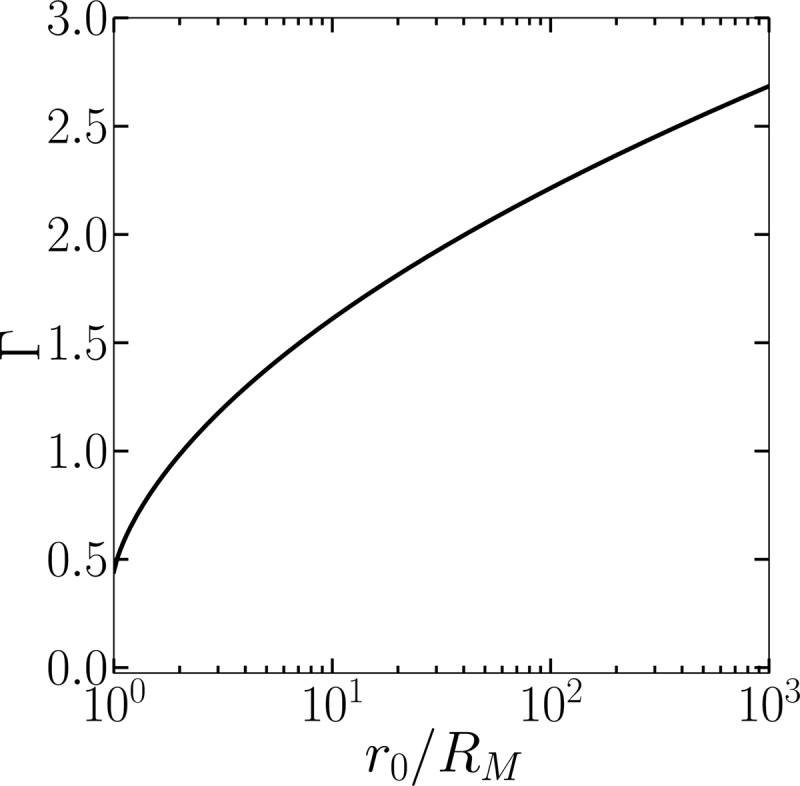
Coefficient appearing in Eq. 56 for collapse time.

The implication of r₀ being a constant is that the mass of liquid surrounding the bubble increases as the bubble collapses. If instead the mass of liquid is held constant, and if r₀ now designates the initial radial extent of the liquid, then the instantaneous radial extent r₁ must decrease according to the relation $r_0^2-R_M^2=r_1^2-R^2$. In this case $r_0/R_M$ in Eq. 57 is replaced by ${\left[{\left(r_0/R_M\right)}^2-\left(1-x^2\right)\right]}^{1/2}$. The difference this makes in Fig. 5 is negligible for $r_0/R_M>2$.

Delale et al.24 take a different approach to handling the singularity in Eq. 45 for an infinite liquid $(r_0=\infty )$. They obtain a solution by requiring that the term multiplying the logarithm vanish, subject to a compatibility condition on the pressure. Thus setting $R\ddot{R}+{\dot{R}}^2=(d/dt)(R\dot{R})=0$ they integrate to obtain $R=R_0{[1+2({\dot{R}}_0/R_0)t]}^{1/2}$, where the subscript zero here signifies initial value. The solution predicts that a bubble initially at rest will remain at rest, which is consistent with the infinite inertia of an unbounded incompressible liquid. Similarly, the solution cannot be used to describe an inertial growth-collapse cycle since ${\dot{R}}_0=0$ when the bubble achieves its maximum radius. In fact, the solution predicts that inertial growth is unbounded, again consistent with infinite inertia.

Maximum volume

For a rigid channel of finite length, a dynamical equation of Rayleigh-Plesset form can be constructed by calculating the inertia of an incompressible liquid for the given geometry.14 Dynamical equations of this sort, valid for channels sufficiently short that liquid compressibility may be ignored, depend on both the length and width of the channel. However, conservation of energy reveals that the maximum volume achieved following growth of a bubble in such channels is practically independent of channel geometry.

If the bubble is initially at rest with volume V₀ and also at rest at maximum volume V_M, if the channel walls are rigid, and if losses during expansion due to viscosity, heat conduction, and radiation are negligible, then the two volumes are related by conservation of potential energy. The change in potential energy, including the change $P_0\Delta V$ in the surrounding liquid, is $\Delta U_p=-{\displaystyle {\int }_{V_0}^{V_M}(P_g+P_v-P_0)}\hspace{0.17em}dV$, which is evaluated using $P_g{V}^{\gamma }=\text{const}$, and with $P_v$ and $P_0$ assumed constant. With the change associated with surface tension written simply as $\Delta U_{\sigma }=U_{\sigma M}-U_{\sigma 0}$ for now, setting $\Delta U_p+\Delta U_{\sigma }=0$ yields

$$\frac{1}{\gamma -1}(P_{\mathit{g}\mathit{M}}{V}_M-P_{g0}{V}_0)+(P_0-P_v)(V_M-V_0)+(U_{\sigma M}-U_{\sigma 0})=0.$$ (58)

This equation can be solved for the maximum bubble volume $V_M$ given the initial conditions of the bubble, and expressions for the surface tension in the initial and final states.

If the bubble starts out spherical, and if $V_M$ is sufficiently large that the Laplace pressure due to surface tension is negligible at maximum volume, then $V_M$ is independent of channel geometry because there is no energy storage in the rigid walls. However, channel geometry does affect the inertia of the liquid, and it therefore affects the time required for the bubble to reach its maximum volume. These observations are consistent with measurements reported recently by Gonzalez-Avila et al.3 of bubble growth in microfluidic channels of variable width D. The results in their Fig. 4 were obtained using a laser to generate a hemispherical bubble on one wall of a channel. The laser energy was kept the same for each bubble in order to maintain the same initial conditions (effectively the same $P_{g0}$ and $V_0$). Channel widths were characterized by the ratio $\eta =D/R_M^{\perp }$, where $R_M^{\perp }$ is the projection of the maximum bubble radius into the plane of the channel wall where the bubble was generated. Measurements were made for four values of $\eta :$ 7.3, 3.1, 1.6, and 0.4. At maximum volume in the narrowest channel $(\eta =0.4)$ the bubble spanned the breadth of the channel and was distinctly cylindrical in shape, whereas for dimensionless channel widths of 1.6 and greater the bubble remained approximately hemispherical at maximum volume (see the photographs in their Fig. 3).

Plotted in their Fig. 4 is the measured equivalent bubble radius $R_{\text{eq}}(t)$, where $R_{\text{eq}}$ is the radius of a hemisphere having the same volume as the bubble. The maximum values of $R_{\text{eq}}$ reported for the four channel widths lie between 133 μm and 143 μm, corresponding to a spread of ±3.6% about the median. This spread may be compared with the authors’ observation that fluctuations in the laser energy resulted in variations of approximately ±4% in the maximum radius. These data are consistent with the conclusion that maximum bubble volume is independent of channel geometry. Their measurements also show significant variations in the time for bubble growth and collapse as a function of channel width, as expected due to the different inertial loads on the bubble.

Equation 58 is now applied to two specific cases of bubble generation between parallel plates. In the first, the shape of the bubble is spherical in both the compressed initial state and at maximum volume. With the energy stored in surface tension given by $U_{\sigma }=4\pi R^2\sigma$, Eq. 58 can be written in the form

$$(P_0-P_v)(x^3-1)+\frac{3\sigma }{R_0}(x^2-1)-\frac{P_{g0}}{\gamma -1}(1-x^{-3(\gamma -1)})=0,$$ (59)

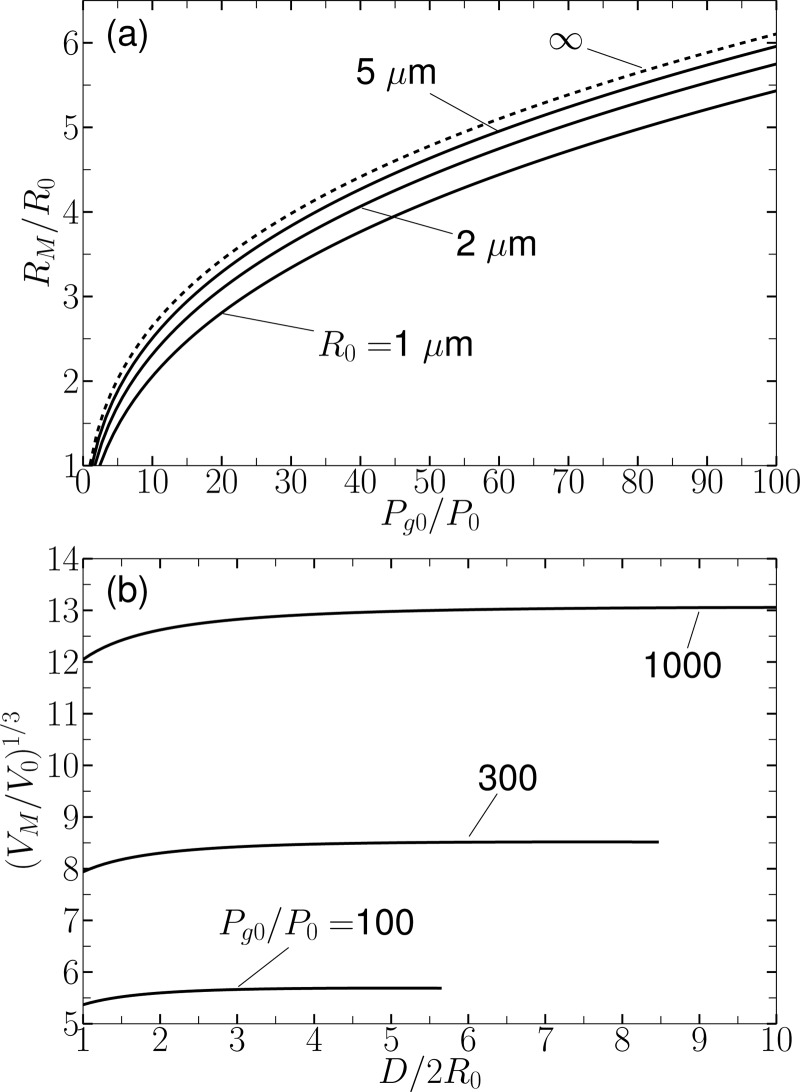
where $x=R_M/R_0$. Equation 59 can be solved numerically for the maximum bubble radius $R_M$ given the initial conditions for the bubble, particularly the initial gas pressure P_g0 and radius R₀. The equation is applicable when the predicted maximum bubble diameter does not exceed the channel width. Shown in Fig. 6a are plots of the normalized maximum bubble radius as a function of initial gas pressure for several initial radii under otherwise standard conditions for air and water (P₀ = 101.3 kPa, P_v = 2.3 kPa, σ = 0.073 N/m). From Eq. 59 it can be seen that for sufficiently large initial radii the solution for $R_M/R_0$ becomes independent of surface tension, and therefore independent of $R_0$. This limit is given by the dashed line in Fig. 6a.

Figure 6.

(a) Maximum radius of a spherical bubble in a channel as a function of initial gas pressure, for several initial bubble radii. (b) Maximum effective radius of a bubble that is initially spherical and becomes cylindrical at maximum volume, as a function of channel width for several initial gas pressures.

In the second case, as depicted in Fig. 1, a bubble between parallel plates starts out spherical with radius $R_0$ in its compressed initial state and becomes cylindrical at maximum volume $V_M=\pi R_M^{2}D$, where $R_M$ here is the radius of the cylinder. The energy stored in surface tension in the initial state is again $U_{\sigma 0}=4\pi R_0^2\sigma$. In the final state, as in the derivation of Eq. 45, we assume that the planar surface at each end of the cylindrical bubble is separated from the channel wall by a thin layer of liquid as in Fig. 1c, such that the total energy stored in surface tension is $U_{\sigma M}=\sigma (2\pi R_{M}D+2\pi R_M^2)$. Under these circumstances Eq. 58 may be expressed as

$$(P_0-P_v)(y-1)+\frac{3\sigma }{R_0}\left[\frac{1}{3}\frac{y}{\alpha }+{\left(\frac{2}{3}\alpha y\right)}^{1/2}-1\right]-\frac{P_{g0}}{\gamma -1}(1-y^{-(\gamma -1)})=0,$$ (60)

where $y=V_M/V_0$ and $\alpha =D/2R_0$. For a bubble to be spherical initially requires $\alpha >1$. The minimum value of $V_M$ in relation to channel width that is required for an initially spherical bubble to become cylindrical at maximum volume is not easily determined. For present purposes it is sufficient to let this requirement be approximately $2R_M>D$, which corresponds to $y^{1/3}>\alpha$. Therefore solutions of Eq. 60 that are relevant to the envisioned evolution of the bubble shape must lie in a parameter space defined nominally by $y^{1/3}>\alpha >1$.

Figure 6b shows the quantity ${\left(V_M/V_0\right)}^{1/3}$, which is a normalized maximum equivalent radius, plotted as a function of the dimensionless channel width $D/2R_0$ for a bubble with initial radius $R_0=2\mu \mathrm{m}$ and for several initial gas pressures. Plot lines are ended where $D/2R_0={\left(V_M/V_0\right)}^{1/3}$ because beyond that point the condition $y^{1/3}>\alpha$ is not satisfied. As noted previously, in the absence of surface tension the maximum bubble volume is independent of channel width. Figure 6b shows that $V_M$ is affected by surface tension only for very narrow channels, and even then the surface tension has relatively little effect on V_M. Therefore when losses are negligible, maximum bubble volume is very nearly independent of channel width.

COMPRESSIBLE LIQUID THEORY

Kedrinskii10 developed the following general Gilmore-type equation for a bubble with a planar (ν = 0), cylindrical (ν = 1), or spherical (ν = 2) surface in a compressible liquid:

$$\left(1-\frac{\dot{R}}{c_L}\right)R\ddot{R}+\left(1-\frac{\dot{R}}{3c_L}\right)\frac{3\nu }{4}{\dot{R}}^2=\left(1+\frac{\dot{R}}{c_L}\right)\frac{\nu }{2}H+\left(1-\frac{\dot{R}}{c_L}\right)\frac{R}{c_L}\dot{H},$$ (61)

where $c_L$ is the sound speed evaluated at the bubble wall, and H is the difference between the specific enthalpy at the bubble wall and at infinity. Derivation of this equation rests on the assumption that the quantity $r^{\nu /2}\left(h+\frac{1}{2}{v}^2\right)$ is an invariant that propagates outward from the bubble wall with velocity $c+v$, where h, v, and c are the local values of specific enthalpy, particle velocity, and sound speed, respectively.

For $\nu =0$ the relation $\ddot{R}=c_L^{-1}\dot{H}$ is obtained. For $\nu =2$ the aforementioned assumption is called the Kirkwood-Bethe approximation,25 and Eq. 61 becomes the Gilmore equation26 for a spherical bubble. The Kirkwood-Bethe approximation follows from recognition that in the linear approximation the quantity $r\left(h+\frac{1}{2}{v}^2\right)$ for the radiated spherical wave is a function of the form $f\left(r-c_{0}t\right)$. However, in the linear approximation for a cylindrical wave the quantity $r^{1/2}\left(h+\frac{1}{2}{v}^2\right)$ can be approximated by a function of the form $f\left(r-c_{0}t\right)$ only at frequencies and distances for which $kr\gg 1$. Accordingly, Eq. 61 can be expected to be less accurate for a cylindrical bubble than for a spherical bubble.

The flow of liquid is assumed to be isentropic despite the possibility of shock formation,25 such that the enthalpy differential is taken to be $dh=dP/\rho$, where here ρ (r, t) is the total liquid density. With terms of order 1/c² neglected integration yields $H=\left(P_L-P_{\infty }\right)/{\rho }_0$, where $P_L$ and $P_{\infty }$ are given by Eqs. 46, 47 for a cylindrical bubble (see, e.g., Prosperetti and Lezzi27 for the calculation for a spherical bubble). Equation 61 may then be rearranged, again neglecting terms of order 1/c², to obtain

$$\left(1-\frac{\dot{R}}{c_0}\right)R\ddot{R}+\left(1-\frac{\dot{R}}{3c_0}\right)\frac{3}{4}{\dot{R}}^2=\left(1+\frac{\dot{R}}{c_0}+2\frac{R}{c_0}\frac{d}{\mathit{d}\mathit{t}}\right)\frac{P_L-P_{\infty }}{2{\rho }_0},$$ (62)

the form of which corresponds to the Keller-Miksis equation27, 28 for a spherical bubble.

In the linear approximation, without surface tension or viscosity, and for $p_{\text{ac}}=p_0{e}^{-i\omega t}$, Eq. 62 becomes

$$\left({\omega }^2+i\omega \frac{2\gamma P_0}{{\rho }_0{c}_0{R}_0}-\frac{\gamma P_0}{{\rho }_0{R}_0^2}\right)R_{\omega }=\left(1-i\omega \frac{2R_0}{c_0}\right)\frac{p_0}{2{\rho }_0{R}_0},$$ (63)

which may be compared with Eq. 52. The product of natural frequency and equilibrium radius is thus $R_0{f}_0={(\gamma P_0/{\rho }_0)}^{1/2}/2\pi$, which for an air bubble in water is 1.7 times greater than the value in Eq. 37. The imaginary term on the left-hand side, which accounts for radiation loss, vanishes as required for an incompressible liquid. However, the resulting loss factor at resonance is an order of magnitude less than that predicted by Eq. 52. Instead, it is comparable to the radiation loss factor obtained from the linear approximation of Eq. 61 for a spherical bubble, ${\delta }_{\text{rad}}=k_0{R}_0=0.014$.

In the limiting case of an incompressible liquid Eq. 62 reduces to

$$R\ddot{R}+\frac{3}{4}{\dot{R}}^2=\frac{P_L-P_{\infty }}{2{\rho }_0},$$ (64)

which does not posses the logrithmic singularity, nor therefore the fitting parameter r₀, for an infinite medium that appears in Eq. 45. While Eq. 64 is unphysical because a cylindrical bubble cannot pulsate in an infinite incompressible liquid, it warrants comparison with Eq. 45. The latter can be made identical to Eq. 64 by setting $\text{ln}\left(r_0/R\right)=2$, such that

$$r_0/R=e^2=\mathrm{7.4.}$$ (65)

This value of $r_0/R$ coincides with the values of $r_0/R_M$ found empirically to be of order 10 by Kedrinskii10 and by Ohl et al.1, 2 from matching numerical solutions of Eq. 45 to observations of bubble growth and collapse. The bubble wall velocity predicted by Eq. 64 for the collapse of an empty cavity, without viscosity and surface tension (such that $P_L=0$ and $P_{\infty }=P_0$), is given by

$${\dot{R}}^2=\frac{2}{3}\frac{P_0}{{\rho }_0}\left(\frac{R_M^{3/2}}{R^{3/2}}-1\right).$$ (66)

Integration yields the collapse time

$$T_c=1.49R_M\sqrt{{\rho }_0/P_0},$$ (67)

as obtained by Kedrinskii.10 The same collapse time is obtained from Eqs. 56, 57 for $r_0/R_M=7.0$, which is again consistent with Eq. 65.

Kedrinskii10 has suggested that uncertainty in the assumption that $r^{1/2}\left(h+\frac{1}{2}{v}^2\right)$ is an invariant leads to arbitrariness in the coefficient $\frac{3}{4}$ multiplying ${\dot{R}}^2$ in Eq. 61 for $\nu =1$. By comparing calculations based on Eq. 61 with the expansion of cylindrical bubbles from approximately 1 to 100 mm following detonation of a hexogen charge, he concluded that better agreement was obtained with the coefficient $\frac{3}{4}$ replaced by 1. Insofar as Eq. 64 is concerned, replacement of $\frac{3}{4}$ by 1 results in a collapse time 5% shorter than predicted by Eq. 67. The distinction between the two coefficients is therefore relatively unimportant when modeling inertial growth and collapse. Additionally, the coefficient does not appear in the linear approximation.

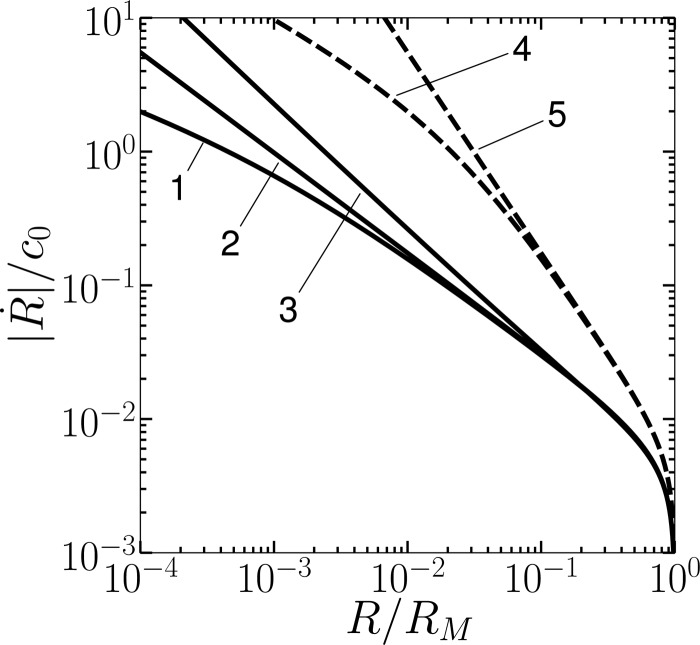
Shown as solid lines in Fig. 7 is a comparison of Eq. 62 (curve 1), Eq. 64 [or equivalently Eq. 66] (curve 2), and Eq. 45 [or equivalently Eq. 55] (curve 3), for the collapse of a cylindrical Rayleigh cavity with $\left|\dot{R}\right|/c_0$ plotted as a function of $R/R_M$. The value $r_0/R_M=7.0$ was used in Eq. 45 to equate the collapse times predicted by Eqs. 45, 64. The dashed lines are the corresponding curves for a spherical cavity, with curve 4 obtained using the Keller-Miksis equation (compressible liquid theory) and curve 5 obtained using Rayleigh’s equation (incompressible liquid theory). Curves 4 and 5 duplicate those in Fig. 1 of Gilmore,26 which is reproduced as Fig. 2 of Flynn.22

Figure 7.

Predictions of Rayleigh collapse for cylindrical bubbles (solid lines) and spherical bubbles (dashed lines). Curve 1: Eq. 62. Curve 2: Eq. 64. Curve 3: Eq. 45 with r₀ = 7.0R_M. Curve 4: Keller-Miksis equation (Ref.28). Curve 5: Rayleigh’s equation (Ref. 23).

Comparing curves 1 and 2, it is observed that the predicted effect of compressibility in Kedrinskii’s model is somewhat less than its effect in the Keller-Miksis equation. However, for both cylindrical and spherical cavity collapse there is little difference between the theories for compressible and incompressible liquids up until $R/R_M=0.1$, so unless rebound is of interest there is typically little reason to account for compressibility when modeling inertial growth and collapse.

CONCLUSION

Three models of cylindrical bubble pulsation have been analyzed: a new model for a compressible liquid in the linear approximation, the standard model in Rayleigh-Plesset form for an incompressible liquid, and a model in the form of the Gilmore equation developed by Kedrinskii for a compressible liquid. Each of these models is limited in its domain of validity.

The linear approximation is of course limited to weak pulsations. Its merit is that it applies to liquids of infinite extent and accounts for viscosity, heat conduction, and radiation loss. It reveals that in contrast with spherical bubbles, acoustic radiation is the dominant loss mechanism. It also provides the natural frequency, which can serve as a benchmark against which other models may be compared in the limit of weak oscillations.

The model in Rayleigh-Plesset form is the one encountered most commonly in the literature. Its application is limited to incompressible liquids of finite radial extent r₀, which typically makes this quantity an arbitrary fitting parameter. The merit of this model is that it provides good agreement with measurements of inertial growth and collapse when r₀ is chosen to be of order 10R_M, where R_M is the maximum bubble radius. In the case of weak oscillations r₀ must be of order 350R₀ to obtain the correct resonance frequency, where R₀ is the equilibrium bubble radius.

Kedrinskii’s model for a compressible liquid follows from an application of the Kirkwood-Bethe approximation that appears to be valid only for bubbles with radii at least on the order of the characteristic wavelength that is radiated. Perhaps for this reason it predicts a resonance frequency for weak oscillations that is too high by a factor of 1.7, and a radiation loss factor that is too small by an order of magnitude. However, its merit is that it is not restricted to liquids of finite extent, and without curve fitting it provides reasonable agreement with measurements of inertial growth and collapse.

We conclude by noting again that the main difficulties arising from the assumption of incompressible flow are associated exclusively with the monopole mode. All higher modes (dipole, quadrupole, etc.) conserve volume and thus are not subject to infinite inertial load in an unbounded incompressible liquid. One may therefore anticipate that shape deformation can be of greater importance in cylindrical bubble dynamics than in spherical bubble dynamics.