Abstract
The human singing and speech spectrum includes energy above 5 kHz. To begin an in-depth exploration of this high-frequency energy (HFE), a database of anechoic high-fidelity recordings of singers and talkers was created and analyzed. Third-octave band analysis from the long-term average spectra showed that production level (soft vs normal vs loud), production mode (singing vs speech), and phoneme (for voiceless fricatives) all significantly affected HFE characteristics. Specifically, increased production level caused an increase in absolute HFE level, but a decrease in relative HFE level. Singing exhibited higher levels of HFE than speech in the soft and normal conditions, but not in the loud condition. Third-octave band levels distinguished phoneme class of voiceless fricatives. Female HFE levels were significantly greater than male levels only above 11 kHz. This information is pertinent to various areas of acoustics, including vocal tract modeling, voice synthesis, augmentative hearing technology (hearing aids and cochlear implants), and training/therapy for singing and speech.
INTRODUCTION
The acoustical characteristics of energy above 5 kHz in singing and speech are not well understood. This high-frequency energy (HFE) in singing and speech has traditionally been neglected in scientific research, but recent findings show that HFE in speech and singing is of perceptual significance and therefore merits some attention. Among the percepts affected by HFE are voice and speech quality (Monson et al., 2011; Füllgrabe et al., 2010; Moore and Tan, 2003), speech intelligibility (Badri et al., 2011; Moore et al., 2010; Pittman, 2008; Apoux and Bacon, 2004; Lippmann, 1996), and localization of speech (Best et al., 2005). Furthermore, humans are apparently sensitive to subtle changes in HFE level in singing (Monson et al., 2011).
Very few spectral details of HFE in speech and singing have been described in the literature. These include a “prominent dip” around 5 kHz that has been found to be consistent in the spectra of sustained vowels produced by normal subjects (Shoji et al., 1991; Ternström, 2008), attributable to an antiresonance caused by the piriform fossa (Dang and Honda, 1997). This spectral dip seems to naturally divide the spectrum into a low-frequency portion (<5 kHz) and a high-frequency portion (>5 kHz). Additionally, harmonic energy, though dropping off at a rate of ∼12 dB/octave (Flanagan, 1958), has been measured above 5 kHz in singing (Fry and Manen, 1957), and out to 20 kHz in loud singing (Ternström, 2008).
A handful of studies have reported levels of certain bands containing HFE, measured from the long-term average spectrum (LTAS) of speech (Sivian, 1929; Dunn and White, 1940; Byrne et al., 1994; Moore et al., 2008). In general these studies reported that female HFE levels are greater than male levels, though no statistical significance was reported. The absolute levels reported in the two most recent studies listed are likely the most valid given the limited technology (i.e., poor high frequency response characteristics of recording equipment) available in the previous studies. Third-octave bands containing HFE ranged in these two latter studies from 29 to 41 dB SPL (with the spectrum normalized to an overall level of 65 dB SPL), which were 16–28 dB below that of the band levels having the greatest amount of energy. Other studies have shown that dysphonic and breathy voices tend to have greater levels of HFE than normal voices (Shoji et al., 1992; Valencia et al., 1994), and that the two voice types can be distinguished quantitatively by an increase in a measure termed the “high-frequency ratio” (Shoji et al., 1992).
Since the high-frequency portion of the speech spectrum tends to be dominated by voiceless fricatives, HFE has been characterized somewhat in relation to this phonetic class. Efforts in this area have revealed that spectral peaks of most English fricatives are found above 5 kHz (Hughes and Halle, 1956; Jongman et al., 2000; Maniwa et al., 2009). These peak locations tended to be higher for voiceless fricatives than for voiced fricatives (Jongman et al., 2000), and higher for females than for males (Jongman et al., 2000; Maniwa et al., 2009). Peak location distinguished place of articulation of fricatives, with /f,v/ and /θ,ð/ having the highest spectral peak locations (∼7.5–8 kHz), followed by /s,z/ (∼7 kHz), and then /∫, ʒ/ (∼4 kHz) (Jongman et al., 2000). In these studies several acoustical parameters were used to effectively quantify fricative class, but third-octave band levels were not examined. (For a more exhaustive review of acoustic properties of fricatives, see Maniwa et al., 2009.)
While technological advances have made accurate presentation and analysis of HFE feasible, detailed acoustical analysis of HFE in speech and singing is lacking. Such analysis is merited since (1) the perceptual significance of HFE has been and continues to be established, and (2) determining the importance of HFE in speech and singing requires an understanding of both the potential information present and the sensitivity of human listeners to this information. In a previous study it was found that humans are sensitive to differences in HFE amplitude level in singing (Monson et al., 2011). The current study examined whether amplitude of HFE differs by production level, production mode, phonetic class, and gender—thereby providing potentially distinguishing information about these different aspects of production. Based on the data available, it was hypothesized that increased production levels of singing and speech exhibit increased SPL of HFE. It was further hypothesized that different production modes (singing vs speech) exhibit different HFE characteristics. It was hypothesized that phonemes of speech exhibit distinct features of HFE content. Finally, it was hypothesized that female singing and speech produces more HFE than does male singing and speech. To examine these hypotheses, a database of high-fidelity anechoic recordings of loud, normal, and soft speech and singing was created and analyzed. Octave- and third-octave band analysis was a logical and standard method to use for this initial effort and examination of the hypotheses. As the natural division of the spectrum (by the piriform fossa antiresonance) at ∼5 kHz falls conveniently close to the 8-kHz octave band low cutoff frequency of ∼5.7 kHz, HFE analysis was performed using the 8- and 16-kHz octave bands. Thus, HFE is defined here as the acoustical energy found in the standard 8 - and 16-kHz octave bands.
METHOD
Recordings
Recordings were made in a fully anechoic chamber located on Brigham Young University campus. The chamber has working dimensions of 8.71 m × 5.66 m × 5.74 m with a low-frequency anechoic cutoff frequency of 80 Hz. An acoustically transparent cable-suspension “floor” horizontally traverses the chamber.
A [1/2]-inch Type 1 precision microphone was used for the recordings. To minimize the effects of high-frequency scattering caused by reflection off of a microphone boom, the microphone was attached to the end of a 0.57-m rod protruding perpendicularly from a metal microphone boom. The microphone was regularly calibrated throughout the recording process (1 kHz, 114 dB). The height of the microphone was set to the level of the mouth of the subject, directly on-axis at a distance of 60 cm from the mouth. The microphone signal was patched into a separate control room located adjacent to the chamber. Acoustical data from the microphone were collected using a National Instruments PXI 36-channel data acquisition system, recording at 24 bits with a 44.1-kHz sampling rate. Data were recorded as binary files using a customized LABVIEW interface, and were then imported into MATLAB for analysis and conversion to wave files.
Subjects
Recordings were made from 15 singer subjects (8 female) who were native speakers of American English with no reported history of a speech or voice disorder. All subjects had at least 2 years of post-high school private voice training. Age ranged from 20 to 71 years (mean = 28.5), and subject voice part breakdown was as follows: 3 baritones, 4 tenors, 2 mezzo-sopranos, and 6 sopranos. One subject was 71 years old, but individual acoustical analysis of this subject’s speech and singing showed no significant difference from other levels. Thus this subject was not excluded as there appeared to be no significant effect of age for the analyses used here. Subjects participated in two recording sessions. The first session was a practice session wherein the subject was trained in the task to be performed and was acclimated to singing and speaking in the anechoic environment. Subjects were given a copy of the material to be recorded and asked to practice speaking and singing the material on their own time before the second session. The second session was the actual recording session and is described in detail in Sec. 2C. Subjects were allowed to take breaks at any time during the recording session.
Corpus and recording procedure
The subject recorded 20 six-syllable low-predictability phonetically representative phrases with alternating syllabic strength. Half of the phrases began with a strong syllable followed by alternating syllabic strength (SWSWSW), while the other half began with a weak syllable followed by alternating syllabic strength (WSWSWS). These phrases were taken from Spitzer et al. (2007) (the first 20 phrases listed in Appendix A of that article). These phrases were selected and used in part because of their ease and usefulness in translation to sung material, as will be described. It was also anticipated that they would be useful for future work, their low predictability lending to study of intelligibility, and their alternating syllabic strength lending to study of prosodics and rhythm information.
The phrases were spoken at 3 different levels: normal, soft, and loud. For normal speech, the subject was instructed to say the phrases in a “normal conversational voice, as if you were speaking them to someone.” For soft speech, the subject was instructed to say the phrases “as quietly as possible without whispering.” For loud speech, the subject was instructed to say the phrases “in a loud manner, as if talking to someone across the room at a cocktail party.” The subject also recorded the 20 test phrases sung at 3 different levels: normal, pianissimo, and fortissimo. For normal singing, the subject was instructed to sing the phrases in his/her “normal performance voice.” For the other two conditions, the subject was instructed to sing “pianissimo” and “fortissimo.” As all phrases had three strong syllables, the subject sang phrases on a 5-4-3-2-1 scale, placing strong syllables on steps 5, 3, and 1. For phrases beginning with a weak syllable, the first weak syllable was also sung on step 5 (“five-FIVE-four-THREE-two-ONE”). For phrases ending with a weak syllable, the last weak syllable was also sung on step 1 (“FIVE-four-THREE-two-ONE-one”). Lower voices (baritone, mezzo) sang in the key of C (G-F-E-D-C; 196-175-165-147-131 Hz for males, 392-349-330-294-262 Hz for females). Higher voices (tenor, soprano) sang in the key of F (C-Bb-A-G-F; 262-233-220-196-175 Hz for males, 523-466-440-392-349 Hz for females).
The phrases were divided into two blocks (10 phrases each), each block consisting of either the SWSWSW syllabic strength pattern or the WSWSWS syllabic strength pattern. The order of block recording was randomized and balanced. Test phrase order within each block was randomized for each subject. Half of the subjects recorded speech first; half recorded singing first. Within each block for both speech and singing, all subjects performed half of the phrases (5 phrases) in the normal condition first. Half of the subjects then recorded the loud condition followed by the soft condition, with the other half of subjects recording soft followed by loud. This process was then repeated for the remaining five phrases of that block. The subject spoke and sang each phrase once, with the exception of the normal speech condition, in which the subject was asked to give two repetitions of each phrase.
During each block the subject was given a 3 × 5-inch note card with the 10 phrases printed on it. The subject was instructed to raise the card to look at (and memorize) the phrase to be spoken/sung, but to hold the card down at his/her side while actually saying/singing the phrase. This method was necessary to avoid the reflection of high-frequency waves off of the card, which would likely affect the distribution of HFE in the recordings. The investigator stood at the far wall of the anechoic chamber with the subject to observe, explain the tasks, and prompt for repetition or change when necessary. (On occasion it was necessary to repeat phrases due to undesired noises, misspoken words, missed phrases, and/or inconsistency in following directions.) During the singing blocks, the investigator sounded starting and ending pitches on a pitch pipe at least once before beginning each block, but repeated the pitches as often as the subject or investigator deemed necessary.
Acoustical analysis
Binary files generated from the PXI system were saved to disk and imported into MATLAB for editing and analysis. Initially, a.wav file for each subject’s session was created in MATLAB and imported into Audacity audio editing software. Separate files were then generated for each of the six conditions for each subject (normal/loud/soft × speech/singing) by recording time points (found by hand using Audacity) marking the beginning and end of the various segments in the original recording of the subject. In this same manner it was also possible to exclude any errors made during recording. These segments were then concatenated to generate a single signal for each of the six conditions for that subject using MATLAB. These signals were each carefully scrutinized to ensure quality and accuracy of the material recorded. The order of the recorded phrases was not rearranged, thus each signal maintained the (random) ordering of the phrases assigned to that subject. All analyses were done using MATLAB except where otherwise stated. All statistical analyses were done using the SPSS statistical analysis software package.
The LTAS of each signal was created using a 2048-point FFT, resulting in a frame length of 2048/44.1 kHz= 46.44 ms, with a Hamming window and 50% overlap. Before taking the LTAS, all signals were high-pass filtered at 50 Hz using a fourth-order Butterworth filter to decrease low-frequency noise. As each signal had a varying amount of silent pauses and breaks—which would affect the overall LTAS of the signal—it was desired to exclude frames containing only silence. The measured noise floor of the anechoic chamber (after high-pass filtering) was less than 30 dBrms. Simply using this value as a threshold for inclusion in the LTAS analysis, however, was insufficient for two reasons: (1) some phonemes (e.g., stop consonants) exhibit silence long enough in duration that their frames could potentially be excluded when they should be included, and (2) ambient noise peaks (with the subject standing in the anechoic chamber) were measured at varying levels up to approximately 50 dB, potentially causing ambient noise frames to be included when they should be excluded. To counteract these two issues, the exclusion decision was implemented by finding the peak level of the current frame of analysis, as well as the peak of the previous frame and the following frame. If two of these three frames were found to have peak levels above the threshold level, the current frame was included in analysis. Given the sporadic nature of the ambient noise peak levels measured (and after some trial and error), a value of 43 dB was selected as the threshold level. To check the validity of this value, a secondary signal was generated for each signal analyzed by concatenating only the frames included in the LTAS analysis (which consisted of all valid speech and singing samples, both vowels and consonants). Upon inspection and listening, the 43-dB value was found to be most successful in generating a signal that had little to no pauses between words and phrases, while still including the silence produced by consonants. (Lower values tended to include unnecessary silent pauses between words and phrases, while higher values tended to exclude stop consonants, plosives, and even some fricatives.)
Overall SPL was calculated from the LTAS for each signal by summing the energy in all frequency bins. Level for each octave and third-octave band was calculated by summing only the energy in frequency bins that fell between the bandedge frequencies of that band. It was not clear, however, that this summing method would be a good estimate of levels calculated in the traditional manner. To verify this, the overall root-mean-square (RMS) level was calculated in the traditional manner by summing the squared-pressure over the duration of the signal, taking the square root, and then dividing by the length of the signal. Comparing this value to the sum of all frequency bins in the LTAS for several different types of signals (noise, speech, singing) revealed that the RMS value was always less than 1 dB greater than the LTAS value. It was expected that the RMS value would be higher than the LTAS value as some energy is lost in the windowing and frequency-bin summing process of the LTAS.
This process was repeated with third-octave band analysis by passing signals through a traditional third-octave digital filter bank and calculating RMS values for the resulting third-octave band signals. For a white noise signal the RMS values were typically close to 1 dB greater than the corresponding third-octave values obtained by the LTAS method, and never more than 3 dB. HFE third-octave band levels were always less than 1.5 dB different, indicating that the method of summing frequency bins in the LTAS is a valid approximation of third-octave band analysis, particularly for the frequency range of interest in this study. Because of the interest in the LTAS for this study, the LTAS method of third-octave band analysis was used.
A “mean” LTAS for each condition was calculated to compare several effects in different conditions. For the most accurate comparison, the mean LTAS was calculated in the following manner. The LTAS for each subject in a given condition was calculated and then normalized to have an overall level of 0 dB. The linear versions of each subject’s normalized LTAS for that condition were averaged across subjects. The resulting LTAS for each condition was then normalized to the mean overall SPL calculated for that condition.
There are at least two other methods by which a mean LTAS could have been calculated: (1) concatenating all of the speech/singing for a given condition and then taking the LTAS of that entire condition; or (2) taking the average LTAS for all subjects without normalizing first. The first method was not used because the resulting LTAS would likely be dominated by those subjects who sung/spoke slower than the other talkers, resulting in a greater number of frames analyzed for these subjects, and thus biasing the LTAS. Similarly, the second method was not used because the resulting LTAS would likely be dominated by those subjects who sung/spoke at a higher SPL than the other subjects. The method selected eliminates both of these errors, but is not without its own limitations. Namely, this method essentially assumes that the LTAS for each subject would have the same relative amounts of energy at all frequencies if the subject’s overall acoustic level changed by only a few dB (to the mean overall level for a given condition). It is recognized that this may not be the case, but this method was deemed the most accurate representation of the mean LTAS, given the limitations of the other methods.
Regarding the phonetic value of HFE, the focus of this study was on voiceless fricatives because this class of phonemes has been distinguished as a class for which HFE is prominent and potentially important for perceptual classification. The voiceless fricatives /s,∫,f,θ/ were extracted from the normal speech condition of the phrases recorded by each subject. The full duration of each fricative was extracted “by hand” to exclude any silence or neighboring phonemes. The extracted fricatives were then concatenated into a single signal for each fricative produced by that subject and the LTAS was calculated. The number of instances for each phoneme in the recorded phrases were as follows: /s/- 19; /∫/- 3; /f/- 5; /θ/- 4 (since phrases were repeated twice in the normal speech condition, the actual number of phonemes extracted for each subject were twice these values). A mean LTAS across subjects was calculated for each fricative.
As standard levels are typically reported as SPL at 1 m from the source, all levels reported here have been converted to the expected level at 1 m given the level recorded at 60 cm using the distance rule in sound propagation. (A distance of 60 cm was used here due to space constraints in the anechoic chamber; see Monson et al., 2012) True mean levels reported here were calculated by converting dB levels to linear squared-pressure amplitudes, taking the mean, and converting this value back to dB. None of the signals were “pre-emphasized” in this study, thus the levels reported represent actual HFE levels of the raw singing/speech signal.
RESULTS AND DISCUSSION
In this study “production level” is defined as the level of phonatory effort as perceived internally (subjectively) by the talker/singer (i.e., soft, normal, or loud for speech; pianissimo, normal, or fortissimo for singing). The term “production mode” is used referring to either the mode of singing or the mode of speech.
Effects of production level
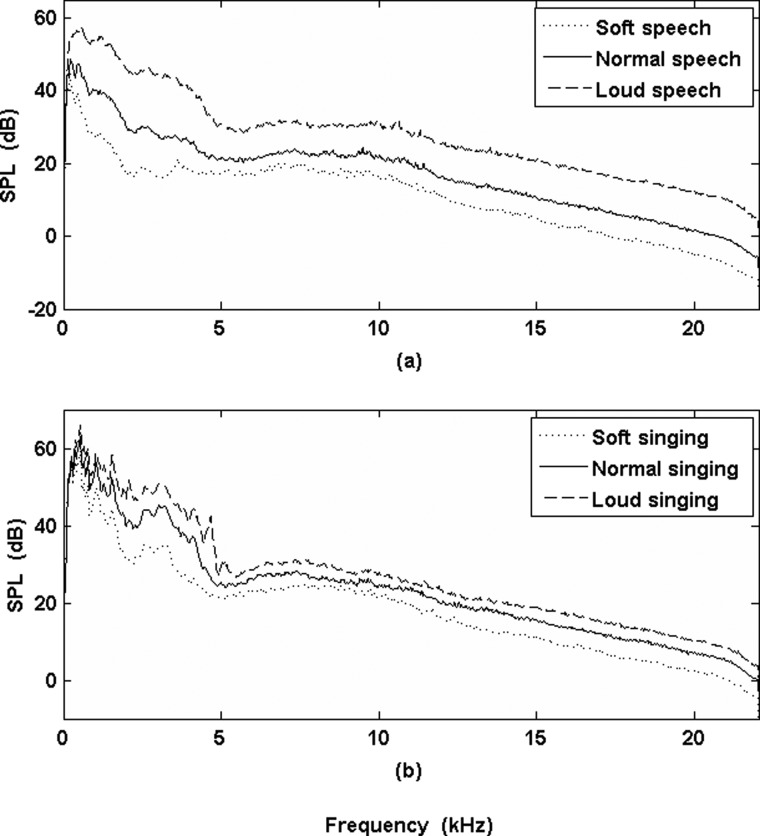
Figure 1 shows the mean LTAS calculated for each of the six production conditions, separated by production mode. Mean SPLs (with standard deviations) for each condition are given in Table Table I.. As expected, increased overall SPL of the LTAS was seen with increased production level in both production modes. The SPL changes from soft speech to loud speech, however, were much greater than the SPL changes from soft singing to loud singing (a difference between production modes that was statistically significant, F(1,14) = 37.628, p < 0.001). The mean SPL of loud speech was approximately the same as the mean SPL for normal singing (∼74 dB), both being about 12 dB greater than that of normal speech (62 dB).
Figure 1.
Mean LTAS calculated for each of the six recording conditions, separated by production mode of speech (a) and singing (b). Overall SPLs for each spectrum correspond to the mean SPLs given in Table Table I..
Table I.
Mean overall SPLs at 1 m (re 20 μPa) of soft, normal, and loud speech and singing. Absolute HFE levels (the combined 8-kHz and 16-kHz octave bands) calculated from the mean LTAS are also given.
| Condition | ||||
|---|---|---|---|---|
| Mode | Level | Mean SPL (dB SPL) | Std Dev (dB) | Mean HFE (dB SPL) |
| Speech | Soft | 54.8 | 2.6 | 42.3 |
| Normal | 62 | 2.4 | 47 | |
| Loud | 73.8 | 4.4 | 55.4 | |
| Singing | Soft | 69.7 | 4.6 | 47.6 |
| Normal | 73.9 | 3.1 | 50.8 | |
| Loud | 77.5 | 2.9 | 53.7 | |
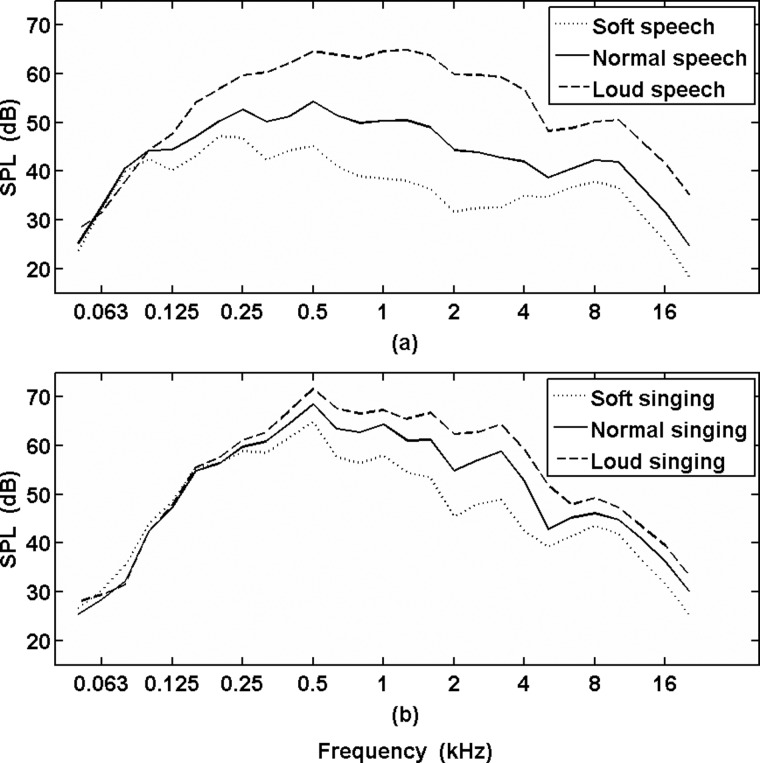
Figure 2 shows the third-octave band levels for each test condition calculated from the mean LTAS (see also Table Table II.). The band levels for normal speech (if adjusted by +3 dB for an overall SPL of 65 dB) are similar to those reported in the two recent LTAS studies (Byrne et al., 1994; Moore et al., 2008), though HFE bands are somewhat higher than that reported by Moore et al. (2008). For the 16-kHz octave bands the results here appear to agree more closely with Byrne et al. (1994). Moore et al. (2008) attributes these higher band levels to noise from the microphone used in the earlier study, but it is possible that microphone placement or the recording material itself caused the differences in HFE, leading to these disparities (e.g., an increase in the number of voiceless fricatives would potentially lead to increased HFE band levels in the LTAS). The SPLs reported here were verified by multiple Type 1 precision microphones recording simultaneously in the anechoic chamber (Monson et al., 2012).
Figure 2.
Third-octave band levels for each test condition calculated from the mean LTAS (see also Table Table II.).
Table II.
Third-octave band levels of soft, normal, and loud speech and singing calculated from the mean LTAS for each condition. Levels correspond to overall SPL given in Table Table I..
| Level (dB SPL) | ||||||
|---|---|---|---|---|---|---|
| fc (kHz) | Soft Speech | Normal Speech | Loud Speech | Soft Singing | Normal Singing | Loud Singing |
| 0.050 | 23.7 | 25.2 | 28.0 | 26.7 | 25.4 | 28.0 |
| 0.063 | 32.5 | 32.7 | 31.5 | 30.3 | 28.5 | 29.4 |
| 0.079 | 39.9 | 40.7 | 37.8 | 35.4 | 32.2 | 31.5 |
| 0.099 | 42.6 | 44.2 | 44.2 | 43.8 | 42.4 | 42.4 |
| 0.125 | 40.1 | 44.4 | 47.7 | 48.6 | 47.3 | 47.8 |
| 0.157 | 43.1 | 47.1 | 54.2 | 55.6 | 54.8 | 55.5 |
| 0.198 | 47.2 | 50.3 | 56.9 | 56.2 | 56.3 | 57.5 |
| 0.250 | 46.8 | 52.7 | 59.7 | 58.9 | 59.8 | 61.1 |
| 0.315 | 42.3 | 50.2 | 60.3 | 58.5 | 60.9 | 62.9 |
| 0.397 | 44.3 | 51.2 | 62.2 | 61.7 | 64.5 | 67.2 |
| 0.500 | 45.2 | 54.4 | 64.6 | 64.9 | 68.5 | 71.7 |
| 0.630 | 41.0 | 51.4 | 63.9 | 57.7 | 63.4 | 67.6 |
| 0.794 | 38.9 | 49.9 | 63.2 | 56.4 | 62.7 | 66.6 |
| 1 | 38.5 | 50.4 | 64.6 | 58.0 | 64.4 | 67.3 |
| 1.260 | 38.0 | 50.4 | 64.9 | 54.4 | 61.0 | 65.6 |
| 1.587 | 36.3 | 49.0 | 63.7 | 53.4 | 61.2 | 66.8 |
| 2 | 31.6 | 44.3 | 59.8 | 45.4 | 54.9 | 62.4 |
| 2.520 | 32.5 | 43.9 | 59.8 | 48.0 | 57.0 | 62.8 |
| 3.175 | 32.6 | 42.8 | 59.4 | 48.9 | 58.9 | 64.4 |
| 4 | 34.9 | 42.0 | 56.7 | 42.4 | 52.7 | 59.2 |
| 5.040 | 34.7 | 38.7 | 48.3 | 39.2 | 42.8 | 51.9 |
| 6.350 | 36.7 | 40.5 | 48.8 | 41.4 | 45.2 | 47.9 |
| 8 | 37.8 | 42.2 | 50.1 | 43.5 | 46.1 | 49.3 |
| 10.079 | 36.6 | 41.9 | 50.5 | 41.9 | 44.8 | 47.4 |
| 12.699 | 30.9 | 36.7 | 46.0 | 36.4 | 40.8 | 43.4 |
| 16 | 25.5 | 31.5 | 41.6 | 31.6 | 36.2 | 39.5 |
| 20.159 | 18.4 | 24.8 | 35.3 | 25.3 | 30.2 | 33.4 |
Note that the most noticeable differences between production levels (and production modes) in the mean LTAS appear to be below 5000 Hz. However, notable differences in HFE level are also readily observable. Table Table I. shows mean HFE levels (the combined 8- and 16-kHz octave levels) calculated from the mean LTAS for each recording condition. An increase in HFE band levels is seen for each increase in production level within mode. The HFE increases tend to be comparable to the overall SPL increases for the singing mode (<1 dB difference), while speech HFE level increases are 2–4 dB less than the overall SPL increase. Interestingly, loud speech exhibits the highest HFE level of all conditions. It was hypothesized that increased production level in singing and speech would cause increased SPL of HFE. A 2 × 3 [production mode × production level] repeated-measures analysis of variance (ANOVA) performed on overall HFE level showed that increasing production level caused significant increases in overall HFE level (F(2,26) = 181.668, p < 0.001) with a significant interaction between production mode and production level (F(2,26) = 13.032, p < 0.001). This interaction was due to the larger increases in HFE for speech than for singing. However, pairwise comparisons showed that all increases between production levels were significant.
Effects of production mode
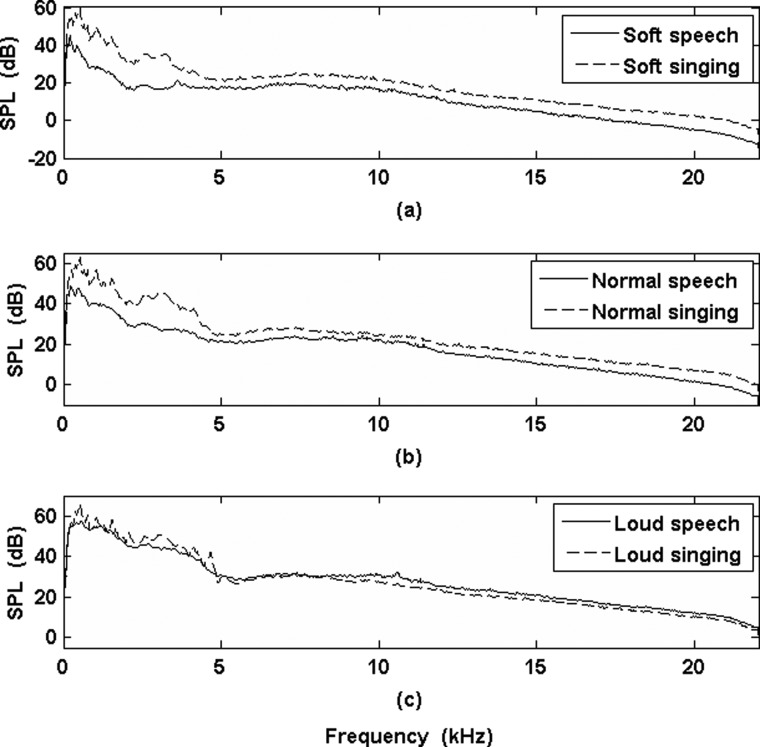
Figure 3 shows the mean LTAS calculated for each condition, separated by production level. Higher amplitude HFE was obtained for singing versus speech in both the soft and normal conditions. These differences were greater than 3 dB and were statistically significant for both soft (t(14) = 3.43, p < 0.005) and normal (t(14) = 5.416, p < 0.001) conditions. Differences in HFE level between loud singing and speech were not statistically significant, however (t(14) = −0.46, p = 0.653). Another point of interest is the observance of the ∼4.5-dB difference in HFE level of loud speech over normal singing, despite both being the same overall SPL.
Figure 3.
Mean LTAS calculated for each of the six recording conditions, separated by production level of soft (a), normal (b), and loud (c). Overall SPLs for each spectrum correspond to the mean SPLs given in Table Table I..
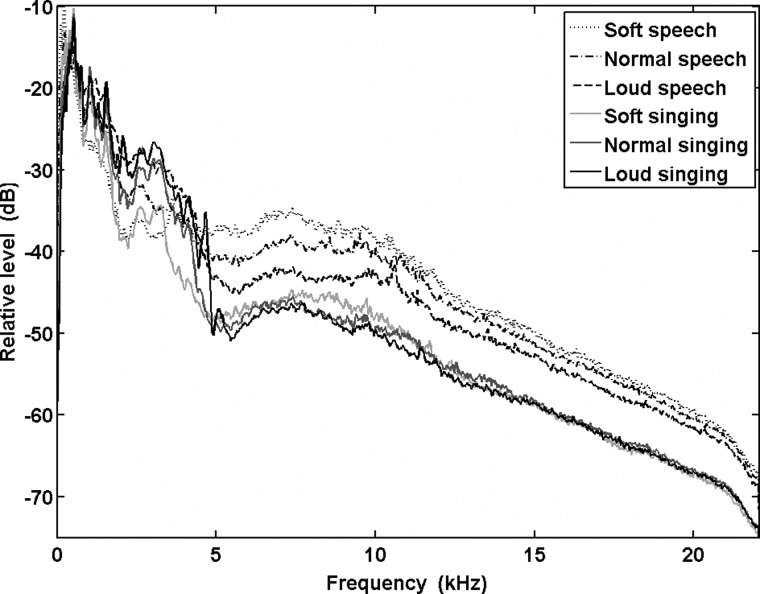
A major difference between speech and singing is seen in the relative levels of HFE for each mode. Figure 4 shows the mean LTAS for each condition, normalized to 0 dB. It can be observed that speech exhibits higher relative levels of HFE than does singing. As speech production level increases, relative HFE level decreases. This is not the case for singing, however, in which relative HFE level remains roughly the same for every production level.
Figure 4.
Mean LTAS calculated for each of the six recording conditions and then normalized to an overall SPL of 0 dB.
Separate 2 × 6 [production mode × third-octave band] repeated-measures ANOVAs were calculated for each production level. Significant main effects for production mode were apparent for both soft (F(1,13) = 14.08, p < 0.005) and normal (F(1,13) = 30.481, p < 0.001) conditions, with a significant interaction between production mode and band center-frequency for both conditions. The main effect of mode was not significant for the loud condition (F(1,13)= 0.786, p = 0.391), but there was a significant interaction between production mode and band center-frequency.
Effects of fricative place of articulation
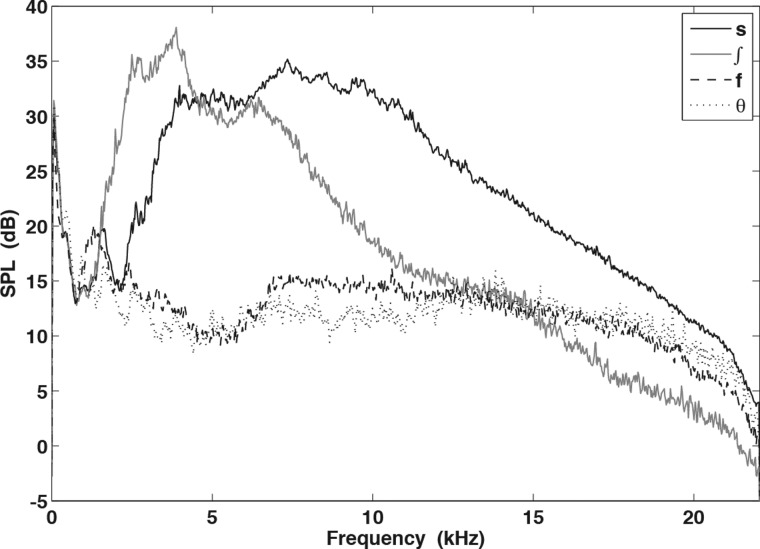
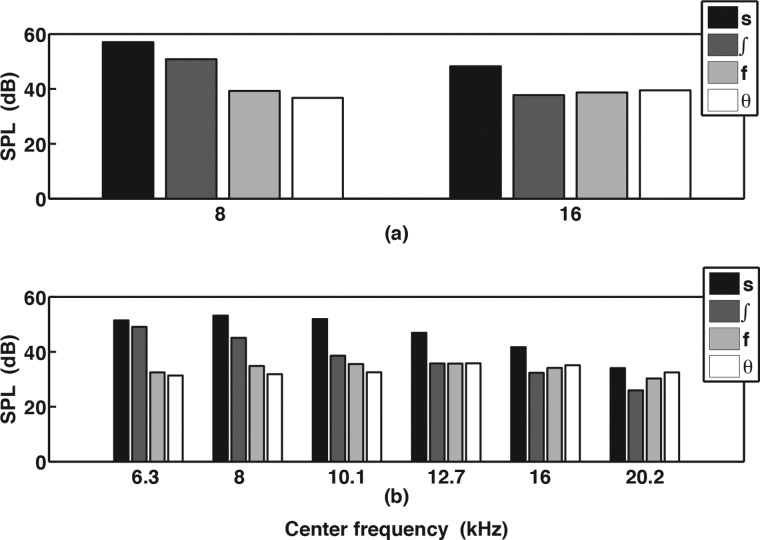
Figure 5 shows the mean LTAS calculated for each of the four voiceless fricatives, normalized to the mean overall SPL at 1 m for each fricative. Clearly /s/ and /∫/ exhibit distinct HFE features, distinguishing them from each other and from the /f,θ/ pair, but the distinction between /f/ and /θ/ is less obvious. Examining octave and third-octave band analysis in Fig. 6 (see also Table Table III.), however, reveals a slight difference in HFE characteristics. Specifically, /f/ appears to exhibit higher octave and third-octave levels in the 8-kHz octave (∼3 dB), with a slight drop in octave level from the 8-kHz to the 16-kHz octave, where /θ/ exhibits a 3-dB increase in octave level.
Figure 5.
Mean LTAS calculated for each of the four voiceless fricatives and then normalized to the mean overall SPL at 1 m for each fricative.
Figure 6.
Octave (a) and third-octave (b) band levels for each fricative calculated from the mean LTAS (see also Table Table III.).
Table III.
HFE octave and third-octave band levels of 4 voiceless fricatives (/s,∫,f,θ/) recorded during normal speech, calculated from the mean LTAS for each fricative.
| Level (dB SPL) | ||||
|---|---|---|---|---|
| Band | /s/ | /∫/ | /f/ | /θ/ |
| 8-kHz (Oct) | 57 | 50.8 | 39.2 | 36.7 |
| 16-kHz (Oct) | 48.2 | 37.7 | 38.7 | 39.5 |
| 6.3 kHz | 51.5 | 49.1 | 32.5 | 31.4 |
| 8 kHz | 53.2 | 45.1 | 34.8 | 31.8 |
| 10.1 kHz | 51.9 | 38.6 | 35.5 | 32.5 |
| 12.7 kHz | 46.9 | 35.8 | 35.7 | 35.8 |
| 16 kHz | 41.7 | 32.3 | 34.1 | 35.1 |
| 20.2 kHz | 34.1 | 26 | 30.3 | 32.5 |
A 4 × 6 [fricative × third-octave band] repeated-measures ANOVA showed significant differences across fricatives (F(3,39) = 93.276, p < 0.001), with a significant interaction between fricative and third-octave band center-frequency (F(15,195) = 80.085, p < 0.001). Pairwise comparisons between fricative classes revealed no significant difference between /f/ and /θ/ third-octave bands levels. However, a paired-samples t test using the 8-kHz octave band levels did result in a significant difference between /f/ and /θ/ (t(14)= 2.569, p < 0.05).
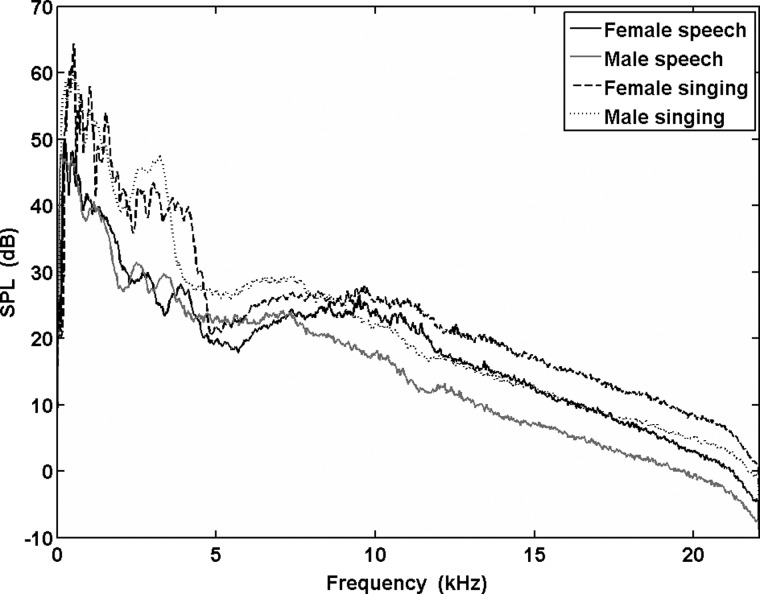
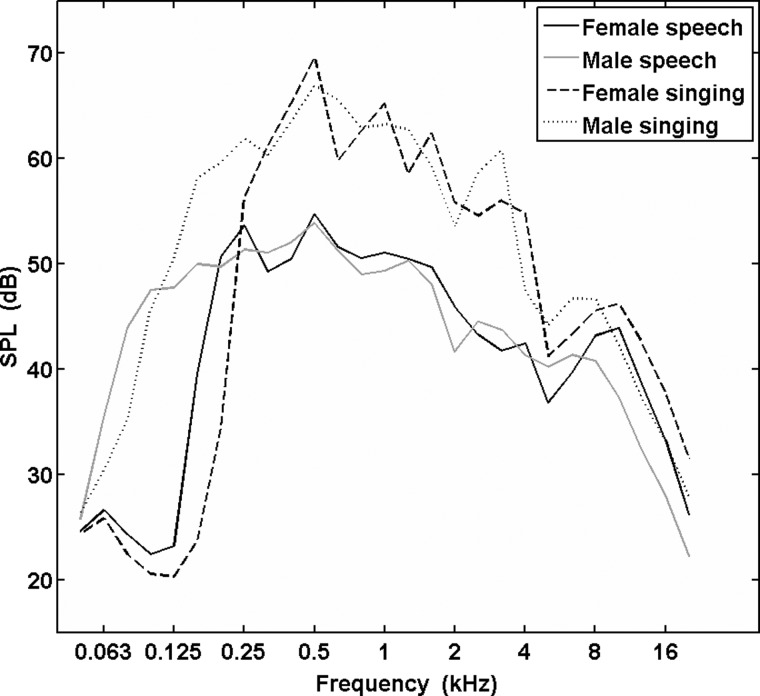
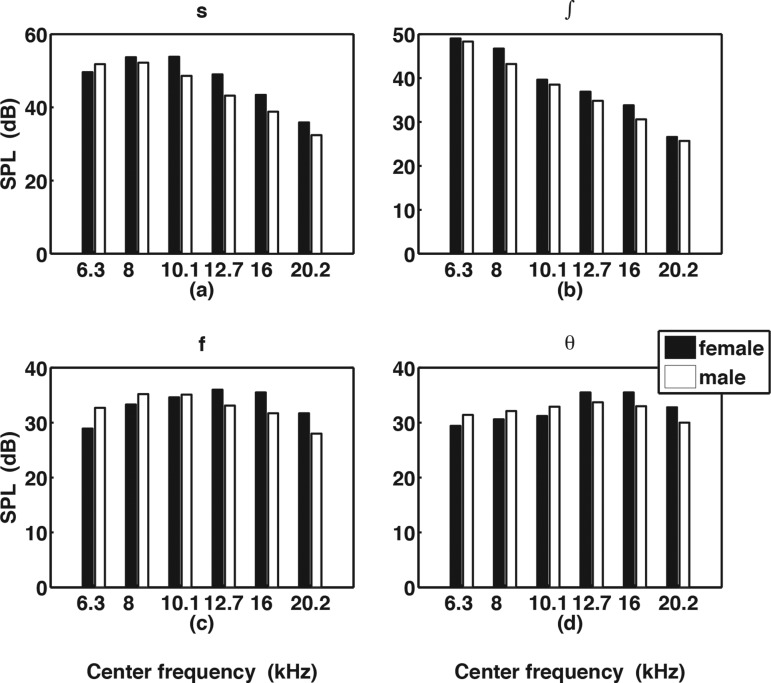
Effects of gender
Figure 7 shows the mean LTAS calculated for each gender in both production modes at normal production levels. Examination of the LTAS reveals that mean male HFE levels are actually greater than female levels for the first part of the HFE range, but then female levels increase and surpass male levels as frequency increases. Octave-band analysis showed that female speech on average exhibits greater HFE levels than male speech for both HFE octaves, but that the mean male 8-kHz octave band level for singing is actually 0.4 dB greater than the female mean level. In the 16-kHz octave, the female singing level was about 5 dB greater than the male level. Breaking this down to third-octave bands shown in Fig. 8 (see also Table Table IV.) revealed that female mean levels were in fact greater than male levels for five of the six HFE bands in speech, and four of the six HFE bands in singing. Interestingly, male singing and female speech exhibit very similar HFE band values.
Figure 7.
Mean LTAS calculated for each gender in both production modes at normal production levels. Overall SPLs correspond to the mean SPLs given in Table Table I. for normal speech and normal singing.
Figure 8.
Third-octave band levels for each gender in both production modes calculated from the mean LTAS (see also Table Table IV.).
Table IV.
Mean third-octave band levels of normal speech and singing separated by gender, calculated from the mean LTAS. Levels correspond to overall SPLs of 62 dB for speech and 73.9 dB for singing.
| Level (dB SPL) | ||||
|---|---|---|---|---|
| fc (kHz) | Female Speech | Male Speech | Female Singing | Male Singing |
| 0.050 | 24.6 | 25.8 | 24.4 | 26.4 |
| 0.063 | 26.6 | 35.4 | 25.8 | 30.3 |
| 0.079 | 24.3 | 43.9 | 22.4 | 35.2 |
| 0.099 | 22.4 | 47.5 | 20.5 | 45.7 |
| 0.125 | 23.2 | 47.7 | 20.3 | 50.6 |
| 0.157 | 39.6 | 50.0 | 23.7 | 58.2 |
| 0.198 | 50.7 | 49.7 | 34.5 | 59.6 |
| 0.250 | 53.6 | 51.4 | 56.3 | 61.9 |
| 0.315 | 49.2 | 51.1 | 61.3 | 60.4 |
| 0.397 | 50.4 | 52.0 | 65.2 | 63.5 |
| 0.500 | 54.7 | 53.9 | 69.6 | 66.9 |
| 0.630 | 51.6 | 51.3 | 59.8 | 65.6 |
| 0.794 | 50.5 | 49.0 | 62.6 | 62.8 |
| 1 | 51.1 | 49.3 | 65.2 | 63.3 |
| 1.260 | 50.5 | 50.3 | 58.6 | 62.8 |
| 1.587 | 49.7 | 48.1 | 62.4 | 59.2 |
| 2 | 45.8 | 41.6 | 55.9 | 53.5 |
| 2.520 | 43.3 | 44.6 | 54.6 | 58.7 |
| 3.175 | 41.8 | 43.8 | 56.0 | 60.8 |
| 4 | 42.5 | 41.3 | 54.8 | 47.4 |
| 5.040 | 36.8 | 40.2 | 41.2 | 44.2 |
| 6.350 | 39.6 | 41.3 | 43.3 | 46.7 |
| 8 | 43.2 | 40.8 | 45.5 | 46.7 |
| 10.079 | 43.9 | 37.3 | 46.2 | 42.3 |
| 12.699 | 38.6 | 32.3 | 42.5 | 37.2 |
| 16 | 33.2 | 28.0 | 37.8 | 33.2 |
| 20.159 | 26.2 | 22.2 | 31.5 | 27.8 |
Examination of gender effects was included in all of the previous analyses reported on production mode and production level, finding few significant effects. A 2 × 3 [production mode × production level] mixed-model ANOVA performed on overall HFE level showed no significant effect of gender (F(1,13) = 0.203, p = 0.66). There was no interaction between gender and production level, nor between gender and production mode. Separate 2 × 6 [production mode× third-octave band] mixed-model ANOVAs showed no significant effect of gender for the soft (F(1,13) = 3.122, p = 0.101), normal (F(1,13) = 1.388, p = 0.26), or loud (F(1,13) = 0.186, p = 0.673) conditions, though in each condition there was a significant interaction between gender and third-octave band center-frequency. For fricatives, a 4 × 6 [fricative × third-octave band] mixed-model ANOVA showed no significant difference between genders (F(1,13)= 0.168, p = 0.688); however, there was a significant interaction between gender and fricative (F(3,39) = 4.504, p < 0.01).
These previous analyses used the actual (raw) levels recorded by each subject, which may not be appropriate for studying gender effects. An alternative is to use each subject’s band levels (for a given condition) that have been normalized to have an overall SPL equivalent to the mean SPL for that production condition. For within-subjects designs this method is inappropriate because it potentially alters the band level differences within subjects across conditions. The advantage of normalizing for a between-subjects design, however, is that it allows one to control for overall SPL differences, with the assumption that comparison between different conditions is not necessary. This is equivalent to comparison of relative HFE levels between subjects, which may be of more interest in analyzing gender differences.
Using normalized levels, a one-way ANOVA showed no significant differences in overall HFE levels between genders for any of the test conditions. However, repeating the analysis using separate HFE octave band levels showed that gender differences in the 16-kHz octave did reach significance for all test conditions, while differences in the 8-kHz octave did not reach significance for any test condition. To ascertain further what bands may be contributing to these differences analysis was performed using third-octave bands for all test conditions. Table Table V. shows the ANOVA results for third-octave band levels. Only two of the six HFE third-octave bands showed differences that consistently reached statistical significance across production conditions. The 12.7-kHz band exhibited significant differences for all six production conditions, while the 16-kHz band did so for five conditions (loud singing being the exception). It is notable that three HFE bands (the 10-, 12.7-, and 16-kHz bands) showed significant gender differences for normal speech. Normal singing differed in only two bands (12.7- and 16-kHz).
Table V.
ANOVA results comparing gender differences in HFE octave and third-octave level across recording conditions. Values that reached significance are in bold font.
| Speech | Singing | ||||
|---|---|---|---|---|---|
| F-ratio | p-value | F-ratio | p-value | ||
| Soft | 6.3 kHz | 0.023 | 0.883 | 0.786 | 0.391 |
| 8 kHz | 2.354 | 0.149 | 1.098 | 0.314 | |
| 10.1 kHz | 11.834 | 0.004 | 4.419 | 0.056 | |
| 12.7 kHz | 20.964 | 0.001 | 10.86 | 0.006 | |
| 16 kHz | 9.386 | 0.009 | 9.653 | 0.008 | |
| 20.2 kHz | 5.304 | 0.038 | 5.481 | 0.036 | |
| Normal | 6.3 kHz | 0.602 | 0.452 | 3.837 | 0.072 |
| 8 kHz | 3.633 | 0.079 | 0.9 | 0.36 | |
| 10.1 kHz | 12.787 | 0.003 | 1.536 | 0.237 | |
| 12.7 kHz | 20.183 | 0.001 | 4.874 | 0.046 | |
| 16 kHz | 10.569 | 0.006 | 4.738 | 0.049 | |
| 20.2 kHz | 4.443 | 0.055 | 2.278 | 0.155 | |
| Loud | 6.3 kHz | 4.034 | 0.066 | 1.529 | 0.238 |
| 8 kHz | 0.002 | 0.966 | 0.577 | 0.461 | |
| 10.1 kHz | 4.273 | 0.059 | 2.208 | 0.161 | |
| 12.7 kHz | 10.205 | 0.007 | 5.249 | 0.039 | |
| 16 kHz | 5.233 | 0.04 | 4.402 | 0.056 | |
| 20.2 kHz | 2.003 | 0.18 | 2.035 | 0.177 | |
| Soft | 8-kHz Octave | 1.849 | 0.197 | 0.551 | 0.471 |
| 16-kHz Octave | 17.17 | 0.001 | 10.741 | 0.006 | |
| Normal | 8-kHz Octave | 3.469 | 0.085 | 0.298 | 0.594 |
| 16-kHz Octave | 17.446 | 0.001 | 4.872 | 0.046 | |
| Loud | 8-kHz Octave | 0.386 | 0.545 | 0.026 | 0.874 |
| 16-kHz Octave | 8.526 | 0.012 | 4.842 | 0.046 | |
| Soft | Total HFE | 2.348 | 0.149 | 0.925 | 0.354 |
| Normal | Total HFE | 4.558 | 0.052 | 0.029 | 0.867 |
| Loud | Total HFE | 0.961 | 0.345 | 0.067 | 0.8 |
Likewise, gender differences in fricative production (using normalized levels) reached significance for only certain fricatives and bands. Figure 9 and Table Table VI. (see also Table Table VII.) show that for /s/ production males had significantly greater 6.3-kHz band levels, while females had significantly greater levels for the 10-, 12.7-. 16-, and 20-kHz bands (leading to a significantly greater overall HFE level). Similarly, male levels for /f/ production were significantly greater than females in the 6.3-kHz band (leading to a significantly greater 8-kHz octave band level), while female levels were significantly greater than males in the last two HFE third-octave bands (16 and 20 kHz, leading to a significantly greater 16-kHz octave band level). The only other difference that reached significance was the 8-kHz band for /∫/, which was greater for females than males.
Figure 9.
Third-octave band levels for fricatives produced by each gender, calculated from the mean LTAS (see also Table Table VII.).
Table VI.
ANOVA results comparing gender differences in HFE octave and third-octave level across voiceless fricatives. Values that reached significance are in bold font.
| F-ratio | p-value | F-ratio | p-value | ||||
|---|---|---|---|---|---|---|---|
| /s/ | 6.3 kHz | 4.699 | 0.049 | /f/ | 6.3 kHz | 7.248 | 0.018 |
| 8 kHz | 3.377 | 0.089 | 8 kHz | 4.26 | 0.06 | ||
| 10.1 kHz | 25.557 | <0.001 | 10.1 kHz | 0.523 | 0.482 | ||
| 12.7 kHz | 35.849 | <0.001 | 12.7 kHz | 4.561 | 0.052 | ||
| 16 kHz | 16.538 | 0.001 | 16 kHz | 9.415 | 0.009 | ||
| 20.2 kHz | 6.935 | 0.021 | 20.2 kHz | 10.507 | 0.006 | ||
| /∫/ | 6.3 kHz | 0.533 | 0.478 | /θ/ | 6.3 kHz | 1.083 | 0.317 |
| 8 kHz | 5.728 | 0.032 | 8 kHz | 0.833 | 0.378 | ||
| 10.1 kHz | 1.112 | 0.311 | 10.1 kHz | 0.785 | 0.392 | ||
| 12.7 kHz | 3.229 | 0.096 | 12.7 kHz | 0.368 | 0.555 | ||
| 16 kHz | 1.412 | 0.256 | 16 kHz | 1.477 | 0.246 | ||
| 20.2 kHz | 0.175 | 0.683 | 20.2 kHz | 2.387 | 0.146 | ||
| /s/ | 8-kHz Octave | 8.943 | 0.01 | /f/ | 8-kHz Octave | 5.996 | 0.029 |
| 16-kHz Octave | 31.65 | <0.001 | 16-kHz Octave | 9.855 | 0.008 | ||
| /∫/ | 8-kHz Octave | 2.373 | 0.147 | /θ/ | 8-kHz Octave | 0.722 | 0.411 |
| 16-kHz Octave | 2.436 | 0.143 | 16-kHz Octave | 1.481 | 0.245 | ||
| /s/ | Total HFE | 14.306 | 0.002 | /f/ | Total HFE | 0.474 | 0.503 |
| /∫/ | Total HFE | 2.448 | 0.142 | /θ/ | Total HFE | 0.469 | 0.505 |
Table VII.
Mean total, octave, and third-octave HFE levels for each of the 4 voiceless fricatives separated by gender, calculated from the mean LTAS for each fricative and gender.
| /s/ | /∫/ | /f/ | /θ/ | |||||
|---|---|---|---|---|---|---|---|---|
| Band | Female | Male | Female | Male | Female | Male | Female | Male |
| Total HFE | 58.3 | 56.2 | 51.5 | 50 | 41.7 | 41 | 40.9 | 40.1 |
| 8-kHz Oct | 57.5 | 55.9 | 51.3 | 49.8 | 37.6 | 39.2 | 35.2 | 36.3 |
| 16-kHz Oct | 50.2 | 44.8 | 38.9 | 36.5 | 39.5 | 36.2 | 39.6 | 37.3 |
| 6.3 kHz | 49.6 | 51.8 | 49 | 48.3 | 28.9 | 32.7 | 29.4 | 31.4 |
| 8 kHz | 53.7 | 52.2 | 46.7 | 43.2 | 33.3 | 35.2 | 30.6 | 32.1 |
| 10.1 kHz | 53.8 | 48.6 | 39.6 | 38.5 | 34.6 | 35.1 | 31.2 | 32.9 |
| 12.7 kHz | 49 | 43.2 | 36.9 | 34.8 | 36 | 33.1 | 35.5 | 33.7 |
| 16 kHz | 43.4 | 38.8 | 33.8 | 30.6 | 35.5 | 31.7 | 35.5 | 33 |
| 20.2 kHz | 35.9 | 32.4 | 26.6 | 25.7 | 31.7 | 28 | 32.8 | 30 |
Here it should be acknowledged that this report of statistical analysis is not ideal as it consists of continuously comparing means between genders across bands and conditions, which increases the risk of a Type I error (inaccurate rejection of the null hypothesis). However, this research has been quite exploratory in nature, and, as there are very little data on HFE in the research literature, this broad multiple comparison approach became necessary as a starting point for future research. It is quite possible that some of the significant gender effects reported here for certain bands and/or conditions are in actuality erroneous, but the best method to establish this would be to conduct future experiments designed to examine the robustness of the hypotheses derived from this report.
It was predicted that female speech/singing would produce more HFE than male speech/singing. This prediction was supported with the caveats that significant differences between genders in HFE level of running speech and singing were only consistent for a limited bandwidth (11.3–18 kHz), and that mean male levels were consistently greater in the 6.3-kHz third-octave band (5.7–7.1 kHz) across conditions and fricatives. Significant gender differences were found for production of the fricatives /s/ and /f/, but not /∫/ or /θ/, with male levels greater in the lower HFE range and female levels greater in the upper HFE range. These differences appear to agree somewhat with the single-subject data given by Stelmachowicz et al. (2001).
CONCLUSIONS
Previous work has shown that mean and median HFE level difference limens for humans listening to samples of singing and speech are close to 4–6 dB (for the 8-kHz octave), with some listeners able to detect differences as small as 1 dB (Monson et al., 2011; Monson, 2011). All differences found between production conditions here in the 8-kHz octave band exceeded 1 dB except gender differences in singing. Several of the differences found here met or exceeded 4 dB. The 8-kHz octave band differences between successive production levels (soft vs normal vs loud) were >4 dB in speech (∼3 dB in singing) and differences between production modes (speech vs singing) were 5.3 and 3.8 dB for soft and normal productions, respectively (1.6 dB for loud production). The fricatives /s/ and /∫/ differed from each other by more than 6 dB in 8-kHz octave, and from /f/ and /θ/ by more than 11 dB (/f/ and /θ/ only differed from each other by 2.5 dB). Gender differences in the 8-kHz octave were only 2.4 dB for speech and 0.4 dB for singing.
While HFE level is greatly reduced relative to the rest of the speech spectrum, the HFE spectral differences found here indicate that there is acoustical information in HFE that distinguishes production modes, production levels, phoneme (fricative) classes, and genders. Since previous work indicates many of these differences are detectable, this information is of potential perceptual value to humans in distinguishing between and identifying human vocalizations. This study was an initial attempt at a general characterization of the acoustical nature of HFE with the long-term goal of quantifying its perceptual role and the potential for volitional control of HFE level during voice and speech production. It is hoped that this report will be of particular value to those in the areas of vocal tract modeling and voice synthesis working on the difficult tasks of modeling HFE and synthesizing “natural” human sounds; to those studying augmentative hearing technology (e.g., hearing aids and cochlear implants) to improve effectiveness of these devices; and to those offering training and therapy for singing and speech, as acoustical measures that emerge from HFE studies may prove useful in assessing and treating different qualitative and quantitative aspects of the human speaking and singing voice.
ACKNOWLEDGMENTS
This work was carried out at Brigham Young University in Provo, UT, and was funded by NIH grants F31DC010533 and R01DC8612. The authors thank Kent Gee, Eric Hunter, and the BYU Acoustics Research Group for use of facilities and equipment.
References
- Apoux, F., and Bacon, S. P. (2004). “ Relative importance of temporal information in various frequency regions for consonant identification in quiet and in noise,” J. Acoust. Soc. Am. 116, 1671–1680. 10.1121/1.1781329 [DOI] [PubMed] [Google Scholar]
- Badri, R., Siegel, J. H., and Wright, B. A. (2011). “ Auditory filter shapes and high-frequency hearing in adults who have impaired speech in noise performance despite clinically normal audiograms,” J. Acoust. Soc. Am. 129, 852–863. 10.1121/1.3523476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best, V., Carlile, S., Jin, C., and van Schaik, A. (2005). “ The role of high frequencies in speech localization,” J. Acoust. Soc. Am. 118, 353–363. 10.1121/1.1926107 [DOI] [PubMed] [Google Scholar]
- Byrne, D., Dillon, H., Tran, K., Arlinger, S., Wilbraham, K. Cox, R., Hagerman, B., Hetu, R., Kei, L., Lui, C., Kiessling, J., Kotby, N. M., Nasser, N. H. A., Wafaa , Nakanishi, Y., Oyer, H., Powell, R., Stephens, D., Meredith, R., Sirimanna, T., Tavartkiladze, G., Frolenkov, G. I., Westerman, S., and Ludvigsen, C. (1994). “ An international comparison of long-term average speech spectra,” J. Acoust. Soc. Am. 96, 2108–2120. 10.1121/1.410152 [DOI] [Google Scholar]
- Dang, J., and Honda, K. (1997). “ Acoustic characteristics of the piriform fossa in models and humans,” J. Acoust. Soc. Am. 101, 456–465. 10.1121/1.417990 [DOI] [PubMed] [Google Scholar]
- Dunn, H. K., and White, S. D. (1940). “ Statistical measurements on conversational speech,” J. Acoust. Soc. Am. 11, 278–288. 10.1121/1.1916034 [DOI] [Google Scholar]
- Flanagan, J. L. (1958). “ Some properties of the glottal sounce source,” J. Speech Hear. Res. 1, 99–116. [DOI] [PubMed] [Google Scholar]
- Fry, D. B., and Manen, L. (1957). “ Basis for the acoustical study of singing,” J. Acoust. Soc. Am. 29, 690–692. 10.1121/1.1909011 [DOI] [Google Scholar]
- Füllgrabe, C., Baer, T., Stone, M. A., and Moore, B. C. (2010). “ Preliminary evaluation of a method for fitting hearing aids with extended bandwidth,” Int. J. Aud. 49, 741–753. 10.3109/14992027.2010.495084 [DOI] [PubMed] [Google Scholar]
- Hughes, G. W., and Halle, M. (1956). “ Spectral properties of fricative consonants,” J. Acoust. Soc. Am. 28, 303–310. 10.1121/1.1908271 [DOI] [PubMed] [Google Scholar]
- Jongman, A., Wayland, R., and Wong, S. (2000). “ Acoustic characteristics of English fricatives,” J. Acoust. Soc. Am. 108, 1252–1263. 10.1121/1.1288413 [DOI] [PubMed] [Google Scholar]
- Lippmann, R. P. (1996). “ Accurate consonant perception without mid-frequency speech energy,” IEEE Trans. Speech Audiol. Proc. 4, 66–69. 10.1109/TSA.1996.481454 [DOI] [Google Scholar]
- Maniwa, K., Jongman, A., and Wade, T. (2009). “ Acoustic characteristics of clearly spoken English fricatives,” J. Acoust. Soc. Am. 125, 3962–3973. 10.1121/1.2990715 [DOI] [PubMed] [Google Scholar]
- Monson, B. B. (2011). “ High-frequency energy in singing and speech,” Ph.D. dissertation, U. Arizona, Tucson, Arizona. [Google Scholar]
- Monson, B. B., Hunter, E. J., and Story, B. H. (2012). “ Horizontal directivitity of low- and high-frequency energy in speech and singing,” J. Acoust. Soc. Am. 132, 433–441. 10.1121/1.4725963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monson, B. B., Lotto, A. J., and Ternström, S. (2011). “ Detection of high-frequency energy changes in sustained vowels produced by singers,” J. Acoust. Soc. Am. 129, 2263–2268. 10.1121/1.3557033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, B. C., Füllgrabe, C., and Stone, M. A. (2010). “ Effect of spatial separation, extended bandwidth, and compression speed on intelligbility in a competing-speech task,” J. Acoust. Soc. Am. 128, 360–371. 10.1121/1.3436533 [DOI] [PubMed] [Google Scholar]
- Moore, B. C., Stone, M. A., Füllgrabe, C., Glasberg, B. R., and Puria, S. (2008). “ Spectro-temporal characteristics of speech at high frequencies, and the potential for restoration of audibility to people with mild-to-moderate hearing loss,” Ear Hear. 29, 907–922. 10.1097/AUD.0b013e31818246f6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, B. C., and Tan, C. T. (2003). “ Perceived naturalness of spectrally distorted speech and music,” J. Acoust. Soc. Am. 114, 408–419. 10.1121/1.1577552 [DOI] [PubMed] [Google Scholar]
- Pittman, A. L. (2008). “ Short-term word-learning rate in children with normal hearing and children with hearing loss in limited and extended high-frequency bandwidths,” J. Speech Lang. Hear. Res. 51, 785–797. 10.1044/1092-4388(2008/056) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoji, K., Regenbogen, E., Yu, J. D., and Blaugrund, S. M. (1991). “ High-frequency components of normal voice,” J. Voice 5, 29–35. 10.1016/S0892-1997(05)80160-2 [DOI] [Google Scholar]
- Shoji, K., Regenbogen, E., Yu, J. D., and Blaugrund, S. M. (1992). “ High-frequency power ratio of breathy voice,” Laryngoscope 102, 267–271. [DOI] [PubMed] [Google Scholar]
- Sivian, L. J. (1929). “ Speech power and its measurement,” Bell Sys. Tech. J. 8, 646–661. [Google Scholar]
- Spitzer, S. M., Liss, J. M., and Mattys, S. L. (2007). “ Acoustic cues to lexical segmentation: A study of resynthesized speech,” J. Acoust. Soc. Am. 122, 3678–3687. 10.1121/1.2801545 [DOI] [PubMed] [Google Scholar]
- Stelmachowicz, P. G., Pittman, A. L., Hoover, B. M., and Lewis, D. E. (2001). “ Effect of stimulus bandwidth on the perception of /s/ in normal- and hearing-impaired children and adults,” J. Acoust. Soc. Am. 110, 2183–2190. 10.1121/1.1400757 [DOI] [PubMed] [Google Scholar]
- Ternström, S. (2008). “ Hi-Fi voice: Observations on the distribution of energy in the singing voice spectrum above 5 kHz,” Proc. Acoustics’08, Paris, June 29 – July 4, http://intellagence.eu.com/acoustics2008/acoustics2008/cd1/data/index.html (Last viewed October 4, 2011).
- Valencia, N. N., Mendoza, L. E., Mateo, R. I., and Carballo, G. G. (1994). “ High-frequency components of normal and dysphonic voices,” J. Voice 8, 157–162. 10.1016/S0892-1997(05)80307-8 [DOI] [PubMed] [Google Scholar]