Relationship between x-ray illumination field size and flat field intensity and its impacts on x-ray imaging

Xue Dong; Tianye Niu; Xun Jia; Lei Zhu

doi:10.1118/1.4750054

. 2012 Sep 11;39(10):5901–5909. doi: 10.1118/1.4750054

Relationship between x-ray illumination field size and flat field intensity and its impacts on x-ray imaging

Xue Dong ¹, Tianye Niu ¹, Xun Jia ², Lei Zhu ^3,^a)

PMCID: PMC3461050 PMID: 23039629

Abstract

Purpose: X-ray cone-beam CT (CBCT) is being increasingly used for various clinical applications, while its performance is still hindered by image artifacts. This work investigates a new source of reconstruction error, which is often overlooked in the current CBCT imaging. The authors find that the x-ray flat field intensity (I₀) varies significantly as the illumination volume size changes at different collimator settings. A wrong I₀ value leads to inaccurate CT numbers of reconstructed images as well as wrong scatter measurements in the CBCT research.

Methods: The authors argue that the finite size of x-ray focal spot together with the detector glare effect cause the I₀ variation at different illumination sizes. Although the focal spot of commercial x-ray tubes typically has a nominal size of less than 1 mm, the off-focal-spot radiation covers an area of several millimeters on the tungsten target. Due to the large magnification factor from the field collimator to the detector, the penumbra effects of the collimator blades result in different I₀ values for different illumination field sizes. Detector glare further increases the variation, since one pencil beam of incident x-ray is scattered into an area of several centimeters on the detector. In this paper, the authors study these two effects by measuring the focal spot distribution with a pinhole assembly and the detector point spread function (PSF) with an edge-spread function method. The authors then derive a formula to estimate the I₀ value for different illumination field sizes, using the measured focal spot distribution and the detector PSF. Phantom studies are carried out to investigate the accuracy of scatter measurements and CT images with and without considering the I₀ variation effects.

Results: On our tabletop system with a Varian Paxscan 4030CB flat-panel detector and a Varian RAD-94 x-ray tube as used on a clinical CBCT system, the focal spot distribution has a measured full-width-at-half-maximum (FWHM) of around 0.4 mm, while non-negligible off-focal-spot radiation is observed at a distance of over 2 mm from the center. The measured detector PSF has an FWHM of 0.510 mm, with a shape close to Gaussian. From these two distributions, the author calculate the estimated I₀ values at different collimator settings. The I₀ variation mainly comes from the focal spot effect. The estimation matches well with the measurements at different collimator widths in both horizontal and vertical directions, with an average error of less than 3%. Our method improves the accuracy of conventional scatter measurements, where the scatter is measured as the difference between fan-beam and cone-beam projections. On a uniform water cylinder phantom, more accurate I₀ suppresses the unfaithful high-frequency signals at the object boundaries of the measured scatter, and the SPR estimation error is reduced from 0.158 to 0.014. The proposed I₀ estimation also reduces the reconstruction error from about 20 HU on the Catphan©600 phantom in the selected regions of interest to less than 4 HU.

Conclusions: The I₀ variation is identified as one additional error source in x-ray imaging. By measuring the focal-spot distribution and detector PSF, the authors propose an accurate method of estimating the I₀ value for different illumination field sizes. The method obtains more accurate scatter measurements and therefore facilitates scatter correction algorithm designs. As correction methods for other CBCT artifacts become more successful, our research is significant in further improving the CBCT imaging accuracy.

Keywords: x-ray focal spot, flat field intensity, x-ray scatter, cone-beam CT

INTRODUCTION

X-ray cone-beam CT (CBCT) imaging is being increasingly used for various clinical applications. For example, on-board CBCT on a radiation therapy machine enables dose verification, patient positioning, and tumor targeting in image-guided radiation therapy (IGRT).¹^,²^,³ C-arm CBCT provides image guidance which is critical in surgical procedures.⁴^,⁵ The performance of these systems, however, is hampered by errors from large scatter contamination and beam hardening effects.⁶^,⁷ Significant research has been conducted on correction methods for these artifacts, which are able to achieve a CT number accuracy of below 50 HU in some scenarios.⁸^,⁹^,¹⁰^,¹¹^,¹²^,¹³ As more accurate CBCT imaging is required, correction for residual CBCT artifacts becomes important. In this paper, we investigate a different type of imaging error, which is often overlooked in the current CBCT studies.

We find that the x-ray flat field intensity (I₀) varies as the illumination field size changes with different collimator settings. Commercial x-ray tubes typically have nominal focal spot sizes of about 1 mm or less. The intensity distribution of the focal spot, however, spills into a large area with a diameter of several millimeters due to off-focal-spot radiation.¹⁴ In this paper, we define the focal spot area as inside the FHWM of the focal spot distribution. All the radiation generated outside the focal spot area is considered as off-focal-spot radiation. The large effective focal spot size at low intensities, together with the fact that x-ray collimator blades have a large magnification factor onto the detector, leads to penumbra effects in the order of centimeters. When the collimator reduces the illumination field size, a detector pixel receives less incident x-ray intensity since it is exposed to partial focal spot. Detector glare is a secondary effect causing the flat field intensity variation. Due to scattering in the mountings of the detector, the point-spread function (PSF) of a-Si/CsI based flat panel detectors shows an extended tail up to 4 cm from the illumination center.¹⁵^,¹⁶ The total intensity of one incident pencil beam is spread into a large area on the detector, and therefore I₀ decreases as less detector field is illuminated.

An accurate I₀ value is important in CBCT imaging. In the current practice, I₀ is usually considered dependent only on the current and voltage of the x-ray tube. Pre-stored I₀ values obtained in the system calibration are used in the reconstruction. When the field size changes, the pre-stored I₀ value becomes inaccurate, which causes errors in the reconstructed images. The problem is more severe especially in the applications of advanced region-of-interest (ROI) imaging techniques with a small illumination field¹⁷ or when the illumination field needs to be continuously changed during scan for minimum-data reconstruction.¹⁸^,¹⁹ Furthermore, ignoring I₀ variation may lead to wrong conclusions in the current CBCT research. For example, an additional fan-beam projection (with a narrowly opened collimator) is commonly used to measure the scatter signals in a cone-beam projection. Considering the fan-beam projection as scatter-free, we can use the fan-beam projection to estimate the primary signals in the cone-beam projection. In the published literature, the scatter signals in the cone-beam projection are measured as the difference of the two projections, with an implicit assumption that the I₀ distributions are unchanged in both projections.¹¹^,²⁰^,²¹ These methods obtain inaccurate scatter measurements especially around the object boundary.

In this paper, we first measure the focal spot distribution and the detector PSF of a flat-panel-based CBCT system. An equation is then derived to estimate the I₀ value for different illumination field sizes based on the measured focal spot distribution and the detector PSF. We validate the proposed formula of I₀ estimation by comparing the estimated I₀ with the measured values for different collimator settings. Effects of accurate I₀ on the improved accuracy of CBCT imaging and scatter measurement are evaluated on the Catphan©600 phantom and a cylindrical water phantom with a diameter of 16.9 cm and height of 22 cm.

METHOD

The I₀ value of an x-ray imaging system depends on many system parameters. In this paper, we assume the x-ray tube settings (i.e., mA, kVp, pulse width, etc.) unchanged in all the experiments. The detector is also calibrated well at the operating kVp such that the I₀ image is uniform across the illuminated area without heel effects²² and the detector has a linear response. We focus on the I₀ variation only due to illumination field size change of the system.

Measurement of focal spot distribution

Several standard methods can be applied in the measurement of focal spot distribution, including pinhole method, the slit method, and coded aperture mask method.¹⁴^,²³^,²⁴ In this work, we choose pinhole method because it is easy to implement and capable of providing two-dimensional distribution of the focal spot. A standard pinhole assembly is attached to the surface of the field collimator in the flat-panel-based CBCT system. After calibration, the focal spot, pinhole, and the center of detector are aligned, and a magnified image of the focal spot is projected onto the detector. The projection image of the pinhole contains background signals, with small magnitudes but comparable to the off-focal-spot radiation. To obtain an accurate distribution of the focal spot, we measure the background image by covering the pinhole using a small piece of lead in a second measurement, and then subtract the image (mainly background signals) from the first measurement.

Measurement of detector PSF

We employ an edge-spread function (ESF) method to estimate the detector PSF.¹⁶^,²⁵ The detector is first illuminated with half of the effective area blocked to obtain the ESF. A lead sheet with a sharp and straight edge is used as the beam blocker. We place the lead sheet directly on the top of the detector to minimize the magnification factor and therefore the penumbra effects. 1D line-spread function (LSF) is obtained by first taking the derivative of the 2D half-blocked projection in the direction perpendicular to the blocker edge and then averaging central 200 line profiles along the other orthogonal direction to reduce noise. Research has shown that on a flat-panel detector, the LSF function can be modeled by three terms, with one dominant Gaussian component and two other components accounting for the extended tails of flat-panel detector LSF.¹⁶ We then fit the measured LSF to the following function to further suppress noise, based on a formula provided in Ref. 16:

\begin{matrix} LSF (x) & = & \frac{a_{1}}{\sqrt{2 π b_{1}^{2}}} e^{- {|x|}^{2} / 2 b_{1}^{2}} + \frac{a_{2}}{π b_{2}^{2}} K_{1} (\frac{|x|}{b_{2}}) \\ + \frac{a_{3}}{π b_{3}} \frac{1}{1 + {|x|}^{2} / b_{3}^{2}}, \end{matrix}

(1)

where a_i, and b_i are fitting coefficients and $K_{1} (\frac{|x|}{b_{2}})$ is a first-order MacDonald (modified Bessel) function. Finally, we assume that the detector response is rotationally symmetric, i.e., the LSF remains unchanged if the beam blocker changes to a different angle. Since the LSF is equivalent to a parallel projection on the PSF, the detector PSF is calculated using a standard filtered-back-projection (FBP) (Ref. ²⁶) reconstruction on the LSF, as also implemented in Ref. 25.

I₀ for different illumination field sizes

The finite size of the focal spot and the nonideal detector PSF jointly affect the I₀ value for different illumination field size. Denote I_p as the ideal flat field image without the above two effects. We assume that the system is well calibrated, the flat field image is normalized, i.e., I_p has values of 1 inside the illuminated area and 0 outside. When the focal spot distribution, f, has a finite size and the detector has an ideal PSF (i.e., the PSF is a unit impulse), the measured flat field, I_f, becomes:

I_{f} (x, y) = I_{p} (x, y) * f (x \cdot L_{1} / L_{2}, y \cdot L_{1} / L_{2}),

(2)

where x and y are the coordinates on the detector in the horizontal and vertical directions respectively, L₁ is the distance from the field collimator to the focal spot, and L₂ is the distance from the field collimator to the detector; * is the convolution operator. Note that, f(x·L₁/L₂, y·L₁/L₂) is normalized to have unit total intensity. In the above calculation, the focal spot image on the detector is obtained by magnifying the focal spot distribution by a factor of L₂/L₁. We approximate that the focal spot distribution is mainly on a plane parallel to the field collimator as well as the detector. The magnification factor therefore remains constant for different x and y locations. On clinical CBCT systems, L₁ is around 25 cm and L₂ is around 125 cm, resulting in a large magnification factor of about 5. It is for this reason that the focal spot distribution has a large effect on I_f, although the majority of the focal spot intensity is allocated in small area of several millimeters.

The detector glare leads to similar blurring effects on the flat field image, which can also be modeled by convolution. The final I₀ image therefore is estimated as

I_{0} (x, y) = I_{p} (x, y) * f (x \cdot L_{1} / L_{2}, y \cdot L_{1} / L_{2}) * p (x, y),

(3)

where p is the detector PSF. Similar to f, p is normalized to have unit total intensity.

Equation 3 gives a 2D estimate of the flat field. For the convenience in practical implementations, we assume that the effects of a finite-size focal spot and detector glare cause a constant I₀ change across the projection field. The I₀ variation, T, is calculated by averaging the flat field intensity around the central area of the detector to reduce the random errors. In our implementations, we select the central illuminated line and eliminate the points that are less than 200 pixels from the detector edge, and then obtain T by averaging the remaining data points. Note that, since both the magnified focal spot distribution and the detector PSF are normalized to have unit total intensity, the calculated T is one when the collimator is fully open, and becomes less than one when the illumination field size decreases. In imaging applications where the illumination field size changes, we simply multiply the flat field intensity acquired when the collimator is fully open by the calculated T to obtain a more accurate I₀.

Evaluation

The measurements of the focal spot distribution and the detector PSF are carried out on our tabletop x-ray CBCT system. The system consists of a Varian RAD-94 x-ray tube, a Eureka MC150-C collimator, a Varian Paxscan 4030CB flat panel detector, and a rotary stage for CT data acquisition. The detector is operated in a two-by-two binning mode with a size of 300 mm × 400 mm, and the effective detector pixel size is 0.38 × 0.38 mm². The x-ray tube operates in the fluoroscopic imaging mode with 125 kVp, 80 mA, and a pulse width of 13 ms. The major components and the geometry of the system match exactly those of a Varian On-Board Imager (OBI) CBCT system on the Trilogy radiation therapy machine. Refer to our previous publication¹⁰ for more details of this system. The pinhole (Fluke Biomedical, Model # 07-633) has a diameter of 0.01 mm and is used to measure the focal spot distribution with a range of 0.1–0.5 mm, which covers the nominal focal spot size (0.4 mm) of our x-ray tube.

Equation 3 estimates the I₀ change value for illumination fields with arbitrary shapes. On commercial x-ray imaging systems, the illumination field is controlled by collimator blades in the horizontal and the vertical directions. Here, we validate the proposed I₀ estimation formula by measuring the flat field intensities with different collimator widths in the horizontal and the vertical directions and comparing them with the estimated values using the proposed method.

The variation of I₀ leads to errors in characterization of the x-ray systems. As one example of conventional scatter measurement methods, we acquire the primary signals on one slice of the projection using a fan-beam geometry and use these signals to obtain scatter in a cone-beam projection on the same object. In published literature, the scatter is measured as the difference between the fan-beam and cone-beam projections, without considering the I₀ variation. We improve the scatter measurement by dividing the primary signals in the fan-beam projection by the scaling factor (T) obtained based on our I₀ estimation [Eq. 3], which accounts for the I₀ increase in the cone-beam geometry. A comparison study is performed on an in-house uniform cylindrical water phantom with a diameter of 16.9 cm and a height of 22 cm. The measured scatter signals and scatter-to-primary ratio (SPR) with and without the proposed I₀ correction are compared with the reference values obtained from a Monte Carlo (MC) simulation on a water phantom with the same geometry.

The MC simulation is conducted using a MC software package developed for graphics-processor-unit (GPU)-based digitally reconstruction radiograph (gDRR) calculations. gDRR obtains both primary and scatter signals via realistically simulating the CBCT projection process. The software is developed in the environment of GPU for its high computational efficiency.²⁷ In our previous work, the accuracy of the scatter signal calculation has been demonstrated by comparing the results with those from EGSnrc, a commonly used MC package for photon transport. We found a good agreement between gDRR results and those using EGSnrc on a head-and-neck (HN) cancer patient with a standard CBCT setup.²⁷ In each projection, a number of photons are transported in parallel by different GPU threads to gain efficiency. Within each thread, a photon is first generated at the x-ray source and is then transported according to the physical interaction process between the photon and the phantom material, till it exits the phantom region or is absorbed. The scatter signal is recorded if the photon exits the phantom, hits the detector, and is scattered at least once inside the phantom. In the simulation, we use a geometrical configuration identical to that in our experiment. The simulated x-ray source has an infinitely small focal-spot area and a flat photon fluence within the collimator area. An x-ray spectrum of 125 kVp as used in our experiment is simulated based on a published method.²⁸ The deposited photon energy on the detector has a nonlinear relationship with the incident photon energy. This detector response is also considered in the gDRR simulation using a realistic detector response curve. The scatter in the detector housing is neglected for the high efficiency of simulation.

The scatter or SPR error, E, is evaluated using the root of the mean square error (RMSE), calculated as

E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {(\frac{s_{e} (i) - s_{0} (i)}{s_{0} (i)})}^{2}} \times 100 %,

(4)

where i is the index of the pixel, s_e is the estimated scatter in the calculation of scatter estimation error, or the estimated SPR in the calculation of SPR error. s₀, is the ground truth obtained from the MC simulation and N is the total number of pixels in the ROI.

A study on the Catphan©600 phantom (The Phantom Laboratory, Salem, NY), with a diameter of 20 cm, is performed to show the influence of a variant I₀ on the CT image quality. To suppress scatter artifacts and study effects on image quality from I₀ variation only, fan-beam projections are taken with an illumination width of about 10 mm on the detector in the vertical direction. Fan-beam CT reconstructions are compared with and without the consideration of the I₀ value change as the illumination field changes from cone-beam to fan-beam. In selected ROIs, we use mean CT number values on the reconstructed images as image quality metrics.

RESULTS

Measurement of focal spot distribution and detector PSF

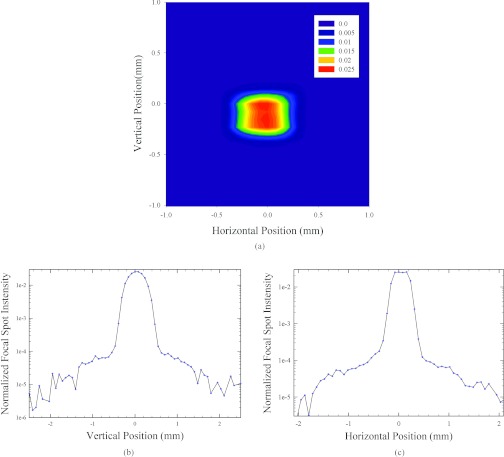
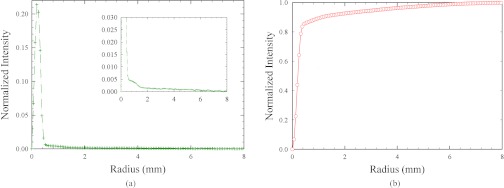
Figure 1 shows the measured focal spot distribution using the pinhole method. The measured FWHM is about 0.463 mm in the vertical direction and about 0.386 mm in the horizontal direction, close to the nominal value of 0.4 mm. However, the radiation source covers an area of up to 4 mm (2 mm on each side). Note that, although the off-focal-spot radiation (i.e., the radiation outside the FWHM) is small, it significantly contributes to the I₀ variation since the integration in Eq. 3 is taken on a large area. For a better illustration of this effect, we calculate the total radiation inside rings well centered at the focal spot but with different radii, as shown in Fig. 2a. The radiation is non-negligible even at a distance of several millimeters from the center. To quantify the contribution from the off-focal-spot radiation in the calculation of I₀, we then calculate the radiation inside a disc with different radii. As seen in Fig. 2b, a disc with a 1 mm radius covers majority of the focal spot, but still misses around 11% of the total x-ray source radiation.

Results of focal spot measurement. Measured focal spot distribution in (a) 2D plot, (b) 1D plot of the central vertical line, and (c) 1D plot of the central horizontal line. The distribution is normalized to have unit total intensity.

Total radiation of the focal spot distribution inside (a) a ring or (b) a disc well centered with different radii.

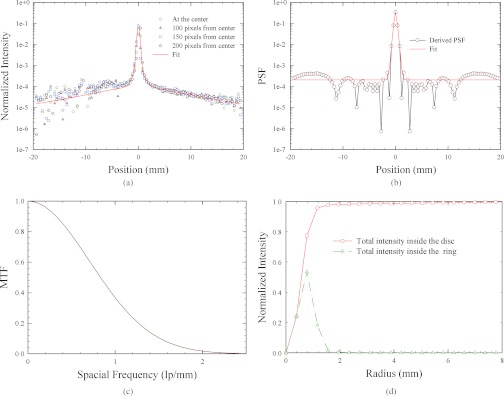
Since the detector response changes with the detector location, we performed the LSF measurements with the beam blocker edge at different positions on the detector, i.e., at the detector center, 100, 150, and 200 pixels away from the center. The results are summarized in Fig. 3a. Coherence is observed in these measurements, indicating the shift-invariant response of the detector. We then use the LSF measured at the detector and suppress the noise via fitting using Eq. 1. The resulting fitting coefficients are presented in Table 1. Using an FBP reconstruction algorithm on the LSF, we obtain the detector PSF shown in Fig. 3b. Gaussian fitting is finally used to suppress numerical errors on the PSF. The resulting fitting function is y(x) = y₀ + a · exp ( − 0.5 · |(x − x₀)/b|^c), where a = 0.3475, b = 0.1746, c = 1.3522, x₀ = 0, y₀ = 0.0002. To verify our measurement, we compute the modulation transfer function (MTF) from the PSF. The result shown in Fig. 3c matches well with the literature.²⁹ The PSF has a long tail as in the focal spot distribution. We therefore plot in Fig. 3d the total intensity of the PSF in a ring or a disc at different radii, similar to Fig. 2. As seen in Fig. 3d, a disc with a 1 mm radius misses around 12% of the total intensity.

(a) 1D profiles of the detector LSFs measured with the beam blocker edge at different detector positions. (b) 1D profile of the calculated detector PSF. The 2D PSF is rotationally symmetric and normalized to the have unit total intensity. (c) MTF. (d) Total intensity of the detector PSF inside a ring or a disc well centered with different radii.

Table 1.

Fitting coefficients in Eq. 1 for estimating LSF on the Varian Paxscan 4030CB flat panel detector.

Coefficient	Value
a1	0.8900
a2	0.0453
a3	0.0647
b1	0.2254
b2	0.4252
b3	8.4792

Open in a new tab

Estimation of I₀ variation

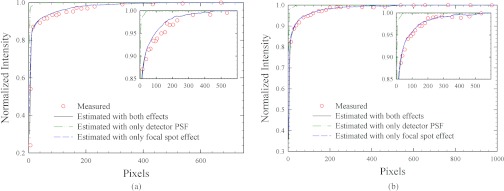
Figure 4 compares the measured I₀ at the detector center and the estimated values using the proposed method for different collimator widths on the detector in the horizontal and vertical directions. The values are normalized by the flat field intensity measured with the collimator fully open. Note that, the I₀ value drops significantly when the illumination field size is small. When the collimator width is about 27 pixels on the detector (10.5 mm), the decrease reaches about 12% as compared to the value in a full cone-beam projection. The estimated flat field intensities considering only the focal spot or the detector PSF effects are shown in Fig. 4 as well. It is seen that a majority of the I₀ variation is attributed to the off-focal-spot radiation. The effects of a nonideal detector PSF are noticeable but relatively small. By considering both effects, the estimated I₀ variation curve using Eq. 3 matches the measured values, with an average error of less than 3.0%.

Comparison of the measured and the estimated I₀ values for different (a) vertical and (b) horizontal illumination widths on the detector. The results considering both focal spot and detector PSF effects almost overlap with those considering only the focal spot effect.

Influence of I₀ variation on scatter measurement

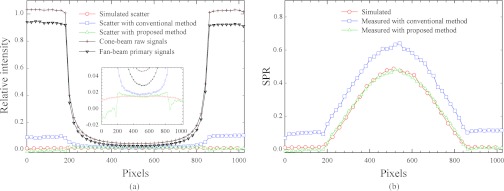
Figure 5 shows the comparison of scatter to flat field intensity ratio and scatter to primary ratio (SPR) on the in-house uniform cylindrical water phantom. Without I₀ variation correction, the measured scatter shows a high frequency component around the object edge, an unrealistic behavior contradictory to the characteristics of scattering process.¹⁶^,³⁰^,³¹ Similar scatter measurements are found in publications from other researchers and even from our own group.⁸^,⁹^,²¹ The discrepancy between the measurement and MC simulation is often ascribed to extra detector scatter.²⁰ In this study, we find that the scatter measurement can be more accurate with the proposed I₀ correction. As shown in Fig. 5a, the high frequency component around the edge of scatter measurement is greatly suppressed. The scatter estimation error is decreased from 40% to 6% inside the phantom volume. Some discrepancies are observed around the object periphery after using our method, which is due to the assumption that the off-focal-spot photons travel a pathlength through the object similar to the photons emitting from the center of the focal spot. As also discussed in a recent publication,³⁰ this assumption is valid in the center of the object, but less accurate around the object edge for the reason that the path length near the edge of the cylinder is changing rapidly between photons arriving at adjacent horizontal pixels. The primary signal change from a fan-beam projection to a cone-beam projection therefore cannot be modeled as a simple scaling by the I₀ variation. It is also noted that, different from simulated scatter, the scatter distribution obtained by the proposed method is asymmetric. This is mainly because our method assumes uniform I₀ variation across the projection field. The assumption becomes less accurate especially around the edge of the detector, where the incident angle is large. However, these discrepancies cause small errors in SPR as compared to the one with conventional measurement because of the large primary intensity outside the object [see Fig. 5b]. With the proposed method, the RMSE of SPR estimation is reduced from 0.158 to 0.014. Since CT reconstruction accuracy is determined by SPR, not by scatter alone,⁶ our method achieves sufficient scatter measurement accuracy for high-quality CT images.

1D profiles of (a) scatter and primary signals and (b) SPRs on the in-house water phantom.

Influence of I₀ variation on the accuracy of CT numbers

Figure 6 shows the reconstructed Catphan©600 fan-beam CT images with and without considering effects of I₀ change from cone-beam to fan-beam geometry. With the collimator width of ∼27 pixels, the proposed method estimates the I₀ variation about 12.0%, and greatly improves the image accuracy. As shown in Table 2, CT number error is up to 23 HU using the cone-beam flat field as the I₀ for the fan-beam reconstruction, while with improved I₀, the error is reduced to less than 4 HU. Note that, fan-beam CT has a superior image quality since scatter signals are inherently suppressed. The image comparison indicates the importance of using an accurate I₀ value in further improvement of CBCT image quality after scatter correction.

Reconstructed images of Catphan©600 phantom from fan-beam projections (a) using cone-beam flat field as I₀ and (b) using estimated I₀ with the proposed method. (c) Reference image, using fan-beam flat field as I₀. Display window: [–26 168] HU.

Table 2.

A comparison of mean CT numbers in the selected ROIs shown in Fig. 6. R_co, R_pro, and R_fan denote the mean CT numbers in Figs. 6a, 6b, 6c, respectively.

Region	R_co	R_pro	R_fan	R_co – R_fan	R_pro – R_fan
1	−39	−54	−53	14	−1
2	−87	−104	−103	16	−1
3	−171	−188	−188	17	0
4	−910	−927	−927	17	0
5	914	894	891	23	3
6	328	314	312	16	2
7	−910	−925	−926	16	1

Open in a new tab

CONCLUSIONS AND DISCUSSION

In this paper, we measure the focal spot distribution and the detector PSF, and investigate their effects on flat field intensities. On a tabletop cone-beam CT system, we find that although the focal spot distribution has an FWHM of about 0.463 mm in the vertical direction and 0.386 mm in the horizontal direction and its low intensity tail reaches several millimeters from the focal spot center. The measured detector PSF has an FWHM of 0.510 mm, with a shape close to Gaussian. The large effective focal spot size at low intensities, together with the detector glare effect, results in I₀ variation for different collimator settings. For example, the I₀ value difference is up to 12% as the geometry changes from cone-beam to fan-beam.

In the studies presented in this paper, the I₀ variation has significant effects on conventional scatter measurements. If the I₀ value change is ignored, large discrepancy up to 410% between the measured scatter and the ground truth (MC simulated scatter) appear around the object edge. Inaccurate I₀ also causes reconstruction errors, although the errors are small as compared to those due to scatter and beam-hardening effects. Scatter and beam-hardening correction methods for CBCT have already been extensively studied and are able to reduce the reconstruction error from over 300 HU to below 50 HU. After these corrections, adjustment of the I₀ value based on the illumination size should be included to further increase the CT number accuracy.

Many factors need to be investigated to improve the proposed I₀ estimation in future studies. For example, in this work, we only study the I₀ variation due to illumination field size change of the system, and assume the x-ray tube settings unchanged in all the experiments and the heel effects eliminated with the detector calibration. These factors degrade the uniformity of the flat field intensity, which is an important assumption in our flat field estimation from Eq. 3.

Our finding of the I₀ value change has several important indications to the current research on volumetric CT imaging. Many system hardware and scatter correction algorithm designs depend on accurate characterization of scatter signals. As we have shown in our evaluation study, scatter measurement without considering the I₀ effect leads to scatter signals with unfaithful characteristics, which degrades the accuracy of the resulting scatter corrections. An inaccurate I₀ results in a CT number error of around 20 HU, which may become critical in more advanced CT imaging scenarios, such as ROI imaging from minimum projection data.¹⁷^,¹⁸^,¹⁹ In these scans, the illumination field is reduced from a conventional setting or even changes constantly to acquire only the projection data that contribute to the ROI reconstruction. To improve the reconstruction accuracy, we can estimate the I₀ variation using the proposed method for each projection based on the illumination field size setting (for example, calculated from beam collimator positions), and then use the corrected I₀ in the calculation of line integrals for reconstruction. As such, our research may facilitate the development of more accurate CT systems.

ACKNOWLEDGMENTS

This project is partially supported by Georgia Institute of Technology new faculty startup funding, the NIH under the Grant No. 1R21EB012700-01A1, and Chiang Chen Overseas Graduate Fellowship. The authors would like to thank Dr. Stephen Rudin and Mr. Amit Jain (Departments of Radiology, Neurosurgery, Physiology and Biophysics, University at Buffalo (SUNY)) and Mr. Jim Mariani (Varian Medical Systems) for their help with the focal spot measurement.

References

Guan H. and Dong H., “Dose calculation accuracy using cone-beam CT (CBCT) for pelvic adaptive radiotherapy,” Phys. Med. Biol. 54(20), 6239–6250 (2009). 10.1088/0031-9155/54/20/013 [DOI] [PubMed] [Google Scholar]
Oldham M., Létourneau D., Watt L., Hugo G., Yan D., Lockman D., Kim L. H., Chen P. Y., Martinez A., and Wong J. W., “Cone-beam-CT guided radiation therapy: A model for on-line application,” Radiother. Oncol. 75(3), 271–278 (2005). 10.1016/j.radonc.2005.03.026 [DOI] [PubMed] [Google Scholar]
Niu T., Zhu L., and Al-Basheer A., “Quantitative cone-beam CT imaging in radiation therapy using planning CT as a prior: First patient studies,” Med. Phys. 39(4), 1991–2000 (2012). 10.1118/1.3693050 [DOI] [PMC free article] [PubMed] [Google Scholar]
Fahrig R., Dixon R., Payne T., Morin R. L., Ganguly A., and Strobel N., “Dose and image quality for a cone-beam C-arm CT system,” Med. Phys. 33(12), 4541–4550 (2006). 10.1118/1.2370508 [DOI] [PubMed] [Google Scholar]
Lauritsch G., Boese J., Wigström L., Kemeth H., and Fahrig R., “Towards cardiac C-arm computed tomography,” IEEE Trans. Med. Imaging 25(7), 922–934 (2006). 10.1109/TMI.2006.876166 [DOI] [PubMed] [Google Scholar]
Niu T. and Zhu L., “Overview of x-ray scatter in cone beam computed tomography and its correction methods,” Curr. Med. Imaging Rev. 6(2), 82–89 (2010). 10.2174/157340510791268515 [DOI] [Google Scholar]
Reitz I., Hesse B.-M., Nill S., Tucking T., and Oelfke U., “Enhancement of image quality with a fast iterative scatter and beam hardening correction method for kV CBCT,” Z. Med. Phys. 19(3), 158–172 (2009). 10.1016/j.zemedi.2009.03.001 [DOI] [PubMed] [Google Scholar]
Gao H., Fahrig R., Bennett N. R., Sun M., Star-Lack J., and Zhu L., “Scatter correction method for x-ray CT using primary modulation: Phantom studies,” Med. Phys. 37(2), 934–946 (2010). 10.1118/1.3298014 [DOI] [PMC free article] [PubMed] [Google Scholar]
Niu T., Sun M., Star-Lack J., Gao H., Fan Q., and Zhu L., “Shading correction for on-board cone-beam CT in radiation therapy using planning MDCT images,” Med. Phys. 37(10), 5395–406 (2010). 10.1118/1.3483260 [DOI] [PubMed] [Google Scholar]
Niu T. and Zhu L., “Scatter correction for full-fan volumetric CT using a stationary beam blocker in a single full scan,” Med. Phys. 38(11), 6027–6038 (2011). 10.1118/1.3651619 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhu L., Bennett R., and Fahrig R., “Scatter correction method for X-ray CT using primary modulation theory and preliminary results,” IEEE Trans. Med. Imaging 25(12), 1573–1587 (2006). 10.1109/TMI.2006.884636 [DOI] [PubMed] [Google Scholar]
Zhu L., Xie Y., Wang J., and Xing L., “Scatter correction for cone-beam CT in radiation therapy,” Med. Phys. 36(6), 2258–2268 (2009). 10.1118/1.3130047 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhu L., Star-Lack J., Li T., Xing L., and Fahrig R., “Improved scatter correction for X-ray cone-beam CT using primary modulation,” Proc. SPIE 6510, 65101U1–65101U8 (2007). 10.1117/12.713678 [DOI] [Google Scholar]
Russo P. and Mettivier G., “Method for measuring the focal spot size of an x-ray tube using a coded aperture mask and a digital detector,” Med. Phys. 38(4), 2099–2115 (2011). 10.1118/1.3567503 [DOI] [PubMed] [Google Scholar]
Bub A., Gondrom S., Maisl M., Uhlmann N., and Arnold W., “Image blur in a flat-panel detector due to compton scattering at its internal mountings,” Meas. Sci. Technol. 18(5), 1270–1277 (2007). 10.1088/0957-0233/18/5/013 [DOI] [Google Scholar]
Poludniowski G., Evans P. M., Kavanagh A., and Webb S., “Removal and effects of scatter-glare in cone-beam CT with an amorphous-silicon flat-panel detector,” Phys. Med. Biol. 56(2011), 1837–1851 (2011). 10.1088/0031-9155/56/6/019 [DOI] [PubMed] [Google Scholar]
Zhang B. and Zeng G. L., “Two-dimensional iterative region-of-interest (ROI) reconstruction from truncated projection,” Med. Phys. 34(3), 935–944 (2007). 10.1118/1.2436969 [DOI] [PubMed] [Google Scholar]
Sidky E. Y., Zou Y., and Pan X., “Minimum data image reconstruction algorithms with shift-invariant filtering for helical, cone-beam CT,” Phys. Med. Biol. 50(8), 1643–1657 (2005). 10.1088/0031-9155/50/8/002 [DOI] [PubMed] [Google Scholar]
Zou Y. and Pan X., “Exact image reconstruction on PI-lines from minimum data in helical cone-beam CT,” Phys. Med. Biol. 49(6), 941–959 (2004). 10.1088/0031-9155/49/6/006 [DOI] [PubMed] [Google Scholar]
Chen Y., Liu B., Connor J. M. O., Didier C. S., and Glick S. J., “Characterization of scatter in cone-beam CT breast imaging: comparison of experimental measurements and Monte Carlo simulation,” Med. Phys. 36(3), 857–869 (2009). 10.1118/1.3077122 [DOI] [PMC free article] [PubMed] [Google Scholar]
Sun M. and Star-Lack J. M., “Improved scatter correction using adaptive scatter kernel superposition,” Phys. Med. Biol. 55(22), 6695–6720 (2010). 10.1088/0031-9155/55/22/007 [DOI] [PubMed] [Google Scholar]
Mori S., Endo M., Nishizawa K., Ohno M., Miyazaki H., Tsujita K., and Saito Y., “Prototype heel effect compensation filter for cone-beam CT,” Phys. Med. Biol. 50(22), N359–N370 (2005). 10.1088/0031-9155/50/22/N02 [DOI] [PubMed] [Google Scholar]
Everson J. D. and Gray J. E., “Focal-spot measurement: Comparison of slit, pinhole, and star resolution pattern techniques,” Radiology 165, 261–264 (1987). [DOI] [PubMed] [Google Scholar]
Kimme-Smith C., Bassett L. W., and Gold R. H., “Focal spot size measurements with pinhole and slit for microfocus mammography units,” Med. Phys. 15(3), 298–303 (1988). 10.1118/1.596264 [DOI] [PubMed] [Google Scholar]
Li H., Mohan R., and Zhu X. R., “Scatter kernel estimation with an edge-spread function method for cone-beam computed tomography imaging,” Phys. Med. Biol. 53(23), 6729–6748 (2008). 10.1088/0031-9155/53/23/006 [DOI] [PubMed] [Google Scholar]
Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1(6), 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
Jia X., Yan H., Cervino L., Folkerts M., and Jiang S. B., “A GPU tool for efficient, accurate, and realistic simulation of cone beam CT projections,” Med. Phys. (submitted), e-print arXiv:1204.6367v1. [DOI] [PMC free article] [PubMed]
Boone J. M. and Seibert J. A., “An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV,” Med. Phys. 24(11), 1661–670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]
Kai Y., “Development and evaluation of a dedicated breast CT scanner,” Ph.D. dissertation, University of California, Davis, CA, 2007. [Google Scholar]
Bootsma G. J., Verhaegen F., and Jaffray D. A., “The effects of compensator and imaging geometry on the distribution of x-ray scatter in CBCT,” Med. Phys. 38(2), 897–914 (2011). 10.1118/1.3539575 [DOI] [PubMed] [Google Scholar]
Kyriakou Y. and Kalender W. A., “X-ray scatter data for ﬂat-panel detector CT,” Phys. Med. 23(1), 3–15 (2007). 10.1016/j.ejmp.2006.12.004 [DOI] [PubMed] [Google Scholar]

[c1] Guan H. and Dong H., “Dose calculation accuracy using cone-beam CT (CBCT) for pelvic adaptive radiotherapy,” Phys. Med. Biol. 54(20), 6239–6250 (2009). 10.1088/0031-9155/54/20/013 [DOI] [PubMed] [Google Scholar]

[c2] Oldham M., Létourneau D., Watt L., Hugo G., Yan D., Lockman D., Kim L. H., Chen P. Y., Martinez A., and Wong J. W., “Cone-beam-CT guided radiation therapy: A model for on-line application,” Radiother. Oncol. 75(3), 271–278 (2005). 10.1016/j.radonc.2005.03.026 [DOI] [PubMed] [Google Scholar]

[c3] Niu T., Zhu L., and Al-Basheer A., “Quantitative cone-beam CT imaging in radiation therapy using planning CT as a prior: First patient studies,” Med. Phys. 39(4), 1991–2000 (2012). 10.1118/1.3693050 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c4] Fahrig R., Dixon R., Payne T., Morin R. L., Ganguly A., and Strobel N., “Dose and image quality for a cone-beam C-arm CT system,” Med. Phys. 33(12), 4541–4550 (2006). 10.1118/1.2370508 [DOI] [PubMed] [Google Scholar]

[c5] Lauritsch G., Boese J., Wigström L., Kemeth H., and Fahrig R., “Towards cardiac C-arm computed tomography,” IEEE Trans. Med. Imaging 25(7), 922–934 (2006). 10.1109/TMI.2006.876166 [DOI] [PubMed] [Google Scholar]

[c6] Niu T. and Zhu L., “Overview of x-ray scatter in cone beam computed tomography and its correction methods,” Curr. Med. Imaging Rev. 6(2), 82–89 (2010). 10.2174/157340510791268515 [DOI] [Google Scholar]

[c7] Reitz I., Hesse B.-M., Nill S., Tucking T., and Oelfke U., “Enhancement of image quality with a fast iterative scatter and beam hardening correction method for kV CBCT,” Z. Med. Phys. 19(3), 158–172 (2009). 10.1016/j.zemedi.2009.03.001 [DOI] [PubMed] [Google Scholar]

[c8] Gao H., Fahrig R., Bennett N. R., Sun M., Star-Lack J., and Zhu L., “Scatter correction method for x-ray CT using primary modulation: Phantom studies,” Med. Phys. 37(2), 934–946 (2010). 10.1118/1.3298014 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c9] Niu T., Sun M., Star-Lack J., Gao H., Fan Q., and Zhu L., “Shading correction for on-board cone-beam CT in radiation therapy using planning MDCT images,” Med. Phys. 37(10), 5395–406 (2010). 10.1118/1.3483260 [DOI] [PubMed] [Google Scholar]

[c10] Niu T. and Zhu L., “Scatter correction for full-fan volumetric CT using a stationary beam blocker in a single full scan,” Med. Phys. 38(11), 6027–6038 (2011). 10.1118/1.3651619 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c11] Zhu L., Bennett R., and Fahrig R., “Scatter correction method for X-ray CT using primary modulation theory and preliminary results,” IEEE Trans. Med. Imaging 25(12), 1573–1587 (2006). 10.1109/TMI.2006.884636 [DOI] [PubMed] [Google Scholar]

[c12] Zhu L., Xie Y., Wang J., and Xing L., “Scatter correction for cone-beam CT in radiation therapy,” Med. Phys. 36(6), 2258–2268 (2009). 10.1118/1.3130047 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c13] Zhu L., Star-Lack J., Li T., Xing L., and Fahrig R., “Improved scatter correction for X-ray cone-beam CT using primary modulation,” Proc. SPIE 6510, 65101U1–65101U8 (2007). 10.1117/12.713678 [DOI] [Google Scholar]

[c14] Russo P. and Mettivier G., “Method for measuring the focal spot size of an x-ray tube using a coded aperture mask and a digital detector,” Med. Phys. 38(4), 2099–2115 (2011). 10.1118/1.3567503 [DOI] [PubMed] [Google Scholar]

[c15] Bub A., Gondrom S., Maisl M., Uhlmann N., and Arnold W., “Image blur in a flat-panel detector due to compton scattering at its internal mountings,” Meas. Sci. Technol. 18(5), 1270–1277 (2007). 10.1088/0957-0233/18/5/013 [DOI] [Google Scholar]

[c16] Poludniowski G., Evans P. M., Kavanagh A., and Webb S., “Removal and effects of scatter-glare in cone-beam CT with an amorphous-silicon flat-panel detector,” Phys. Med. Biol. 56(2011), 1837–1851 (2011). 10.1088/0031-9155/56/6/019 [DOI] [PubMed] [Google Scholar]

[c17] Zhang B. and Zeng G. L., “Two-dimensional iterative region-of-interest (ROI) reconstruction from truncated projection,” Med. Phys. 34(3), 935–944 (2007). 10.1118/1.2436969 [DOI] [PubMed] [Google Scholar]

[c18] Sidky E. Y., Zou Y., and Pan X., “Minimum data image reconstruction algorithms with shift-invariant filtering for helical, cone-beam CT,” Phys. Med. Biol. 50(8), 1643–1657 (2005). 10.1088/0031-9155/50/8/002 [DOI] [PubMed] [Google Scholar]

[c19] Zou Y. and Pan X., “Exact image reconstruction on PI-lines from minimum data in helical cone-beam CT,” Phys. Med. Biol. 49(6), 941–959 (2004). 10.1088/0031-9155/49/6/006 [DOI] [PubMed] [Google Scholar]

[c20] Chen Y., Liu B., Connor J. M. O., Didier C. S., and Glick S. J., “Characterization of scatter in cone-beam CT breast imaging: comparison of experimental measurements and Monte Carlo simulation,” Med. Phys. 36(3), 857–869 (2009). 10.1118/1.3077122 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c21] Sun M. and Star-Lack J. M., “Improved scatter correction using adaptive scatter kernel superposition,” Phys. Med. Biol. 55(22), 6695–6720 (2010). 10.1088/0031-9155/55/22/007 [DOI] [PubMed] [Google Scholar]

[c22] Mori S., Endo M., Nishizawa K., Ohno M., Miyazaki H., Tsujita K., and Saito Y., “Prototype heel effect compensation filter for cone-beam CT,” Phys. Med. Biol. 50(22), N359–N370 (2005). 10.1088/0031-9155/50/22/N02 [DOI] [PubMed] [Google Scholar]

[c23] Everson J. D. and Gray J. E., “Focal-spot measurement: Comparison of slit, pinhole, and star resolution pattern techniques,” Radiology 165, 261–264 (1987). [DOI] [PubMed] [Google Scholar]

[c24] Kimme-Smith C., Bassett L. W., and Gold R. H., “Focal spot size measurements with pinhole and slit for microfocus mammography units,” Med. Phys. 15(3), 298–303 (1988). 10.1118/1.596264 [DOI] [PubMed] [Google Scholar]

[c25] Li H., Mohan R., and Zhu X. R., “Scatter kernel estimation with an edge-spread function method for cone-beam computed tomography imaging,” Phys. Med. Biol. 53(23), 6729–6748 (2008). 10.1088/0031-9155/53/23/006 [DOI] [PubMed] [Google Scholar]

[c26] Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1(6), 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]

[c27] Jia X., Yan H., Cervino L., Folkerts M., and Jiang S. B., “A GPU tool for efficient, accurate, and realistic simulation of cone beam CT projections,” Med. Phys. (submitted), e-print arXiv:1204.6367v1. [DOI] [PMC free article] [PubMed]

[c28] Boone J. M. and Seibert J. A., “An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV,” Med. Phys. 24(11), 1661–670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]

[c29] Kai Y., “Development and evaluation of a dedicated breast CT scanner,” Ph.D. dissertation, University of California, Davis, CA, 2007. [Google Scholar]

[c30] Bootsma G. J., Verhaegen F., and Jaffray D. A., “The effects of compensator and imaging geometry on the distribution of x-ray scatter in CBCT,” Med. Phys. 38(2), 897–914 (2011). 10.1118/1.3539575 [DOI] [PubMed] [Google Scholar]

[c31] Kyriakou Y. and Kalender W. A., “X-ray scatter data for ﬂat-panel detector CT,” Phys. Med. 23(1), 3–15 (2007). 10.1016/j.ejmp.2006.12.004 [DOI] [PubMed] [Google Scholar]

PERMALINK

Relationship between x-ray illumination field size and flat field intensity and its impacts on x-ray imaging

Xue Dong

Tianye Niu

Xun Jia

Lei Zhu

Abstract

INTRODUCTION