Abstract
Background:
Selecting patients with ‘sufficient life expectancy’ for Phase I oncology trials remains challenging. The Royal Marsden Hospital Score (RMS) previously identified high-risk patients as those with ⩾2 of the following: albumin <35 g l−1; LDH > upper limit of normal; >2 metastatic sites. This study developed an alternative prognostic model, and compared its performance with that of the RMS.
Methods:
The primary end point was the 90-day mortality rate. The new model was developed from the same database as RMS, but it used Chi-squared Automatic Interaction Detection (CHAID). The ROC characteristics of both methods were then validated in an independent database of 324 patients enrolled in European Organization on Research and Treatment of Cancer Phase I trials of cytotoxic agents between 2000 and 2009.
Results:
The CHAID method identified high-risk patients as those with albumin <33 g l−1 or ⩾33 g l−1, but platelet counts ⩾400.000 mm−3. In the validation data set, the rates of correctly classified patients were 0.79 vs 0.67 for the CHAID model and RMS, respectively. The negative predictive values (NPV) were similar for the CHAID model and RMS.
Conclusion:
The CHAID model and RMS provided a similarly high level of NPV, but the CHAID model gave a better accuracy in the validation set. Both CHAID model and RMS may improve the screening process in phase I trials.
Keywords: phase I oncology trials, sufficient life expectancy, decision tree analysis, performance, discrimination, calibration
The selection of patients to be enrolled in phase I cancer trials is critical, as investigators must identify those with a ‘sufficient’ life expectancy (Ploquin et al, 2012). In most study protocols, the required life expectancy is at least 3 months (90 days). Several arguments support the use of this eligibility criterion. From a clinical perspective, it is not ethical to expose very frail patients to a new drug usually with little prospect of benefit; such patients, who have exhausted all effective treatments, may be better receiving palliative care alone. In addition, from a research perspective, the enrolment of patients at relatively high risk of early death could jeopardise the study and subsequent drug development.
To date, several models predictive of early death in this context have been proposed (Janisch et al, 1994; Yamamoto et al, 1999; Bachelot et al, 2000; Verweij, 2000; Han et al, 2003; Arkenau et al, 2008a, 2008b, 2009; Penel et al, 2008, 2009, 2010; Wheler et al, 2009; Olmos et al, 2011). Arkenau et al (2008a, 2008b) developed a score based on overall survival, which then was validated by logistic regression analysis for prediction of 90-day survival. This logistic regression analysis identified three factors (albumin <35 g l−1, LDH > upper limit of normal and the presence of >2 metastatic sites), and this Royal Marsden Hospital score (RMS) predicted early death. Another three potential factors (ECOG-PS, alkaline phosphatase and weeks per line of prior treatment) were also identified, but these factors did not improve the overall performance of the RMS for 90-day mortality prediction. Two groups of patients were identified: low-risk patients with 0 or 1 prognostic factor and high-risk patients with >1 prognostic factor. The median overall survival for low- and high-risk patients was 74.1 (95% confidence interval (CI; 53.2–96.2)) vs 24.9 (95% CI (19.5–30.2)) weeks, respectively (Arkenau et al, 2008b). The variables used for RMS are easily obtained at the bedside. The performance of the RMS was subsequently evaluated in a large international database that included more than 2100 patients treated in cancer research centres (Olmos et al, 2012); the proportion of patients correctly classified using this model was ∼80%. To date, more complex scores generated by logistic regression analysis (Olmos et al, 2012) have not outperformed the RMS.
In this study, we conducted an additional analysis in order to (i) develop a model based on an alternative methodological approach that relies on decision tree analysis, specifically Chi-squared Automatic Interaction Detection (CHAID), and to (ii) assess the performance (prediction/calibration) of both the RMS and CHAID model using an independent validation database that comprised 324 patients enrolled in the phase I trials, conducted by the European Organization on Research and Treatment of Cancer (EORTC).
Patients and methods
Primary end point
The primary end point was 90-day mortality (early death), which corresponds to the clinical eligibility criterion required in most contemporary phase I trials.
Patients
We analysed two databases. The training set was the European New Drug Development Network Database (Olmos et al, 2012), which included 2182 patients treated in 14 centres between 2005 and 2007. Seventy-two patients were excluded because they were lost to follow-up before the 90 days. The collected variables have been extensively described in another study (Olmos et al, 2012) and from this database, the RMS based on logistic regression analysis had previously been developed (Olmos et al, 2012).
The validation set comprised 324 patients treated in EORTC phase I cancer trials between 2000 and 2009. In this database, the same variables were available (Olmos et al, 2012). Eighteen patients were excluded because they were lost to follow-up before the 90 days, and 134 patients were excluded because of missing values for at least one parameter used in the one or other of the models (Table 1).
Table 1. Flowchart of (A) the development data set and (B) the validation data set.
| Development data set | Validation data set | |
|---|---|---|
| Total number of patients | 2182 | 324 |
| Lost to follow-up within the 90 first days | 72 | 16 |
| Missing data for albumin | 49 | 51 |
| Missing data for the number of metastatic site | 0 | 83 |
| Missing data for LDH | 337 | 76 |
| Assessable patients for both models | 1760 | 172 |
Abbreviation: LDH=lactate dehydrogenase.
Development of the new model
In this study, Exhaustive CHAID was used to create a growing tree analysis (SIPINA Software, version 3.5, Sipina Research, Lyon, France). This technique uses a systematic algorithm to detect the strength of association between potential prognostic factors and the outcome variable, in this case early death. The algorithm reveals which prognostic factor best correlates with the greatest changes in the outcome variable. At each step, the CHAID algorithm recursively partitions data into mutually exclusive and exhaustive subsets that are maximally different in terms of the dependent variable (i.e., early death), as assessed with the use of Bonferroni-adjusted χ2-statistics. In addition, the cohort was then divided into subsets based on the best prognostic factor (i.e., splitter), and child ‘nodes’ were created. The process continued to search each node for the next best prognostic factor until the CHAID model stopping rules came into effect; end nodes were then created.
The CHAID algorithm performed three successive actions: (i) it merged the subgroups with similar occurrences of the target variable (αmerge=0.01), (ii) then split the subgroups using the best prognostic factor (αsplit=0.01) and finally (iii) it terminated the tree when the observed number of early deaths was ∼30 (Biggs et al, 1991; Melchior et al, 2001; Ambalavanan et al, 2006; Chan et al, 2006). All of the collected data have been tested as potential splitters in a non-supervised approach. Because of the inherent instability of the method, we conducted an internal validation using a bootstrapping approach. From the initial training data set, we generated 100 randomly generated subsets, including 20% of the initial population. We then verified that the main splitters remained constant across the different CHAID analyses.
We have applied this method to 2172 patients from the training database (after exclusion of the 72 patients lost to follow-up within the 90 first days).
Assessment of performance of both models
We then assessed the performance of both the CHAID model and RMS, using the subgroup of patients without missing data from the independent validation data set (Harell et al, 1996; Bleeker et al, 2003). We assessed the discrimination performance of both models using the classical parameters, including sensitivity, specificity, positive predictive value and NPV, rate of well-classified patients and the discriminative slope, as well as their 95% CI (Italiano et al, 2008). The discriminative slope was the absolute difference in average predictions (risk of early death) in low- and high-risk patients, as defined by the analysed model. To measure the calibration (or generalisability of the prediction made), we also calculated the Brier score (Blattenberger and Lad, 1985), which is simply defined as (Y−p)2, where Y is the outcome and p the prediction for each patient. The Brier score for a model can range from 0, for a perfect model, to 0.25, for a non-informative model (Blattenberger and Lad, 1985).
Results
General
The main characteristics of both populations are presented in Table 2.
Table 2. Description of both populations.
| Training data set ( n =2110) | Validation data set ( n =306) | ||
|---|---|---|---|
| Parameters | n , % (95 CI) | n , % (95 CI) | P -value ( χ 2 -test) |
| Early death | 0.003 | ||
| Yes | 344, 16.3% (14.7–17.8) | 30, 9.8% (6.4–13.1) | |
| Missing data | 0 | 0 | |
| Gender | <0.001 | ||
| Women | 1194, 56.6% (54.5–58.7) | 135, 44.1% (38.5–49.7) | |
| Missing data | 0 | 0 | |
| Primaries | <0.001 | ||
| Colorectal cancers | 367/17.4% (15.7–19.0) | 87/28.4% (23.3–33.4) | |
| Oesophago-gastric cancers | 275/13.0% (11.6–14.4) | 15/4.9% (2.5–7.3) | |
| Gynaecological cancers | 249/11.8% (10.4–13.2) | 18/5.9% (3.2–8.5) | |
| Sarcomas | 216/10.2% (8.9–11.5) | 15/4.9% (2.5–7.3) | |
| Lung cancers | 214/10.1% (8.8–11.4) | 10/3.3% (1.3–5.3) | |
| Melanoma | 157/7.4% (6.3–8.5) | 21/6.9% (4.1–9.7) | |
| Prostate cancer | 148/7.0% (5.9–8.1) | 1/0.3% (0–0.9) | |
| Breast cancers | 142/6.7% (5.6–7.8) | 40/13.1% (9.3–16.9) | |
| Other genitourinary cancers | 108/5.1% (4.2–6.0) | 17/5.6% (3.0–8.2) | |
| Head and neck | 94/4.5% (3.6–5.4) | 71/23.2% (18.5–27.9) | |
| Others | 140/6.6% (5.5–7.6) | 11 (3.6%) | |
| Missing data | 0 | ||
| ECOG-PS | <0.001 | ||
| 0 | 857/40.6% (38.4–42.8) | 155/50.7% (45.1–56.3) | |
| 1 | 1186/56.2% (54.1–58.4) | 140/45.8% (40.2–51.4) | |
| 2 | 67/3.2% (2.4–3.9) | 11/3.6% (1.5–5.7) | |
| Missing data | 0 | 0 | |
| First-in-man | |||
| Yes | 930/44.1% (42.0–46.1) | 0/0% (−) | |
| Missing data | 0 | ||
| Investigational treatments | <0.001 | ||
| Targeted agent (single-agent) | 940/44.5% (42.4–46.6) | ||
| Cytotoxic agents | 460/21.8% (19.3–24.3) | 306/100% (−) | |
| Targeted+cytotoxic agents | 543/25.7% (23.8–27.6) | ||
| Combination of targeted agents | 167/7.9% (6.7–9.0) | ||
| Missing data | 0 | ||
Abbreviation: CI=confidence interval.
In the training set, the rate of early death was 16.3% (95% CI (14.7–17.9)). Median age was 58.5 and the sex ratio was 0.44. In this database, the most frequent primary cancer was colorectal (17.4%). The vast majority of patients (96.8%) had very good general performance status (ECOG-PS ⩽1). Furthermore, 34.7% of patients had two metastatic sites. The investigational treatments were single agents in 59.8% of cases, and 44.1% of patients received an investigational treatment within a first-in-man trial. In addition, 88.2% of trials investigated molecularly targeted therapies alone or in combination.
In the validation set, the rate of early death was 9.8% (95% CI (6.4–13.1)). Median age was 56.9 and the sex ratio was 55.9. The most frequent primary cancer was again colorectal (28.4%). The rate of patients with ECOG-PS ⩽1 was 96.5%, and 27.8% of patients had two metastatic sites. All patients enrolled in these trials received cytotoxic agent(s).
Decision tree analysis in the training data set
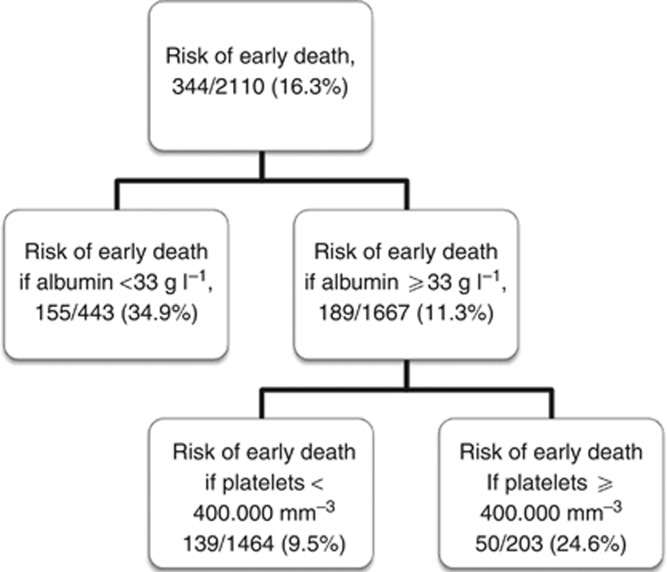
The CHAID analysis separated the patients into five subgroups based on the serum albumin, LDH, platelet count and alkaline phosphatase. The early death rates ranged from 6.0% to 71.0% (Figure 1). The overall discrimination performance of this model assessed, by a ROC curve, was 0.72 (95% CI (0.69–0.75)). The ROC curve identified two categories of patients. High-risk patients were those with albumin <33 g l−1 or albumin ⩾33 g l−1, but platelet counts ⩾400.000 mm−3; all other patients were of low-risk. The rates of early death for the high- and low-risk patients were 31.7% (95% CI (28.2–35.5)) and 9.5% (95% CI (7.2–11.5)), respectively.
Figure 1.
Decision tree generated by the CHAID analysis in the training data set.
The stability of the model was explored by bootstrapping. In every randomly generated subset, the CHAID analysis was applied. Albumin remained the most powerful splitter in 66.0% of the randomly generated subsets/trees. The discriminative thresholds for albumin, defining high- and low-risk patients ranged between 32 and 34 g l−1 in 85.4% of the randomly generated subsets/trees. Platelet count and LDH were the first splitters in a further 23.0% of the generated subsets/trees.
Performance of both models in the training data set
We then repeated the analysis after excluding 350 patients who had missing values for at least one parameter used in one or the other of the two models (Table 1). The performances of both models (discrimination/calibration) assessed in the training set were similar (Table 3).
Table 3. Performance of both models in the training data set.
| Royal Marsden Model | Model derived from the decision tree analysis | |
|---|---|---|
| Definition of high-risk patients | Patients with at least two of the following prognostic factors (albumin <35 g l−1, LDH > ULN and more than two metastatic sites) | Patients with albumin <33 g l−1 or patients with albumin ⩾33 g l−1 and with platelet counts ⩾400.000 mm−3 |
| Evaluable patients | 1760 (80.6%) | 1760 (80.6%) |
| Rate of early death in low-risk group | 137/1256 (10.9% (9.3–12.8)) | 122/1241 (9.8% (8.3–11.7)) |
| Rate of early death in high-risk group | 157/504 (31.1% (27.2–35.4)) | 172/519 (33.1% (29.1–37.4)) |
| Sensitivity | 0.53 (0.47–0.59) | 0.58 (0.53–0.64) |
| Specificity | 0.76 (0.74–0.78) | 0.76 (0.74–0.78) |
| Positive predictive value | 0.31 (0.27–0.35) | 0.33 (0.29–0.37) |
| Negative predictive value | 0.89 (0.87–0.90) | 0.90 (0.88–0.92) |
| Rate of well-classified patients | 0.72 (0.70–0.74) | 0.73 (0.71–0.75) |
| Discriminative slope | 20.1% (14.9–25.5) | 23.0% (18.0–28.0) |
| Brier score | 0.014 | 0.010 |
Abbreviations: LDH=lactate dehydrogenase; ULN=upper limit of normal.
Performance of both models in the validation data set
Table 4 summarises the results of the external validation of the performance of both models.
Table 4. Performance of both models in the validation data set.
| Royal Marsden Model | Model derived from the decision tree analysis | |
|---|---|---|
| Definition of high-risk patients | Patients with at least two of the following prognostic factors (albumin <35 g l−1, LDH > ULN and more than two metastatic sites) | Patients with albumin <33 g l−1 or patients with albumin ⩾33 g l−1 and with platelet counts ⩾400.000 mm−3 |
| Evaluable patients | 172 (56.2%) | 172 (56.2%) |
| Rate of early death in low-risk group | 1/103 (1.0% (0.1–6.0)) | 6/133 (4.5% (1.8–10.0)) |
| Rate of early death in high-risk group | 14/69 (20.3% (12.0–32.0)) | 9/39 (23.1% (11.7–39.7)) |
| Sensitivity | 0.93 (0.66–1.00) | 0.60 (0.33–0.82) |
| Specificity | 0.65 (0.57–0.72) | 0.81 (0.73–0.86) |
| Positive predictive value | 0.20 (0.12–0.32) | 0.23 (0.12–0.40) |
| Negative predictive value | 0.99 (0.94–1.00) | 0.95 (0.90–0.98) |
| Rate of well-classified patients | 0.67 (0.60–0.74) | 0.79 (0.73–0.85) |
| Discriminative slope | 19.3% (9.2–29.4) | 18.0% (4.0–32.0) |
| Brier score | 0.098 | 0.010 |
Abbreviations: LDH=lactate dehydrogenase; ULN=upper limit of normal.
The model derived from the CHAID decision tree analysis provided higher specificity (0.81 vs 0.65) and a superior overall rate of correctly classified patients than the RMS (0.79 (95% CI (0.73–0.85)) vs 0.67 (95% CI (0.60–0.74))). By contrast, the RMS had a better sensitivity (0.93 vs 0.60). Discriminative slopes were similar for the CHAID model and RMS (18% and 19.3%, respectively) as well as the NPV (0.95 (95% CI (0.90–0.98)) and 0.99 (95% CI (0.94–1.00))), respectively) and the calibration (0.010 vs 0.098).
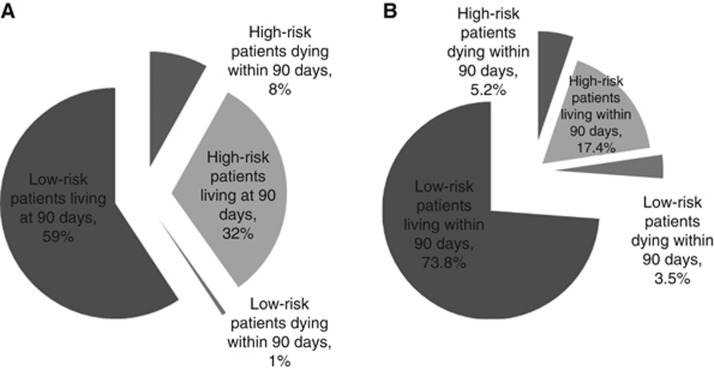
With regard to the RMS, 69 out of 172 patients were considered high risk, but 55 patients were erroneously excluded (Figure 2A). With the new model, 39 out of 172 patients were considered high risk, and 30 were erroneously excluded, that is they would have been considered ineligible but did not subsequently die early (Figure 2B).
Figure 2.
Repartition of patients from the validation database using (A) the RMS and (B) the new model.
Discussion
We have developed and validated a new model to identify patients at risk of early death in phase I clinical trials based on an alternative methodological approach, decision tree analysis. The new model is based on two objective criteria easily obtained at bedside, serum albumin and platelet count. Low level of serum albumin, as a marker of cancer-related malnutrition, is a well-known prognostic factor in cancer patients (Bachelot et al, 2000; Han et al, 2003; Penel et al, 2008, 2010). High number of platelets is also a poor prognostic factor (Janisch et al, 1994; Wheler et al, 2009). It is a marker of inflammation induced by cancer; the high number of platelets can increase the risk of thrombosis and then early mortality, and is also an activator of tumour angiogenesis (Lip et al, 2002). The model did not retain one highly subjective criterion (Ando et al, 2001), ECOG-PS, which is the most important criterion in many other studies using logistic regression methods. Likewise, although both the CHAID model and the RMS include serum albumin (although with slightly different thresholds), the CHAID model did not include LDH, which may not always be routinely available. Rather, the CHAID model included platelet count, which was not a part of the RMS even though included in their analysis as a candidate predictive factor.
Both the RMS and CHAID model were able to identify those at higher or lower risk of early death. There were, however, notable differences between the two models. The RMS defined a higher proportion of the population as being high risk (40% and 23%, respectively), so would exclude more patients; by contrast the CHAID model would be more ‘inclusive’. The proportion of patients dying early in the low-risk group was, however, higher with the CHAID model than the RMS (4.5% and 1%, respectively). This higher risk of dying within 90 days among low-risk patients using the CHAID model probably reflects its greater inclusivity. Nevertheless, the 4.5% risk of death that would result from restricting phase I trial entry to patients in the low-risk group, as defined by the CHAID model, is still substantially lower than the risk of death in the unselected validation populations (9.3% and 10.9%). The new model provides, therefore, a rather better prediction of the risk for being alive at 90 days (specificity) at the expense of lesser prediction of the risk of death within 90 days (sensitivity). When selecting patients for phase I trials, the NPV, or the ability to correctly identify patients who will survive 90 days, is arguably the most important criterion, and the CHAID model and RMS provided a similarly high NPV. The CHAID model was, however, more accurate at correctly classifying individual patients (79% and 67%, respectively). In several previous studies, using both methods (logistic regression analysis and CHAID method), the identified prognostic factors are different; several methodological points explained the identification of different factors. Logistic regression analysis tends to identify factors associated with the outcome in the whole data set. The CHAID method creates some mutually exclusive subgroups of patients in which the model identify the optimal splitter (or discriminator) at each level. At the end, the prognostic factors identified could be different (Peter, 2007; Kurt et al, 2008).
This study does have some limitations. The validation set is considerably smaller than the training set, thus restricting the power to make comparisons of the two approaches. Moreover, the patient population from which the CHAID model and RMS were derived are different, having been diagnosed and treated in different institutions over different periods of time. They also received different novel agents, most of the patients of the European New Drug Development Network Database having received molecularly targeted therapies, mainly in first-in-man trials; by contrast, the majority of patients in the EORTC trials received cytotoxic agents, mainly in phase Ib trials. The performance of both models was, however, good in the single validation database, indicating that the prediction performance of both models is generalisable. Both study populations are highly selected because already enrolled in phase I trials, we plan to conduct a new study in a cohort of patients screened for phase I trial participation. Furthermore, both models identify the risk of early death, regardless its cause (toxicity-related mortality, underlying disease, cancer progression or their combinations); nevertheless the primary objective here is to identify patients assessable for the primary end points regardless the cause of death.
Despite the fact that the patients analysed met all the conventional eligibility criteria required for phase I trial entry, including excellent general condition and normal baseline biological parameters, the early death rate was relatively high (9.8−16.3%) in these highly experienced centres. For the purpose of patient selection with such predictive models, the most important evaluation criterion is the NPV, which is the probability of low-risk patients not dying within 90 days. Both models provided the same NPV of ∼95% when applied to the validation cohort. It is likely to be difficult to improve on this level prediction using basic clinical and laboratory parameters. This suggests that the integration of more sophisticated parameters reflecting other dimensions than tumour burden and its consequences, such as tumour growth dynamics (Gomez-Roca et al, 2011) or the presence of circulating tumour cells (Olmos et al, 2011), may need to be incorporated if the predictive value of models is to improve.
Large retrospective studies have demonstrated that the main cause of death for patients in early trials is not toxicity, which occurs in <0.5% of the enrolled patients, but deaths related to the underlying cancer (Kurzrock and Benjamin, 2005). An erroneous assessment of life expectancy carries some obvious detrimental consequences for the patient (Lipsett, 1995). The impact of enrolling many patients who will die within 90 days, frequently before study completion, on the effective delivery of phase I trials should also be better evaluated. By using predictive models it is now possible to select patients with a low risk of early death. In this analysis, using the RMS to restrict study entry to those could reduce the early death rate to 1%, but only at the expense of excluding 40% of patients who would otherwise have been eligible. Using the CHAID model, entering only patients with albumin 33 g l−1 or platelet count <400.000 mm−3 would reduce the early death rate to 4.5%, while excluding <25%. Restricting entry to a low-risk subgroup of patients using either method implies a need to slow down, to a greater or lesser extent, the recruitment of patients, or to increase the number of phase I centres. Either approach would have significant impact on the conduct and delivery of early clinical trials.
In summary, both the RMS and the new CHAID model perform well, but with notable differences, in predicting patients at risk of early death in phase I trials. We recommend, therefore, that the clinical utility of both approaches be validated and compared in a large, multicentre international prospective study. Such a study should also assess the impact of the use of predictive models on the ability to deliver key trial end points, that is to evaluate cumulative toxicities, gain an initial indication of anti-tumour activity and describe drug pharmacokinetics.
Acknowledgments
This work was supported by G Luca (Milan), TRJ Evans (Beatson, Glasgow), R Wilson (Belfast), C Sessa (Bellinzona), R Plummer (Newcastle), EORTC Staff (Vicky Minas and Ann Marinus) and Séverine Marchant (manuscript editing).
This work is published under the standard license to publish agreement. After 12 months the work will become freely available and the license terms will switch to a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License.
Presented in part at the 48th American Society of Clinical Oncology (ASCO) Annual Meeting 2012, 01–05 June 2012, Chicago, Illinois, USA (Abstract 2540).
09/10/2012
This paper has been modified since advance online publication, an acknowledgement has been added
References
- Ambalavanan N, Carlo WA, Shankaran S, Bann CM, Emrich SL, Higgins RD, Tyson JE, O’Shea TM, Laptook AR, Ehrenkranz RA, Donovan EF, Walsh MC, Goldberg RN, Das A (2006) National Institute of Child Health and Human Development Neonatal Research Network Predicting outcomes of neonates diagnosed with hypoxemic-ischemic encephalopathy. Pediatrics 118: 2084–2093 [DOI] [PubMed] [Google Scholar]
- Ando M, Ando Y, Hasewaga Y, Shimokata K, Minami H, Wakai K, Ohno Y, Sakai S (2001) Prognostic value of performance status assessed by patients themselves, nurses and oncologists in advanced non-small cell lung cancer. Br J Cancer 85: 1634–1639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkenau HT, Barriuso J, Olmos D, Ang JE, de Bono J, Judson I, Kaye S (2009) Prospective validation of a prognostic score to improve patient selection for oncology phase I trials. J Clin Oncol 27: 2692–2696 [DOI] [PubMed] [Google Scholar]
- Arkenau HT, Olmos D, Ang JE, Barriuso J, Karavasilis V, Ashley S, de Bono J, Judson I, Kaye S (2008a) 90-Days mortality rate in patients treated within the context of a phase-I trial: how should we identify patients who should not go on trial? Eur J Cancer 44(1): 536–540 [DOI] [PubMed] [Google Scholar]
- Arkenau HT, Olmos D, Ang JE, de Bono J, Judson I, Kaye S (2008b) Clinical outcome and prognosis factors for patients treated within the context of a phase I study: the Royal Marsden Hospital experience. Br J Cancer 98: 1029–1033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachelot T, Ray-Coquard I, Catimel G, Ardiet C, Guastalla JP, Dumortier A, Chauvin F, Droz JP, Philip T, Clavel M (2000) Multivariate analysis of prognostic factors for toxicity and survival for patients enrolled in phase I clinical trials. Ann Oncol 11: 151–156 [DOI] [PubMed] [Google Scholar]
- Biggs D, de Ville B, Suen E (1991) A method of choosing multiway partitions for classification and decision trees. J Appl Stat 18: 49–62 [Google Scholar]
- Blattenberger G, Lad F (1985) Separating the Brier score into calibration and refinement component: a graphical exposition. Am Stat 39: 26–32 [Google Scholar]
- Bleeker SE, Moll HA, Steyerberg EW, Donders AR, Derksen-Lubsen G, Grobbee DE, Moons KG (2003) External validation is necessary in prediction research: a clinical example. J Clin Epidemiol 56: 826–832 [DOI] [PubMed] [Google Scholar]
- Chan F, Cheing G, Chan JYC, Rosenthal DA, Chronister J (2006) Predicing employment outcomes of rehabilitation clients with orthopedic disabilities: a CHAID analysis. Disabil Rehabil 28: 257–270 [DOI] [PubMed] [Google Scholar]
- Gomez-Roca C, Koscielny S, Ribrag V, Dromain C, Marzouk I, Bidault F, Bahleda R, Ferté C, Massard C, Soria JC (2011) Tumour growth rates and RECIST criteria in early drug development. Eur J Cancer 47: 2512–2516 [DOI] [PubMed] [Google Scholar]
- Han C, Braybrooke JP, Deplanque G (2003) Comparison of prognostic factors in patients in phase I trials of cytotoxic drugs vs new noncytotoxic agents. Br J Cancer 89: 1166–1171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harell FE, Lee KL, Mark DB (1996) Multivariable Prognostic Models: issues in developing models, evaluating assumptions and adequacy, and mesuring and reducing errors. Stat Med 15: 361–388 [DOI] [PubMed] [Google Scholar]
- Italiano A, Massard C, Bahleda R, Vataire AL, Deutsch E, Magné N, Pignon JP, Vassal G, Armand JP, Soria JC (2008) Treatment outcome and survival in participants of phase 1 oncology trials carried out from 2003 to 2006 at Institute Gustave Roussy. Ann Oncol 19: 787–792 [DOI] [PubMed] [Google Scholar]
- Janisch L, Mick R, Schilsky RL, Vogelzang NJ, O’Brien S, Kut M, Ratain MJ (1994) Prognostic factors for survival in patients treated in phase I clinical trials. Cancer 74: 1965–1973 [DOI] [PubMed] [Google Scholar]
- Kurt I, Ture M, Kurum AT (2008) Comparing performances of logistic regression, classification and regression tree, and neural networks for predicting coronary artery disease. Expert Syst Appl 34: 366–374 [Google Scholar]
- Kurzrock R, Benjamin RS (2005) Risks and benefits of phase 1 oncology trials, revisited. N Engl J Med 352: 930–932 [DOI] [PubMed] [Google Scholar]
- Lip GY, Chin BS, Blann AD (2002) Cancer and prothrombosis state. Lancet Oncol 3: 27–34 [DOI] [PubMed] [Google Scholar]
- Lipsett MB (1995) On the nature and ethics of phase I trials. J Clin Oncol 13: 1049–1051 [DOI] [PubMed] [Google Scholar]
- Melchior LA, Huba GJ, Gallagher T, Jean-Louis E, McDonald SS, Smereck GA, German VF, Brown VB, Panter AT (2001) Unmet needs in groups of traditionally underserved individuals with HIV/AIDS: empirical models. Home Health Care Services Quaterly 19: 29–51 [DOI] [PubMed] [Google Scholar]
- Olmos D, A’Hern R, Marsoni S, Morales R, Gomez-Roca C, Verweij J, Voest EE, Schöffski P, Ang JE, Penel N, Schellens JH, Del Conte G, Brunetto AT, Evans TR, Wilson R, Gallerani E, Plummer R, Tabernero J, Soria JC, Kaye SB (2012) Patient selection for oncology phase I trials – a multi-institutional study of prognostic factors. J Clin Oncol 30: 996–1004 [DOI] [PubMed] [Google Scholar]
- Olmos D, Baird RD, Yap TA, Massard C, Pope L, Sandhu SK, Attard G, Dukes J, Papadatos-Pastos D, Grainger P, Kaye SB, de Bono JS (2011) Baseline circulating tumor cell counts significantly enhace a prognostic score for patients participating in phase I oncology trials. Clin Cancer Res 17: 5188–5196 [DOI] [PubMed] [Google Scholar]
- Penel N, Clisant S, Lefebvre JL, Adenis A (2009) ‘Sufficient life-expectancy’: an amazing inclusion criteria in cancer phase II-III trials. J Clin Oncol 27: 105. [DOI] [PubMed] [Google Scholar]
- Penel N, Delord JP, Bonneterre ME, Bachelot T, Ray-Coquard I, Blay JY, Pascal LB, Borel C, Filleron T, Adenis A, Bonneterre J (2010) Development and validation of a model that predicts early death among cancer patients participating in phase 1 clinical trials investigating cytotoxics. Invest New Drugs 28: 76–82 [DOI] [PubMed] [Google Scholar]
- Penel N, Vanseymortier M, Bonneterre ME, Clisant S, Dansin E, Vendel Y, Beuscart R, Bonneterre J (2008) Prognostic factors among cancer patients with good performance status screened for phase I trials. Invest New Drugs 26: 53–58 [DOI] [PubMed] [Google Scholar]
- Peter CA (2007) A comparison of regression trees, logistic regression, generalized additive models, and multivariate adaptive regression splines for predicting AMI mortality. Stat Med 26: 2937–2957 [DOI] [PubMed] [Google Scholar]
- Ploquin A, Olmos D, Ferté C, Cassier PA, Kramar A, Duhamel A, Penel N (2012) Life-expectancy of patients enrolled in phase 1 clinical trials: a systematic review of published prognostic models. Crit Rev Oncol Hematol 83(2): 242–248 [DOI] [PubMed] [Google Scholar]
- Verweij J (2000) The prognosis of prognostic factors in phase I clinical trials. Ann Oncol 11(2): 131–132 [DOI] [PubMed] [Google Scholar]
- Wheler J, Tsimberidou AM, Hong D, Naing A, Jackson T, Liu S, Feng L, Kurzrock R (2009) Survival of patients in a Phase 1 clinic: the M.D. Anderson Cancer Center experience. Cancer 115(5): 1091–1099 [DOI] [PubMed] [Google Scholar]
- Yamamoto N, Tamura T, Fukuoka M, Saijo N (1999) Survival and prognostic factors in lung cancer patients treated in phase I trials: Japanese experience. Int J Oncol 15(4): 737–741 [PubMed] [Google Scholar]