Fisher information matrix for branching processes with application to electron-multiplying charge-coupled devices

Abstract

The high quantum efficiency of the charge-coupled device (CCD) has rendered it the imaging technology of choice in diverse applications. However, under extremely low light conditions where few photons are detected from the imaged object, the CCD becomes unsuitable as its readout noise can easily overwhelm the weak signal. An intended solution to this problem is the electron-multiplying charge-coupled device (EMCCD), which stochastically amplifies the acquired signal to drown out the readout noise. Here, we develop the theory for calculating the Fisher information content of the amplified signal, which is modeled as the output of a branching process. Specifically, Fisher information expressions are obtained for a general and a geometric model of amplification, as well as for two approximations of the amplified signal. All expressions pertain to the important scenario of a Poisson-distributed initial signal, which is characteristic of physical processes such as photon detection. To facilitate the investigation of different data models, a “noise coefficient” is introduced which allows the analysis and comparison of Fisher information via a scalar quantity. We apply our results to the problem of estimating the location of a point source from its image, as observed through an optical microscope and detected by an EMCCD.

1 Introduction

The charge-coupled device (CCD) is an important digital imaging technology that has found utility in many applications. It plays crucial roles, for example, in areas as disparate as high sensitivity cellular microscopy and astronomy. A typical CCD has high quantum efficiency, which enables it to detect a large percentage of the photons which impinge upon its surface. However, a CCD is generally not suitable for imaging under extremely low light conditions. This is mainly due to the measurement noise of the CCD, which can overwhelm the signal when relatively few photons are detected from the imaged object. Measurement noise is added when the signal is read out from the device, and is commonly called the readout noise (e.g., Snyder et al. 1995).

A technology that is intended to overcome the detrimental effect of the readout noise under low light conditions is the electron-multiplying charge-coupled device (EMCCD). Similar to a CCD, an EMCCD is a device which accumulates electrons in proportion to the number of photons it detects. Unlike a CCD, however, an EMCCD can significantly increase the number of electrons through a multiplication process before they are read out. Therefore, whereas the readout noise can overwhelm the signal detected by a CCD under low light conditions, it is effectively drowned out by the amplified signal in the case of an EMCCD.

An EMCCD achieves signal amplification by transferring the electrons through a multiplication register that consists of a sequence of typically several hundred stages. Electrons are moved through the stages in sequence, repeatedly exiting one stage and entering the next until they exit the last stage. Multiplication occurs because in any given stage, each input electron can, with certain probabilities, generate secondary electrons via a physical phenomenon called impact ionization. All secondary electrons are transferred to the next stage for further amplification along with the input electrons. In this way, even when the probabilities of secondary electron generation (typically 0.01 to 0.02 (Basden et al. 2003) for one secondary electron per input electron, and even smaller for more than one per input electron) are small in each stage, the cascading effect can potentially produce a large number of electrons per initial electron. An important observation is that while multiplication is intended to drown out the readout noise, it is a random process, and hence introduces stochasticity of its own. Therefore, when enough photons can be detected from the imaged object such that the readout noise level is already low in comparison to the signal, the use of electron multiplication can actually have the adverse effect of unnecessarily introducing increased stochasticity in the acquired data.

From an image acquired using a CCD-based camera, parameters of interest can be estimated to obtain useful information about the imaged object. In single molecule microscopy (e.g., Walter et al. 2008; Moerner 2007), for example, a major topic of interest has been the accurate estimation of the location of a fluorescent molecule (e.g., Thompson et al. 2002; Ober et al. 2004; Andersson 2008; Pavani and Piestun 2008; Ram et al. 2008), which has important applications in, for instance, the study of intracellular processes (e.g., Ram et al. 2008). In this context, we have proposed a general framework (Ram et al. 2006) for calculating the Fisher information, and hence the Cramer-Rao lower bound (Rao 1965), for the estimation of parameters from an image produced by a microscope. Based on this framework, accuracy limits have been obtained for estimating, for example, the positional coordinates of a single molecule (e.g., Ober et al. 2004). These performance measures, however, assume the image to have been acquired by a CCD, and hence do not apply to EMCCD imaging.

Our current purpose is then to develop the theory that is necessary for deriving performance measures for estimating parameters from an EMCCD image. To obtain the Fisher information for EMCCD data, we need to find the probability distribution of the electron count that results from the multiplication process described above. To this end, we consider the stochastic multiplication as a branching process (e.g., Harris 1963; Athreya and Ney 2004), as others have done for EMCCDs (e.g., Hynecek and Nishiwaki 2003; Basden et al. 2003; Tubbs 2003) and other electron-multiplying devices (e.g., Matsuo et al. 1985; Hollenhorst 1990). The probability distribution for the output of the branching process depends on the model that is used to describe the secondary electron generation in each multiplication stage. While multiple secondary electrons can be generated per input electron per stage (Hynecek and Nishiwaki 2003), for simplicity it is common to describe the electron generation as a Bernoulli event (i.e., a secondary electron is generated per input electron per stage with probability b, or not generated with probability 1 − b). However, since no explicit expression exists for the probability distribution of the output electron count of such a branching process, different approximating distributions have been proposed (e.g., Hynecek and Nishiwaki 2003; Basden et al. 2003; Tubbs 2003). Rather than starting with the assumption of Bernoulli multiplication, here we propose using the geometric distribution to describe the probability of secondary electron generation.

The main contribution of the current work lies in the derivation of Fisher information expressions for data that can be described as the output of a branching process, with or without added readout noise. The expressions differ in the random variable, and hence the probability distribution, that is used to model the data. In all cases, however, the input to the branching process is modeled as a Poisson random variable. This assumption of a Poisson-distributed initial signal is significant, in that many physical processes that give rise to stochastic signals can be modeled as a Poisson process. Photon emission by a fluorescent molecule (and hence the detection of those photons by a camera), for example, is typically modeled as a Poisson process.

Importantly, in the process of presenting our theory, illustrations and comparisons are made of different data models in terms of their Fisher information. To facilitate the investigation, we use a quantity which we call the “noise coefficient”. The noise coefficient allows us to analyze and compare the Fisher information of different data models via a scalar quantity, and its definition is based on the assumption that information about the parameters of interest is contained in the Poisson-distributed signal.

We note that in the context of EMCCD image analysis, little has been done, to the best of our knowledge, in the way of Fisher information which importantly allows the computation of Cramer-Rao lower bound-based accuracy limits for estimating parameters of interest from the acquired data. The studies performed in Hynecek and Nishiwaki (2003) and Basden et al. (2003), for example, consider the stochasticity of electron multiplication, but not from the perspective of Fisher information. Note however that in Mortensen et al. (2010), the Fisher information has been presented for an EMCCD data model that is characterized by a probability distribution that has previously been described in Basden et al. (2003). This distribution is also the probability density for what we refer to as the high gain approximation (see Section 5.1) of our geometric model of electron multiplication. In their analysis, Mortensen et al. ultimately arrive at a simple approximation of the Fisher information for EMCCD data that is based on the “excess noise factor,” a well known quantity in electron multiplication literature (e.g., Matsuo et al. 1985; Hollenhorst 1990; Hynecek and Nishiwaki 2003). Specifically, the Fisher information for EMCCD data is approximated as half the Fisher information for the ideal scenario where the data consists of just the initial Poisson-distributed signal. However, as suggested in their work, as well as by our analysis here (see Section 5.2), this approximation is appropriate only when a relatively large number of photons are detected by an EMCCD operating at a high level of amplification. In contrast, the Fisher information corresponding to our geometric model of multiplication is suitable for arbitrary photon counts and amplification levels.

This paper is organized as follows. We begin in Section 2 with a general result from which all ensuing Fisher information expressions can be derived. This result immediately gives rise to the Fisher information for the ideal scenario of an uncorrupted signal and the practical scenario of a signal that is corrupted by readout noise. Based on this result, we also define the noise coefficient. In Section 3, general Fisher information expressions are presented which pertain to a signal that is amplified according to a branching process. These results assume a general model of multiplication, and allow the straightforward derivation of expressions for specific multiplication models. In Section 4, explicit Fisher information expressions are derived for the geometric model of multiplication. Using these results, we examine multiplication in terms of the stochasticity that it introduces and its ability to drown out the device readout noise. In Section 5, Fisher information expressions are presented for two approximations of an amplified signal that are relatively easy to work with computationally and/or analytically. In Section 6, we generalize the theory developed in previous sections for a single signal to a collection of independent signals such as that which comprise an EMCCD image. This is followed by an example which applies the generalized theory to the localization of a single molecule from an EMCCD image. In this example, the calculation of the Fisher information matrix and the Cramer-Rao lower bound-based limit of the localization accuracy is accompanied by the results of maximum likelihood estimations performed with simulated images. Finally, we conclude in Section 7.

2 The noise coefficient

The first part of this paper deals with the analysis of the information content of a scalar random variable that models the data in a single pixel of an electron multiplication imaging sensor or a similar device. The signal that impacts the detector is modeled as a Poisson random variable, but the data is a readout noise-corrupted version of the signal that may have been amplified with the intention to overcome the added noise.

Of particular interest in this paper is the calculation of the Fisher information matrix related to various parameter estimation problems such as the localization of a single molecule from its image. These estimation problems take on a typical form. The probability mass function of the incident Poisson random variable is parameterized by its mean ν. The mean ν itself is, however, typically a function of the parameter vector θ that is of interest, e.g., the positional coordinates of a single molecule. Since these problems form the basis of what follows, we first state an expression for the Fisher information of a random variable using the specific parameterization that will be of importance for the later developments.

Theorem 1 Let Z_ν be a continuous (discrete) random variable with probability density (mass) function p_ν, where ν is a scalar parameter. Let ν = ν_θ be a reparameterization of p_ν through the possibly vector-valued parameter θ ∈ Θ, where Θ is the parameter space. We use the notation Z_θ (p_θ) to denote Z_νθ (p_νθ), θ ∈ Θ. Then the Fisher information matrix I(θ) of Z_θ with respect to θ is given by

$$\mathbf{I}(\theta )={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·E\left[{(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta }(z)))}^2\right].$$ (1)

Proof Let L(θ|z) be the log-likelihood function for θ. By the definition of the Fisher information matrix,

$$\mathbf{I}(\theta )=E\left[{\left(\frac{\partial L(\theta |z)}{\partial \theta }\right)}^T\frac{\partial L(\theta |z)}{\partial \theta }\right]=E[{(\frac{\partial }{\partial \theta }\text{ln}(p_{\theta }(z)))}^T\frac{\partial }{\partial \theta }\text{ln}(p_{\theta }(z))]={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·E\left[{\left(\frac{1}{p_{\theta }(z)}\frac{\partial p_{\theta }(z)}{\partial {\nu }_{\theta }}\right)}^2\right]={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·E\left[{(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta }(z)))}^2\right].\text{\hspace{1em}\hspace{1em}\hspace{1em}□}$$

Note that the above theorem can be seen to be a special case of the transformation result for Fisher information matrices (e.g., Kay 1993) that applies to our specific conditions, and that the scalar expectation term in Eq. 1 is just the Fisher information of Z_θ with respect to ν_θ.

Theorem 1 importantly breaks the Fisher information matrix I(θ) into two parts: a matrix portion ${\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }$ which does not depend on the specific probability distribution p_θ of Z_θ, and a scalar portion E $\left[{\left(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta }(z))\right)}^2\right]$ which does depend on p_θ. This formulation provides the foundation of our definition of a “noise coefficient” for comparing the Fisher information of different data models. To motivate the purpose and definition of this coefficient, we first present two corollaries which follow immediately from Theorem 1. The results of both corollaries have been presented in our earlier work (e.g., Ober et al. 2004; Ram et al. 2006), but are given here again as two important realizations of the general Fisher information expression of Eq. 1.

The two corollaries pertain to data acquired under two important scenarios. The first gives the Fisher information matrix for the ideal scenario where a Poisson-distributed number of detected particles are read out from a device without being corrupted by measurement noise. This scenario thus represents the best case wherein a CCD is able to read out a signal without introducing readout noise, and will serve as the benchmark against which practical scenarios are compared. In this and all ensuing scenarios, the function ν_θ will represent the mean of the Poisson-distributed signal.

Corollary 1 Let Z_θ be a Poisson random variable with mean ν_θ > 0, such that its probability mass function is $p_{\theta ,P}(z)=\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^z}{z!}$, z = 0, 1,…. The Fisher information matrix I_P(θ) of Z_θ is given by

$${\mathbf{I}}_P(\theta )={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·\frac{1}{{\nu }_{\theta }}.$$ (2)

Proof Since p_θ,P is parameterized by θ through the function ν_θ, by Theorem 1 I_P(θ) takes the form of Eq. 1. To prove the result, we need only evaluate the expectation term of Eq. 1, with p_θ = p_θ,P:

$$\begin{gathered} E\left[{(\frac{\partial }{\partial {\nu }_{\theta }}[\text{ln}(p_{\theta ,P}(z))])}^2\right]=E\left[{\left(\frac{\partial }{\partial {\nu }_{\theta }}\right[\text{ln }\left(\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^z}{z!}\right)\left]\right)}^2\right]=E\left[{(\frac{z}{{\nu }_{\theta }}-1)}^2\right] \\ =\frac{1}{{\nu }_{\theta }^2}E\left[z^2\right]-\frac{2}{{\nu }_{\theta }}E[z]+1=\frac{{\nu }_{\theta }+{\nu }_{\theta }^2}{{\nu }_{\theta }^2}-2\frac{{\nu }_{\theta }}{{\nu }_{\theta }}+1=\frac{1}{{\nu }_{\theta }}.\text{\hspace{1em}\hspace{1em}\hspace{1em}□} \end{gathered}$$

Note that Eq. 2 reduces to the familiar result of ${\mathbf{I}}_P(\theta )=\frac{1}{{\nu }_{\theta }}$ if the parameter to be estimated happens to be the mean of the Poisson distribution (i.e., if θ = ν_θ).

The second corollary is of significance in that it gives the Fisher information matrix for the practical scenario where measurement noise is added to a Poisson-distributed number of detected particles when they are read out from a device. Measurement noise is typically modeled as a Gaussian random variable, and is assumed to be such by this corollary (see Appendix for the proof). This scenario importantly corresponds to the practical operation of a CCD, which adds measurement noise when electrons are read out (e.g., Snyder et al. 1995).

Corollary 2 Let Z_θ = V_θ + W, where V_θ is a Poisson random variable with mean ν_θ > 0, and W is a Gaussian random variable with mean η_w and variance ${\sigma }_w^2$. Let V_θ and W be stochastically independent of each other, and let W be not dependent on θ. The probability density function of Z_θ is then the convolution of the Poisson probability mass function with mean ν_θ and the Gaussian probability density function with mean η_w and variance ${\sigma }_w^2$, given by $p_{\theta ,R}(z)=\frac{1}{\sqrt{2\pi }{\sigma }_w}{\displaystyle {\sum }_{j=0}^{\mathrm{\infty }}}\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^j}{j!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}$, z ∈ ℝ. The Fisher information matrix I_R(θ) of Z_θ is given by

$${\mathbf{I}}_R(\theta )={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }{·({\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{1}{p_{\theta ,R}(z)}·(\frac{1}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2})}^2\mathit{\text{dz}}-\mathrm{1}).$$ (3)

Note that the density function p_θ,R in the above corollary can be found in Snyder et al. (1995).

According to Theorem 1 and demonstrated by Corollaries 1 and 2, different probability distributions of the random variable Z_θ will result in Fisher information matrices that differ from one another through the Fisher information of Z_θ with respect to ν_θ (i.e., the scalar expectation term of Eq. 1). We therefore introduce, for the purpose of comparing the Fisher information of different data models, a “noise coefficient” based on this quantity. (We call it the “noise coefficient” because, as illustrated by Corollaries 1 and 2, different data models will typically share the same signal, but differ by the type of noise that corrupts the signal.) Since Eq. 2 represents the best case scenario (where we have Poisson-distributed data that is not corrupted by measurement noise), we take its Fisher information with respect to ν_θ (i.e., the quantity $\frac{1}{{\nu }_{\theta }}$) as the reference, and define the noise coefficient as follows.

Definition 1 Let Z_θ be a continuous (discrete) random variable with probability density (mass) function p_θ. Let p_θ be parameterized by θ through the mean ν_θ > 0 of a Poisson-distributed random variable. Then the noise coefficient (with respect to ν_θ) of Z_θ, denoted by α, is given by

$$\alpha ={\nu }_{\theta }·E\left[{(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta }(z)))}^2\right].$$ (4)

The noise coefficient of Eq. 4 is just the ratio of the Fisher information of Z_θ to that of the ideal, uncorrupted Poisson-distributed signal, both with respect to ν_θ. Using this quantity, the Fisher information matrix I(θ) of a random variable which satisfies the conditions of Definition 1 can be expressed as I(θ) = α·I_P(θ), where I_P(θ) is the Fisher information matrix of Eq. 2. Note that the noise coefficient α as defined is a nonnegative scalar, and that the larger its value, the larger the Fisher information matrix I(θ) (i.e., the higher the amount of information I(θ) contains about the parameter vector θ, and hence the better the accuracy with which θ can be estimated).

For the ideal scenario of Corollary 1 where the data is Poisson-distributed, the noise coefficient is trivially α_P = 1. For the practical scenario of Corollary 2 where Gaussian-distributed measurement noise is added to the detected Poisson-distributed signal, the noise coefficient α_R is just

$${\alpha }_R={\nu }_{\theta }·({\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{1}{p_{\theta ,R}(z)}·{\left(\frac{1}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\right)}^2\mathit{\text{dz}}-\mathrm{1}),$$ (5)

and the Fisher information matrix I_R(θ) can be written as I_R(θ) = α_R · I_P(θ).

In this paper, most results will involve data that can be described as a Poisson-distributed signal with mean ν_θ that is stochastically multiplied (i.e., amplified) by some random function M before being corrupted by some additive measurement noise W. Since neither the stochasticity introduced by the multiplication nor the measurement noise is dependent on θ, they contribute no additional information about θ. If anything, they can deteriorate the Fisher information. Therefore, the noise coefficient α for these data models can be expected to be at most 1 (i.e., at most α_P). We state and prove this result formally in the following theorem.

Theorem 2 Let Θ be a parameter space and let Z_θ = M(V_θ) + W, θ ∈ Θ, where V_θ is a Poisson random variable with mean ν_θ > 0, M is a random function, and W is a scalar-valued random variable. We assume that V_θ, M, and W are stochastically independent. Then, for the noise coefficient α of Z_θ, 0 ≤ α ≤ 1.

Proof Trivially, we have α ≥ 0 because by Definition 1, it is the product of a positive value ν_θ and the expectation of a squared expression. We next show that α ≤ 1.

For any random variable U_θ that depends on the parameter θ ∈ Θ, we denote by S_Uθ its score function and by I_Uθ(θ) = E [(S_Uθ)^T S_Uθ] its Fisher information matrix with respect to the parameter θ. If we let Y_θ = M(V_θ), we first show that I_Yθ(θ) ≤ I_Vθ(θ).

We explicitly denote the dependence of the multiplication random function M on the random event ω ∈ Ω, i.e., M : ℕ × Ω → ℝ; (n, ω) ↦ M(n, ω). For a fixed ω₀ ∈ Ω, M(·, ω₀) can be considered as a constant statistic for the Poisson random variable V_θ. Then by the monotonicity of the Fisher information matrix (e.g., Rao 1965), we have that for each ω₀ ∈ Ω, I_M(Vθ,ω0)(θ) ≤ I_Vθ(θ).

Using the identity E [E [A|B]] = E [A], where A and B are random variables, we condition on the random events that yield constant (i.e., non-random) multiplication functions to obtain the required inequality

$$\begin{gathered} {\mathbf{I}}_{Y_{\theta }}(\theta )={\mathbf{I}}_{M(V_{\theta })}(\theta )=E\left[{\left(S_{M(V_{\theta })}\right)}^T{S}_{M(V_{\theta })}\right]=E\left[E\right[{\left(S_{M(V_{\theta })}\right)}^T{S}_{M(V_{\theta })}|M]] \\ =E[E[{\left(S_{M(V_{\theta })}\right)}^T{S}_{M(V_{\theta })}|M(·,·)=M(·,{\omega }_0)\left]\right]=E[{\mathbf{I}}_{M(V_{\theta },{\omega }_0)}(\theta )]\le E[{\mathbf{I}}_{V_{\theta }}(\theta )]={\mathbf{I}}_{V_{\theta }}(\theta ). \end{gathered}$$

We next consider the addition of the random variable W to Y_θ. Let F be the statistic defined by F ([A B]^T) = [1 1][A B]^T = A + B, where A and B are random variables. We then have that Z_θ = F ([Y_θ W]^T), and by the monotonicity of the Fisher information matrix, we have I_Zθ(θ) ≤ I_{[Yθ W]^T}(θ).

By the stochastic independence of Y_θ and W, the joint probability density function of [Y_θ W]^T is the product of their respective density functions p_Yθ and p_W. (Note that Y_θ and W can each be either discrete or continuous, but for ease of treatment, we consider them both to be characterized by density functions.) Then,

$${\mathbf{I}}_{{[Y_{\theta }\mathit{\text{ W}}]}^T}(\theta )=E[{(\frac{\partial }{\partial \theta }\text{ln}[p_{Y_{\theta }}(y)p_W(w)])}^T\frac{\partial }{\partial \theta }\text{ln}[p_{Y_{\theta }}(y)p_W(w)]]=E\left[{(\frac{\partial }{\partial \theta }\text{ln}[p_{Y_{\theta }}(y)]+\frac{\partial }{\partial \theta }\text{ln}[p_W(w)])}^T\right(\frac{\partial }{\partial \theta }\text{ln}[p_{Y_{\theta }}(y)]+\frac{\partial }{\partial \theta }\text{ln}[p_W(w)]\left)\right]=E\left[{(\frac{\partial }{\partial \theta }\text{ln}[p_{Y_{\theta }}(y)])}^T\right(\frac{\partial }{\partial \theta }\text{ln}[p_{Y_{\theta }}(y)]\left)\right]={\mathbf{I}}_{Y_{\theta }}(\theta ).$$

Therefore, we have I_Zθ(θ) ≤ I_Yθ(θ) ≤ I_Vθ(θ). Since I_Vθ(θ) is just I_P(θ) of Corollary 1, and since I_Zθ(θ) = α · I_P(θ), it follows that α ≤ 1. □

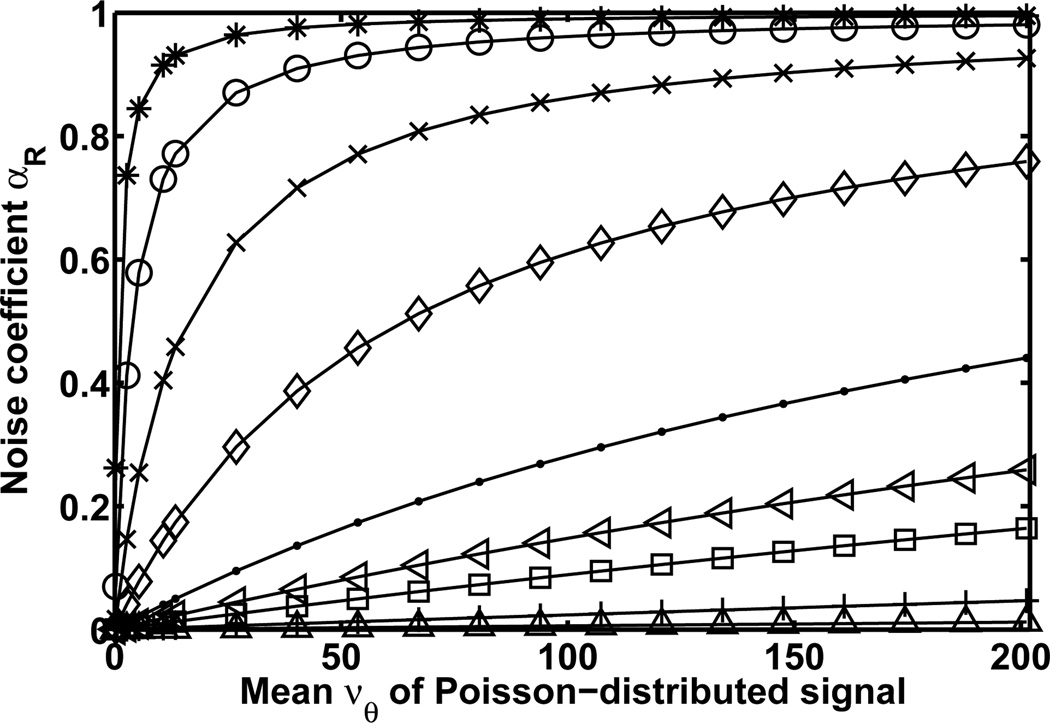
Note that if the multiplication random function M in Theorem 2 is the identity function (i.e., M(V_θ) = V_θ), then we recover the signal plus measurement noise scenario of Corollary 2. Hence, Theorem 2 immediately implies that the noise coefficient α_R of Eq. 5 is between 0 and 1, and that the Fisher information matrix I_R(θ) is no greater than I_P(θ) of the ideal scenario of Corollary 1. For illustration, Fig. 1 plots, for η_w = 0 and different values of σ_w corresponding to different levels of readout noise, the noise coefficient α_R as a function of the mean ν_θ of the Poisson-distributed signal. The plot shows that for all readout noise levels and for all values of ν_θ, the value of the noise coefficient α_R is no less than 0 and no greater than 1.

Fig. 1.

Noise coefficient α_R (Eq. 5), for the scenario of a Poisson-distributed signal with Gaussian-distributed measurement noise, as a function of the mean ν_θ of the signal. The values of ν_θ range from 0.27 to 201.28. The different curves correspond to measurement noise with mean η_w = 0 and standard deviation σ_w = 1 (*), 2 (◦), 4 (×), 8 (⋄), 16 (·), 24 (◁), 32 (□), 64 (+), and 128 (△).

For each value of ν_θ, Fig. 1 shows that the value of α_R decreases with increasing levels of the readout noise. This agrees with the expectation that the Fisher information deteriorates in proportion to the amount of noise. Moreover, for each readout noise level, we see that the value of α_R increases with increasing values of ν_θ. This demonstrates that, by increasing the signal to effectively drown out the readout noise, the Fisher information matrix I_R(θ) can be expected to approach I_P(θ) of the ideal scenario. Practically, however, it may be impossible to acquire the necessary amount of signal. In this case, the signal can be amplified before it is read out. Signal amplification that can be modeled as a branching process is the subject of what follows.

3 Fisher information for signal multiplication

In a basic multiplication, or branching, process (e.g., Harris 1963; Athreya and Ney 2004), an initial number of particles are fed into a series of stages where, in each stage, an input particle can generate secondary particles of the same kind with certain probabilities. The particles at the output of one stage become the input of the next, resulting in a cascading effect that can produce a large number of particles, and hence an amplification of the initial particle count. While motivated by electron multiplication in an EMCCD, the theory we present is general and can be used for other multiplication applications. Therefore, consistent with the literature on branching processes, we will use the generic term “particle” to refer to the physical entities that are multiplied. We begin by giving the definition of a basic branching process, in a form similar to that found in Kimmel and Axelrod (2002).

Definition 2 A branching process with an initial particle count probability distribution (q_k)_k=0,1,… and an individual offspring count probability distribution (p_k)_k=0,1,… is a sequence of nonnegative integer-valued random variables (X_n)_n=0,1,…, given by

$$X_n=\{\begin{array}{cc}U,\hfill & n=0,\hfill \\ {\displaystyle {\sum }_{j=1}^{X_{n-1}}}{Y}_j,\hfill & n=1,2,\dots ,\hfill \end{array}$$ (6)

where the initial particle count random variable U is nonnegative and integer-valued with probability distribution (q_k)_k=0,1,…, and for each X_n, n = 1, 2, …, the individual offspring count random variables Y_j, j = 1, …, X_n−1, are nonnegative and integer-valued, and are mutually independent and identically distributed with probability distribution (p_k)_k=0,1,…. Note that if X_n−1 = 0, then ${\displaystyle {\sum }_{j=1}^{X_{n-1}}}{Y}_j=0$.

In Definition 2, the random variable X_n denotes the number of particles at the output of the n^th stage of multiplication, with X₀ understood to be the initial number of particles U prior to multiplication. In the definition of X_n for n = 1, 2, …, the random variable Y_j, j = 1, …, X_n−1, denotes the number of offspring particles due to the j^th of the X_n−1 particles at the output (input) of the previous (current) stage. In this way, the cascading effect of the multiplication process is captured. Note that the number of offspring particles Y_j includes the j^th input particle itself.

For a branching process with N stages of multiplication, where N is a nonnegative integer, the mean and variance of the number of particles X_N at the output of the N^th stage are well known results (e.g., Harris 1963; Athreya and Ney 2004). For a general initial particle count probability distribution (q_k)_k=0,1,… (which by Definition 2 has mean E[X₀] and variance Var[X₀]) and a general individual offspring count probability distribution (p_k)_k=0,1,… with mean m and variance σ², the mean E[X_N] and variance Var[X_N] of X_N are as given in Table 1. The table also gives expressions for E[X_N] and Var[X_N] that correspond to combinations of different definitions of (q_k)_k=0,1,… and (p_k)_k=0,1,…. These expressions are easily verified by substituting E[X₀] = Var[X₀] = ν_θ, and/or appropriate expressions for m and σ² (see Section 4 for definitions of the standard and zero modified geometric distributions), into the general expressions for E[X_N] and Var[X_N].

Table 1.

The mean E[X_N] and variance Var[X_N] of the number of particles X_N at the output of an N-stage branching process for various combinations of the initial particle count probability distribution (q_k)_k=0,1,… and the individual offspring count probability distribution (p_k)_k=0,1,…. The mean and variance of a general (p_k)_k=0,1,… are denoted by m and σ², where m ≥ 0 for E[X_N], and m > 0, m ≠ 1 for Var[X_N].

(qk)k=0,1,…	(pk)k=0,1,…	E[XN]	Var[XN]
General	General	mNE[X0]	$\frac{{\sigma }^2{m}^{N-1}(m^N-1)}{m-1}E[X_0]+m^{2N}\mathit{\text{Var}}[X_0]$
Poisson(νθ)	General	mNνθ	${\nu }_{\theta }(\frac{{\sigma }^2{m}^{N-1}(m^N-1)}{m-1}+m^{2N})$
Poisson(νθ)	Geometric(b)	${\left(\frac{1}{1-b}\right)}^N{\nu }_{\theta }$	${\nu }_{\theta }(2{\left(\frac{1}{1-b}\right)}^{2N}-{\left(\frac{1}{1-b}\right)}^N)$
Poisson(νθ)	Zero modified geometric(a, b)	${\left(\frac{1-a}{1-b}\right)}^N{\nu }_{\theta }$	${\nu }_{\theta }(\frac{2b}{b-a}{\left(\frac{1-a}{1-b}\right)}^{2N}-\frac{b+a}{b-a}{\left(\frac{1-a}{1-b}\right)}^N)$

From Table 1, we see that E[X_N] is the product of the mean initial particle count E[X₀] and the term m^N, which is the mean of X_N given a single initial particle (i.e., given that X₀ = 1). The term m^N is commonly called the mean gain of the branching process, and is an indicator of the amount of multiplication that can be expected from a branching process.

Definition 2 specifies a general branching process by leaving the initial particle count probability distribution (q_k)_k=0,1,… and the individual offspring count probability distribution (p_k)_k=0,1,… to be defined. We are, however, interested in the scenario where the initial particle count random variable is Poisson-distributed (e.g., photons detected as electrons by an EMCCD according to a Poisson process). Using the Poisson distribution for (q_k)_k=0,1,…, the next theorem gives the probability distribution, the noise coefficient, and the Fisher information matrix of the particle count X_N,θ at the output of an N-stage branching process.

Theorem 3 Let X_N,θ, N ∈ {0, 1, …}, be the number of particles at the output of an N-stage branching process with an initial particle count probability distribution $q_k=\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^k}{k!}$, k = 0, 1, … and an individual offspring count probability distribution (p_k)_k=0,1,… that is not dependent on θ.

1. The probability distribution of X_N,θ is given by the probability mass function

   $$p_{\theta ,M}\left(x\right)=P(X_{N,\theta }=x)={\displaystyle \sum _{j=0}^{\mathrm{\infty }}}P(X_{N,\theta }=x|X_{0,\theta }=j)·\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^j}{j!},x=0,1,\dots .$$ (7)
2. The noise coefficient corresponding to the probability mass function p_θ,M is given by

   $${\alpha }_M={\nu }_{\theta }·({\displaystyle \sum _{x=0}^{\mathrm{\infty }}}\frac{1}{P(X_{N,\theta }=x)}{({\displaystyle \sum _{j=1}^{\mathrm{\infty }}}P(X_{N,\theta }=x|X_{0,\theta }=j)·\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^{j-1}}{(j-1)!})}^2-1),$$ (8)

   and the Fisher information matrix of X_N,θ is I_M(θ) = α_M · I_P(θ), where I_P(θ) is as given in Eq. 2.

Proof 1. By the law of total probability, for x = 0, 1, …,

$$\begin{gathered} p_{\theta ,M}(x)=P(X_{N,\theta }=x)={\displaystyle \sum _{j=0}^{\mathrm{\infty }}}P(X_{N,\theta }=x|X_{0,\theta }=j)·q_j \\ ={\displaystyle \sum _{j=0}^{\mathrm{\infty }}}P(X_{N,\theta }=x|X_{0,\theta }=j)·\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^j}{j!}. \end{gathered}$$

2. Since the individual offspring count probability distribution (p_k)_k=0,1,… is not dependent on θ, the conditional probability P(X_N,θ = x|X_0,θ = j), j = 0, 1, …, is not dependent on θ. Hence, p_θ,M is parameterized by θ through the mean ν_θ of a Poisson-distributed random variable. By Definition 1, α_M is then given by Eq. 4 with p_θ = p_θ,M, and the resulting expectation term can be evaluated analogously in step-by-step fashion as in the proof of Corollary 2. The matrix I_M(θ) then follows directly from Definition 1. □

Eqs. 7 and 8 are expressed in terms of P(X_N,θ = x|X_0,θ = j), which is the general probability mass function of the output particle count X_N,θ conditioned on the initial particle count X_0,θ. They therefore allow the straightforward realization of concrete expressions for the probability mass function and the noise coefficient of X_N,θ once the conditional mass function is determined. The conditional mass function, in turn, needs to be defined through a specific individual offspring count probability distribution (p_k)_k=0,1,…, which specifies how the particles are multiplied. Indeed, this approach is taken in Section 4 to arrive at the Fisher information matrix for the case where (p_k)_k=0,1,… is a geometric probability distribution.

Theorem 3 assumes that the output particle count X_N,θ of the multiplication process is the data from which θ is to be estimated. In a device such as an EMCCD, however, measurement noise is added to X_N,θ during the readout process. In this case, the data Z_θ is the sum of X_N,θ and a Gaussian random variable W which models the noise. By the stochastic independence of X_N,θ and W, the density function p_θ,MR (Eq. 31) of Z_θ is the convolution of the mass function of X_N,θ (Eq. 7) and a Gaussian density function. Using p_θ,MR, application of Definition 1 and a calculation analogous to the proof of Corollary 2 will readily yield the noise coefficient α_MR (Eq. 32). These results are stated as Corollary 4 in the Appendix.

4 Fisher information for geometric multiplication

Theorem 3 and Corollary 4 provide general Fisher information expressions for a Poisson-distributed initial particle count that has been stochastically multiplied according to some individual offspring count probability distribution (p_k)_k=0,1,…. In this section, we consider the case where (p_k)_k=0,1,… is a zero modified geometric distribution, which we define as follows (Haccou et al. 2005).

Definition 3 A zero modified geometric distribution is a probability distribution (p_k)_k=0,1,… given by

$$p_k=\{\begin{array}{cccc}a,\hfill & k=0,\hfill & \hfill & \hfill \\ (1-a)(1-b)b^{k-1},\hfill & k=1,2,\dots ,\hfill & 0\le a<1,\hfill & 0\le b<1.\hfill \end{array}$$ (9)

The zero modified geometric distribution has mean $m=\frac{1-a}{1-b}$ and variance ${\sigma }^2=\frac{(1-a)(b+a)}{{(1-b)}^2}$, which can be easily verified. It has a probability generating function of linear fractional form. Due to this special property, the probability distribution of the number of particles X_N,θ at the output of an N-stage branching process with a geometrically distributed individual offspring count can be expressed explicitly without recursion (e.g., Harris 1963; Athreya and Ney 2004). From Eq. 9, it can be seen that the zero modified geometric distribution allows the individual offspring count to take on increasing positive integer values with decreasing probabilities, and if desired, the value zero with a non-zero probability. This makes it suitable for modeling processes like electron multiplication in an EMCCD, where higher offspring counts per input particle per stage can be assumed to become increasingly unlikely. (Note that this assumption is inferred from Hynecek and Nishiwaki (2003), where it is suggested that the generation of more than one secondary electron per input electron per stage in an EMCCD multiplication register can be assumed to be an event that practically does not occur.) The ability to define a non-zero probability for a zero individual offspring count also enables the modeling of any particle loss mechanisms that may exist.

By setting the parameter a = 0, the zero modified geometric distribution of Eq. 9 reduces to the standard geometric distribution p_k = (1 − b)b^{k − 1}, k = 1,2,…. This distribution has easily verifiable mean $m=\frac{1}{1-b}$ and variance ${\sigma }^2=\frac{b}{{(1-b)}^2}$. We will use the more general zero modified geometric distribution in the theory that follows. However, the standard geometric distribution will be used for illustration purposes since it produces a branching process where there is no possibility of losing a particle. The absence of particle loss is often assumed in the modeling of, for example, electron multiplication in an EMCCD.

For an N-stage branching process with a Poisson-distributed initial particle count and a geometrically distributed individual offspring count, the following theorem gives the probability distribution, the noise coefficient, and the Fisher information matrix of the output particle count X_N,θ. In brief, the proof (see Appendix) for this theorem uses the theory of probability generating functions to derive the conditional probability mass function of X_N,θ given an initial particle count X_0,θ (see Eq. 34). The results then follow by using the conditional mass function in the general mass function and noise coefficient of Eqs. 7 and 8.

Theorem 4 Let X_N,θ, N ∈ {0, 1, …}, be the number of particles at the output of an N-stage branching process with an initial particle count probability distribution $q_k=\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^k}{k!}$, k = 0, 1, …, and a zero modified geometric individual offspring count probability distribution (p_k)_k=0,1,… that is not dependent on θ.

1. The probability distribution of X_N,θ is given by the probability mass function

   $$p_{\theta ,\mathit{\text{Geom}}}(x)=P(X_{N,\theta }=x)=\{\begin{array}{cc}{e}^{-{\nu }_{\theta }\frac{A}{B}},\hfill & x=0,\hfill \\ e^{-{\nu }_{\theta }\frac{A}{B}}{\displaystyle {\sum }_{j=0}^{x-1}}\left(\begin{array}{c}\hfill x-1\hfill \\ \hfill j\hfill \end{array}\right)\frac{C^{x-1-j}{D}^{j+1}}{B^{j+x+1}}\frac{{\nu }_{\theta }^{j+1}}{(j+1)!},\hfill & x=1,2,\dots ,\hfill \end{array}$$ (10)

   where A = (1 − a)(m − 1)m^N, B = b(m^N − 1)m + (1 − a)(m − 1), C = b(m^N − 1)m, D = m^N(1 − a)²(m − 1)², $m=\frac{1-a}{1-b}\ne 1,\mathit{\text{ and }}\left(\begin{array}{c}\hfill x-1\hfill \\ \hfill j\hfill \end{array}\right)$ denotes “x − 1 choose j”.
2. The noise coefficient corresponding to the probability mass function p_θ,Geom is given by

   $${\alpha }_{\mathit{\text{Geom}}}={\nu }_{\theta }·[{\displaystyle \sum _{x=1}^{\mathrm{\infty }}}\frac{e^{-2{\nu }_{\theta }\frac{A}{B}}}{p_{\theta ,\mathit{\text{Geom}}}(x)}{\left({\displaystyle \sum _{j=0}^{x-1}}\right(\begin{array}{c}\hfill x-1\hfill \\ \hfill j\hfill \end{array}\left)\frac{C^{x-1-j}{D}^{j+1}}{B^{j+x+1}}\frac{{\nu }_{\theta }^j}{j!}\right)}^2-{\left(\frac{A}{B}\right)}^2],$$ (11)

   and the Fisher information matrix of X_N,θ is I_Geom(θ) = α_Geom · I_P(θ), with I_P(θ) as given in Eq. 2.

For the special case where we have a standard geometric individual offspring count probability distribution, setting a = 0 in Eqs. 10 and 11 yields, for $m=\frac{1}{1-b}$, the simpler expressions

$$p_{\theta ,\mathit{\text{Geom}}}(x)=\{\begin{array}{cc}{e}^{-{\nu }_{\theta }},\hfill & x=0,\hfill \\ e^{-{\nu }_{\theta }}{\displaystyle {\sum }_{j=0}^{x-1}}\frac{\left(\begin{array}{c}\hfill x-1\hfill \\ \hfill j\hfill \end{array}\right)}{(j+1)!}{(1-\frac{1}{m^N})}^{x-1-j}{(\frac{{\nu }_{\theta }}{m^N})}^{j+1},\hfill & x=1,2,\dots ,\hfill \end{array}$$ (12)

$${\alpha }_{\mathit{\text{Geom}}}={\nu }_{\theta }·[{\displaystyle \sum _{x=1}^{\mathrm{\infty }}}\frac{e^{-2{\nu }_{\theta }}}{p_{\theta ,\mathit{\text{Geom}}}(x)}{\left({\displaystyle \sum _{j=0}^{x-1}}\right(\begin{array}{c}\hfill x-1\hfill \\ \hfill j\hfill \end{array}\left){(1-\frac{1}{m^N})}^{x-1-j}{\left(\frac{1}{m^N}\right)}^{j+1}\frac{{\nu }_{\theta }^j}{j!}\right)}^2-1].$$ (13)

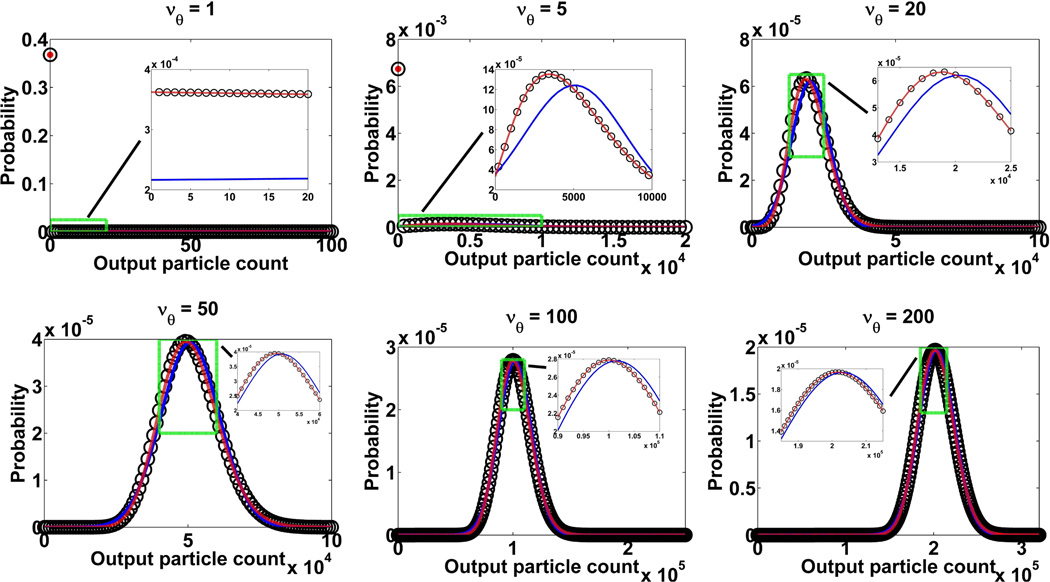
Fig. 2 plots, in open circles, the probability mass function p_θ,Geom(x) of Eq. 12 for six different values of the mean initial particle count ν_θ. For small values of ν_θ (1 and 5), the shape of the function is characterized by a large value at x = 0. This is because the output particle count of the multiplication will be 0 whenever the initial particle count is 0, a likely event given the small ν_θ. However, as ν_θ becomes larger, the shape of the probability mass function starts to resemble that of a Gaussian density function (see Section 5.2).

Fig. 2.

Probability mass function (Eq. 12) of X_536,θ, the particle count at the output of a 536-stage branching process with a standard geometric (◦) individual offspring count probability distribution and a mean gain of m⁵³⁶ = 1015.46, for six different values of the mean ν_θ of the Poisson-distributed initial particle count. For each value of ν_θ, the probability density functions resulting from the high gain approximation (Eq. 21) (red curve) and the Gaussian approximation (see discussion of Theorem 6) (blue curve) of the output of the standard geometric multiplication are also shown.

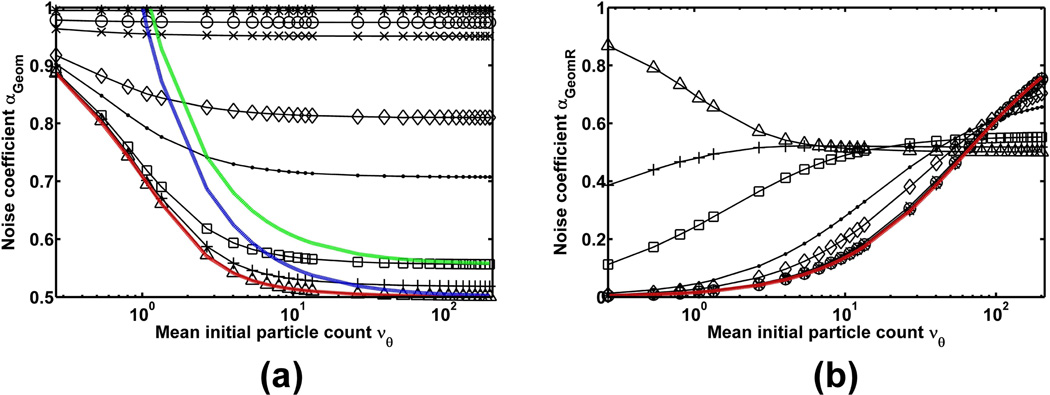
Multiplication is a random process, and hence adds stochasticity to the detected signal. This is illustrated by Fig. 3(a), which plots the noise coefficient α_Geom of Eq. 13 as a function of the mean ν_θ of the initial particle count. The figure shows curves for different values of the mean gain m^N of the multiplication process, with N set to 536 stages. (The value 536 is the number of multiplication stages in a CCD97 chip (E2V Technologies, Chelmsford, UK), a sensor which is used in many EMCCD cameras.) In accordance with Theorem 2, the stochasticity added by the multiplication is seen in the fact that the noise coefficient α_Geom is less than one for all values of the mean gain and ν_θ shown in the plot. This directly implies that the corresponding Fisher information matrix I_Geom(θ) is smaller than I_P(θ) of the ideal scenario.

Fig. 3.

(a) Noise coefficient α_Geom (Eq. 13), for the scenario of a Poisson-distributed signal that is amplified by multiplication, and (b) noise coefficient α_GeomR (Eq. 38), for the scenario of a Poisson-distributed signal that is amplified by multiplication and subsequently corrupted by measurement noise. In both (a) and (b), the noise coefficient is shown as a function of the mean ν_θ of the signal, which ranges in value from 0.27 to 201.28. The signal is amplified through N = 536 stages of standard geometric multiplication, and the different curves correspond to mean gain values of m^N = 1.01 (*), 1.03 (◦), 1.06 (×), 1.31 (⋄), 1.71 (·), 4.98 (□), 14.49 (+), and 1015.46 (△). In (a), the red curve represents the noise coefficient α_H (Eq. 22) of the high gain approximation, while the blue and green curves represent the noise coefficient α_Gauss (Eq. 25) of the Gaussian approximation for mean gains of 1015.46 and 4.98, respectively. In (b), the measurement noise is Gaussian-distributed with mean η_w = 0 and standard deviation σ_w = 8, and as a reference, the red curve represents the noise coefficient α_R (Eq. 5) for the scenario where there is no signal amplification.

For each value of ν_θ, Fig. 3(a) shows that multiplication with a higher mean gain results in a smaller value of α_Geom, indicating that the amount of added stochasticity is proportional to the mean gain. Moreover, for each mean gain value, we see that the value of α_Geom decreases with increasing values of ν_θ, suggesting that multiplication adds the least amounts of stochasticity when the signal to be amplified is small.

Despite the fact that multiplication adds stochasticity to the data, it can be useful in the practical scenario wherein measurement noise is introduced by the device. In this case, the derivations of the probability density p_θ,GeomR (Eq. 35) of the final data Z_θ and the associated noise coefficient α_GeomR (Eq. 36) will be analogous to the proof of Theorem 4 in the Appendix, using instead the general expressions of Eqs. 31 and 32 of Corollary 4, which account for the added Gaussian noise. The results are stated as Corollary 5 in the Appendix, where expressions for the special case of standard geometric multiplication are also given.

To illustrate that multiplication can be beneficial when readout noise is present, Fig. 3(b) plots the noise coefficient α_GeomR of Eq. 38 as a function of the mean ν_θ of the initial particle count. Curves are shown for the same set of mean gain values as in Fig. 3(a), and a zero mean Gaussian readout noise with a standard deviation of σ_w = 8 is assumed. As a reference for comparison, the noise coefficient α_R of Eq. 5, which corresponds to the absence of multiplication, is shown for the same readout noise level as a red curve.

Fig. 3(b) shows that, for the given set of mean gain values, multiplication yields a better noise coefficient than no multiplication (i.e., α_GeomR is greater than α_R) for ν_θ values of up to roughly 60 particles. In this range of ν_θ values, a higher mean gain generally yields a larger α_GeomR. Beyond roughly ν_θ = 60 particles, however, multiplication starts to produce, in order of decreasing mean gain, a noise coefficient that is worse than no multiplication (i.e., α_GeomR starts to drop below α_R). By roughly ν_θ = 130 particles, multiplication with any of the given mean gain values offers no benefit, with a higher mean gain yielding a smaller α_GeomR.

Fig. 3(b) therefore demonstrates that multiplication, especially at high mean gain, is beneficial when the signal level is relatively small (or equivalently, when the readout noise level is relatively significant). On the other hand, when the signal level is relatively large such that the readout noise level is already relatively insignificant, multiplication has the undesirable net effect of introducing additional stochasticity.

5 Approximations of the output of multiplication

Though exact, the probability distributions and noise coefficients of Theorem 4 and Corollary 5 can be difficult to analyze and time-consuming to compute. In this section, we present two ways to approximate the output of geometric multiplication that yield expressions that are relatively simple to analyze and/or compute. The first approximation is based on the behavior of a branching process as its mean gain converges to infinity, and applies specifically to geometric multiplication. The second approximation models the output of a branching process as a Gaussian random variable, and can be used with any multiplication model. This approximation allows for a relatively easy analytical demonstration of the behavior of the noise coefficient.

5.1 High gain approximation

Let (X_n,θ)_n=0,1,… be a branching process with initial particle count X_0,θ = 1 and a zero modified geometric individual offspring count probability distribution with mean $m=\frac{1-a}{1-b}>1$. Then it is shown in Harris (1963) that as the number of multiplication stages n converges to infinity, the sequence of random variables (Y_n = X_n,θ/mⁿ)_n=0,1,… converges, with probability 1 and in mean square, to a random variable Y with a zero modified exponential distribution given by

$$p(y)=\{\begin{array}{ccc}\frac{a}{b},\hfill & y=0,\hfill & \hfill \\ {(1-\frac{a}{b})}^2{e}^{-(1-\frac{a}{b})y},\hfill & y>0,\hfill & 0\le a<b<1.\hfill \end{array}$$ (14)

Based on this result, for a large N, the particle count X_N,θ at the output of an N-stage branching process with initial particle count X_0,θ = 1 and a zero modified geometric individual offspring count probability distribution with mean m > 1, can be approximated by the random variable m^NY, whose probability density function can be verified to be a scaled version of Eq. 14:

$$p(x)=\{\begin{array}{ccc}\frac{a}{b},\hfill & x=0,\hfill & \hfill \\ \frac{1}{m^N}{(1-\frac{a}{b})}^2{e}^{-(1-\frac{a}{b})\frac{x}{m^N}},\hfill & x>0,\hfill & 0\le a<b<1.\hfill \end{array}$$ (15)

If instead the branching process has an initial particle count of X_0,θ = j, j = 1, 2, …, then the distribution of the output particle count X_N,θ can be approximated by the j-fold convolution of p(x) of Eq. 15 with itself. The resulting density function can be shown to be, for 0 ≤ a < b < 1,

$$p(x|j)=\{\begin{array}{cc}{\left(\frac{a}{b}\right)}^j,\hfill & x=0,\hfill \\ \frac{1}{m^N}{(1-\frac{a}{b})}^2{e}^{-(1-\frac{a}{b})\frac{x}{m^N}}{\displaystyle {\sum }_{l=0}^{j-1}}\frac{\left(\begin{array}{c}\hfill j-1\hfill \\ \hfill l\hfill \end{array}\right)j}{(l+1)!}{\left(\frac{a}{b}\right)}^{j-l-1}{(1-\frac{a}{b})}^{2l}{\left(\frac{x}{m^N}\right)}^l,\hfill & x>0.\hfill \end{array}$$ (16)

To obtain the approximating probability density function and noise coefficient for the case where the initial particle count X_0,θ is Poisson-distributed with parameter ν_θ, we note that Eq. 16 is the approximating probability density function of the output particle count X_N,θ conditioned on X_0,θ. It is thus similar to the conditional probability mass function that is required by the general expressions of Eqs. 7 and 8. However, since it is a density function, continuous analogues of Eqs. 7 and 8 are needed. By proceeding in similar fashion as in the proof of Theorem 3, the general expressions for the continuous case can be verified to be

$$p(x)=\{\begin{array}{cc}{e}^{-{\nu }_{\theta }}(1+{\displaystyle {\sum }_{j=1}^{\mathrm{\infty }}}\frac{p(0|j){\nu }_{\theta }^j}{j!}),\hfill & x=0,\hfill \\ e^{-{\nu }_{\theta }}{\displaystyle {\sum }_{j=1}^{\mathrm{\infty }}}\frac{p(x|j){\nu }_{\theta }^j}{j!},\hfill & x>0,\hfill \end{array}$$ (17)

$$\alpha ={\displaystyle {\int }_0^{\mathrm{\infty }}}\frac{1}{p(x)}{\left(e^{-{\nu }_{\theta }}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{p(x|j){\nu }_{\theta }^{j-1}}{(j-1)!}\right)}^2\mathit{\text{dx}}+\frac{\mathrm{1}}{p(0)}{\left(e^{-{\nu }_{\theta }}{\displaystyle \sum _{j=\mathrm{1}}^{\mathrm{\infty }}}\frac{p(0|j){\nu }_{\theta }^{j-\mathrm{1}}}{(j-\mathrm{1})!}\right)}^2-\mathrm{1}.$$ (18)

Substituting Eq. 16 into Eq. 17 gives the required density function, which we use in our next theorem.

Theorem 5 Let X_θ be a random variable with probability density function

$$p_{\theta ,H}(x)=\{\begin{array}{cc}{e}^{-{\nu }_{\theta }(1-\frac{a}{b})},\hfill & x=0,\hfill \\ \frac{{(1-\frac{a}{b})}^2{e}^{-(1-\frac{a}{b})\frac{x}{m^N}-{\nu }_{\theta }}}{m^N}{\displaystyle {\sum }_{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^j}{(j-1)!}{\displaystyle {\sum }_{k=0}^{j-1}}\frac{\left(\begin{array}{c}\hfill j-1\hfill \\ \hfill k\hfill \end{array}\right){\left(\frac{a}{b}\right)}^{j-k-1}}{(k+1)!{\left({(1-\frac{a}{b})}^2\frac{x}{m^N}\right)}^{-k}},\hfill & x>0,\hfill \end{array}$$ (19)

where 0 ≤ a < b < 1 and $m=\frac{1-a}{1-b}$. Then the noise coefficient corresponding to p_θ,H is

$${\alpha }_H={\nu }_{\theta }·[{\displaystyle {\int }_0^{\mathrm{\infty }}}\frac{{(1-\frac{a}{b})}^2{\left({\displaystyle {\sum }_{j=1}^{\mathrm{\infty }}}\frac{j{\nu }_{\theta }^{j-1}}{(j-1)!}{\displaystyle {\sum }_{k=0}^{j-1}}\frac{\left(\begin{array}{c}\hfill j-1\hfill \\ \hfill k\hfill \end{array}\right){\left(\frac{a}{b}\right)}^{j-k-1}}{(k+1)!{\left({(1-\frac{a}{b})}^{2}x\right)}^{-k}}\right)}^2}{e^{(1-\frac{a}{b})x+{\nu }_{\theta }}{\displaystyle {\sum }_{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^j}{(j-1)!}{\displaystyle {\sum }_{k=0}^{j-1}}\frac{\left(\begin{array}{c}\hfill j-1\hfill \\ \hfill k\hfill \end{array}\right){\left(\frac{a}{b}\right)}^{j-k-1}}{(k+1)!{\left({(1-\frac{a}{b})}^{2}x\right)}^{-k}}}\mathit{\text{dx}}+\frac{a^2}{b^2{e}^{{\nu }_{\theta }(\mathrm{1}-\frac{a}{b})}}-\mathrm{1}],$$ (20)

and the Fisher information matrix of X_θ is I_H(θ) = α_H · I_P(θ), where I_P(θ) is as given in Eq. 2.

Proof The noise coefficient α_H follows by substituting Eqs. 19 and 16 into Eq. 18 and simplifying. The Fisher information matrix I_H(θ) then follows directly from Definition 1. □

To approximate standard geometric multiplication, setting a = 0 in Eqs. 19 and 20 yields the simpler expressions

$$p_{\theta ,H}(x)=\{\begin{array}{cccc}{e}^{-{\nu }_{\theta }},\hfill & x=0,\hfill & \hfill & \hfill \\ \frac{e^{-(\frac{x}{m^N}+{\nu }_{\theta })}\sqrt{{\nu }_{\theta }x/m^N}{I}_1\left(2\sqrt{{\nu }_{\theta }x/m^N}\right)}{x},\hfill & x>0,\hfill & m=\frac{1}{1-b},\hfill & 0<b<1,\hfill \end{array}$$ (21)

$${\alpha }_H={\nu }_{\theta }·\left[\frac{e^{-{\nu }_{\theta }}}{4{\nu }_{\theta }^2}{\displaystyle {\int }_0^{\mathrm{\infty }}}\frac{x^2{e}^{-\frac{x^2}{4{\nu }_{\theta }}}{I}_0^2(x)}{I_1(x)}\mathit{\text{dx}}-\mathrm{1}\right].$$ (22)

The functions I₁ and I₀ are the first and zeroth order modified Bessel function of the first kind, respectively, and they are obtained by applying the identity (Abramowitz and Stegun 1965)

$$I_{\upsilon }(u)={\left(\frac{1}{2}u\right)}^{\upsilon }{\displaystyle \sum _{j=0}^{\mathrm{\infty }}}\frac{{\left(\frac{1}{4}{u}^2\right)}^j}{j!(\upsilon +j)!},\upsilon \in \{0,1,\dots \},u\in ℝ,$$

with v = 1 and v = 0 during the simplification. Note that Eq. 21 appears in an equivalent form, without the jump at x = 0 and without the modified Bessel function representation, in Basden et al. (2003). It can also be found, in identical form as presented here and along with some associated Fisher information analysis, in Mortensen et al. (2010). Note also that whereas the mean gain m^N is present in the density functions of Eqs. 19 and 21, it disappears by simple substitution in deriving the noise coefficients of Eqs. 20 and 22.

According to its derivation, the high gain approximation can be expected to apply only in the case of a large mean gain. For illustration, the probability density function of Eq. 21 is shown, for a relatively large mean gain of m^N = 1015.46, as a red curve in each plot of Fig. 2. For each of the six values of the mean initial particle count ν_θ, a close agreement can be seen between this density function and the probability mass function of Eq. 12 (◦). Similarly, a close match can be seen in Fig. 3(a) between the noise coefficient α_H of Eq. 22 (red curve) and the noise coefficient α_Geom of Eq. 13 computed for m^N = 1015.46 (△). As expected, Fig. 3(a) also demonstrates that the agreement between α_H (which again does not depend on the mean gain m^N) and α_Geom becomes increasingly poor with decreasing mean gain values for α_Geom.

When measurement noise is present, the approximating probability distribution of the final data will be the convolution of the approximating distribution of Eq. 19 and a Gaussian distribution. The resulting density function p_θ,HR (Eq. 39) and the associated noise coefficient α_HR (Eq. 40) are stated as Corollary 6 in the Appendix, where expressions pertaining to standard geometric multiplication are also given.

The high gain approximation offers the important advantage of computational efficiency. At least for the case of standard geometric multiplication, we have found that its associated expressions can be evaluated in significantly less time than their exact counterparts in Section 4. Importantly, as demonstrated above, they produce values which are similar to that of their exact counterparts at high mean gain. In Section 6.2.2, we will make use of this approximation when performing maximum likelihood estimations where the probability distribution of the data is computed many times with different values of the estimated parameters.

5.2 Gaussian approximation

In this section, we present a Gaussian approximation of the output of multiplication. Unlike the high gain approximation, its applicability is not restricted to geometric multiplication. It has been reported (e.g., Hynecek and Nishiwaki 2003; Basden et al. 2003) that given a large initial particle count, the probability distribution of the output particle count Y of a branching process can be approximated by a Gaussian distribution with the same mean and variance as that of Y. For an N-stage branching process with a Poisson initial particle count probability distribution and a general individual offspring count probability distribution (p_k)_k=0,1,…, the mean and variance of the number of particles X_N,θ at its output are given in Table 1. Taking this mean and variance to be that of a Gaussian random variable X_θ, the following theorem gives the noise coefficient and the Fisher information matrix of the particle count Z_θ = X_θ + W, where W is a Gaussian random variable representing measurement noise. In contrast to previous sections, here we are presenting the more general case first because the case without measurement noise is a trivial special case of the more general result.

Theorem 6 Let Z_θ = X_θ + W, where X_θ and W are Gaussian random variables that are stochastically independent of each other, and W is not dependent on θ. Let X_θ have mean η_x,θ = m^Nν_θ and variance ${\sigma }_{x,\theta }^2={\nu }_{\theta }\left(\frac{{\sigma }^2{m}^{N-1}(m^N-1)}{m-1}+m^{2N}\right)$, where ν_θ > 0, m > 0, m ≠ 1, σ² ≥ 0, and N ∈ {0, 1, …}. Let W have mean η_w and variance ${\sigma }_w^2$. Then the noise coefficient corresponding to the probability density function of Z_θ, which is Gaussian with mean η_z,θ = η_x,θ + η_w and variance ${\sigma }_{z,\theta }^2={\sigma }_{x,\theta }^2+{\sigma }_w^2$, is given by

$${\alpha }_{\mathit{\text{GaussR}}}={\nu }_{\theta }·\left[{\left({\nu }_{\theta }\left(\frac{{\sigma }^2(1-\frac{1}{m^N})}{m(m-1)}+1\right)+\frac{{\sigma }_w^2}{m^{2N}}\right)}^{-1}+\frac{1}{2}{\left({\nu }_{\theta }+\frac{{\sigma }_w^2{m}^{-2N}}{\frac{{\sigma }^2(1-\frac{1}{m^N})}{m(m-1)}+1}\right)}^{-2}\right],$$ (23)

and the Fisher information matrix of Z_θ is I_GaussR(θ) = α_GaussR · I_P(θ), with I_P(θ) as given in Eq. 2.

Proof By Definition 1, α_GaussR is the product of ν_θ and the Fisher information of the Gaussian random variable Z_θ with respect to ν_θ. The Fisher information of a Gaussian random variable is well known (e.g., Kay 1993). For Z_θ with mean η_z,θ and variance ${\sigma }_{z,\theta }^2$, its Fisher information with respect to ν_θ is

$$\mathbf{I}(\theta )=\frac{1}{{\sigma }_{z,\theta }^2}{\left(\frac{\partial {\eta }_{z,\theta }}{\partial {\nu }_{\theta }}\right)}^2+\frac{1}{2{\sigma }_{z,\theta }^4}{\left(\frac{\partial {\sigma }_{z,\theta }^2}{\partial {\nu }_{\theta }}\right)}^2.$$ (24)

By evaluating Eq. 24 and multiplying the result by ν_θ, we arrive at Eq. 23. □

For the case where measurement noise is absent, the random variable Z_θ of Theorem 6 reduces to the Gaussian random variable X_θ as defined in the theorem. By making this adjustment in the proof of Theorem 6, one can easily verify the resulting noise coefficient to be, for m > 0, m ≠ 1, and σ² ≥ 0,

$${\alpha }_{\mathit{\text{Gauss}}}={\left(\frac{{\sigma }^2(1-\frac{1}{m^N})}{m(m-1)}+1\right)}^{-1}+\frac{1}{2{\nu }_{\theta }}.$$ (25)

The Fisher information matrix of X_θ is then just I_Gauss(θ) = α_Gauss · I_P(θ), with I_P(θ) as given in Eq. 2.

In electron multiplication literature (e.g., Matsuo et al. 1985; Hollenhorst 1990; Hynecek and Nishiwaki 2003), the excess noise factor is defined as the ratio of the variance of the output particle count of a multiplication process to the variance of the initial particle count, normalized by the square of the mean gain. It is thus a measure of the increase in the stochasticity of the data as a result of the multiplication. Interestingly, the expression $\frac{{\sigma }^2(1-1/m^N)}{m(m-1)}+1$ in Eqs. 23 and 25 is easily verifiable to be the excess noise factor for the case of a Poisson-distributed initial particle count. We will revisit the excess noise factor later in this section.

By substituting $m=\frac{1}{1-b}\text{ and }{\sigma }^2=\frac{b}{{(1-b)}^2}$ for the standard geometric distribution into the mean η_x,θ and the variance ${\sigma }_{x,\theta }^2$ of X_θ, the resulting Gaussian density function is plotted, for a mean gain of m⁵³⁶ = 1015.46, as a blue curve in Fig. 2 for each of the six values of the mean initial particle count ν_θ. We see that for small values of ν_θ, the Gaussian density matches poorly with the probability mass function of Eq. 12 (◦). However, with increasing values of ν_θ, the Gaussian density starts to coincide more and more with the mass function. The same observation can be made with the noise coefficient α_Gauss of Eq. 25. Computed for $m=\frac{1}{1-b},{\sigma }^2=\frac{b}{{(1-b)}^2}$, and m⁵³⁶ = 1015.46, Fig. 3(a) shows that, for small values of ν_θ, α_Gauss (blue curve) is in poor agreement with α_Geom of Eq. 13 that has been computed for the same mean gain (△). With increasing values of ν_θ, however, it becomes an increasingly better match of α_Geom. Hence, unlike the high gain approximation which applies for all values of ν_θ, the Gaussian approximation only applies for large ν_θ as indicated in Hynecek and Nishiwaki (2003) and Basden et al. (2003). However, unlike the high gain approximation, the Gaussian approximation also applies for low mean gain values. For example, Fig. 3(a) shows that for a low mean gain of m⁵³⁶ = 4.98, α_Gauss (green curve) becomes an increasingly better match of α_Geom (□) with increasing values of ν_θ.

As is evident from Eq. 25 and its curves in Fig. 3(a), the Gaussian approximation can produce noise coefficients that converge to infinity when ν_θ converges to 0. This might appear to contradict Theorem 2, which states that the noise coefficient can be at most 1. However, this is not the case since the Gaussian random variable does not fall under the category of random variables to which the theorem applies. Specifically, it is not the sum of a random function of a Poisson random variable and a scalar-valued random variable.

Besides being easy to compute, the expressions associated with the Gaussian approximation allow for relatively simple analytical studies. For example, it is easily verified that as the mean gain m^N converges to infinity in Eqs. 23 and 25, in both cases we obtain the same noise coefficient

$${\alpha }_{\mathit{\text{GaussR}}}={\alpha }_{\mathit{\text{Gauss}}}={\left(\frac{{\sigma }^2}{m(m-1)}+1\right)}^{-1}+\frac{1}{2{\nu }_{\theta }},m>1.$$ (26)

This shows that, in practice, we can drown out the measurement noise by using multiplication with a large mean gain to amplify the signal. Furthermore, the dependence of the noise coefficient on the inverse of ν_θ indicates that the high mean gain multiplication is more beneficial when low signal levels are expected. This is consistent with what we observed from Fig. 3(b).

Using mean $m=\frac{1}{1-b}$ and variance ${\sigma }^2=\frac{b}{{(1-b)}^2}$ for standard geometric multiplication, Eq. 26 yields

$${\alpha }_{\mathit{\text{GaussR}}}={\alpha }_{\mathit{\text{Gauss}}}=\frac{1}{2}+\frac{1}{2{\nu }_{\theta }}.$$ (27)

The first summand in Eq. 27 is the inverse of the excess noise factor (see above) in the limit that the mean gain converges to infinity. Therefore, in this limiting scenario, standard geometric multiplication yields an excess noise factor of 2, indicating a two-fold increase in the stochasticity of the data due to the amplification. Interestingly, for the Bernoulli multiplication model (see Section 1) which is commonly used to describe electron multiplication in an EMCCD, the excess noise factor has been shown to also approach the value 2 as the mean gain converges to infinity (e.g., Matsuo et al. 1985; Robbins and Hadwen 2003). However, the convergence to 2 for Bernoulli multiplication is dependent on the probability of secondary particle generation tending to 0.

If we further let the mean initial particle count ν_θ converge to infinity in Eq. 27, we obtain α_GaussR = α_Gauss = 0.5. This importantly suggests that when standard geometric multiplication with a high mean gain is unnecessarily used to amplify an already large signal, the Fisher information matrices I_GaussR(θ) and I_Gauss(θ) will be no smaller than half of I_P(θ) of the ideal Poisson data scenario. This agrees with Figs. 3(a) and 3(b), which suggest that α_Geom and α_GeomR converge to 0.5 as the mean gain and ν_θ are increased.

6 Application to EMCCD imaging

When imaging with a CCD or an EMCCD, photons from the imaged object arrive, and hence are detected, according to a Poisson process. In each pixel of the device, electrons accumulate in proportion to the detected photons, and in the case of an EMCCD, are subsequently multiplied using a register consisting of several hundred stages. The readout process then converts the electric charge to a digital count, during which time measurement noise is added. The data in each pixel of a CCD (EMCCD) can therefore be modeled as a Poisson-distributed particle count (that is multiplied according to a branching process), plus a Gaussian-distributed random variable that models the readout noise. As such, the Fisher information expressions derived thus far will readily apply for a single CCD or EMCCD pixel. In this section, we first build on our theory by deriving results pertaining to the Fisher information for a collection of pixels (i.e., an image). We then give an example that applies the results to a concrete estimation problem in single molecule microscopy.

6.1 Fisher information for an EMCCD image

An image acquired by a CCD or an EMCCD consists of a two-dimensional array of pixels. Since the data in different pixels can be assumed to be independent measurements, the Fisher information matrix for an image is the sum of the Fisher information matrices for its pixels. For an image of K pixels, its Fisher information matrix is thus ${\mathbf{I}}_{\mathit{\text{im}}}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_k(\theta )$, where I_k(θ) is the Fisher information matrix for the k^th pixel.

Moreover, since the theory from previous sections applies to the data in each pixel, we can write ${\mathbf{I}}_{\mathit{\text{im}}}(\theta )={\displaystyle {\sum }_{k=1}^K}{\alpha }_k·{\mathbf{I}}_{P,k}(\theta )$, where α_k is the noise coefficient for the k^th pixel, and ${\mathbf{I}}_{P,k}(\theta )={\left(\frac{\partial {\nu }_{\theta ,k}}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta ,k}}{\partial \theta }·\frac{1}{{\nu }_{\theta ,k}}$ is the Fisher information matrix for the k^th pixel in the ideal scenario where the data at that pixel is just the initial electron count which is Poisson-distributed with mean ν_θ,k. It follows that for the ideal K-pixel image, α_k = 1 for k = 1, …,K, and its Fisher information matrix is ${\mathbf{I}}_{\mathit{\text{im}},P}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_{P,k}(\theta )$. We now give an inequality which relates I_im(θ) for a practical image to I_im,P(θ) for its corresponding ideal image.

Theorem 7 Let ${\mathbf{I}}_{\mathit{\text{im}}}(\theta )={\displaystyle {\sum }_{k=1}^K}{\alpha }_k·{\mathbf{I}}_{P,k}(\theta )$, and let ${\mathbf{I}}_{\mathit{\text{im}},P}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_{P,k}(\theta )$. Let α_min and α_max denote, respectively, the smallest and the largest elements in the sequence (α_k)_k=1,…,K. Then we have

$${\alpha }_{\mathit{\text{min}}}·{\mathbf{I}}_{\mathit{\text{im}},P}(\theta )\le {\mathbf{I}}_{\mathit{\text{im}}}(\theta )\le {\alpha }_{\mathit{\text{max}}}·{\mathbf{I}}_{\mathit{\text{im}},P}(\theta ).$$

Proof Let J = I_im(θ)−α_min ·I_im,P(θ). Then for the left-hand side inequality, we need to show that J ≥ 0. Writing out the matrices I_im(θ) and I_im,P(θ) explicitly as defined, we get

$$\mathbf{J}={\displaystyle \sum _{k=1}^K}{\alpha }_k·{\mathbf{I}}_{P,k}(\theta )-{\alpha }_{\mathit{\text{min}}}{\displaystyle \sum _{k=1}^K}{\mathbf{I}}_{P,k}(\theta )={\displaystyle \sum _{k=1}^K}({\alpha }_k-{\alpha }_{\mathit{\text{min}}})·{\mathbf{I}}_{P,k}(\theta ).$$

Then, for any x ∈ ℝⁿ, where J is n × n, we have that

$$x^T\mathbf{J}x={\displaystyle \sum _{k=1}^K}{x}^T[({\alpha }_k-{\alpha }_{\mathit{\text{min}}})·{\mathbf{I}}_{P,k}(\theta )]x={\displaystyle \sum _{k=1}^K}({\alpha }_k-{\alpha }_{\mathit{\text{min}}})·x^T{\mathbf{I}}_{P,k}(\theta )x\ge 0.$$

Note that we have the inequality at the end since, for all k, (α_k − α_min) ≥ 0 and x^T I_P,k(θ)x ≥ 0. The latter is true because for each k, I_P,k(θ) is a Fisher information matrix, and therefore positive semidefinite. Since x^T Jx ≥ 0 for all x ∈ ℝⁿ, we have that J ≥ 0. The proof for the right-hand side inequality is analogous. □

Theorem 7 is of importance in that it can be used to assess, in terms of the Fisher information, how close a practical image is to its corresponding ideal image. If, for example, the smallest noise coefficient for a practical image is close to 1, then the image contains nearly the same amount of information about θ as the ideal image. On the other hand, if the largest noise coefficient is small compared to 1, then the image contains very little information about θ compared to the ideal image. In general, provided that suitable models are used to compute I_im,P(θ) and the noise coefficients (α_k)_k=1,…,K, Theorem 7 can be used to obtain a quantitative lower and upper bound of an image’s information content.

We now consider the case where the data in each pixel of a K-pixel EMCCD image is modeled using the Gaussian approximation of Theorem 6. Specifically, we assume the approximation of a standard geometric multiplication process with infinite mean gain, such that the noise coefficient for each pixel is in the form of α_GaussR of Eq. 27. For this special scenario, we give a corollary which follows directly from Theorem 7.

Corollary 3 Let ${\mathbf{I}}_{\mathit{\text{im}},\mathit{\text{GaussR}}}(\theta )={\displaystyle {\sum }_{k=1}^K}{\alpha }_{\mathit{\text{GaussR}},k}·{\mathbf{I}}_{P,k}(\theta )$, where for k = 1, …,K, ${\alpha }_{\mathit{\text{GaussR}},k}=\frac{1}{2}+\frac{1}{2{\nu }_{\theta ,k}}$. Let ${\mathbf{I}}_{\mathit{\text{im}},P}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_{P,k}(\theta )$, and let ν_θ,max and ν_θ,min denote, respectively, the smallest and the largest elements in the sequence (ν_θ,k)_k=1,…,K. Then we have the inequality

$$(\frac{1}{2}+\frac{1}{2{\nu }_{\theta ,\mathit{\text{max}}}}){\mathbf{I}}_{\mathit{\text{im}},P}(\theta )\le {\mathbf{I}}_{\mathit{\text{im}},\mathit{\text{GaussR}}}(\theta )\le (\frac{1}{2}+\frac{1}{2{\nu }_{\theta ,\mathit{\text{min}}}}){\mathbf{I}}_{\mathit{\text{im}},P}(\theta ).$$ (28)

Corollary 3 is a realization of Theorem 7 which, due to the simpler form of the noise coefficient for the assumed conditions, gives an inequality that depends on just the maximum and the minimum mean initial electron counts in the pixels comprising the image. Importantly, Eq. 28 shows that if we let ν_θ,k converge to infinity for all pixels k = 1, …,K, then ${\mathbf{I}}_{\mathit{\text{im}},\mathit{\text{GaussR}}}(\theta )=\frac{1}{2}{\mathbf{I}}_{\mathit{\text{im}},P}(\theta )$. Practically, assuming that the data can be modeled using the Gaussian approximation, this indicates that when standard geometric multiplication is used at high mean gain to amplify an image with an already high signal level in every pixel, the Fisher information of the amplified image will at worst be half of that of its corresponding ideal image.

6.2 Example: Limit of the accuracy for localizing a point source

In this section, we apply our theory to an important estimation problem in single molecule microscopy, namely the localization of a fluorescent molecule. We first compute and compare the noise coefficients for three different data models of an image acquired of a single molecule. These data models consist of the ideal scenario of an image with Poisson-distributed data, the practical scenario of a readout noise-corrupted CCD image, and the practical scenario of a stochastically multiplied and readout noise-corrupted EMCCD image. We then use the noise coefficients to compute Fisher information matrices for the estimation of the location of the single molecule from its image. From the matrices, we readily obtain the Cramer-Rao lower bound-based limits of the accuracy for the location estimation, which we compare with the standard deviations of maximum likelihood location estimates obtained with simulated image data sets. (For other studies involving point source parameter estimation from EMCCD images, see, for example, DeSantis et al. (2010), Mortensen et al. (2010), Quan et al. (2010), Thompson et al. (2010), and Wu et al. (2010).)

Note that in the material that follows, a standard geometric model of electron multiplication is assumed for the EMCCD. To perform the same analyses using a different model of multiplication, the results presented in Section 3 for a general model of multiplication may be used to obtain the necessary mathematical expressions.

6.2.1 Noise coefficient comparison

We consider the estimation of the location of an in-focus point source (e.g., single molecule) from its image as observed through a fluorescence microscope and detected by a CCD or EMCCD camera. For this problem, the mean of the Poisson-distributed photon count (or equivalently, electron count) that is detected from the point source at the k^th pixel of the device can be shown to be

$${\nu }_{\theta ,k}=\frac{N_{\mathit{\text{photon}}}}{M^2}{\displaystyle {\int }_{C_k}}q(x/M-x_0,y/M-y_0)\mathit{\text{dxdy}},$$ (29)

where N_photon is the expected number of photons detected from the point source, M is the magnification of the microscope, C_k is the region in the xy-plane occupied by the pixel, x₀ and y₀ are the x and y coordinates of the point source in the object space where it resides, and q is a function which describes the image formed from the detected photons. More specifically, q is called the “image function”, and gives the image at unit magnification of a point source that is located at the origin of the object space coordinate system (Ram et al. 2006). Eq. 29 is a realization of a more general formula in Ram et al. (2006), as it assumes the rate at which photons are detected from the point source to be a constant. In general, ν_θ,k can also include as additional summands the means of Poisson-distributed components (e.g., photon count detected from something other than the point source) which are stochastically independent of one another, and of the electron count due to the point source.

We assume that q is given by the Airy point spread function (Born and Wolf 1999), a model which has classically been used to describe the image of an in-focus point source. The Airy image function can be written as (Ram et al. 2006)

$$q(x,y)=\frac{J_1^2\left(\frac{2\pi n_a}{\lambda }\sqrt{x^2+y^2}\right)}{\pi (x^2+y^2)},(x,y)\in {ℝ}^2,$$ (30)

where n_a is the numerical aperture of the objective lens, λ is the wavelength of the detected photons, and J₁ is the first order Bessel function of the first kind. The Airy image function is circularly symmetric, with a strong central peak and ripples that increasingly diminish in amplitude away from the center.

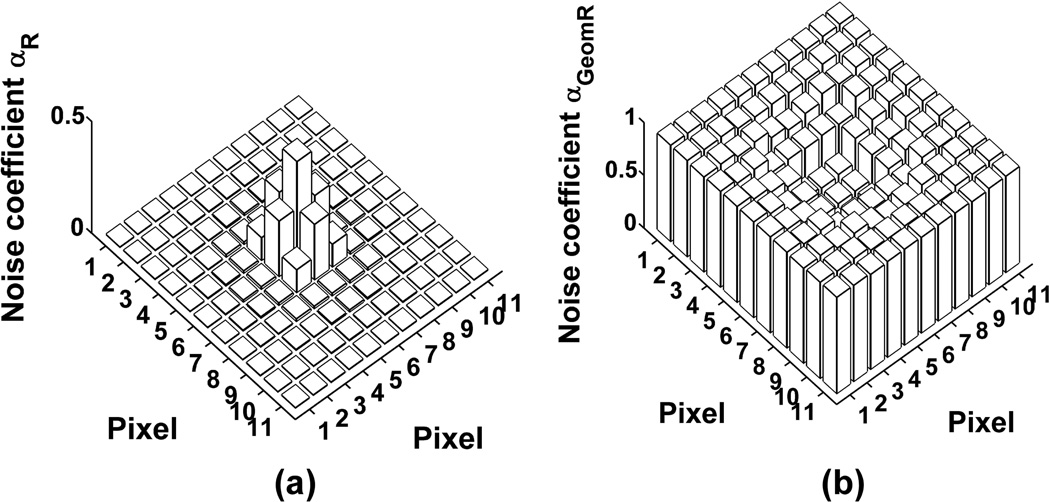
Noise coefficients are computed for an 11-by-11 pixel array (i.e., image), with the mean initial electron count ν_θ,k (Eq. 29) at the k^th pixel calculated with the point source attributes and imaging parameters given in Fig. 4. Mirroring the shape of the Airy image function of Eq. 30, and due to the centering of the point source image on the pixel array, the resulting profile of ν_θ values over the pixel array is circularly symmetric, with the largest values in the center region and a maximum value of 53.48 electrons at the center pixel.

Fig. 4.

Noise coefficient (α_R for (a), α_GeomR for (b)) profile for (a) a CCD image and (b) an EMCCD image of an in-focus point source. The point source is assumed to emit photons of wavelength λ = 655 nm, which are collected by an objective lens with magnification M = 100 and numerical aperture n_a = 1.3. The image of the point source is given by the Airy image function, and is centered on an 11-by-11 array of 16 µm by 16 µm pixels (i.e., x₀ = y₀ = 880 nm, assuming the upper left corner of the pixel array is (0, 0)). The expected number of detected photons is set to N_photon = 200, a reasonable number that could be detected from a single fluorescent molecule. In (a), readout noise with mean η_w = 0 e⁻ and standard deviation σ_w = 8 e⁻ is assumed for every pixel. In (b), the standard deviation is higher at σ_w = 24 e⁻, and standard geometric multiplication with a mean gain of m⁵³⁶ = 1015.46 is assumed.

For the ideal Poisson data model, the noise coefficient is, by definition, 1 for each pixel of the image. For the two practical data models, the noise coefficients for all pixels in the image are plotted in Fig. 4. For the CCD scenario, a Gaussian readout noise with mean η_w = 0 e⁻ and standard deviation σ_w = 8 e⁻ in every pixel is assumed. The chosen standard deviation represents a noise level that is typical of a CCD, and is the number specified, for example, for the normal readout mode of our laboratory’s Hamamatsu C4742-95-12ER CCD camera. In this case, Fig. 4(a) shows that α_R of Eq. 5 is relatively small for every pixel. The center region of the image has the largest α_R values, with the center pixel having the maximum value of only 0.456. This and the circular symmetry of the α_R values correspond to the profile of ν_θ values, which is in accordance with Fig. 1 showing the value of α_R to be proportional to the value of ν_θ. By Theorem 7, the maximum α_R value of 0.456 implies that the Fisher information for this scenario is less than half of that for the ideal scenario.

For the EMCCD scenario, standard geometric multiplication using a 536-stage register is assumed. The mean gain is set to m⁵³⁶ = 1015.46, and a Gaussian readout noise with mean η_w = 0 e⁻ and standard deviation σ_w = 24 e⁻ in every pixel is assumed. The higher readout noise level of 24 e⁻ is within the range of typical values for an EMCCD, and is representative of the noise level for the settings at which our laboratory’s Andor iXon EMCCD cameras are often operated. In this case, Fig. 4(b) shows that the value of α_GeomR of Eq. 38 is at least 0.5 in every pixel. This demonstrates a significant increase in the information content of every pixel due to the high mean gain multiplication. Moreover, the pixels in the center of the image have α_GeomR values that are closer to 0.5, while the rest have α_GeomR values that are closer to 1. This is in accordance with the curve with the same high mean gain in Fig. 3(b) which, though shown for σ_w = 8 e⁻, indicates that the value of α_GeomR decreases with increasing values of ν_θ. The minimum α_GeomR value in this case is 0.503, which implies, by Theorem 7, that the Fisher information for this scenario is greater than half of that for the ideal scenario.

6.2.2 Limit of the localization accuracy comparison

To arrive at the limit of the localization accuracy for each data model, the estimated parameters are defined as the coordinates of the point source, i.e., θ = (x₀, y₀). Given θ and the noise coefficients computed above, we readily obtain the Fisher information matrix for each data model as described in Section 6.1. The limit of the localization accuracy for x₀ (y₀) is then defined as the square root of the Cramer-Rao lower bound on the variance of the estimates of x₀ (y₀), and is thus a lower bound on the standard deviation of any unbiased estimator of x₀ (y₀). Due to the centering of the circularly symmetric Airy image function on a square pixel array, the accuracy limits for x₀ and y₀ are the same. Hence, we give only a single limit for each data model.

The limits of the localization accuracy for the three data models are shown in Table 2. As expected, the ideal scenario of Poisson-distributed data has the best (i.e., the smallest) accuracy limit of 8.50 nm. In comparison, the CCD scenario has a significantly higher accuracy limit of 21.14 nm due to the readout noise of standard deviation σ_w = 8 e⁻ in every pixel. In contrast, by using high mean gain multiplication to drown out the readout noise, the EMCCD scenario has an accuracy limit of 11.58 nm that is only a little higher than that of the ideal scenario. Note that this is despite a larger readout noise standard deviation of σ_w = 24 e⁻ per pixel, which for the CCD scenario would more than double its accuracy limit to 57.27 nm.

Table 2.

Limits of the localization accuracy and results of maximum likelihood estimations for the ideal Poisson-distributed data model and the practical CCD and EMCCD image models. Attributes of the imaged point source and all imaging-related parameters are as in Fig. 4. For each data model, the positional coordinates (x₀, y₀) of the point source are estimated from 1000 simulated images, and the results for x₀ are shown.

Data model	No. of x0 estimates	True x0 (nm)	Mean of x0 estimates (nm)	Limit of the localization accuracy (nm)	Standard deviation of x0 estimates (nm)
Ideal	1000	880	880.16	8.50	8.69
CCD	998a	880	880.47	21.14	20.94
EMCCD	1000	880	879.74	11.58	11.75

^aTwo outlier estimates which place the center of the point source’s image outside the pixel array have been removed.

Table 2 also shows, for each data model, the mean and standard deviation of the estimates of the x₀ coordinate from maximum likelihood estimations carried out on 1000 simulated images of the point source. The image simulation and the estimation are performed in MATLAB (The MathWorks, Inc., Natick, MA). For an ideal image, the k^th pixel value, with mean ν_θ,k of Eq. 29, is generated using MATLAB’s poissrnd function. For a CCD image, the k^th pixel value is the sum of a similarly generated Poisson random number and a Gaussian random number with mean 0 and standard deviation 8 generated using MATLAB’s randn function. For an EMCCD image, the k^th pixel value is the sum of a number generated from the standard geometric multiplication probability mass function of Eq. 12 (with m^N = 1015.46 and ν_θ = ν_θ,k) using the inverse transform method, and a Gaussian random number with mean 0 and standard deviation 24.

By the independence of the pixels, the log-likelihood function that is maximized for a given image is the sum of the log-likelihood functions of its individual pixels. For an ideal and a CCD image, the log-likelihood function of the k^th pixel is the logarithm of, respectively, the Poisson mass function with mean ν_θ,k of Eq. 29 and the density function given in the statement of Corollary 2 with ν_θ = ν_θ,k, η_w = 0, and σ_w = 8. For an EMCCD image, the k^th pixel’s log-likelihood function is approximated by the density function of Eq. 41 with m^N = 1015.46, ν_θ = ν_θ,k, η_w = 0, and σ_w = 24. The high gain approximation is used (as opposed to the standard geometric multiplication density function of Eq. 37) because it computes significantly faster while, as the results will show, retaining reasonable accuracy. In all cases, the maximization is realized by minimizing the negative of the log-likelihood function using MATLAB’s fminunc function. Also, initial estimates for x₀ and y₀ are randomly generated per image to be within 20% of the true value of 880 nm.

For each data scenario, Table 2 shows that the standard deviation of the maximum likelihood estimates of x₀ comes reasonably close to the corresponding limit of the localization accuracy. In each case, the mean of the estimates also recovers reasonably closely the true value of x₀. (For the results of maximum likelihood estimations performed on additional simulated EMCCD data sets that differ in the expected number of detected photons N_photon, see Table 3 in the Appendix. As in the case of the results of Table 2, the mean values and the standard deviations of the x₀ estimates of these data sets reasonably recover, respectively, the true value of x₀ and their corresponding limits of the localization accuracy.)

Table 3.

Limits of the localization accuracy and results of maximum likelihood estimations for four simulated data sets of the EMCCD image model. Except for the expected number of detected photons N_photon, for each data set the attributes of the imaged point source and all imaging-related parameters are as in Fig. 4(b). For each data set, the positional coordinates (x₀, y₀) of the point source are estimated from 1000 simulated images, and the results obtained from the 1000 x₀ estimates are shown. In addition, limits of the localization accuracy for the corresponding ideal Poisson-distributed data model and CCD image model (with readout noise parameters as given in Fig. 4(a)) are provided for comparison.

Expected photon count Nphoton	True x0 (nm)	Mean of x0 estimates (nm)	Limit of the localization accuracy (nm)	Standard deviation of x0 estimates (nm)	Ideal limit of the localization accuracy (nm)	CCD limit of the localization accuracy (nm)
150	880	879.56	13.28	13.19	9.82	27.44
100	880	879.80	16.07	16.18	12.02	39.99
50	880	880.45	21.98	22.23	17.00	77.53
25	880	879.35	29.61	31.32	24.04	152.53

7 Conclusion

We have derived various Fisher information expressions pertaining to data that can be described as the output of a branching process with potentially added measurement noise. All expressions assume a Poisson-distributed initial signal which is characteristic of many physical processes. General expressions which make no assumptions about the model of signal amplification allow the straightforward derivation of specific expressions once the probability distribution of the amplified signal is known. On the other hand, specific results which assume the geometric model of amplification can readily be applied to, for example, imaging with an EMCCD. Meanwhile, expressions based on two approximations of an amplified signal offer computational efficiency and/or ease of analysis. Throughout the presentation, illustration and comparison of different data models have been performed using a noise coefficient that has been defined based on the common form taken by the data models. As demonstrated with a point source localization example, the developed theory has applications in the Fisher information analysis of practically important problems.

Biographies

Fig. 5 Jerry Chao obtained his B.S. and M.S. degrees in computer science from the University of Texas at Dallas, Richardson, in 2000 and 2002, respectively. He received the Ph.D. degree in electrical engineering from the same institution in 2010. From 2003 to 2005, he developed software for microscopy image acquisition and analysis at the University of Texas Southwestern Medical Center, Dallas. He is currently carrying out postdoctoral research in the Department of Electrical Engineering, University of Texas at Dallas, and the Department of Immunology, University of Texas Southwestern Medical Center. His research interests include biomedical image and signal processing, with particular application to cellular microscopy, and the development of software for bioengineering applications.

Fig. 6 E. Sally Ward received the Ph.D. degree from the Department of Biochemistry, Cambridge University, Cambridge, U.K., in 1985. From 1985 to 1987, she was a Research Fellow at Gonville and Caius College while working at the Department of Biochemistry, Cambridge University. From 1988 to 1990, she held the Stanley Elmore Senior Research Fellowship at Sidney Sussex College and carried out research at the MRC Laboratory of Molecular Biology, Cambridge. In 1990, she joined the University of Texas Southwestern Medical Center, Dallas, as an Assistant Professor. Since 2002, she has been a Professor in the Department of Immunology at the same institution, and currently holds the Paul and Betty Meek-FINA Professorship in Molecular Immunology. Her research interests include antibody engineering, molecular mechanisms that lead to autoimmune disease, questions related to the in vivo dynamics of antibodies, and the use of microscopy techniques for the study of antibody trafficking in cells.

Fig. 7 Raimund J. Ober received the Ph.D. degree in engineering from Cambridge University, Cambridge, U.K., in 1987. From 1987 to 1990, he was a Research Fellow at Girton College and the Engineering Department, Cambridge University. In 1990, he joined the University of Texas at Dallas, Richardson, where he is currently a Professor with the Department of Electrical Engineering. He is also Adjunct Professor at the University of Texas Southwestern Medical Center, Dallas. He is an Associate Editor of Mathematics of Control, Signals, and Systems, and a past Associate Editor of Multidimensional Systems and Signal Processing, IEEE Transactions on Circuits and Systems, and Systems and Control Letters. His research interests include the development of microscopy techniques for cellular investigations, in particular at the single molecule level, the study of cellular trafficking pathways using microscopy investigations, and signal/image processing of bioengineering data.

Appendix

Corollary 2 Proof:

Since p_θ,R is parameterized by θ through ν_θ, by Theorem 1 I_R(θ) takes the form of Eq. 1. To prove the result, we need only evaluate the expectation term of Eq. 1 with p_θ = p_θ,R:

$$E\left[{(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta ,R}(z)))}^2\right]=E\left[{\left(\frac{1}{p_{\theta ,R}(z)}\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=0}^{\mathrm{\infty }}}\frac{j{\nu }_{\theta }^{j-1}-{\nu }_{\theta }^j}{j!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\right)}^2\right]=E\left[{\left(\frac{1}{p_{\theta ,R}(z)}\left(\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}-p_{\theta ,R}(z)\right)\right)}^2\right]=E\left[{\left(\frac{1}{p_{\theta ,R}(z)}\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\right)}^2\right]-2·E\left[\frac{1}{p_{\theta ,R}(z)}\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\right]+1={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{1}{p_{\theta ,R}(z)}{\left(\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\right)}^2\mathit{\text{ dz}}-\frac{2·e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\left(\frac{{\nu }_{\theta }^{j-1}}{(j-1)!}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\mathit{\text{ dz}}\right)+1={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{1}{p_{\theta ,R}(z)}{\left(\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}}{(j-1)!}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}\right)}^2\mathit{\text{ dz}}-\mathrm{1}.\text{\hspace{1em}\hspace{1em}\hspace{1em}□}$$

Corollary 4 Let Z_θ = X_N,θ + W, where X_N,θ is as defined in Theorem 3, and W is a Gaussian random variable with mean η_w and variance ${\sigma }_w^2$. Let X_N,θ and W be stochastically independent of each other, and let W be not dependent on θ.

1. The probability distribution of Z_θ is given by the probability density function

   $$p_{\theta ,\mathit{\text{MR}}}(z)=\frac{1}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{l=0}^{\mathrm{\infty }}}{e}^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}\left[{\displaystyle \sum _{j=0}^{\mathrm{\infty }}}P(X_{N,\theta }=l|X_{0,\theta }=j)·\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^j}{j!}\right],z\in ℝ.$$ (31)
2. The noise coefficient corresponding to the probability density p_θ,MR is given by

   $${\alpha }_{\mathit{\text{MR}}}={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }·e^{-2{\nu }_{\theta }}}{p_{\theta ,\mathit{\text{MR}}}(z)}{\left({\displaystyle \sum _{l=0}^{\mathrm{\infty }}}\frac{e^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{P(X_{N,\theta }=l|X_{0,\theta }=j)·{\nu }_{\theta }^{j-1}}{(j-1)!}\right)}^2\mathit{\text{ dz}}-{\nu }_{\theta }.$$ (32)

The Fisher information matrix of Z_θ is given by I_MR(θ) = α_MR · I_P(θ), with I_P(θ) as given in Eq. 2.

Theorem 4 Proof:

1. Let f be the probability generating function of the zero modified geometric distribution (p_k)_k=0,1,… of Eq. 9. By the definition of the generating function, for s ∈ ℂ and |s| ≤ 1,

$$\begin{gathered} f(s)={\displaystyle \sum _{k=0}^{\mathrm{\infty }}}{p}_k{s}^k=p_0{s}^0+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}}{p}_k{s}^k \\ =a+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}}(1-a)(1-b)b^{k-1}{s}^k=\frac{a-(a-(1-b))s}{1-\mathit{\text{bs}}}. \end{gathered}$$

Given an N-stage branching process with initial particle count 1 (i.e., U = 1 in Definition 2) and an individual offspring count probability distribution (p_k)_k=0,1,…, the probability generating function of the probability distribution of the particle count X_N,θ at the output of the branching process is well known to be the N^th iterate of the probability generating function of (p_k)_k=0,1,… (e.g., Harris 1963; Athreya and Ney 2004; Grimmett and Stirzaker 2001). Denoted by f_N(s), the N^th iterate of f(s) can be shown by induction to be, for $m=\frac{1-a}{1-b}\ne 1$,

$$f_N(s)=1-\frac{(1-a)(m-1)m^N(1-s)}{b(m^N-1)m(1-s)+(1-a)(m-1)},N=0,1,\dots ,s\in ℂ,|s|\le 1.$$ (33)

According to Definition 2, each initial particle of a branching process multiplies independently of the other initial particles, but according to a common stochastic model. Therefore, if the initial particle count is a positive integer j, then the probability mass function of the output particle count X_N,θ will be the j-fold convolution of, in this case, the probability mass function corresponding to Eq. 33 with itself. By a well known result from the theory of generating functions, the generating function of X_N,θ is then just [f_N(s)]^j (e.g., Grimmett and Stirzaker 2001).

Using this generating function, the conditional probability that the output particle count X_N,θ = x given j ∈ {1, 2, …} initial particles can be obtained based on the definition of the generating function. For x = 0, it is given by [f_N(s)]^j evaluated at s = 0, and for x = 1, 2, …, it is given by the x^th derivative of [f_N(s)]^j evaluated at s = 0 and divided by x! (e.g., Grimmett and Stirzaker 2001). This can be shown to yield, for A, B, C, and D as given for Eq. 10,

$$P(X_{N,\theta }=x|X_{0,\theta }=j)=\{\begin{array}{c}{\left[1-\frac{A}{B}\right]}^j,x=0,\hfill \\ {\displaystyle {\sum }_{l=0}^{x-1}}\frac{\left(\begin{array}{c}\hfill x-1\hfill \\ \hfill l\hfill \end{array}\right)C^{x-1-l}{D}^{l+1}}{(l+1)!B^{x+l+1}}\frac{{\partial }^{l+1}}{\partial {\left(1-\frac{A}{B}\right)}^{l+1}}\left({\left[1-\frac{A}{B}\right]}^j\right),x=1,2,\dots .\hfill \end{array}$$ (34)

Note that Eq. 34 also applies for j = 0, since P(X_N,θ = x|X_0,θ = 0) is 1 for x = 0, and is 0 otherwise. Finally, for an initial particle count that is Poisson-distributed with mean ν_θ, using the conditional mass function of Eq. 34 in the general expression of Eq. 7 gives the desired probability mass function of X_N,θ.

2. The noise coefficient α_Geom follows by substituting Eqs. 34 and 10 into Eq. 8 and simplifying. The Fisher information matrix I_Geom(θ) then follows directly from Definition 1. □

Corollary 5 Let Z_θ = X_N,θ + W, where X_N,θ is as defined in Theorem 4, and W is a Gaussian random variable with mean η_w and variance ${\sigma }_w^2$. Let X_N,θ and W be stochastically independent of each other, and let W be not dependent on θ.

1. The probability density function of Z_θ is, for z ∈ ℝ, given by

   $$p_{\theta ,\mathit{\text{GeomR}}}(z)=\frac{e^{-{\nu }_{\theta }\frac{A}{B}}}{\sqrt{2\pi }{\sigma }_w}\left[e^{-{\left(\frac{z-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}+{\displaystyle \sum _{l=1}^{\mathrm{\infty }}}{e}^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}{\displaystyle \sum _{j=0}^{l-1}}\frac{\left(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array}\right)C^{l-1-j}{(D{\nu }_{\theta })}^{j+1}}{(j+1)!B^{j+l+1}}\right].$$ (35)
2. The noise coefficient corresponding to the probability density p_θ,GeomR is given by

   $${\alpha }_{\mathit{\text{GeomR}}}={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }{D}^2{e}^{-2{\nu }_{\theta }\frac{A}{B}}}{p_{\theta ,\mathit{\text{GeomR}}}(z)}{\left({\displaystyle \sum _{l=1}^{\mathrm{\infty }}}\frac{e^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=0}^{l-1}}\frac{(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array})C^{l-1-j}}{j!B^{j+l+1}{(D{\nu }_{\theta })}^{-j}}\right)}^2\mathit{\text{dz}}-{\nu }_{\theta }\frac{A^2}{B^2}.$$ (36)

The Fisher information matrix of Z_θ is I_GeomR(θ) = α_GeomR · I_P(θ), with I_P(θ) as given in Eq. 2.

For standard geometric multiplication, setting a = 0 in Eqs. 35 and 36 yields, for $m=\frac{1}{1-b}$,

$$p_{\theta ,\mathit{\text{GeomR}}}(z)=\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}\left[e^{-{\left(\frac{z-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}+{\displaystyle \sum _{l=1}^{\mathrm{\infty }}}{e}^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}{\displaystyle \sum _{j=0}^{l-1}}\frac{\left(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array}\right){\left(1-\frac{1}{m^N}\right)}^{l-j-1}}{(j+1)!{\left(\frac{m^N}{{\nu }_{\theta }}\right)}^{j+1}}\right],z\in ℝ,$$ (37)

$${\alpha }_{\mathit{\text{GeomR}}}={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }·e^{-2{\nu }_{\theta }}}{p_{\theta ,\mathit{\text{GeomR}}}(z)}{\left({\displaystyle \sum _{l=1}^{\mathrm{\infty }}}\frac{e^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{\sqrt{2\pi }{\sigma }_w{m}^N}{\displaystyle \sum _{j=0}^{l-1}}\frac{\left(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array}\right){\left(1-\frac{1}{m^N}\right)}^{l-j-1}}{j!{\left(\frac{m^N}{{\nu }_{\theta }}\right)}^j}\right)}^2\mathit{\text{ dz}}-{\nu }_{\theta }.$$ (38)

Corollary 6 Let Z_θ = X_θ + W, where X_θ is as defined in Theorem 5, and W is a Gaussian random variable with mean η_w and variance ${\sigma }_w^2$. Let X_θ and W be stochastically independent of each other, and let W be not dependent on θ.

1. The probability density function of Z_θ is, for 0 ≤ a < b < 1 and

   $m=\frac{1-a}{1-b}$,

   $$p_{\theta ,\mathit{\text{HR}}}(z)=\frac{1}{\sqrt{2\pi }{\sigma }_w}\left[\frac{e^{-{\left(\frac{z-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{e^{{\nu }_{\theta }(1-\frac{a}{b})}}+\frac{{(1-\frac{a}{b})}^2}{m^N}{\displaystyle {\int }_0^{\mathrm{\infty }}}\frac{e^{-{\left(\frac{z-u-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{e^{(1-\frac{a}{b})\frac{u}{m^N}+{\nu }_{\theta }}}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^j}{(j-1)!}{\displaystyle \sum _{k=0}^{j-1}}\frac{\left(\begin{array}{c}\hfill j-1\hfill \\ \hfill k\hfill \end{array}\right){(\frac{a}{b})}^{j-k-1}}{(k+1)!{\left({(1-\frac{a}{b})}^2\frac{u}{m^N}\right)}^{-k}}\mathit{\text{ du}}\right].$$ (39)
2. The noise coefficient corresponding to the probability density p_θ,HR is given by

   $$\begin{gathered} {\alpha }_{\mathit{\text{HR}}}={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }}{2\pi {\sigma }_w^2·p_{\theta ,\mathit{\text{HR}}}(z)}{ \\ \left(\frac{a·e^{-{\left(\frac{z-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{b·e^{{\nu }_{\theta }(1-\frac{a}{b})}}+\frac{{\left(1-\frac{a}{b}\right)}^2}{m^N}{\displaystyle {\int }_0^{\mathrm{\infty }}}\frac{e^{-{\left(\frac{z-u-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{e^{\left(1-\frac{a}{b}\right)\frac{u}{m^N}+{\nu }_{\theta }}}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{j{\nu }_{\theta }^{j-1}}{(j-1)!}{\displaystyle \sum _{k=0}^{j-1}}\frac{\left(\begin{array}{c}\hfill j-1\hfill \\ \hfill k\hfill \end{array}\right){\left(\frac{a}{b}\right)}^{j-k-1}}{(k+1)!{\left({\left(1-\frac{a}{b}\right)}^2\frac{u}{m^N}\right)}^{-k}}\mathit{\text{du}}\right)}^2\mathit{\text{dz}}-{\nu }_{\theta }. \end{gathered}$$ (40)

The Fisher information matrix of Z_θ is given by I_HR(θ) = α_HR · I_P(θ), where I_P(θ) is as in Eq. 2.

To approximate standard geometric multiplication, setting a = 0 in Eqs. 39 and 40 yields, for $m=\frac{1}{1-b}$, 0 < b < 1,

$$p_{\theta ,\mathit{\text{HR}}}(z)=\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}\left[e^{-{\left(\frac{z-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}+{\displaystyle {\int }_0^{\mathrm{\infty }}}{e}^{-{\left(\frac{z-u-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2-\frac{u}{m^N}}\frac{\sqrt{\frac{{\nu }_{\theta }u}{m^N}}{I}_1\left(2\sqrt{\frac{{\nu }_{\theta }u}{m^N}}\right)}{u}\mathit{\text{du}}\right],z\in ℝ,$$ (41)

$${\alpha }_{\mathit{\text{HR}}}={\nu }_{\theta }·\left[{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{1}{p_{\theta ,\mathit{\text{HR}}}(z)}{\left(\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle {\int }_0^{\mathrm{\infty }}}\frac{e^{-\frac{1}{2}{\left(\frac{z-u-{\eta }_w}{{\sigma }_w}\right)}^2-\frac{u}{m^N}}}{m^N}{I}_0\left(2\sqrt{\frac{{\nu }_{\theta }u}{m^N}}\right)\mathit{\text{ du}}\right)}^2\mathit{\text{ dz}}-\mathrm{1}\right].$$ (42)