Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2012 Aug 3;160(2):1097–1109. doi: 10.1104/pp.112.202200

Diffusion Limitations in Root Uptake of Cadmium and Zinc, But Not Nickel, and Resulting Bias in the Michaelis Constant1,[W],[OA]

Fien Degryse 1,*, Afsaneh Shahbazi 1, Liesbeth Verheyen 1, Erik Smolders 1
PMCID: PMC3461532  PMID: 22864584

Abstract

It has long been recognized that diffusive boundary layers affect the determination of active transport parameters, but this has been largely overlooked in plant physiological research. We studied the short-term uptake of cadmium (Cd), zinc (Zn), and nickel (Ni) by spinach (Spinacia oleracea) and tomato (Lycopersicon esculentum) in solutions with or without metal complexes. At same free ion concentration, the presence of complexes, which enhance the diffusion flux, increased the uptake of Cd and Zn, whereas Ni uptake was unaffected. Competition effects of protons on Cd and Zn uptake were observed only at a very large degree of buffering, while competition of magnesium ions on Ni uptake was observed even in unbuffered solutions. These results strongly suggest that uptake of Cd and Zn is limited by diffusion of the free ion to the roots, except at very high degree of solution buffering, whereas Ni uptake is generally internalization limited. All results could be well described by a model that combined a diffusion equation with a competitive Michaelis-Menten equation. Direct uptake of the complex was estimated to be a major contribution only at millimolar concentrations of the complex or at very large ratios of complex to free ion concentration. The true Km for uptake of Cd2+ and Zn2+ was estimated at <5 nm, three orders of magnitude smaller than the Km measured in unbuffered solutions. Published Michaelis constants for plant uptake of Cd and Zn likely strongly overestimate physiological ones and should not be interpreted as an indicator of transporter affinity.

Internalization of metals by biota is traditionally described by Michaelis-Menten kinetics (Wilkinson and Buffle, 2004). The Km corresponds to the concentration in solution at which the uptake is one-half of the maximal uptake, Fmax. The Michaelis-Menten equation relates the uptake flux, F, to the free ion concentration at the site of uptake, [M]s:

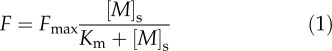graphic file with name PP_202200E01_LW.jpg

If diffusion of a metal across a diffusive boundary layer adjacent to the roots is the rate-limiting step for uptake, the concentration at the site of uptake will be lower than that in the bulk solution. As a result, diffusion limitations result in an overestimate of the Km, if the concentration at the root surface is assumed to be the same as in the bulk solution, as is usually done. This bias in Km has been discussed in detail by Winne (1973) and has, for instance, been demonstrated experimentally for uptake of Glc in rabbit jejunum (Thomson and Dietschy, 1980) and for uptake of several sugars, amino acids, and bile acids in rat ileum (Wilson and Dietschy, 1974).

Models used to predict ion availability and toxicity of metals by plants usually rely on the assumption that uptake is controlled by the free metal ion activity and the activity of competing ions in the bulk solution. For instance, the biotic ligand model (BLM), originally developed to predict metal toxicity to aquatic organisms, assumes that toxicity of an ion is mitigated by the presence of competing ions that bind on the biotic ligand (Paquin et al., 2002). Hough et al. (2005) used a free ion activity model taking into account proton competition effects to predict cadmium (Cd) uptake by soil-grown ryegrass (Lolium perenne). The uptake was reasonably well predicted; however, as the authors pointed out, it was not clear whether the derived constants truly represented physiological affinity constants or were just fitting parameters in a rate-limited uptake process. In case of strong diffusion limitation, ion competition effects on the internalization are expected to have negligible effect on the uptake, as the uptake is controlled by diffusion and not by internalization (Campbell et al., 2002; Degryse and Smolders, 2012).

In previous studies, we found strong evidence that uptake of Cd and zinc (Zn) is limited by the diffusive transport of the free metal ion to the root at low free ion concentration. At constant free ion concentration, the uptake of Cd and Zn increased in presence of metal complexes and the contribution of the complex increased with increasing dissociation rate of the complex (Degryse et al., 2006a, 2006c). In unbuffered solutions, i.e. solutions without metal complexes, stirring increased Cd uptake by plants (Degryse and Smolders, 2012). For nickel (Ni), however, contribution of complexes was small or undetectable, and stirring did not increase the uptake (Degryse and Smolders, 2012). Given this evidence that Cd and Zn uptake by plants is limited by diffusion, it is likely that published Km values for uptake of Cd2+ and Zn2+ by plants overestimate true physiological values. This bias in the Km when a diffusive boundary layer is present has been largely ignored in plant-physiological research. Indeed, in numerous studies the Km value has been interpreted as a characteristic of the carrier-mediated transport process, while in many cases it may reflect mass transfer properties. In addition, these diffusion limitations may mask ion competition effects in the uptake.

The aim of this article was (1) to present evidence that Km values determined for Cd2+ and Zn2+ uptake by plants in general reflect transport limitations rather than transporter affinity; (2) to derive true Km values by determining the Km under conditions where the uptake is not transport limited; (3) to identify the consequence of diffusion limitations on competition effects; and (4) to describe uptake of Cd, Zn, and Ni by plants in a single comprehensive model that combines competitive Michaelis-Menten kinetics with a diffusion equation.

Theoretical Framework

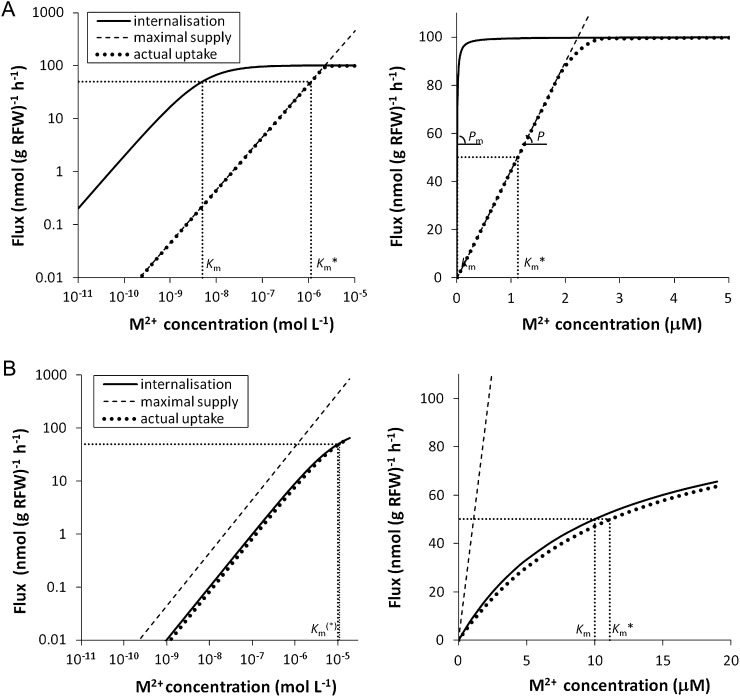
In the following, we qualitatively discuss the bias in the Km because of diffusion limitations, based on Figure 1. Equations are given in the “Materials and Methods” section. Figure 1A presents a case where the potential internalization flux by the plant at low concentrations is much larger than the maximal rate at which the free ion can be supplied through diffusive transport of the ion to the root surface. In this case, the actual uptake flux by the plant will approach the maximal diffusive flux, and the free ion concentration at the root surface is much smaller than that in the bulk solution. The apparent Km (Km*; determined as the concentration where the uptake flux is one-half of the maximal uptake) is much larger than the true Km value. In Figure 1B, the potential internalization flux at low concentration is of the same order of magnitude as the maximal diffusion flux. In this case, the concentration at the root surface is slightly smaller than that in the bulk solution, and there is only a slight bias in the Km value.

Figure 1.

Figure 1.

Open in a new tab

Conceptual diagram of the internalization flux (Michaelis-Menten curve; full line), maximal diffusive supply from solution to root (dashed line), and actual uptake flux (dotted line) as a function of free ion concentration for two theoretical cases. Left and right sections show the same curves, on log (left) or linear (right) scale. In A, the potential internalization flux is much larger than the maximal diffusive supply at low concentrations, i.e. the uptake is strongly limited by the transport of the free ion to the root. The plant acts as a near-zero sink, and the actual plant uptake equals the maximal diffusive flux. The Km* is much larger than the true Km, and the experimental permeability P (slope of the actual uptake curve) is much smaller than the membrane permeability Pm (slope of the internalization curve). In B, the maximal diffusive flux is larger than the potential internalization flux. The uptake is not limited by diffusive transport, and the Km* and true Km are almost equal.

Given the evidence that uptake of Cd and Zn by plants is diffusion limited, even in stirred nutrient solutions, we hypothesize that reported Km values of Cd2+ and Zn2+ are biased, and that the physiological Km values are much smaller. To test this hypothesis, we measured the uptake of Cd, Zn, and Ni in solution, in absence or in presence of labile hydrophilic metal complexes. If diffusion limitations prevail, the complexes dissociate within the diffusion layer and thus enhance the diffusion flux and therefore the metal uptake. By adding labile complexes in large amounts, it should be possible to abolish the diffusion barrier completely, in which case the physiological Km can be determined.

In addition, the effect of competitive ions on uptake was tested. The presence of competitive ions decreases the internalization flux. However, if uptake is rate limited by the diffusive transport to the uptake site and not by internalization, competition effects should theoretically not affect the uptake flux.

RESULTS

Short-term (4-h) uptake experiments were carried out with radiolabeled solutions. As most of our experiments were done with spinach (Spinacia oleracea), the full model description is applied on the data for spinach. Also for tomato (Lycopersicon esculentum), experiments were carried out using a high degree of metal buffering to determine the physiological Km. Smaller datasets were obtained for three other plant species (rapeseed [Brassica napus], wheat [Triticum aestivum], and the Zn-Cd-hyperaccumulator Thlaspi caerulescens), for which the effect of stirring and buffering by metal complexes on Cd uptake was investigated.

Effect of Stirring

Cd uptake at low concentration (1 nm) in a solution without metal buffering was significantly (P < 0.05) increased by stirring the solution during the 4-h uptake period (Table I). The effect of stirring was more pronounced for the hyperaccumulator (7-fold increase) than for the other species (1.2- to 3.4-fold increase).

Table I. Effect of stirring and buffering with complexes on uptake of Cd by four plant species, at a Cd2+ concentration of 1 nm.

The 4-h uptake (in nmol per g root fresh weight [RFW] per hour) was determined in solutions with 2 mm Ca(NO3)2, 2 mm MES (pH 6.0), 15 μm H3BO3 in absence or presence of complexes of different dissociation rate. The total ligand concentration, [Ltot], and the ratio of total Cd concentration to the free Cd2+ concentration (1 nm), [Cdtot]/[Cd2+], in the solution is specified in the table. se of n replicates between brackets. y, Solution stirred; n, solution unstirred during the uptake period.

Liganda [Ltot] [Cdtot]/[Cd2+] Stirred Spinach Rapeseed T. caerulescens Wheat
n Cd uptake n Cd uptake n Cd uptake n Cd uptake
mm nmol (g RFW)−1 h−1 nmol (g RFW)−1 h−1 nmol (g RFW)−1 h−1 nmol (g RFW)−1 h−1
– 1 n 6 0.070 (0.009) 12 0.051 (0.007) 2 0.170 (0.008) 2 0.078 (0.001)
– 1 y 13 0.239 (0.018) 17 0.114 (0.012) 3 1.17 (0.17) 2 0.093 (0.004)
NTA 0.10 100 n 3 4.55 (0.49) 3 2.08 (0.52) 2 6.24 (0.41)
NTA 0.30 310 n 3 11.2 (1.1) 3 5.91 (0.46) 2 14.5 (1.7)
NTA 1.0 1,260 n 3 26.2 (1.3) 3 12.1 (1.8) 2 28.2 (3.7)
NTA 3.0 5,700 n 2 39.3 (8.1) 3 32.5 (4.4) 2 72.6 (10.0)
NTA 4.9 10,000 n 2 2 7.22 (2.08)
HEDTA 0.029 10,000 n 3 8.25 (0.81) 2 16.5 (0.7) 2 24.8 (8.9) 2 2.37 (0.32)
CDTA 0.014 10,000 n 2 1.62 (0.23) 2 4.13 (0.03) 2 11.5 (1.5) 2 1.15 (0.45)
Open in a new tab
a

Dissociation rate constant, kd, of the Cd-ligand complex: >10−2, 10−2.8, and 10−5 s−1 for NTA, HEDTA, and CDTA, respectively.

As previously discussed, no effect of stirring on Cd uptake was observed at high Cd2+ concentration (1 μm; Degryse and Smolders, 2012) or at low Cd2+ concentration (1 nm) in presence of complexes (Degryse et al., 2006b). For Ni, no effect of stirring was observed even at low Ni2+ concentration (1 nm) in unbuffered solution (Degryse and Smolders, 2012).

Effect of Complexes

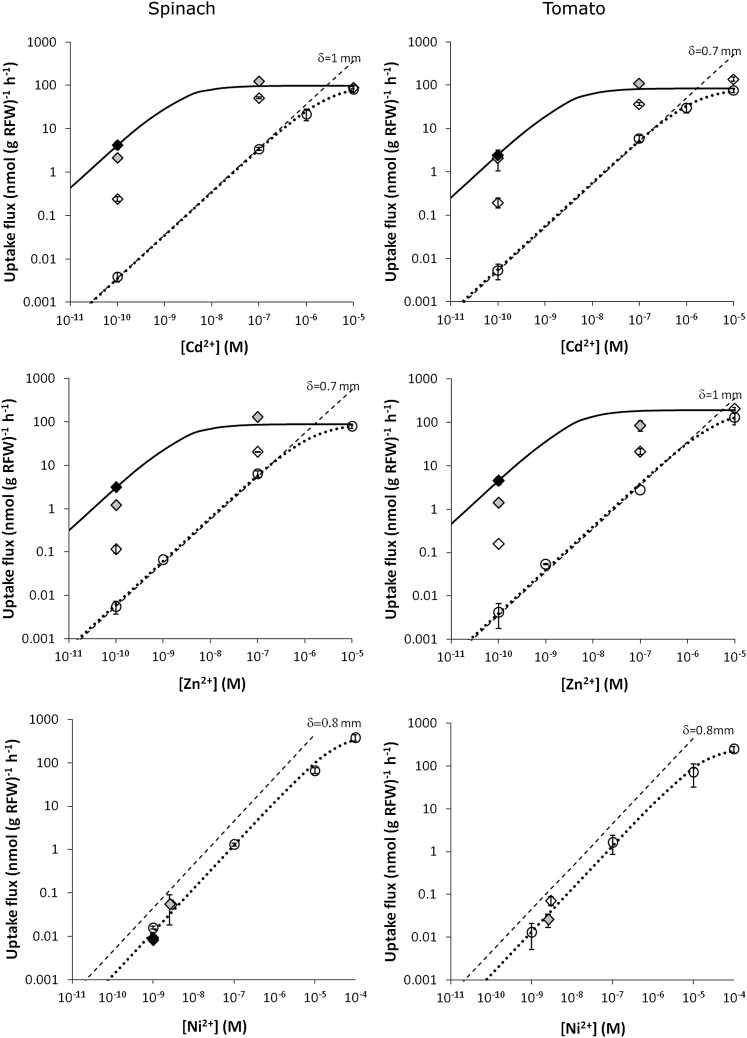
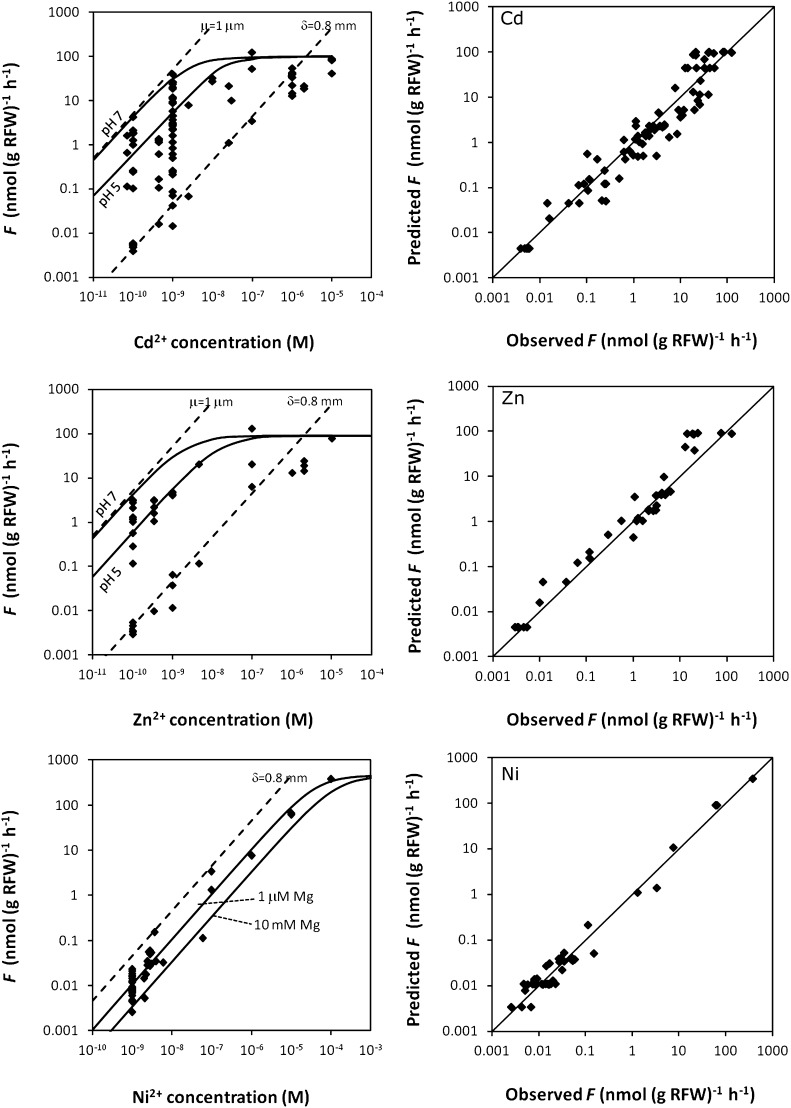
For spinach and tomato, the effect of complexes on the uptake was assessed at different free metal ion concentrations. At a free ion concentration of 1 nm, the uptake of Cd and Zn strongly increased in the presence of complexes with nitrilotriacetate (NTA; Fig. 2). There was relatively less contribution of the complexes to the uptake at a free ion concentration of 0.1 μm and only a very small contribution at a free ion concentration of 10 μm. These findings are in agreement with our hypothesis that the complexes mainly contribute to the uptake through their effect on the diffusive flux, which limits the uptake at low free ion concentrations (Fig. 1A). If uptake is strongly limited by diffusion, the plant roots act as a near-zero sink and the uptake equals the maximal diffusion flux. An effective diffusion layer thickness of 0.7 to 1 mm was estimated based on the uptake in the solutions without complexes. In contrast to Cd and Zn, the presence of complexes had no or little effect on the Ni uptake (Fig. 2), suggesting that the diffusive transport was not limiting the uptake. This was corroborated by the circa 3-fold lower uptake flux for Ni than for Cd and Zn at free ion concentrations below 1 μm.

Figure 2.

Figure 2.

Open in a new tab

Short-term (4-h) uptake flux of Cd, Zn, and Ni by spinach (left) or tomato (right) as a function of the free ion concentration in solution for solutions without complexes (circles) or in solutions with complexes (diamonds). The complex to free ion concentration ratio was 100 (white symbols), 104 (gray), or 105 (black) for Cd and Zn, or approximately 30 (white), 40 (gray), or 100 (black) for Ni. The dashed line show the maximal diffusion flux for a diffusive layer thickness δ as indicated in the figures (fitted to correspond to the uptake in unbuffered solutions at low concentrations). The dotted line gives Michaelis-Menten curve fitted to the uptake in unbuffered solutions. The full line gives the Michaelis-Menten curve for Cd and Zn fitted to the uptake in the most strongly buffered solution where uptake was likely internalization limited. Error bars indicate ses of two replicates. The parameters of the fitted Michaelis-Menten curves are listed in Table II.

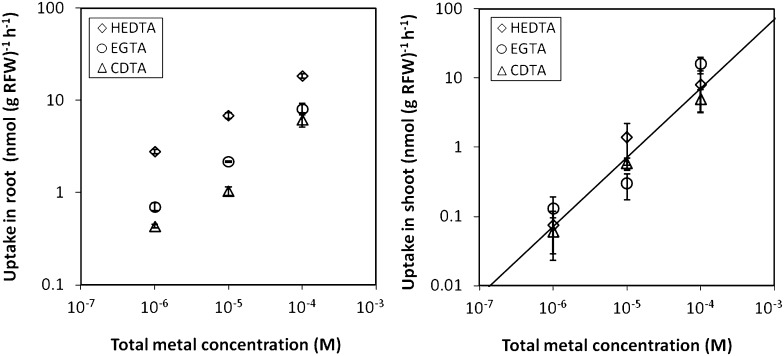
Table I shows results for the effect of complexes on Cd uptake at 1 nm Cd2+ for different plant species. As discussed before for spinach (Degryse et al., 2006a), the uptake ranged over more than two orders of magnitude despite the identical free ion concentration. The uptake increased with increasing concentration of complex or, at a same concentration of complexes, with increasing dissociation rate of the complex [NTA > N-(2-hydroxyethyl)-ethylenediamine-N,N\x{2019},N\x{2019}-triacetate (HEDTA) > trans-1,2-cyclohexyldiamine-N,N,N\x{2019},N\x{2019}-tetraacetate (CDTA)].

The percentage of Cd recovered in the shoots was generally less than 10%. However, at high degrees of buffering by metal complexes, larger recoveries in the shoot were observed. In a few cases, even more than 50% of Cd taken up was recovered in the shoots. In contrast with the total uptake flux or the uptake in the root, the uptake in the shoot showed no relation to the dissociation rate of the complex (Fig. 3), suggesting that there is also a passive, indiscriminate uptake mechanism.

Figure 3.

Figure 3.

Open in a new tab

The Cd uptake in root (left) and shoot (right) of spinach for a 4-h uptake period, expressed as root fresh weight (RFW)-based uptake flux, as function of the total metal concentration in solution, for solutions with 1 nm Cd2+ and 1, 10, or 100 μm Cd complex [basic solution composition: 2 mm Ca(NO3)2 and 2 mm MES at pH 6.0]. The uptake in the root follows the same order as the dissociation rate of the complex. The uptake in the shoot does not show any consistent differences between the complexes and increases proportionally to the total concentration, suggesting passive uptake. The line shows the relationship for a passive permeability coefficient of 10−7 cm s−1. Error bars give ses of the mean for three replicates.

Effect of Competitive Ions

No competitive effects of protons or Ca2+ (for calcium) on the uptake of Cd and Zn were observed in unbuffered solutions. However, a proton competition effect on the uptake was observed in solutions where the concentration of Cd-NTA complexes was 104 times larger than the free Cd2+ concentration, as discussed recently (Degryse and Smolders, 2012). This suggests that this strong buffering increased the diffusion flux to the point where the internalization flux was limiting the uptake. For Zn, a proton competition effect only became apparent at an even larger degree of buffering (Zn-NTA to Zn2+ concentration ratio of 105; Supplemental Fig. S1).

The presence of complexes did not increase Ni uptake at pH 5 or 6, but slightly increased the uptake at pH 7, suggesting that the smaller proton activity at pH 7 increased the internalization flux to the extent that the diffusive transport became partly rate limiting (Degryse and Smolders, 2012).

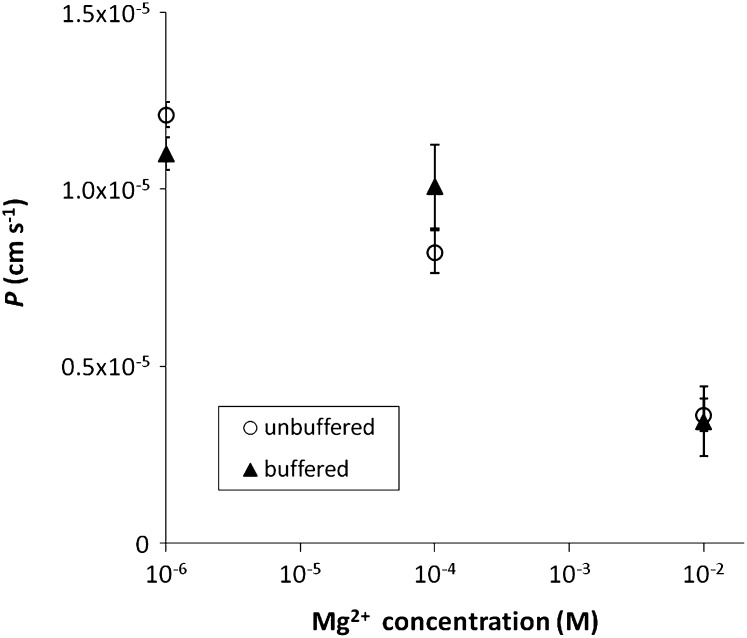
At all pH values, a very clear competition effect of Mg2+ (for magnesium) on Ni uptake was observed (Fig. 4). Increasing the Mg2+ concentration from micromolar range to 10 mm decreased the uptake 3- to 5-fold. Varying Ca2+ concentrations over this range did not have any significant effect on the Ni uptake.

Figure 4.

Figure 4.

Open in a new tab

Observed permeability (ratio of surface based uptake flux to free Ni2+ concentration) for Ni uptake by spinach as function of Mg concentration, in solution without or with complex (Ni-IDA). The Ni2+ free ion concentration was circa 1 nm and the complex to free ion concentration in the buffered solution was circa 30. Error bars indicate ses of two replicates.

Michaelis Constants for Uptake of Cd, Zn, and Ni

The Michaelis-Menten equation (Eq. 1) was fitted to the uptake curves measured in unstirred solutions at pH 6 without complexes and to those measured at the largest degree of buffering (at a complex to free ion concentration ratio of 105 for Cd and Zn). In these latter solutions, the uptake of Cd and Zn is supposedly internalization limited (i.e. controlled by the transporters), given the proton competition effect appearing at this degree of buffering (Supplemental Fig. S1). In the unbuffered solutions, the Km* was between 1.5 and 6 μm for uptake of Cd2+ and Zn2+ by both spinach and tomato. In contrast, Km values in the metal-buffered solutions were in the nanomolar order, about three orders of magnitude smaller than corresponding Km* values determined in unbuffered solutions (Table II).

Table II. Kinetic parameters for uptake of Cd, Zn, and Ni by spinach and tomato in unbuffered solutions or in solutions buffered with metal complexes.

The Km was determined based on uptake in unstirred, unbuffered solutions (Km*) or in solutions that were buffered with complexes and in which uptake was likely internalization limited (Km). The permeability P corresponds to the slope of the uptake curve at low concentrations and is calculated as the ratio of Fmax to Km, with Fmax expressed on a surface area basis (based on a specific root area of 200 cm2 per g root fresh weight [RFW]). Data for solutions with 2 mm Ca(NO3)2 at pH 6.0.

Plant Species/Element Fmax Unbuffered
 Buffereda
Km* P Km Pmb
nmol (g RFW)−1 h−1 μm cm s−1 μm cm s−1
Spinach
 Cd 99.4 (0.2)c 2.83 (0.01) 4.9 × 10−5 0.0021d 6.6 × 10−2
 Zn 89.6 (0.1) 1.43 (0.02) 8.7 × 10−5 0.0029d 4.5 × 10−2
 Ni 460 (1) 36.8 (0.1) 1.7 × 10−5 22–57 1.1–3.0 × 10−5
Tomato
 Cd 83.4 (0.1) 1.49 (0.01) 7.8 × 10−5 0.0033d 3.5 × 10−2
 Zn 190 (3) 4.72 (0.26) 5.6 × 10−5 0.0040d 6.5 × 10−2
 Ni 270 (1) 19.8 (0.1) 1.9 × 10−5 11–36 1.1–3.3 × 10−5
Open in a new tab
a

For Cd and Zn: buffered at a ratio of metal-NTA complex to free ion concentration of 105; for Ni: range of Km derived for solutions buffered at complex to Ni2+ concentration ranging between 30 and 100.  bAssumed to correspond to the membrane permeability Pm since uptake was likely internalization limited.  csds (between brackets) were calculated from the correlation matrix, using the SolverAid macro from de Levie (1999).  dsd estimated at less than 0.1 nm, but this does not take into account the uncertainty in the complexation constants used to calculate the solution speciation of the buffered solutions.

For Ni, no systematic difference in Km was found between buffered and unbuffered solutions (Table II). The estimated Km ranged from 11 to 57 μm.

Model Predictions

We modeled the uptake of Cd, Zn, and Ni by spinach using a diffusion equation combined with a Michaelis-Menten equation (Fig. 1). The data on which the model was fitted cover a wide range of free metal ion activities and solution competition (Supplemental Table S1). A competitive Michaelis-Menten equation was used to account for the Mg2+ and proton competition effects observed for Ni2+ uptake and for the proton competition effects observed for Cd and Zn uptake at a high degree of buffering.

The effective diffusive layer thickness δ was assumed to be 0.8 mm in unstirred solutions and 0.3 mm for stirred solutions, as our previous experiments on Cd uptake suggested approximately these values (Degryse et al., 2006b; Degryse and Smolders, 2012), and these values are also in reasonable agreement with estimated provided in literature for unstirred layer thicknesses near membranes (Barry and Diamond, 1984).

The metal-binding constants of the competitive Michaelis-Menten equation were fitted by minimizing the residual sum of squares of the log-transformed uptake data (Table III). The least-square solution for the Ni parameters was logKNi 4.5 and logKMg 2.5. Even though we found some indication of a proton competition effect (Degryse and Smolders, 2012), the proton-binding parameter was nonsignificant. For Zn, binding parameters of logKZn 8.7 and logKH 5.8 were derived. For Cd, the proton- and metal-binding parameter were very strongly covaried and, as a result, no reliable estimates could be derived by fitting both parameters together. This strong covariation between binding parameters has been discussed in more detail by Mertens et al. (2007). Since the binding constant KM corresponds to the reciprocal of the Km in a competition-less, internalization-limited scenario, we calculated the KCd as the reciprocal of the Km derived at pH 7 (little proton competition) and at the highest degree of metal buffering (in which case uptake is supposedly internalization limited). The estimated binding parameters were nearly identical to those for Zn (Table III). Predicted values for Cd uptake are almost unaffected and the model R2 remains at 0.90 if logKCd and logKH are increased by the same value because of the strong covariation, but decreasing the logK values results in a decrease in the model R2 because of underprediction of the uptake in the most strongly buffered solutions.

Table III. Estimated binding constants of metal and competitive ions for metal uptake by spinach.

Binding constants were derived by fitting the model, which combines a diffusion equation with a competitive Michaelis-Menten equation (Eq. 7), to the observed data. sd of parameter estimates (in parentheses) was calculated from the correlation matrix, using the SolverAid macro from de Levie (1999). The model R2 (calculated as 1 − SSE/SSTO, with SSE the error sum of squares and SSTO the total sum of squares of log-transformed uptake fluxes) was 0.90 for Cd, 0.94 for Zn, and 0.97 for Ni. n = Number of data points.

Binding Constant Cd Zn Ni
n = 78 n = 39 n = 43
logKM 8.7a 8.7 (0.1) 4.5 (<0.1)
logKH 5.8 (< 0.1) 5.8 (0.3)
logKMg 2.5 (0.6)
Open in a new tab
a

The covariation between logKCd and logKH was too large to fit them together. The binding constant for Cd was calculated as the reciprocal of the Km at pH 7 and high degree of buffering (complex [Cd-NTA] to free ion concentration ratio of 105).

The uptake predicted by the model was in good agreement with measured uptake (Fig. 5). For Cd and Zn, uptake was predicted to be diffusion limited in most cases. Only at large degree of buffering by labile complexes, the diffusion flux is increased to the point where the internalization flux is limiting the uptake (Fig. 5). For Ni, the uptake was predicted to be mostly internalization limited, though a slight diffusion limitation was still predicted at low Mg concentrations. For instance, the actual uptake flux at pH 6 at low Mg (<10−4 m) was predicted to be 27% less than the internalization flux. At high Mg concentrations, the uptake was predicted to be fully internalization limited.

Figure 5.

Figure 5.

Open in a new tab

Predicted versus observed uptake of Cd, Zn, and Ni by spinach (right sections, the line is the 1:1 line), using a model that combines the diffusion equation with a competitive Michaelis-Menten equation (Fig. 1). The model was fitted on a dataset that covered a range of pH (5–7), free ion concentration, degree of buffering, and Ca and Mg concentration (full details in Supplemental Table S1). The left sections show all experimental uptake fluxes as function of the free ion concentration. For comparison, the left figures also show the diffusion flux in an unstirred, unbuffered solution (assuming an effective diffusive layer thickness δ of 0.8 mm) or, for Cd and Zn, in the most strongly buffered medium (reaction layer thickness μ of 1 μm) and the modeled internalization fluxes (solid lines) at low or high concentration of competitive ions (H+ for Cd and Zn uptake, Mg2+ for Ni uptake).

To summarize these effects of buffering and competition effects, we plotted theoretical curves and experimental points as proposed by Smulders and Wright (1971; Fig. 6). The experimentally observed permeability P (uptake flux normalized against free ion concentration) at low concentrations, corresponding to the slope of the uptake curve, was plotted against the estimated membrane permeability Pm (ratio of Fmax to estimated true Km, i.e. the slope of the internalization curve; Fig. 1). If the membrane permeability is smaller than the diffusional permeability, internalization is limiting the uptake and the observed permeability equals the membrane permeability. If the membrane permeability is larger than the diffusional permeability, diffusion limits the uptake and the observed permeability equals the diffusional permeability. In unstirred, unbuffered solutions, the diffusional permeability is approximately 6 × 10−5 cm s−1, corresponding to D/δ, and uptake is, therefore, diffusion limited if the membrane permeability exceeds 6 × 10−5 cm s−1, as is the case for Cd and Zn (Table II). In strongly buffered solution, the diffusional permeability is much larger because the complexes enhance the diffusion flux, and diffusion limitations only occur at much larger values of the membrane permeability. Competition effects on the internalization flux (i.e. on the membrane permeability) only become apparent if the uptake is not limited by the diffusive transport. This explains why the Mg2+ competition effect on Ni2+ uptake (for which the estimated Pm is around 2 × 10−5 cm s−1 or less in presence of competitors) is apparent in unbuffered solutions, while the proton competition effect on Cd2+ and Zn2+ uptake (for which the estimated Pm is around 5 × 10−2 cm s−1) is apparent only in very strongly buffered solutions.

Figure 6.

Figure 6.

Open in a new tab

Theoretical curves relating the apparent measured permeability P to the membrane permeability Pm (adapted from Smulders and Wright, 1971). The curves are shown for an unstirred, unbuffered solution (diffusive layer thickness δ of 0.8 mm) or for a very strongly buffered solution (reaction layer thickness μ of 1 μm). The symbols show measured permeability for spinach against estimated membrane permeability (using the best-fit model parameters; Table III) for Ni uptake at low or high Mg concentration and for Cd and Zn uptake at different pH values in unbuffered (black symbols) or strongly buffered solutions (white symbols).

The model was also fitted when taking into account a passive uptake component (Eq. 10). The fitted value for the passive permeability (passive uptake flux divided by total metal concentration) was 9.0 × 10−8 cm s−1 for Zn and 1.7 × 10−7 cm s−1 for Cd (see Supplemental Text S2 and Supplemental Table S4), i.e. of similar magnitude as the value estimated based on Cd measured in the shoot in solutions strongly buffered with complexes (Fig. 3). The improvement in the predictions was very small, however, as most variation was explained by only taking into account the active uptake. Only in treatments with very high degree of buffering, this passive uptake was estimated to have a large contribution to the overall uptake.

DISCUSSION

Effect of Complexes to Cd and Zn Uptake: Diffusion Alleviation or Direct Uptake

Several authors have reported the contribution of complexes to Cd or Zn uptake by plants, e.g. for barley (Hordeum vulgare; Bell et al., 1991), Lactuca sativa (McLaughlin et al., 1997), wheat (Wang et al., 2009), and Triticum turgidum (Panfili et al., 2009). Usually, two hypotheses are given that may explain this contribution of complexes to the uptake: (1) the uptake is rate limited by diffusion of the free ion to the site of uptake and the presence of complexes increases the diffusive supply, or (2) the complexes are directly taken up. Some studies have indeed shown direct uptake of the complex, but at large (mm) concentration of complexes, mostly in phytoremediation studies. For instance, Niu et al. (2012) found that copper (Cu) in plants grown on soil treated with [S, S]-ethylenediamine disuccinic acid (EDDS; lowest concentration 0.5 mmol/kg) was mainly as Cu-EDDS. At all concentrations, plant yield was significantly reduced, suggesting damage to the plants. Collins et al. (2002) tested the effect of EDTA addition to soil on Zn uptake and measured Zn-EDTA in the xylem. No Zn-EDTA in the xylem sap was detected at a rate of 0.034 mmol/kg or 0.34 mmol/kg (except for one species). At 3.4 mmol/kg, Zn-EDTA concentrations in the xylem were small compared with those in the soil solution, except for barley, the species that showed evidence of physiological stress at this rate (decreased transpiration rate). Also results of Schaider et al. (2006) suggested that physiological stress increased the unrestricted uptake of metal-chelate complexes.

At low concentrations of complexes, there is to our knowledge no evidence in literature of a large contribution of direct uptake to the overall uptake. Panfili et al. (2009) determined uptake of citrate (at 0.26 mm) and Cd by wheat in nutrient solutions using double labeling (14C and 109Cd). Uptake of citrate was observed, but was small and could not explain the observed increase in Cd uptake in solutions with citrate compared to a control solution at the same Cd2+ activity. As pointed out by the authors, contribution of the complexes through dissociation with the diffusive boundary layer was the most likely explanation for the observed increase in uptake in presence of Cd-citrate, as the calculated limiting diffusion flux was similar to the observed uptake flux in the unbuffered solution. Also in our previous work, we argued that the contribution of complexes to the uptake was likely due to alleviation in diffusion limitations, and this for several reasons: (1) the contribution of the complexes to the uptake follows the same order as the dissociation rate of the complex, (2) at constant free ion concentration and increasing concentration of complex, the uptake increases not proportional to the total concentration, but in general follows a square-root relationship (10-fold increase in concentration results in approximately 3-fold increase in uptake) that is in agreement with diffusion-limited uptake (Eq. 9), (3) the uptake flux in unbuffered solution is of similar magnitude as the calculated limiting diffusion flux, (4) stirring the solution increases the uptake, and (5) complexes contribute much less at high free ion activity when the uptake saturates.

We found indications, however, that complexes can also be directly taken up, as evident from the strong relationship between total metal concentration in solution and Cd measured in the shoot at the end of the 4-h uptake period in strongly buffered solutions. The fraction of Cd recovered in the shoot was only large (>20%) for large degrees of buffering. Both the relationship between uptake flux into the shoot and total metal solution concentration (Fig. 3) and the inclusion of a passive uptake component in our model (Eq. 10) suggest a passive permeability coefficient of circa 10−7 cm s−1 for spinach. Also for the other plant species, the relationship between uptake flux into the shoot and total metal solution concentration suggested values in this order. This value is of the same order as water uptake rates (Tinker and Nye, 2000). Our modeling and experimental results suggest that this passive uptake only prevails at high degree of buffering with slowly dissociating complexes or at millimolar concentrations of complexes (see Supplemental Text S2 and Supplemental Table S5). These conditions are not likely to occur in soils, except in chelate-amended soils as is the case with chelate-assisted phytoremediation.

Our results suggest that also in soils, Cd and Zn uptake by plants is likely to be limited by diffusion at low (submicromolar) Cd2+ and Zn2+ concentrations, in which case labile complexes in soil solution are expected to contribute to the uptake. A large degree of buffering (total to free ion concentration ratio of at least 104) with fast dissociating complexes is necessary to increase the diffusion flux till the point where the uptake is most likely internalization limited at low metal concentrations (Fig. 2). Such a large degree of solution buffering is unlikely under environmentally relevant conditions. For instance, Nolan et al. (2003) found that the fractions of dissolved Cd and Zn present as free ion were >10% in solutions of soils covering a wide range of properties.

Internalization-Limited Ni Uptake?

The lower uptake of Ni2+ than of Cd2+ or Zn2+, the negligible contribution of Ni complexes to the Ni2+ uptake (Fig. 2), the Mg2+ competition effect in unbuffered solutions (Fig. 4), and the lack of effect on stirring on Ni uptake (Degryse and Smolders, 2012) all suggest that Ni uptake was mostly limited by internalization. Morel et al. (1991) already hypothesized that Ni uptake is less likely to be limited by diffusive transport than uptake of Cd or Zn because of its slower water-loss rate. The rate-limiting step in binding to the biotic uptake site is likely to be the loss of a water molecule from the inner hydration sphere of the metal ion, and the internalization flux is therefore expected to be smaller for Ni than for Cd and Zn. The water exchange constants of Cd and Zn are around 5 × 108 s−1, while that of Ni is only 2.7 × 104 s−1, i.e. four orders of magnitude smaller (Kobayashi et al., 1998; Inada et al., 2005). This corresponds to the difference in our fitted binding constants (Table III).

Competition Effects

A clear Mg competition effect on Ni uptake was observed. Similar observations have been made for Ni uptake by green algae (Worms and Wilkinson, 2007). Lock et al. (2007) developed a BLM for Ni toxicity to barley root elongation, and also found that Mg2+ was the main competitive ion, while Ca2+, K+ (for potassium), and H+ (for hydrogen) had negligible effects on the toxicity of Ni2+. Similar observations were made by Li et al. (2009) who further refined the BLM.

For Cd and Zn, we found no effect of Ca concentration or pH on the uptake, except at a very high degree of buffering, where a proton competition effect became apparent (Supplemental Fig. S1). An apparent competition effect has also been observed for uptake of Cd (Vigneault and Campbell, 2005) and Zn (Harrison et al., 1986) by freshwater algae. This effect of pH is likely not a true competition effect, but may be caused by conformational changes in the surface transport proteins, as suggested by François et al. (2007).

The strong diffusion limitation in uptake of Cd and Zn explains why competition effects on the internalization only become apparent in very strongly buffered solutions. Few studies have reported competition effects on Cd or Zn uptake in short-term experiments at low (submicromolar) solution concentrations. However, Hart et al. (2002) observed a decrease in Cd uptake, even at low concentrations (below those where the uptake saturates) when adding 10 μm Zn to the uptake solution. We speculate that this competition effect may be related to less transporters being available for Cd at this relatively high Zn concentration. As explained above, a lower transporter density can decrease the uptake even under transport-limited conditions.

Effect of Transporter Density and Other Biotic Factors on Diffusion-Limited Uptake

Pence et al. (2000) reported an increase in ZNT1 expression in T. caerulescens plants in response to low Zn status and larger ZNT1 expression in the hyperaccumulator T. caerulescens than in a related nonhyperaccumulator. In this study, we observed a larger Cd uptake for T. caerulescens ‘Ganges’ than for nonhyperaccumulating plant species (Table I), in agreement with the high Cd uptake observed by Lombi et al. (2001) for this ecotype. Several authors have suggested that large uptake of Zn and Cd by hyperaccumulators is related to the presence of high-affinity, highly expressed transporters (e.g. Lombi et al., 2001). However, according to the theoretical framework presented here, no effect of increasing the transporter affinity (i.e. a lower true Km) on the uptake is expected under diffusion-limited conditions (Fig. 1A). An increase in transporter density (number of transporters per unit root surface area), on the other hand, can theoretically increase the uptake flux even under diffusion-limited conditions. Only at high transporter density, the diffusion flux to the surface equals that to a fully covered surface. In that case, further increasing the transporter density will theoretically not affect the uptake under diffusion-limited conditions. At low transporter density, however, the diffusion zones of the individual transporters do not overlap, and the total diffusive flux to the surface is proportional to the number of transporters (Supplemental Fig. S2). In the intermediate case, increasing transporter density increases the diffusion flux to the surface, but less than proportionally (Wilkinson and Buffle, 2004). The larger effect of stirring on the Cd uptake by T. caerulescens than by the other species (Table I) is in agreement with this theoretical framework (see Supplemental Text S1 and Supplemental Fig. S3 for a quantitative analysis).

In our model description, we considered the root surface to be fully active in the uptake. Based on the uptake in unbuffered solutions at low Cd2+ and Zn2+ concentrations, we estimated the effective diffusive layer thickness at approximately 800 μm for an unstirred solution and approximately 300 μm for a stirred solution. However, at low transporter density, the diffusive layer thickness to reach the observed uptake flux would need to be smaller. Thus, our estimate for the diffusive layer thickness takes into account both the physical boundary layer and the effect of fractional surface coverage. The physical diffusive layer thickness is likely to be smaller (Supplemental Text S1).

Not only transporter density, but also other biotic factors affect the uptake even when uptake is transport limited. An increase in the active root surface, e.g. by an increase in the root:shoot ratio or by development of thinner roots or long root hairs, will increase the diffusive flux, and has indeed been reported as a response of plants to low availability of phosphorus (Ma et al., 2001) or Zn (Dong et al., 1995). Root exudates that increase the solution concentrations in the rhizosphere will also increase the diffusion flux to the root surface. For instance, Hoffland et al. (2006) found an increase in root exudation of organic acids at low Zn and phosphorus availability in soils.

Biased Michaelis Constants for Cd and Zn Uptake

Based on the uptake in strongly buffered solutions, we estimate that true Km values for Cd and Zn are in the nanomolar order, i.e. three orders of magnitude smaller than the values determined in unbuffered solutions. Similarly, Hacisalihoglu et al. (2001) reported a much lower Km value for Zn uptake in buffered than in unbuffered solutions. These authors interpreted this as evidence of a second, high-affinity Zn transport system that operates at low Zn2+ concentrations. However, at a same Zn2+ concentration, uptake is larger in buffered than in unbuffered solutions (Fig. 2). Therefore, the difference in uptake between both types of solutions cannot be explained by different transport systems being active in different concentration ranges. It seems a far more plausible explanation that the uptake in the unbuffered solutions was limited by diffusion, and the experimentally determined Km value was therefore biased by this diffusion limitation.

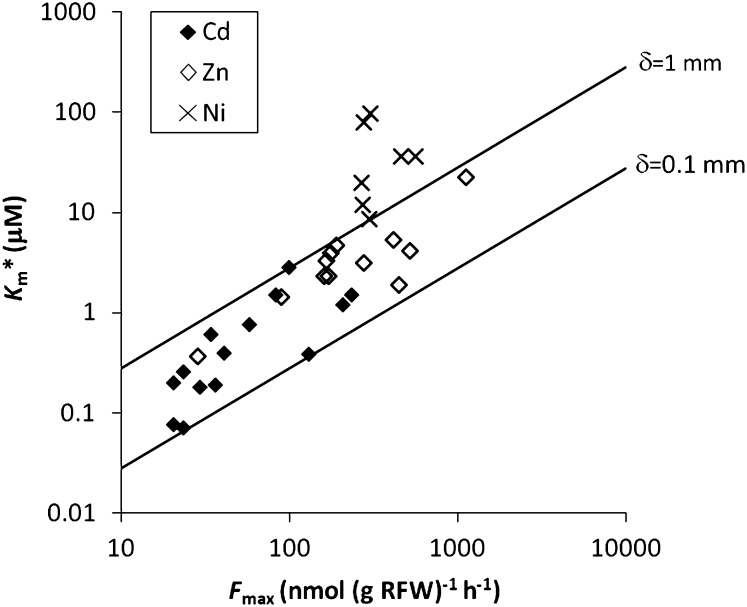
To further corroborate our findings about this bias in Km values of Cd and Zn, published Michaelis constants for plant uptake of Cd, Zn, and Ni were collated. Only short-term uptake data for nonhyperaccumulating plants in unbuffered solutions were considered (see Supplemental Table S2). The maximal uptake flux, which is mostly reported on a fresh root weight basis, was converted to a surface area basis assuming a specific root surface of 200 cm2 per g root fresh weight. As the ratio Fmax/Km* (i.e. the slope of the uptake curve at low concentrations) corresponds to the ratio D/δ under strong diffusion limitations, a positive correlation between Fmax and Km* is to be expected (provided the variation in δ is small compared to the variation in Fmax) if Cd and Zn uptake is indeed diffusion limited in the low concentration range, as we postulate here. Indeed, such a positive correlation was observed for both Cd and Zn, and nearly all data fell within the range for δ values between 100 and 1,000 μm (Fig. 7). Differences in δ values between studies and plant species might be related to different agitation of the solution during the plant uptake or to differences in active root surface area or in surface density of the transporters. For Ni, there was no positive correlation between Fmax and Km and the data generally fell in the range for δ values above 1,000 μm, supporting our hypothesis that plant uptake parameters for Ni determined in hydroponics are not, or only marginally, affected by diffusion limitations.

Figure 7.

Figure 7.

Open in a new tab

Literature reported Michaelis constants determined in unbuffered solutions (Km*) versus the maximal uptake flux for uptake of Cd, Zn, or Ni by different plant species. The lines show the expected relation between Fmax and Km* if uptake is diffusion limited for an effective diffusive layer thickness of 1 or 0.1 mm (details in Supplemental Table S2).

The possible bias in Km values because of transport limitations has been long recognized (Winne, 1973), but has been largely overlooked in plant physiological research. The experimentally determined Km for uptake of solutes by plants is usually assumed to represent the affinity of the uptake system. Our results strongly suggest that, at least for Cd and Zn, the experimentally determined Km is an indication of the diffusion barrier rather than a transporter characteristic. The theoretical framework we present is based on multiple lines of indirect evidence and all our experimental uptake data fit well within this framework. We speculate that also for other ions than Cd and Zn, diffusion limitations in uptake may prevail, even in solutions. For instance, contribution of complexes to the plant uptake has also been shown for Cu uptake by plants (Bell et al., 1991; Degryse et al., 2006c). It is therefore likely that Km values determined for Cu uptake in solutions may often also be biased by transport limitations, as was discussed by Bravin et al. (2010). Recently, we also provided evidence, in collaboration with colleagues from Austria, that phosphorus uptake by plants in solutions is also diffusion limited, resulting in overestimates of the Km value (Santner et al., 2012).

MATERIALS AND METHODS

The data used in this study include the Cd uptake data reported by Degryse et al. (2006a) and Cd and Ni uptake data reported by Degryse and Smolders (2012), but most of the data has not been reported before. These data were gathered over several years, but were determined using the same experimental methods. We studied five plant species, but most data were gathered for spinach (Spinacia oleracea), and the modeling is therefore based on the data for spinach. A full overview of the uptake solutions and measured uptake for spinach can be found in Supplemental Table S1.

Plant Cultivation

Seeds of spinach, tomato (Lycopersicon esculentum), rapeseed (Brassica napus), wheat (Triticum aestivum), and Thlaspi caerulescens ‘Ganges’ (obtained from Dr. Fang-Jie Zhao) were germinated for 5 d at 25°C between sheets of germination paper continuously wetted with metal-free nutrient solution. Seedlings were transferred to a Cd-free nutrient solution [composition in mm: 2 Ca(NO3)2, 0.5 MgSO4, 1.2 KNO3, 0.1 KH2PO4; in μm: 25 NaCl, 5 MnSO4, 15 H3BO3, 0.5 CuSO4, 0.07 (NH4)6Mo7O24, 1 ZnSO4, 10 FeNaEDTA]. The solutions were buffered with 2 mm MES at pH 6. Plants were grown in a growth chamber with 14/10-h day/night cycle, day/night temperature of 22°C/16°C, and photosynthetic photon flux density of 400 μmol m2 s−1. Plants were taken from the nutrient solutions between 14 and 20 d after transplanting, for use in the uptake experiments.

Uptake Solutions

The uptake solutions had a basal composition of 2 mm Ca(NO3)2, 15 μm H3BO3, and 2 mm pH buffer (MES for pH 5 and 6; HEPES for pH 7). The solutions were radiolabeled with 109Cd (approximately 10 kBq L−1), 65Zn (approximately 100 kBq L−1), or with 63Ni (approximately 200 kBq L−1), and were left to equilibrate overnight before the uptake experiment was carried out.

The solutions covered a range in pH (5–7), free ion concentration (10−10–10−5 m for Cd and Zn, 10−9–10−4 m for Ni), degree of complexation (up to a complex to free ion concentration ratio of 105 for Cd and Zn and up to a ratio of 100 for Ni), and Ca and Mg concentration. For Cd, complexes with varying dissociation rate constant were used (Degryse et al., 2006a). The free ion concentration in solutions with metal complexes was calculated with GEOCHEM-PC (Parker et al., 1995).

In one of the experiments, Chelex was used to buffer the Cd and Zn activities in solution at a constant value (Checkai et al., 1987). The chelex resin was first loaded with Ca, Cd, and Zn (at three different metal levels). Solutions with 2 mm Ca(NO3)2 and ligands (NTA or HEDTA) in different concentrations were equilibrated with the resin for 2 d. The solution was separated from the Chelex by filtration and total Cd and Zn concentrations were determined. Using this buffering method has the advantage that the assumption of same free metal concentration (for solutions buffered with the same Chelex resin) does not rely on speciation calculations. The results of this experiment were in good agreement with those of the other experiments.

For Ni, a lower degree of complexation was used than for Cd and Zn. A very large degree of buffering was not practical for two reasons. The radioactivity in the plant strongly decreased as the degree of buffering increased at given radioactivity in solution, because the complexes had negligible contribution to the uptake. To still have measurable 63Ni activities in the plant, we would have needed to use much larger radioactivity in solution at higher degrees of buffering. Even more importantly, as the contribution of the complexes was so small, it was essential to exactly know the free ion concentration in the solution for the interpretation of the results. The free ion activity was therefore experimentally determined with Donnan dialysis in the buffered solutions (Degryse and Smolders, 2012), and these experimental values were used in the data analysis. At very high degrees of buffering, it is much harder to obtain reliable measurements of free ion concentrations. As our experimental results at lower degrees of buffering already pointed to Ni uptake being (mostly) limited by internalization, we avoided the use of larger degrees of buffering.

Uptake Experiments

The uptake experiments were carried out as described by Degryse and Smolders (2012). Two or three plants were transferred to 1 L of the radiolabeled uptake solution. At the end of the 4-h uptake period, the plants were transferred to a solution with 10 mm Ca(NO3)2 to remove cell wall bound metal. This desorption step was carried out as these experiments were carried out to obtain more insight in the uptake process, and therefore only absorbed metal should be considered. Preliminary experiments showed that the amount of adsorbed Cd was small (<5%) compared to absorbed Cd for our 4-h uptake period. Shoots and roots were separated and weighed. The γ-activity of 109Cd or 65Zn was determined by counting shoots and roots separately in a γ counter (Minaxi 5530 auto-γ). The β-activity of 63Ni in shoots and roots was determined with a liquid scintillation counter (Packard Tri-Carb 1600CA) after acid extraction (10 mL of 5% HCl, 5 d equilibration). Preliminary experiments showed that this method was effective at extracting nearly all radioactivity from the seedlings. The amount of metal taken up by the plants was calculated from the radioactivity in the plant and the specific activity (radioactivity relative to stable concentration) of the solution. The root weight based uptake flux was calculated by dividing the amount of metal taken up by the root fresh weight and the uptake period (4 h). The surface area based uptake flux was calculated from the ratio of the root weight based uptake flux assuming a specific root surface of 200 cm2 (g root fresh weight)−1.

The solutions were not stirred during the uptake, except for the treatments where the effect of stirring was assessed (see Supplemental Table S1).

Model

The theoretical treatment of the effect of a diffusive boundary layer on active transport has been presented by Winne (1973), and is shortly summarized here. The diffusional flux in a medium without metal complexes, equals:

graphic file with name PP_202200E02_LW.jpg

where F is the area based diffusion flux (nmol cm−2 s−1), δ is the diffusion layer thickness (cm), D is the diffusion coefficient (cm2 s−1), and [M] and [M]s is the (free) metal ion concentration in the bulk solution and at the root surface (μm).

The active transport rate is given by the Michaelis-Menten equation:

graphic file with name PP_202200E03_LW.jpg

where Fmax is the maximal uptake flux (nmol cm−2 s−1) and Km the (true) Km.

In steady state, the diffusion rate flux equals the internalization flux. Combining Equations 2 and 3 results in a quadratic equation in [M]s of which the positive root is:

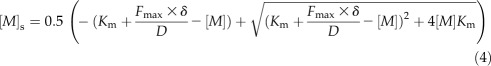graphic file with name PP_202200E04_LW.jpg

Substituting Equation 4 in Equation 2 yields:

graphic file with name PP_202200E05_LW.jpg

At low concentrations, in the linear part of the curve (Fig. 1), a simpler equation can be derived (Winne, 1973):

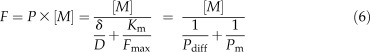graphic file with name PP_202200E06_LW.jpg

where Pdiff is the diffusional permeability (cm s−1), corresponding to D/δ, and Pm the membrane permeability (cm s−1), corresponding to Fmax/Km. Thus, the experimentally determined permeability P, i.e. the ratio of the uptake flux to the free ion concentration in solution, results from a diffusion barrier in series with a membrane barrier (1/P = 1/Pdiff + 1/Pm).

We further refined this model by taking into account the effect of labile complexes on the diffusion flux (Eq. 2) and competition effects on the internalization flux (Eq. 3). The latter were taken into account by using a competitive Michaelis-Menten equation (Slaveykova and Wilkinson, 2005), in which Km was calculated as:

graphic file with name PP_202200E07_LW.jpg

where [Ci] is the concentration of the competitive ion Ci and KC,i is the binding constant for this competitive ion and KM is the binding constant of the metal ion of interest. This metal-binding constant KM corresponds to the reciprocal of the Km in a competition-less scenario.

To take into account the effect of buffering by complexes on the diffusion flux, we made use of the reaction layer theory (Van Leeuwen et al., 2002; Degryse et al., 2006c). Complexes dissociate within the diffusion layer, thus increasing the supply of free ion. At a constant free ion concentration, complexes enhance the diffusion flux, because they dissociate within the diffusion layer and thus increase the supply of the free ion. The reaction layer is the zone near the surface where the equilibrium between complex and free ion cannot be maintained and there is a strong decrease in free ion concentration compared to the bulk solution. The diffusion equation in presence of complexes can be quantified as:

graphic file with name PP_202200E08_LW.jpg

where μ is the thickness of the reaction layer (cm). The thickness of the reaction layer decreases with increasing dissociation rate of the complex and increasing degree of buffering:

graphic file with name PP_202200E09_LW.jpg

where kd is the first order rate dissociation constant (s−1) and [ML] and [M] are concentrations of complex and free ion. A competitive ligand exchange method was used to measure the dissociation rate of the complex (Degryse et al., 2006a).

Equation 5 was used to predict the data, with Km corrected for competition effects (Eq. 7) and using μ (Eq. 9) instead of δ in solution with complexes (if μ < δ). In unbuffered solutions, δ was assumed to be 800 μm for unstirred solutions and 300 μm for stirred solutions. A value of 5 × 10−6 cm2 s−1 was used for the diffusion coefficient of Cd2+, Zn2+, and Ni2+. The value of Fmax was taken from the fit of the Michaelis-Menten curves on the data shown in Figure 2.

Fitted parameters were the metal-binding constant KM and the binding constants of the competitive ions (H+ for Cd and Zn uptake, Mg2+ and H+ for Ni uptake). The parameters were optimized by minimizing the residual sum of squared of the log-transformed uptake.

We did the modeling on the uptake data for spinach, since this dataset was bigger than for tomato. However, the observed uptake was very similar for spinach and tomato. Application of the model to the more limited dataset for tomato resulted in very similar parameter values (Supplemental Table S3).

As we found indications of passive uptake (Fig. 3), we also tested the model with inclusion of a passive uptake component:

graphic file with name PP_202200E10_LW.jpg

with Fpassive the passive uptake flux (nmol cm−2 s−1), [Mtot] the total metal concentration in solution (μm), and Ppassive the passive permeability coefficient (cm s−1). The active uptake was calculated as described above (Eq. 5, using δ for unbuffered solutions and μ for buffered solutions). In this case, both the binding parameters and Ppassive were optimized by minimizing the residual sum of squared of the log-transformed uptake (see Supplemental Text S2).

Supplemental Data

The following materials are available in the online version of this article.

Glossary

Cd

cadmium

Zn

zinc

Ni

nickel

BLM

biotic ligand model

Mg

magnesium

Cu

copper

Ca

calcium

H

hydrogen

Km*

apparent Km

NTA

to be defined
HEDTA: to be defined

CDTA

to be defined

References

  1. Barry PH, Diamond JM. (1984) Effects of unstirred layers on membrane phenomena. Physiol Rev 64: 763–872 [DOI] [PubMed] [Google Scholar]
  2. Bell PF, Chaney RL, Angle JS. (1991) Free metal activity and total metal concentrations as indices of micronutrient availability to barley (Hordeum vulgare (L.) ‘Klages’). Plant Soil 130: 51–62 [Google Scholar]
  3. Bravin MN, Le Merrer B, Denaix L, Schneider A, Hinsinger P. (2010) Copper uptake kinetics in hydroponically-grown durum wheat (Triticum turgidum durum L.) as compared with soil’s ability to supply copper. Plant Soil 331: 91–104 [Google Scholar]
  4. Campbell PGC, Errécalde O, Fortin C, Hiriart-Baer VP, Vigneault B. (2002) Metal bioavailability to phytoplankton—applicability of the biotic ligand model. Comp Biochem Physiol C Toxicol Pharmacol 133: 189–206 [DOI] [PubMed] [Google Scholar]
  5. Checkai RT, Hendrickson LL, Corey RB, Helmke PA. (1987) A method for controlling the activities of free metal, hydrogen and phosphate ions in hydroponic solutions using ion exchange and chelating resins. Plant Soil 99: 321–334 [Google Scholar]
  6. Collins RN, Merrington G, McLaughlin MJ, Knudsen C. (2002) Uptake of intact zinc-ethylenediaminetetraacetic acid from soil is dependent on plant species and complex concentration. Environ Toxicol Chem 21: 1940–1945 [PubMed] [Google Scholar]
  7. de Levie R. (1999) Estimating parameter precision in nonlinear least squares with Excel’s solver. J Chem Educ 76: 1594–1598 [Google Scholar]
  8. Degryse F, Smolders E. (2012) Cadmium and nickel uptake by tomato and spinach seedlings: plant or transport control? Environ Chem 9: 48–54 [Google Scholar]
  9. Degryse F, Smolders E, Merckx R. (2006a) Labile Cd complexes increase Cd availability to plants. Environ Sci Technol 40: 830–836 [DOI] [PubMed] [Google Scholar]
  10. Degryse F, Smolders E, Parker DR. (2006b) An agar gel technique demonstrates diffusion limitations to cadmium uptake by higher plants. Environ Chem 3: 419–423 [Google Scholar]
  11. Degryse F, Smolders E, Parker DR. (2006c) Metal complexes increase uptake of Zn and Cu by plants: implications for uptake and deficiency studies in chelator-buffered solutions. Plant Soil 289: 171–185 [Google Scholar]
  12. Dong B, Rengel Z, Graham RD. (1995) Root morphology of wheat genotypes differing in zinc efficiency. J Plant Nutr 18: 2761–2773 [Google Scholar]
  13. François L, Fortin C, Campbell PGC. (2007) pH modulates transport rates of manganese and cadmium in the green alga Chlamydomonas reinhardtii through non-competitive interactions: implications for an algal BLM. Aquat Toxicol 84: 123–132 [DOI] [PubMed] [Google Scholar]
  14. Hacisalihoglu G, Hart JJ, Kochian LV. (2001) High- and low-affinity zinc transport systems and their possible role in zinc efficiency in bread wheat. Plant Physiol 125: 456–463 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Harrison GI, Campbell PGC, Tessier A. (1986) Effects of pH changes on zinc uptake by Chlamydomonas variabilis grown in batch culture. Can J Fish Aquat Sci 43: 687–693 [Google Scholar]
  16. Hart JJ, Welch RM, Norvell WA, Kochian LV. (2002) Transport interactions between cadmium and zinc in roots of bread and durum wheat seedlings. Physiol Plant 116: 73–78 [DOI] [PubMed] [Google Scholar]
  17. Hoffland E, Wei C, Wissuwa M. (2006) Organic anion exudation by lowland rice (Oryza sativa L.) at zinc and phosphorus deficiency. Plant Soil 283: 155–162 [Google Scholar]
  18. Hough RL, Tye AM, Crout NMJ, McGrath SP, Zhang H, Young SD. (2005) Evaluating a ‘Free Ion Activity Model’ applied to metal uptake by Lolium perenne L. grown in contaminated soils. Plant Soil 270: 1–12 [Google Scholar]
  19. Inada Y, Mohammed AM, Loeffler HH, Funahashi S. (2005) Water-exchange mechanism for zinc(II), cadmium(II), and mercury(II) ions in water as studied by umbrella-sampling molecular-dynamics simulations. Helv Chim Acta 88: 461–469 [Google Scholar]
  20. Kobayashi S, Nagayama S, Busujima T. (1998) Lewis acid catalysts stable in water: correlation between catalytic activity in water and hydrolysis constants and exchange rate constants for substitution of inner-sphere water ligands. J Am Chem Soc 120: 8287–8288 [Google Scholar]
  21. Li B, Zhang X, Wang X, Ma Y. (2009) Refining a biotic ligand model for nickel toxicity to barley root elongation in solution culture. Ecotoxicol Environ Saf 72: 1760–1766 [DOI] [PubMed] [Google Scholar]
  22. Lock K, Van Eeckhout H, De Schamphelaere KAC, Criel P, Janssen CR. (2007) Development of a biotic ligand model (BLM) predicting nickel toxicity to barley (Hordeum vulgare). Chemosphere 66: 1346–1352 [DOI] [PubMed] [Google Scholar]
  23. Lombi E, Zhao FJ, McGrath SP, Young SD, Sacchi GA. (2001) Physiological evidence for a high-affinity cadmium transporter highly expressed in a Thlaspi caerulescens ecotype. New Phytol 149: 53–60 [DOI] [PubMed] [Google Scholar]
  24. Ma Z, Bielenberg DG, Brown KM, Lynch JP. (2001) Regulation of root hair density by phosphorus availability in Arabidopsis thaliana. Plant Cell Environ 24: 459–467 [Google Scholar]
  25. McLaughlin MJ, Smolders E, Merckx R, Maes A. (1997) Plant uptake of Cd and Zn in chelator-buffered nutrient solution depends on ligand type. In Ando T, Fujita K, Mae T, Matsumoto H, Mori S, , Plant Nutrition—For Sustainable Food Production and Environment. Kluwer Academic Publishers, Dordrecht, The Netherlands, pp 113–118 [Google Scholar]
  26. Mertens J, Degryse F, Springael D, Smolders E. (2007) Zinc toxicity to nitrification in soil and soilless culture can be predicted with the same biotic ligand model. Environ Sci Technol 41: 2992–2997 [DOI] [PubMed] [Google Scholar]
  27. Morel FMM, Hudson RJM, Price NM. (1991) Limitation of productivity by trace-metals in the sea. Limnol Oceanogr 36: 1742–1755 [Google Scholar]
  28. Niu L, Shen Z, Luo C, Deng Y-e, Wang C. (2012) Accumulation mechanisms and subcellular distribution of Cu in maize grown on soil treated with S,S-ethylenediamine disuccinic acid. Plant Soil 351: 237–247 [Google Scholar]
  29. Nolan AL, Mclaughlin MJ, Mason SD. (2003) Chemical speciation of Zn, Cd, Cu, and Pb in pore waters of agricultural and contaminated soils using Donnan dialysis. Environ Sci Technol 37: 90–98 [DOI] [PubMed] [Google Scholar]
  30. Panfili F, Schneider A, Vives A, Perrot F, Hubert P, Pellerin S. (2009) Cadmium uptake by durum wheat in presence of citrate. Plant Soil 316: 299–309 [Google Scholar]
  31. Paquin PR, Gorsuch JW, Apte S, Batley GE, Bowles KC, Campbell PGC, Delos CG, Di Toro DM, Dwyer RL, Galvez F, et al. (2002) The biotic ligand model: a historical overview. Comp Biochem Physiol C Toxicol Pharmacol 133: 3–35 [DOI] [PubMed] [Google Scholar]
  32. Parker DR, Chaney RL, Norvell WA. (1995) Chemical equilibrium models: applications to plant nutrition research. In Loeppert RH, Schwab AP, Goldberg S, eds, Chemical Equilibrium and Reaction Models. SSSA, Madison, WI, pp 163–200 [Google Scholar]
  33. Pence NS, Larsen PB, Ebbs SD, Letham DLD, Lasat MM, Garvin DF, Eide D, Kochian LV. (2000) The molecular physiology of heavy metal transport in the Zn/Cd hyperaccumulator Thlaspi caerulescens. Proc Natl Acad Sci USA 97: 4956–4960 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Santner J, Smolders E, Wenzel WW, Degryse F. (2012) First observation of diffusion-limited plant root phosphorus uptake from nutrient solution. Plant Cell Environ 35: 1558–1566 [DOI] [PubMed] [Google Scholar]
  35. Schaider LA, Parker DR, Sedlak DL. (2006) Uptake of EDTA-complexed Pb, Cd and Fe by solution- and sand-cultured Brassica juncea. Plant Soil 286: 377–391 [Google Scholar]
  36. Slaveykova VI, Wilkinson KJ. (2005) Predicting the bioavailability of metals and metal complexes: critical review of the Biotic Ligand Model. Environ Chem 2: 9–24 [Google Scholar]
  37. Smulders AP, Wright EM. (1971) The magnitude of nonelectrolyte selectivity in gallbladder epithelium. J Membr Biol 5: 297–318 [DOI] [PubMed] [Google Scholar]
  38. Thomson ABR, Dietschy JM. (1980) Experimental demonstration of the effect of the unstirred water layer on the kinetic constants of the membrane transport of D-glucose in rabbit jejunum. J Membr Biol 54: 221–229 [DOI] [PubMed] [Google Scholar]
  39. Tinker PB, Nye PH. (2000) Solute Movement in the Rhizosphere. Oxford University Press, New York [Google Scholar]
  40. Van Leeuwen HP, Puy J, Galceran J, Cecilia J. (2002) Evaluation of the Koutecky-Koryta approximation for voltammetric currents generated by metal complex systems with various labilities. J Electroanal Chem 526: 10–18 [Google Scholar]
  41. Vigneault B, Campbell PGC. (2005) Uptake of cadmium by freshwater green algae: effects of pH and aquatic humic substances. J Phycol 41: 55–61 [Google Scholar]
  42. Wang P, Zhou DM, Luo XS, Li LZ. (2009) Effects of Zn-complexes on zinc uptake by wheat (Triticum aestivum) roots: a comprehensive consideration of physical, chemical and biological processes on biouptake. Plant Soil 316: 177–192 [Google Scholar]
  43. Wilkinson KJ, Buffle J. (2004) Critical evaluation of physicochemical parameters and processes for modelling the biological uptake of trace metals in environmental (aquatic) systems. In van Leeuwen HP, Köster W, eds, Physicochemical Kinetics and Transport at Biointerfaces. John Wiley and Sons, Ltd, Chichester, UK, pp 445–533 [Google Scholar]
  44. Wilson FA, Dietschy JM. (1974) The intestinal unstirred layer: its surface area and effect on active transport kinetics. Biochim Biophys Acta 363: 112–126 [DOI] [PubMed] [Google Scholar]
  45. Winne D. (1973) Unstirred layer, source of biased Michaelis constant in membrane transport. Biochim Biophys Acta 298: 27–31 [DOI] [PubMed] [Google Scholar]
  46. Worms IAM, Wilkinson KJ. (2007) Ni uptake by a green alga. 2. Validation of equilibrium models for competition effects. Environ Sci Technol 41: 4264–4270 [DOI] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES