Gone in 0.6 Seconds: The Encoding of Motor Memories Depends on Recent Sensorimotor States

Abstract

Real-world tasks often require movements that depend on a previous action or on changes in the state of the world. Here we investigate whether motor memories encode the current action in a manner that depends on previous sensorimotor states. Human subjects performed trials in which they made movements in a randomly selected clockwise or counterclockwise velocity-dependent curl force field. Movements during this adaptation phase were preceded by a contextual phase that determined which of the two fields would be experienced on any given trial. As expected from previous research, when static visual cues were presented in the contextual phase, strong interference (resulting in an inability to learn either field) was observed. In contrast, when the contextual phase involved subjects making a movement that was continuous with the adaptation-phase movement, a substantial reduction in interference was seen. As the time between the contextual and adaptation movement increased, so did the interference, reaching a level similar to that seen for static visual cues for delays >600 ms. This contextual effect generalized to purely visual motion, active movement without vision, passive movement, and isometric force generation. Our results show that sensorimotor states that differ in their recent temporal history can engage distinct representations in motor memory, but this effect decays progressively over time and is abolished by ∼600 ms. This suggests that motor memories are encoded not simply as a mapping from current state to motor command but are encoded in terms of the recent history of sensorimotor states.

Introduction

In real-world tasks, actions rarely take place in isolation but are often preceded by a previous action or change in the environment. These previous states may have significant effects on the performance of a subsequent movement. For example, in tennis, performing the appropriate backswing and linking one's swing to the visual motion of the ball are crucial in achieving a quality stroke. Here we examine whether previous motion, be it physical or visual, influences learning in the subsequent movement.

When two opposing visuomotor or dynamic (force-field) perturbations are presented sequentially, there is substantial interference (Brashers-Krug et al., 1996; Krakauer et al., 1999; Karniel and Mussa-Ivaldi, 2002; Caithness et al., 2004). However, if contextual cues are associated with each perturbation, interference can be reduced (Imamizu et al., 2007; Howard et al., 2008; Cothros et al., 2009; Addou et al., 2011; Hirashima and Nozaki, 2012). By the “contextual cues” of a movement we refer to states of the world and body excluding those directly associated with the arm while it experiences the perturbation. Therefore, context can be visual cues, movement of other body parts, or states of the arm before the perturbed movement. Such cues are typically presented concurrently with movement, allowing the formation and recall of separate motor memories. For example, motion versus no motion of the contralateral arm (Nozaki et al., 2006) or the relative direction of movement between the two arms (Howard et al., 2010; Yokoi et al., 2011) provide strong cues that can substantially reduce interference.

Despite the relevance for real-world tasks, few studies have examined the contextual effects of cues presented before the movement. In one exception, when a perturbed movement followed distinct previous movements, there was a reduction in interference by a small but significant amount (Wainscott et al., 2005). The shortest delay examined between the movements was 500 ms. However, evidence from classical conditioning in the cerebellum suggests that cue effectiveness decays with time: cues provided within 500 ms are most effective (Ohyama et al., 2003). Similarly, the relationship between Purkinje cell activity and arm kinematics shows a correlation that decays over a 500 ms period into the past (Hewitt et al., 2011). Because the cerebellum is also known to play an important role in adaptation to dynamic force fields (Maschke et al., 2004; Smith and Shadmehr, 2005), we hypothesized that a temporal window of 500 ms may exist during which previous motion can provide a cue for learning opposing perturbations.

To test this hypothesis, we used an interference paradigm in which each trial consisted of a contextual phase followed by an adaptation phase. During the adaptation phase, subjects made a movement in one of two opposing curl fields, with field direction in each trial predictable from the contextual phase. The paradigm allowed us to examine the effectiveness of different contextual cues before movement, including active and passive movement cues, and static and dynamic visual cues. We also varied the delay between the contextual and adaptation phases. Our results show that immediate past movement or visual motion provides strong contextual cues for motor learning. This effect decays progressively over a 600 ms window to reach levels comparable with the weak effects reported for serial order cues (Wainscott et al., 2005).

Materials and Methods

A total of 78 right-handed subjects (37 male, 41 female) took part in four experiments (one additional subject was also used but was excluded from the final analysis as described below). Subjects provided written informed consent and were naive to the aims of the experiments. A local ethics committee approved the protocol, and all subjects completed an Edinburgh handedness questionnaire.

Apparatus

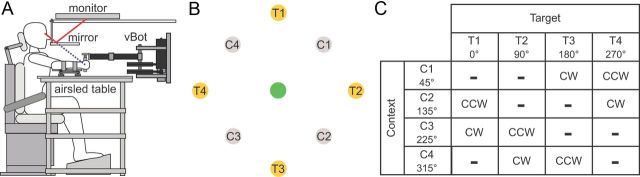
All experiments were performed using a vBOT planar robotic manipulandum, with associated virtual reality system and air table (Howard et al., 2009). The vBOT is a custom-built back-drivable planar robotic manipulandum, which exhibits low mass at its handle. Position is measured using optical encoders sampled at 1000 Hz, and torque motors allow endpoint forces to be specified. The position signal was used unfiltered, whereas velocity was computed by fitting a quadratic motion equation, assuming constant acceleration, over a window that consisted of the 30 most recent position samples and associated time stamps. The vBOT was equipped with a force transducer (Nano 25; ATI Industrial Automation) mounted at the handle to measure the applied forces. Before digitization, the output channels of the force transducers were low-pass filtered at 500 Hz using analog fourth-pole Bessel filters. Subjects were seated in a sturdy chair in front of the apparatus and firmly strapped against the backrest with a four-point seatbelt to reduce body movement (Fig. 1A). Subjects grasped the robot handle in their right hand while an air sled (constraining movement to the horizontal plane) supported their right forearm. Visual feedback was provided using a computer monitor mounted above the vBOT and was projected veridically to the subject via a mirror. Subjects were prevented from viewing their hand directly, and the virtual reality system was used to overlay images such as targets, visual cues, and starting locations (all 1.25-cm-radius disks) and a hand cursor (0.5-cm-radius red disk) in the plane of movement.

Figure 1.

Experimental paradigm. A, The subject grasps the handle of the robotic manipulandum (vBOT) while seated. Visual feedback of movements is presented veridically using a top-mounted computer screen viewed via a mirror. The subject's forearm is fixed to the handle and supported by an air sled. B, Workspace layout of the experiment. There were four possible cue locations (gray circles, C1–C4), one central target (green circle; note that in the experiment this was displayed as gray), and four final targets (yellow circles, T1–T4). C, Table of the force-field directions as a function of cue and target location. During the exposure phase of the experiments, force fields were applied on the subjects' hands by the robot as the subject performed a movement between the central location and the final target. The force field applied—CW or CCW—depended on both the target direction (0°, 90°, 180°, and 270°) and the cue location (45°, 135°, 225°, and 315°), but not every combination was used. For each target location, two possible cue locations could be chosen (one for each force-field direction) corresponding to ±135° relative angle around the central target. Only the combination of the cue location and final target location specified the force-field direction. In a block of trials, all cue locations and final target locations were pseudorandomly presented such that CW and CCW trials were mixed equally. The table shows the association of force field and cue–target location used in half the subjects for a given experiment. In the other half, the association was reversed.

Paradigm overview

Throughout all experiments, each trial consisted of a contextual phase, followed by an adaptation phase. The adaptation phase was identical in all experiments, requiring subjects to make a reaching movement from a central location to one of four peripheral targets (T1–T4; Fig. 1B). During this movement, the subject's hand could be subjected to either a clockwise (CW) or a counterclockwise (CCW) velocity-dependent curl field. Field direction (CW or CCW) varied pseudorandomly from trial to trial. There were four contextual cues that related to positions C1–C4 (Fig. 1B) in ways that depended on the particular experiment. The direction of the field (Fig. 1C) was predictable based on the cues presented during the contextual phase (C1–C4) and the target location (T1–T4). Movements to each target were associated with two cues (for example, movements from the central point to target T1 were associated with either cue C2 or C3). The combination of the cue position and target location specified the force-field direction (Fig. 1C). The experiments were counterbalanced such that, in each experiment, half of the subjects experienced the contextual cues matched to one set of force-field directions (as in Fig. 1C), whereas the other half of the subjects experienced the contextual cues matched to the opposite force-field directions. This was performed to avoid any bias arising from associations between a particular context and field direction.

The contextual phase of each trial allowed us to examine the ability of different cues to reduce the interference between the two fields (CW and CCW) experienced in the subsequent adaptation phase. In different experiments, we examined two classes of cues: movement cues and visual cues. In experiments that examined movement cues, subjects were required to make a movement (or were passively moved or generated a force) during the contextual phase of the trial. The field for the adaptation phase (CW or CCW) was determined by the direction of this movement. Movements made during the contextual phase of the trial were never perturbed. In experiments that examined visual cues, subjects did not move during the contextual phase of the trial. Rather, the context was provided by either a static or dynamic visual cue that determined the field direction for the adaptation phase (CW or CCW).

Adaptation phase

We first describe the second part of each trial, the adaptation phase, because this was identical across all experiments. The adaptation phase consisted of a 12 cm reaching movement from a central location (located in the midsagittal plane ∼30 cm below the eyes and 30 cm in front of the chest) to one of four radial target locations: 0°, 90°, 180°, and 270° (Fig. 1B).

During this movement, either a null field or a viscous curl field (Gandolfo et al., 1996) was applied, which ramped up linearly over 50 ms after subjects had moved 2 cm away from the center location. The force at the handle was given by the following:

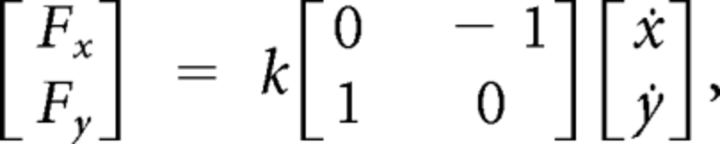where k was set equal to ±13 N · s/m. The sign of k determined the direction of the force field (CW or CCW), depending on the previous contextual phase of the trial, which varied across experimental conditions.

Within each experiment, blocks of 18 trials were performed consisting of 16 field trials and two clamp trials. In the field trials, each of the four targets and two possible field directions were repeated twice. The order of the movements within each block was pseudorandom, except that a clamp trial always occurred in the first and last four trials of each block. The two clamp trials always occurred for movements to the 0° target (straight ahead): one trial with a contextual cue for a CW field and one trial with a contextual cue for a CCW field (randomizing which came first within each block). In a clamp trial, the movement was confined to a simulated mechanical channel with a spring constant of 10,000 N/m (Milner and Franklin, 2005; Smith et al., 2006).

Each experiment began with a preexposure phase consisting of 12 blocks in which no forces were applied (216 null trials), followed by an exposure phase of 75 blocks (1350 field trials), and finally a postexposure phase consisting of four blocks (72 null trials). Subjects were given a short rest on average every 200 trials (195–205 trials).

Contextual phase

The contextual phase varied across experiments. The contextual cue combined with the target direction for the subsequent adaptation-phase movement always defined a specific force field (Fig. 1C).

Experiment 1: static visual contexts (n = 16)

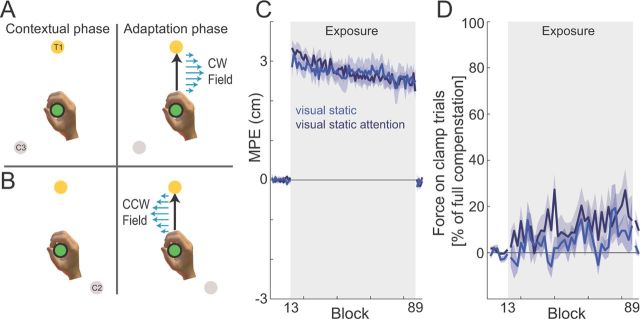
The first condition of experiment 1 was designed to examine the contextual effects of a static visual cue (n = 8). On each trial, a visual cue, the center location, and the final target were displayed and the vBOT applied a force to guide the subject's hand to the center location (following a minimum jerk trajectory). A trial began when the hand cursor had remained within the center location at a speed below 0.1 cm/s for 500 ms. On each trial, a single visual cue (gray disk, one of C1–C4; Fig. 1B) was displayed 10 cm from the central location. The position of the cue depended on the target and field direction that would be applied during the adaptation phase of the trial. That is, the cue location was either −135° or +135° rotated from the target location (relative to the center location), with the sign dependent on the direction of the upcoming curl field (two trials are shown in Fig. 2A,B for CW and CCW fields, respectively). Therefore, the visual cue location was predictive of the direction of the curl field in the adaptation phase.

Figure 2.

Static visual cue experiments. A, Experimental design. Subjects started the trial with their hand at the central location (green circle) while both the cue location (gray circle) and final target (yellow circle) were visually presented. Movement initiation was either signified by an acoustic beep (static visual cue condition) or the cue color changing from gray to white (static visual cue attention experiment). The combination of cue (e.g., C3) and target (e.g., T1) uniquely specified the CW force field (Fig. 1B), applied once the subjects initiated the movement to the final target. B, For the same final target (T1), if cue C2 was visually presented to the subjects, this uniquely specified the CCW force field, applied once the movement was initiated. C, MPE plotted against block number. The mean across all subjects (solid line) and SE across subjects (shaded region) for each block in both the static visual cue (blue) and static visual cue attention (navy blue) experiments are shown. Although the two force fields produce error in the opposite directions, the sign of errors on trials on which the CCW field was presented have been reversed so that all errors in the direction of the force field are shown as positive. On block 13, the two curl fields were introduced (exposure, gray shaded region), which remained on until block 89, when subjects returned to the null force field. D, Percentage force compensation computed from clamp trials throughout the experiment. The mean ± SE force across subjects over two blocks is plotted as a percentage of the force required for estimated complete compensation. Gray shaded region indicates exposure blocks in which the curl force fields were applied.

The start of the trial was cued by an acoustic tone. At a fixed time interval after the tone (510 ms), the central location disk changed color from gray to white, indicating that the subject should initiate a movement to the target (within 50–400 ms of the color change, or the trial was aborted). The red hand cursor then reflected the hand position during the movement. If the duration of the movement (measured from the time the cursor had moved 2 cm from the center location until it entered the target) was between 150 and 300 ms, a “correct speed” message was displayed; otherwise, a too fast/slow warning was given.

The correspondence between visual cue location (±135°) and curl-field direction (CW/CCW) was counterbalanced across the eight subjects. One subject was excluded from the final analysis as a result of inconsistent and highly variable hand paths throughout the experiment.

To investigate the effect of attention, an additional static visual condition was examined (n = 8). The condition was identical to the previous one except, to ensure that subjects attended to the static visual cue, the signal to start the movement was indicated by the static visual cue changing from gray to white (with no auditory cue). To prevent subjects predicting movement onset, the timing of the movement initiation signal was set to 0.4 s plus a random time chosen from an exponential distribution with mean 0.5 s truncated at 2.1 s (the start cue always occurred between 0.4 and 2.5 s). If subjects did not initiate the movement between 50 and 400 ms of the cue color change, the trial was aborted.

Experiment 2: temporal decay of contextual motion effect (n = 16)

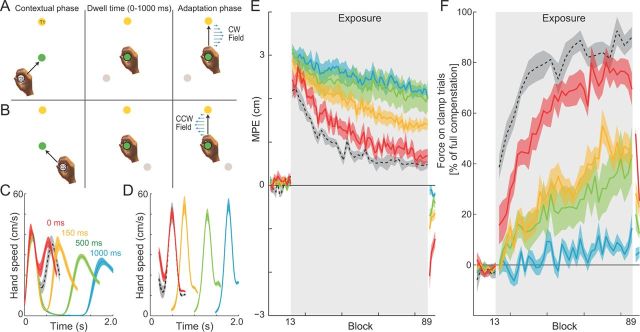
Experiment 2 was designed to examine the contextual effects of previous movement. On each trial, the contextual phase consisted of a 10 cm movement (in a null field) to the central location, which acted as the starting position for the adaptation-phase movement. Therefore, the center location can be considered as a via point from the starting location to the final target. The starting location of the contextual-phase movement depended on the target and field direction that would be applied for the adaptation phase. That is, the starting location was either −135° or +135° from the target location, with the sign dependent on the direction of the curl field (two trials are shown in Fig. 4A,B for CW and CCW fields, respectively). Thus, the movement in the contextual phase was predictive of the direction of the curl field in the adaptation phase. On each trial, the starting location, via point, and final target were displayed, and the vBOT applied a force to guide the subject's hand to the start location. Subjects were cued to start the movement by an acoustic tone.

Figure 4.

Dwell time contextual effect experiments. A, Experimental design. In the contextual phase, subjects moved from the cue location to the central target while the final target was visually displayed. No forces were applied during this movement at any stage of the experiment. Subjects were then required to remain in the central location for a set dwell time (0, 150, 500, or 1000 ms). After remaining in the central target for the correct time, subjects moved to the final target. The curl force fields were applied during this phase of the trial. For example, the movement from cue C3 and to target T1 uniquely specified the CW force field. B, The movement from cue C2 and to final target T1 uniquely specified the CCW force field. C, Speed profiles for the single force-field condition (black) and dwell time conditions of 0 ms (red), 150 ms (yellow), 500 ms (green), and 1000 ms (cyan) aligned on the contextual movement initiation. The mean and SE of the hand speed profiles are shown across all subjects. D, Speed profiles for the single force-field condition (black) and the dwell time conditions of 0 ms (red), 150 ms (yellow), 500 ms (green), and 1000 ms (cyan) aligned on the peak velocity of the second movement. The mean and SE of the hand speed profiles are shown across all subjects. E, Mean hand path error (MPE) and SE as a function of block, averaged across all subjects for dwell times of 0, 150, 500, and 1000 ms as well as for the single force-field condition (black dashed line). Shaded region indicates exposure blocks in which the curl force fields were applied. Each block in the single force-field condition consisted of nine trials (8 force-field trials and 1 clamp trial) and consecutive blocks were averaged together. This provides an even comparison across blocks with all other experimental conditions as the identical number of force-field trials (of any one field direction) are presented in a block. F, Percentage force compensation computed from clamp trials throughout the experiment. The mean ± SE force over two blocks across subjects is plotted as a percentage of the force required for estimated complete compensation, for dwell times of 0 ms (red), 150 ms (yellow), 500 ms (green), and 1000 ms (cyan), as well as the corresponding values for the single force-field condition (black dashed). Shaded region indicates exposure blocks in which the curl force fields were applied.

We varied the time subjects were required to pause at the central location before continuing to the final target (dwell time). One group was required to make a continuous movement (∼0 ms dwell time), whereas the other groups were required to have a dwell time within one of three ranges: 150–300, 500–1000, or 1000–1500 ms (we refer to these as 150, 500 and 1000 ms dwell time groups). Subjects were required to stay within the radius of the central location disc with a speed <5 cm/s for the duration of the dwell time. If they left the central location outside of the specified dwell time range, this generated a mistrial (no forces were generated) and they were required to repeat the trial.

Subjects were required to repeat a trial if they failed to achieve a speed >30 cm/s in the first movement or had a speed perpendicular to the target direction on leaving the via point >10 cm/s (in both these cases, the force field was not experienced). The latter condition ensured that the movement was composed of two approximately straight segments so that the initial kinematics in the adaptation phase was independent of the starting location. If the duration of the second movement (measured from the time the cursor had moved 2 cm from the center location until it entered the target) was between 150 and 250 ms, a “correct speed” message was displayed; otherwise, a too fast/slow warning was given.

Sixteen subjects each participated in two of the four dwell time conditions on separate days (assigned pseudorandomly) so that eight subjects participated in each condition. To reduce possible bias of the first session on the second, we reversed the assignment between starting location and curl-field direction for each subject across the two experiments.

To contrast the learning of the opposing force fields with interference free learning of a single force field, six naive subjects were recruited (n = 6). Three of the subjects learned the CW curl force field (for all cue conditions), whereas the other three subjects learned the CCW curl force field (for all cue conditions). Each block consisted of nine trials (eight force-field trials and one clamp trial). This provides an even comparison across blocks with all other experimental conditions as the identical number of force-field trials (of any one field direction) are presented in a block. All other conditions were identical to the continuous (∼0 ms dwell time) group.

Experiment 3: contextual motion before target location (n = 8)

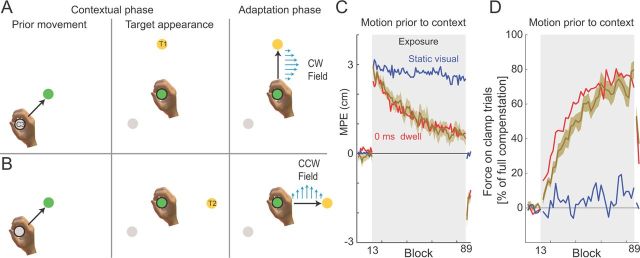
In all the previous experiments, subjects could plan the motor command required for the adaption phase from the start of the contextual phase, because sufficient information was available to specify the direction of the force field. In experiment 3, we examined whether it was necessary to know the final target direction right from the onset of movement or whether the sensorimotor system was still able to use information from the contextual phase without initially knowing what the adaptation phase would be. Specifically, whereas the cue location and central location were presented from the start of the trial, the final target was only displayed when subjects reached the central location (two trials are shown in Fig. 5A,B for CW and CCW fields, respectively). Because the starting location by itself does not specify the direction of the curl field, it is only when the target is displayed (angled either at −135° or +135° relative to the contextual motion) that the field direction is defined. The experiment was similar to the continuous movement condition of experiment 2, with subjects required to make a continuous movement (∼0 ms dwell time).

Figure 5.

Motion before contextual information cues learning. A, Experimental design. The contextual phase comprised two components. Prior movement, The first movement (cue location to central target) occurred before the complete contextual information (presentation of target), which determined the force-field direction. The trial was initiated with the subject's hand at one of the cue locations (C3 in this case) while the central location was visually presented. The subject then moved to the central location. Target appearance, Once the subject was within the central location, the target appeared. Adaptation phase, Subjects then moved to the final target, and the force field was applied as soon as subjects initiated the movement. In this case, the previous movement from cue C3 combined with the current target presentation of T1 specified the CW force field. B, The identical previous movement from cue C3 to the central target was performed. However, in the target appearance phase, target T2 was presented. This combination specified the CCW force field on the adaptation phase of the movement. C, Mean MPE (green trace) and SE (green shaded region) across all subjects and blocks during the motion before contextual presentation experiment. For comparison, the mean results for the static visual (blue trace) and 0 ms dwell time (red trace) conditions are shown. Shaded gray region indicates the exposure period in which the two curl force fields were applied. D, Percentage force compensation computed from clamp trials throughout the experiment. The mean ± SE force over two blocks across subjects is plotted as a percentage of the force required for estimated complete compensation. For comparison, the mean results for the static visual normal (blue trace) and 0 ms dwell time (red trace) conditions are shown. Shaded region indicates exposure blocks in which the curl force fields were applied.

Experiment 4: sensorimotor cues that may mediate contextual effects

To examine the sensorimotor cues that may mediate contextual effects, experiments were performed examining visual cursor motion without arm movement, visual cursor motion without arm or eye movement, active arm movement without visual motion, passive arm movement without visual motion, and isometric force generation without visual motion.

Dynamic visual motion (n = 8).

This condition was similar to the static visual cue experiment (experiment 1), with the subject's hand starting at the center location. However, during the contextual phase of each trial, the red cursor simulated a 510 ms minimum jerk trajectory between the visual cue location and the central location. The form of this cursor trajectory was chosen to be biologically plausible (Flash and Hogan, 1985), thereby giving rise to sensory feedback that would match as closely as possible to the cursor motion experienced in the dwell time conditions. The adaptation phase commenced when the cursor reached the central location. At this point, the color of the central location changed from gray to white, indicating that the subject should initiate a movement to the target within 50–250 ms. The red cursor now tracked the hand as in previous experiments. Eye movements were unconstrained, and subjects were therefore free to track the cursor if they wished.

Dynamic visual motion during eye fixation (n = 6).

This condition was similar to the previous, except that subjects were required to fixate the central location during the contextual phase of the trial. The position of the right eye was monitored using an eye tracker (Eyelink 1000 Tower Mount system; SR Research) sampled at 1000 Hz. If the subject moved their eye >3 cm from the central location during the contextual phase, the trial was immediately aborted. The trial was then repeated. During the adaptation phase, subjects were free to move their eyes.

Active motion without vision (n = 6).

This condition was similar to the dwell time experiments (experiment 2) with a 50 ms dwell time (maximum allowed dwell time of 250 ms). However, the red hand cursor was not displayed during the contextual-phase movement to the central location. To assist subjects reaching the central location, a weak channel (with a spring constant of 500 N/m) was used to guide them.

Passive motion without vision (n = 6).

This condition investigated the contextual effect of proprioception. It was identical to the previous one, except that the vBOT passively moved the subject's hand to the central location during the contextual phase. The passive movement began after the “go” signal and followed a minimum jerk trajectory as described above. Subjects were asked to relax their arm during the passive movement. As with experiment 2, the red hand cursor for this passive movement was not displayed. After a dwell time of 50 ms (maximum allowed dwell time of 250 ms) subjects were required to actively move to the final target during which the hand cursor followed the hand.

To establish that the movements were passive, two techniques were used. The first was performed online to provide immediate feedback to subjects. After each trial, linear regression was used to fit the measured force (exerted on the handle by the subject) against the measured acceleration. The assumption is that, in the case of a purely passive movement, the measured force would be linearly related to the acceleration through the effective mass of the arm. Therefore, an r² < 0.7 (315° target) or r² < 0.8 (other targets) was used as an indication that subjects may have produced either some resistance or assistance to the motion, and an online error was provided. Offline, a second technique was used to confirm that movements were passive. During the experiment, surface electromyography (EMG) was recorded (Delsys Bagnoli DE-2.1 Single Differential Electrodes) from two primary shoulder muscles (the pectoralis major and posterior deltoid) and two primary elbow muscles (the biceps brachii and triceps lateralis). The skin was cleansed with alcohol and prepared by rubbing an abrasive gel into the skin. This was removed with a dry cloth, and the gelled electrodes were secured to the skin using double-sided tape. The EMG signals were bandpass filtered between 20 and 450 Hz (within the Delsys Bagnoli EMG system) and then sampled at 2.0 kHz using a National Instruments data acquisition card. To provide a signal to compare active and passive movements, each subject performed a short block of 90 active movement trials in the null field (similar to the active motion context condition above). The relative EMG signals were compared between the active and passive phases of the experiments. We confirmed that all subjects were passive during this experiment, with the mean integrated electrical activity measured across all muscles during the passive movements being 2.2% of that measured during normal active movements in the null field.

Isometric force generation (n = 6).

In both the dwell time experiment (experiment 2) and the active motion without vision condition, the contextual phase consisted of an active movement, the generation of which required the production of force by the arm muscles. To investigate whether force generation alone could provide a contextual cue, subjects performed an isometric force generation task during the contextual phase. As before, a trial began when the hand cursor had remained within the center location at a speed below 0.1 cm/s for 500 ms. Subjects were then required to push the handle in one of two opposite directions while it was firmly held stationary by a simulated spring (10,000 N/m). The push direction was indicated by the location of a disc placed 6 cm from the home position and at either 90° or 270° from the movement target. Force was measured at a 1 kHz rate using the force transducer at the base of the handle, and its running average was computed over the past 20 ms. Subjects were required to achieve a force of appropriate magnitude and direction such that its value fell within a range delineated by a circular region centered on 7.5 N with a radius of 2.5 N. When the running average of force met this condition, the central starting position changed from gray to white and was held white for 200 ms. This indicated that successful force generation had been achieved without giving any visual motion cues and informed subjects to stop pushing. After the magnitude of force fell below 1.6 N, a cursor appeared at the home position to indicate hand position, and subjects were required to move the cursor from the center position to the final target location.

Data analyses

Data were collected from the manipulandum encoders and force transducer at 1000 Hz and logged to disk for offline analysis using MATLAB (MathWorks). Movement error was calculated on each trial by analyzing the hand movement from the central to target location (the adaptation phase). We calculated the maximum perpendicular error (MPE) of the hand path from a straight path between the center location to the middle of the target. For each subject, we computed the average of the MPE for all exposure trials within a block and adjusted the sign appropriately so that errors from CW and CCW field trials could be combined. We then calculated the mean and SE for each block across subjects. The endpoint forces were examined on the clamp trials to further measure the amount of adaptation. The force produced by subjects into the wall of the simulated channel was integrated across the adaptation-phase movement. To quantify the amount of specific compensation at the end of each experiment, we examined the forces on the clamp trials over the final 25 exposure blocks. To evaluate the degree of compensation, the measured force was divided by the amount of force that would be required for perfect compensation in the force field (calculated as the field constant multiplied by the actual velocity on each trial). The values of percentage force compensation throughout the experiment are based on the compensation required in the curl force field. Therefore, values in the null force field before learning (preexposure phase) should be close to zero.

We perform hypothesis-based planned comparisons and report uncorrected p values to determine statistical significance. Although we performed a number of tests, overall only a few are truly critical for the conclusions of the study. Statistical differences were determined using an ANOVA in SPSS 16.0 using the general linear model. In the dwell time experiment (experiment 2), three ANOVAs were performed. First, a general linear model, with a factor of dwell time (four levels: 0, 150, 500, and 1000), was used to test the size of the initial errors (MPEs) experienced within the first block of the force field. Next, the difference in the amount of adaptation across the four dwell times was examined in two ways: (1) using the MPE at the end of exposure (MPE on last four exposure blocks; blocks 84–87), and (2) using the MPE on the postexposure trials (MPE on all four blocks in the final null field; blocks 88–91). For all three tests, if a significant main effect of dwell time was found, differences were examined using Tukey's HSD post hoc test. For all other experiments, a general linear model was used to test whether the error was significantly different at the end of exposure (MPE on last four exposure blocks; blocks 84–87) compared with initial exposure (MPE on first four exposure blocks; blocks 13–16), with subjects as a random effect. A second linear model was used to test whether there were significant aftereffects (MPE on all four blocks in the final null field; blocks 88–91) compared with the initial null field trials (MPE on last four blocks in the null field; blocks 9–12), with subjects as a random effect. Similar tests were also performed on percentage force compensation when appropriate. Statistical significance was considered at the p < 0.05 level for all statistical tests.

Results

In all experimental conditions, subjects performed trials consisting of a contextual phase followed by an adaptation phase. During the adaptation phase, subjects made reaching movements to four different targets from a central location (target locations T1–T4; Fig. 1B). During the preceding contextual phase, a cue was provided that was associated with one of four locations (cue locations C1–C4; Fig. 1B). The combination of the cue location and the target location uniquely specified the direction (CW or CCW) of the velocity-dependent curl field, which was applied during the movement in the adaptation phase. Specifically, the relative angle between the target and the cue location (±135°) determined which of the two field directions would be experienced. This produced eight unique contexts (Fig. 1C). Each experiment began with a preexposure period consisting of 12 blocks (216 trials) in the null field, followed by an exposure period consisting of 75 blocks (1350 trials) during which the opposing force fields were applied to movements in the adaptation phase. Finally, a postexposure period consisting of four blocks (72 trials) in the null field followed, in which cue-dependent aftereffects were examined. Two clamp trials were presented in each block of 18 trials. Across the last third of clamp trials in the field condition across all main experiments (excluding the static field control condition) and subjects, the mean ± SD peak displacement into the channel was 0.67 ± 0.46 mm. The isometric experiment showed the largest displacement, with a mean ± SD peak displacement into the channel of 1.23 ± 0.51 mm.

Experiment 1: static visual context

In the static visual condition of experiment 1, the experimental conditions were set to be as close as possible to all subsequent experiments to permit comparison. The contextual phase consisted of a static visual cue presented at one of the four cue locations (Fig. 2A,B). On each trial, both the visual cue and final target were displayed to the subjects while their hand remained stationary at the central location. This provided information indicating which force field would be presented during the adaptation-phase movement on that trial (Fig. 1C shows the relationship of field to cue and target location for half the subjects; we counterbalanced the relationship between cue–target location and force-field direction across subjects). Movement initiation was indicated by an acoustic signal. Subjects initially performed movements in the null field, making straight movements to each of the four targets, regardless of the cue context (Fig. 3A, Pre-exposure). When the force fields were introduced, the initial movements showed large deviations from a straight line, in the direction of the force field (Fig. 3A, Initial exposure). Over the course of the exposure period, these deviations did not diminish (Fig. 3A, Final exposure). After removal of the field during the postexposure period, no deviation of trajectories from a straight line were observed, indicating that subjects did not learn a specific compensation for the two field directions (Fig. 3A, Post exposure). We quantified performance by the MPE on each trial (Fig. 2C, blue trace) and also the amount of force compensation as determined by the force produced against the channel wall on clamp trials (Fig. 2D, blue trace). Using an ANOVA, we found a significant increase in MPE during the initial exposure period (F_(1,7) = 351.503; p < 0.001) but no significant reduction in MPE from the initial to final trials of the exposure period (F_(1,7) = 3.89; p = 0.089). During the null field trials of the postexposure period, MPE was not significantly different from the preexposure period (F_(1,7) = 0.24; p = 0.882). Overall, these findings demonstrate that static visual cues do not provide effective contextual information suitable for learning opposing force fields, resulting in very slow or minimal learning of the two force fields. These results thus provide a baseline for the following experiments.

Figure 3.

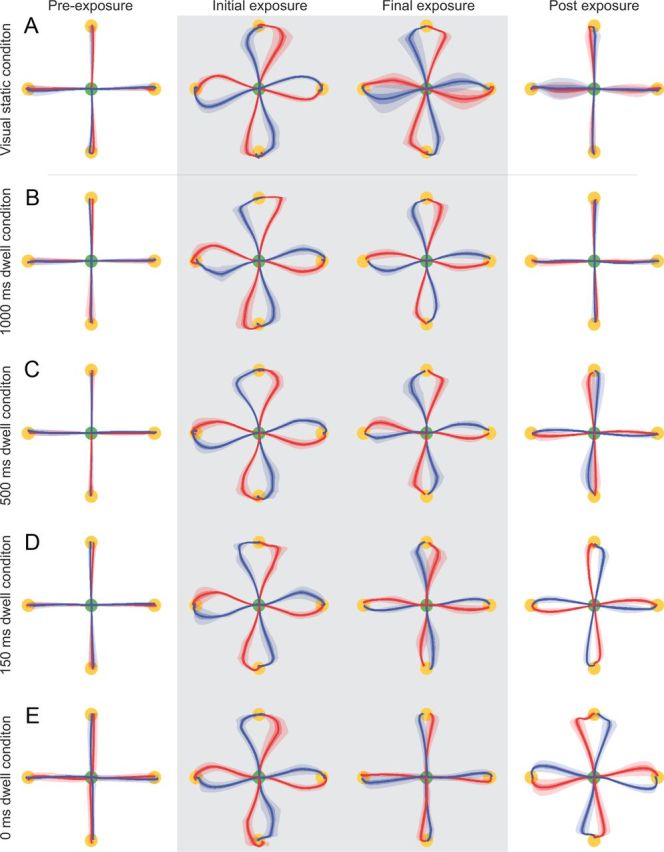
Hand paths during the movements between the central location (green circle) and final target (yellow circle) for the static visual cue and dwell time experiments. The mean (solid line), SE (dark shaded region), and SD (light shaded region) across all subjects for each condition are plotted. The trials on which the CW force field was applied are shown in red, and the trials in which the CCW force field was applied are shown in blue. Pre-exposure, The mean of the last eight trials in the initial null field (block 12). Initial exposure, The first eight trials in the curl force fields (block 13). Final exposure, The last eight trials in the curl field (block 88). Post exposure, The first eight trials in the null field during the washout (aftereffect trials) (block 89). Trials in which the force field is applied are shown with the shaded gray background. A, Paths in the visual static condition. B, Paths in the 1000 ms dwell condition. C, Paths in the 500 ms dwell condition. D, Paths in the 150 ms dwell condition. E, Paths in the 0 ms dwell condition.

The attention condition of experiment 1 was similar to the above condition except movement initiation was cued by the cue location changing color from gray to white. This forced subjects to attend to the cue. We again quantified performance by MPE on each trial (Fig. 2C, navy blue trace), and the force compensation values were computed from clamp trials (Fig. 2D, navy blue trace). Using an ANOVA, we found a large increase in MPE during the initial exposure period (F_(1,7) = 240.917; p < 0.001) and a small reduction in MPE from the initial to final trials of the exposure period (F_(1,7) = 115.646; p < 0.001). However, the MPE on the null field trials of the postexposure period were not significantly different from the preexposure period (F_(1,7) = 2.523; p = 0.156).

Differences between the two conditions were further investigated by a comparison of the error measures in the two static visual cue experiments. There were no significant differences between the final level of MPE in the late exposure stage between the static visual cue experiment and the static attentional cue experiment (F_(1,7) = 0.111; p = 0.748). Similarly, no significant differences were found between the two static visual experiments results for the force compensation in the final trials of exposure (F_(1,7) = 0.843; p = 0.389).

There were small but significant decreases in the MPE during the field exposure, which taken in isolation could be interpreted as subjects learning a small amount of compensation for the force fields. However, the absence of aftereffects (significant deviations of the trajectory during the postexposure phase) suggests that this field-specific compensation is very small. Instead, these results imply that the reduction in MPE during the exposure period is likely to have occurred through a field-independent increase in limb stiffness (Burdet et al., 2001; Franklin et al., 2007), driven by increases in muscular co-contraction (Osu et al., 2002; Franklin et al., 2003) and feedback gains (Franklin et al., 2012). Thus, these findings suggest that spatial attention to different locations is not effective as a contextual cue, resulting in very slow or minimal learning of the two force fields.

Experiment 2: temporal decay of contextual motion effect

Experiment 2 examined whether a movement made before the adaptation-phase movement could provide a contextual cue for learning opposing fields. As in experiment 1, the combination of cue location and target determined the field direction (Fig. 1C). However, in this case, subjects were required to make a movement during the contextual phase, from the cue location to the central location (Fig. 4A,B). The central location thus acted as a via point between the contextual- and adaptation-phase movements. No force fields were applied during the contextual-phase movement. We examined the effect of increasing time delays (dwell times) between the two movements. That is, in different experimental conditions, subjects were required to either make a continuous movement (0 ms dwell time) or pause at the central location for a dwell time of 150–300, 500–1000, or 1000–1500 ms. The actual dwell times (mean ± SE) across subjects for the 0, 150, 500, or 1000 ms conditions were 17.3 ± 3.4, 246 ± 7.5, 680 ± 13.1, and 1211 ± 26.3 ms, respectively.

Figure 4C shows the mean speed profile for the four dwell times, aligned to the initiation of the first movement. The 0 ms dwell group exhibited a small dip in the speed profile as the paths passed through the central location. In contrast, for the other three groups, speed was close to zero during the dwell period. Because of natural movement variability, aligning the speed profiles with the start of the movement tends to blur the peak of the second movement for longer dwell times. Figure 4D shows the same data aligned to the peak speed of each trial, showing that the second movement has similar peak speeds across different dwell times.

Learning was quantified using MPE during the adaptation-phase movement (Fig. 4E), as in experiment 1. During the preexposure period, subjects made approximately straight movements characterized by a low MPE. The hand paths for the second movement did not differ as a function of the first movement direction; see preexposure MPE (Fig. 4E) and movement trajectories (Fig. 3B–E, Pre-exposure). During introduction of the curl fields, movement paths became curved (Fig. 3B–E, Initial exposure) and MPE increased correspondingly. MPE during the first block of the exposure period was not significantly different across the four groups of subjects (F_(3,112) = 2.647; p = 0.068). However, by the end of exposure (Fig. 3B–E, Final exposure), MPE differed significantly across the different dwell time groups (F_(3,112) = 46.386; p < 0.001). Specifically, using a post hoc test, we found that the lowest MPE occurred for the continuous condition (0 ms dwell time, p < 0.001), followed by the 150 ms dwell time (p < 0.001). In contrast, we found no differences between the MPE in either the 500 or 1000 ms conditions (p = 0.792). Similar results were found for the level of force compensation during final exposure (Fig. 4F), with a significant main effect for dwell time (F_(3,112) = 39.545; p < 0.001). Post hoc tests indicated that the 0 ms dwell time had the highest compensation (p < 0.001), whereas the 150 and 500 ms conditions were not significantly different from each other (p = 0.893), and the 1000 ms condition had the lowest compensation (p < 0.001). Therefore, the development of force compensation was strongly affected by dwell time. For the 0 ms dwell condition, compensation grew steadily, reaching a value of ∼80% by the end of the field trial exposure phase (Fig. 4F). This effect was reduced as dwell time was increased, with little compensation present for 1000 ms dwell times.

For 0 ms dwell times, postexposure movements exhibited large aftereffects in the opposite direction to the field (Figs. 3E, Post exposure, 4E), indicating that the subjects had learned to specifically compensate for the field dynamics. These aftereffects reduced in the postexposure period but were not completely absent by the end of the experiment. As dwell time increased, the size of the postexposure aftereffects progressively reduced (F_(3,112) = 68.865; p < 0.001; Fig. 3B–E, Post exposure). A post hoc comparison demonstrated that the aftereffects were largest for 0 ms dwell times (p < 0.001 for all comparisons), followed by the 150 and 500 ms conditions (not significantly different from each other, p = 0.066; but different from the 1000 ms conditions, p < 0.001). For the 1000 ms dwell time, the aftereffects during the postexposure period were almost completely abolished (Fig. 3B, Post-exposure). The degree of force compensation in the postexposure trials showed significant differences (monotonically decreasing with dwell time) between all four dwell times (post hoc, all p < 0.05) after a significant main effect (F_(3,112) = 34.788; p < 0.001).

Results from these experiments show that associating opposing force fields with distinct previous movements allowed subjects to co-represent each perturbation and learn independent representations for dynamics that would otherwise interfere. However, as the dwell time between the movements in the contextual and adaptation phase increased, the influence of the first movement on the second decayed and was no longer present at 1000 ms. These effects can be clearly seen in both the final exposure and postexposure trajectories across the dwell time conditions (Fig. 3). Specifically, final exposure paths become progressively straighter as dwell time decreases (indicating progressively greater degrees of adaptation), whereas postexposure paths become progressively more perturbed as dwell time decreases (indicating larger aftereffects associated with greater degrees of adaptation). The amount and speed of learning for the various dwell time conditions can be compared against the learning of a single force field under similar conditions as for the continuous group (Fig. 4, black dashed lines).

Experiment 3: contextual motion before target location cues learning

In the experiments described above, subjects were presented with contextual information before the adaptation-phase movement that specified the direction of the upcoming force field. Specifically, both the cue location associated with the contextual phase and the target locations associated with the adaptation-phase movement were displayed at the start of each trial. In experiment 3, we investigated whether it was necessary for the complete contextual information to be provided before subjects initiated the movement or whether subjects could use information from the contextual phase in “real-time” without initially knowing what the adaptation-phase target would be. The experiment was similar to the continuous movement condition experiment 2, with subjects required to make a continuous movement (∼0 ms dwell time). However, during the contextual phase, only the cue position and the central location were presented. The final target was presented only once subjects had reached the central location. In this case, the initial contextual movement alone does not specify the direction of the force field, because the subsequent adaptation phase of the trial could be made to one of two targets, each associated with one of two opposing fields (Fig. 5, compare A, B). Therefore, complete contextual information specifying the direction of the field is only available once subjects have entered the central location and the target location appears.

Despite not knowing which target, and hence which field, they would experience until reaching the central position, subjects were able to learn the opposing fields, exhibiting similar levels of adaptation to the 0 ms dwell time condition (Fig. 5C). Over the course of the exposure period, MPE significantly decreased (F_(1,7) = 560.560; p < 0.001), and significant aftereffects were present in the postexposure period (F_(1,7) = 185.172; p < 0.001). The force compensation values computed from clamp trials (Fig. 5D) exhibit similar levels of adaptation to the 0 ms dwell time condition. The results suggests that a motor plan, which incorporates an adaptation appropriate for the particular force field, can be generated in real time, after the movement associated with the contextual phase has finished. Such an ability could also arise from subject planning for the two potential targets, and hence field directions, and then selecting the appropriate plan (Cisek and Kalaska, 2005). However, we note that, if subjects were indeed planning two complex movements, we might expect that there would be some decrement in learning compared with the condition in which they only need to plan one movement. No such decrement was observed.

Experiment 4: sensory and motor signals involved in the contextual effect

The previous experiment demonstrates that previous motion has a contextual effect on the representation of dynamics during a subsequent movement. However, it is not clear what particular aspects of the previous motion were critical for this effect. For example, during the contextual-phase movement, subjects viewed a moving cursor that represented their hand, may have made eye movements that depend on the motion, actively generated force that led to the motion of their hand, and received feedback information arising from the sensory consequences of its motion. Any of these could be generating the cue responsible for contextual partitioning. Five additional experiments were therefore performed to examine these cues. All five conditions caused large increases in MPE during the presentation of the force fields (all p < 0.001).

Visual cursor motion

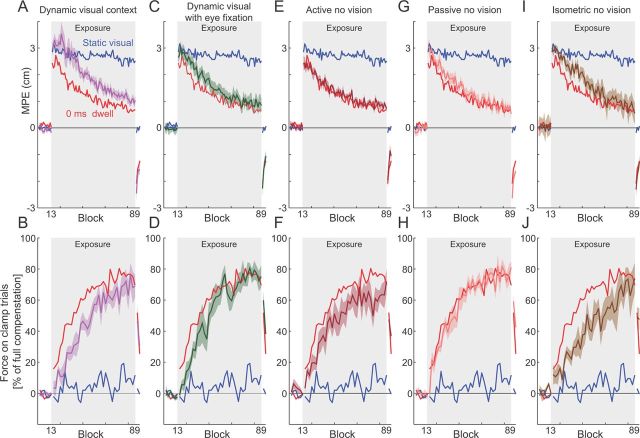
This condition investigated whether visual motion of the cursor alone could provide a contextual cue. Whereas in experiment 2 the contextual phase consisted of an active movement from the cue position to the central location, in this experiment the visual cursor moved although the subject's hand remained stationary at the central location. The subjects actively performed only the second movement (from the central location to the final target during the adaptation phase) once the visual cursor had reached the central location. During the preexposure phase, subjects made approximately straight movements characterized by a low MPE (Fig. 6A). At the onset of the exposure period, subjects exhibited large deviations from straight-line movements that significantly reduced over the course of the exposure period (F_(1,7) = 71.881; p < 0.001; Fig. 6A). Similarly, during the postexposure period, MPE values were significantly larger than those of the preexposure period, consistent with the presence of aftereffects (F_(1,7) = 50.363; p < 0.001). Force compensation values were similar to the 0 ms dwell time condition (Fig. 6B). This indicates that a moving cursor that was predictive of the upcoming force field provides a strong contextual cue for representing the opposing dynamics.

Figure 6.

Sensorimotor cues involved in contextual effects. In all conditions, to aid comparison, the mean results for the normal condition static visual (blue trace) and 0 ms dwell time (red trace) conditions are shown on both MPE and force compensation plots. Shaded gray region indicates exposure period in which the two curl force fields were applied. A, MPE in the dynamic visual context condition. The mean MPE (purple trace) and SE (purple shaded region) across all subjects, as a function of experimental block. In this condition, the cursor was moved visually from the cue location to the central location while the subject's hand was stationary at the central location before the subject actively moved to the final target. B, Percentage force compensation in the dynamic visual condition. C, MPE in the dynamic visual context with eye fixation. Subjects were required to maintain eye fixation at the central target during the dynamic visual presentation. D, Percentage force compensation in the dynamic visual context with eye fixation. E, MPE in the active previous motion with no visual cursor condition. F, Percentage force compensation in the active previous motion with no visual cursor condition. G, MPE in the passive previous motion with no visual cursor condition. H, Percentage force compensation in the passive previous motion with no visual cursor condition. I, MPE in the isometric force context condition. J, Percentage force compensation in the isometric force context condition.

Visual cursor motion during eye fixation

In the previous condition, while the cue was purely visual motion of the cursor, the subjects may have tracked the cursor with their eyes. To exclude any possible contextual effects associated with such previous movement, an additional group of subjects performed the same experiment but were required to fixate the central location during the contextual phase of each trial, while the visual cursor was in motion. Over the course of the exposure period in this experiment, MPE significantly decreased (F_(1,5) = 99.377; p < 0.001). In addition, significant aftereffects were present in the postexposure period of the experiment (F_(1,5) = 169.605; p < 0.001; Fig. 6C). Force compensation values were similar to the 0 ms dwell time condition (Fig. 6D). This confirms that visual motion independent of eye movement provides strong contextual information for the motor system.

Active movement without vision

The previous experiments demonstrate that a moving visual cursor is sufficient to provide a contextual cue to allow two opposing force fields to be learned simultaneously. In this condition, we investigated whether active movement of the limb in the absence of visual feedback could also provide a contextual cue. During the contextual phase, subjects actively moved from the cue position to the central target without the presentation of a visual cursor but instead guided by a mechanical channel. On the introduction of the field during the exposure period, MPE values during the adaptation phase initially increased and then significantly reduced over the course of exposure (F_(1,5) = 66.622; p < 0.001; Fig. 6E). Similarly, significant aftereffects were present during the postexposure period (F_(1,5) = 156.539; p < 0.001), indicating that subjects had learned the appropriate compensation for each field. Force compensation values were similar to the 0 ms dwell time condition (Fig. 6F). In fact, the results from this experiment gave near identical results to those of experiment 2 (active movement with visual feedback), indicating that active movement in the absence of vision provides a strong contextual cue.

Passive motion without vision

Proprioceptive feedback associated with the motion of the arm is another component of an actively generated movement, which could play a contextual role. Although we cannot generate the identical feedback received during active movement, we can approximate this by imposing a passive movement on the limb. To investigate whether such sensory feedback alone can also act as a contextual cue, we passively moved the subject's arm during the contextual phase. MPE values and force compensation are shown in Figure 6, G and H, respectively. Overall, the results from this experiment were similar to those from the 0 ms dwell time condition of experiment 2, indicating that passive movement in the absence of vision is also a strong contextual cue for the motor system. Over the course of the exposure period, MPE significantly decreased (F_(1,5) = 255.052; p < 0.001), and significant aftereffects were present in the postexposure period (F_(1,5) = 262.509; p < 0.001).

Isometric force generation

To investigate whether force generation alone in the absence of arm movement could act as a cue to the motor system, in this experiment subjects were required to generate an isometric force in one of two directions during the contextual phase of each trial. During isometric force generation, the mean ± SD peak displacement of the handle across all clamp trials and subjects was small (1.4 ± 0.79 mm). After the contextual phase, subjects were required to move a cursor from the home position to the final target. The direction of the force field during the movement was uniquely specified by the direction of the isometric force for each subject. After introduction of the field during the exposure period, MPE values initially increased and then significantly reduced over the course of exposure (F_(1,5) = 146.827; p < 0.001; Fig. 6I). Similarly, significant aftereffects were present during the postexposure period (F_(1,5) = 140.277; p < 0.001), indicating that subjects had learned the appropriate compensation for each field. The amount of force compensation rose slowly during exposure, reaching a similar level to the other experiments by the end of exposure (Fig. 6J). These results indicate that isometric force generation produces a strong contextual effect on subsequent dynamic learning, demonstrating that motion per se is not necessary. We hypothesize that the sensorimotor state associated with isometric force generation during the contextual phase leads to this contextual learning effect, although it is not possible to rule out contributions from somatosensory feedback.

Consistent contextual effects across conditions

In each experiment, two channel trials (toward the T1 target) were randomly interspersed in each block of trials to examine feedforward adaptation. Although a reduction in kinematic error during force-field learning can be achieved through co-contraction (Franklin et al., 2003; Milner and Franklin, 2005), this does not result in the appropriate force applied against the channel wall. For each subject, the integrated force applied against the channel wall was divided by the integrated force required to completely compensate for the field (as determined by the field strength and movement velocity on each trial). To compare this measure across all of the experiments, the average dwell times used by each subject in each condition were calculated. An ANOVA indicated a significant main effect of experimental condition (F_(11,76) = 21.137; p < 0.001), and this was further examined using post hoc tests. For conditions with small dwell times, the force-field compensation over the last third of the exposure period approached 80% (Fig. 7A). This amount of compensation was consistent across all contextual conditions that were associated with small dwell times (active or passive movement, dynamic visual motion, isometric force, 0 ms dwell condition; all p > 0.9 for post hoc comparisons). However, as the dwell time increased, the percentage of force compensation decreased, and, by 1000 ms, it was not different from the static visual or static visual attention conditions (all p > 0.99 for post hoc comparisons). The level of adaptation measured on clamp trials during the exposure period were also mirrored by MPE, in both the final exposure period (Fig. 7B) and the postexposure aftereffects (Fig. 7C). In both of these measures, after a significant main effect of experimental condition (final exposure MPE, F_(11,76) = 11.176, p < 0.001; postexposure MPE, F_(11,76) = 23.622, p < 0.001), post hoc tests found similar results. There were no differences across all experimental conditions with short dwell times (all p > 0.67 for post hoc comparisons), and the two static visual conditions were not significantly different from both the 500 and 1000 ms dwell conditions based on post hoc comparisons (all p > 0.3 for post hoc comparisons). However, these two groups were significantly different from one another (all p < 0.05 for post hoc comparisons). These effects were not a result of any systematic change in peak velocity with dwell time (Fig. 7D). Specifically, an ANOVA found no significant main effect for experimental condition on peak velocity (F_(11,76) = 1.735; p = 0.081).

Figure 7.

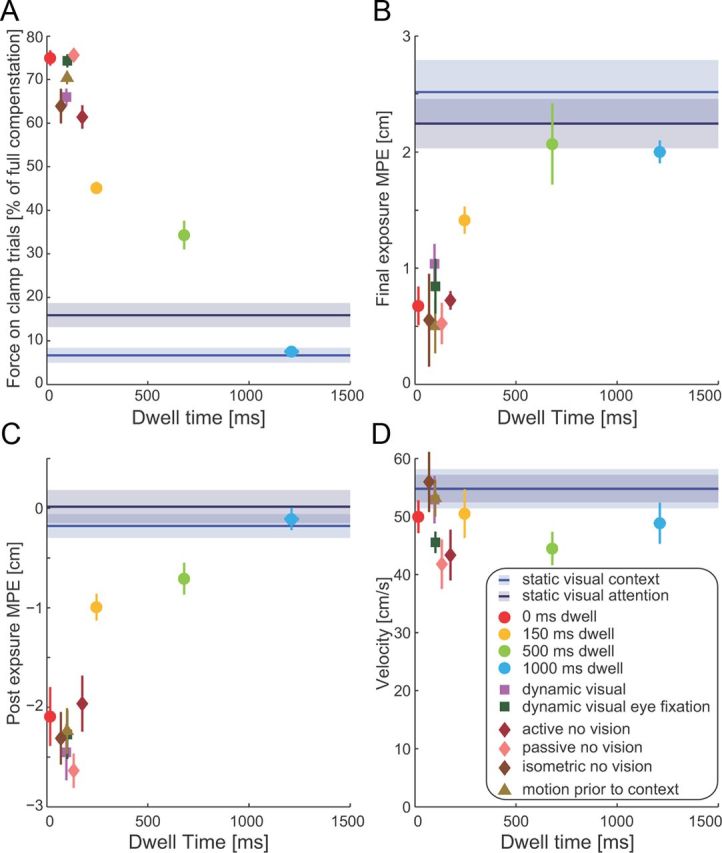
Contextual effects vary with dwell time. A, The mean ± SE force on clamp trials (in direction toward target T1) as a percentage of the force required for estimated complete compensation. Values for all experiments (on the last third of trials during force-field exposure) are plotted as a function of the mean dwell time that subjects used in these conditions, with SE indicated by horizontal error bars. Note that most of the horizontal error bars are so small that they disappear under the symbols. For comparison, the results from the visual static conditions are plotted as a line (shaded region indicates SE) across all dwell times, because they are not related to a particular dwell time. B, The mean ± SE MPE over the last block of trials during force-field exposure. C, The mean ± SE MPE over the first block of trials in the postexposure session in all experiments. D, The mean ± SE peak velocity across all subjects in all experimental conditions experiments (on the last third of trials during force-field exposure), plotted as a function of dwell time.

Discussion

Using an interference paradigm involving opposing dynamic force fields, we examined how the contextual effect of past states affects the formation of motor memory. Our task consisted of a contextual phase followed by an adaptation phase, allowing us to investigate the effectiveness and time course of contextual cues. Consistent with previous studies (Gandolfo et al., 1996), static visual cues resulted in strong interference. In contrast, movements made during the contextual phase resulted in substantial adaptation. When the contextual- and adaptation-phase movements were close to continuous, interference was minimal and performance approached 80% of full adaptation, comparable with that reported for adaptation to a single force field (Joiner and Smith, 2008; Sing et al., 2009; Joiner et al., 2011). As the time between the contextual and adaptation phase movements increased (the dwell time), adaptation fell to ∼45 and 30% for the 150 and 500 ms dwell times, respectively. By 1000 ms, the contextual effect of previous movement was abolished, and performance did not differ significantly from that observed with static visual cues.

Interference was similarly reduced when subjects simply observed a moving cursor during the contextual phase (while their hand was stationary), regardless of whether eye movements were allowed or not, suggesting an important contextual role for visual motion. Active or passive arm movements in the absence of visual motion and isometric force generation in the absence of movement also exerted strong contextual effects. All these experiments exhibited similar patterns of adaptation to the 0 ms dwell time experiment (in which all cues are present), suggesting that each component is as effective as the combination of cues.

Consistent with previous studies (Gandolfo et al., 1996), we show that static visual cues are not sufficient to reduce interference over short timescales, even when spatial attention is required on the cue. Although visual cues have been reported to have some ability to reduce interference, this was only after extensive training (Krouchev and Kalaska, 2003; Wada et al., 2003; Osu et al., 2004). In contrast, previous studies have found stronger contextual effects for concurrent movements, such as unimanual versus bimanual contexts (Nozaki et al., 2006) and different types of bimanual movement (Howard et al., 2008, 2010). In the current study, we focus on the contextual effect of previous movement during a unimanual task. Our results are consistent with a previous study that looked at sequential motion (i.e., dwell times of 500 ms or more), which found a small but significant reduction in interference (Wainscott et al., 2005). However, we show that interference markedly decreases with shorter dwell times. At 0 ms dwell time and for purely visual or passive motion, we see a reduction in interference that is unprecedented in the literature, with final adaptation levels close to single force-field learning (although the initial rate of adaptation was slower than for single fields).

Previous computational studies of dynamic learning suggest that subjects learn a mapping from current state to the force required to compensate for the field (Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Franklin et al., 2008). That is, the force vector (F_t) at time t is some function of position (x_t) and velocity (v_t), F_t = g(x_t, v_t). Such a model can account for standard single field learning but cannot account for our observed findings. Our results suggest that the representation may not simply depend on the current state but also on previous states. For example, we can write that force at time t depends on previous states s (including visual and proprioceptive inputs as well as motor output) over a 600 ms window as follows F_t = g(s_t, s_{t − 1}, s_{t − 2}, _… s_{t − 600}), representing time discretely in 1 ms steps. Such a representation would allow opposing fields to be learned, provided the states in the 600 ms before opposing force-field exposure were different. If we assume that the state s_{t − k} represents the true state with additive noise, such a model can also explain why adaptation increases with shorter dwell times. As dwell time decreases, more elements of {s_t, s_{t − 1}, s_{t − 2}, … s_{t − 600}} are different for the two fields, and hence more terms contribute to disambiguate them. As dwell time increases, fewer elements will be different, leading qualitatively to decay in adaptation with dwell time. Our results suggest that s_t may represent active and passive arm motion, visual motion, or isometric force generation. Such a mechanism may also explain the ability of pairing rhythmic and discrete movements with opposing kinematics or dynamics to reduce interference (Ikegami et al., 2010; Howard et al., 2011), because these different movement classes exhibit speed profiles with different recent histories.

Contextual cues in cerebellar-based motor learning have been extensively studied for classical conditioning of the eyelid response. In eyeblink conditioning, a finite temporal window exists during which the conditioned stimulus (such as a tone), when paired with the unconditioned stimulus (a puff of air), can come to elicit a behaviorally adaptive motor response (the protective blink). The range of effective conditioned stimuli can be regarded as contextual cues, which modulate upcoming movements. They are presented to Purkinje cells via the parallel fiber system (Kim and Thompson, 1997). In eyelid conditioning, Purkinje cells learn which contextual cues (which parallel fiber inputs) can predict (and correct) the erroneous motor output. Of relevance to the current study, Purkinje cells can encode the kinematics of active movements (Harvey et al., 1977), passive movements (Rubia and Kolb, 1978), and target motion during a tracking task (Shidara et al., 1993). More recently, Purkinje cell activity was found to correlate with arm kinematics over a window extending 500 ms into the past (Hewitt et al., 2011). Moreover, the cerebellum plays an important role in dynamic force-field learning (Maschke et al., 2004; Smith and Shadmehr, 2005) and may implement internal models in the motor system (Miall et al., 2007; Ebner and Pasalar, 2008; Hewitt et al., 2011). The view emerging from these previous studies is consistent with our current results, suggesting that cues related to physical or visual motion have important contextual roles during motor learning, decaying in effectiveness over a finite contextual window.

From a behavioral perspective, there is evidence for preactivation of upcoming actions in serially ordered sequences (Lashley, 1951). Several lines of evidence have suggested that 500 ms is a key temporal boundary for such interactions to occur. For example, in saccadic adaptation studies, when a delay of 400–600 ms is introduced between the saccade and the displaced target reappearing, there is a substantial reduction in saccadic gain adaptation (Fujita et al., 2002). In addition, a recent study has challenged the idea that the dorsal action-related visual stream has little or no memory. In an obstacle-avoidance task, when trials were performed with an intertrial interval of <1000 ms, there was a significant effect of the kinematics of the previous trial on the current one, with the effect increasing with decreasing intertrial intervals (Jax and Rosenbaum, 2009). Our results suggest that similar time periods associated with previous motion have substantial impact on the ability to store motor memories.

There are many ways in which recent states could affect motor learning. One proposed mechanism involves engaging separate populations of neurons (Wolpert and Kawato, 1998; Nozaki et al., 2006). Several recent multicompartment models have been developed to mathematically formalize the context-dependent reduction in interference (Lee and Schweighofer, 2009; Nozaki and Scott, 2009). In our case, recent sensorimotor states—possibly encoded by cerebellar output—appear to engage such different representations. An alternative view is to regard the neural ensemble (such as primary motor cortex M1 activity) as a dynamical system. Movement initiation (or planning) leads to a transition of ensemble activity from a wandering state to a specific location in neural state space, thereby initializing the dynamical system to a state that generates the required movement (Churchland et al., 2010, 2012). In the case in which one movement follows another, the initial state would be different from a movement de novo, allowing a separation in the representation of opposing dynamics.

Our study provides the first evidence for a dramatic reduction in interference based on previous sensorimotor state. Naturally, we acknowledge that this study raises a number of interesting questions. For example, the strong effect of purely visual motion needs additional investigation to understand the role of the location and form of the visual motion that leads to the reduction in interference. Also, although we expect a similar temporal decay in adaptation for visual motion and isometric contexts, this is yet to be demonstrated. We regard it as strength of our findings that they lead naturally to a range of additional questions that can be addressed.

In conclusion, we have shown that the recent history of previous states plays a fundamental role in reducing interference. However, this ability decays progressively with increasing temporal separation between the contextual and adaptation phases. Our results show that many state-dependent sensorimotor cues have a strong contextual effect on subsequent movements. As such, they can lead to the formation of separate motor memories for the representations of dynamics in movements that would otherwise form a single memory.