Lagrangian transport properties of pulmonary interfacial flows

Abstract

Disease states characterized by airway fluid occlusion and pulmonary surfactant insufficiency, such as respiratory distress syndrome, have a high mortality rate. Understanding the mechanics of airway reopening, particularly involving surfactant transport, may provide an avenue to increase patient survival via optimized mechanical ventilation waveforms. We model the occluded airway as a liquid-filled rigid tube with the fluid phase displaced by a finger of air that propagates with both mean and sinusoidal velocity components. Finite-time Lyapunov exponent (FTLE) fields are employed to analyse the convective transport characteristics, taking note of Lagrangian coherent structures (LCSs) and their effects on transport. The Lagrangian perspective of these techniques reveals flow characteristics that are not readily apparent by observing Eulerian measures. These analysis techniques are applied to surfactant-free velocity fields determined computationally, with the boundary element method, and measured experimentally with micro particle image velocimetry (μ-PIV). We find that the LCS divides the fluid into two regimes, one advected upstream (into the thin residual film) and the other downstream ahead of the advancing bubble. At higher oscillatory frequencies particles originating immediately inside the LCS experience long residence times at the air–liquid interface, which may be conducive to surfactant transport. At high frequencies a well-mixed attractor region is identified; this volume of fluid cyclically travels along the interface and into the bulk fluid. The Lagrangian analysis is applied to velocity data measured with 0.01 mg ml⁻¹ of the clinical pulmonary surfactant Infasurf in the bulk fluid, demonstrating flow field modifications with respect to the surfactant-free system that were not visible in the Eulerian frame.

1. Introduction

Pulmonary surfactant is a surface-active compound comprising lipids and proteins that is incorporated in the lining fluid that coats the alveoli and bronchioles in the lower respiratory tract. Surfactant is produced by the cells lining the alveoli and functions to prevent atelectasis and atelectrauma by dynamically reducing surface tension in the lungs (Grotberg 2001). Pulmonary surfactant deficiency is a hallmark of respiratory distress syndrome (RDS) and acute lung injury (ALI), diseases that are further characterized by the closure and fluid occlusion of pulmonary airways. Mechanical ventilation and treatment strategies such as surfactant replacement therapy (SRT) must be administered to restore airway patency. Unfortunately, these lifesaving treatments carry the risk of ventilator-induced lung injury (VILI). According to Rubenfeld et al. (2005), 74 500 persons die of acute lung injury in the USA each year, a figure comparable to the number of adult deaths attributed to breast cancer or human immunodeficiency virus disease in 1999. At the same time, 57% of patients survive acute lung injury each year (Zambon & Vincent 2008), many of whom require care for cognitive abnormalities, weakness, depression, or post-traumatic stress disorder. Mechanical stresses at the airway wall, due to migrating air–liquid interfaces, play an important role in airway damage during RDS, ALI, and VILI (Matthay et al. 2002).

The mechanics of single-airway reopening have been modelled by the propagation of a semi-infinite bubble through a fluid-occluded flexible tube (Gaver, Samsel & Solway 1990) or channel (Gaver et al. 1996; Jensen et al. 2002; Halpern et al. 2005). However, airway reopening phenomena may also be explored in rigid geometries (Halpern & Gaver 1994; Zimmer, Williams & Gaver 2005; Smith & Gaver 2008). The rigid-wall assumption allows utilization of previous studies of semi-infinite bubble propagation, including Bretherton (1961) , Shen & Udell (1985), Lu & Chang (1988) and Heil (2001).

In vitro experiments and computations presented in Bilek, Dee & Gaver (2003) and Kay et al. (2004) demonstrate that the pressure gradient near the bubble tip sweeps across the epithelial layer and is instrumental to its damage. Bilek et al. (2003) showed that the exogenously delivered clinical pulmonary surfactant Infasurf (ONY Inc., Amherst NY) reduces airway epithelial cell damage during steady airway reopening. More advanced models of airway reopening have explored physicochemical characteristics including the time-dependent damaging mechanical stresses during pulsatile flow (Smith & Gaver 2008) or the effects of surfactant on the flow field (Ghadiali, Halpern & Gaver 2001; Ghadiali & Gaver 2003; Naire & Jensen 2005). These studies show that surfactant uptake at the migrating air–liquid interface is instrumental in reducing the magnitude of the pressure gradient that can lead to cell damage in atelectrauma. However, transport limitations in steady flow can significantly reduce the efficacy of surfactant delivery (Ghadiali & Gaver 2000). Furthermore, delivery of exogenous surfactant to the deep lung is difficult; therefore, it is advantageous to utilize existing low concentrations of endogenous surfactant through a novel engineered ventilation waveform.

Surfactant transport is a multi-step process that depends upon convection and diffusion in the liquid phase, and sorption to and from the air–liquid interface (Stebe & Barthes-Biesel 1995; Yap & Gaver 1998; Ghadiali & Gaver 2003). As discussed in § 7, in airway reopening the Péclet number describing the relationship between convective and diffusive transport is extremely large; therefore, convection is the dominant transport process in the bulk fluid. Unfortunately, the instantaneous Eulerian velocity profiles computed in prior investigations do not fully clarify the time-dependent convective transport properties of the flow.

The goal of the current study is to develop and use Lagrangian methods to elucidate convective transport properties that are fundamental to surfactant transport. This will help to develop insight into the trajectories that surfactant molecules will follow as they migrate to the air–liquid interface, from which the adsorption process is a critical step. In this investigation we study pulsatile airway reopening and seek to identify coherent structures that may be exploited to improve mechanical ventilation strategies. These strategies may enhance surfactant transport from the bulk to the interface, thereby reducing the damaging mechanical stresses and stress gradients at the wall. We first consider finite-time Lyapunov exponent (FTLE) fields and Lagrangian coherent structures (LCSs) computed from boundary element method (BEM) velocity fields to identify transport processes and validate our experimental results under surfactant-free conditions. This helps to demonstrate the existence of convective flows that can be used to distribute surfactant near a bubble tip. These Lagrangian techniques are then extended to velocity distributions measured with micro-particle image velocimetry (μ-PIV) to investigate transport modifications in a surfactant-doped solution using the clinical pulmonary surfactant Infasurf (ONY Inc., Amherst NY) during pulsatile bubble motion. We hypothesize that pulsatile flow conditions will modify surfactant transport and enhance adsorption to the interface, thereby reducing damaging stresses on the airway wall.

2. Analytic methods

2.1. Flow field simulation

In this section, we review the model of Smith & Gaver (2008), which computes the fluid velocity field during pulsatile semi-infinite bubble propagation. These simulations are used to establish the convective transport behaviour in an idealized system. This provides the foundation for the subsequent analysis of transport processes observed experimentally with and without pulmonary surfactant. The boundary velocities and stresses are first computed with the BEM and a subsequent algorithm is used to determine the Lagrangian particle trajectories and the FTLE field.

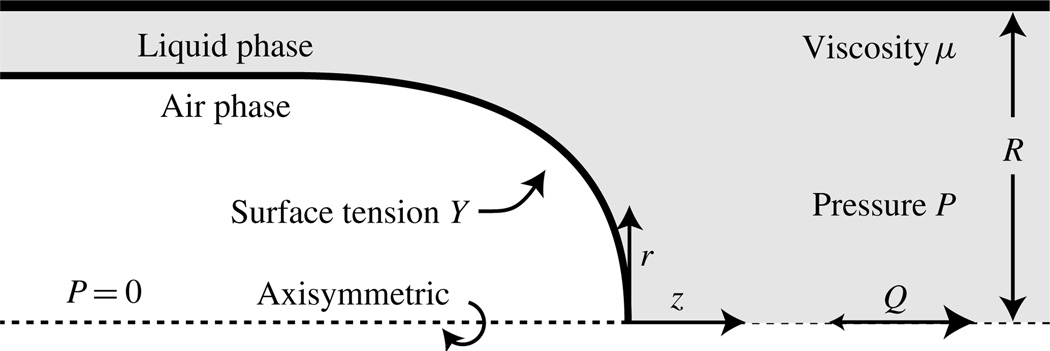
The system is modelled using the BEM coupled to a lubrication theory approximation in the upstream film region, as shown in figure 1, with the equations formulated in cylindrical coordinates. The liquid occlusion is assumed to be surfactant-free; the fluid viscosity μ and surface tension γ are held constant.

Figure 1.

Computational domain from Smith & Gaver (2008). The model is divided into two regions described by the boundary element region (BEM) and lubrication theory (LUBE). In the BEM region, bounding surfaces are described by 3-node quadratic elements.

We scale the governing equations as in Smith & Gaver (2008) using the following scales:

$$(r^{*},z^{*})=R(r,z),(u_z^{*},u_r^{*})=\left(\frac{\gamma }{\mu }\right)(u_z,u_r),P^{*}=\frac{\gamma }{R}P,t^{*}=\left(\frac{R\mu }{\gamma }\right)t.$$ (2.1)

Using these scales, the dimensionless flow field is governed by the capillary number Ca = μQ^*(t^*)/πR²γ, which represents the relationship between viscous and surface-tension-induced forces and is defined by the dimensional flow rate Q^* and tube radius R. Pulsatility is imposed by the unsteady capillary number

$$\mathit{\text{Ca}}={\mathit{\text{Ca}}}_M+{\mathit{\text{Ca}}}_{\Omega }\text{sin}(\Omega t),$$ (2.2)

which comprises mean (Ca_M) and oscillatory (Ca_Ω) components. The system is further parametrized by the dimensionless driving frequency Ω = μωR/γ, which represents the balance between the dimensional frequency ω and the interfacial relaxation time scale, and the oscillatory amplitude A = 2Ca_Ω/Ω, which describes the dimensionless oscillatory stroke length.

The flow field is described by the dimensionless Stokes equations (2.2) and the continuity (equation 2.3):

$$\mathbf{\nabla }P(\mathit{x},t)={\nabla }^2\mathit{u}(\mathit{x},t),$$ (2.3)

$$\mathbf{\nabla }•\mathit{u}=0,$$ (2.4)

for the fluid velocity u(x, t) and the pressure P(x, t). The governing equations and boundary conditions are posed in the laboratory frame of reference. Since simulation in this frame would result in an extremely long domain when solved over a long period of time, the solution is kinematically translated to the bubble tip frame of reference as described by Smith & Gaver (2008).

The axisymmetric domain (figure 1) includes the downstream surface where a time-dependent flow rate is imposed, the tube walls (no-slip and no penetration condition), and the interfacial surface (stress condition). The air–liquid interface is a free surface; as such the geometry is computed as part of the solution process. This time-dependent domain is used as a guide for seeding a uniform grid of particles to compute the FTLE at a given initial time.

2.2. Convective transport analysis overview

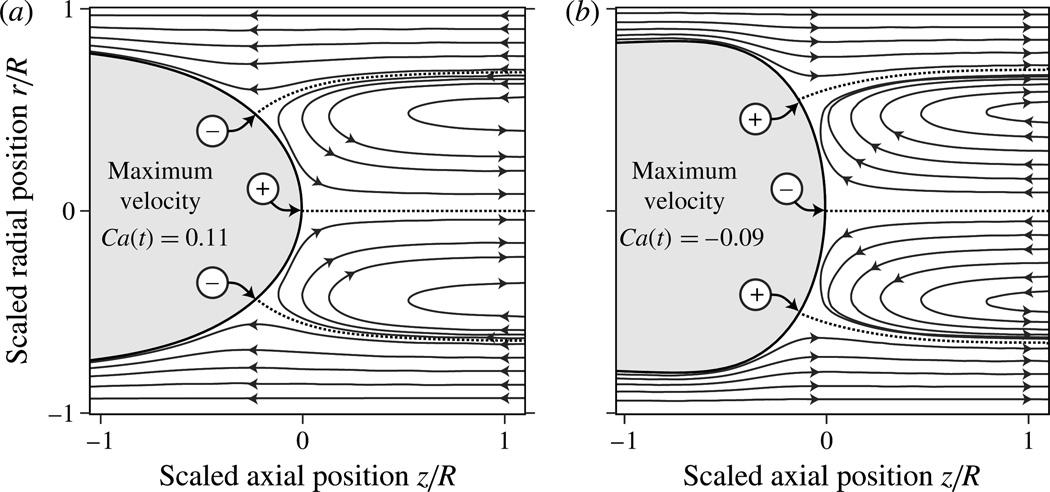
If the mean capillary number dominates (Ca_M > Ca_Ω) the system is approximated by steady-state behaviour, as discussed in the context of the normal stress gradient by Smith & Gaver (2008). Interesting dynamics occur when Ca_Ω > Ca_M, resulting in retrograde bubble motion (reverse flow). Instantaneous streamlines (figure 2) for the ‘case III’ parameters in table 1 demonstrate converging (+) and diverging (−) stagnation points that move along the air–liquid interface tip as a function of time.

Figure 2.

Streamlines computed at the (a) maximum and (b) minimum velocities during pulsatile bubble propagation for the ‘case III’ parameters in table 1. Dashed lines indicate stagnation streamlines, (+) and (−) denote the locations of converging and diverging stagnation points, respectively.

Table 1.

Non-dimensional parameter values for the different cases in the study. Here, A is the amplitude of the oscillations, Ω is the frequency, and Ca_M and Ca_Ω are the mean and oscillatory capillary numbers.

	BEM Case I Low A, high Ω	BEM Case II High A, low Ω	BEM Case III High A, high Ω	PIV Case IV Water	PIV Case V Infasurf
CaM	0.01	0.01	0.01	8.3 × 10−5	2.5 × 10−4
CaΩ	0.02	0.025	0.1	1.7 × 10−4	5.2 × 10−4
Ω	0.04	0.01	0.04	4.7 × 10−5	1.4 × 10−4
A	1	5	5	7.4	7.4
TI	20T	3T	20T	2T	2T

However, for unsteady flow, frozen snapshots in time are not adequate to fully describe Lagrangian transport properties (Mancho & Wiggins 2006). The analysis techniques presented in the current study integrate the effects of the temporally and spatially dependent velocity field to describe convective transport as the system evolves through time. Time-periodic velocity fields have traditionally been explored with Poincaré sections (Ottino 1989). This technique provides geometric information about the flow for a given set of initial conditions, and may also be applied to quasi-periodic and chaotic trajectories. Poincaré maps also reduce the dimensionality of the system because the time-dependent velocity field is converted into a map that yields a discrete dynamical system. In other words, rather than studying a tracer particle trajectory as a curve in space as time progresses, a periodic particle trajectory may be viewed as a discrete set of points. As such, we use this approach to analyse the high-frequency behaviour of the computational model in §§ 4.3 and 4.4.

In addition to Poincaré sections, we employ FTLE analysis. This technique has previously been employed to study periodic, pulsatile blood flow in the carotid artery by Shadden & Taylor (2008). That study identified Lagrangian coherent structures that characterize underlying transport structures in turbulent flow, such as vortices that occur in the presence of an aneurysm. In the current study, identifying an LCS in the bubble tip region allows us to investigate the Lagrangian transport properties of the fluid and identify flow regimes that may improve surfactant transport.

2.3. Lagrangian coherent structures

We define a coherent structure as one that is present in flow for long time periods. In steady flows, this corresponds to stable and unstable manifolds that act as separatrices, or boundaries, that separate regions of qualitatively different flow. Haller, in a series of papers (Haller & Poje 1998; Haller 1999, 2001a,b, 2002), investigated the notion of time-independent and finite-time hyperbolic trajectories, which are individual trajectories to which other trajectories are either attracted to or repelled from over a prescribed time interval. In unsteady flows, these are referred to as Lagrangian coherent structures (LCSs).

In the current study we construct FTLE fields from both computed and measured Eulerian velocity distributions in order to locate Lagrangian coherent structures. Over a prescribed time interval, the FTLE field gives a scalar measure of the average amount of stretching of initially nearby trajectories from each initial condition (Shadden, Dabiri & Marsden 2006).

Shadden, Lekien & Marsden (2005) defines LCSs as manifolds that locally maximize the scalar field, and they develop a flux estimate showing that LCSs converge to material lines for long integration times. It is also important to note that finite-time hyperbolicity properties may change depending on the choice of time interval (Mancho & Wiggins 2006).

2.4. Finite-time Lyapunov exponent fields

Identifying hyperbolic trajectories by computing Lyapunov exponents over a finite-time interval reveals the time-average maximal and minimum stretching between initially adjacent fluid markers (‘particles’) over the fixed interval of time. By plotting these maximal strains as a scalar field, hyperbolic trajectories may be detected.

To compute the FTLE a regular grid of particles is defined at time t = t₀ and the Lagrangian trajectory of each particle from the initial position x₀ may be constructed by solving the initial value problem:

$$\frac{\mathrm{d}\mathit{x}}{\mathrm{d}t}=\mathit{u}(\mathit{x}(t),t),$$ (2.5a)

$$\mathit{x}(t_0)={\mathit{x}}_0.$$ (2.5b)

This describes the relationship of the Eulerian fluid velocity field u to the flow map

$${\varphi }_{t_0}^{t_0+T_I}(\mathit{x}):\mathit{x}(t_0)\to \mathit{x}(t_0+T_I),$$ (2.6)

that describes the position of the particle after an integration time T_I. As in Shadden et al. (2005), we define the finite-time version of the right Cauchy–Green deformation tensor

$$\mathit{\Delta }(\mathit{x})=\mathit{J}{({\varphi }_{t_0}^{t_0+T_I}(\mathit{x}))}^{\mathrm{T}}\mathit{J}({\varphi }_{t_0}^{t_0+T_I}(\mathit{x}))$$ (2.7)

where J is the Jacobian matrix and superscript T indicates the transpose. The FTLE field is then defined by

$${\sigma }_t^{T_I}=\frac{1}{|T_I|}\text{log}\sqrt{{\mathrm{\lambda }}_{\mathit{\text{max}}}(\mathit{\Delta }(\mathit{x}))},$$ (2.8)

where λ_max(Δ(x) is the maximum eigenvalue of the symmetric matrix Δ(x), and designates the maximal divergence of fluid particles near x over the integration time T_I. Haber et al. (2000) present a mathematically similar technique in their investigation of the transport properties of inhaled particulates, considering Lagrangian stretching as suggested by Ottino (1989). The rate of strain tensor for the displacement of a single particle over an entire breathing cycle is analysed, instead of the instantaneous velocity rate of strain.

The computed FTLE value (σ) is referred to as a ‘forward-time’ FTLE if T_I > 0 (figure 3a). Here, the maximal ridges in the FTLE field define the location of the repelling LCSs, which corresponds to the most rapid deviation of trajectories between particles that were adjacent at time t₀. Therefore, the repelling LCSs represent unstable manifolds and repel trajectories. Particles cannot cross the repelling LCSs. In steady bubble propagation, the repelling LCS intersects the air–liquid interface at the diverging stagnation point.

Figure 3.

(a) Forward-time (T_I = 20 periods), (b) backward-time (T_I = −20 periods), and (c) overlaid forward- and backward-time FTLE fields for case III (high A, high Ω computations: see table 1) at time D (figure 6). The repelling LCS is shown in red in (a) (forward-time FTLE) and (c) (overlaid forward- and backward-time FTLEs). The attracting LCS is determined from the backward-time FTLE in (b) and is also shown in (c). The colour bar (d) corresponds to (a) and (b).

In contrast, the ‘backward-time’ FTLE (figure 3b) is computed using tracer particle trajectories for negative integration times (T_I < 0). This reveals the location at which the particles must have been previously located in order to convect to the regular grid positions defined at time t₀. Therefore, the attracting LCSs define attracting manifolds. During steady propagation the attracting LCS intersects the interface at the converging stagnation point. The forward- and backward-time FTLEs are overlaid, as shown in figure 3(c), to investigate the spatial relationship between these two coherent structures.

3. Methodology – simulated flow field

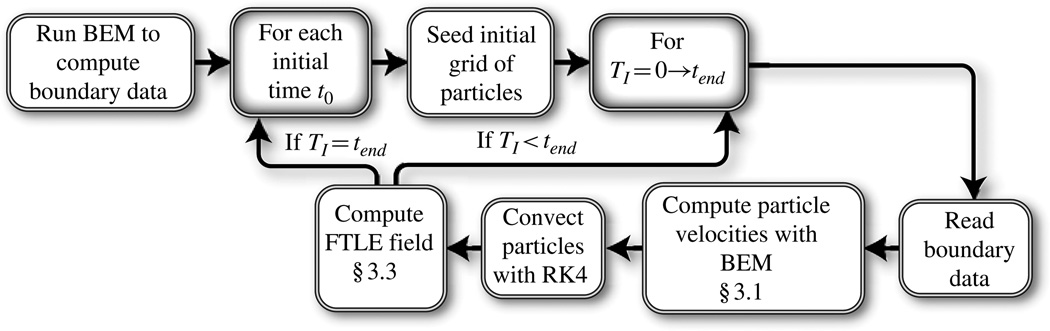
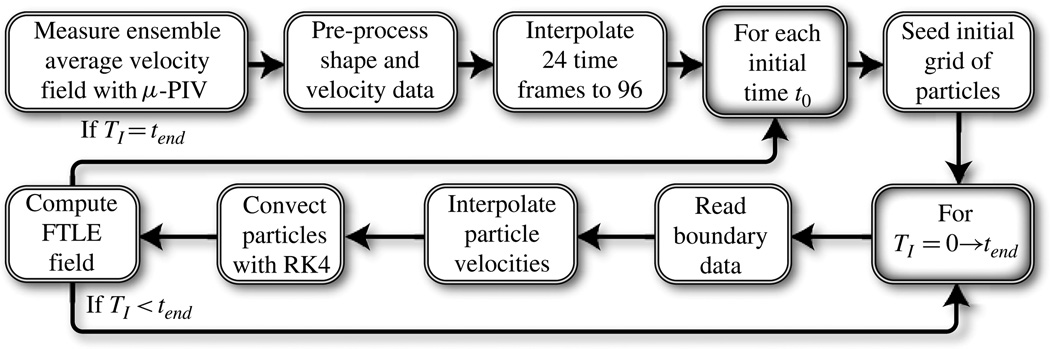
Extending the work of Smith & Gaver (2008) we couple the fluid model with particle integration techniques in order to compute fluid trajectories; a schematic of the algorithm is shown in figure 4. We first solve for the boundary velocities u(r, z) and stresses τ(r, z) at 144 time steps in the oscillatory cycle. For each starting time t₀ we seed a regular grid of particles within the domain, removing points that fall in the air phase.

Figure 4.

Steps to compute the FTLE field from BEM velocity results. Shaded boxes indicate the start of an iterative (for) loop.

To evaluate the flow map ϕ, which describes the translation of a fluid particle x(t₀) at time t₀ to its later position x(t₀ + T_I) at time t₀ + T_I, we compute the Lagrangian displacement following (2.4). To advance the particles to the next time step (t_n) we first read the boundary velocities u(r, z, tⁿ) and stresses τ(r, z, tⁿ) from files; this information is used to evaluate the particle velocity as described in § 3.1. A fourth-order Runge–Kutta (RK4) integrator is used to advance the positions of the particles ${\mathit{X}}_n^i\text{to}{\mathit{X}}_{n+1}^i$ and the FTLE field is computed as described in § 2.4.

3.1. Computing velocity data

The boundary element method is used to solve the Stokes equations and determine the stress and velocity distribution at the domain boundaries. The flow is allowed to develop to a stationary state (Smith & Gaver 2008) and the boundary data for a single oscillation is stored. This information is then used to compute the velocity for each particle. For a point x₀ in the flow domain הי, the internal velocity may be computed exactly by the integral equation (Pozrikidis 1992):

$$u_j({\mathit{x}}_0)={\displaystyle {\int }_{\partial (יה)}{u}_i(\mathit{x})}{T}_{ijk}(\mathit{x},{\mathit{x}}_0)n_k(\mathit{x})\mathrm{d}s-\frac{1}{\mathit{\text{Ca}}}{\displaystyle {\int }_{\partial (יה)}{f}_i(\mathit{x})}{S}_{ij}(\mathit{x},{\mathit{x}}_0)\mathrm{d}s,$$ (3.1)

where f = τ • n is the traction on the boundary, and the tensors S and T are the free-space fundamental solutions for velocity and stress for Stokes flow, respectively. At the air–liquid interface f = κγn, with κ describing the interfacial curvature.

The accuracy of the BEM implementation used in the present study is well established. This includes our studies of the steady propagation of a semi-infinite bubble in a channel, with direct comparisons to analytical solutions (Park & Homsy 1984) under low-Ca conditions, and finite difference simulations for larger Ca (Reinelt & Saffman 1985). Unsteady flows have been validated in Zimmer et al. (2005) and most importantly in Smith & Gaver (2008), which provides the time-dependent Eulerian velocity fields used for the present study. These BEM simulations are executed until stationary state occurs, which is established when the bubble tip curvature, velocity, and pressure drop differ from the previous cycle by < 5 × 10⁻⁸.

We use (3.1) to compute the solution for the velocity at any point in the domain, using the boundary velocities and stresses computed over one period in our preprocessing. To evaluate the velocity of our fluid markers, we use Gaussian elimination with an adaptive quadrature, which we discuss in greater detail below. Singularities exist in the integrands of (3.1) near the boundaries of the domain; to overcome this difficulty we compute the velocity at a safe distance (described below) from the boundary and use the known boundary velocity to interpolate values in the singular region. The distance from the boundary at which interpolation is necessary is determined by comparing the computed velocity to the known downstream velocity, as discussed below.

3.2. Implementation

FTLE simulation requires tracking of the trajectory of many particles (> 50 000) by integrating the time-dependent particle velocity over 2–20 periods of oscillation, depending on the time scales of the particular parameters in question. Furthermore, the choice of initial condition strongly influences the behaviour of the LCSs, necessitating evaluation of many starting times. Because of this tremendous computational expense we employ an adaptive quadrature to reduce run-times while increasing the error in the computed particle velocities by less than 1 × 10⁻⁶. The improvement in computational efficiency afforded by this procedure was substantial; for 56 606 particles running on 160 threads the adaptive quadrature provides a 69% reduction in the run-time for a single time step, from 26.5 to 8.2 s.

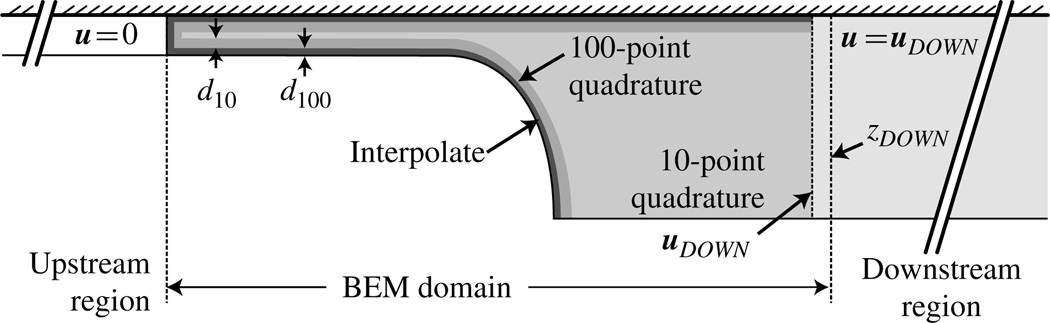
Figure 5 shows a schematic of the adaptive quadrature employed in the BEM velocity evaluations. Inside the BEM domain and far from the boundaries (d > d₁₀ = 0.1), a 10-point Gaussian quadrature is sufficient (figure 5, light grey). Closer to the domain boundaries (d₁₀ ⩾ d > d₁₀₀ = 0.0075), a 100-point quadrature is employed, shown in dark grey. Immediately adjacent to the boundary (d < d₁₀₀ = 0.0075), where the integrand of (3.1) is singular, bilinear interpolation is employed to determine the velocity. The locations of the quadrature transitions (d₁₀, d₁₀₀) are determined by computing the error in the downstream region, where the solution is known. These bounds were established at the distance where the error between the BEM and known values is ε < 1 × 10⁻⁶; we refer to this as a ‘safe’ distance from the boundary.

Figure 5.

The adaptive quadrature employed to increase computational efficiency. A 10-point Gaussian quadrature is used far from the edges of the BEM domain, the quadrature is increased to 100 points near the boundaries. Immediately adjacent to the edges, interpolation is used to determine the velocity.

3.3. Computation of the FTLE field

Following determination of the final positions x(t₀ + T) of each particle we compute the spatial gradient of the flow map $(\mathrm{d}/\mathrm{d}x){\varphi }_{t_0}^{t_0+T_I}(\mathit{x})$ via second-order central differencing. In the case of particles along the boundaries a one-sided second-order finite difference is used. This result is used to evaluate the Cauchy–Green deformation tensor from (2.6). Once the gradient of the flow map is computed, as in Shadden et al. (2005), we obtain the FTLE field by direct evaluation of (2.7). Here, a two-dimensional formulation is appropriate because the velocity field is radially symmetric about the tube centreline.

4. Analysis of the simulated flow field surrounding a pulsatile finger of air

We compute the FTLE fields using the algorithm outlined in figure 4, considering the three computational cases described in table 1. These are as follows.

• Case I: low A, high Ω. Particles are initialized on a 700 × 100 grid on (z, r) ∈ [−2, 5] × [0, 1], with approximately 53 000 particles in the domain.

• Case II: high A, low Ω. Particles are initialized on a 1400 × 100 grid on (z, r) ∈ [−5, 9] × [0, 1] with approximately 97 000 total markers.

• Case III: high A, high Ω. Particles are initially seeded on a 1000 × 100 grid on (z. r) ∈ [−5, 5] × [0, 1] with approximately 60 000 particles.

In all three cases the spatial mesh size is h = 0.01 and the time step Δt is 1/72 period. The BEM domain for all runs consists of 211 total boundary points: 15 downstream, 60 on the upper wall, 6 on the upstream BEM/LUBE boundary, and 130 on the air–liquid interface. The lubrication (LUBE) region contains 100 points.

The integration times T_I vary depending on the oscillation frequency of each case; therefore, T_I is chosen to coincide with the time scales of the problem. We select T_I to be sufficiently large to allow the tracer particles advect far into the upstream (thin film) or downstream regions of the domain. In cases I and III (Ω = 0.04) the integration time T_I = 20T (20 periods), because the flow patterns in these cases require a greater number of oscillations to advect the tracer particles away from the bubble tip region where the FTLE is computed. However, at low frequency (Ω = 0.01), the particles are swept quickly from the tip region and the integration time is only T_I = 3T (3 periods). The experimental data are recorded at extremely low frequencies (Ω < 1.5 × 10⁻⁴); in these cases (IV–V) we use T_I = 2T. This provides an adequate integration duration to visualize the convective transport properties of the field.

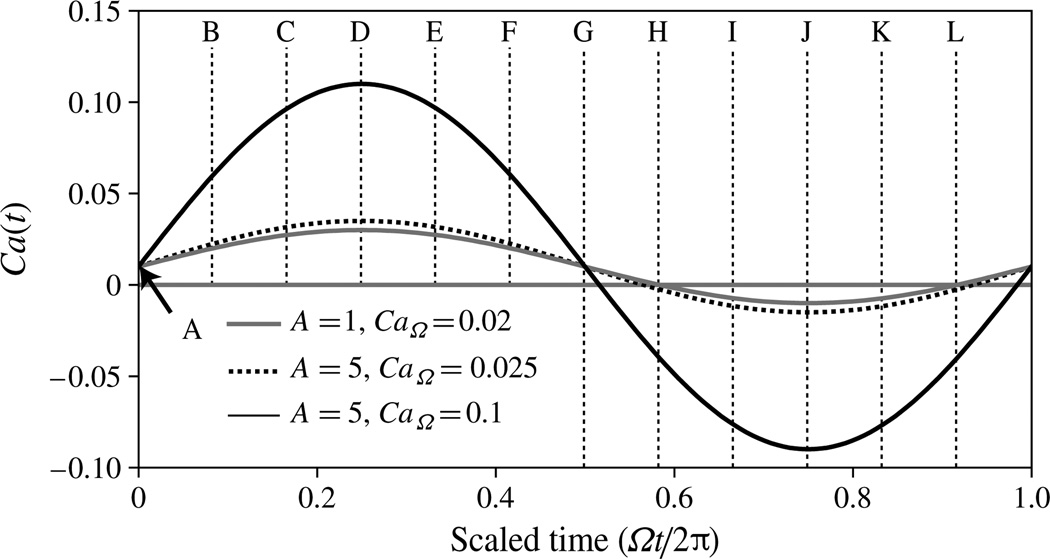
For all of our FTLE computations we investigate a range of starting times t₀. Since the unsteady capillary number Ca(t) = Ca_M + Ca_Ω sin(Ωt) is sinusoidal, we study initial starting times with respect to different portions of the pulsatile cycle. The unsteady capillary numbers for the computational cases are illustrated in figure 6 with letters A–L demarcating initial times t₀ that are explored in more detail below.

Figure 6.

Time-dependent capillary number Ca(t) for the three BEM cases (I–III), showing the time-points A–L at which particles are initially seeded (t₀).

4.1. Case I: low amplitude, high frequency (Ca_Ω = 0.02, A = 1, Ω = 0.04)

In figure 7(a) we provide a four-panel description of the FTLE field and LCS for the low-amplitude case I (A = 1, Ω = 0.04), with particle positions and pathlines in the neighbourhood of the LCS. The LCS extends from the interface into the bulk fluid, which is visible as a red (high-value) codimension-one manifold (line) denoting the boundary between two regions of qualitatively different flow. In steady flows the location of the LCS would be identical to that of the stagnation streamline, and would terminate at the diverging stagnation point. However, in unsteady flows the LCS may not correspond to the average stagnation streamline due to temporal effects. Because we focus on the behaviour of the maximal-value region that defines the LCS, all FTLE fields presented herein are scaled on a range 0 to 1 to facilitate comparison between cases.

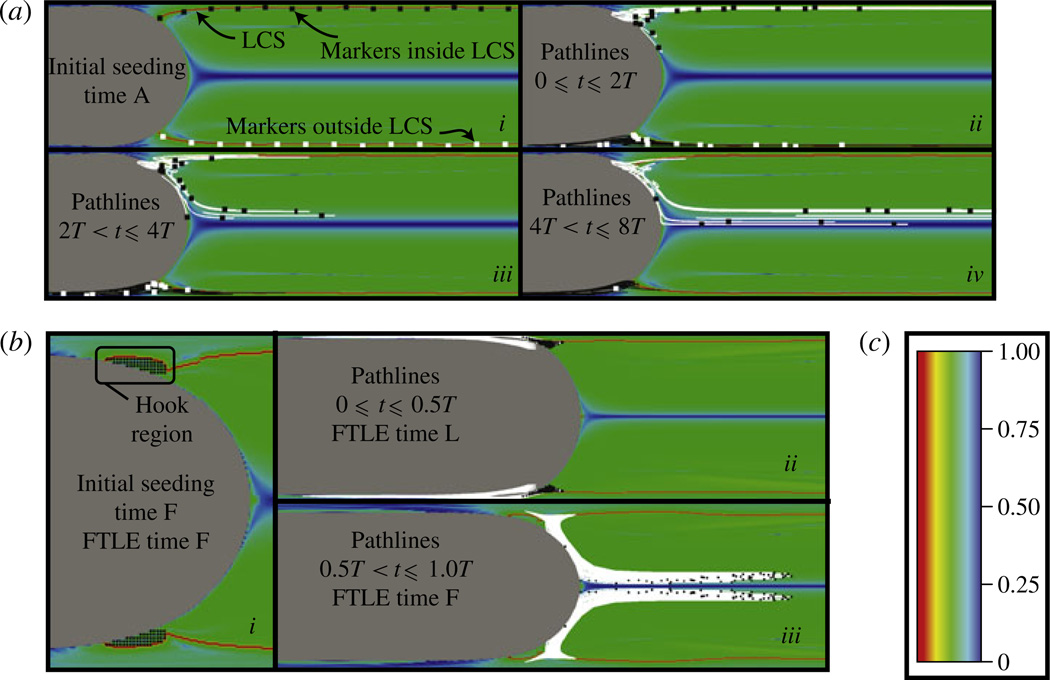
Figure 7.

FTLE field and particle pathlines for (a) A = 1 case: (i) initial seeding and (ii–iv) the time course of the particle pathlines. Particles inside the LCS (top plane) are demarcated by black symbols with white pathlines, particles outside the LCS (bottom plane) are shown with white particles and black pathlines. (b) A = 5,= 0.025 case with (i) particles initialized inside the ‘hook’ region and (ii) subsequently swept upstream into the thin film and then (iii) downstream ahead of the bubble tip. In this and all subsequent figures the FTLE field is scaled on a range zero to one; the corresponding colour scale is shown in (c).

We track the motion of virtual fluid markers (particles) in order to elucidate the Lagrangian motion of fluid in the vicinity of the LCS. We refer to particles positioned at a greater radius than the LCS as ‘outside’, and those closer to the tube centreline as ‘inside’ (figure 7a,i). To simplify the presentation, we exploit symmetry to demonstrate the particles inside the LCS on the top half (black particles, white pathlines), and particles initialized outside the LCS are shown in the lower half (white particles, black pathlines).

Figure 7(a,ii–iv) clearly demonstrates the importance of the LCS and shows the extreme sensitivity of the particle trajectories to the initial seeding positions. As such, the LCS divides the flow field into distinctly separate regions, with the fluid outside the LCS advecting into the residual film and fluid inside the LCS advecting downstream into the bulk fluid. In this low-A case, the intersection point of the LCS at the air–liquid interface remains relatively constant. As such, particles that advect downstream do not enter the thin-film region upstream of the bubble tip and are exposed to only a short section of air–liquid interface between the LCS and the tube centreline.

4.2. Case II: high amplitude, low frequency (Ca_Ω = 0.025, A = 5, Ω = 0.01)

In contrast to the low-A scenario, the high-amplitude cases (II and III) exhibit a region where fluid particles are periodically advected between the thin-film region and the bulk fluid ahead of the advancing interface. For this reason, particles in this region are exposed to a significant portion of air–liquid interface between the LCS and the tube centreline. To elucidate the dynamics responsible for this oscillatory trajectory for case II, we choose our initial seeding at time F (figure 6) and initialize particles in the ‘hook’-shaped region of the LCS, as shown in the black box in figure 7(b,i). Tracer locations and pathlines following a half-period of convection (T_I = 0.5) are illustrated in figure 7(b,ii), showing the white recirculatory particle path upstream along the bubble interface that subsequently returns to locations near the starting position. These particles are next advected downstream as demonstrated in figure 7(b,iii), which shows the pathlines from 0.5T < t ⩽ 1.0T. This simulation shows that these particles spend approximately one full period immediately adjacent to the interface before they are ejected ahead of the advancing bubble. This extended exposure to the free surface could enhance pulmonary surfactant transport along the interface in comparison to steady flow with the same mean velocity.

4.3. Case III: high amplitude, high frequency (Ca_Ω = 0.1, A = 5, Ω = 0.04)

As the frequency is increased (Ω = 0.04) we observe an increase in the complexity of the flow field. For example, an increase in Ω increases the magnitude of the hook-shaped region of the LCS that was shown in figure 7(b,i). This structure now extends much further into the thin-film region. Figure 8(a) shows that the particles oscillate in the vicinity of the bubble tip for seven cycles, yielding surprising Lagrangian convection patterns that are revealed through Poincaré sections. Below we demonstrate that the dynamic flow field results in a time-periodic expulsion of groups of fluid particles from the interfacial region into the bulk, hereafter referred to as an ‘ejection loop’, as shown in figure 8, and related to the downstream pathlines shown in figure 7(b,iii). In addition the periodic particle trajectories shown in figure 10 demonstrate time-dependent attractor regions that collect and dispense particles according to the phase of the flow.

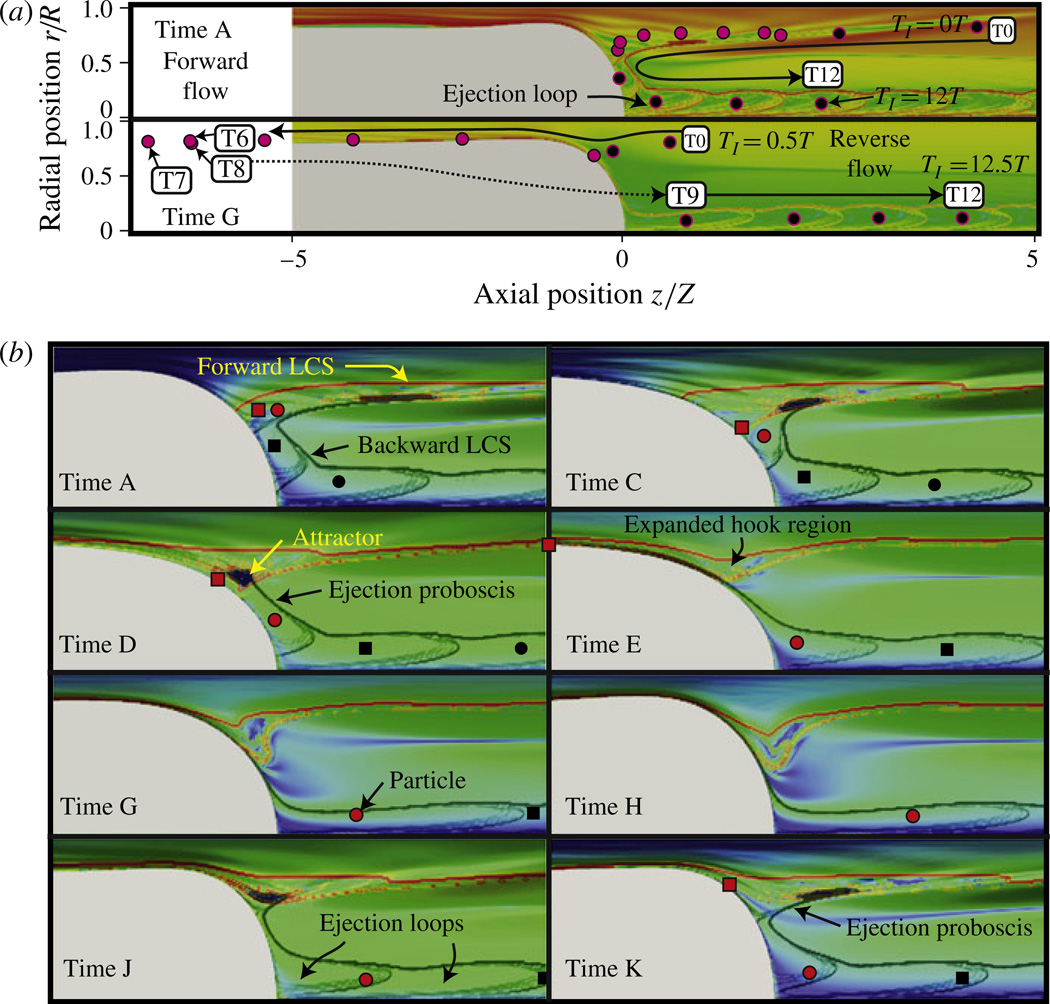
Figure 8.

(a) Backward-time (T_I = −20T) FTLE fields for case III (A = 5, Ca_Ω = 0.1), demonstrating cyclic LCS formation and shedding at the tip. Poincaré sections for a single particle located in a backward-time FTLE ‘loop’ downstream of the bubble tip are shown in the upper half of the domain for four time-points in the pulsatile cycle. The particle originates at a location (T₀) at time A and convects forward in time for 20 periods (T₁₉). (b) Overlay of the forward-time (T_I = 20T) and backward-time (T_I = −20T) FTLE fields for case III (A = 5, Ca_Ω = 0.1). Particle positions at several points over a single cycle show the downstream ejection of a particle (red circle) that has spent 7 periods traversing the thin-film region. The particle denoted by the red square leaves the fields of view (in the upstream direction) for times G–J.

Figure 10.

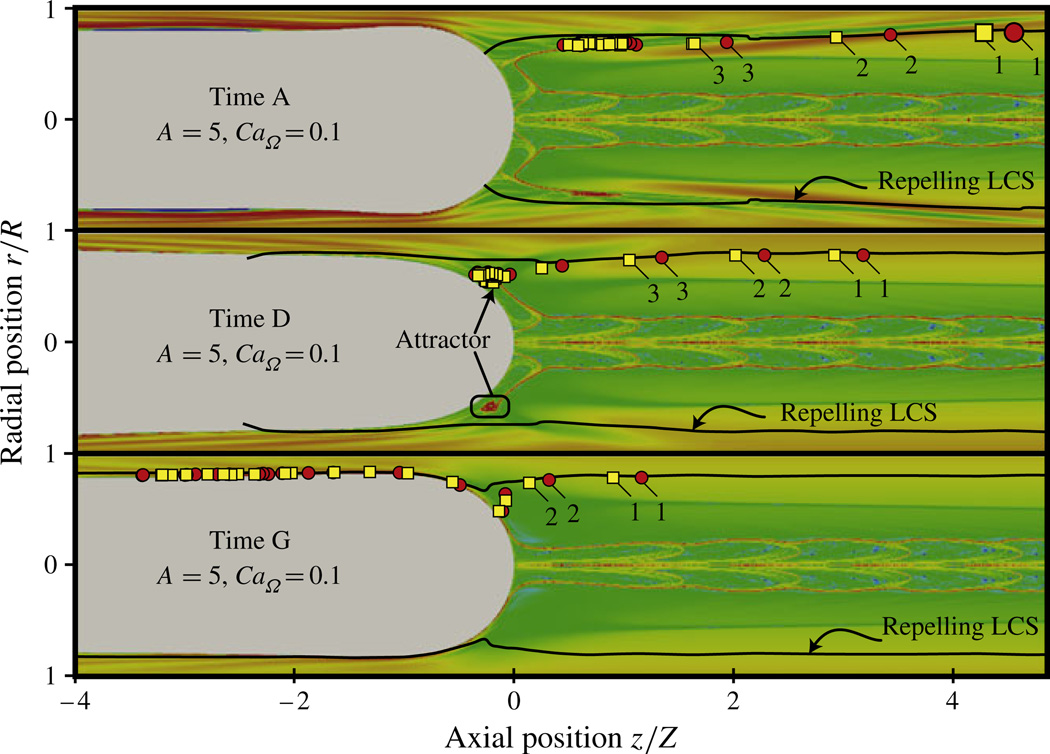
The backward-time FTLE field (T_I = 20T) for case III (high A, high Ω) at times A, D and G shown in figure 6. Poincaré sections for three points over 20 periods are shown in the upper half of each domain, demonstrating particle trapping in the attractor region visible at time D. Large symbols indicate the starting position of the tracer particles at time A, numbers indicate the time course of the Poincaré sections. The repelling LCS is shown as a black line.

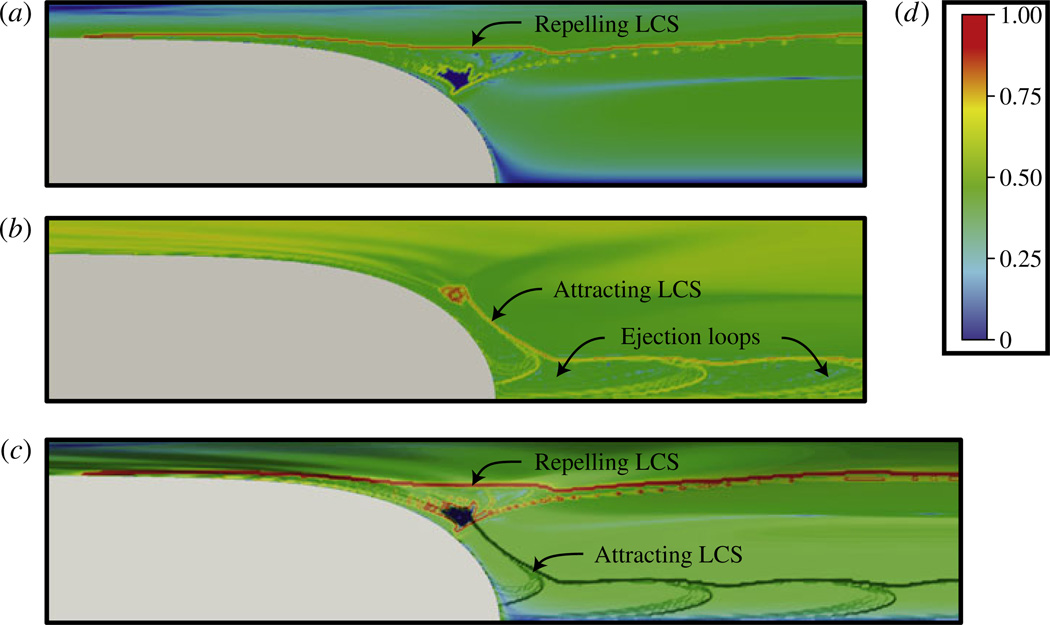
4.3.1. Ejection loop

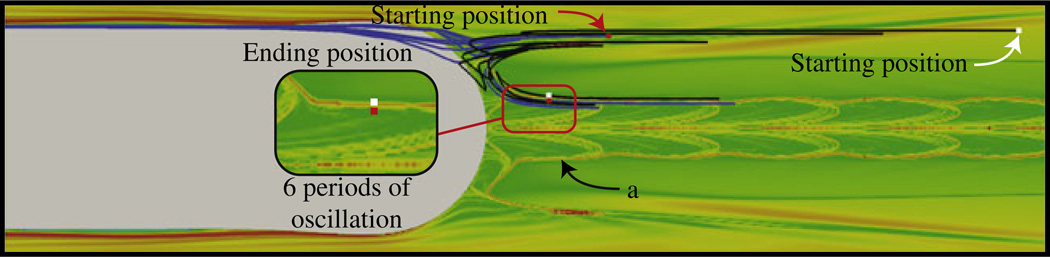
As described above, as Ω is increased the oscillatory trajectory behaviour of particles near the interface becomes more prominent. The hook region of the LCS encompassing these points, shown for case II in figure 7(b,i), expands upstream into the thin-film region for case III as shown in red in figure 8(b) at time E. To explore this phenomenon we consider Poincaré sections for a single particle as depicted in figure 8(a), which overlays the backward-time FTLE field. In each panel of figure 8(a) the backward-time FTLE field is computed at a starting time t₀ associated with the time A (top) or G (bottom) and the integration time T_I = −20T. The tracer particle originates at T_I = 0 immediately inside the repelling LCS. The subsequent position of the particle over 12 periods is tracked. Near the onset of retrograde bubble motion (figure 8a, time G) a volume of fluid containing the particle is drawn into the thin-film region. As the bubble resumes forward motion, the particle convects into the bulk fluid downstream of the tip (figure 8a, time A). This behaviour occurs for 7 oscillations, and for clarity the particle is shown in magenta during this stage.

We observe a notable Lagrangian characteristic through this analysis. Once per cycle a volume of fluid is ‘pinched off’ and expelled ahead of the bubble tip, never to return to the air–liquid interface. This portion of fluid is surrounded by an attracting manifold (the attracting LCS, determined from the backward-time FTLE), and is labelled as the ‘ejection loop’ in figure 8(a), time A.

To further explore particle ejection from the bubble tip we overlay the forward- and backward-time FTLE fields as well as the positions of 4 tracer particles, initialized at time A. These particles are followed as they advect forward in time (figure 8b). In each panel of figure 8(b) the FTLE integration starting time t₀ is associated with the time A–K and the integration time T_I = 20T (forward-time FTLE) and T_I = −20T (backward-time FTLE). The repelling LCS (determined from the forward-time FTLE) is represented in red while the reverse-time LCS (attracting manifold) is shown in dark green. Forward, backward, and overlaid FTLE fields for time A are shown in figure 9, figure 8(a), and figure 8(b) respectively. At time A one ejection loop contains a black square tracer that will separate from the interface in subsequent time steps. As the oscillation continues to the maximum velocity (time D), a second ejection loop (red circular tracer) forms at the bubble tip when the attracting LCS and an attractor move to intersect the interface. This protruding attracting LCS, which terminates in the attractor region, is termed the ‘ejection proboscis’ (figure 8b, times D and K). At the maximum reverse velocity (time J) the attractor region and the attached attracting LCS and migrate away from the bubble tip to form a new ejection proboscis. This structure then expands into the fluid as the bubble once again resumes forward motion (times K–C), only to pinch back to the interface to create another ejection loop that is subsequently expelled downstream. The volume of the ejection loop is a measure of volume of material that is temporarily cycled along the air–liquid interface during pulsatile bubble propagation.

Figure 9.

Backward FTLE field (time A) and forward particle trajectories (6 periods) for case III (A = 5, Ca_Ω = 0.1). The particles are initialized downstream so that convection carries one inside the ejection loop (red particle, blue pathline) and one immediately outside the same ejection loop (white particle, black pathline).

Large values of the backward-time FTLE field, which define the attracting LCSs, occur because particles must be originally located much further apart than the initial grid spacing and then advect forward in time to the location where the FTLE is computed. This behaviour is demonstrated in figure 9, which shows the backward-time FTLE field at time A and the trajectories of two particles (red and white) that are initially seeded far apart in the downstream region. As the particles are advected forward in time the red particle with the blue pathline travels into the thin-film region before it is ejected from the bubble tip; this behaviour corresponds to figure 8(a). In contrast, the white particle with a black pathline does not enter the thin-film region. Because of the difference in trajectories, these two particles that are initially seeded far apart in the downstream are brought close together. It is this behaviour that is responsible for the maximal ridge in the FTLE field (LCS) denoted a in figure 9.

4.4. Attractor region

For case III (high A and high Ω) the backward-time FTLE fields (figure 10, time D) indicate an attractor region that develops inside the LCS that is not present in case II. The particle behaviour in this area is similar to that in the hook region of case II, wherein the tracers migrate along the interface in the thin film and are then swept downstream of the bubble tip. However, in this high-Ω scenario an attractor region exists where particles enter and remain trapped near the interface for the duration of the simulation (20 periods).

In order to investigate particle trapping we compute the Poincaré maps for different phases in the pulsatile period. For three times A, D and G we plot the positions of two particles at each period for 20 periods in figure 10. The particles are initialized at the locations demarcated by the larger symbols at time A and are then advected for 20 periods. At time A the particles are located downstream of the bubble and inside the repelling LCS (black line). At the maximum of the sinusoidal velocity curve (time D), the tracers gather in the attractor region near the interface. At time G the points are then pushed upstream along the interface and into the thin-film region. This demonstrates cyclic behaviour of tracers in a region that translates with the migrating bubble tip. From this analysis it is observed that these particles are repetitively drawn into the attractor region shown in figure 10 at time D. Further inspection of the Poincaré sections shows apparently chaotic behaviour in this region – a tracer will return to different locations within the attractor at time D in subsequent cycles. This indicates that we have identified a fluid mixing region near the bubble interface.

5. Methods – experimental data

We next consider the FTLE computed from velocity data measured experimentally with micro-particle image velocimetry (μ-PIV). This permits the validation of methods described above and provides an avenue to explore the effect of pulmonary surfactant physicochemical interactions.

Particle image velocimetry (PIV) is a well-established technique for investigating the hydrodynamic properties of macro- and micro-scale flows (Adrian 2005). This technique uses a precisely timed pulsed light source to illuminate and record the position of fluorescent particles in two separate images at known times. The particle displacement is then estimated statistically by correlating the particle pairs (Adrian 1991). In μ-PIV volumetric laser illumination is used: the shallow focal depth of the microscope objective lens yields a pseudo-two-dimensional plane of focused particles for correlation (Santiago et al. 1998). The pulsatile bubble propagation velocity fields analysed herein are measured with the μ-PIV techniques described extensively in Yamaguchi, Smith & Gaver (2009), and post-processed as described in Smith, Yamaguchi & Gaver (2010).

Because of experimental considerations, the data are available on a 73 × 47 grid over (z, r) ∈ [−284 µm, 568 µm] × [−272 µm, 272 µm] for case IV (pure water) and a 58 × 37 grid over (z, r) ∈ [−281 µm, 562 µm] × [−266 µm, 266 µm] for case V (0.01 mg ml⁻¹ Infasurf). There are fewer interrogated vectors in the Infasurf measurements (case V) because the increased opacity of the solution necessitates a decreased particle concentration. This, in turn, yields fewer vectors in the interrogation. Nevertheless, the Infasurf measurements provide a detailed description of the flow field that allows for Lagrangian analysis.

5.1. Pre-processing

To compute the FTLE field we must numerically determine a flow map from the measured data (§ 2.4) by integrating particle positions through time, a summary of the algorithm is depicted in figure 11. The ensemble-averaged velocity (μ-PIV) and bubble shape (shadowgraphy) are measured at 24 points in the oscillatory cycle; further temporal refinement is not experimentally tractable. To decrease the integration time steps we interpolate with quintic smoothing splines to create a total of 96 time-points, making use of the temporal periodicity to interpolate points at the beginning and end of the cycle. This yields an integration time step of 1/48 of the period with fourth-order Runge–Kutta.

Figure 11.

Program steps to compute the FTLE field from μ-PIV data.

The MATLAB smoothing spline spaps (MathWorks) is used to calculate the smoothest function f that lies within a tolerance E_max of the data points (Reinsch 1967). The distance of the spline from the unsmoothed data is defined by

$$E(f)={\displaystyle \sum _{j=1}^{n}w(j)}{|y(j)-f(t(j))|}^2,$$ (5.1)

where t is time, y is the measured velocity (in the r or z direction), and w(j) is the weight of a specific data point. Smoothness is enforced by minimizing the roughness measure,

$$F({\mathrm{D}}^{3}f)={\displaystyle {\int }_{\mathit{\text{min}}(t)}^{\mathit{\text{max}}(t)}{|{\mathrm{D}}^{3}f(g)|}^2\mathrm{d}g,}$$ (5.2)

with D³f representing the third derivative of the interpolating function f. The spline f is the unique minimizer of ρE(f ) + F(D³f ), with ρ chosen so that E(f ) = E_max. In the current study, we employ E_max = 0.5 to interpolate the velocities and bubble shapes. To account for grid points that are temporarily located in the air-phase for a portion of the cycle, we set the weight w(j) = 0 when the point is in the air phase and w(j) = 1 when the point resides in the fluid domain, effectively ignoring time-points in the air phase. The smoothing properties of the spline serve to reduce the effects of noise in the experimental data without requiring knowledge of the form of the velocity–time relationship.

5.2. Flow map

As with the BEM analysis, we compute the flow map by integrating with a fourth order Runge–Kutta method. Tracer particles are initialized on a 500 × 250 grid on (z/R, r/R) ∈ [−2, 2] × [−1, 1], with approximately 65 000 particles in the domain fluid domain and a grid spacing h/R = 0.008, compared with h/R = 0.01 for the BEM. However, since the experimental data do not provide an avenue to evaluate the velocities directly at all locations in space, it is necessary to spatially interpolate the discrete velocity data at each time-point. Although the μ-PIV velocities are interrogated on a regular grid, our current experimental configuration does not measure velocities in the air phase. Therefore, interpolation techniques that necessitate a regular grid provide erroneous results near the air–liquid interface as information in this region is unavailable. To overcome this difficulty, we compute the Delaunay triangulation of the points in the liquid phase and employ linear interpolation to determine the velocity using the MATLAB intrinsic function TriScatteredInterp.

6. Analysis of experimental data

Figure 12 compares the predictions of Lagrangian transport properties from computational simulations (figure 12a,b) and estimates that are based upon experimental velocity field measurements in surfactant-free (figure 12c,d) and surfactant-doped (figure 12e,f) conditions. Table 1 gives the values of the relevant non-dimensional parameters. For the experimental data (cases IV–V) we use an integration time span of T_I = 2T, and for the computational data (case II) we use an integration time span of T_I = 3T, making note of the faster time scales in the experimental cases. The qualitative differences of the centreline FTLE field between theory and experiments are due to velocity field noise in our experimental data. This results from the fact that measurements from this region must be taken through a larger volume of fluid in the cylindrical tube geometry. In addition, errors exist in the interpolation of velocities immediately adjacent to the bubble tip because we cannot precisely measure the interfacial velocity.

Figure 12.

Forward FTLE fields comparing computational results to experimental measurements in pure water and water with 0.01 mg ml⁻¹ of the pulmonary surfactant Infasurf. T_I = 2T for the experimental data and T_I = 3T for the computational simulations. Numbers indicate the time course of the particle trajectories. (a) BEM, time E; (b) BEM, time H; (c) water, time E; (d) water, time H; (e) Infasurf, time E; (f) Infasurf, time H.

6.1. Surfactant-free behaviour

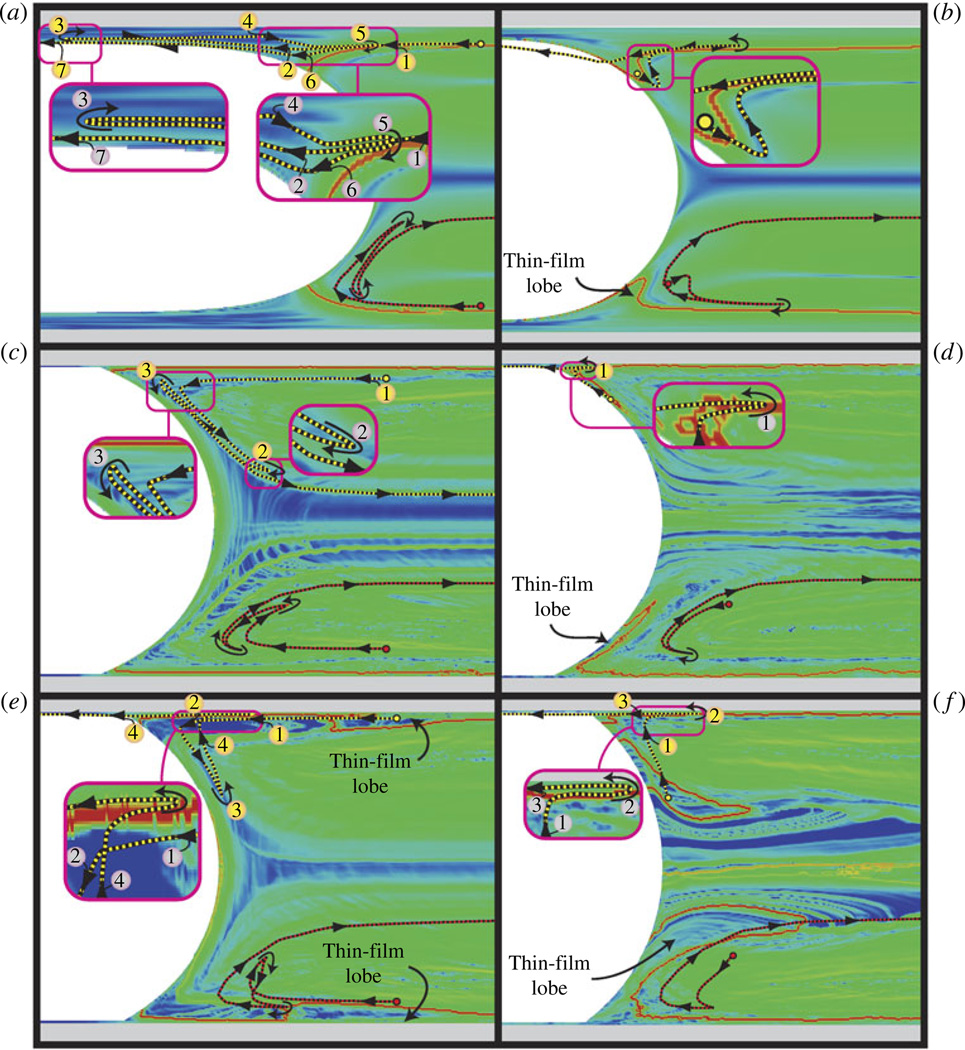
Comparing figure 12(a,b) (computational data) with figure 12(c,d) (experimental data) demonstrates the excellent agreement between the forward-time FTLE fields in the surfactant-free experimental (μ-PIV) and computational (BEM) cases. Note that because the experiments are conducted at significantly lower Ca than the BEM computations, and therefore deposit less residual fluid following bubble passage, the experimentally determined LCS intersects the bubble tip closer to the tube wall (figure 12c). Nevertheless, in both cases the LCS denotes the boundary separating regions where particles are advected either upstream (into the thin film), or downstream from the bubble tip. This behaviour is demonstrated by the BEM particle trajectories in figure 12(a). The red particle (lower half of domain) is initially seeded inside the LCS and oscillates near the interface during the reverse flow phase before advecting into the downstream bulk fluid. In contrast the yellow particle trajectory (top half of domain) is seeded outside the LCS and oscillates in the thin-film region during retrograde bubble motion (time-points 2–6) and then remains in the residual film following bubble passage (time 7). Similar behaviour occurs in the experimental analysis.

Likewise, at time H in the reverse-flow regime, we again find good agreement between the Lagrangian characteristics of the BEM computations and μ-PIV experiments conducted in pure water. The BEM analysis (figure 12b) shows the LCS deforming towards the bubble tip, labelled ‘Thin-film lobe’. As before, the LCS defines the boundary between particles destined to travel upstream or downstream of the bubble tip. A particle seeded outside this region of the LCS (yellow particle in top half of domain) will initially travel ahead of the bubble tip during the retrograde motion phase of the driving flow, and as forward bubble motion resumes the particle advects into the thin film. In this figure the particle pathline appears to cross through the air phase. However, this is an artefact that occurs because the bubble geometry is represented during the initial seeding time of the particle. As the simulation progresses, the film thickens during the forward phase and the particle resides immediately inside the air–liquid interface. The low-Ca experimental measurements in water (figure 12d) demonstrate a qualitatively similar LCS, with a clearly defined thin-film lobe. Again, a particle initialized outside the LCS (yellow particle in top half of domain) in the thin-film lobe advects to the wall and is subsequently deposited in the residual film. A particle on the inside of the LCS (red particle in bottom half of domain) eventually convects downstream.

6.2. Behaviour of surfactant-doped solutions

The presence of 0.01 mg ml⁻¹ of Infasurf in the bulk fluid (case V) yields significant modification of the flow field, as shown in figure 12(e). The FTLE during the forward phase (time E) presents an LCS that exists near the outer wall and curves inward toward the tube centreline, demarcated as ‘Thin-film lobe’. Fluid particles within this structure travel along the wall and then towards the centreline adjacent to the air–liquid interface, as demonstrated by the yellow particle-trace (top half of figure 12e). Reverse flow then sweeps the fluid back towards the wall to be advected into the thin film in the subsequent forward stroke. In contrast, a particle originating at a similar position in pure water (figure 12c, yellow pathline) oscillates once near the bubble tip before travelling into the downstream region. From this comparison, it is clear that surfactant has moved the LCS inward, and thus surfactant dramatically affects the trajectories of Lagrangian fluid markers in this vicinity. Furthermore, the particle trajectories represented in red in figures 12c and 12e are both seeded inside the LCS and eventually migrate downstream. The overall trajectories are similar in this region of the flow. The local variation in the pathlines results from the blunting of the air–liquid interface during retrograde motion in the presence of surfactant.

The FTLE from the reverse-flow phase (time H) demonstrates significant modifications due to surfactant effects (figure 12f). The thin-film lobes that are visible in the BEM computations (case II) and water experiments (case IV) extend much farther downstream in the presence of surfactant. Fluid in the thin-film lobe region, characterized by the yellow particle trace in the top half of figure 12(e,f ), travels towards the wall during the retrograde motion portion of the pulsatile cycle and is then advected into the thin film as forward bubble motion resumes. These particles migrate along the air–liquid interface in the bubble cap region to a much greater extent than in the surfactant-free case shown in figure 12(d). The increased size of the thin-film lobe in the presence of surfactant implies an increased net convective transport of surfactant to the thin-film region due to pulsatility.

The changes observed in FTLE fields computed from water and water/Infasurf measurements are due solely to the physicochemical behaviour of the air–liquid interface. The driving flow and other fluid properties, such as viscosity, are held constant between experiments. Furthermore, the modifications in the flow field due to Infasurf discussed above, such as the thin-film lobe, were not observed in measurements conducted in the presence of sodium dodecyl sulphate (SDS), an anionic surfactant. The physicochemical hydrodynamics of pulmonary surfactant, specifically Infasurf, dynamically alter the interfacial tension to yield changes in the bubble shape and flow field that are not present with SDS or pure water.

Dynamic changes in the surface concentration of Infasurf Γ alter the flow field by changing the stress condition at the air–liquid interface. In a surfactant-free solution, the surface tension γ is constant and the interfacial stress is defined by the Young–Laplace equation. In the presence of surfactant, the surface tension γ(s) is a function of the local surfactant concentration Γ(s) and varies in both space and time, where s is the arclength coordinate. These changes in stress at the interface alter the bubble shape and flow field which, in turn, affect surfactant transport and the mechanical stresses at the wall. Additionally, tangential (Marangoni) stresses at the air–liquid boundary occur due to the non-equilibrium surface tensions, rigidifying the interface and further modifying flow and transport. These changes in bubble geometry, interfacial stress, and fluid velocity – due solely to the presence of Infasurf – account for the significant modification of the FTLE field, particularly during retrograde bubble motion.

7. Assumptions and limitations

In this study we have investigated the convective transport properties of fluid markers through an investigation of Lagrangian trajectories. We have conducted this investigation to elucidate the bulk transport processes with the assumption that convection dominates diffusion during airway reopening. This representation is most accurate if the Péclet number (Pe = UR/D), representing the ratio of convection to diffusion, is much greater than unity. Here U is the magnitude of the velocity, R is the tube radius, and D is the molecular diffusivity. Experiments were designed to replicate the reopening of a bronchial airway, so U ~ 1 cm s⁻¹ and R ~ 0.025 cm. The diffusivity of surfactant is assumed to be in the range of 10⁻⁸ cm² s⁻¹ < D < 10⁻⁶ cm² s⁻¹, with D = 10⁻⁷ cm² s⁻¹ providing an estimate for the diffusivity of the primary surface-active molecule dipalmitoylphosphatidylcholine (DPPC) (Launois-Surpas et al. 1992), and smaller diffusivities for liposomes and larger values of D for components with smaller molecular weights. Therefore, 10⁴ < Pe < 10⁶ and convection clearly dominates diffusion for the transport of surfactant in the bulk phase.

Although convection dominates diffusion, it is possible that lateral diffusion of particles crossing streamlines could affect the trajectories demonstrated by our Lagrangian simulations. To estimate the magnitude of this effect we approximate the diffusion distance during one oscillatory period as $l_{\mathit{\text{Diff}}}^{*}=\sqrt{DT}$, where T = 1 s is the period of oscillation. For the surface-active component DPPC $l_{\mathit{\text{Diff}}}^{*}=3\times {10}^{-4}\text{cm}$, or $l_{\mathit{\text{Diff}}}^{*}/R~0.01$. Therefore, we would expect that a molecule of DPPC would be displaced by approximately 1% of the tube radius during an oscillation. While this could smear the trajectories from the idealized representation provided by our Lagrangian analysis, the overall trends should not be greatly affected. On the other hand, the Lagrangian description cannot model the adsorption of surfactant to the air–liquid interface, which is the critical step in the transport of surface-active substances. Nevertheless, our Lagrangian calculations can demonstrate the increased time that surfactant molecules can remain in the proximity of the bubble tip during pulsatility, which may enhance surfactant sorption.

The present study has not used simulation of the surfactant-doped system to predict the Lagrangian trajectories of fluid particles. Unfortunately, the computational exploration of surfactant physicochemical interactions during pulsatile flow is beyond the scope of the present study. However, we have validated our ability to use μ-PIV data to accurately predict Lagrangian trajectories in surfactant-free situations (by comparison to BEM). Therefore, by incorporating surfactant into our experimental systems and calculating the modification of the Lagrangian trajectories, the present study can accurately demonstrate the modification of the FTLE description and location of the LCSs that occur with the incorporation of surfactant, which is likely to influence transport processes. Nevertheless, the detailed correlation between Lagrangian motion and surfactant physicochemical hydrodynamics during pulsatile flow must await high-resolution computational simulation.

8. Conclusions

We compute FTLE fields describing pulsatile air-finger propagation using velocity data computed with the BEM and measured with μ-PIV. The maximal ridges of the FTLE field represent boundaries between regions of qualitatively different flow. We have found that these LCSs describe the boundary between fluid advected downstream into the bulk and fluid advected upstream into the thin residual film. However, depending on values of the non-dimensional parameters, different flow regimes are observed. Increasing the oscillatory stroke length A yields fluid regions that oscillate upstream and then downstream along the bubble interface. As the frequency Ω is increased a subset of particles remains in residence near the interface for an increasing number of pulsatile cycles before ejection from the bubble tip region.

The dynamic behaviour of this fluid region has potentially important surfactant transport implications in pulmonary airway reopening. In steady-velocity reopening non-equilibrium pulmonary surfactant distribution along the air–liquid interface causes the surface tension to vary along the length of the free surface. This, in turn, yields Marangoni stresses that rigidify the interface and increase the driving pressure necessary to restore patency in the airway. FTLE analysis indicates that pulsatile flows have the potential to redistribute surfactant along the length of the interface to yield a reduced surface tension, driving pressure, and Marangoni stresses. Furthermore, the high-A, high-Ω simulations (case III) demonstrate a well-mixed reservoir region that sweeps along the interface once per period, periodically returning to an attractor region. As the accumulated fluid is spread along the interface, surfactant may adsorb, lowering surface tension and reducing airway damage. These results are consistent with the macroscale measurements by Pillert & Gaver (2009) and the observed protection of epithelial cells from the temporary reverse flow (Glindmeyer, Smith & Gaver 2011).

We compare the FTLE fields computed from BEM simulations to those computed from experimentally measured (μ-PIV) velocities in pure water and water doped with 0.01 mg ml⁻¹ of Infasurf, a clinical pulmonary surfactant. Excellent agreement is found between the forward-time FTLEs calculated from the BEM computations (case II) and μ-PIV measurements in pure water. FTLEs computed from measurements in the presence and absence of Infasurf show that the pulmonary surfactant significantly expands the thin-film lobe of the LCS that projects ahead of the bubble cap during retrograde motion. This region draws fluid from near the tube wall towards the centreline adjacent to the interface and is directly attributed to the physicochemical hydrodynamics of Infasurf.

In summary, the Lagrangian analysis provides an excellent technique for elucidating convective transport properties in time-dependent free-surface flows such as that occurring during pulsatile bubble propagation. In particular, this technique identifies parameter spaces in which regions of the flow can be modified to enhance surfactant delivery.

We offer this paper as a contribution to the Festschrift in honour of T. Pedley in light of his extraordinary contributions to our understanding of biofluid mechanics and, in particular, the relationship between transport processes and biological function in the pulmonary (Pedley & Kamm 1988) and circulatory systems (Pedley 1980), and aquatic motion (Lewis & Pedley 2000; Drescher et al. 2009). We look forward to many more years of contributions from this friend and colleague. Computational resources were provided by the Tulane Center for Computational Science and the Louisiana Optical Network Infrastructure. We appreciate the insight provided by Professor L. Fauci.