Abstract
The shear strength of human trabecular bone may influence overall bone strength under fall loading conditions and failure at bone-implant interfaces. Here, we sought to compare shear and compressive yield strengths of human trabecular bone and elucidate the underlying failure mechanisms. We analyzed 54 specimens (5-mm cubes), all aligned with the main trabecular orientation and spanning four anatomic sites, 44 different cadavers, and a wide range of bone volume fraction (0.06–0.38). Micro-CT-based non-linear finite element analysis was used to assess the compressive and shear strengths and the spatial distribution of yielded tissue; the tissue-level constitutive model allowed for kinematic non-linearity and yielding with strength asymmetry. We found that the computed values of both the shear and compressive strengths depended on bone volume fraction via power law relations having an exponent of 1.7 (R2=0.95 shear; R2=0.97 compression). The ratio of shear to compressive strengths (mean ± SD, 0.44 ± 0.16) did not depend on bone volume fraction (p=0.24) but did depend on microarchitecture, most notably the intra-trabecular standard deviation in trabecular spacing (R2=0.23, p<0.005). For shear, the main tissue-level failure mode was tensile yield of the obliquely oriented trabeculae. By contrast, for compression, specimens having low bone volume fraction failed primarily by large-deformation-related tensile yield of horizontal trabeculae and those having high bone volume failed primarily by compressive yield of vertical trabeculae. We conclude that human trabecular bone is generally much weaker in shear than compression at the apparent level, reflecting different failure mechanisms at the tissue level.
Keywords: shear, finite element, trabeculae, microarchitecture, yield
1. Introduction
Since trabecular bone is thought to be primarily adapted to sustain compressive loads along its main trabecular orientation, most focus to date in biomechanical studies of human trabecular bone has been placed on understanding its compressive strength behavior (Carter and Hayes 1976; Ciarelli et al. 1991; Goldstein 1987; Goulet et al. 1994; Morgan and Keaveny 2001; Rice et al. 1988; Keller 1994). However, obliquely oriented external loads can generate substantial shear stress within a bone with respect to the main trabecular orientation, which may be relevant for understanding bone trauma, including hip fracture etiology (Ford and Keaveny 1996; Keyak 2000; Lotz et al. 1991). Likewise, large shear stresses can develop near bone-implant interfaces, which may influence orthopaedic implant loosening (Cheal et al. 1992). In analyzing such situations, the shear strength of trabecular bone may be equally or even more relevant than its compressive strength.
To date, only a few studies have addressed the apparent-level shear strength behavior of trabecular bone, particularly for humans (Garnier et al. 1999; Fenech and Keaveny 1999; Ford and Keaveny 1996; Halawa et al. 1978; Kasra and Grynpas 2007; Mitton et al. 1997; Stone et al. 1983; Rincón-Kohli and Zysset 2009; Saha and Gorman 1981; Garrison et al. 2011). It has been proposed that the structure-function relations may differ between compression vs. shear loading because trabecular bone may maintain structural integrity for habitual (compressive) loading, but may be degraded for non-habitual (shear) loading, particularly for individuals prone to fracture (Ciarelli et al. 2000; Homminga et al. 2004). Similarly, while the shear strength of bovine trabecular bone may be low because of pronounced bending of individual trabeculae (Fenech and Keaveny 1999), little is known about the associated shear failure mechanisms in human trabecular bone — which may differ from bovine mechanisms because of inter-species differences in bone volume fraction and micro-architecture. Thus, to further understanding of the shear strength behavior of human trabecular bone, we sought here to compare the apparent-level shear and compressive strengths of a wide range of human trabecular bone and to explore the underlying failure mechanisms.
2. Methods
A total of 65 human cadaver specimens of trabecular bone, from four anatomic sites, were initially chosen for this analysis. These specimens, taken from prior studies in our laboratory (Bevill et al. 2006; Kopperdahl and Keaveny 1998; Morgan and Keaveny 2001), were originally machined as 8 mm-diameter cylindrical cores, along their principal trabecular orientation, and were scanned at a spatial resolution of 10–22μm using either micro-CT (n=44; μCT 20; Scanco Medical AG, Brüttisellen, Switzerland) or serial milling (n=21) (Beck et al. 1997). Standard trabecular microarchitecture parameters (Hildebrand et al. 1999; Laib et al. 2001) were available for all specimens that were scanned with micro-CT. A subset (n=22) of these specimens were also mechanically tested to failure in compression (Bevill et al. 2006; Kopperdahl and Keaveny 1998; Morgan and Keaveny 2001).
For the purposes of this study, one voxel-based finite element model was generated for each specimen, the model comprising a 5 mm cube (Figure 2a) that was virtually extracted from the images of the central portion of the larger cylindrical specimen. An element size of 66 μm was used for the femoral neck specimens, and 22 μm for the greater trochanter, proximal tibia and vertebral body specimens. These resolutions were based on convergence requirements that the ratio of mean trabecular thickness to element size be at least 4 (Guldberg et al. 1998; Neibur et al. 1999). Individual models had between about 1–5 million elements. To ensure that these extracted cube specimens were adequately aligned (within ±10° of the principal trabecular orientation), six uniaxial linear elastic finite element analyses were performed on each specimen to calculate the Euler angles of misalignment (van Rietbergen et al. 1996). Eight specimens from the greater trochanter and three specimens from the proximal tibia were eliminated because of misalignment. This resulted in a final cohort of 54 specimens, which together spanned four anatomic sites, were taken from 44 different cadavers, and displayed a wide range (0.06–0.38) of bone volume fraction (Table 1). For this final cohort, the trabecular microarchitecture parameters were available only for the specimens there were imaged using micro-CT (n=39).
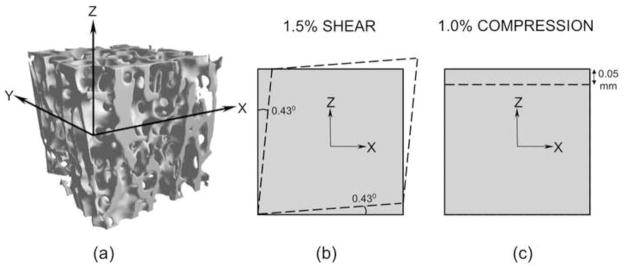
Figure 2.
(a) A 5mm cube trabecular bone specimen with its Z-axis oriented along the main material orientation (the X-axis was selected randomly in the transverse plane) (b) An engineering XZ shear strain of 1.5% was applied for shear strength analysis, the dashed lines denoting the prescribed displacement boundary condition on four faces, the other two faces remaining unconstrained (c) A compressive normal strain of 1.0% was applied for compressive strength analysis, the dashed lines denoting the prescribed displacement boundary condition on the top face, the bottom face minimally fixed on rollers and the sides faces unconstrained.
Table 1.
Specimen details for the final cohort (mean ± SD).
| Anatomic Site | No. of Specimens †(male/female) | Age (years) | Bone Volume Fraction |
|---|---|---|---|
| Femoral Neck | 25 (12/13) | 70 ± 10 | 0.25 ± 0.07 |
| Greater Trochanter | 4 (4/0) | 67 ± 12 | 0.11 ± 0.04 |
| Proximal Tibia | 8 (8/0) | 64 ± 10 | 0.12 ± 0.04 |
| Vertebral body | 17 (12/5) | 66 ± 8 | 0.09 ± 0.03 |
|
| |||
| Pooled | 54 (36/18) | 68 ± 10 | 0.17 ± 0.09 |
Number of trabecular bone cube specimens; altogether these specimens were taken from a total of 44 different cadavers.
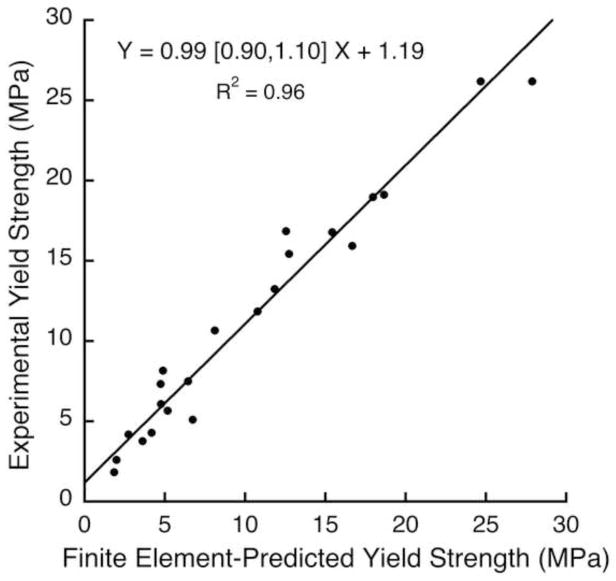
Two non-linear finite element analyses were performed on each specimen to calculate both the apparent-level shear and compressive yield strengths. In all analyses, all finite elements were assigned the same hard tissue material properties having an isotropic elastic modulus of 18.0 GPa, a Poisson’s ratio of 0.3, and a rate-independent elastic-plastic material model (Papadopoulos and Lu 2001). The models also included kinematic non-linearity (“large-deformation” effects), which are important to include for specimens having low bone volume fraction (Bevill et al. 2006). In the voxel-level constitutive model, tissue-level failure was allowed to occur only by tissue-level yield. Such yielding comprised a modified von-Mises criterion with tension-compression strength asymmetry, which was achieved by introducing pseudo kinematic hardening to shift the yield envelope. The tissue-level yield strains of 0.33% in tension and −0.81% in compression were chosen based on a prior calibration study (Bevill et al. 2006). This overall implementation provided excellent agreement (Y~X, R2=0.96) for compressive apparent-level yield strength between model and experiment for the 22 specimens for which we had both mechanical testing and finite element yield strength data (Figure 1). For each model, displacement boundary conditions were applied to impose uniaxial shear stress for shear strength assessment (Figure 2b) and uniaxial compressive stress for compressive strength assessment (Figure 2c). All analyses were performed using a highly scalable, implicit parallel finite element framework, Olympus (Adams et al. 2004) on a Sun Constellation Linux Cluster (Ranger; Texas Advanced Computing Center, TX, USA), each analysis requiring about 100 CPU hours.
Figure 1.
Validation of predictions of compressive yield strength, for the 22 specimens in this study that had both micro-CT scans and experimental measures of compressive yield strength. The same tissue-level effective modulus of 18.0 GPa was used in all models. Orthogonal regression was used since there were measurement errors in both experimental and finite element strength measures. Values in brackets represent the 95% confidence interval for the slope.
The main outcomes from these analyses were the apparent-level shear and compressive yield strengths, which were obtained using an offset of 0.2% strain applied to the computed apparent-level stress-strain curves. To gain insight into tissue-level failure mechanisms, the proportion of yielded tissue (equivalent to number of elements for which the maximum or minimum principal stress at the element centroid had exceeded the tissue-level tensile or compressive yield strength respectively, divided by total number of elements) and the tissue-level yield mode (tensile or compressive) was calculated at the apparent-level 0.2% offset yield point. For all yielded elements, those elements having a ratio of maximum principal stress to tensile strength of greater than the ratio of minimum principal stress to compressive strength were considered to yield in tension at the tissue level; otherwise they were considered to yield in compression at the tissue level. For our statistical analyses, non-linear and general linear regression modeling (JMP, Version 9.0.0, SAS Institute Inc., Cary, NC) was used to determine the dependence of the various apparent-level and tissue-level outcomes on apparent-level loading mode and on bone volume fraction, anatomic site, and microarchitecture.
3. Results
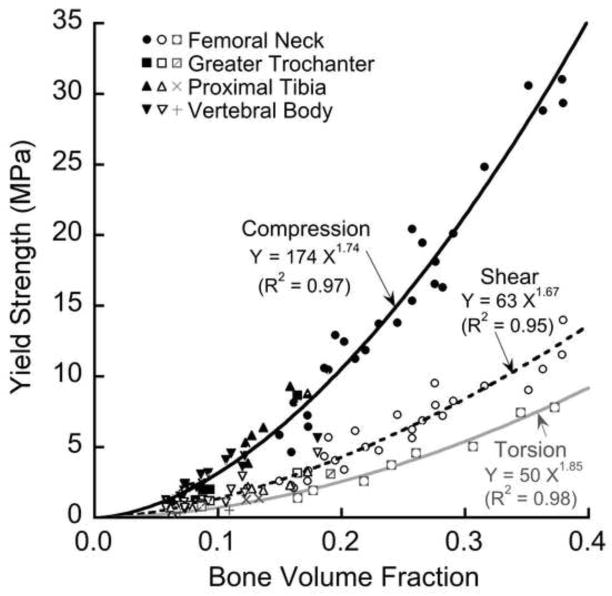
Both the apparent-level shear (R2=0.95) and compressive (R2=0.97) yield strengths depended on bone volume fraction in a non-linear fashion, each relation having an exponent of 1.7 (Figure 3). Because the relation between apparent-level yield strength and bone volume fraction relation did not depend on anatomic site (p = 0.55 for shear; p = 0.09 for compression), data from the four different anatomic sites were pooled in most subsequent results. Both the shear and compressive yield strengths were highly correlated with almost all the microarchitecture parameters (Table 2), which was expected since most microarchitecture parameters generally have high correlation with bone volume fraction (Hildebrand et al. 1999). The apparent-level yield strain decreased slightly with bone volume fraction for shear loading (R2=0.07, p=0.05) but clearly increased for compressive loading (R2=0.42, p < 0.001).
Figure 3.
Variation of compressive (solid line), shear (dashed line), and torsion (light line) apparent-level 0.2% offset yield strengths with bone volume fraction.
Table 2.
Pearson correlation coefficients for yield strength, shear-to-compression yield strength ratio, and the proportion of yielded tissue, all versus bone volume fraction (BV/TV) and various architecture parameters (n=39). Data are shown stratified by bone volume fraction (Pooled, n=39; Low, BV/TV < 0.20, n=23; High, BV/TV > 0.20, n=16). Italicized values have p < 0.05 at least.
|
Yield Strength
|
Shear-to-Compression Strength Ratio
|
Proportion of Yielded Tissue (%)
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shear
|
Comp
|
Pooled | Low | High | Shear
|
Comp
|
|||||||||
| Pooled | Low | High | Pooled | Low | High | Pooled | Low | High | Pooled | Low | High | ||||
| BV/TV | 0.97 | 0.90 | 0.90 | 0.97 | 0.91 | 0.96 | −0.24 | −0.22 | −0.27 | 0.62 | 0.25 | 0.54 | 0.55 | 0.11 | 0.67 |
| Conn-Den | 0.39 | 0.42 | −0.35 | 0.37 | 0.38 | −0.35 | −0.16 | −0.19 | 0.04 | 0.15 | −0.29 | −0.05 | 0.09 | −0.31 | −0.05 |
| SMI | −0.84 | −0.38 | −0.79 | −0.88 | −0.64 | −0.82 | 0.32 | 0.36 | 0.19 | −0.56 | −0.25 | −0.36 | −0.53 | −0.31 | −0.43 |
| Tb.N | 0.73 | 0.55 | 0.21 | 0.73 | 0.64 | 0.15 | −0.29 | −0.36 | 0.04 | 0.45 | −0.15 | 0.48 | 0.39 | −0.06 | 0.39 |
| Tb.Th | 0.86 | 0.71 | 0.61 | 0.88 | 0.67 | 0.72 | −0.22 | −0.12 | −0.32 | 0.40 | −0.04 | 0.09 | 0.40 | −0.05 | 0.30 |
| Tb.Sp | −0.69 | −0.52 | −0.23 | −0.70 | −0.65 | −0.16 | 0.40 | 0.48 | −0.07 | −0.39 | 0.13 | −0.51 | −0.39 | −0.07 | −0.41 |
| Tb.(1/N).SD | −0.36 | 0.07 | −0.29 | −0.41 | −0.21 | −0.17 | 0.43 | 0.53 | −0.14 | −0.29 | 0.17 | −0.61 | −0.42 | −0.26 | −0.44 |
| Tb.Th.SD | 0.59 | 0.77 | 0.06 | 0.62 | 0.65 | 0.24 | −0.16 | 0.03 | −0.34 | 0.18 | 0.05 | −0.26 | 0.22 | −0.05 | 0.02 |
| Tb.Sp.SD | −0.53 | −0.01 | −0.45 | −0.58 | −0.32 | −0.37 | 0.48 | 0.56 | −0.01 | −0.34 | 0.16 | −0.62 | −0.47 | −0.29 | −0.50 |
| DA | 0.19 | 0.40 | 0.13 | 0.3 | 0.71 | 0.31 | −0.41 | −0.43 | −0.25 | 0.14 | 0.18 | 0.03 | 0.36 | 0.47 | 0.26 |
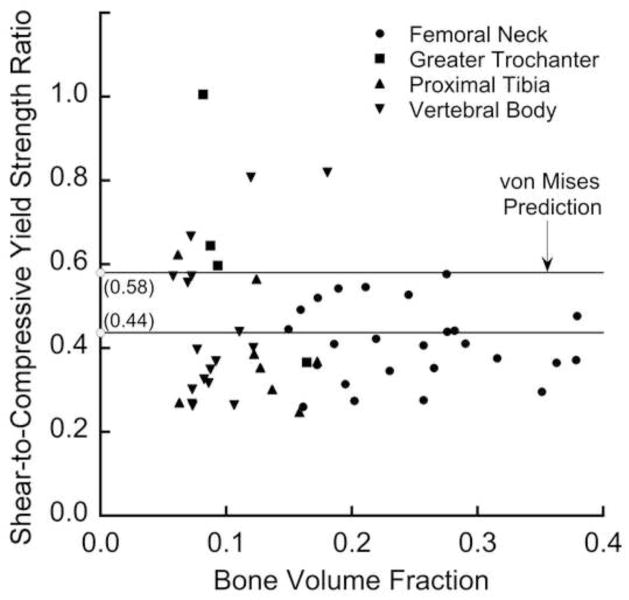
With the exception of one specimen, the shear strength was always appreciably lower than the compressive strength. Consistent with the similar exponents for shear and compression in the strength-bone volume fraction relation, the ratio of shear to compressive strengths (Figure 4) did not depend on bone volume fraction (p = 0.24) or anatomic site (p = 0.13). However, this ratio did vary appreciably (mean ± SD = 0.44 ± 0.16; range = 0.25–1.00) and was partially explained by microarchitecture (Table 2), most notably the intra-specimen standard deviation of trabecular separation (Tb.Sp.SD, R2=0.23, p< 0.005). For some specimens having low bone volume fraction (BV/TV < 0.20), the ratio of shear to compressive strengths was close to the value of 0.58 as predicted by a traditional (assuming isotropy and strength symmetry) von Mises criterion, but at higher bone volume fraction the von Mises criterion over-predicted this ratio.
Figure 4.
Variation of the ratio of shear to compressive yield strengths with the bone volume fraction. This ratio (mean ± SD = 0.44 ± 0.16 for 54 specimens) displayed additional scatter below a bone volume fraction of about 0.20. This ratio for the traditional von Mises criterion is 0.58.
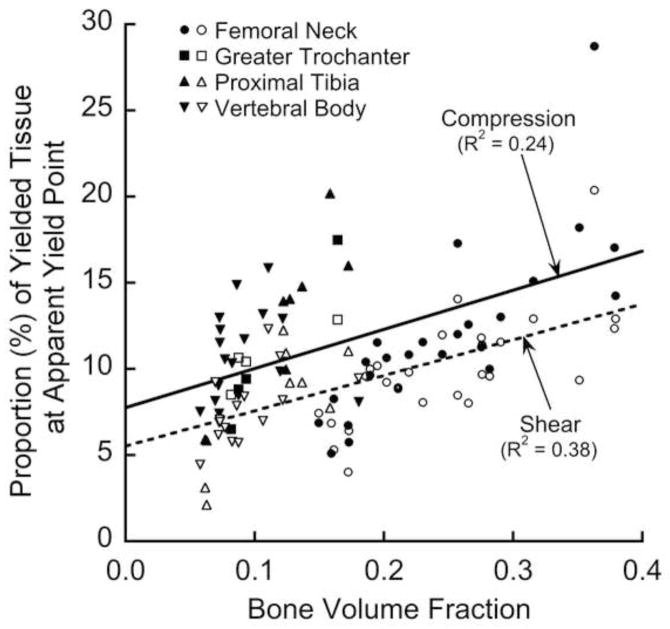
Analysis of the amount of yielded tissue at the apparent-level yield point revealed a number of differences in the underlying failure mechanisms. While the total proportion of yielded tissue yielded was only slightly lower for shear than compression loading (Figure 5), there were much greater differences in the mode of tissue-level failure. For shear, there was predominantly tensile tissue-level yielding regardless of bone volume fraction, whereas for compression, there was tensile tissue-level yielding at low bone volume fraction and compressive tissue-level yielding otherwise (Figure 6). Visual inspection revealed that for shear loading, there was mainly tensile stretching of the obliquely oriented trabeculae regardless of bone volume fraction (Figure 7). This tensile yield pattern appeared to occur primarily along continuous load paths that were oriented at approximately 45° with respect to the main trabecular orientation. However, for compression loading, there was mainly tensile failure of horizontal trabeculae for specimens with low bone volume fraction and otherwise mainly compressive failure of longitudinal trabeculae (Figure 7). This tensile failure of the horizontal trabeculae was the result of kinematic large-deformation-related bending of the vertical trabeculae: when neighboring vertical trabeculae bent away from each other in opposite directions, the interconnecting horizontal trabeculae were stretched.
Figure 5.
Variation of the proportion of yielded tissue (expressed as a percentage of total tissue in the bone specimen) at the apparent-level 0.2% offset yield point for shear and compression loading.
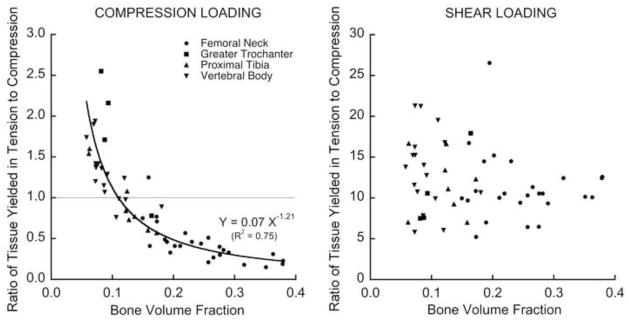
Figure 6.
Variation of the ratio of tissue yielded in tension to tissue yielded in compression at the apparent-level 0.2% offset yield point, for compression (left) and shear (right) loading. Note the 10-fold difference in the vertical scales between plots.
Figure 7.
Distribution of tissue-level yielding for a thin slice for two specimens, of low (BV/TV = 0.07) and high (BV/TV = 0.26) bone volume fraction. Red regions denote tissue-level yield in tension and blue regions denote tissue-level yield in compression. The Z-axis denotes the main trabecular orientation.
4. Discussion
These results show that human trabecular bone is generally much weaker in shear than compression at the apparent level, reflecting different failure mechanisms at the tissue level. Although the ratio of shear to compressive strengths did not depend on bone volume fracture, it did depend on the trabecular microarchitecture, particularly at low bone volume fraction for which the compressive and shear strengths were almost equal for some specimens. This dependence reflected a change in tissue-level failure mechanism for compressive loading as bone volume fraction decreases whereby kinematic large-deformation effects become important (Bevill et al. 2006; Stolken and Kinney 2003) as adjacent vertical trabeculae bend apart from each other and stretch the connecting horizontal trabeculae. There was not any such dependence of the failure mechanism on bone volume fraction for shear loading. Thus, for some specimens with low bone volume fraction, depending on the micro-architecture, the compressive strength could fall low enough to approach the shear strength.
At the tissue level, one novel finding was the dominance of tensile yield of obliquely oriented trabeculae for pure shear loading. Because of the difficulty of probing failure mechanisms using purely experimental models, most previous studies on pure shear (Garnier et al. 1999; Mitton et al. 1997; Saha and Gorman 1981) loading have described only apparent-level strength properties and have been unable to directly address tissue-level failure mechanisms. In general, pure shear loading along the main trabecular orientation, as simulated in our study, is equivalent to compression-tension biaxial loading at 45° to the main trabecular orientation. This equivalence is reflected in the observed failure pattern (Figure 7, left panels) of predominantly tensile yield due to stretching of the trabeculae oriented along the principal tensile stress direction at an angle of 45° with respect to main trabecular orientation. There is only a minor degree of compressive yield along the (perpendicular) principal compressive stress direction because the tissue is weaker in tension than compression, and thus yielding will occur preferentially for tensile loading even if tissue-level tensile and compressive stresses are equal. Interestingly, these failure mechanisms appear to be different than those for uniaxial apparent-level 45° off-axis loading. For example, our earlier work (Bevill et al. 2009b) showed that uniaxial compression of human trabecular bone caused predominantly tissue-level tensile yielding due to bending of individual trabeculae (again, which fail primarily in tension because the tissue is so weak in tension). It is not clear how a superimposed apparent-level tensile loading perpendicular to such 45° off-axis uniaxial compressive loading would alter such failure mechanisms and study of such bi-axial failure mechanisms remains a topic for future research. Previously, we also proposed that torsion of bovine tibial trabecular bone causes failure via appreciable bending of individual trabeculae (Fenech and Keaveny 1999). Although torsion and shear loading both produce shear stresses in the specimen at the apparent level, those torsion results cannot be directly compared to those from our pure shear simulations because shear stresses across the specimen are not uniform in a pure torsion test and for trabecular bone this may cause different tissue-level failure mechanisms.
These observations on tissue-level failure mechanisms constitute computer-generated predictions and therefore await direct experimental validation. In the meanwhile, microdamage in trabecular bone induced from mechanical testing has been correlated with the structure model index (Arlot et al. 2008; Karim and Vashishth 2011). Consistent with that finding, we found that the total amount (proportion) of yielded tissue was also significantly correlated to SMI (Table 2). For specimens with low bone volume fraction loaded under compression, we found that failure occurred mostly in the horizontal trabeculae. This is consistent with the findings from experiments on human vertebral bone (Fyhrie and Schaffler 1994) in which it was observed that complete fracture of trabeculae was confined to the horizontal trabeculae — presumably fracture of individual trabeculae only occurs when trabecular are excessively stretched primarily uniaxially. Finite element studies by other investigators have also shown good agreement between predicted distributions of tissue-level stress and directly imaged histological sections of microdamage (Nagaraja et al. 2005; Shi et al. 2010).
At the apparent level, we found an influence of intra-specimen heterogeneity in trabecular microarchitecture on the ratio of shear to compressive strengths. Interestingly, this intra-specimen variation contributed more to a decrease in compressive strength of low volume fraction specimens than to any effect on the shear strength (Table 2). Similarly, the negative correlation between the degree of anisotropy (DA) and the shear-to-compressive strength ratio implies that a more anisotropic structure renders the bone equally susceptible to shear or compressive failure, more so due to the decrease in compressive strength than any effect on shear strength. Other investigators have reported similar observations, in which an increase in intra-specimen variability of microarchitecure of vertebral bone decreased stiffness (Wegrzyn et al. 2010; Yeh and Keaveny 1999; Yeni et al. 2011) and strength (Wegrzyn et al. 2010) under compression. Similarly, it has been proposed that heightened trabecular anisotropy might render the proximal femur more susceptible to fracture (Ciarelli et al. 2000). Our results suggest that these intra-specimen heterogeneity effects primarily degrade the compressive strength and have less influence on the shear strength.
The validity of our computational results for apparent-level strength is supported by results from various previous experiments. Our compressive strength results were directly validated by our own experiments, and the exponent of about 1.7 in our strength-bone volume relation is consistent with reported power law relations from various other compression experiments, which are in range 1.5–2.0 (Carter and Hayes 1976; Morgan and Keaveny 2001). Since many experimental studies have studied shear failure by testing cylindrical cores of trabecular bone in torsion (Garnier et al. 1999; Ford and Keaveny 1996; Kasra and Grynpas 2007; Rincón-Kohli and Zysset 2009), to help interpret that body of work we performed a sub-study to directly compare apparent-level yield strength derived from torsion vs. pure shear loading (Appendix). That study found statistically similar exponents in the yield strength-bone volume fraction relation for the two loading modes, but much lower strength for torsion than pure shear (ratio of mean strengths = 0.57 for n=15 specimens). This ratio is close to the value of 0.61 obtained for the ratio of mean torsion to shear ultimate strengths as measured experimentally for human femoral bone bone (Garnier et al. 1999). Similarly, the ratio of mean torsion strength to mean compression strength for these 15 specimens was 0.24 (Appendix), which is in close agreement with the value of 0.22 obtained in a much larger experiment on human trabecular bone (Rincón-Kohli and Zysset 2009). Further, after accounting for variations in bone volume fraction, average values of torsional yield strength from our simulations agreed well in an absolute sense with the literature data from multiple experiments (Figure 8). Finally, a recent experiment on human trabecular bone reported statistically similar exponents for the strength-density relation for compression vs. torsion (Rincón-Kohli and Zysset 2009), just as we did (1.74 vs. 1.85, p=0.25, see Figure 3).
Figure 8.
Literature comparison (Garnier et al. 1999; Ford and Keaveny 1996; Rincón-Kohli and Zysset 2009; Garrison et al. 2011) of torsional yield strength vs. bone volume fraction, for 15 specimens from this study. The error bars show one standard deviation around the mean value of bone volume fraction and yield strength. For studies that did not report apparent density, the bone volume fraction was calculated assuming a tissue density of 2.0 g/cm3. The data from (Bevill et al. 2009a) is unpublished (n=6 vertebral body specimens).
Our study has a number of limitations. Although our models were well validated for compressive yield strength, we relied on computational models to extrapolate from compressive strength to shear strength. In general, the models had sufficiently high spatial resolution for numerical convergence but did not include such micro-scale features as intra-specimen variations in mineral density or tissue material properties, anisotropy of the bone tissue, or the geometric detail of any resorption spaces. While inclusion of such features can affect overall behavior (Bourne and van der Meulen 2004; Gross et al. 2012; Jaasma et al. 2002; van der Linden et al. 2001; Verhulp et al. 2008), their exclusion is unlikely to appreciably alter the relation between compression vs. shear yield strengths, which was our main focus. Even so, it is possible that more complex tissue-level material behavior, such as anisotropy in tissue yielding and post-yield hardening (Carnelli et al. 2010; Schwiedrzik and Zysset 2012), or mechanical effects of micro-damage or micro-fracture, might lead to different tissue-level failure mechanisms, particularly in the post-yield region of the apparent-level stress-strain curve. Further, particularly for specimens having low volume fraction, the apparent-level properties as estimated by these finite element models may be sensitive to the applied boundary condition (Pahr and Zysset 2008, Bevill et al. 2009a), which may introduce some error in these estimates compared to the in vivo behavior. Finally, we only explored shear behavior in the axial-transverse plane and the shear failure behavior may differ for other planes. Despite these limitations, these new results should provide an improved basis for assessing the role of shear failure of trabecular bone in structural analyses of whole bones and bone-implant systems.
Acknowledgments
Funding was provided by the National Institutes of Health (NIH AR43784). Cadaveric material was supplied by the Anatomic Gift Foundation and NDRI. Micro-CT imaging was performed at the laboratory of Dr. Sharmila Majumdar at UC San Francisco. Supercomputer resources were obtained from the National Partnership for Advanced Computational Infrastructure (NPACI UCB266).
Appendix
In this sub-study, we used the computational techniques described above to measure the yield strength of 15 cylindrical cores (8mm diameter, 12–15 mm length, BV/TV = 0.19±0.10, 0.07–0.38) under torsion loading. These cores were chosen from the original image set of the 54 cubes specimens. The nodes on the bottom face of the cores were fully constrained and a rotational displacement was applied on the nodes of the top face equivalent to 1.5% apparent engineering shear strain. The shear stress was calculated from the apparent-level torque vs. angle of twist curve using the following equation (Nádai 1950):
where T is the calculated torque, r is the radius of the specimen and 3 is the angle of twist per unit length. The term dT/d3 was determined by fitting a fifth-degree polynomial to the torque vs angle of twist curve. While this equation has been used in various studies of trabecular bone (Garnier et al. 1999; Ford and Keaveny 1996; Kasra and Grynpas 2007; Rincón-Kohli and Zysset 2009), it applies directly only to isotropic homogenous continuum materials and works well also for transversely isotropic materials that have an axis of symmetry along the axis of the cylindrical specimen (Ford and Keaveny 1996). We found that the torsion strength varied in a power law fashion with bone volume fraction (Figure 3, R2 = 0.96). The constant in the power law regression for torsional strength was significantly different from the constant of the regression of shear strength (p<0.001), but the exponents were not different (p=0.25, Tukey HSD test). After adjusting for bone volume fraction, general linear regression modeling indicated that the ratio of mean torsional strength to mean shear strength was 0.57, confirming that the apparent-level yield strength of trabecular bone is much lower under torsional loading relative to pure shear loading. Likewise, the ratio of the adjusted mean for torsion strength to compression strength was 0.24.
Footnotes
Conflict of interest statement
Dr. Keaveny has a financial interest in O.N. Diagnostics and both he and the company may benefit from the results of this research. All other authors have no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams MF, Bayraktar HH, Keaveny TM, Papadopoulos P. Ultrascalable implicit finite element analyses in solid mechanics with over a half a billion degrees of freedom. ACM/IEEE Proceedings of SC2004: High Performance Networking and Computing.2004. [Google Scholar]
- Arlot ME, Burt-Pichat B, Roux JP, Vashishth D, Bouxsein ML, Delmas PD. Microarchitecture influences microdamage accumulation in human vertebral trabecular bone. Journal of Bone and Mineral Research. 2008;23(10):1613–1618. doi: 10.1359/jbmr.080517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck JD, Canfield BL, Haddock SM, Chen TJ, Kothari M, Keaveny TM. Three-dimensional imaging of trabecular bone using the computer numerically controlled milling technique. Bone. 1997;21(3):281–287. doi: 10.1016/s8756-3282(97)00122-1. [DOI] [PubMed] [Google Scholar]
- Bevill G, Eswaran SK, Farahmand F, Keaveny TM. The influence of boundary conditions and loading mode on high-resolution finite element-computed trabecular tissue properties. Bone. 2009a;44(4):573–578. doi: 10.1016/j.bone.2008.11.015. [DOI] [PubMed] [Google Scholar]
- Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39(6):1218–1225. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
- Bevill G, Farhamand F, Keaveny TM. Heterogeneity of yield strain in low-density versus high-density human trabecular bone. Journal of Biomechanics. 2009b;42(13):2165–2170. doi: 10.1016/j.jbiomech.2009.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourne BC, van der Meulen MC. Finite element models predict cancellous apparent modulus when tissue modulus is scaled from specimen CT-attenuation. Journal of Biomechanics. 2004;37(5):613–621. doi: 10.1016/j.jbiomech.2003.10.002. [DOI] [PubMed] [Google Scholar]
- Carnelli D, Gastaldi D, Sassi V, Contro R, Ortiz C, Vena P. A finite element model for direction-dependent mechanical response to nanoindentation of cortical bone allowing for anisotropic post-yield behavior of the tissue. Journal of Biomechanical Engineering. 2010;132(8):081008. doi: 10.1115/1.4001358. [DOI] [PubMed] [Google Scholar]
- Carter DR, Hayes WC. Bone compressive strength: the influence of density and strain rate. Science. 1976;194(4270):1174–1176. doi: 10.1126/science.996549. [DOI] [PubMed] [Google Scholar]
- Cheal EJ, Spector M, Hayes WC. Role of loads and prosthesis material properties on the mechanics of the proximal femur after total hip arthroplasty. Journal of Orthopaedic Research. 1992;10(3):405–422. doi: 10.1002/jor.1100100314. [DOI] [PubMed] [Google Scholar]
- Ciarelli MJ, Goldstein SA, Kuhn JL, Cody DD, Brown MB. Evaluation of Orthogonal Mechanical Properties and Density of Human Trabecular Bone from the Major Metaphyseal Regions with Materials Testing and Computed Tomography. Journal of Orthopaedic Research. 1991;9(5):674–682. doi: 10.1002/jor.1100090507. [DOI] [PubMed] [Google Scholar]
- Ciarelli TE, Fyhrie DP, Schaffler MB, Goldstein SA. Variations in three-dimensional cancellous bone architecture of the proximal femur in female hip fractures and in controls. Journal of Bone and Mineral Research. 2000;15(1):32–40. doi: 10.1359/jbmr.2000.15.1.32. [DOI] [PubMed] [Google Scholar]
- Fenech CM, Keaveny TM. A cellular solid criterion for predicting the axial-shear failure properties of trabecular bone. Journal of Biomechanical Engineering. 1999;121(4):414–422. doi: 10.1115/1.2798339. [DOI] [PubMed] [Google Scholar]
- Ford CM, Keaveny TM. The dependence of shear failure properties of bovine tibial trabecular bone on apparent density and trabecular orientation. Journal of Biomechanics. 1996;29(10):1309–1317. doi: 10.1016/0021-9290(96)00062-0. [DOI] [PubMed] [Google Scholar]
- Fyhrie DP, Schaffler MB. Failure mechanisms in human vertebral cancellous bone. Bone. 1994;15(1):105–109. doi: 10.1016/8756-3282(94)90900-8. [DOI] [PubMed] [Google Scholar]
- Garnier KB, Dumas R, Rumelhart C, Arlot ME. Mechanical characterization in shear of human femoral cancellous bone: torsion and shear tests. Medical Engineering & Physics. 1999;21(9):641–649. doi: 10.1016/s1350-4533(99)00096-x. [DOI] [PubMed] [Google Scholar]
- Garrison JG, Gargac JA, Niebur GL. Shear strength and toughness of trabecular bone are more sensitive to density than damage. Journal of Biomechanics. 2011;44(16):2747–2754. doi: 10.1016/j.jbiomech.2011.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein SA. The mechanical properties of trabecular bone: dependence on anatomic location and function. Journal of Biomechanics. 1987;20(11/12):1055–1061. doi: 10.1016/0021-9290(87)90023-6. [DOI] [PubMed] [Google Scholar]
- Goulet RW, Goldstein SA, Ciarelli MJ, Kuhn JL, Brown MB, Feldkamp LA. The relationship between the structural and orthogonal compressive properties of trabecular bone. Journal of Biomechanics. 1994;27(4):375–389. doi: 10.1016/0021-9290(94)90014-0. [DOI] [PubMed] [Google Scholar]
- Gross T, Pahr DH, Peyrin F, Zysset PK. Mineral heterogeneity has a minor influence on the apparent elastic properties of human cancellous bone: a SRμCT-based finite element study. Computer Methods in Biomechanics and Biomedical Engineering. 2012 doi: 10.1080/10255842.2011.581236. [DOI] [PubMed] [Google Scholar]
- Guldberg RE, Hollister SJ, Charras GT. The accuracy of digital image-based finite element models. Journal of Biomechanical Engineering. 1998;120(4):289–295. doi: 10.1115/1.2798314. [DOI] [PubMed] [Google Scholar]
- Halawa M, Lee AJ, Ling RS, Vangala SS. The shear strength of trabecular bone from the femur, and some factors affecting the shear strength of the cement-bone interface. Arch Orthop Trauma Surg. 1978;92(1):19–30. doi: 10.1007/BF00381636. [DOI] [PubMed] [Google Scholar]
- Hildebrand T, Laib A, Müller R, Dequeker J, Rüegsegger P. Direct three-dimensional morphometric analysis of human cancellous bone: microstructural data from spine, femur, iliac crest, and calcaneus. Journal of Bone and Mineral Research. 1999;14(7):1167–1174. doi: 10.1359/jbmr.1999.14.7.1167. [DOI] [PubMed] [Google Scholar]
- Homminga J, Van-Rietbergen B, Lochmuller EM, Weinans H, Eckstein F, Huiskes R. The osteoporotic vertebral structure is well adapted to the loads of daily life, but not to infrequent “error” loads. Bone. 2004;34(3):510–516. doi: 10.1016/j.bone.2003.12.001. [DOI] [PubMed] [Google Scholar]
- Jaasma MJ, Bayraktar HH, Niebur GL, Keaveny TM. Biomechanical effects of intraspecimen variations in tissue modulus for trabecular bone. Journal of Biomechanics. 2002;35(2):237–246. doi: 10.1016/s0021-9290(01)00193-2. [DOI] [PubMed] [Google Scholar]
- Karim L, Vashishth D. Role of trabecular microarchitecture in the formation, accumulation, and morphology of microdamage in human cancellous bone. Journal of Orthopaedic Research. 2011;29(11):1739–1744. doi: 10.1002/jor.21448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasra M, Grynpas MD. On shear properties of trabecular bone under torsional loading: effects of bone marrow and strain rate. Journal of Biomechanics. 2007;40(13):2898–2903. doi: 10.1016/j.jbiomech.2007.03.008. [DOI] [PubMed] [Google Scholar]
- Keller TS. Predicting the Compressive Mechanical-Behavior of Bone. Journal of Biomechanics. 1994;27(9):1159–1168. doi: 10.1016/0021-9290(94)90056-6. [DOI] [PubMed] [Google Scholar]
- Keyak JH. Relationships between femoral fracture loads for two load configurations. Journal of Biomechanics. 2000;33(4):499–502. doi: 10.1016/s0021-9290(99)00202-x. [DOI] [PubMed] [Google Scholar]
- Kopperdahl DL, Keaveny TM. Yield strain behavior of trabecular bone. Journal of Biomechanics. 1998;31(7):601–608. doi: 10.1016/s0021-9290(98)00057-8. [DOI] [PubMed] [Google Scholar]
- Laib A, Kumer JL, Majumdar S, Lane NE. The temporal changes of trabecular architecture in ovariectomized rats assessed by MicroCT. Osteoporosis International. 2001;12(11):936–941. doi: 10.1007/s001980170022. [DOI] [PubMed] [Google Scholar]
- Lotz JC, Cheal EJ, Hayes WC. Fracture prediction for the proximal femur using finite element models: Part I-Linear analysis. Journal of Biomechanical Engineering. 1991;113(4):353–360. doi: 10.1115/1.2895412. [DOI] [PubMed] [Google Scholar]
- Mitton D, Rumelhart C, Hans D, Meunier PJ. The effects of density and test conditions on measured compression and shear strength of cancellous bone from the lumbar vertebrae of ewes. Medical Engineering & Physics. 1997;19(5):464–474. doi: 10.1016/s1350-4533(97)00001-5. [DOI] [PubMed] [Google Scholar]
- Morgan EF, Keaveny TM. Dependence of yield strain of human trabecular bone on anatomic site. Journal of Biomechanics. 2001;34(5):569–577. doi: 10.1016/s0021-9290(01)00011-2. [DOI] [PubMed] [Google Scholar]
- Nádai A. Theory of flow and fracture of solids. McGraw-Hill; New York: 1950. pp. 347–352. [Google Scholar]
- Nagaraja S, Couse TL, Guldberg RE. Trabecular bone microdamage and microstructural stresses under uniaxial compression. Journal of Biomechanics. 2005;38(4):707–716. doi: 10.1016/j.jbiomech.2004.05.013. [DOI] [PubMed] [Google Scholar]
- Neibur GL, Yuen JC, Hsia AC, Keaveny TM. Convergence Behavior of High Resolution Finite Element Models of Trabecular Bone. Journal of Biomechanical Engineering. 1999;121:629–635. doi: 10.1115/1.2800865. [DOI] [PubMed] [Google Scholar]
- Pahr DH, Zysset PK. Influence of boundary conditions on computed apparent elastic properties of cancellous bone. Biomechanics and Modeling in Mechanobiology. 2008;7(6):463–476. doi: 10.1007/s10237-007-0109-7. [DOI] [PubMed] [Google Scholar]
- Papadopoulos P, Lu J. On the formulation and numerical solution of problems in anisotropic finite plasticity. Computer Methods in Applied Mechanics and Engineering. 2001;190(37–38):4889–4910. [Google Scholar]
- Rice JC, Cowin SC, Bowman JA. On the dependence of the elasticity and strength of cancellous bone on apparent density. Journal of Biomechanics. 1988;21(2):155–168. doi: 10.1016/0021-9290(88)90008-5. [DOI] [PubMed] [Google Scholar]
- Rincón-Kohli L, Zysset PK. Multi-axial mechanical properties of human trabecular bone. Biomechanics and Modeling in Mechanobiology. 2009;8(3):195–208. doi: 10.1007/s10237-008-0128-z. [DOI] [PubMed] [Google Scholar]
- Saha S, Gorman PH. Strength of human cancellous bone in shear and its relationship to bone mineral content. Transactions of Orthopaedic Research Society. 1981;217 [Google Scholar]
- Schwiedrzik JJ, Zysset PK. An anisotropic elastic-viscoplastic damage model for bone tissue. Biomechanics and Modeling in Mechanobiology. 2012 doi: 10.1007/s10237-012-0392-9. [DOI] [PubMed] [Google Scholar]
- Shi X, Liu XS, Wang X, Guo XE, Niebur GL. Effects of trabecular type and orientation on microdamage susceptibility in trabecular bone. Bone. 2010;46(5):1260–1266. doi: 10.1016/j.bone.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stolken JS, Kinney JH. On the importance of geometric nonlinearity in finite-element simulations of trabecular bone failure. Bone. 2003;33(4):494–504. doi: 10.1016/s8756-3282(03)00214-x. [DOI] [PubMed] [Google Scholar]
- Stone JL, Beaupre GS, Hayes WC. Multiaxial strength characteristics of trabecular bone. Journal of Biomechanics. 1983;16(9):743–752. doi: 10.1016/0021-9290(83)90083-0. [DOI] [PubMed] [Google Scholar]
- van der Linden JC, Birkenhager-Frenkel DH, Verhaar JA, Weinans H. Trabecular bone’s mechanical properties are affected by its non-uniform mineral distribution. Journal of Biomechanics. 2001;34(12):1573–1580. doi: 10.1016/s0021-9290(01)00146-4. [DOI] [PubMed] [Google Scholar]
- van Rietbergen B, Odgaard A, Kabel J, Huiskes R. Direct mechanics assessment of elastic symmetries and properties of trabecular bone architecture. Journal of Biomechanics. 1996;29(12):1653–1657. doi: 10.1016/0021-9290(96)00093-0. [DOI] [PubMed] [Google Scholar]
- Verhulp E, van Rietbergen B, Muller R, Huiskes R. Indirect determination of trabecular bone effective tissue failure properties using micro-finite element simulations. Journal of Biomechanics. 2008;41(7):1479–1485. doi: 10.1016/j.jbiomech.2008.02.032. [DOI] [PubMed] [Google Scholar]
- Wegrzyn J, Roux JP, Arlot ME, Boutroy S, Vilayphiou N, Guyen O, Delmas PD, Chapurlat R, Bouxsein ML. Role of trabecular microarchitecture and its heterogeneity parameters in the mechanical behavior of ex vivo human L3 vertebrae. Journal of Bone and Mineral Research. 2010;25(11):2324–2331. doi: 10.1002/jbmr.164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh OC, Keaveny TM. Biomechanical effects of intraspecimen variations in trabecular architecture: A three-dimensional finite element study. Bone. 1999;25(2):223–228. doi: 10.1016/s8756-3282(99)00092-7. [DOI] [PubMed] [Google Scholar]
- Yeni YN, Zinno MJ, Yerramshetty JS, Zauel R, Fyhrie DP. Variability of trabecular microstructure is age-, gender-, race- and anatomic site-dependent and affects stiffness and stress distribution properties of human vertebral cancellous bone. Bone. 2011;49(4):886–894. doi: 10.1016/j.bone.2011.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]