Intraocular Pressure Magnitude and Variability as Predictors of Rates of Structural Change in Non-Human Primate Experimental Glaucoma

Abstract

The purpose of this study is to determine the effects of intraocular pressure (IOP) mean, maximum and variability on the rate of structural change in experimental glaucoma. Data were taken retrospectively from 59 non-human primates involved in ongoing studies of experimental glaucoma. IOP was measured by tonometry every 1–3 weeks, and these readings split into non-overlapping fixed-length windows. First, different characterizations of IOP variability were tested to find the one that was least correlated with the mean IOP within the same window. Next, the rates of change of the Mean Position of the Disc (MPD) from confocal scanning laser tomography, and Retinal Nerve Fiber Layer Thickness (RNFLT) from spectral domain ocular coherence tomography, were calculated over each window. Mixed effects models were formed to predict these rates based on the characterizations of IOP. Normalized root mean squared residual (RMSR) from the trend of IOP during windows of five IOP measurements provided a characterization of variability showing lowest correlation with mean IOP (r<0.001). In univariate analyses, rate of change of MPD and RNFLT were predicted by mean IOP (p<0.001 for both) and maximum IOP (p<0.001 for both). IOP variability did not significantly predict change in MPD (p=0.129) or RNFLT (p=0.438). In bivariate models, maximum IOP was the most significant predictor of change. We conclude that normalized RMSR allows the effects of IOP variability to be assessed independently of mean IOP. Maximum IOP provided the best predictability of structural change, either causally or because it captures the contributions of both mean and variability.

1. Introduction

Glaucoma is a major cause of blindness and visual disability, and therefore it is important to identify the factors associated with rapid disease progression. Elevated intra-ocular pressure (IOP) is a risk factor for development and progression of glaucoma (AGIS Investigators, 2000; Kass et al., 2002; Kass et al., 2010; Leske et al., 2003). However, the roles of diurnal (Asrani et al., 2000; Bengtsson and Heijl, 2005; Realini et al., 2010, , 2011) and intervisit (Medeiros, 2010; Nouri-Mahdavi et al., 2004a; Nouri-Mahdavi et al., 2004b) fluctuations in IOP are less well understood.(Medeiros, 2010) In part, this is because clinical studies typically measure IOP with an insufficient sampling rate to truly measure this variability. For example, the Advanced Glaucoma Intervention Study (AGIS) measured IOP at a frequency of just once every six months (Nouri-Mahdavi et al., 2004b). Additionally, the level of variability in IOP may not be independent of the chronic level of IOP, depending on the measure of variability being used.

The Advanced Glaucoma Intervention Study (AGIS) reported that the standard deviation of IOP values was predictive of progression in glaucoma (Nouri-Mahdavi et al., 2004a), yet it was not found to be predictive of visual field status four years later (Nouri-Mahdavi et al., 2004b). A later AGIS analysis found that variability was associated with progression in low IOP patients but not in high IOP patients (Caprioli and Coleman, 2008). The Early Manifest Glaucoma Trial (EMGT) and the European Glaucoma Prevention Study both found no relation between the standard deviation of IOP values and subsequent progression (Bengtsson et al., 2007; Miglior et al., 2007). However, IOP variability was associated with progression in a study of post-operative glaucoma patients (Hong et al., 2007). An analysis of data from the Malmö Ocular Hypertension Study found that IOP variability as measured by office-hours diurnal IOP curves was associated with increased risk of developing glaucoma, but was not a significant predictor in a model that also included Mean IOP as a predictor (Bengtsson and Heijl, 2005). Progression has also been reported to be associated with the maximum IOP (Bergea et al., 1999) and the range of IOP (Asrani et al., 2000; Bergea et al., 1999) observed within the study period. Most recently, the Collaborative Initial Glaucoma Treatment Study reported that the standard deviation, range and maximum IOP were all more predictive of visual field progression than the mean IOP, in a cohort undergoing IOP-lowering medication (Musch et al., 2011).

The issue is confounded by the fact that each of these variability measures is correlated with the mean level of IOP (Caprioli and Coleman, 2008; Saccà et al., 1998), possibly contributing to the disparate nature of these results. This makes it difficult to distinguish effects of variability from effects of chronically elevated IOP. In this retrospective study of data from non-human primates with experimental glaucoma and frequent IOP monitoring over time, we seek to separate the effects of high IOP with those of IOP variability, and determine the power of each to predict structural changes to the optic nerve head (ONH) and peripapillary retinal nerve fiber layer (RNFL).

2. Methods

2.1. Animals

Data were taken from non-human primates (NHPs) involved in ongoing studies of experimental glaucoma, including 59 rhesus macaques (Macaca mulatta) aged 2 to 22 years. In each animal, one eye underwent laser treatment to the trabecular meshwork to induce chronic elevation of IOP (Quigley and Hohman, 1983). Laser treatments were performed under ketamine only, ketamine and xylazine, or ketamine and dexmedetomidine anesthesia initially in two separate treatment sessions (180° of the trabecular meshwork in each session separated by 2 weeks). Laser treatments were repeated in subsequent weeks (but limited to a 90° sector) unti l an IOP elevation was first noted or if post-laser IOP had returned to normal levels. The duration of post-laser longitudinal imaging and the degree of structural change in the treated eye of each animal at endpoint varied according to the criteria of the primary study in which each animal was involved. This enabled a wide range of experimental glaucoma stages to be evaluated in this study. However, we excluded from analysis all data from eyes after they had reached end-stage glaucoma, defined as 60% reduction of retinal nerve fiber layer thickness (RNFLT) as compared to the baseline average in a given eye. This was done because eyes do not exhibit further change beyond this end-stage (at least for RNFLT) (Hood and Kardon, 2007). Note that the endpoints were defined based on various criteria for structural change, rather than being based on the magnitude of IOP insult, so this should not cause bias when comparing different characterizations of IOP. IOP characterizations were compared between the three primary studies using a linear regression model to ensure consistency between cohorts.

The Legacy Health Institutional Animal Care and Use Committees approved all of the protocols in this study, and all animals were treated in accordance with the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research.

2.2. IOP measurement

IOP was measured by Tonopen XL (Reichert Inc, Depew NY) in both eyes of each animal (mean of n=3 measures per eye) every 1 to 3 weeks at the start of each imaging session (see below for imaging details). Anesthesia for imaging sessions always began with an induction dose of ketamine (15 mg/kg IM) and either xylazine (0.8–1.5 mg/kg IM) or midazolam (0.2 mg/kg IM). Depending on the specific protocol for the session, isoflurane gas (1–2%; typically 1.25%) was also administered via endotracheal tube. Thus, IOP measurements were acquired under varied anesthetic agents and at variable times after administration of anesthetic agents, though typically within 30 min of anesthesia induction.

2.3. Imaging

Imaging of the ONH and retinal nerve fiber layer (RNFL) occurred every 1 to 3 weeks after the start of unilateral laser treatments. All imaging was performed 30 minutes after IOP was lowered to 10 mmHg by anterior chamber manometer. As such, all image data were captured at the same IOP, and after sufficient time to eliminate any reversible component of ONH deformation that was due to the chronically elevated level of IOP on a given imaging day. Hence, we captured only the permanent alterations in each eye relative to its baseline imaging data (Bellezza et al., 2003; Burgoyne et al., 2002; Burgoyne et al., 1995).

Three Confocal Scanning Laser Tomography (CSLT) images (with each being the mean of n=3 data sets) were acquired from both eyes at each imaging session, using a Heidelberg Retina Tomograph II (Heidelberg Engineering GmbH, Heidelberg, Germany). Scans were included in the study if they had an acceptable quality score, defined as SD ≤ 50. For the current study, the CSLT parameter mean position of the disc (MPD) was calculated for each CSLT image as described in previous publications (Burgoyne et al., 2004; Burgoyne et al., 1994). Briefly, MPD refers to the height of the surface of the ONH (i.e. average height of all pixels located within the disc margin contour line) relative to the height of a reference plane located on the peripapillary surface. The MPD value used in this analysis was the mean MPD of the three acquired CSLT images.

Spectral Domain Ocular Coherence Tomography (sdOCT) RNFL imaging was performed using a commercially available device (Spectralis, Heidelberg Engineering GmbH, Heidelberg, Germany). For this study, the average peripapillary RNFLT was measured from a single circular B-scan consisting of 1536 A-scans (RNFLT samples). Nine individual sweeps were averaged in real time to comprise the final stored B-scan at each session. The position of the scan was centered on the ONH at the first imaging session and all follow-up scans were pinned (identical) to this location. A trained technician manually corrected the accuracy of the native automated image segmentation prior to exporting the data for extraction of thickness values by custom software. Images met the minimum acquisition requirements for the instrument, and were included if the quality score was no worse than 15.

2.4. Statistical Analysis

Only data collected after the date of the initial laser treatment for each NHP was included for analysis. For analysis, the IOP sequences were split into non-overlapping windows of a fixed number of testing sessions. Each NHP had to have undergone at least this number of testing sessions to be included in the analysis. For example, when the window width was five sessions, the first window consisted of sessions 1–5 post-laser; the second window consisted of sessions 6–10; etc. The mean, maximum and ‘variability’ (defined below) of IOP were characterized within each window, along with the MPD and RNFLT at the start of the window. The rate of change in MPD and RNFLT over the time period was defined by linear regression over time when there were at least three structural measurements present within that window of IOP measurements; and by the difference between the first and last structural measurements within the window divided by the time between them when only two measurements were available within that window.

The first stage of analysis was to choose a suitable parameterization to summarize IOP variability. The aim was to pick a measure of variability that is independent of the mean IOP. Six summary measures of variability were considered:

• SD: the standard deviation of the IOP measurements within the window (Bengtsson et al., 2007; Miglior et al., 2007; Nouri-Mahdavi et al., 2004a; Nouri-Mahdavi et al., 2004b).

• Range: the absolute difference between the greatest and least IOP measurements within the window (Asrani et al., 2000; Bergea et al., 1999).

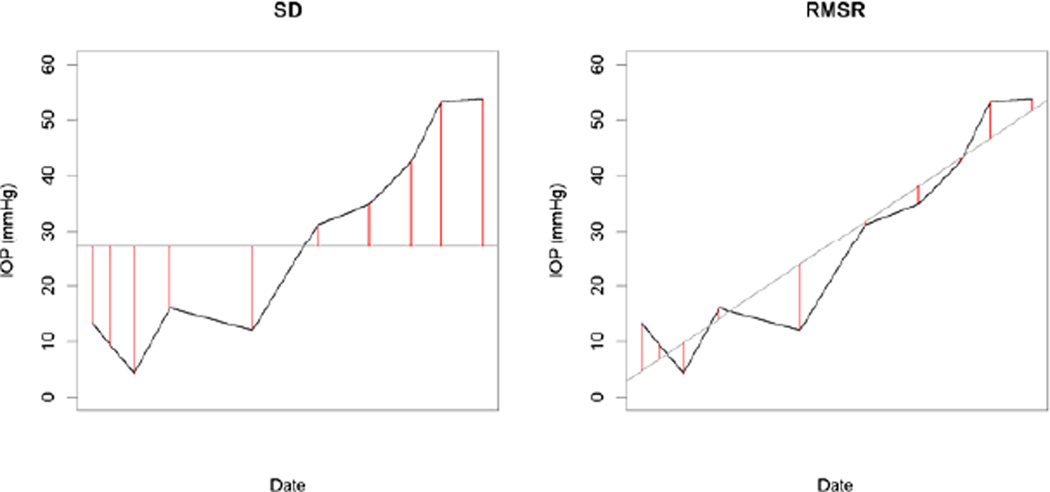
• RMSR: the root mean square residual from the regression line of IOP over time within the window. This is equivalent to calculating the standard deviation after first adjusting for any trend over time, as illustrated in Figure 1.

• SD/mean: the standard deviation normalized by dividing by the mean within the same window, sometimes referred to as the coefficient of variance.

• Range/mean: the absolute difference divided by the mean within the window.

• RMSR/mean: the root mean square residual divided by the mean within the window.

Figure 1.

Example showing the difference between the calculations of standard deviation (SD) and root mean square residual (RMSR), in this case for a window length of ten IOP measurements. SD equals the square root of the mean of the squared lengths of the red lines in the left-hand plot; RMSR equals the equivalent value based on the red lines in the right-hand plot. For SD, the lines extend from each data point to the mean value within the window. For RMSR, the red lines extend from each data point to the trend line over time.

A mixed effects linear model was constructed to predict the variability from the mean IOP, for each measure of variability considered. This method accounts for the fact that there are multiple windows per eye and two eyes per NHP. A first-order autoregressive correlation structure was assumed due to the longitudinal nature of the data (measures from two windows will be better correlated when those windows are closer together in time). A high p-value indicates that mean IOP is not predictive, i.e. that the measure of variability can be considered to be independent of the mean IOP. This process was repeated for different window lengths.

In order to demonstrate the magnitude of the relations between mean IOP and each measure of variability, the Pearson correlation was also calculated, since there is no simple equivalent available when using the mixed effects model. Comparisons between correlations were performed using Steiger’s Z₂* test statistic, which follows an asymptotic standard normal distribution, N(0,1), under the null hypothesis that the two correlations are equal (Steiger, 1980). While this reduces the power of the test to detect a difference when compared with using the simple Z statistic, it is more valid since it accounts for the fact that the correlations come from data drawn from the same subjects. A measure of variability was sought that had a low correlation with mean IOP.

Having chosen the measure of variability, further mixed effects models (with the same correlation structure as above) were constructed, to predict the rate of change of each structural measure (MPD and RNFLT). First, univariate models were constructed, using as the predictor the age of the animal, treatment (whether this was the lasered eye or the fellow control eye), the three characterizations of IOP (mean, maximum and variability), the same three characterizations of IOP during the previous window of measurements (when available; the first window for each eye was omitted from analyses when results from the previous window were used), and the initial value of the structural measurement (the first value measured within that window). Bivariate models were then constructed to predict the rate of structural change based on combinations of predictors. During the experiment, most animals underwent multiple laser insults in order to achieve the desired elevation in IOP. Therefore for this primary analysis, this analysis was performed omitting any windows that contained a laser insult (and starting a new window with the next measurement after the laser insult), giving 264 windows of tests. Since this resulted in too few consecutive windows of measurements for the effects of IOP in the previous window to be assessed, a secondary analysis was performed including measurements from dates on which a laser insult took place, giving a total of 341 windows of tests. To ensure that the results were robust to the analysis chosen, the main univariate analyses (the effects of IOP mean, maximum and variability on the rate of change of MPD and RNFLT) were repeated using different window lengths. These univariate analyses were also repeated within cohorts restricted to each of the three primary study cohorts.

Longer series of data typically came from those NHPs that did not show early change in response to IOP elevation. There is a significant relation between series length (number of windows) and the rate of change of MPD, with p=0.0098. The relation between series length and the rate of change of RNFLT was not significant, p=0.109, although the trend was in the expected direction. Therefore to address this potential bias, we repeated the analyses using only the last window in the sequence for each animal. This gives a sample size of 113 windows, rather than the 341 windows when using the entire dataset. None of these windows contained a laser insult.

3. Results

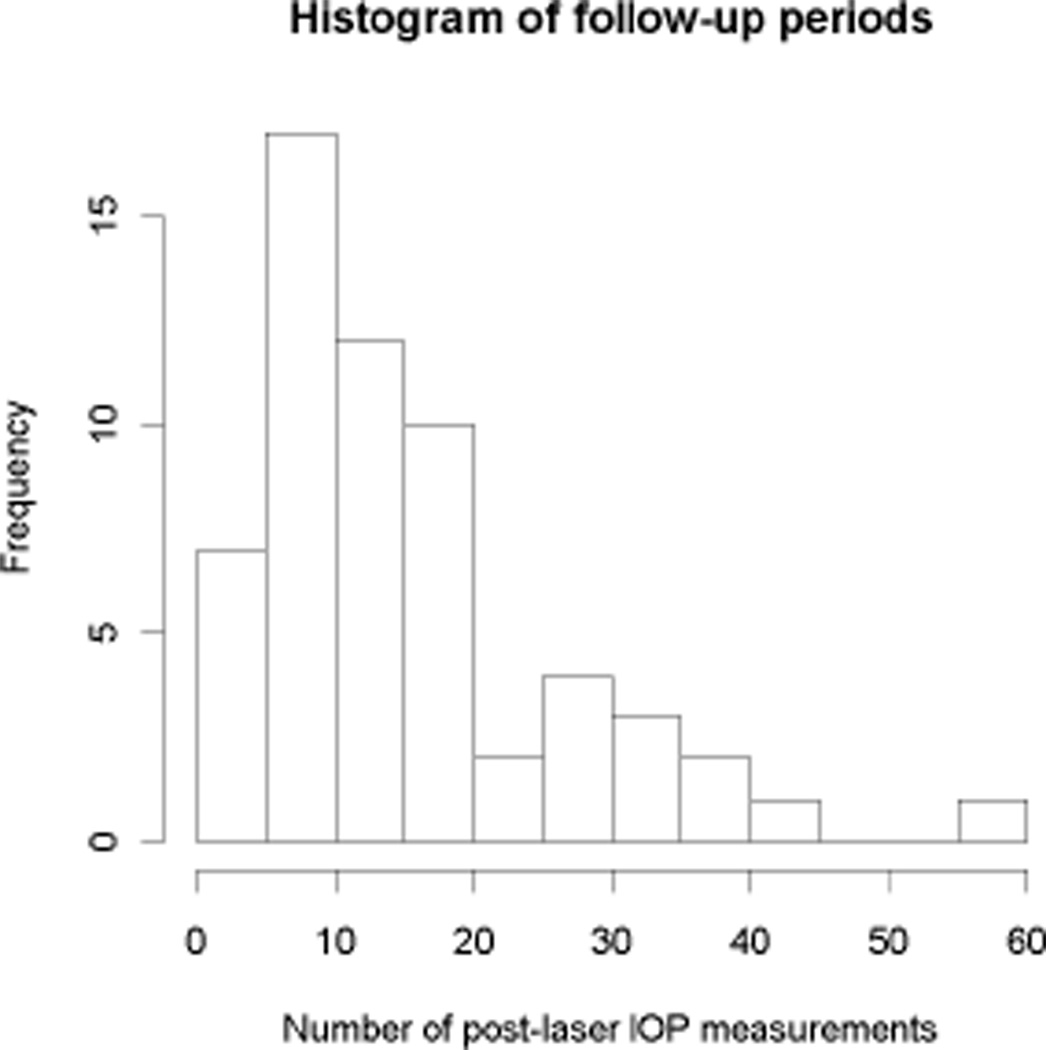
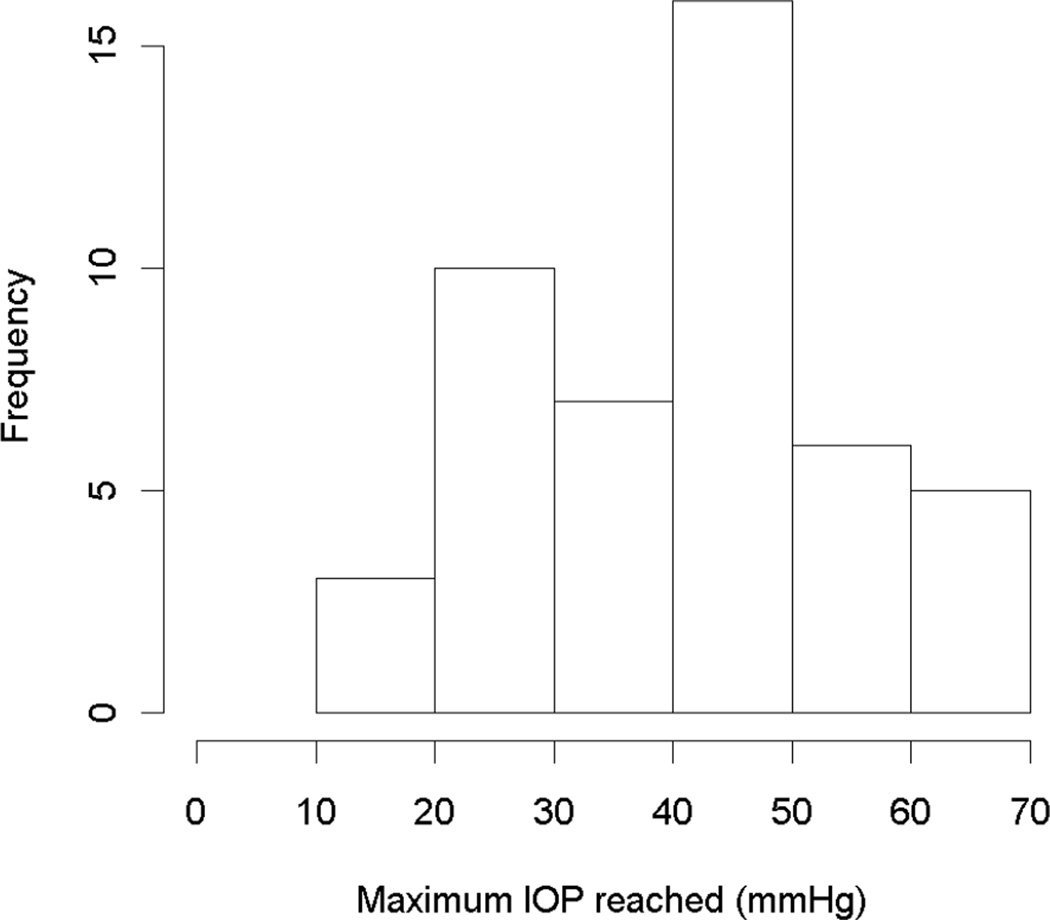
Table 1 shows the characteristics of the NHPs in the study, and the scan quality scores for both HRT and OCT. In all, 59 NHPs were included. No significant differences were found between the characteristics of the three primary study cohorts. Figure 2 shows a histogram of the number of (post-laser, pre-endstage) IOP measurements per animal. Figure 3 shows a histogram of the maximum IOP measurements throughout the study in the treated eyes.

Table 1.

Characteristics of the study dataset over the entire duration of the study. Changes from baseline in the mean position of the disc (MPD) and retinal nerve fiber layer thickness (RNFLT) are for the treated eyes only.

	Mean	Standard Deviation	Range
# IOP measurements	30	22	8 – 113
# MPD measurements	17	15	4 – 61
# RNFLT measurements	14	14	0 – 59
Overall Duration (days)	268	214	43 – 900
IOP in treated eye (mmHg)	19.7	11.3	0.0 – 65.7
Maximum IOP recorded (mmHg)	40.7	12.5	15.3 – 65.7
IOP in untreated eye (mmHg)	11.2	3.1	0.0 – 31.3
MPD change from baseline (µm)	−154	159	−759 – +22
RNFLT change from baseline (%)	−20	20	−75 – +15
HRT Standard Deviation	14.1	5.2	0 – 50
OCT Quality Score	29.6	4.6	15 – 44

Figure 2.

Histogram of the number of post-laser IOP measurements per NHP in the study.

Figure 3.

Histograms of the maximum post-laser IOP measurements reached in the treated eyes.

Table 2 shows the p-values for each of the six measures of variability that were considered as predictors of mean IOP, for different window lengths. Table 3 shows the correlation between mean IOP and each measure, demonstrating the magnitude of the relation. Note that the values in Table 2 are not simply the p-values of the correlation coefficients, since they take into account that there are multiple longitudinal data points for each eye of each NHP by using a mixed effects model. It is seen that in order to be considered independent of the mean IOP, measures of variability must be normalized by dividing by the mean IOP. When assessing the effect of IOP variability, these mean-normalized characterizations of the variability should be used in place of the raw SD, Range or RMSR.

Table 2.

p-values for Mean IOP as a predictor of different measures of IOP fluctuation, using a linear mixed effects model as specified in the Methods section, for different lengths of windows of IOP measurements. Low numbers indicate that the parameter is well correlated with Mean IOP. SD = standard deviation; Range = absolute difference between the maximum and minimum IOP; RMSR = root mean square residual compared with the trend over time. N shows the number of non-overlapping windows of that length that are available for analysis.

Window	N	SD	Range	RMSR	SD/Mean	Range/Mean	RMSR/Mean
3	689	<0.0001	<0.0001	<0.0001	0.027	0.026	0.002
4	504	<0.0001	<0.0001	<0.0001	0.557	0.431	0.343
5	375	<0.0001	<0.0001	<0.0001	0.078	0.068	0.020
6	341	<0.0001	<0.0001	<0.0001	0.152	0.079	0.265
7	259	<0.0001	<0.0001	<0.0001	0.065	0.111	0.098
8	255	<0.0001	<0.0001	<0.0001	0.775	0.751	0.446
9	209	<0.0001	<0.0001	<0.0001	0.789	0.998	0.885
10	193	<0.0001	<0.0001	<0.0001	0.259	0.425	0.647

Table 3.

The correlation between Mean IOP and each different measure of IOP fluctuation, for different lengths of windows of IOP measurements. In contrast with Table 2, high numbers indicate that the parameter is well correlated with Mean IOP. Lower correlations indicate a greater degree of independence between the two, allowing the effects of IOP magnitude and fluctuation to be better separated. SD = standard deviation of IOP measures; Range = absolute difference between the maximum and minimum IOP measures; RMSR = root mean square residual compared with the trend from linear regression over time.

Window	SD	Range	RMSR	SD/Mean	Range/Mean	RMSR/Mean
3	0.588	0.590	0.470	0.016	0.016	−0.041
4	0.673	0.674	0.634	0.060	0.056	0.020
5	0.686	0.684	0.650	0.035	0.032	−0.000
6	0.675	0.674	0.687	0.083	0.073	0.059
7	0.671	0.679	0.678	0.100	0.094	0.039
8	0.675	0.689	0.730	0.162	0.138	0.102
9	0.696	0.700	0.746	0.195	0.154	0.131
10	0.726	0.734	0.756	0.201	0.160	0.133

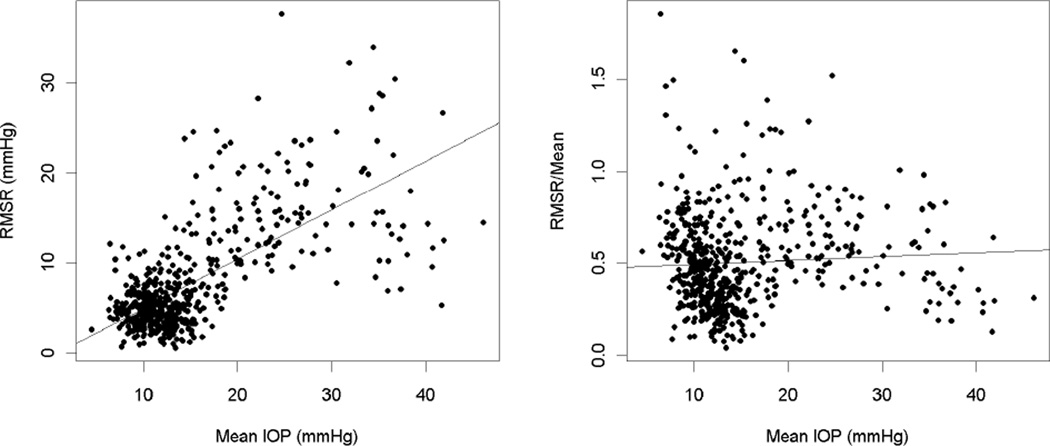
As seen in Table 2, the best parameterization of variability (indicated by higher p-values) varied depending on the window length chosen. Based on the strength of the correlations in Table 3, RMSR/Mean was the characterization of variability that was least correlated with mean IOP for all window lengths greater than three measurements. This is demonstrated in the plot in Figure 4. Thus, RMSR/Mean was used as the measure of variability for the rest of the study, enabling the effects of chronic elevated IOP to be better separated from the effects of IOP variability. Of the different window lengths, windows of six measurements demonstrated good independence between variability and mean (the magnitude of the correlation between mean IOP and RMSR/Mean was 0.059, p=0.265), while also being sufficiently long to detect longitudinal change. Therefore, for subsequent analyses, variability was defined as the value of RMSR/Mean within windows of six IOP measurements. This measure was then used as a predictor of the rate of structural change within the window, along with the other predictors given in the Methods section.

Figure 4.

In the left-hand plot, variability defined as the root mean squared residual from the trend of IOP over time (RMSR), within each window of six tests, is significantly correlated with the mean IOP within that window. The least-squares fitted regression line shows RMSR increasing with mean IOP. In the right-hand plot, this variability is normalized by dividing by the mean (RMSR/Mean), and becomes independent of mean IOP, with the regression line becoming nearly horizontal.

Table 4 shows the results of univariate analyses, in the 264 windows during which no laser insult took place. Table 5 shows the equivalent results based on 341 windows of tests with or without a laser insult, enabling the effect of IOP in the previous time window to be assessed. In each case, the p-value (from the mixed effects model) associated with the predictor is given. Mean, Variability and Maximum IOP were all significant predictors of the rate of change of MPD, and both Mean and Maximum IOP were significant predictors of the rate of change of RNFLT. Since the measure of variability was chosen to be independent of mean IOP, this is evidence that IOP variability is associated with increased damage, and that this is not merely an artefactual result caused by the association between the measure of variability and IOP level. Maximum IOP within the window was found to be the best predictor of the rate of structural change. It was better for predicting the change in MPD than the variability (p=0.007 from Steiger’s Z₂* test) or mean (not significant, Z₂* p=0.368). For predicting change in RNFLT, Maximum IOP was better than either mean (not significant, Z₂* p=0.668) or variability (Z₂* p<0.001). Age was not found to be a significant predictor; this is likely due to the narrow range of ages of the animals in the study, and should not be taken as indicative of the presence or absence of age as an independent risk factor (although it does mean that age need not be included as a predictor in the bivariate models considered below). All trends in these results were consistent across the three study cohorts, although the significance levels varied between cohorts due to the reduced sample sizes.

Table 4.

Results of univariate models using each potential predictor of the rate of structural change, as defined by either MPD or RNFLT. The predictors considered were three characterizations of the IOP within the same window of six measurements (in mmHg), the age of the animal (in years), and the value of the structural parameter at the start of the window. Only windows of six measurements during which no laser insult took place are included for this analysis. The coefficient gives the predicted change in the outcome variable for a one unit increase in the specified predictor.

Predictor	Rate of change of MPD			Rate of change of RNFLT
	Coefficient	Standard Error	p-value	Coefficient	Standard Error	p-value
IOP Mean	−0.037	0.008	<0.001	−0.013	0.002	<0.001
IOP Fluctuation	−0.538	0.353	0.129	0.052	0.066	0.438
IOP Maximum	−0.029	0.006	<0.001	−0.010	0.002	<0.001
Age	0.043	0.024	0.080	−0.006	0.009	0.498
Initial MPD	0.003	0.001	<0.001	0.0004	0.0002	0.049
Initial RNFLT	0.020	0.005	<0.001	0.0071	0.0012	<0.001

Table 5.

Results of univariate models using each potential predictor of the rate of structural change, as defined by either MPD or RNFLT. The predictors considered were three characterizations of the IOP within the same window of six measurements (in mmHg), the same three characterizations over the previous window of six measurements when available, the age of the animal (in years), and the value of the structural parameter at the start of the window. Windows are included whether or not a laser insult took place during that time period. The coefficient gives the predicted change in the outcome variable for a one unit increase in the specified predictor.

Predictor	Rate of change of MPD			Rate of change of RNFLT
	Coefficient	Standard Error	p-value	Coefficient	Standard Error	p-value
IOP Mean	−0.037	0.012	0.003	−0.012	0.002	<0.001
IOP Fluctuation	−2.590	0.353	<0.001	−0.043	0.059	0.474
IOP Maximum	−0.050	0.008	<0.001	−0.008	0.001	<0.001
Previous IOP Mean	−0.016	0.010	0.116	−0.003	0.002	0.228
Previous IOP Fluctuation	−0.832	0.263	0.002	−0.073	0.061	0.234
Previous IOP Maximum	−0.022	0.006	0.001	−0.005	0.002	0.006
Age	−0.016	0.047	0.731	−0.005	0.011	0.632
Initial MPD	0.006	0.001	<0.001	0.001	0.000	<0.001
Initial RNFLT	0.002	0.005	0.767	0.008	0.001	<0.001

Tables 6 and 7 show the results of univariate models using the IOP mean, variability and maximum to predict the rates of structural change when the analyses were performed using different window lengths. Similar patterns are observed for different window lengths. The rate of change of MPD can be predicted by IOP maximum or variability; the rate of change of RNFLT can be predicted by IOP maximum or mean. Maximum IOP is not only the most significant predictor in most cases, but is also the only characterization that consistently predicts both rates of change.

Table 6.

Results of univariate models using three characterizations of the IOP to predict the rate of change of MPD, using different window lengths.

Predictor	IOP Mean		IOP Fluctuation		IOP Maximum
	Coef	p	Coef	p	Coef	p
3 measurements	−0.028	0.055	−3.038	<0.001	−0.047	<0.001
4 measurements	−0.023	0.021	−1.423	0.001	−0.024	0.001
5 measurements	−0.037	<0.001	−1.144	<0.001	−0.038	<0.001
6 measurements	−0.037	0.003	−2.590	<0.001	−0.050	<0.001
7 measurements	0.009	0.423	−0.953	<0.001	−0.013	0.147
8 measurements	−0.023	0.067	−1.127	<0.001	−0.057	<0.001
9 measurements	−0.001	0.918	−0.790	0.002	−0.024	0.001
10 measurements	−0.007	0.532	−1.180	<0.001	−0.035	<0.001

Table 7.

Results of univariate models using three characterizations of the IOP to predict the rate of change of RNFLT, using different window lengths.

Predictor	IOP Mean		IOP Fluctuation		IOP Maximum
	Coef	p	Coef	p	Coef	p
3 measurements	−0.007	<0.001	0.131	0.160	−0.004	0.007
4 measurements	−0.014	<0.001	−0.223	0.007	−0.010	<0.001
5 measurements	−0.008	<0.001	−0.044	0.442	−0.007	<0.001
6 measurements	−0.012	<0.001	−0.043	0.474	−0.008	<0.001
7 measurements	−0.009	<0.001	−0.075	0.103	−0.006	<0.001
8 measurements	−0.009	<0.001	−0.135	0.004	−0.007	<0.001
9 measurements	−0.006	<0.001	−0.048	0.216	−0.004	<0.001
10 measurements	−0.005	<0.001	−0.111	<0.001	−0.004	<0.001

To ensure that our conclusions were not being biased by the fact that there were a greater number of windows available for slower progressing eyes, the analysis was repeated using only the most recent window per eye, rather than all available windows. Results are presented in Table 8, in the same format as Table 4 above. It is seen that the magnitudes of the coefficients have generally increased, as the effects are not being diluted by as long periods of stability. However, the standard errors have also increased, due to the reduced sample size. As a result, the p-values are very similar with those obtained using the entire dataset. In particular, no p-values have changed from significant to non-significant or vice-versa.

Table 8.

Results of univariate models using each potential predictor of the rate of structural change, as defined by either MPD or RNFLT, using only the most recent window of six measurements per eye (instead of all available windows as in Table 4). The predictors considered were three characterizations of the IOP within the same window (in mmHg), the age of the animal (in years), and the value of the structural parameter at the start of the window. The coefficient gives the predicted change in the outcome variable for a one unit increase in the specified predictor.

Predictor	Rate of change of MPD			Rate of change of RNFLT
	Coefficient	Standard Error	p-value	Coefficient	Standard Error	p-value
IOP Mean	−0.155	0.039	<0.001	−0.027	0.003	<0.001
IOP Fluctuation	−4.763	0.719	<0.001	−0.121	0.094	0.206
IOP Maximum	−0.145	0.019	<0.001	−0.013	0.002	<0.001
Age	−0.038	0.070	0.590	−0.017	0.013	0.219
Initial MPD	0.013	0.002	<0.001	0.001	0.0002	<0.001
Initial RNFLT	0.004	0.012	0.738	0.010	0.002	<0.001

In a bivariate model to predict the rate of structural change, IOP mean and maximum had coefficients of opposite sign. A high IOP maximum was associated with a more negative rate of change of MPD (coefficient = −0.034, p=0.119), but this effect was tempered if the mean IOP was also high (coefficient = +0.007, p=0.806). Using single backwards elimination would result in a more parsimonious model with Maximum IOP as the sole predictor, in which case it becomes significant as shown above. When a similar bivariate model was constructed using Maximum and Mean IOP as predictors of change in RNFLT, Maximum IOP was again found to be the more significant predictor retained after backwards elimination, while Mean was not significant (p=0.433). When Maximum and Variability were used, Variability was not significant when predicting change in MPD (p=0.781) or change in RNFLT (p=0.347); Maximum IOP was significant in both cases (p<0.001).

Using bivariate analyses, in the dataset including windows of tests containing a laser insult, the IOP mean from the current and previous windows were both significant predictors of the rate of change of MPD in the current window (p<0.001 for both). However the IOP maximum and variability from the previous window were not significant independently of the value in the current window (p=0.256 and p=0.371 respectively), indicating that no additional information was gained from their inclusion. Similar results were found from bivariate models to predict the change in RNFLT; the mean IOP from the previous window had p=0.001, and the maximum had p=0.940, and the variability had p=0.232.

When predicting change in MPD or RNFLT using the current and previous IOP means, or the current and previous IOP maxima, the regression coefficients associated with each were of opposite sign. An elevated current IOP mean was associated with a greater change in MPD; but if the previous IOP mean was also elevated, the change in MPD was smaller. This would be consistent with the structural damage having already taken place when IOP first became elevated, with little additional damage caused by that elevated IOP being subsequently maintained.

In an additional assessment of IOP as a risk factor, we calculated the Cumulative IOP Difference (Yang et al., 2011) for each experimental glaucoma eye. This was defined as the difference between the area under its IOP-time curve and that of the contralateral normal eye, spanning the period between laser onset and the start of each window. We then formed mixed effects models to predict the change in either MPD or RNFLT (as before) that also included this measure. The predictors were the cumulative difference up to the start of the window; the mean, maximum and variability of IOP in the current window; and the interactions between cumulative difference and each of these three IOP measures. After using the stepwise backwards elimination technique, the only significant predictor of the rate of change was still IOP maximum. While these relationships may change over the course of the neuropathy, our data suggest that for a given window of time, the maximum level of IOP during that window influenced structural progression more than the IOP exposure prior to that window.

4. Discussion

The most important result from this study is the finding that RMSR/Mean provides a suitable measure of IOP variability. Although other mean-normalized measures of IOP variability were also shown to not be significantly correlated with mean IOP, RMSR/Mean exhibited the lowest correlation when windows of length 5 measurements were used. Because these normalized measures are independent of mean IOP, their use allows the effects of chronic IOP elevation to be better separated from the effects of IOP variability. This removes the confounding effect caused by IOP range and SD being approximately proportional to mean IOP, as seen in analysis of the data from previous clinical trials (Caprioli and Coleman, 2008; Saccà et al., 1998).

As shown in Figure 1, during periods coinciding with true change to the chronic IOP level, SD and range are both increased, even though this is not indicative of true IOP variability. RMSR from the trend over time does not have this drawback, making it more suitable for analyses. This will become even more important when using increased sampling frequencies from IOP telemetry (Downs et al., 2011). In this retrospective study, it was found that maximum IOP within a time window was the IOP characterization that best predicted the rates of two forms of structural change within that window. No additional information was gained by also including mean IOP or IOP variability (neither was found to be consistently significant as a predictor in a bivariate model with IOP maximum). Maximum IOP will tend to increase with both mean IOP and IOP variability. In our dataset, maximum IOP was significantly correlated with both mean IOP (r=0.922, p<0.001) and IOP variability (r=0.368, p<0.001).

It is possible that the maximum IOP is indeed the most significant factor causing progression. However, it is also possible that both elevated mean IOP and more variable IOP cause increased damage, and that maximum IOP appears to be the best predictor because it captures both of these sources. Either possibility would be consistent with the findings of the AGIS study, which stated: “We hypothesize that greater IOP fluctuation is damaging in eyes with low mean IOPs, but when the mean IOP is higher, the role of IOP fluctuation becomes less important” (Caprioli and Coleman, 2008). Although the results in Tables 2 and 3 indicate a way to distinguish effects of chronic IOP elevation from effects of variability, it is not possible in this retrospective dataset to separate the effect of peaks in IOP from those two factors. This could only be achieved by a prospective study altering either mean IOP or the level of IOP variability while maintaining the other at a constant value.

The characterization of IOP in this study was based on measurements that were an average of 11.6 days apart. While this is a much higher frequency than in clinical trials (which typically have only two or three IOP measurements per year), it may still not be sufficient to accurately assess the most important aspects of variability. The maximum IOP is very unlikely to occur at the precise moment of testing. Therefore, while the greatest recorded IOP measurement within any given time period should be correlated with the true maximum that occurred during that period, the relation will not be perfect. The temporally sparse nature of clinical IOP data will also affect the accuracy of estimates of mean IOP. However, it will have an even greater effect on the accuracy of estimates of maximum IOP, since the noise is not reduced by averaging over several readings. Therefore, while this sparseness is problematic if chronic IOP elevation is driving glaucomatous damage, it becomes even more problematic if peaks in IOP are in fact driving the process. Our study does not include any aspect of short-term (seconds to minutes) or diurnal variations of IOP or vascular perfusion pressure. A better characterization of IOP, and hence more definitive conclusions concerning the most important factors related to progression, may be achieved using continuous monitoring by IOP telemetry, and work to develop such a system is underway (Downs et al., 2011).

Sequences for each eye were divided into non-overlapping windows, instead of using the entire sequence. This reduces the effect of the fact that the rate of change was not constant throughout the testing period, since it will be far closer to a constant rate when restricted to one shorter window. It also makes the study more relevant when translated to a clinical setting, since the clinician will wish to detect any acceleration in the rate of progression compared with earlier time windows for that same patient, so that appropriate treatment can be given. Based on the results shown in Table 3, windows of length 5 measurements were felt to be optimal. However as shown by Tables 6 and 7, the conclusions were robust to this choice.

The main limitation of this study is that the analysis was retrospective and our protocols were not designed to acquire IOP measurements under identical conditions. In particular, the IOP data we report were measured under variable degrees and types of anesthesia, all known to lower IOP. Due to this anesthesia effect, it is likely that we are underestimating the mean and peak IOPs throughout the study. Both eyes of each animal undergo a consistent period of lower IOP after anesthesia that can persist for up to 8 hours, which could also have a variable impact on progression. Moreover, our manometrically controlled imaging protocols induced IOP fluctuation in the treated eye that was both uncharacterized and variable (i.e. depending on the ambient IOP prior to cannulation).

5. Conclusions

In summary, our study suggests that IOP maximum was the single most important predictor of the rate of global ONH and RNFLT change in 59 NHPs with unilateral experimental glaucoma. These data and their analysis do not find IOP variability to be an independent risk factor; however definitive conclusions regarding the consequences of IOP variability and ocular perfusion pressure must await a prospective trial based on continuous telemetric data. Our data additionally suggest that measures of variability should be normalized by dividing by the mean IOP to effectively separate the effects of IOP variability from chronic IOP level.

Highlights.

• Intraocular pressure (IOP) is associated with glaucoma, but the mechanism is unclear.

• Many measures of IOP variability are correlated with the mean IOP.

• 59 non-human primates with early experimental glaucoma were followed.

• IOP mean and maximum were both predictive of rapid structural change, but variability was not.

• Maximum IOP showed the strongest association with the rate of change.

Acronyms Used

AGIS

Advanced Glaucoma Intervention Study

CSLT

Confocal Scanning Laser Tomography

IOP

Intraocular Pressure

MPD

Mean Position of the Disc

NHP

Non-Human Primate

ONH

Optic Nerve Head

RNFL

Retinal Nerve Fiber Layer

RNFLT

Retinal Nerve Fiber Layer Thickness

RMSR

Root Mean Squared Residual

sdOCT

Spectral Domain Ocular Coherence Tomography