Abstract
Amyloid β protein (Aβ), the principal component of the extracellular plaques found in the brains of Alzheimer’s disease patients, forms fibrils well suited to structural study by X-ray fiber diffraction. Fiber diffraction patterns from the 40-residue form Aβ(1–40) confirm a number of features of a three-fold symmetric Aβ model from solid state NMR, but suggest that the fibrils have a hollow core, not present in the original ssNMR models. Diffraction patterns calculated from a revised hollow three-fold model with a more regular β-sheet structure are in much better agreement with the observed diffraction data than patterns calculated from the original ssNMR model. Refinement of a hollow-core model against ssNMR data led to a revised ssNMR model, similar to the fiber diffraction model.
Keywords: amyloid structure, amyloid-β peptide, X-ray fiber diffraction, solid state NMR, Alzheimer’ disease
Introduction
Amyloid β protein (Aβ) is a 38–43 amino acid peptide, the principal component of the extracellular plaques found in the brains of Alzheimer’s disease patients.1 It is derived from the β-amyloid precursor protein by proteolysis, and variations in the exact sites of proteolysis account for the slight variations in the length of the peptide. The most abundant form is the 40-residue peptide Aβ(1–40),2 but other forms, differing mostly in the C-terminal site of proteolysis, are found, particularly Aβ(1–42). Amyloids are aggregates of misfolded proteins associated with over 20 human diseases including Alzheimer’s and Parkinson’s;3 the aggregates consist of long, unbranched fibrils 40–100 Å in diameter, often made up of twisted subfilaments that give the fibrils a rope-like appearance. X-ray fiber diffraction patterns from amyloids are dominated by a sharp reflection at a spacing close to 4.75 Å on the meridian (the axis parallel to the fibril axis), an indication of β-strands running perpendicular to the fibril axis, called cross-β structure.4,5 In many cases there is also a more diffuse intensity maximum at 8–10 Å on the equator (the axis at right-angles to the meridian). Many amyloids, perhaps most or all amyloids associated with disease,6 have the unique ability to propagate their own structure, recruiting other molecules of the same protein to the misfolded form as first described for infectious prions.7
Aβ structure has been studied by a variety of methods including cryo-electron microscopy (cryo-EM),8,9 fiber diffraction,10–13 solid state NMR (ssNMR),14–19 and molecular dynamics simulations.20–22 Aβ fibrils are known to be highly polymorphic, with subtle variations in fibril growth conditions leading to significant differences in molecular structure.23 The most detailed models have come from ssNMR, and consist of cross-β subfilaments (cross-β units15) made up of Aβ(1–40) molecules in which each Aβ molecule has two β-strands, in different β-sheets. The two strands form a U-shape, and are hydrogen-bonded to equivalent parallel strands in adjacent Aβ molecules. The number and orientation of U-shaped cross-β subfilaments varies, depending upon the conditions under which the fibrils are formed.14,15,24
We have obtained fiber diffraction data from Aβ (1–40) fibrils, and considered some of the proposed Aβ models in the light of those data. We particularly considered the three-fold symmetric model of Paravastu et al.,15 since some of our diffraction data were obtained from fibrils formed under identical conditions to those used in the ssNMR experiments from which that model was derived. Fiber diffraction is complementary to ssNMR because it is sensitive to large-scale structural features, while providing information at higher resolution than has so far been available from cryo-EM for Aβ. While we confirmed many of the general features of the original three-fold symmetric model, we found some discrepancies between the observed diffraction data and data predicted by that model. We have constructed new models more consistent with the fiber diffraction data, and shown that these models can also account for the ssNMR data.
Results and Discussion
Overview
We obtained fiber diffraction data from fibrils prepared at pH 2 and pH 7.4. The pH 7.4 fibrils were prepared under conditions identical to those used for ssNMR experiments,15 but the pH 2 fibrils yielded much better diffraction data. The diffraction patterns and electron microscopy suggested that the fibrils from both preparations had the same general structure, so we analyzed the data from the pH 2 fibrils, comparing them to data calculated from variations of the ssNMR model. The diffraction data also suggested that the fibrils had the general form of a hollow cylinder, so we constructed models based on the three-fold symmetric ssNMR model, but with a hollow core. These reconstructions led to a model (the fiber diffraction model) that fit the diffraction data well. In a separate modeling experiment, we further refined the original three-fold symmetric model against the ssNMR data, with small changes in the restraints that allowed the model to have a hollow core. The resulting refined model accounts for the ssNMR data and fits the fiber diffraction data much better than did the original ssNMR model, although not as well as the fiber diffraction model.
Diffraction from Aβ fibers
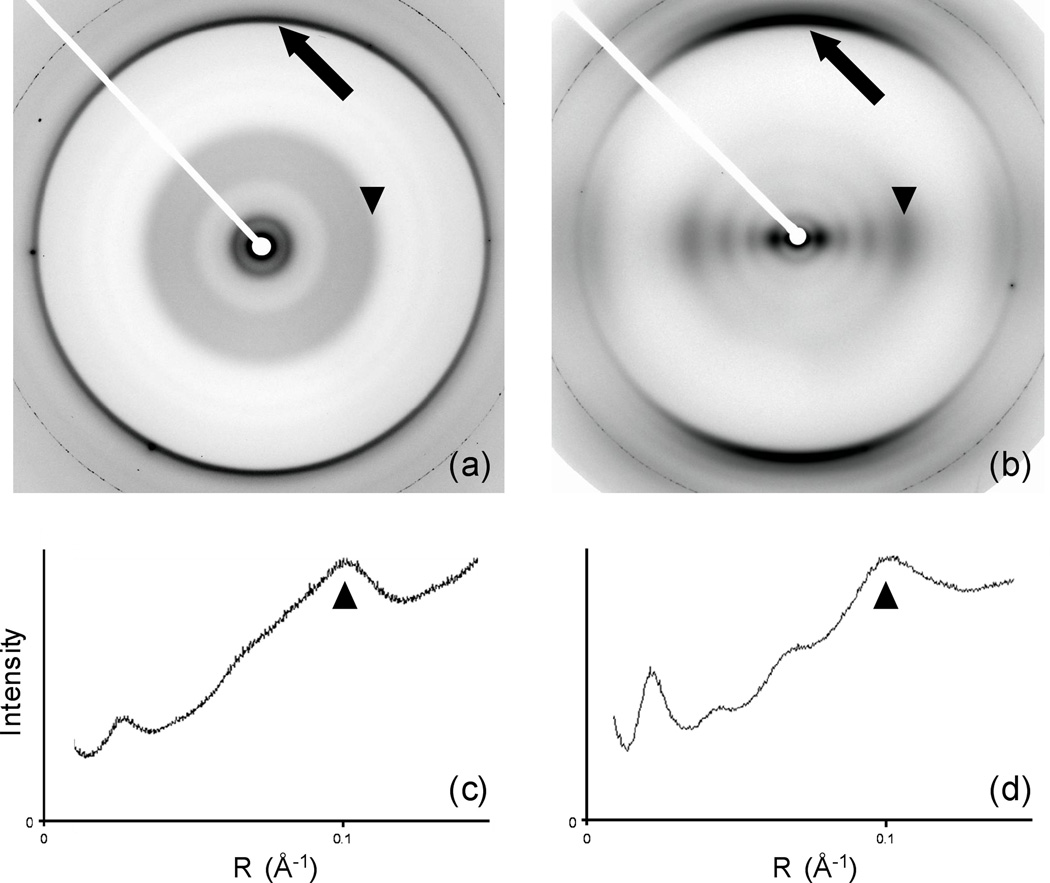
Diffraction patterns from Aβ fibers (Fig. 1a and b) all show typical amyloid cross-β diffraction, with an intense meridional reflection at 4.7 Å. Patterns from fibrils grown at pH 7.4 under quiescent conditions identical to those in the ssNMR measurements of Paravastu et al.15 were highly disoriented, although meridional and equatorial diffraction could still be distinguished (Fig. 1a). Despite the difference in orientation, sector plots (Materials and Methods) show that the pattern of intensities on the equator is very similar at neutral and low pH (Fig. 1 c and d). Diffraction on the equator is continuous, with no evidence for crystallinity even at low angles. The strongest equatorial features are intensities at about 40 Å and 10 Å resolution (44 and 9.8 Å at low pH; ~43 and ~10 Å at neutral pH). Under both conditions, there are weaker intensities at ~15 Å and ~22 Å, although because of disorientation the 22 Å intensity is too weak to be confidently identified in the neutral-pH patterns. Only the low-pH patterns were sufficiently ordered for quantitative analysis, but the similarities in the diffraction patterns, together with the similar appearances of the fibrils in electron microscopy images (Fig. S1), imply that the low-pH structure is similar to the neutral-pH structure. We therefore concluded that it was appropriate to use the three-fold-symmetric fibril model derived by Paravastu et al.15 as the starting point for comparisons with our diffraction data.
Fig. 1. Diffraction patterns and equatorial diffracted intensity from Aβ fibers.
(a) Diffraction pattern from fibrils made at pH 7.4, using fibrils from ssNMR measurements as seeds. (b) Diffraction pattern from fibrils made without buffer, at pH ~2. (c) Equatorial intensity (from a sector plot (Materials and Methods), integrated azimuthally) from (a) as a function of reciprocal space radius. (d) Equatorial intensity from (b). Arrows: meridional intensity at 4.7 Å. Arrowheads: equatorial intensity at ~10 Å.
Aβ models: comparison of experimental and calculated diffraction patterns
The low-pH Aβ diffraction pattern (Fig. 1b) was sufficiently well-oriented to allow the accurate determination of equatorial diffracted intensities by angular deconvolution.25,26 Intensities calculated from a variety of models were compared to these measured intensities.
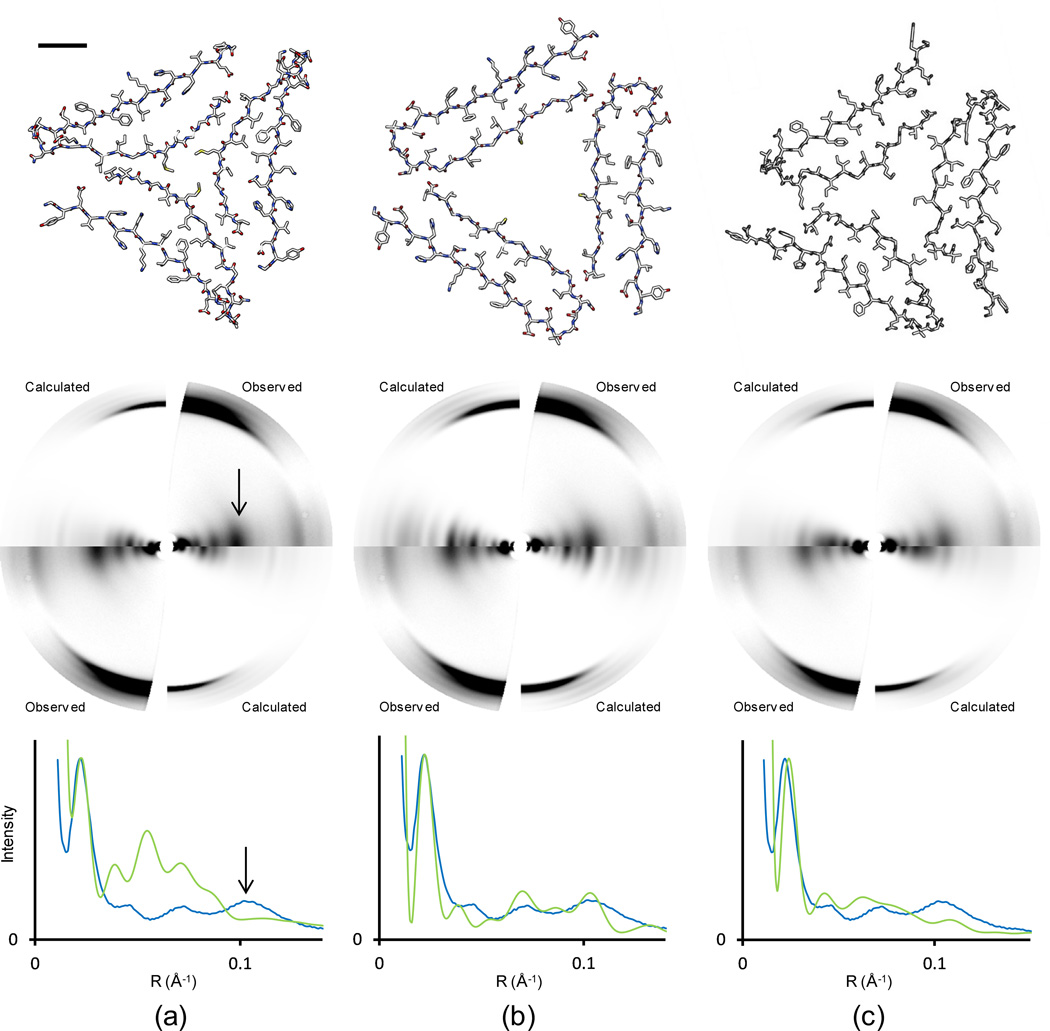
A diffraction pattern calculated from the published ssNMR model for three-fold symmetric Aβ fibrils15 reproduced the observed strong equatorial intensity close to R = 0.02 Å−1 (50 Å), but beyond that resolution, neither the peak positions nor the relative intensities fit the observed data (Fig. 2a). In particular, the model did not predict the strong equatorial intensity at R = 0.1 Å−1 (10 Å) and the intensity at R = 0.037 Å−1 was much greater than observed. The model also predicted very strong diffraction at R = 0.053 Å−1, where the observed data actually fell to a minimum. Overall, the calculated intensities were much stronger at medium resolution (R between 0.03 and 0.10 Å−1) than the observed intensities.
Fig. 2. Comparison of diffraction predicted from Aβ models with observed data.
(a) ssNMR model published by Paravastu et al.15 (b) Model adjusted to better fit fiber diffraction data. (c) Revised ssNMR model, PDB file 2LMP. Within each part, the top image is the cross-section of the three-subfilament Aβ models (bar = 10 Å), the middle image compares predicted with observed fiber diffraction data, and the bottom image represents intensity on a line through the equator of the corresponding diffraction pattern. Observed equatorial intensities were extracted by angular deconvolution; calculated intensities were from the corresponding models (Materials and Methods). Observed (blue) and calculated (green) intensities are scaled to match the peak intensities at R = 0.02 Å−1 (50 Å). Arrows in (a) indicate the strong equatorial intensity at R = 0.1 Å−1 (10 Å).
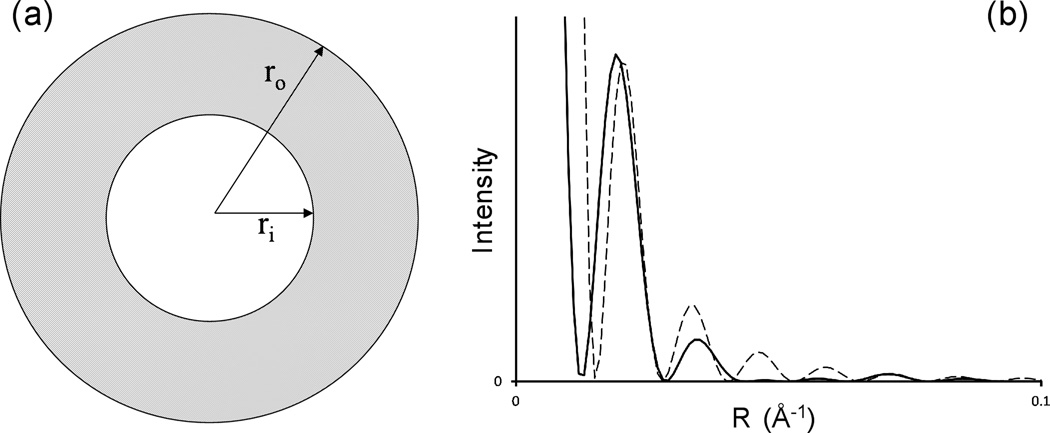
The diffraction calculated from the published ssNMR model qualitatively resembled diffraction from a solid cylinder, which is a reasonable approximation to the model at very low resolution. The observed diffraction intensities, however, are more typical of diffraction from a hollow cylinder (Fig. 3), falling off very rapidly at low angles (around R = 0.04 Å−1 in Fig. 1d) and then recovering to a considerable extent (around R = 0.1 Å−1 in Fig. 1d). While intensities calculated from homogeneous cylinders are of limited significance, since diffraction is influenced by molecular structures even at low resolution, these observations did suggest to us that the exploration of hollow models might improve the fit between the calculated and observed data. We therefore calculated the diffraction pattern that would be produced by the ssNMR model with the cross-β units simply moved to higher radius, approximating a hollow cylinder. This model predicted a diffraction pattern (Fig. S2a) that qualitatively resembled the experimental data more closely than the pattern from the unmodified ssNMR model, but still greatly underestimated the diffraction near R = 0.1 Å−1, and included diminished but still distinct intensity at R = 0.05 to 0.06 Å−1.
Fig. 3. Diffraction from solid and hollow cylinders.
(a) Cross-section of a hollow cylinder, outer diameter ro, inner diameter ri. (b) Calculated diffracted intensity from a solid cylinder, ro = 40 Å (dashed line), and from a hollow cylinder, ro = 40 Å, ri= 20 Å (solid line), as a function of reciprocal space radius R. This figure illustrates the nature of diffraction from solid and hollow cylinders, although it does not represent actual experimental data.
A model similar to the expanded ssNMR model, retaining a number of key molecular interactions but with β sheets much closer to the canonical structure (Materials and Methods), predicted a diffraction pattern with a greatly improved fit to the observed pattern at resolutions below about 8 Å (Fig. 2b) (higher resolution agreement is at present beyond the scope of this work). The more regular β sheets spaced close to 10 Å apart give rise to strong diffraction at 10 Å (R = 0.1 Å−1), as observed, and other parts of the equatorial diffraction are also in much better qualitative agreement with the observed data.
Other possible models
Alternative models for Aβ based on cryo-EM data, in which the fibrils are made up of two rather than three cross-β subfilaments, have been published.9,27 Aβ structures are known to depend on solution and fibrillization conditions24 as well as the exact peptide sequence, so these models are not necessarily appropriate for our fibrils, but they were nevertheless considered. Coordinates for one model27 were not available, but this model would not be expected to predict the observed diffraction data, since it includes a solid fibril core and the diffraction data imply a hollow core, as discussed above. Similarly, the separation of the subfilaments in a cryo-EM model9 of Aβ(1–42) is inconsistent with the peak positions in our diffraction data.
A model derived by ssNMR from fibrils formed under agitating conditions contains two rather than three subfilaments.14 Diffraction data calculated from this model were in very poor agreement with the observed diffraction data (Fig. S2b). The diffraction data thus readily distinguish among structural models that are qualitatively different from one another. We emphasize that the two- and three-subfilament models apply to distinct Aβ(1–40) structures, so our diffraction data do not contradict the two-subfilament model of Petkova et al.14
Hollow models and ssNMR data
The collapsed core of the published ssNMR model was largely a consequence of restraints on the distances between Met35 side chains in different cross-β units. These restraints were imposed during model development in order to explain the strength of magnetic dipole-dipole couplings among 13C-labeled Met35 methyl carbons, which was found experimentally to be somewhat greater than expected if only couplings within each cross-β unit were considered.15 An alternative explanation for the experimental data is that Met35 methyl carbons are randomly displaced along the fibril axis. The inverse-cube dependence of dipole-dipole couplings then leads to an enhancement of the average coupling strength, without requiring short distances between cross-β units.
Revised ssNMR models (PDB ID: 2LMP and 2LMQ) were calculated with the program Xplor-NIH (Materials and Methods), using the experimental restraints from Paravastu et al.15 and additional conformational restraints from backbone 13C-13C and 15N-15N dipolar recoupling measurements.28 Restraints on distances between Met35 methyl carbons in different cross-β units, which had the effect of collapsing the central pore in the earlier modeling calculations by Paravastu et al.,15 were not included in the Xplor-NIH calculations. These models are similar to the fiber diffraction model in Fig. 2b, in that the center of the fibril is hollow and the β sheets are more regular in structure (Fig. 2c). Diffraction predicted by one of the lowest-energy refined models (chains C, I, and O from PDB ID: 2LMP) is in much better agreement with the observed diffraction data (Fig. 2c) than the diffraction predicted by the original ssNMR model. Although the agreement does not appear to be as good as the agreement from the fiber diffraction model (Fig. 2b), it is good enough to support the hollow fibril core and more regular β sheet structure.
Precise quantitative agreement is not necessarily expected between the experimental fiber diffraction data and data calculated from ssNMR-based models, since the low-pH fibrils used to obtain an oriented diffraction pattern need not be completely identical structurally to the neutral-pH fibrils used in ssNMR measurements. Nevertheless, the results in Fig. 2c show that the principal features of the three-fold symmetric ssNMR-based model are consistent with the diffraction data, once the restraint on Met35-Met35 distances is removed as described above. Related conclusions regarding Met35-Met35 interactions were reached in recent molecular dynamics studies of three-fold symmetric Aβ fibrils.22
The revised models
Fiber diffraction confirms the cross-β amyloid structure of Aβ, as well as the three-fold symmetric structure of Aβ under the conditions used; no other structural model achieved even the qualitative agreement between calculated and observed diffraction seen in Figs. 2b and 2c. Electron micrographs and the strong equatorial intensity at R = 0.022 Å−1 are consistent with a structure approximating a cylinder of diameter ~80 Å, and to this extent the general features of the earlier ssNMR model for fibrils formed under quiescent conditions15 are confirmed. However, the weaker equatorial intensities at higher resolution suggested that unlike the earlier model, the cylinder is hollow, and this suggestion is supported by both diffraction pattern predictions (Fig. 2b) and the revised ssNMR analysis (Fig. 2c). Molecular dynamics simulations22 also favor a hollow rather than a solid core; the increased accessible surface area of a hollow model could bind small molecules, with important consequences for therapeutic and diagnostic applications. The hollow core may perhaps be surprising at first, given the hydrophobicity of the side chains lining the inner surface, but the molecular dynamics simulations show that the cavity is energetically stable and hydrated.
Other fiber diffraction studies of Aβ
Earlier workers10–13 obtained diffraction patterns from dried fibers or disks of Aβ(1–40) and Aβ(1–42). Modeling studies were limited, however, perhaps because the diffraction patterns were not as well-ordered as those described here. The published patterns are similar to those we have presented in that all include cross-β meridional intensity and equatorial intensity close to 10 Å, but other intensity maxima vary in position and relative strength, as might be expected given the diversity of conditions under which the fibers were made.
Fiber diffraction and ssNMR
Our analysis demonstrates the valuable complementarity between fiber diffraction and ssNMR for structural studies of filamentous assemblies. Fiber diffraction can only in exceptionally favorable cases29,30 image molecular details, but can often provide accurate overall shapes and dimensions; in contrast, ssNMR provides large numbers of accurate restraints on short interatomic distances, but the combination of many such distances and angles can lead to much less well-determined large-scale distances and dimensions. Combining the two methods overcomes these problems. To obtain the maximum benefit from this complementarity, it will be necessary to refine models against fiber diffraction and ssNMR data simultaneously; such refinements are being developed,31,32 and although they cannot yet handle data from fibrous systems as disoriented as amyloids, they should eventually be able to resolve any remaining disagreements between fiber diffraction models and the revised ssNMR models.
Materials and Methods
Sample preparation
For the low-pH studies, synthetic Aβ(1–40) (Bio-Synthesis Inc., Lewisville, TX) was dissolved without further purification in Milli-Q (Millipore Corp., Bedford, MA) water to a concentration of 13 mg/ml and stored at 4 °C. In contrast to the neutral-pH studies, no seeding step was used. The pH of the peptide solution after resuspension in water was ~2.0. Mature fibrils developed in about three months as observed by negative stain electron microscopy (EM).
For the neutral-pH studies, fibrils of synthetic Aβ(1–40) were prepared under quiescent conditions as described by Paravastu et al.15 The fibrils used for diffraction experiments were made identically to the fibrils used for ssNMR experiments, using multiple generations of seeding.15 Once mature fibrils had formed, the solution was centrifuged at 344,000 g and the resulting pellet was resuspended in 10 mM Tris-HCl pH 7.4 to a concentration of 5 mg/ml.
Under both sets of conditions, EM revealed twisted fibrils with diameters from 80–100 Å (Fig. S1), comparable to earlier observations of quiescent Aβ.15
Electron microscopy
Aβ(1–40) at a concentration of 1 mg/ml was applied to carbon-coated 400 square mesh copper grids (Electron Microscopy Sciences, Hatfield, PA). The grids were rinsed with buffer, negatively stained with 0.05% uranyl formate and 1% uranyl acetate, blotted, and allowed to dry. Electron micrographs were collected on a Philips CM12 transmission electron microscope operating at 80 kV in the Vanderbilt University Cell Imaging Shared Resource.
Fiber diffraction
Fibers of Aβ were prepared by suspending a 5 µl drop of fibril solution between two glass rods with beeswax tips approximately 1.5 mm apart. The fibers were allowed to dry over a period of hours to days in a closed chamber.33 Hydration was found to be important in maintaining the orientation and order of the fibers; saturated potassium sulfate was used to maintain relative humidity at 98%.
Fiber diffraction data were collected at the BioCAT and BioCARS beamlines of the Advanced Photon Source synchrotron, Argonne National Laboratory, and at beamline 4–2 at the Stanford Synchrotron Radiation Laboratory. Fibers were dusted with calcite and specimen-to-detector distances were determined from the 012 calcite diffraction ring at 3.8547 Å resolution and the 104 ring at 3.0355 Å.34
Patterns were obtained from numerous fibers, prepared under various conditions of pH, salt concentration, and humidity, seeded15 and unseeded. The patterns were all qualitatively very similar, as described above (Results) for the best-oriented fibers from each pH class.
Fiber diffraction analysis
Diffraction patterns were analyzed using the program WCEN35 to determine experimental parameters and positions of reflections. Equatorial intensities for the low-pH data were determined by the method of angular deconvolution.25,26 Deconvoluted intensities fit the observed intensities well for the low-pH data, but the disorientation in the neutral-pH data was too great to allow this approach. However, qualitative representations of intensities could be obtained even from poorly oriented patterns (provided that there was some orientation) using the sector plot feature of WCEN. This feature plots integrated intensity at a given radius within a sector centered on the equator of the diffraction pattern. The angular width of the sector was 10° for the better-oriented low-pH patterns, 20° for the poorly oriented neutral-pH patterns. Sector plots (Fig. 1) present intensities integrated azimuthally, that is, along the arcs that arise from sample disorientation, as a function of reciprocal space radius R. In contrast, the intensities shown in other plots (Figs. 2 and 3) are not integrated along the arcs, and are thus more easily compared to the observed intensities in the diffraction patterns. This difference should be considered when comparing such plots; effectively, the sector plots are corrected for sample disorientation, but the other plots are not. The difference approximates36 to a weighting of all the plots except the sector plots by R−1.
Diffraction simulations were carried out using the program DISORDER from the FiberNet website (www.fiberdiffraction.org). DISORDER performs Fourier-Bessel transforms to calculate diffraction from helical structures37 and simulates orientational disorder.38 For these simulations, a repeating unit of three Aβ molecules related by rotational symmetry was used. All three molecules were at the same axial position; varying their relative axial positions does not affect the equatorial intensities. An arbitrary symmetry of 200 repeating units in one turn of a helix, with each unit axially displaced from the previous unit by 4.7 Å, was used; after disorientation, the simulated diffraction pattern is not sensitive to the number of repeating units provided that it is large. An isotropic temperature factor of 40 was used in all simulations. Displays of fiber diffraction patterns used the programs WCEN (Fig. 1) and FIT2D (www.esrf.eu/computing/scientific/FIT2D/) (Fig. 2). Background subtraction from experimental data for comparison with data calculated by DISORDER used the program FibreFix,39 using the circularly-symmetric background option.
Intensities of equatorial diffraction from solid and hollow cylinders were calculated from the equation40
where the intensity at reciprocal space radius R is G(R)2, ro and ri are the outer and inner radii respectively of a hollow cylinder, and J1 is a first-order Bessel function.
Construction of models to fit the fiber diffraction data
Molecular models were constructed using UCSF CHIMERA.41 The model shown in Fig. 2b was developed by adjusting the three-subfilament model of Paravastu et al.,15 increasing the distance apart of the subfilaments to obtain a hollow cylindrical model, and regularizing the structure of the β-sheets. Adjustments were constrained by retaining the D23-K28 salt bridge and the I31-V39 contacts between adjacent β-strands.
Refinement of models against ssNMR data
Refinement of models against the ssNMR data used the program Xplor-NIH,42 using the experimental restraints from Paravastu et al.15 and additional conformational restraints from backbone 13C-13C and 15N-15N dipolar recoupling measurements.28
Supplementary Material
Highlights.
The Aβ peptide forms fibrils in plaques in the brains of Alzheimer’s patients.
X-ray fiber diffraction data are complementary to ssNMR data.
Combining fiber diffraction and ssNMR data leads to a new Aβ model.
The three-fold symmetric model has a hollow core.
The hollow core may be significant for therapeutics and diagnosis.
Acknowledgements
Supported by US National Institutes of Health grants AG002132 and by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases. The Stanford Synchrotron Radiation Laboratory is a national user facility operated by Stanford University on behalf of the U.S. Department of Energy, Office of Basic Energy Sciences. The SSRL Structural Molecular Biology Program is supported by the Department of Energy, Office of Biological and Environmental Research, and by the NIH National Center for Research Resources. Use of the Advanced Photon Source was supported by the US Department of Energy. BioCAT and BioCARS are NIH-supported Research Centers RR-007707 and RR-008630. We thank Sarah Tiggelaar and Adrianne Eyman for assistance with preliminary fiber diffraction experiments.
Abbreviations used
- Aβ
amyloid β protein
- cryo-EM
cryo-electron microscopy
- ssNMR
solid state nuclear magnetic resonance
- EM
electron microscopy
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Glenner GG, Wong CW. Alzheimer’s disease: initial report of the purification and characterization of a novel cerebrovascular amyloid protein. Biochem. Biophys. Res. Comm. 1984;120:885–890. doi: 10.1016/s0006-291x(84)80190-4. [DOI] [PubMed] [Google Scholar]
- 2.Mori H, Takio K, Ogawarag M, Selkoe DJ. Mass spectrometry of purified amyloid β protein in Alzheimer's disease. J. Biol. Chem. 1992;267:17062–17086. [PubMed] [Google Scholar]
- 3.Chiti F, Dobson CM. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 4.Rudall KM. The Society of Dyers and Colourists: Symposium on Fibrous Proteins. Leeds: Chorley and Pickersgill Ltd.; 1946. The structure of epidermal protein; pp. 15–23. [Google Scholar]
- 5.Eanes ED, Glenner GG. X-ray diffraction studies on amyloid filaments. J. Histochem. Cytochem. 1968;16:673–677. doi: 10.1177/16.11.673. [DOI] [PubMed] [Google Scholar]
- 6.Frost B, Diamond MI. Prion-like mechanisms in neurodegenerative diseases. Nat. Rev. Neurosci. 2010;11:155–159. doi: 10.1038/nrn2786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Prusiner SB, Scott M, Foster D, Pan KM, Groth D, Mirenda C, Torchia M, Yang SL, Serban D, Carlson GA, Hoppe PC, Westaway D, DeArmond SJ. Transgenetic studies implicate interactions between homologous PrP isoforms in scrapie prion replication. Cell. 1990;63:673–686. doi: 10.1016/0092-8674(90)90134-z. [DOI] [PubMed] [Google Scholar]
- 8.Sachse C, Fändrich M, Grigorieff N. Paired β-sheet structure of an Aβ(1–40) amyloid fibril revealed by electron microscopy. Proc. Natl. Acad. Sci. USA. 2008;105:7462–7466. doi: 10.1073/pnas.0712290105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang R, Hu X, Khant H, Ludtke SJ, Chiu W, Schmid MF, Frieden C, Lee J-M. Interprotofilament interactions between Alzheimer’s Aβ1–42 peptides in amyloid fibrils revealed by cryoEM. Proc. Natl. Acad. Sci. USA. 2009;106:4653–4658. doi: 10.1073/pnas.0901085106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Malinchik SB, Inouye H, Szumowski KE, Kirschner DA. Structural analysis of Alzheimer's β(1–40) amyloid: protofilament assembly of tubular fibrils. Biophys. J. 1998;74:537–545. doi: 10.1016/S0006-3495(98)77812-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sikorski P, Atkins ED, Serpell LC. Structure and texture of fibrous crystals formed by Alzheimer's Aβ(11–25) peptide fragment. Structure. 2003;11:915–926. doi: 10.1016/s0969-2126(03)00149-7. [DOI] [PubMed] [Google Scholar]
- 12.Jahn TR, Makin OS, Morris KL, Marshall KE, Tian P, Sikorski P, Serpell LC. The common architecture of cross-beta amyloid. J. Mol. Biol. 2010;395:717–727. doi: 10.1016/j.jmb.2009.09.039. [DOI] [PubMed] [Google Scholar]
- 13.Pauwels K, Williams TL, Morris KL, Jonckheere W, Vandersteen A, Kelly G, Schymkowitz J, Rousseau F, Pastore A, Serpell LC, Broersen K. Structural basis for increased toxicity of pathological Aβ42:Aβ40 ratios in Alzheimer disease. J. Biol. Chem. 2012;287:5650–5660. doi: 10.1074/jbc.M111.264473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Petkova AT, Yau WM, Tycko R. Experimental constraints on quaternary structure in Alzheimer's β-amyloid fibrils. Biochemistry. 2006;45:498–512. doi: 10.1021/bi051952q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Paravastu AK, Leapman RD, Yau WM, Tycko R. Molecular structural basis for polymorphism in Alzheimer’s β-amyloid fibrils. Proc. Natl. Acad. Sci. U.S.A. 2008;105:18349–18354. doi: 10.1073/pnas.0806270105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ahmed M, Davis J, Aucoin D, Sato T, Ahuja S, Aimoto S, Elliot JI, Van Nostrand WE, Smith SO. Structural conversion of neurotoxic amyloid-β1–42 oligomers to fibrils. Nat. Struct. Mol. Biol. 2010;17:561–567. doi: 10.1038/nsmb.1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bertini I, Gonnelli L, Luchinat C, Mao J, Nesi A. A new structural model of Aβ40 fibrils. J. Am. Chem. Soc. 2011;133:16013–16022. doi: 10.1021/ja2035859. [DOI] [PubMed] [Google Scholar]
- 18.Parthasarathy S, Long F, Miller Y, Xiao Y, McElheny D, Thurber K, Ma B, Nussinov R, Ishii Y. Molecular-level examination of Cu2+ binding structure for amyloid fibrils of 40-residue Alzheimer’ β by solid-state NMR spectroscopy. J. Am. Chem. Soc. 2011;133:3390–3400. doi: 10.1021/ja1072178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Scheidt HA, Morgado I, Rothemund S, Huster D. Dynamics of amyloid β fibrils revealed by solid-state NMR. J. Biol. Chem. 2012;287:2017–2021. doi: 10.1074/jbc.M111.308619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Buchete NV, Tycko R, Hummer G. Molecular dynamics simulations of Alzheimer’s beta-amyloid protofilaments. J. Mol. Biol. 2005;353:804–821. doi: 10.1016/j.jmb.2005.08.066. [DOI] [PubMed] [Google Scholar]
- 21.Fawzi NL, Okabe Y, Yap EH, Head-Gordon T. Determining the critical nucleus and mechanism of fibril elongation of the Alzheimer’s Abeta(1–40) peptide. J. Mol. Biol. 2007;365:535–550. doi: 10.1016/j.jmb.2006.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Miller Y, Ma B, Nussinov R. The unique Alzheimer’s β-amyloid triangular fibril has a cavity along the fibril axis under physiological conditions. J. Am. Chem. Soc. 2011;133:2742–2748. doi: 10.1021/ja1100273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kodali R, Williams AD, Chemuru S, Wetzel R. Abeta(1–40) forms five distinct amyloid structures whose beta-sheet contents and fibril stabilities are correlated. J. Mol. Biol. 2010;401:503–517. doi: 10.1016/j.jmb.2010.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Petkova AT, Leapman RD, Guo Z, Yau WM, Mattson MP, Tycko R. Self-propagating, molecular-level polymorphism in Alzheimer's β-amyloid fibrils. Science. 2005;307:262–265. doi: 10.1126/science.1105850. [DOI] [PubMed] [Google Scholar]
- 25.Makowski L. Processing of X-ray diffraction data from partially oriented specimens. J. Appl. Crystallogr. 1978;11:273–283. [Google Scholar]
- 26.Namba K, Stubbs G. Solving the phase problem in fiber diffraction. Application to tobacco mosaic virus at 3.6Å resolution. Acta Crystallogr., Sect. A: Found. Crystallogr. 1985;41:252–262. [Google Scholar]
- 27.Schmidt M, Sachse C, Richter W, Xu C, Fändrich M, Grigorieff N. Comparison of Alzheimer Aβ(1– 40) and Aβ (1– 42) amyloid fibrils reveals similar protofilament structures. Proc. Natl. Acad. Sci. USA. 2009;106:19813–19818. doi: 10.1073/pnas.0905007106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hu K-N, Qiang W, Bermejo GA, Schwieters CD, Tycko R. Restraints on backbone conformations in solid state NMR studies of uniformly labeled proteins from quantitative amide 15N-15N and carbonyl 13C-13C dipolar recoupling data. J. Magn. Reson. 2012;218:115–127. doi: 10.1016/j.jmr.2012.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Stubbs G. Developments in fibre diffraction. Curr. Opin. Struct. Biol. 1999;9:615–619. doi: 10.1016/s0959-440x(99)00014-7. [DOI] [PubMed] [Google Scholar]
- 30.Chandrasekaran R, Stubbs G. Fibre diffraction. In: Arnold E, Himmel DM, Rossman MG, editors. International Tables for Crystallography, Vol. F: Crystallography of Biological Macromolecules. 2nd edn. Chichester: Wiley; 2012. pp. 583–592. [Google Scholar]
- 31.Wang H, Stubbs G. Molecular dynamics in refinement against fiber diffraction data. Acta Crystallogr., Sect. A: Found. Crystallogr. 1993;49:504–513. doi: 10.1107/s0108767392011255. [DOI] [PubMed] [Google Scholar]
- 32.Straus SK, Scott WRP, Schwieters CD, Marvin DA. Consensus structure of Pf1 filamentous bacteriophage from X-ray fibre diffraction and solid-state NMR. Eur. Biophys. J. 2011;40:221–234. doi: 10.1007/s00249-010-0640-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McDonald M, Kendall A, Tanaka M, Weissman JS, Stubbs G. Enclosed chambers for humidity control and sample containment in fiber diffraction. J. Appl. Crystallogr. 2008;41:206–209. [Google Scholar]
- 34.Effenberger HK, Mereiter K, Zemann J. Crystal structure refinement of magnesite, calcite, rhodochrosite, siderite, smithonite, and dolomite, with discussion of some aspects of the stereochemistry of calcite type carbonates. Z. Kristallogr. 1981;156:233–243. [Google Scholar]
- 35.Bian W, Wang H, McCullough I, Stubbs G. WCEN: a computer program for initial processing of fiber diffraction patterns. J. Appl. Crystallogr. 2006;39:752–756. [Google Scholar]
- 36.Stubbs GJ. The effect of disorientation on the intensity distribution of non-crystalline fibres. Acta Crystallogr., Sect. A: Found. Crystallogr. 1974;30:639–645. [Google Scholar]
- 37.Klug A, Crick FHC, Wyckoff HW. Diffraction by helical structures. Acta Crystallogr. 1958;11:199–213. [Google Scholar]
- 38.Holmes KC, Barrington Leigh J. The effect of disorientation on the intensity distribution of non-crystalline fibres. I. Theory. Acta Crystallogr., Sect. A: Found. Crystallogr. 1974;30:635–638. [Google Scholar]
- 39.Rajkumar G, AL-Khayat HA, Eakins F, Knupp C, Squire JM. The CCP13 FibreFix program suite: Semi-automated analysis of diffraction patterns from non-crystalline materials. J Appl. Crystallogr. 2007;40:178–184. doi: 10.1107/S0021889806048643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Franklin RE, Holmes KC. Tobacco mosaic virus: application of the method of isomorphous replacement to the determination of the helical parameters and radial density distribution. Acta Crystallogr. 1958;11:213–220. [Google Scholar]
- 41.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera - A visualization system for exploratory research and analysis. J. Comput. Chem. 2004;15:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 42.Schwieters CD, Kuszewski JJ, Tjandra N, Clore GM. The Xplor-NIH NMR molecular structure determination package. J. Mag. Reson. 2003;160:65–73. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.