Slow unfolded-state structuring in ACBP folding revealed by simulation and experiment

Abstract

Protein folding is a fundamental process in biology, key to understanding many human diseases. Experimentally, proteins often appear to fold via simple two- or three-state mechanisms involving mainly native-state interactions, yet recent network models built from atomistic simulations of small proteins suggest the existence of many possible metastable states and folding pathways. We reconcile these two pictures in a combined experimental and simulation study of acyl-coenzyme A-binding protein (ACBP), a two-state folder (folding time ~10 ms) exhibiting residual unfolded-state structure, and a putative early folding intermediate. Using single-molecule FRET in conjunction with side-chain mutagenises, we first demonstrate that the denatured state of ACBP at near-zero denaturant is unusually compact and enriched in long-range structure that can be perturbed by discrete hydrophobic core mutations. We then employ ultrafast laminar-flow mixing experiments to study the folding kinetics of ACBP on the microsecond timescale. These studies, along with with Trp-Cys quenching measurements of unfolded-state dynamics, suggest that unfolded-state structure forms on a surprisingly slow (~100 µs) timescale, and that sequence mutations strikingly perturb both time-resolved and equilibrium smFRET measurements in a similar way. A Markov State Model (MSM) of the ACBP folding reaction, constructed from over 30 milliseconds of molecular dynamics trajectory data, predicts a complex network of metastable stables, residual unfolded-state structure and kinetics consistent with experiment, but no well-defined intermediate preceding the main folding barrier. Taken together, these experimental and simulation results suggest that the previously characterized fast kinetic phase is not due to formation of a barrier-limited intermediate, but rather a more heterogeneous and slow acquisition of unfolded-state structure.

Introduction

Solving the mystery of how proteins fold requires a combination of advances which collectively have remained elusive: (1) experiments with sufficient spatial and temporal resolution to yield a detailed characterization of folding kinetics, (2) simulation methodology that can make successful quantitative predictions of multiple experiments at atomic resolution, and (3) to apply these methodologies to large, slow-folding proteins with biological relevance, instead of designed mini-proteins. Towards this end, we have conducted an extensive study of bovine acyl-CoA binding protein (ACBP) using a combination of experimental and computational methods.

ACBP is an 86-residue four-helix bundle protein reported to fold on the ~10 millisecond timescale, typical of the single-domain proteins often used as model systems for folding. ACBP has been described as a two-state folder, with a transition state consisting of an ensemble of structures with helices 1 and 4 packed against one another¹, although higher-resolution experiments have suggested slightly more complex models, with each new experimental probe revealing previously undetectable intermediates². NMR and FRET studies have shown that the unfolded state is not a random coil, but compact with significant residual structure under denaturing conditions^3–5. Continuous-flow capillary mixing, and more recent laminar-flow mixing experiments⁶ revealed an ~80 µs kinetic phase, suggesting a three-state phenomenological model U→I→N where I is a partially-structured intermediate⁷.

We were particularly interested to probe the molecular events underlying this fast kinetic phase of ACBP folding, as this timescale is now jointly accessible by simulation and experiment. Here, we use single-molecule FRET (smFRET) studies and mutational analysis to provide a detailed characterization of residual structure in the denatured state of ACBP. We then use ultrafast laminar-flow mixing experiments to study the folding kinetics of ACBP on the microsecond timescale. These studies, along with with Trp-Cys quenching measurements of unfolded-state dynamics, suggest that unfolded-state structure forms on a surprisingly slow (~100 µs) timescale, and that sequence mutations strikingly perturb both time-resolved and equilibrium FRET measurements in a similar way.

To gain further insight into folding mechanism, we independently perform a large-scale molecular simulation study of ACBP folding. Previously, systems such as ACBP have been too large and slow for simulation studies, which have been limited to nanosecond to microsecond timescales for proteins with less than 40 residues. Today, recent advances in simulation methodology^8–10 and network models called Markov State Models (MSMs), in which conformational dynamics is modeled as transitions between kinetically metastable states, make it possible to model folding on the millisecond timescale.^11,12 Here, we use over 30 milliseconds of trajectory data to construct a MSM of ACBP folding, which predicts residual unfolded-state structure and kinetics consistent with experiment, but no well-defined intermediate.

Taken together, these experimental and simulation results suggest that the fast kinetic phase is not due to formation of a well-defined intermediate, but rather a much more heterogeneous acquisition of unfolded-state structure. Moreover, our analysis provides a way to reconcile the large numbers of metastable states predicted by MSMs with simpler models derived from fits to experimental kinetic data. The MSM model of ACBP folding predicts that, despite the complexity of the underlying dynamics, spectroscopic probes of end-to-end distance most sensitively report on two main dynamical timescales, implying a phenomenological three-state mechanism.

Experimental Methods

Protein expression, purification and labeling

A plasmid encoding for wild type acyl-CoA binding protein (ACBP) was provided by Dr. Kaare Teilum (University of Kopenhagen, Denmark)¹³. Site directed mutagenesis was accomplished with the Quickchange mutagenesis kit (Stratagene, Carlsbad). Expression, purification and fluorophore-labeling of ACBP was performed as described in detail elsewhere⁵. For protein L (ProL) details, see SI section A.1.

Single molecule measurements

Single-molecule measurements were performed with a water-immersion objective mounted on an inverted fluorescence microscope (Olympus IX17, 60 × 1.2 NA water-immersion objective, 100 µm pin-hole), equipped with an acousto-optical modular (N48058-XX-55, Neos Technologies, Melbourne, FL) to allow alternating-laser-excitation (ALEX) using a two-laser excitation source (488 nm Ar⁺-laser for the D-, 634 nm diode-laser for the A-fluorophore)^14,15. A laser alternation period of 100 µs was employed, allowing simultaneous and direct probing of both D and A-fluorophores in a single, diffusing molecule. Emitted photons were separated into donor and acceptor channels and imaged onto a single-photon counting avalanche photodiode. All measurements were carried out in 20 mM sodium phosphate, pH 7.0 (ProL and ACBP), or 20 mM sodium acetate, pH 4.20 (ACBP) containing various concentrations of GuHCl (0–6 M) as chemical denaturant. See SI section A.2 for more details.

Real FRET-efficiencies (E_FRET) were calculated from the experimentally measured proximity ratio (PR) according to E_FRET = PR/[PR +γ·(1-PR)]. The correction factor γ is the product of an instrument-specific constant η_A/η_D (ratio of A- and D-detection efficiencies), and a dye-specific term Q_A/Q_D (ratio of A- and D-quantum yields). The quantum yields of the D- and A-fluorophores were measured with singly-labeled proteins, relative to the quantum yields of the free maleimide dyes (Q_D = 0.92, Q_A = 0.32). For ACBP, we estimated Q_D = 0.66 ± 0.06 (measured at 6 M GuHCl, with C-terminally labeled ACBP). For ProL, we found Q_D = 0.68 ± 0.04 for ProL (measured at 6 M with a protein sample labeled at Cys16). These values are consistent with previously reported quantum yields of Alexa488 measured under similar conditions using unrelated proteins (0.63 < Q_D < 0.78)^16–18. See SI for details on determining γ.

The Förster radius (R₀) was calculated as R₀ = 0.211 · [k² · n⁻⁴ · Q_D · J(λ)]^1/6 (in units of Å), where J(λ) is the spectral overlap integral of the D-emission and the A-absorbance spectra, Q_D is the quantum yield of the protein conjugated D-fluorophore, n is the refractive index of the solution, and k² = 2/3 is the orientational factor. A Gaussian-chain model was used to calculate radius of gyration R_g from E_PR. See SI for full details.

The time-resolved FRET and Trp-Cys quenching measurements are described in detail in SI sections A.4 and A.5.

Simulation Methods

Molecular Dynamics simulation

Distributed molecular dynamics simulations were performed using an accelerated version of GROMACS¹⁹ written specifically for GPUs²⁰ using the Folding@Home platform²¹. The AMBER ff96²² forcefield (AMBER ff03²³ was also tested) with a popular GBSA implicit solvent model²⁴ was used for production runs. Up to 10,000 parallel simulations were simulated at 300K, 330K, 370K and 450K, started from roughly equal numbers of native, extended, and random-coil starting states (the five different initial coil states used as initial structures were generated from a Monte Carlo procedure rewarding compactness.) Starting conformations for the native state of ACBP were taken from the minimized crystal structure (PDB code 1hb6). The aggregate simulation time was 31.7 ms (31.0 ms for the AMBER ff03 simulations). Stochastic integration (Langevin dynamics) was performed using a time step of 2 fs, Berendsen temperature coupling, full nonbonded interactions (no cutoff), a viscosity of 91 ps⁻¹, hydrogen bond lengths constrained using SHAKE; and trajectory snapshots recorded every 1 ns.

Calibration of simulated temperature and experimental denaturant concentration

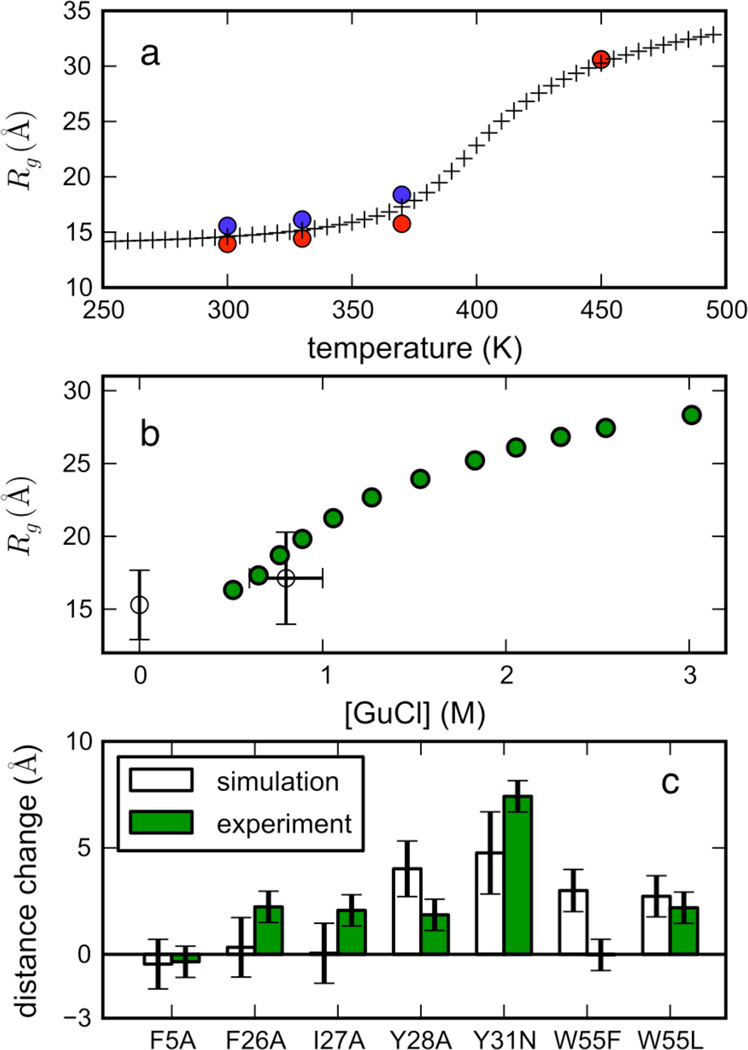
Unfolded-state simulations at increasing temperatures exhibit a globule-to-coil transition (see Figure 6a), allowing us to calibrate each simulation temperature to an effective experimental [GuHCl] using a polymer-theory approach, as described previously^25,26. This method—similar in spirit to several recent molecular transfer models of denaturant-dependent unfolded-state chain expansion^26–29—circumvents the inaccuracies of current forcefield models for GuHCl, and instead uses a tangible order parameter (the extent of expansion in the denatured-state ensemble) to compare simulated and experimental ensembles. The calibration results were corroborated by direct comparisons of simulated average end-to-end distances against those calculated from experimental FRET efficiencies, as well as comparsions of the Flory χ parameter (the monomeric transfer free energy from protein to solvent) obtained from fitting experimental and simulated ensembles to the polymer theory model (see SI for details). Simulations at 330 K, 370 K, and 450 K were calibrated to 0 M, 0.6–1.0 M, and >6 M GuHCl, respectively.

Figure 6.

(A) Radius of gyration (R_g) vs. temperature for simulated unfolded-state ensembles started from extended (blue) and coil (red) conformations (after ~5 µs), shown with the best-fit (i.e. maximum-likelihood) polymer theory model (crosses, see SI for details). Note that the R_g values superimpose at 450K. (B) Estimated radius of gyration (average of extended and coil values) from simulations (unfilled circles) at 0 M GuHCl (330 K) and ~0.8 M GuHCl (370 K) agree well with experimental R_g for ACBP 1–88 measured by smFRET (green circles) (see SI for details of the calibration of simulated temperature with experimental denaturant concentration). Horizontal error bars reflect uncertainty in the calibration, while vertical error bars denote the variance of Rg values across extended and coil ensembles. (C) Predicted (white) versus experimental (green) changes in average end-to-end distances due to perturbing mutations. Changes in the expectation value of interresidue distance 17–86 for several ACBP mutants were calculated from simulated unfolded-state ensembles (370 K, 0.6–1.0 M GuHCl) using coarse-grained FEP calculations (see Methods, SI section B.6). The experimental changes in end-to-end distances ΔR_ee, were calculated from the smFRET R_g values at 0.5 M GuHCl, using the random coil identity 〈R_g²〉 = 〈R_ee²〉/6. Error bars for ΔR_ee are calculated from uncertainties in R_g.

Long-range contact propensities in unfolded-state ensembles

Interresidue contact propensities were calculated using 2000 conformations chosen at random from simulated unfolded-state ensembles after 5 µs. Two residues were defined to be in contact if their C_α atoms were closer than 8.5 Å. Propensities were calculated as a contact free energy −kT log (p_ij/p_ij^ref) for residues i and j, where T=300K, p_ij is the probability of contact for residues i and j, and p_ij^ref is a reference state for contact probabilities averaged over all contacts at sequence separation s = |i-j|, i.e. p_ij^ref = <p_kl> where |k-l| = s. Pseudocounts of 1/2000 were added to each p_ij to correct for finite sampling error.

Modeling sequence-dependent unfolded-state expansion

Changes in simulated unfolded-state ensembles upon mutation were computed with a free energy perturbation approach, using a coarse-grained potential with two terms: (1) a statistical potential derived from sequence-dependent backbone dihedral propensities³⁰, and (2) interresidue contact energies computed from the Miyazawa-Jernigan³¹ matrix. Because this potential is sufficiently smooth, accurate reweighting was possible using twenty thousand snapshots (taken after 5 µs from ensembles simulated at 370K). The relative free energy between wildtype and mutants were calculated using the MBAR algorithm, with expectation values of intramolecular distances calculated as described in³². Full details are in SI section B.6.

Markov State Model (MSM) construction and validation

The MSMBuilder³³ software was used to build MSMs for ACBP under folding conditions (0M GuHCl, 330K simulations) and unfolding conditions (0.6–1.0 1M GuHCl, 370K simulations). We found that a 20,000-microstate decomposition yielded a good balance of state connectivity and adequate transition sampling. Conformations were clustered using a subset of 258 atoms (backbone N, C_α and C); 20% of the data was used to generate an initial clustering, and the remaining 80% of the data was assigned to the generators. The 20,000-microstate model was used for predicting experimental observables, while a 2000-macrostate MSM obtained by kinetic-based lumping³⁴ was used to analyze the distribution of folding pathway fluxes from unfolded to folded states.

Transition probabilities T_ij of transitioning from state i to state j (within a lag time τ) are estimated by counting the number of transitions n_ij observed between time t and t+τ, and normalizing by rows: T_ij = n_ij/(Σ_j n_ij). To enforce detailed balance, we symmetrize the forward and backward counts as (n_ij+n_ji)/(Σ_j n_ij+n_ji). Artifacts from symmetrization are mostly limited to transitions with very few counts (and hence low populations that have negligible effects). Sliding-window counts were used to alleviate finite-sampling errors. To validate the robustness of these assumptions in estimating transition rates, we performed importance sampling of the posterior distribution of 2000-macrostate transition matrices, using a reversible conjugate prior for Markov chains as described in³⁵. We generated ~5000 Markov chain realizations (samples of transition counts ñ_ij, with no sliding window used; calculations are limited by storage space), from which expectation values (mean and variance) of equilibrium populations p_i ∝ (Σ_j ñ_ij) were calculated. The expectation equilibrium populations calculated using the reversible prior were very similar to the symmetrization results (Supplementary Fig. S7e,f). For example, the native macrostate population (p_nat) using this procedure was 28.13% +/− 0.069%, whereas the transition matrix constructed directly from from sliding-window counts yielded p_nat = 30.3%, a discrepancy of only ~0.07 kT.

A lag time of τ=20 ns was determined to be suitable by building a series of MSMs at different lag times to find a region where the spectrum of implied timescales^36,37 τ_i = −τ/ln(λ_i) are relatively insensitive to lag time. To check the accuracy of the MSM, we compared average inter-residue distances over time (17–86, 1–86 and 17–50) seen in the trajectory data, to predictions from the MSM, and found reasonable agreement (see SI section B.1). While the implied timescales become accelerated after lumping (it is difficult to achieve a perfect separation of timescales), distributions of folding pathway fluxes remain mostly intact for analysis. A Bayesian inference model described in³⁸ was used to estimate Arrhenius barriers ΔG^‡_ij separating microstates and macrostates.

Committor (p_fold) values and mean first passage times were computed for each macrostate using methods described in^37,39. The p_fold values we compute for MSM macrostates are defined as the probability of reaching the native macrostate before the unfolded extended-chain macrostate. Transition Path Theory (TPT)^40–42 was used to calculate pathways of reactive folding flux, using a modified “greedy backtracking” algorithm (see SI section B.2). MSM equilibrium population vectors were calculated from the largest eigenvector of the transition matrix, i.e. from p_eq = p_eqT. Macrostate free energies F_i were calculated from MSM equilibrium populations p_i as F_i = −kT log p_i at room temperature. The free energy of folding as a function of the kinetic reaction coordinate p_fold was calculated as F(p_fold) = −kT log Z(p_fold) where, Z(p_fold) = Σ_i χ_ip_i where χ_i is a bin indicator variable for bins with left edges p_fold = 0, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95.

Master Equation formalism

The continuous-time master equation describing the microstate dynamics is dp/dt = pK, where p is the vector of state populations, and K is a 20,000 × 20,000 matrix of rate coefficients, related to the discrete-time transition probability matrix by T = exp(τK)^36,43. The solution of the master equation is

$$\mathbf{p}(t)={\mathrm{\Sigma }}_n{{\mathbf{\psi }}^{\mathrm{L}}}_n[{{\mathbf{\psi }}^{\mathrm{R}}}_n·\mathbf{p}(t=0)]\text{ exp}({\mathrm{\lambda }}_{n}t)={\mathrm{\Sigma }}_n{\mathbf{p}}_n(t),$$

where ψ^L_n, ψ^R_n, λ_n are the left and right eigenvectors and eigenvalues of K, respectively. The kinetics can thus be described as a superposition of exponential relaxation modes p_n(t) at implied timescales τ*_n = −λ_n⁻¹, each with amplitude a_n = [ψ^R_n · p(t=0)].

MSM predictions of observables

Predicted values of observables over time were computed as F(t) = p(t) · f, where p(t) is a vector of state populations over time, and f is a vector of observables values for each microstate. Uncertainty estimates were propagated assuming statistical independence of each state. For some observables, time courses were obtained by discrete propagation of the transition probability matrix T, using p(t+τ) = p(t)T. For others, p(t) was calculated from the 1000 slowest relaxation modes of the master equation solution. RMSD pseudo-trajectories were calculated using a simple Monte Carlo algorithm to generate a trajectory of (20 ns) microstate jumps, and selecting at random (uniformly) a simulation snapshot to report observables at each time step (see SI section B.3 for more examples). Predictions of FRET observables over time were computed with special corrections for FRET probe linkers not present in the simulations (see SI section B.4), and corrections for native state stability (see below). Trp-Cys quenching rates and intramolecular diffusion coefficients for T17C-W58 and W58-I86C were predicted using methods described in²⁵ from simulated distributions of intramolecular Trp-Cys distances P(r) calculated from simulated unfolded ensembles (330 K, 0 M GuHCl and 370 K, 0.6–1.0 M GuHCl, starting from extended and coil states, snapshots taken after 1 µs), where r is the distance between side-chain centroids (see also SI section A.5). Intramolecular diffusion coefficients D were computed from trajectory data, by fitting the mean-squared displacements of Trp-Cys distances over time in blocks of 50 ns (sampled in 1-ns intervals), as described previously²⁵.

Correcting predicted FRET values for native-state stability

A consequence of symmetrization of the transition probability matrix is that the equilibrium populations are proportional to the total number of observed counts⁴⁴: p_i ∝ (Σ_j n_ij). Because of this, our MSM predicts an equilibrium distribution of states with ~2:1 unfolded vs. folded populations, even under folding conditions. To correct predicted observables, we compute FRET values by subtracting the equilibrium unfolded-state component of the signal (i.e. we assume that the simulated unfolded state is “invisible”). The stationary state p_eq = (n_coil + n_ext + n_nat)/(N_coil + N_ext + N_nat) is the (normalized) number of counts observed in the trajectories, where n_coil, n_ext, and n_nat are the vectors of observed microstate counts for simulations initiated from coil, extended and native states, respectively, and N = N_coil + N_ext + N_nat is the total number of counts observed in all simulations. We propagate the discrete-time transition matrix as described above to get populations over time, and calculate FRET using a modified projection operator S′:

$$S\prime (\mathbf{p})=(N/N_{\text{nat}})·[S(\mathbf{p})-S([{\mathbf{n}}_{\text{ext}}+{\mathbf{n}}_{\text{coil}}]/N)]$$

This projection operator has the property that as t→∞, S′(p(t→∞)) = S(n_nat/N_nat). We use this correction for the FRET predictions in Figure 2d, setting the starting configuration p(t=0) to a single microstate corresponding to the extended state. A caveat of this approach is that negative FRET values may be obtained at very early times, when initial popultions are from unfolded states. For all cases we considered, we find that this effect only occurs for t < 1 µs, faster than the time resolution of the mixer experiments with which we make comparisons.

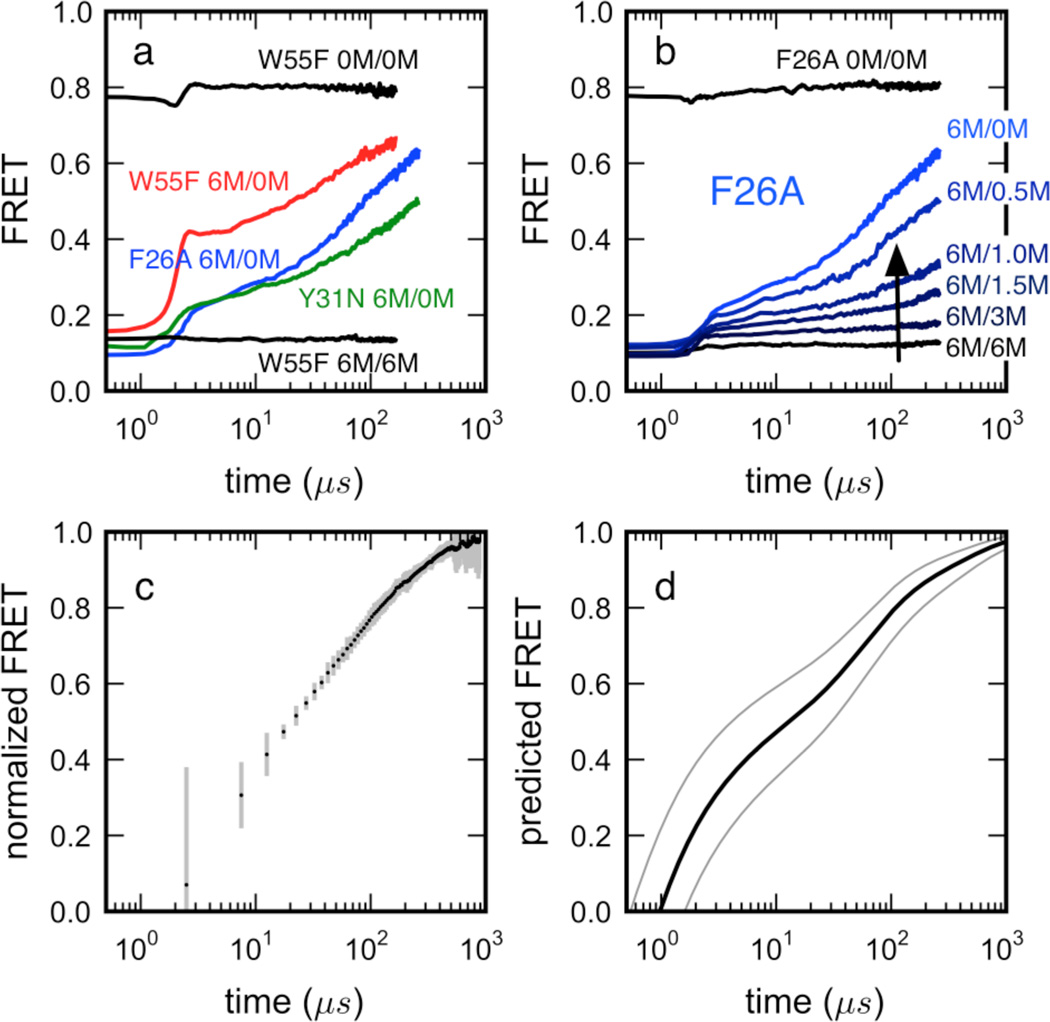
Figure 2.

Folding kinetics of hydrophobic core mutants of ACBP 17–88 measured in an ultrafast microfluidic mixer. (a) Mutations F26A and Y31N (shown to disrupt unfolded-state structure in smFRET experiment) decrease the relaxation amplitudes of the fast kinetic phase, but do not significantly affect relaxation rates (see Supplementary Figure S11 and SI section B.4 for fitting details). Burst-phase amplitudes occurring within the mixing time (< 4 µs) are evidence of residual structure already formed at early times. (b) Disruption of residual structure induced by chemical denaturant, exemplified by the F26A variant. (c) Average FRET-trajectories of the W55F variant measured in separate mixing experiments out to ~800 µs. Five independent measurements, normalized to initial and final asymptotic values, were averaged, with the error bars representing the standard deviations of this average. (d) MSM predictions of FRET time courses (see below, Methods) show kinetic time scales in qualitative agreement with experiment. Confidence intervals (thin lines) reflect uncertainty in R₀ and probe distances (see SI).

Results

Experimental evidence for a highly structured denatured state

To study the denatured-state structure of ACBP under a wide range of experimental conditions, smFRET studies^45,46 were performed. Pairs of Cys residues were engineered into the ACBP sequence (wild type ACBP is Cys-free) that were subsequently labeled with a FRET dye pair (Alexa488/Alexa647). The FRET pairs were positioned such that they report on distance changes within discrete substructures of the four-helix bundle topology (Figure 1a, top). For example, labeling at position 1–68 reports on distance changes within the first three N-terminal helices, while labeling at positions 17–88 reports on changes in the three C-terminal helices. Likewise, ACBP 1–40 reports predominantly on the integrity and interaction of helix 1 (previously reported to be flexible and engaging in little long-range residual structure⁴), while ACBP 1–88 probes end-to-end distance changes (SI section A.3 for additional information). These FRET-pair variants contained an additional, highly destabilizing W55F mutation to populate the denatured subensemble at very low denaturant concentrations. Comparison with wild type ACBP suggests that the W55F mutation does not significantly perturb residual structure in denatured state, at least under conditions where both mutant and wild type populate the denatured state to measurable quantities (0.8–6 M GuHCl) (Supplementary Fig. S1a).

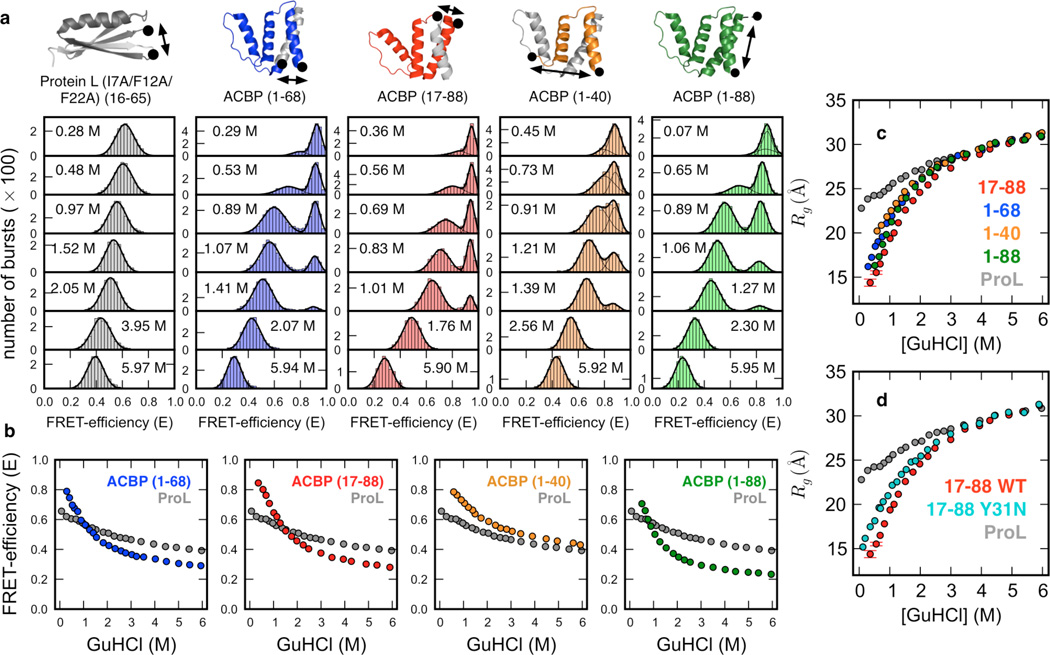
Figure 1.

Unfolded-state structure studied by smFRET experiments at equilibrium. (a) Single molecule FRET histograms measured with site-specifically labeled ProL (grey, reference), and four ACBP variants (blue, red, orange, green) at various denaturant concentrations. (b) Unfolded-state FRET-efficiencies versus denaturant concentration for each variant, shown with the ProL reference (c) FRET-based random coil R_g estimates for ACBP revealing non-uniform compaction, and compaction to a greater extent than the ProL random-coil reference. R_g values were normalized to the R_g estimate of ACBP 17–88 by multiplying by the Flory scaling factor (see SI section A.4). (d) Mutant Y31N produces a significant expansion of the unfolded state, indicating a disruption of long-range structure. (Data for other mutants shown in Supplementary Figure S1.)

FRET-efficiency histograms of the four FRET-pair mutants of ACBP exhibit folded (high-FRET) and unfolded (low-FRET) subpopulations that coexist at intermediate denaturant concentration, as expected for a thermodynamic two state folder with a free energy barrier separating folded and unfolded subpopulations (Figure 1a, bottom). Mean FRET-efficiencies of the folded and denatured subpopulations were extracted from Gaussian fitting of the histograms. The mean FRET-efficiencies of the denatured subpopulation of each FRET-pair mutant at a particular denaturant concentration are plotted in Figure 1b, together with the mean-FRET efficiency of a highly destabilized and constitutively unfolded triple-Ala variant of ProL (see SI section A.1 for details), that serves here as a pseudo-random coil reference. Clearly, all four interresidue distances of ACBP probed by smFRET experience significantly larger contractions than the single distance probed in the ProL reference, particularly below 3 M GuHCl, suggesting a compact ensemble of structures under conditions that favor folding.

To compare the mutant effects more quantitatively and to better connect the experimental results with simulation predictions, we next converted the FRET-efficiencies into radii of gyration (R_g), which were then normalized to identical chain length (88 residues) by multiplication with the Flory scaling factor (Figure 1c, SI section A.2 for additional information). Under strongly denaturing conditions (> 3 M GuHCl), all five proteins show (within error) identical polymer behavior, suggesting that under those conditions, chain contraction is sequence-independent and probably unspecific (see SI section A.3). Below 3 M GuHCl, however, we not only observe a significant shortening of each of the four ACBP distances beyond that measured in the ProL reference (suggesting acquisition of compact residual structure beyond that seen in the ProL random coil), but also significant differences among the ACBP distances themselves, demonstrating non-uniform compaction. The 1–40 distance exhibits the weakest contraction, which is consistent with previous reports^4,47 that helix 1 is more flexible and engages in less residual structure than the remaining three helices. The largest distance change is experienced by 17–88, with 1–68 exhibiting a behavior in between 1–40 and 17–88. The latter observation is noteworthy, as the interdye distance in 17–88 (72 residues) and 1–68 (68 residues) is almost identical, the only difference being that 17–88 includes the structured C-terminal helix (45 % folded in isolation), while 1–68 includes the weakly structured and more flexible N-terminal helix.

To provide further evidence for residual structure in denatured ACBP, additional mutants were made in the 17–88 FRET-pair context by replacing large, hydrophobic residues that engage in long-range residual structure in folded ACBP (F5A in helix 1, F26A, I27A, Y28A, Y31N in helix 2, and W55L in helix 3; SI section A.3 for additional information). Indeed, for the non-conservative Y31N mutant, we observe a significant perturbation of residual structure (Figure 1d), a result that is also predicted by reweighting of the simulated unfolding ensembles (Figure 6c, Supplementary Figure S2). Interestingly, even though the F5A mutation perturbs the same long-range interactions as the Y31N in the folded protein, it doesn’t affect denatured-state structure measureably. Perturbation of native-like structure in the denatured ensemble is thus likely not to be the cause of the disruptive effect of the Y31N mutant.

We do not see significant denatured-state expansion in the F26A, I27A and Y28A mutants (Figure S1), which is perhaps surprising, given that the mutated residues F26, I27, Y28 and Y31 are all positioned in helix 2, and are separated by less than two helix turns in the folded protein. This could simply be because Y31N is more disruptive than the other, more conservative, alanine mutations. Another, more provocative explanation, is that these differential disruptive effects are reporting the presence of specific long-range helix-helix contacts in denatured ACBP. Such an interaction was first postulated by Poulsen and co-workers for helix 2 and helix 4 fro spin-sensitized NMR experiments, a hypothesis that is supported by more recent molecular dynamics simulations that reveal similar contacts persisting in acid-denatured ACBP (pH 2.3), i.e. conditions where ACBP is > 99% unfolded. Such long-range interaction might be favored by the amphipathic nature of the two heices and the high helical propensity of helic 4 (60% folded in isolation) that may act as a hydrophobic docking site for helix 2. Indeed a helical wheel plot suggests that residue Y31 would be positioned right in the center of the putative hydrophobic helix interface, while residues F26, I27 and Y28 would adopt more peripheral positions (Supplementary Figure S1b). It is therefore plausible that a Y31N mutation would exert a more perturbing effect. As the rate-limiting step for folding is the formation of side chain contacts between helices 1, 2 and 4, long-range contacts between helices 2 and 4 in the denatured state might be advantageous for barrier-limited folding¹. A much more extensive mutational analysis, however, is required to fully support this model.

Surprisingly slow formation of unfolded structure

We hypothesized that the ~80 µs kinetic phase seen previously⁷ might reflect a gradual (microsecond timescale) collapse to a heterogeneous ensemble of unfolded, yet highly compact structures, rather than the formation of a classical folding intermediate. Strong support for this hypothesis comes from non-equilibrium FRET experiments measured with the F26A, Y31N and W55F mutants of ACBP 17–88 in an ultrafast laminar-flow mixing device.

The FRET-trajectories of the three mutants, measured upon refolding of denatured protein (6 M GuHCl) into refolding buffer (0 M GuHCl), are biphasic, with a submicrosecond burst phase occurring within the mixing time of the mixer (< 4 µs), followed by a fast, kinetically resolvable relaxation process occurring on the ~100 µs timescale (Figure 2a). The W55F trajectory (Figure 2b, red) is best fit by either a single exponential (relaxation time scale = 48 ± 4 µs), or a stretched-exponential (relaxation time scale = 46 ± 3 µs; β = 0.80; see SI section A.4 for further details on curve fitting). Additional measurements for the W55F variant at both high and low flow rates were made in separate mixing experiments to extend the time range of FRET-trajectories to ~800 µs (Figure 2c). The results (after normalization to account for minor differences in detection efficiencies) agree well with the shorter trajectories after 20 µs (see SI section A.4). The full time course of FRET vs. time predicted by the MSM (which does not predict a stable folding intermediate, Figure 5) seems to qualitatively reproduce the ~800 µs FRET-trajectory (Figure 2d). We note that the simulated dynamics predicted by the MSM are slightly faster (~1–10 µs). This agreement with experiment is reasonable considering potential systematic error from forcefield and rate estimation effects (see below).

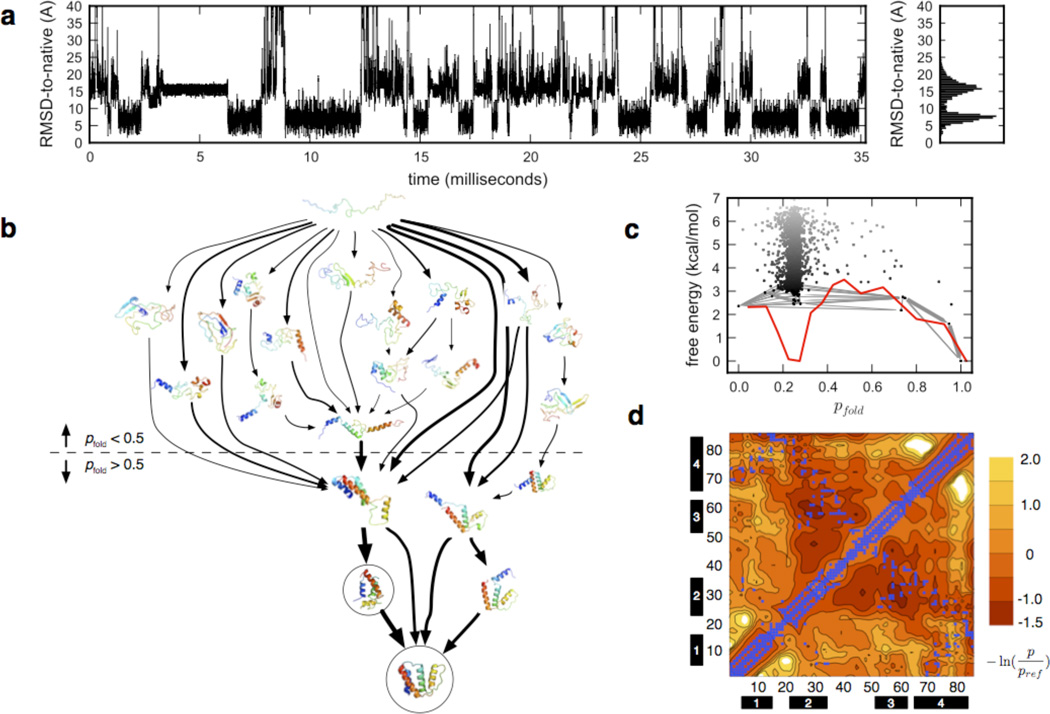
Figure 5.

Markov State Model (MSM)-based simulation of ACBP folding in all-atom detail on the tens of millisecond timescale. (a) Folding pseudo-trajectories generated from the MSM, projected onto a single degree of freedom such as the RMSD-C_α to the native crystal structure, suggests cooperative folding to the native state via a simple two-state mechanism, near the millisecond timescale. The MSM, however, is a complex network of metastable states, and the full picture of the folding dynamics is predicted to be more complex. (b) Shown are the 15 highest-flux folding pathways bridging the extended and native states in a 2000-macrostate MSM, as calculated by Transition Path Theory (TPT)⁴¹. Line thicknesses are proportional to pathway folding flux (on a log-scale). Circled are the macrostates corresponding to the native and near-native state identified by Teilum et al.² (c) Free energy vs. p_fold (a kinetic reaction coordinate defined as the probability of reaching the native state versus the extended state), plotted for each macrostate (black dots), shows a highly diffuse network of unfolded states, yet a simple basin structure in a 1D projection (red line). Gray edges represent the network of fluxes shown in (b). (d) Average inter-residue contact propensities calculated from unfolded-state simulations corresponding to ~1M GuHCl (see Methods for details on the conversion of temperature into denaturant concentration), taken after 5 µs, show long-range contacts between helices 2 and 3, and helices 2 and 4. Contours show free energies of contacts (units kT) compared to a reference normalized by loop length. Blue squares denote native contacts.

The slow, barrier-limited folding transition occurring on the ~10 ms time scale, and accounting for the remaining 5–10 % of the expected FRET amplitude change upon folding, cannot be resolved at the high flow rates employed in this study. However, previous laminar-flow mixing studies at substantially slower flow rates and different mixer design revealed an additional slower phase with a rate constant (~ 9 ms) almost identical to the rate constant reported from Trp-fluorescence detection⁷, thus ruling out a major perturbation of the energy landscape by the bulky fluorophores.

Increasing the denaturant concentration in the refolding buffer results in a nonlinear decrease of the amplitude of the kinetically resolvable relaxation process (Figure 2b). The relaxation rates of the three mutants, obtained from single exponential fits and rate spectra analysis (see below) of the FRET-trajectories, agree within a factor of 2.5 and are only weakly affected by denaturant, as found previously⁷. Interestingly, mutants Y31N and F26A result in lower dead-time collapse amplitudes than the W55F mutant, indicating that there is already long-range residual structure developing within the first few microseconds of refolding. This hypothesis is supported by earlier experiments and simulations that show that contacts between helices 2 and 3 persist at moderately high denaturant concentrations (3 M GuHCl)⁴, and our own simulation predictions (see below) that similar interhelical contacts persist at moderately denaturing temperature (370 K, corresponding to 0.6–1.0 M GuHCl) (Supplementary Figure S3). It is therefore plausible that helix 2–helix 3 contacts form early in the folding process while helix 2-helix 4 contacts (which form at lower denaturant concentrations⁴) form later. Similar fits for for F26A and Y31N yield ~90 µs and ~120 µs, respectively.

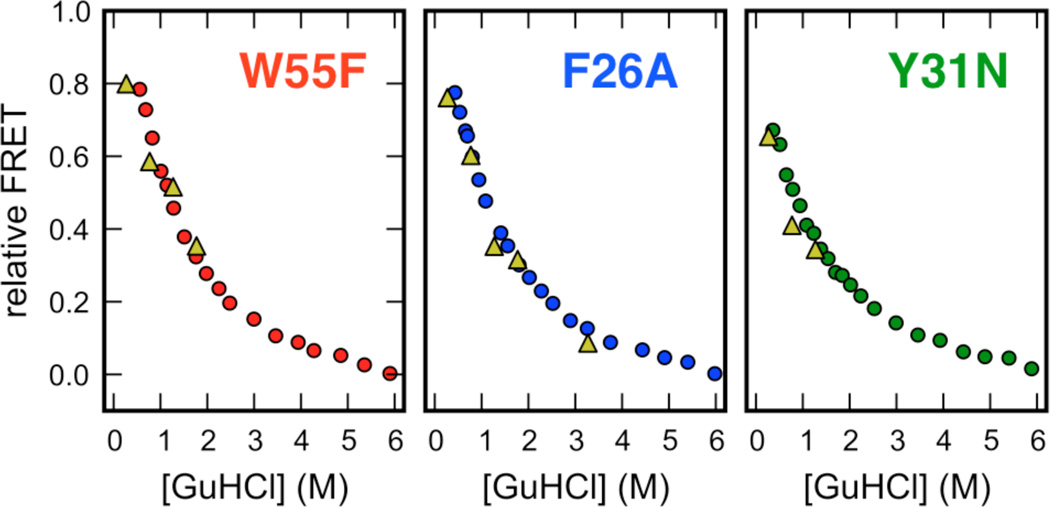
To our surprise, we also found that extrapolations of the (normalized) asymptotic FRET efficiencies estimated from non-equilibrium mixing agreed within experimental error with the FRET-efficiencies of the denatured subpopulation of ACBP inferred from smFRET experiments at equilibrium (Figure 3). Such good agreement between normalized transient and equilibrium FRET efficiencies is difficult to rationalize in the framework of a folding intermediate (see Discussion).

Figure 3.

Comparison of relative FRET-efficiencies for the denatured subpopulation measured by equilibrium smFRET (circles) and the asymptotic FRET-efficiency of the time-resolvable microsecond kinetic phase measured by ultrafast laminar-flow mixing (triangles). A comparison of relative FRET efficiencies was necessary to account for minor differences in detection efficiencies between the microscopic setups used for the smFRET and ensemble mixing experiments and the presence of donor-only species in the ensemble mixing experiment that were digitally removed in the smFRET experiments. For the smFRET experiments, raw FRET efficiencies of the denatured subpopulation at a particular denaturant concentration were normalized to the difference in FRET efficiency between the folded subpopulation at 0 M GuHCl, and the FRET efficiency of the denatured subpopulation at 6 M GuHCl. For the ensemble mixing experiments, raw asymptotic FRET efficiencies for the microsecond phase at a particular denaturant concentration were normalized to the difference in FRET efficiency of the denatured protein at 6 M (unfolded baseline in Fig. 3a, main text) and the folded protein at 0 M (folded baseline in Fig. 3a, main text). Note that some asymptotic FRET values are not shown: W55F (6 M to 3 M), Y31N (6 M to 1.5 M) and Y31N (6 M to 3 M); these traces were poorly fit by a single-exponential.

Trp-Cys quenching studies suggest slow intramolecular diffusion in the denatured state

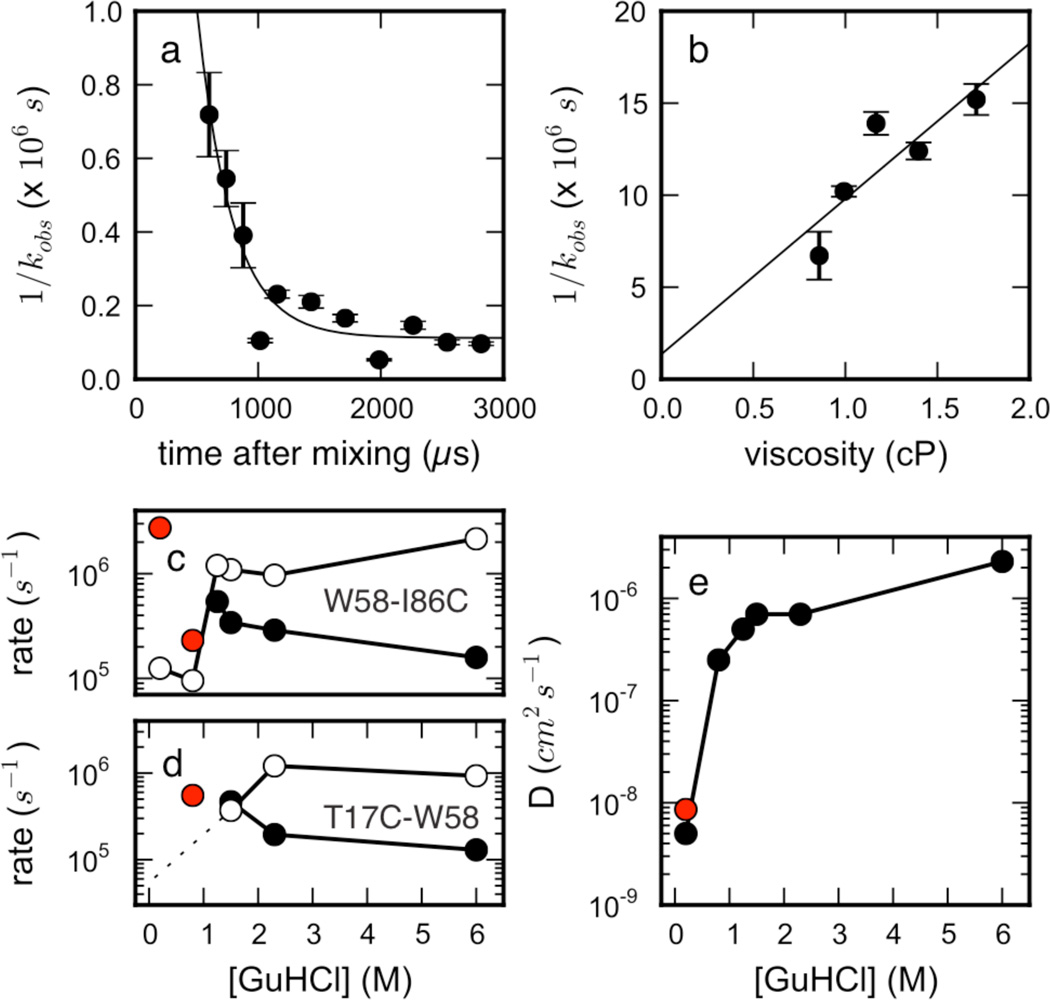
To further probe unfolded-state structure and dynamics, Trp-Cys contact quenching studies were performed. These studies measure the time-resolved decay of the excited triplet state of tryptophan, and its quenching by cysteine in the unfolded state, to give insight into intramolecular dynamics in the unfolded state⁴⁸. Studies were performed for two single-cysteine mutants of the same W55F variant of ACBP which were also used for the smFRET and fast mixing experiments. The first mutant contains a single Cys at position 17 and probes intramolecular diffusion within the T17C-W58 loop that comprises helices 2 and 3 and the long connecting loop that connects the two helices. The second mutant contains a Cys at the C-terminus and reports on chain dynamics in the W58-I86C loop, i.e. on dynamics within the two C-terminal helices. Measurements were performed at equilibrium from 1 M to 6 M GuHCl, as well as in a fast mixer⁴⁹ which diluted denaturant from 5 M to 0.2 M and 0.8 M GuHCl (0.8 M GuHCl only for T17C-W58) in order to observe intramolecular diffusion before barrier-limited folding. A previous study has shown good agreement between equilibrium and mixer measurements at the same denaturant concentration⁴⁹. The observed quenching rates k_obs are modeled as resulting from a combination of a reaction-limited rate, k_R, and diffusion-limited rate, k_D+, which can be extracted by varying viscosity and temperature independently. An effective diffusion coefficient can be determined from the measured rates and simulated Trp-Cys distance distributions, using methods described previously²⁵ (see SI section A.5). Within the mixer, the observed quenching rate slows down within the mixing time (Figure 4a). The slope of a linear fit of 1/k_obs vs. viscosity for W58-I86C gives k_D+ = 1.18 ± 0.41 × 10⁵ s⁻¹ at η=1 cP (Figure 4b).

Figure 4.

Trp-Cys quenching studies of ACBP report slow unfolded-state intramolecular dynamics under folding conditions. (a) Observed quenching rates vs. time for loop W58-I86C in a fast mixer after diluting from 5 M to 0.2 M GuHCl, shown with an exponential fit to the data. (b) Linear dependence of W58-I86C quenching times (T=23C) with viscosity at ~1.4 ms, shown with a least-squares linear fit, R² = 0.729. (T17C-W58 times are not shown as they are too slow to accurately measure.) (c and d) Reaction-limited kR (filled) and diffusion-limited kD+ (open) vs. [GuHCl] for (c) W58-I86C and (d) T17C-W58 loops. Red circles denote k_R predictions from simulation data, and the dotted line reflects a lower limit of D at 0.2 M (see SI). (e) Intramolecular diffusion coefficients extracted from the W58-I86C data using SSS theory (see SI section B.4), and the red circle marks D calculated from simulated mean-squared displacements vs. time at 300K (0 M GuHCl).

Qualitatively, the intramolecular dynamics of ACBP exhibits a pattern similar to previously studied proteins (protein L, protein G): Decreasing the denaturant concentration induces a chain compaction, which increases k_R and decreases k_D+, suggesting less diffusivity (Figures 4c,d). For both loops, k_R and k_D+ cross at ~1.5 M GuHCl, near the denaturation midpoint, behavior seen previously for protein L, although the midpoint is much lower for ACBP. For the T17C-W58 loop, k_D+ becomes too slow to accurately measure (< 4×10⁴ s⁻¹) suggesting this loop is less diffusive than the W58-I86C loop, consistent with the pattern of long-range contacts seen in simulation.

Intramolecular diffusion coefficients at low denaturant concentrations, estimated using experimental rates and a simulated Trp-Cys distribution, were estimated to be ~6 × 10⁻⁹ cm²/s, suggesting that the unfolded state in the absence of denaturant is highly collapsed and slowly diffusing, though the level of diffusivity may vary across the chain (Figure 4e). Significantly, a independent estimate of the diffusion coefficient entirely from simulation gives the same estimate (red point in Figure 4e), showing agreement between simulation and experiment. This result is ~10 times higher than observed for protein L⁴⁹, despite the fact that it is more compact (see also Figure 1b). The diffusion coefficient decreases dramatically below the denaturation midpoint. Along with the crossing of k_R and k_D+, and the dramatic increase in FRET from single molecule studies at the denaturant midpoint, this behavior shows the unfolded chain becomes compact and undergoes slow dynamics as the probability of folding becomes significant.

A Markov State Model of ACBP folding predicts a complex network of metastable states

Recently, discrete-state master equation or Markov state models (MSMs) have had success at modeling long-time statistical dynamics^{11,12,42,43,50}. In these kinetic network models, metastable states are identified such that conformational transitions within each state are much faster than transitions between states, so that the process can be considered to be Markovian⁵¹. The transition rates between states are estimated from Molecular Dynamics (MD) simulations. If the model can self-consistently reconstruct the statistical dynamics of the trajectories it was constructed from, and if it obeys the Markov property, it can be used to simulate the statistical evolution of a non-interacting ensemble of molecules over much longer timescales than the lengths of the individual trajectories from which it is constructed (validation efforts described in Methods). MSM dynamics can be directly compared with bulk experimental data by computing observables from the predicted state populations over time, as expectation values averaged over each state (see Methods).

We built MSMs from over 30 milliseconds of atomistic MD simulation trajectories³³ (distributions of trajectory lengths are shown in Supplementary Figure S4), for both folding conditions (330 K, 0 M GuHCl) and unfolding conditions (370 K, 0.6–1.0 M GuHCl). The native state is stable at 330 K, with a ~3 Å RMSD-C_α to the crystal structure (PDB code 1hb6) maintained after 1 µs. Trajectories from the 330 K ensemble, initiated from folded and unfolded conformations, were used to construct a 20,000-microstate MSM. The continuous-time master equation solution of the microstate kinetics gives a spectrum of implied timescales (see Methods), with the slowest implied timescale corresponds to the overall folding time. The folding time predicted from the MSM is ~3 ms, comparable to the ~ 9 ms experimental folding time (Supplementary Figure S5).

Although no complete folding events were observed in any one trajectory, the network of microstates is fully connected by the many unfolding and partial re-folding events simulated (Supplementary Fig. S6). The lowest-free energy microstate contains the native state, and has a cluster center with RMSD-C_α to the crystal structure of ~0.6 Å (Supplementary Fig. S7). The average RMSD-C_α between pairs of conformations in each microstate (i.e. the microstate radius) is 6.89 ± 1.47 Å, slightly larger than previously MSM models of folding (for example, a 100,000-microstate MSM built from simulations of NTL9 (1–39)¹¹ had an average microstate radius of ~4.5Å), due to the larger size of ACBP (86 residues) and the correspondingly larger accessible conformational volume.

For comparison, we also built an MSM from the 370 K data. The average microstate radius in this model was 8.40 ± 1.88 Å. The lowest free-energy microstate still contains the native state, although the relative free energies of the other microstates are lower (Supplementary Fig. S7). For the discussion below, we will restrict our attention to the 330 K MSM constructed for folding conditions.

Macroscopically, the MSM predicts cooperative transitions between the folded and denatured subpopulations on the millisecond timescale, consistent with experiment (Figure 5a). Microscopically, however, the model is considerably more complex. Consistent with recent simulation and experimental studies showing kinetic heterogeneity⁵², our MSM model predicts a striking heterogeneity of metastable states and folding pathways existing on the mesoscopic scale. MSMs of protein folding for several proteins have previously been reported to have a hub-like network of states around the native state^12,38,53. We report a similar hub-like structure for ACBP, consistent with these findings. Mean first passage times (MFPTs) to the native microstate are three orders of magnitude faster than MFPTs to non-native states (Supplementary Figure S8).

A 2000-macrostate MSM obtained from the 20,000-microstate MSM by kinetic-based lumping³⁴ was used to analyze the distribution of folding pathway fluxes from unfolded to folded states. The highest-flux pathways connecting a fully extended state to the native state show contact formation between helices 1 and 4 that are coupled to the folding transition, consistent with phi-value analysis by Kragelund et al¹ (Figure 5b). Furthermore, our model predicts a near-native state with a displaced helix 3, corresponding well to a near-native intermediate identified by Teilum et al².

A surprising feature predicted by the MSM is the absence of a single well-defined folding intermediate postulated in earlier kinetic studies. The free energy of folding as a function of the kinetic reaction coordinate p_fold was calculated as F(p_fold) = −kT log Z(p_fold) where, Z(p_fold) was estimated at 300K as the sum of equilibrium macrostate populations for binned values of p_fold (see Methods). The free energy diagram shows two low-free energy basins corresponding to the unfolded and folded state, but no other intermediates along the reaction coordinate. Preceding the main folding barrier is a highly diffuse network of compact metastable states with residual unfolded-state structure (Figure 5c). These states contain both native and non-native contacts, consistent with the predictions of past simulations¹¹ and a recent analytical model of hub-like folding networks⁵⁴.

Unfolded-state compaction in simulated ensembles

Simulated unfolded-state ensembles were generated from trajectories starting from fully extended and random-coil conformations, and used to compute several observables directly comparable with experiment. The extended ensemble shows significant chain compaction by ~100 ns (see SI section B.5), reaching a radius of gyration (R_g) by ~5 µs similar to the coil ensemble, although slightly less compact (Figure 6a), in agreement with previous unfolded-state simulations²⁵. A polymer-theory of the coil-globule transition fits the simulated R_g values well for simulated ensembles at different temperatures (Figure 6a, see Methods, SI section C). While these fits show unrealistically high melting temperatures (as found previously²⁵), they are useful in obtaining transfer free energies per monomer as a function of simulation temperature, which can then be used to find experimental denaturant concentrations where ACBP exhibits a similar extent of chain compaction (see Methods). The comparison of simulated versus experimental R_g obtained by smFRET at the calibrated denaturant concentrations compares favorably (Figure 6b).

To model the sequence-dependent unfolded-state expansions measured by smFRET, we used a free energy perturbation approach to reweight conformations from simulated unfolded-state ensembles. By using a sufficiently coarse-grained and smooth potential to model sequence perturbations (see Methods; SI section B.6), accurate reweighting was possible using twenty thousand snapshots from simulated unfolded-state ensembles (taken after 5 µs). We calculated expectation values of interresidue distance 17–86 for the simulated wild-type (86-residue) sequence, as well as several mutant sequences characterized by smFRET. Our results generally agree with changes in end-to-end distances observed by smFRET: mutation Y31N is predicted to have the largest disruption of unfolded-state structure, as seen experimentally (Figure 6c). The relatively coarse resolution of our perturbation method, along with effects not accounted for in the model (such as the speculated amphipathic helix packing between helices 2 and 4; see above), are likely the main source of disagreement.

Unfolded-state structure in simulated ensembles

Interresidue contact propensities after 5 µs were calculated for unfolded-state ensembles generated from extended starting structures (see Methods). Similar patterns of unfolded-state structure were found in the low-temperature (330 K, 0 M GuHCl) and high-temperature (370 K, 0.6–1.0 M GuHCl) simulated ensembles. Significant helical secondary structure is predicted for residues in helix 1, 2, and 4 (as calculated by DSSP⁵⁵, Supplementary Figure S9), in a pattern consistent with chemical shift measurements of the acid-denatured state of ACBP at pH 2.3^56,57 (Supplementary Figure S10). Consistent with previous NMR chemical shift³ and PRE⁴ studies, our simulations predict long-range contacts in the unfolded-state ensemble between residues in helix 2 and 3, and helix 2 and 4 (Figure 5d, Supplementary Figure S3). We find fewer contacts involving helix 1, supporting earlier reports that helix 1 is largely detached from the rest of the ACBP structure⁴, only forming experimentally detectable long-range contacts late in folding reaction^3,58. Average RMSD-to-native values for individual helices over time (at 330K starting from the extended state) show helix 1 has a relaxation timescale of ~350 ns, while helices 2, 3 and 4 form compact, non-native structures by ~100 ns, with helix folding/unfolding presumably occurring on timescales slower than ~15 µs (data not shown).

Slightly more helicity (~20%) and more specific long-range contacts (mostly between residues in helix 2 and 3) are seen in the higher temperature simulations (370K, ~0.6–1.0 M GuHCl). This is likely due to the GBSA solvent model used, which does not model temperature-dependent effects, and to the increased conformational sampling at higher temperature. The exact prediction of helix content has little impact on our polymer-theory analysis, as scaling statistics are insensitive to secondary structure content⁵⁹. We note, however, that overestimates of helicity could bias the folding seen in the MSM toward a ‘diffusion-collision’ mechanism.

Complexity underlies simple kinetics

The network of transition rates in an MSM model specifies a continuous-time chemical master equation whose solution yields a spectrum of implied timescales, each corresponding to a relaxation mode describing population flux on that timescale^36,37,43. This spectrum is broad and continuous, reflecting the large number of dynamic transitions between competing metastable states occurring on many timescales (Supplementary Figure S5). This kinetic detail may be difficult to fully resolve experimentally, as structural observables typically report ensemble-averaged quantities, sensitive to specific kinds of structural transitions (e.g. FRET is most sensitive to changes in interatomic distances near the Förster radius.)

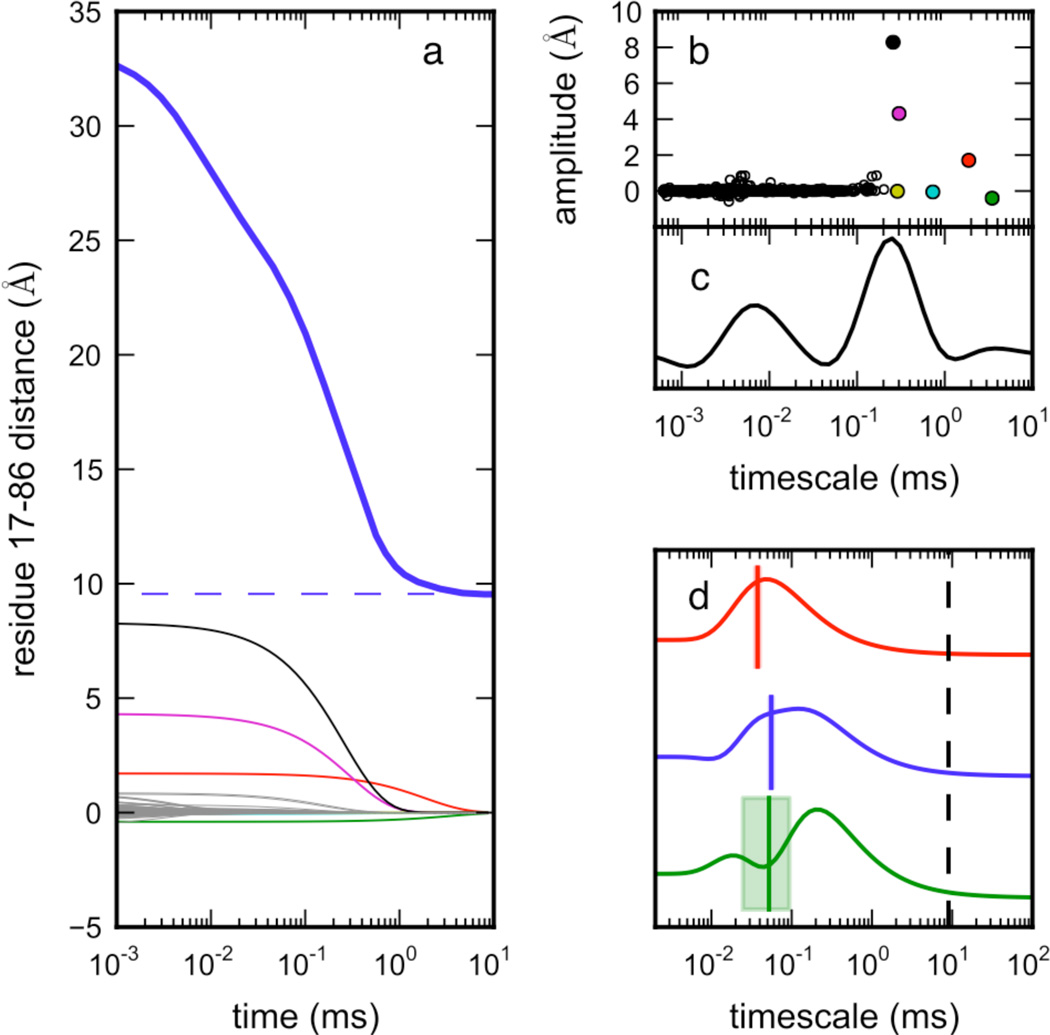
Which relaxation modes of ACBP are most sensitively reported by FRET probes? To predict the relaxation timescales observable by the ACBP 17–88 FRET probe, we projected the MSM population dynamics onto a proxy observable, the distance between residues 17 and 86, which can be more easily computed from simulations (since our simulations do not include C-terminal Gly-Cys residues 87 and 88). The predicted (ensemble-average) time course of this proxy distance is a superposition of relaxation modes of different amplitudes (Figure 7a, see Methods). Interestingly, the model shows only two timescale regimes^* expected to exhibit a large signal. A prudent experimentalist would fit such observed traces to a bi-exponential curve, postulating a three-state model, even though the underlying dynamics are considerably more complex.

Figure 7.

The FRET distance observable is sensitive to two main relaxation timescales. The continuous-time dynamics of the MSM state populations was calculated via the chemical master equation (see Methods). Observable values over time were computed as the sum of projections to the 1000 slowest relaxation modes. Shown in (a) are the MSM dynamics, starting from initial unfolded populations, projected onto the distance between 17 and 86 (blue, thick), with traces of individual modes shown below this. (Since our simulations do not include the C-terminal Gly-Cys residues, 17–86 is used as a proxy for the FRET distance observable 17–88.) (b) The amplitudes of each mode, plotted versus each implied timescale, reveal that, despite a broad distribution of kinetic timescales in the model, only two regimes contribute appreciably to the observed signal: ~0.1–3 ms (folding) and ~10 µs (unfolded-state structuring). Note that these timescales are slightly faster than experiment due to forcefield and rate estimation effects. (c) The calculated rate spectrum for the projection in (a) shows these two regimes clearly. (d) Rate spectra calculated from experimental FRET mixer traces for W55F, F26A and Y31N (data from Figure 2a) show relaxations corresponding to unfolded-state structuring on the ~100 µs timescale (colored lines and shaded rectangles are timescales calculated from single-exponential fits to the data, and their uncertainties). The ~9 ms folding timescale (black dashed line) is not accessible in the FRET mixer experiments, so peaks corresponding to the global folding rate are absent.

The relaxation modes with significant amplitudes cluster around two important timescale regimes: ~0.1–3.0 ms, corresponding to the overall folding relaxation, and timescales near ~1–10 µs, corresponding to structuring in the unfolded state (Figure 7b). We note that these predicted timescales are faster than experiment by an order of magnitude, with a broad spread in the slowest (folding) relaxation timescales, both of which are likely due to forcefield and transition rate estimation effects. The resolution of the MSM can be improved in the future with additional sampling.

To better compare these predictions to experimental FRET traces, we used a new method to calculate spectra of relaxation timescales from time series data^60,61. These so-called rate spectra are obtained by finding a spectrum of rate amplitudes a_i such that Σ_i a_i exp(−t/τ_i) best fits an observed time course for a set of timescales τ_i. The spectra thus obtained are “dynamical fingerprints”⁶² of the observed kinetics, and can be thought of as a numerical inverse Laplace transform, in which regularization methods are used to avoid overfitting to noise.

The rate spectra of both simulation data (Figure 7c) and mixer traces (Figure 7d) reveal similar kinetic phases. Rate spectra calculated from experimental FRET mixer traces for W55F, F26A and Y31N (data from Figure 2a) show relaxations corresponding to unfolded-state structuring on the ~100 µs timescale. While experimental limitations (e.g. signal-to-noise) limit the resolution of the rate spectra, we see a strong qualitative connection between the complex behavior seen in simulation to experiment, as well as quantitative agreement of the location of the peaks in the experimental rate spectra. In most cases, the relaxation timescales obtained from exponential curve fits match the peaks in the rate spectra, although the rate spectra approach is more robust and less sensitive to noise (Supplementary Figure S11, see SI section A.4).

We additionally note the presence of a very small peak at ~3 ms in the rate spectrum of the simulated time course, near the slowest implied timescale of the MSM. The existence of this separate peak is likely an artifact due to the broad spread of relaxation timescales (~0.1–3 ms), and should be attributed to the folding transition. Inspection of the transition matrix eigenvectors corresponding to each implied timescale show similar structural events for all of these relaxation modes: ensembles of compact unfolded conformations transitioning to the native state (Supplementary Figure S12).

Discussion

We believe that complex, multi-state kinetics is a general phenomenon in biopolymer folding studies, and find it plausible that a great deal of complexity in protein folding is commonly masked in a macroscopic interpretation of ensemble, and even single-molecule experiments⁶². It is very noteworthy that several new single-molecule studies of protein folding have found conformational fluctuations indicating multiple distinct metastable states^63,64. Even the most sophisticated single-molecule experiments, however, cannot resolve the entire microscopic complexity of folding due to the limited number of photons that can be detected on the microsecond timescale. It is therefore likely that ensemble and single molecule fast kinetic observables cannot capture the full complexity of folding, and instead we must turn to computer simulation. We expect Markov State Model approaches to be increasingly useful in this regard, as direct comparisons to experiment can made by projecting predicted microscopic dynamics onto macroscopic observables.

Our combined experimental results and MSM of the ACBP folding reaction suggest that residual unfolded-state structure forms on the ~100 µs timescale, in the absence of a well-defined intermediate. This timescale agrees well with the rates previously reported by Teilum et al. using Trp-Dansyl FRET and a continuous flow mixer⁷, and thus we believe the same molecular process is observed in the two studies. Even in that study, the putative intermediate was described as being mostly unstructured, with only a ~30% increase in buried of surface area compared to the unfolded state, and with the fast ~80 µs kinetic phase insensitive to denaturant concentration.

Intriguingly, our results suggest that the slow formation of unfolded-state structure is not due to barrier-limited formation of a folding intermediate, but rather due to slow unfolded-state structuring, possibly through a continuum of states. We find strong agreement between the mean-FRET efficiency of the denatured subpopulation at equilibrium and the asymptotic mean-FRET efficiency of the slow, kinetically resolvable phase in the nonequilibrium mixing experiment. In our mixing experiments (from 6 M to 0 M GuHCl), the measured FRET reaches ~90% of the native-state FRET over the course of ~200 µs. This implies that any intermediate I must have native-like FRET (as characterized previously⁷), and that the unfolded U state must have low FRET and be highly populated at high denaturant concentrations. But if the time-resolved FRET we observe is indeed due to the relatively slow (~100 µs) interconversion of discrete low-FRET and high-FRET states, we would likely see significant line-broadening of the denatured subpopulation in our sm-FRET experiments. Such line broadening has been shown by Rieger et al.⁴⁷ using smFRET with ALEX and a similar confocal transit time to detect an unfolded intermediate of RNase H at ~ 0.7 FRET, differentiated from the native state (0.8 – 1.0 FRET). A signature of such an intermediate is a very broad unfolded-state FRET histogram that results from averaging and shot noise. In contrast, our unfolded-state FRET histograms are narrow, comparable with Protein L, which does not populate a folding intermediate. Although we cannot rule out the possibility that U and I substates are obscured by shot noise or fast averaging, and note that we can only make relative comparisons of single-molecule and time-resolved FRET, we believe the weight of the evidence argues against the barrier-limited formation of an intermediate.

Instead, we believe that the changes in FRET over time observed in the mixer must correspond very closely to the unfolded-state compaction seen in decreasing concentrations of denaturant by smFRET. Early events in the folding reaction are predicted by the MSM to be structurally heterogeneous, suggesting collapse-like behavior with a gradual acquisition of non-local residual structure. Non-specific hydrophobic collapse has been characterized as occurring on the ~100 ns timescale⁶⁵, so slow collapse in ACBP is surprising, although other studies have characterized non-specific collapse forming on timescales less than 150 µs^66–68. Consistent with this picture is slow dynamics in protein unfolded states characterized here and elsewhere⁴⁹, as well as slow dynamics predicted by the MSM. We note that Bayesian estimates of average Arrhenius folding barriers separating MSM metastable states³⁸ are small— ~1.64 ± 1.04 kcal/mol for the 20k-microstate model (Supplementary Figure S13)—but the overall hub-like connectivity structure of the network can contribute to slow kinetics.

It is interesting to compare our predictions of unfolded structure with the results of a recent simulation study by Shaw et al. of the acid-denatured unfolded state of ACBP, in which a single 200 µs-trajectory was simulated⁴⁷. We utilized tens of thousands of independent trajectories amounting to tens of milliseconds of aggregate simulation time. Not surprisingly, even though both simulations predict long-range structure between helices 2 and 4, we see a great deal more heterogeneity in long-range contacts, reflecting both native and non-native interactions between residues normally participating in the hydrophobic core of ACBP. The relaxation timescales we observe for individual helices is consistent with the faster folding/unfolding timescales of helix 1 observed by Shaw et al.

Conclusion

In this work, we have constructed an MSM model of ACBP folding that reveals a complex network of metastable states with slow dynamics in the unfolded ensemble due to non-random residual structure and heterogeneous folding pathways. Validation of this model using smFRET, intramolecular diffusion and fast microfluidic mixing experiments suggests that the folding reaction for ACBP involves a surprisingly slow acquisition of unfolded-state structure in helix 2, 3 and 4 on the ~100 µs timescale, followed by barrier-limited folding to the native state on the ~10 millisecond timescale.

Moreover, our combined simulation and experimental studies of ACBP show how the microscopic complexity of folding can be reconciled with the simple macroscopic behavior often seen in bulk experiments. Despite its inherent microscopic complexity, our MSM model of ACBP predicts that experimental observables probing intramolecular distance should exhibit simple bi-exponential kinetics. In many other molecular systems—vesicle fusion, polymer dynamics, small molecule conformers, etc.—complex dynamics may also underlie simpler experimental observations. MSM approaches like those described here may provide a general framework for taming these processes and explaining how their simple macroscopic behavior arises.

ABBREVIATIONS

ACBP

acyl-coenzyme A-binding protein

FRET

Förster resonance energy transfer

smFRET

single-molecule FRET

GuHCl

guanidinium hydrochloride

PR

proximity ratio

MSM

Markov State Model

GPU

graphics processing unit

GBSA

generalized Born-surface area

MBAR

multi-state Bennett acceptance ratio

NTL9

N-terminal domain of ribosomal protein L9

RMSD

root-mean-squared deviation

PRE

paramagnetic relaxation enhancement