Abstract
The three-dimensional (3-D) structure prediction of proteins, given their amino acid sequence, is addressed using the first principles–based approach ASTRO-FOLD 2.0. The key features presented are: (1) Secondary structure prediction using a novel optimization-based consensus approach, (2) β-sheet topology prediction using mixed-integer linear optimization (MILP), (3) Residue-to-residue contact prediction using a high-resolution distance-dependent force field and MILP formulation, (4) Tight dihedral angle and distance bound generation for loop residues using dihedral angle clustering and non-linear optimization (NLP), (5) 3-D structure prediction using deterministic global optimization, stochastic conformational space annealing, and the full-atomistic ECEPP/3 potential, (6) Near-native structure selection using a traveling salesman problem-based clustering approach, ICON, and (7) Improved bound generation using chemical shifts of subsets of heavy atoms, generated by SPARTA and CS23D. Computational results of ASTRO-FOLD 2.0 on 47 blind targets of the recently concluded CASP9 experiment are presented.
Keywords: protein structure prediction, first-principles, global optimization
Introduction
The protein structure prediction problem continues to represent a proverbial “holy grail” in computational chemistry and structural biology communities. Stated simply, the problem can be described as an attempt to elucidate the three-dimensional (3-D) structure of a protein, given its amino acid sequence. To do this, most algorithms base their approach on Anfinsen's thermodynamic hypothesis.1 According to the hypothesis, the native structure of a protein in a given environment corresponds to the global minimum free energy of the system.
Given the expanding collection of proteins in the Protein Data Bank (PDB),2 along with the inherently difficult task of ab initio protein structure prediction, a number of database- driven methods have been developed, which exploit information from the experimentally determined structures of proteins in the PDB. Although clear classification between approaches toward protein structure prediction has become difficult, most approaches toward protein folding can be classified into the following three categories: (a) homology-based methods, (b) fold recognition–based techniques, and (c) first principles–based methods. A detailed review of various protein folding approaches has been presented in literature.3–5 Homology, or comparative, modeling methods aim to directly identify the template of a homologous protein, which can then be used as a starting point for refining the structure to suit the target protein better. Typically, these methods are most successful when there is a high degree of similarity between the target and parent structures, which exist in the database. Many methods are based on sequence alignment methods such as BLAST or PSI-BLAST.6 Although the implementation of sequence alignment or machine learning methods provides a good starting point for these algorithms, the challenge of loop building and side chain modeling persists. To address these issues, many methods use well-known algorithms for model building7 and side chain placement.8 A detailed review of approaches and drawbacks in comparative protein modeling can be found elsewhere.9,10
Fold-recognition approaches aim to identify distant homologs to a target sequence by working in the structural space instead of the sequence space. The premise for these methods lies in the observation that the fold space is much more limited than the sequence space. Based on the evaluation of researchers that the PDB2 is almost complete in terms of observed folds,11 a number of “threading” algorithms have been developed. Threading algorithms aim to find the best fit for a target protein sequence onto the structure of a template in the database. For distantly related proteins, a successful prediction would require accurate atomic prediction of the dissimilar regions, along with the aligned regions. A number of successful methods have been proposed that use fold recognition, including dynamic programming methods,12 iterative methods,13 and optimization-based methods.14,15
An intermediate category between pure fold-recognition techniques and pure first principles–based methods can be considered to be the fragment assembly–based methods. Here, a target protein is divided into short oligopeptides, which are used to identify fragments of structures from various templates in the database. This way, separate fragments can be selected from unique template structures. The individual fragments can then be brought together using statistical potentials and optimization-based algorithms. Optimization algorithms such as simulated annealing16,17 have been successfully used to bring fragments together to identify a fold, before using all-atom scoring functions to refine the model further. Skolnick and coworkers have aimed to combine multiple sequence alignment and threading with a unified atom lattice model to generate initial folds, before refining and clustering structures to identify the best structures from an ensemble.18
The final category of methods for protein structure prediction, the first principles–based methods, avoids the direct use of homology or structural alignment information. These algorithms work with a much larger search space and base their search algorithms on Anfinsen's hypothesis,1 that is, the structure sought would lie at the global free energy minimum of the system. Despite the increased computational complexity of first principles–based methods, the primary advantage of these methods is the ability to predict the structure of a protein in the absence of a good structural or sequence homolog. Furthermore, the use of physics-based scoring or energy functions would allow the extension of the protein structure prediction algorithms to various environments. Physics-based energy functions would also provide an insight into the protein folding process, along with creating a picture of the energy landscape of a protein.19
A number of first principles–based structure prediction algorithms aim to use a hierarchical process to protein folding. The use of a hierarchical process sequentially reduces the search space for the search algorithms. Dill and coworkers use replica exchange molecular dynamics for the search algorithm, in conjunction with a zipping and assembly model to bring distant parts of the sequence together to form the protein fold.20 Rose and coworkers have proposed a Metropolis Monte Carlo-based search algorithm for the structure prediction problem and identify conformational biases based on discrete moves selected using a physics-based force field.21,22 Using a distributed grid computation algorithm, Folding@Home, Pande and coworkers have used cartesian molecular dynamics to fold protein villin.23 A number of methods have aimed to use coarse grained potential at an early stage to determine the fold of a protein, followed by a model refinement procedure with a more detailed atomistic force field. One of the more popular force fields in this regard is the united-residue (UNRES) force field introduced by Scheraga and coworkers.24–26 By representing each amino acid to two interaction sites and using a stochastic conformational space annealing,27 the conformational space is reduced to the low energy regions. Recently, researchers have successfully managed to fold small proteins such as WW protein domain to high-resolution structures using molecular dynamics and improved all atom force fields.28–30
Another first principles–based approach to protein folding is the ASTRO-FOLD approach developed by Floudas and coworkers.31–38 The framework follows a hierarchical approach to the protein structure prediction problem, by combining the all-atom physics-based ECEPP/3 energy function,39 deterministic αBB global optimization algorithm, stochastic conformational space annealing algorithm, and a molecular dynamics approach in the torsion angle space. The deterministic global minimization algorithm, αBB,40,41 guarantees convergence to the global optimum for a problem with twice differentiable objective function and constraints, by creating a converging series of lower and upper bounds. Given the highly nonlinear nature of the force field, and the complex terrain defining the conformational search space, the deterministic global optimization algorithm is supported by torsion angle dynamics and conformational search annealing procedures. The torsion angle dynamics routine is used to generate low energy, feasible solutions, by using a simple steric-based energy function in a molecular dynamics routine. The conformational search annealing procedure, which is based on a combination of genetic algorithms and simulated annealing methods, is used for enhanced searching of the conformational space to identify better upper bounding function values.
This article has been arranged as follows. The Methods section presents the entire ASTRO-FOLD 2.0 framework in seven major steps: (a) secondary structure prediction, (b) β-sheet topology prediction, (c) contact prediction, (d) loop structure prediction, (e) tertiary structure prediction, (f) selection of near-native structures, and (g) improvement of distance bounds based on identification of chemical shifts in the target protein. This is followed by a presentation of blind target prediction results in the recently concluded CASP9 experiment.
Methods
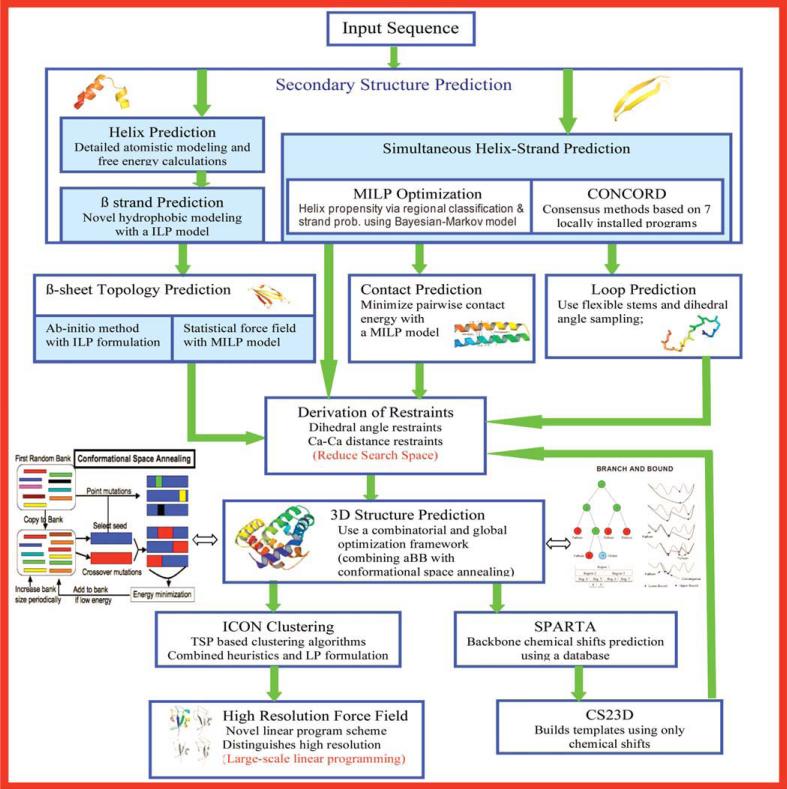
Given an amino acid sequence for a protein, the aim, in a blind prediction, is to identify a small set of proteins, that are likely to be closest to the native structure. The ASTRO-FOLD 2.0 approach is presented in flowchart form in Figure 1, and the individual steps are explained below. We focus on the novel components of ASTRO-FOLD 2.0 and provide an overview of algorithms and approaches from the previous version of ASTRO-FOLD.
Figure 1.
Flowsheet representing the ASTRO-FOLD 2.0 approach.
Secondary structure prediction
A number of methods for secondary structure have been previously used as an initial step in the ASTRO-FOLD procedure. For the purpose of α-helix prediction, two approaches have been previously implemented, which divide a target protein into overlapping oligopeptides. In the first approach, the target is divided into overlapping pentapeptides.34 For each pentapeptide, the helical propensity for the central residue is determined through rigorous probability calculations using detailed atomistic level modeling, and the use of deterministic global optimization targeting the global free energy minimum of the system. The free energy values for all structures predicted are used to calculate individual occupational probabilities for each meta-stable state. When the α-helical probability for three consecutive amino acids is greater than a threshold, the region is assigned as helical. In the second approach (Subramani and Floudas, in preparation), a target protein is divided into overlapping nonapeptides. As the presence of α-helices is marked by hydrogen bonding networks, which run almost parallel to the helical axis, the probability for the central residue of this nonapeptide to be in an α-helix is taken as a linear combination of probabilities of the surrounding amino acid pairs to form i,i + 3 and i,i + 4 hydrogen bonds. At the ends of α-helices, the probability evaluated from hydrogen bonding pairs is supported by the probability of hydrophobic amino acid occurence at specific positions at the ends of the helix. The model is implemented as an infeasibility minimization model, which aims to evaluate the threshold probability and weights of individual terms in the probability evaluation expression. For a given target protein, the model is implemented as a mixed-integer linear programming model that aims to identify the helical regions in the protein, using the parameter values evaluated in the training model. Furthermore, chemical shifts from a large chemical shift database are used to identify a superstructure of possible helical residues in a target protein.
A new consensus secondary structure prediction method (CONCORD) based on mixed integer linear optimization (MILP) has been developed (Wei et al., submitted). Based on seven secondary structure prediction methods, SSpro,42 DSC,43 PROF,44 PROFphd,45 PSIPRED,46 Predator,47 and GorIV,48 the MILP-based consensus method combines the strengths of different methods, and a better prediction accuracy is achieved through this model, which maximizes the number of correctly predicted amino acids in the training protein set.
The objective function of the consensus secondary structure prediction method takes the following form:
| (1) |
In this equation, yp,i is a set of binary variables, and it equals 1 if the sum of the scores of the correct secondary structure predictions is higher than the sum of the incorrect ones for amino acid i of protein p by at least εp,i; y2p is another set of binary variables, and it equals 1 if the sum of the scores of the correct predictions of all amino acids of protein p is greater than the sum of the scores of the incorrect predictions of the same protein p by at least ε2p. The first term in the objective function maximizes the total number of amino acids whose correct prediction has a higher score than the incorrect ones by at least εp,i. The second term in the objective function maximizes the total number of proteins whose sum of the scores of the correct predictions is higher than that of the incorrect predictions by at least ε2p. The third and fourth terms are included here to minimize the sum of soft margins. Note in the first term, 139 is the average length of proteins in the training set, and it is used to balance the weights of the first and second terms.
Two types of constraints are introduced. The first type of constraints ensures that, for an amino acid of a protein, when the difference between the sum of the scores of correct secondary structure predictions and the sum of the scores of incorrect predictions from different methods is lower than εp,i, then the binary variable yp,i equals to zero. This constraint takes the following form:
| (2) |
in which confSp,i,m is the confidence score predicted by method m for the ith amino acid of protein p, and predSSp,i,m is the prediction result of method m for the ith amino acid of protein p (a value of 1 corresponds to a true prediction).
The second type of constraints used in the model normalizes the weights terms, km, of each individual methods.
| (3) |
The consensus method is shown to perform better than any of the seven individual methods when tested on the PDBselect25 training protein set using six-fold cross validation. It also outperforms another set of ten online secondary structure prediction servers when tested on the CASP9 (http://predictioncenter.org/casp9/) targets. The average prediction accuracy is 83.6% for the six-fold cross validation and 82.3% for the CASP9 targets (107 released proteins). A web server, CONCORD, is freely available to the scientific community at http://helios.princeton.edu/CONCORD.
β-Sheet prediction
Once the secondary structure of a target protein has been predicted, we are now aware of the locations of the α-helices and β-strands in the protein. This information only provides local information in terms of the backbone dihedral angle ranges for the amino acids in the respective secondary structure elements. To reduce the search space for the tertiary structure prediction algorithm, it is vital to incorporate information about predicted nonlocal contacts in the set of constraints for the tertiary structure prediction problem. The first step toward this is the prediction of the β-sheet topology of the protein. Note that if the predicted secondary structure does not contain any β-strands, one can directly move to the next stage of the framework.
Previously, Floudas and Klepeis35 developed a method that aimed for the simultaneous prediction of β-strands, β-sheet topologies, and the location of disulfide bridges. Three separate formulations were presented, a residue–residue contact prediction model, strand–strand prediction model, and a combined model. In the residue–residue contact prediction, all hydrophobic residues that are not predicted as helical are identified, and an integer linear optimization model was established, which maximizes the hydrophobic contacts in the target protein. Additional terms are added for cystine–cystine contacts. In the second formulation, a protocol was established to predict a superstructure of potential β-strands. The objective then is to maximize the total strand–strand contact potential. The potential associated with each β-strand is the linear sum of hydrophobic potentials of each hydrophobic amino acid in the strand. The third formulation combines the objective functions from both the residue–residue and strand–strand formulations, thus, allowing both the energies to influence the final topology prediction. For each formulation, a number of constraints are implemented to ensure that biologically meaningful results are obtained. In addition, the presence of integer-cut constraints allows the generation of a rank-ordered list of solutions.
A new β-sheet topology prediction approach has been recently developed, which aims to ensure that the most likely strand pairings are predicted and subjected to biologically restrictive constraints (Subramani and Floudas, in preparation). It has been implemented in a MILP formulation (Subramani and Floudas, in preparation), and this allows us to create a rank-ordered list of preferred β-sheet arrangements. Opposing theories propose varying models for the formation of β-sheets. Although the hierarchical theory suggests that β-sheets nucleates at the hairpins and proceeds through the sheet formation in a zipper-style,49 an increased degree of support has been put forward to the hydrophobic collapse theory of β-sheet formation.50–52 To determine the arrangement of a given number of β-strands, we first evaluate the propensity of amino acid pairs in separate β-strands to form contacts. This model is implemented as a two-dimensional recursive neural network.53 For any amino acid pair (i, j) in separate β-strands, the input vector contains terms representing residue identity, secondary structure, and solvent accessibility. One additional element represents the sequential separation of the two amino acids. Equipped with the residue–residue contact potential matrix derived from the neural network model as described above, a dynamic programming algorithm is introduced to evaluate the best alignment between any pair of strands. The alignment score for any pair of strands si and sj is given by
| (4) |
In Eq. 4, ri and si are indices of amino acids in strands si and sj, respectively. PairPotentialri,si is the residue–residue pair potential for the residue pair (ri, si), as evaluated by the recursive neural network model. For any alignment of two strands, depending on whether the alignment is antiparallel or parallel, the indices ri and si would change in the same or opposite directions. Finally, for any pair of strands si and sj, the highest antiparallel and parallel alignment scores are taken as the strand–strand contact potentials EAP, si, sj and EP, si, sj, respectively.
We define three sets of binary variables, as defined under:
| (5) |
Here, residues i and j belong to different strands.
| (6) |
| (7) |
Given the aim to maximize the hydrophobic contact potential of the predicted β-sheet topology, the objective function can be written as
| (8) |
A variety of constraints are included to ensure that we obtain physically realistic sheet topologies. The first set of constraints links the binary variables for residue–residue contacts (yi,j) to the binary variables for strand–strand contacts (wAPsi,sj and wPsi,sj). By evaluating the strand–strand contact potentials EP,si,sj and EAP,si,sj, we know the best alignment of any strand pair. We hence define two binary matrices ResidueContactAPi,j and ResidueContactPi,j, wherein entries are 1 if i and j can form a contact at all. In addition, we define parameters Strand(i) that determine the strand to which residue i belongs. Note that this contact would be subject to whether their parent strands are contacting. This condition can be expressed as:
| (9) |
Any two strands si and sj can at most form one type of contact with each other, expressed as:
| (10) |
A strand residue can have a maximum of two contacts. However, this does not mean that the strand itself can only have two contacts. It is possible for a long strand to pair up with more than one strand on one side. Hence, the maximum number of contacts a strand can make is taken as 3. In the entire set of proteins that were tested, only four proteins had one strand with four contacts. At the same time, it is required that each strand have at least one contact. These constraints can be represented as:
| (11) |
| (12) |
| (13) |
In addition to relational constraints as shown above, a number of additional biological constraints have been added to the model so as to ensure that the resulting β-sheet topologies are biologically meaningful (Subramani and Floudas, in preparation). To ensure that β-strands with similar lengths contact, and that the predicted contacts do not get guided by single residue contacts, which are highly favorable, constraints are introduced to ensure that the number of contacting residues for any β-strand fall within observed minimum and maximum values, which are dependent on the length of the strand. Furthermore, in order to ensure that one β-strand wrapping around another β-strand (i.e., a contact between two β-strands is restricted to one side only) does not take place, a parameter set is introduced, which ensures that if more than two strands contact a given strand, there is at least one pair of strands, which do not have any overlaps with respect to residues participating in contacts. In addition, a number of constraints have been introduced to model nonlocal contacts, especially those involving super-secondary structures.54–57 Additional constraints ensure that all nonlocal contacts satisfy the formation of a previously occuring super-secondary structure, so as to ensure that the entropy loss due to the formation of the nonlocal contact is not so restrictive as to not be compensated by the resulting hydrogen bond formation. Further, constraints are introduced to ensure that strands, which form only one contact would either be the ones which are shorter, or with lesser hydrophobicity than other strands. A complete description of the mathematical model and extensive computational studies on 2405 pure β and mixed α/β proteins from the PDBSelect25 data set (pairwise sequence similarity ≤ 25%) is presented elsewhere (Subramani and Floudas, in preparation).
In addition to the biological constraints, integer cut constraints are added to generate multiple topology solutions for any given target protein. The advantage of creating an integer optimization-based model is the creation of a rank-ordered list of solutions. We aim to get a set of five topologies for each protein. As we are fixing the anchor points for contacts between two strands, the integer cuts would not involve the residue specific binary variables yi,j. In a number of cases, the objective function value of two topologies are highly similar to each other. By enlisting a small subset of top solutions, it enables us to differentiate between the topologies using a more detailed force field at the final stage. At each iteration, the addition of an integer cut eliminates the current top solution from the feasible set, thus, forcing the model to look for the next best solution.
The resulting MILP must be solved to global optimality to identify the predicted alignment of strands. While in general, MILP problems fall into the category of NP complete problems,58 available solvers typically use a branch-and-bound technique to reach the optimal solution by creating a sequence of LP relaxations of the original problem.
Contact prediction
Given the protein sequence and secondary structure information, residue contacts and protein topology (relative positions of various secondary structure elements) can be predicted. This is done in ASTRO-FOLD 2.0 through an integer linear optimization model. This model predicts residue contacts in α, β, α + β, and α/β proteins.59,60
The total energy of a protein in this model is expressed as sum of a Cα—Cα distance-dependent contact energy contribution and a hydrophobic contribution. Contacts are predicted by minimizing the total energy while satisfying a set of constraints that are included in the model to enforce certain physically observed topological information.
| (14) |
The objective function is shown in Eq. 14. Ei,j,b is the contact energy between two interacting amino acids (i, j) in distance bin b; wi,j,b is a binary variable indicating a contact between residue pair (i, j) in distance bin b (1–9 bins). The first term of Eq. 14 is the energetic contribution from all the contacting residues. Each of the binary variables wi,j,b assigned an energy value Ei,j,b based on the identity of the contacting residues (i, j) and the distance (bin b) at which they contact. If the predicted distance bin for residue pair (i, j) is in bins 1–8 then it means that these two residues are contacting. An extra bin, bin 9, is used to denote a “no-contact” between a pair of residues. Thus, a contact between two residues (i, j) in bin ‘9’ (wi,j,9 = 1) implies the residue pair is not contacting. An energy value of zero is assigned for all contacts in bin 9 (Ei,j,b = 0). Thus, the total energy of a protein can be calculated by taking the sum of such energy contributions over all the residue pairs.
The second term of Eq. 14 is the hydrophobic contribution when the residues of two different strands contact each other to form a β-sheet. The residue pair (si, sj), denote all pairs of residues that are in different β-strands (i.e., ). PRIFT, a hydrophobicity scale,61 is used to assign hydrophobicity value HP(si) to every amino acid in β-strands. A binary variable yci,j is defined for each residue pair and this variable is active only when the pair (i, j) forms a residue contact in the first eight bins. Hydrophobicity for a strand pair is added only when they are contacting (i.e., ycsi,sj = 1). For every contact, the hydrophobic contribution from both participating residues is considered by taking their sum. To calculate the overall hydrophobic contribution, an arithmetic sum is taken over all such strand pairs. The hydrophobic contribution is then multiplied with an optimal weight and added to the first term.
Many different constraints are included in the model, for example, β strand–based constraints: for two strands interacting in parallel or antiparallel fashion; if two strands are contacting then at least some of the residues of these strands should contact each other and so on. Helix-based constraints, general constraints, and integer cut constraints are also included.
The model was first tested on four independent α-helical protein sets. An average prediction accuracy of 66% was obtained for amino acid pairs that are at least six apart in the sequence.59 The average true and false positive distances were 8.87 and 14.67Å, respectively. The model was also tested on three-independent protein test sets and CASP8 test proteins consisting of β, α + β, and α/β proteins and was found to perform very well.60 The average accuracy of the predictions (separated by at least six residues) was ~ 61%. The average true positive and false positive distances were also calculated for each of the test sets and they are 7.58 and 15.88 Å, respectively.
Loop structure prediction
Using the set of constraints generated thus far, we can implement a tertiary structure prediction algorithm, which minimizes the energy of a protein conformer. However, for all dihedral angles where we do not have bounds, default bounds of [−180,180] are used. In particular, this would be applicable to amino acids outside the predicted secondary structure regions (i.e., loop regions). For proteins with a large number of loops, this would result in a large conformational search space for the tertiary structure algorithm. To address this issue, we have developed a novel iterative procedure to derive tight dihedral angle bounds on loop residues in a target protein (Subramani and Floudas, in preparation). An important intermediate step in the homology modeling paradigm is the loop structure prediction. In most approaches, one would be required to carry out a fixed stem loop structure prediction, rather than a flexible stem loop structure prediction. For a fixed stem loop structure prediction algorithm, we have information on the crystallographic coordinates of the amino acids in the flanking secondary structures of any loop. In our case, the problem becomes more difficult, because we only know of the type of secondary structure the stem residues fall into and have no information on their coordinates.
The conformational space of a loop segment is difficult to navigate, because loop segments with very similar sequences form very different structures. Furthermore, sequence similarity between loop segments are typically very low. These restrictions make the exclusive use of databases to predict loop structures challenging. Hence, the generation and optimization of loop segments that are close to native would have to be carried out in a manner similar to the physics-based ab initio tertiary structure algorithm. Most loop structure prediction algorithms implement procedures, which cover three basic steps. First, initial structures are derived by analyzing the loop regions of sequentially dissimilar proteins from a large database. This initial structure is subjected to energy minimization, typically preceded by a fast side chain rotamer optimization step. The side chain rotamer optimization aims to alleviate steric clashes between the backbone and the side chain rotamers, so as to provide local optimization routines a better initial point to work with. Energy optimization of the entire structure is then carried out, either using physics-based or database-derived all-atom potentials. Finally, clustering algorithms are used to identify the best structure from the generated ensemble, or a collection of structures are used to generate tight bounds on the loop angles. Further details on specific algorithms for loop structure prediction are available elsewhere.62–64
The generation of initial structures is a vital step toward getting good final structures, especially when using local optimization techniques. To this end, we take up the latest PDBSelect25 database of proteins. This set of proteins contains 4092 single chain proteins, with pairwise sequence similarity below 25%. We collect loop segments between the lengths of 4 and 20 from this database, as longer lengths provide a more random distribution of amino acid dihedral angles. For each amino acid, we discretize the Ramachandran plot into a grid of size 10° 10° . On the basis of the database of collected loop segments, we count the frequency of backbone dihedral angle occurences for each amino acid in each dihedral angle bin. Further, this distribution is generated separately for each kind of loop (i.e., separate distributions are generated from loops between helices, strands, and any combination of them). At this stage, we generate 2000 initial loop structures from this distribution. The process of generating initial structures generated is similar to the method followed by Mönnigmann and Floudas.64
Side-chain rotamer optimization is an important intermediate step toward structure prediction. A rotamer, short for rotational isomer, is a combination of side chain dihedral angles for any amino acid. Unlike the backbone dihedral angles, the most successful side chain optimization algorithms pose the problem as a combinatorial optimization problem, by approximating the continuous space of dihedral angles using a library of potential rotamers. A detailed review of the limitations and role of rotamer libraries can be found elsewhere.65
Most rotamer optimization algorithms divide the energy associated with a rotamer into two parts, the self energy and the pair energy. The self energy of a rotamer is the energetic interaction of this rotamer with all atoms that are considered fixed during rotamer optimization. Pair energy of a pair of rotamers is the energetic interaction between a pair of rotamers on different amino acids. For each of our algorithms, we precalculate the self and pair energies of all rotamers in our rotamer libraries (the “Penultimate” library66 and the Xiang-Honig Library67).
The first algorithm is an implementation of the FASTER algorithm. For the implementation of the FASTER algorithm, we use the smaller Penultimate rotamer library. Details of algorithmic implementations can be found elsewhere.68 The second algorithm is a cyclic search algorithm, which steps through the larger Xiang-Honig library and saves rotamer changes at specific amino acid positions, which lead to an improvement of the ECEPP/3 energy function. The final rotamer optimization is a random local search algorithm, which bases itself on a new, generated rotamer library. The new rotamer library is generated from a Gaussian distribution in the region of the current rotamer for each amino acid. Finally, we use the previous cyclic search algorithm to identify the best rotamer at each amino acid position. Further implementation details of the rotamer optimization algorithms in Ref. 38 have been presented previously.
Following the side chain rotamer optimization stage, we carry out a constrained non-linear optimization of the loop structures. The objective function for this optimization is the full atom ECEPP/3 potential, given by Eq. 15. The constraints in the model are the dihedral angle constraints derived from the same probability distribution as the initial structure. Once we collect 2000 optimized loop structures, we aim to identify the structures closest to the native by carrying out a traveling-salesman based clustering algorithm, known as ICON.69 The details of the algorithm are presented subseqently. Using the densest clusters identified by ICON, we regenerate a distribution for each amino acid in the target loop. Thus, the probability distribution is modified to address the specific loop in question. The entire algorithm is carried out five times, and the final set of densest clusters are used to generate dihedral angle bounds on each loop residue.
Tertiary structure prediction
On the basis of the approaches presented in the previous sections, we can generate the following set of constraints: (1) Backbone dihedral angle bounds for amino acids identified as lying in α-helices and β-strands; (2) Cα-Cα distance constraints for amino acids in α-helices that are separated by three or four residues in sequence; (3) distance constraints between amino acids that are predicted to contact each other based on the β-sheet topology; (4) residue–residue distance constraints between amino acids as predicted by the contact prediction algorithm; and (5) dihedral angle bounds on amino acids in all intermediary loops of the protein. In addition, optimization-based methods have been developed to improve the bounds on dihedral angles in the predicted secondary structures, as well as improvement in distance bounds based on the predicted secondary structure and sheet topology.37 The tertiary structure prediction algorithm has been implemented as a combination of the deterministic global optimization (αBB algorithm), stochastic global optimization (conformational space annealing), and molecular dynamics in the torsion angle space (torsion angle dynamics).
Energy function
According to Anfinsen's hypothesis,1 the native state of the protein lies at the global free energy minimum of the system. Hence, while solving for the protein structure, it is imperative that the energy function be a reflection of the free energy landscape of the protein. Common physics-based energy functions include energetic contributions from terms based on atomic bonds, atomic angles, torsional angles, van der Waals interactions, and electrostatics. Some examples of force fields, which include all of such terms are AMBER70 and CHARMM.71 A modified approach is to assume the covalent bond lengths and bond angles to lie at their mean values. This way, one can ignore the energetic contributions, which arise from the first two terms previously mentioned. By fixing these parameters to their mean values, force fields such as ECEPP,72 ECEPP/339 and ECEPP-0573 can define their energy expressions purely based on the protein dihedral angles. Modeling the protein using only its dihedral angles significantly reduces the variable space when compared with the cartesian representation that one would have to adopt if bond lengths and angles were included. For ASTRO-FOLD 2.0, we use the ECEPP/3 potential function, which contains terms representing electrostatic, van der Waals, hydrogen bonding, and torsion angle contributions given by:
| (15) |
In Eq. 15, rij represents the distance between a pair of atoms i and j, given that both the atoms fall into the set of atoms over which the summation is carried out. The parameter Fij, which represents the relative impact of the repulsive part of the Lennard–Jones expression, is taken as 0.5 for one to four interactions, and 1.0 for one to five interactions. Non-bonding parameters such as Aij, A′ij, Bij, and Cij are atom pair dependent. The sets ES, NB, and HB are defined over the set of pairs of atoms i and j that can have electrostatic, nonbonded, and hydrogen bonding interactions, respectively. The set TOR runs over all torsion angles of the protein that can contribute to the last term of the expression.
Problem formulation
The problem of finding the global energy minimum of a protein can be formulated as:
| (16) |
In Eq. 16, EECEPP/3(θ) is the ECEPP/3 energy of the protein described previously. and represent the lower and upper bounds on any dihedral angle θk. The distance penalty term , for a given conformation θ can be written out as a combination of lower and upper distance penalty terms given by:
| (17) |
| (18) |
Deterministic global optimization using αBB
To solve the constrained minimization problem given by Eq. 16, we need to use global optimization-based search techniques. One such global optimization technique, which avoids dependence on initial conditions and search heuristics, is the αBB global optimization approach.40,41,74–76 The algorithm is a deterministic global optimization approach, which provides theoretical guarantee of convergence to the global optimum solution for problems with twice-continuously differentiable objective functions and constraints. The αBB global optimization approach guarantees convergence to an ε-global optimum solution by creating a sequence of nondecreasing lower bounds, along with a sequence of nonincreasing upper bounds on the optimum value. Eventual convergence of these sequences lead to the identification of the global optimum. The method has been applied successfully to the problem of protein structure prediction previously,31,38 and we only highlight the key aspects of the algorithm.
The lower bounding problems are constructed by augmenting the objective function and constraints with separable quadratic functions. Mathematically, the lower bounding function is represented as:
| (19) |
The term LECEPP/3(θ) refers to the convex lower bounding function representation of the objective function and is expressed as shown in Eq. 20. The α-parameters represent non-negative parameters, which must be greater than or equal to negative one-half of the minimum eigenvalue of the hessian of the original energy function over the defined domain.77 Mathematically, the aim of the additional quadratic terms is to overpower the nonconvexities of the original terms by adding a value of 2α to the eigenvalues of the hessian of the original energy function. Given solutions to the lower and upper bounding problems, the algorithm branches on the subproblem, which holds the infimum of all the lower bounding function values. This ensures that we get a series of non-increasing lower bounds. The series of nondecreasing upper bounds is determined by identifying the protein structure with the minimum energy value. Any region where the lower bounding energy value exceeds the best current upper bound can be safely fathomed, as the global minimum would definitely not be present in this region.
| (20) |
Torsion angle dynamics
Before the implementation of the deterministic global optimization, it is vital to get initial structures, which fall into the feasible space of the optimization problem. Here, the feasible space of the problem is defined by the dihedral angle and distance bounds generated in the previous sections. Various algorithms have been used for the problem of identifying structures, which satisfy a sparse set of distance and dihedral angle constraints. For protein structure prediction problems, distance geometry algorithms such as EMBED78 and dgsol79 have been used to produce feasible initial structures. In addition to distance geometry methods, a number of other algorithms such as variable target methods80 and molecular dynamics81 have also been used for this problem. A detailed review on algorithms for constrained protein structure determination is available elsewhere.82
The ASTRO-FOLD framework involves an interface with the torsion angle dynamics package CYANA.83 By fixing the covalent bonds and bond angles to their mean values, the torsion angle dynamics package works in the dihedral angle space, thus reducing the number of variables drastically. Further, unlike target minimization, molecular dynamics allows itself the possibility of overcoming energy barriers, due to the presence of kinetic energy. Unlike classical molecular dynamics simulations, the torsion angle dynamics algorithms combine steric clashes-based energy terms and constraint-based penalties in a simplified target function. This allows for faster calculations and results in the algorithm aiming to identify structures, which are fairly low in energy, but are more importantly, feasible. Algorithmic implementation details of the initial point selection can be found elsewhere.38
Conformational space annealing
In conjunction with the αBB deterministic global optimization approach presented, we can use stochastic or heuristic search techniques to improve the search process for the identification of low energy conformations. While the lower bounding problem, as presented in the αBB algorithm provides the theoretical guarantee to create a nondecreasing sequence of lower bounds which would approach the global optimum solution from below, we can integrate heuristic search techniques into the process of creating the sequence of nonincreasing upper bounds. This would provide multiple advantages. First, a faster, albeit stochastic, method would identify new regions of the search space, which may hold the global minimum solution. In addition, by identifying such regions and their corresponding upper bounds, one can fathom other regions of the space where the minimum structure is such that the lower bounding function has an energy value greater than the best current upper bound.
One such algorithm is conformational space annealing (CSA),27,84,85 proposed by Scheraga and coworkers. Although the CSA approach lacks theoretical guarantees, given its high efficiency, a hybrid implementation of the αBB and CSA would be highly favorable.
Starting with a bank (Nbank) of conformers generated by the αBB global optimization algorithm, a distance metric for evaluating separation between structures i and j in the bank is given by:
| (21) |
where Nϕ is the number of dihedral angles of the protein, and , are the kth dihedral angle of conformers i and j, respectively. Given this definition of distance, the average distance between structures in the bank (Davg) can be evaluated by:
| (22) |
The conformational space is searched using heuristics based on genetic algorithms. This involves alteration of conformers, which exist in the bank using two heuristic modifications: mutations and crossover operations. The mutation operation identifies between one and four ϕ, Ψ and ξ1 dihedral angles and changes their values to the ones held by another conformer in the bank. Simultaneously, the crossover operation replaces a randomly selected continuous range of dihedral angles (between 1/8 and 1/4 of the total number of dihedral angles) from a given conformer with the values from a second conformer. Once a mutation or crossover operation is carried out, the new conformer is subjected to local minimization. To ensure that any new structures identified by the genetic algorithm does not fall too close to a structure already existing in the bank, a “radius of influence,” Dcut, is determined. This ensures that the conformer bank does not become too biased towards a specific region in the search space too early.
Further implementation details of the hybrid αBB/CSA algorithm can be found elsewhere.38
Selection of near-native structures
Protein structure prediction encompasses two major challenges: (1) the generation of a large ensemble of high-resolution structures for a given amino acid sequence and (2) the identification of the structure that is closest to the native structure from this ensemble, especially for a blind structure prediction problem. A number of approaches have been used for the identification of near-native structures from large ensembles of predicted conformers. These can be broadly classified into force field-based techniques and clustering-based techniques. Force field-based techniques can be further classified into physics-based and knowledge-based force field techniques. Physics-based force field techniques aim to evaluate coefficients of individual terms in potentials such as AMBER,70 CHARMM,71 and ECEPP/3,39 so as to increase correlation between nearness to native structure and energy value. Knowledge-based potentials aim to derive parameters for distances between Cα atoms,86 Centroids,87 or all atoms,88 so as to separate out the native structure from the non-native decoys. However, the success of all force-field-based techniques would depend on the similarity of the training data set to the conformational ensemble of the blind target protein.
In the ASTRO-FOLD 2.0 framework, we address this challenge by implementing an iterative novel traveling salesman problem (TSP)-based clustering approach, known as ICON.69 By considering each conformer generated from the ASTRO-FOLD 2.0 framework as a node on a traveling salesman path, we identify the globally optimal path through each of these nodes. Once the optimal path is determined, this path is partitioned into clusters such that the clusters minimize the global sum of intracluster differences in values. An overview of each of the steps of ICON is presented below, and the details can be found elsewhere.69,89
With each conformer of the target protein as a node on the TSP path, we define binary variables yi,i′ for any pair of nodes i and i′ as:
| (23) |
The objective function is then defined as90:
| (24) |
where ϕmi,j,mi′,j is given by:
| (25) |
Here, the index j runs over all the pairs of (ϕ,Ψ) angles of each amino acid of the target protein. Constraints, which ensure that each node has exactly one node preceding and following it on the TSP path, are implemented. In addition, efficient TSP solvers such as Concorde91 introduce additional cuts, which eliminate circular tours and subtours. Once the optimal path through all conformers is determined, we propose an integer linear programming (ILP) model to determine the cluster boundaries for a given optimal ordering.89 As for any node on the TSP path, we know the immediate neighbors on the path, the aim is to simply determine the points on the TSP path where immediate neighbors on the path fall into separate clusters. This would be sufficient to identify the boundaries of clusters. To do this, we generate a distribution of ϕi,i+1 (where ϕi,i+1 are defined as in Eq. 25). For any local window of x elements, we identify nodes where the neighbor distance falls below one standard deviation of the global average of this distribution. In addition, this distance would be the minimum in its local window, so as to ensure that we do not separate out elements that are very similar. By selecting local minima points of this distribution as cluster “seeds,” we now have the problem of placing the remaining “outlier” points with the cluster seed element immediately before or after them in the optimal TSP path. This has been modeled as an integer linear programming (ILP) model, with binary variables assigning the outlier points to either the cluster before or after them. The objective function includes terms, which account for the fixed cost (distance between an outlier and the seed of the cluster) and variable cost (distance between two outliers both assigned to the same cluster seed). Constraints are introduced to ensure that there are no crossovers, that is, for any pair of outliers i,i + 1, the assigned cluster of element i + 1 should be greater than or the same as that of element i. Details of the mathematical implementation of the model can be found elsewhere.89 Subsequently, the cluster centroids for each cluster are identified by determining the cluster element with the minimum distance to all other elements of the cluster, with the distance being defined again as in Eq. 25.
Following this, we eliminate loosely bound clusters by analyzing cluster densities. All clusters with cluster densities greater than the median value are retained for future iterations. At the end of 10 iterations or when left with half the initial number of conformers, we rerank the final list of cluster centroids using high-resolution distance-dependent force fields.86,87 The lowest energy structures are identified as the structures nearest to the native.
Improved distance and dihedral bound generation using chemical shifts
Chemical shift information is widely used for protein structure prediction.92–99 This is based on the fact that chemical shifts of protein backbone atoms are very sensitive to the local structures of the protein, thus, chemical shifts can help protein structure prediction in various ways. Shen et al. developed a protocol chemical-shift-Rosetta (CS-Rosetta), to study the influence of the completeness of chemical shifts on protein structure prediction.94 TALOS98 is an algorithm for backbone dihedral angle prediction using chemical shift database information. The database consists of amino acid triplets with corresponding secondary chemical shift and sequence information. By searching the best match of triplet of the query protein against the database, the dihedral angles can be predicted using a consensus scheme of the top 10 matches. The test shows that the predicted dihedral angles are on average 15° from the X-ray derived backbone angles. TOUCHSTONEX99 predicts protein structure by using some long-range distance restraints derived from NMR experimental data (including chemical shifts, NOE contacts, slow amide protein exchange, etc.). A NOE-specific pairwise potential is incorporated to tackle the NMR experimental data-derived constraints. A total of 108 of 125 test proteins are folded below 6.5 Å of Cα RMSD.
In ASTRO-FOLD 2.0, the structures resulting from the clustering are subject to the SPARTA92 algorithm, which predicts the backbone chemical shifts from tertiary structure. The predicted chemical shifts are then used by CS23D (chemical shift to 3-D structure)93 to predict the protein 3-D structure. SPARTA92 predicts backbone chemical shifts for a given protein structure by searching a database of amino acid triplets with chemical shift data of 15N, 1HN, 1Ha, 13Ca, 13Cb, and 13C′ atoms. The triplet database of SPARTA is expanded by adding more proteins from Biological Magnetic Resonance Data Bank (BMRB). The same procedure is used for adding triplet into the database as in Ref. 92. For example, completeness of chemical shifts data for 1Ha, 13Ca, 13Cb, and 13C′ is checked by ensuring at least four of five chemical shifts for these five atoms should exist. For Glycine and Proline, three of four chemical shifts should exist to be added into the database; Only PDBs with 2.4 Å resolution or less are selected for analysis from the BMRB.
CS23D predicts the protein structure given the protein backbone chemical shift information and sequence information. No NOE or J-coupling information is needed for CS23D to predict the protein structure. It consists of several steps involving maximal sub-fragment assembly, chemical shift threading, or chemical shift based de novo structure prediction, chemical shift refinement. The performance of CS23D is dependent on the completeness and correctness of the chemical shift data and the sequence similarity between the query protein and the proteins in the database.
Both SPARTA and CS23D are installed locally.92,93 By generating the modified protein structure from CS23D, we identify improved distance constraints between pairs of amino acids. In addition, consensus methods between the original dihedral angle constraints and the angles of structures generated by CS23D are taken to generate improved dihedral angle bounds. These improved constraints are used to rerun the tertiary structure prediction algorithm discussed previously. The final ensemble of collected structures is compiled and clustered using the novel traveling salesman problem-based clustering algorithm ICON, shown in the previous section. From this stage, the final subset of structures closest to the native are identified.
Computational Studies
A major test of protein structure prediction methods is done through a biennial world wide competition, critical assessment of techniques for protein structure prediction (CASP). In this section, several examples of CASP9 prediction (http://predictioncenter.org/casp9/) using the ASTRO-FOLD 2.0 framework will be presented. Detailed analysis of secondary structure prediction is presented in terms of the three-state (Q3) prediction accuracy, contact prediction is evaluated by its prediction accuracy, and tertiary structure prediction is evaluated by root mean square deviation (RMSD), template modeling (TM) score, and global distance test (GDT) score of the Cα atoms from the native structure.
Forty seven tertiary structure predictions made by ASTRO-FOLD 2.0 during CASP9 are presented in this section. The identification of domains for analysis was carried out by the organizers of CASP9. The detailed structure evaluations are listed in Table 1. In this table, RMSD, GDT, and TM scores are listed first for the top submitted prediction of the ASTRO-FOLD 2.0 models, followed by the same information for the best of the five ASTRO-FOLD 2.0 submitted models. As it is shown in this section, ASTRO-FOLD 2.0 successfully predicts good quality structures and substructures for a number of proteins. In this section, a few of the protein structures predicted by ASTRO-FOLD 2.0 are selected for detailed analysis. We present the results from the secondary structure and contact prediction algorithms, along with the tertiary structure prediction results, thus, representing the impact and importance of these intermediate algorithms toward the final 3-D prediction algorithm.
Table 1.
Structure Evaluations of CASP9 Targets for ASTRO-FOLD 2.0
| Top 1 model |
Best model |
|||||
|---|---|---|---|---|---|---|
| Prot | GDT | TM | RMSD | GDT | TM | RMSD |
| T531-D1 | 0.25 | 0.19 | 11.94 | 0.28 | 0.21 | 11.94 |
| T544-D1 | 0.19 | 0.23 | 15.14 | 0.26 | 0.31 | 10.46 |
| T553-D1 | 0.40 | 0.32 | 7.53 | 0.44 | 0.32 | 6.59 |
| T553-D2 | 0.32 | 0.29 | 12.11 | 0.38 | 0.35 | 8.53 |
| T561-D1 | 0.31 | 0.39 | 11.66 | 0.31 | 0.39 | 11.66 |
| T578-D1 | 0.23 | 0.24 | 17.66 | 0.23 | 0.24 | 15.91 |
| T581-D1 | 0.36 | 0.37 | 12.08 | 0.36 | 0.37 | 12.08 |
| T616-D1 | 0.35 | 0.31 | 14.75 | 0.36 | 0.35 | 12.30 |
| T618-D1 | 0.21 | 0.26 | 18.66 | 0.26 | 0.32 | 13.92 |
| T621-D1 | 0.13 | 0.21 | 19.08 | 0.18 | 0.26 | 17.16 |
| T624-D1 | 0.24 | 0.19 | 12.08 | 0.34 | 0.30 | 8.44 |
| T517-D1 | 0.35 | 0.46 | 14.48 | 0.35 | 0.46 | 9.28 |
| T520-D1 | 0.60 | 0.72 | 3.98 | 0.60 | 0.74 | 3.74 |
| T523-D1 | 0.62 | 0.67 | 5.16 | 0.62 | 0.67 | 3.72 |
| T540-D1 | 0.27 | 0.27 | 12.68 | 0.36 | 0.34 | 7.55 |
| T562-D1 | 0.35 | 0.41 | 10.80 | 0.35 | 0.41 | 10.80 |
| T564-D1 | 0.43 | 0.40 | 13.40 | 0.43 | 0.40 | 11.35 |
| T566-D1 | 0.34 | 0.43 | 7.90 | 0.50 | 0.61 | 4.50 |
| T568-D1 | 0.25 | 0.28 | 12.31 | 0.28 | 0.31 | 12.02 |
| T569-D1 | 0.22 | 0.20 | 12.89 | 0.73 | 0.72 | 3.02 |
| T574-D1 | 0.40 | 0.41 | 7.54 | 0.40 | 0.41 | 7.54 |
| T576-D1 | 0.16 | 0.20 | 17.59 | 0.35 | 0.44 | 9.12 |
| T579-D1 | 0.53 | 0.40 | 4.94 | 0.53 | 0.40 | 4.94 |
| T579-D2 | 0.39 | 0.36 | 10.09 | 0.39 | 0.36 | 8.37 |
| T580-D1 | 0.89 | 0.91 | 1.37 | 0.89 | 0.91 | 1.37 |
| T582-D1 | 0.23 | 0.28 | 10.00 | 0.35 | 0.38 | 8.31 |
| T584-D1 | 0.28 | 0.43 | 23.07 | 0.28 | 0.43 | 13.83 |
| T586-D1 | 0.79 | 0.79 | 2.18 | 0.79 | 0.79 | 2.18 |
| T586-D2 | 0.81 | 0.64 | 2.87 | 0.81 | 0.64 | 2.87 |
| T590-D1 | 0.74 | 0.70 | 2.59 | 0.74 | 0.70 | 2.59 |
| T592-D1 | 0.56 | 0.64 | 8.69 | 0.60 | 0.68 | 8.32 |
| T594-D1 | 0.40 | 0.48 | 7.00 | 0.53 | 0.61 | 4.85 |
| T596-D1 | 0.83 | 0.72 | 1.60 | 0.85 | 0.74 | 1.58 |
| T596-D2 | 0.51 | 0.54 | 4.92 | 0.66 | 0.72 | 3.30 |
| T598-D1 | 0.50 | 0.55 | 5.81 | 0.50 | 0.55 | 5.81 |
| T602-D1 | 0.72 | 0.57 | 2.87 | 0.72 | 0.61 | 2.47 |
| T605-D1 | 0.85 | 0.73 | 1.61 | 0.87 | 0.77 | 1.36 |
| T606-D1 | 0.57 | 0.62 | 7.91 | 0.57 | 0.62 | 7.91 |
| T610-D1 | 0.62 | 0.71 | 6.43 | 0.62 | 0.71 | 6.43 |
| T612-D1 | 0.40 | 0.39 | 8.36 | 0.40 | 0.42 | 8.07 |
| T614-D1 | 0.30 | 0.29 | 12.47 | 0.46 | 0.41 | 5.76 |
| T619-D1 | 0.73 | 0.78 | 2.22 | 0.77 | 0.83 | 1.80 |
| T622-D1 | 0.51 | 0.55 | 7.32 | 0.53 | 0.62 | 7.32 |
| T625-D1 | 0.29 | 0.40 | 13.66 | 0.29 | 0.40 | 13.66 |
| T627-D1 | 0.40 | 0.60 | 7.58 | 0.40 | 0.60 | 7.58 |
| T629-D1 | 0.27 | 0.21 | 10.55 | 0.44 | 0.34 | 9.02 |
| T630-D1 | 0.51 | 0.55 | 5.45 | 0.51 | 0.55 | 5.45 |
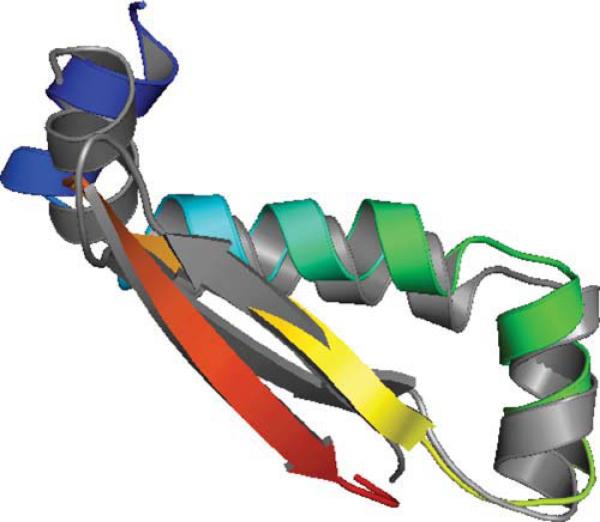
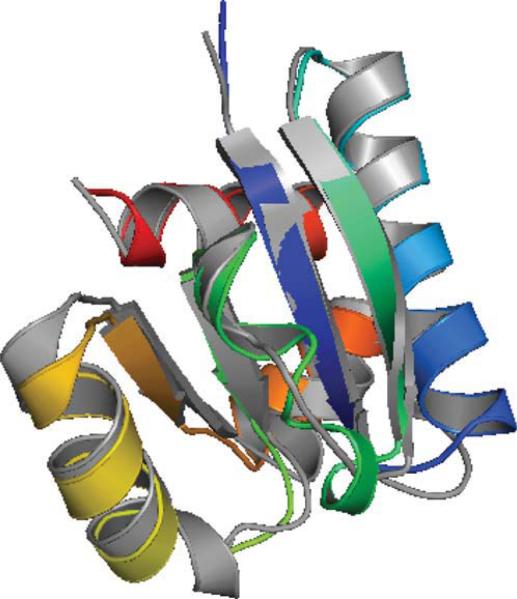
T581:3NPD
Target T581 has been categorized as a free modeling target (PDB code: 3NPD). 3NPD is a one-chain protein with 112 amino acids having specified native coordinates (amino acids 20–131). Out of the 136 amino acids of T581, only amino acids 20–131 are used for evaluation.
As shown in Figure 2, there are five strands in T581 forming a beta sheet with all neighboring strands contacting in antiparallel fashion. In the native structure, the positions of the five β strands are: strand 1 from amino acids 44–45, strand 2 from amino acids 50–58, strand 3 from amino acids 61–68, strand 4 from amino acids 106–113, and strand 5 from amino acids 119–125. In addition, the protein contains five helices located at: helix 1 from amino acids 22–39, helix 2 from amino acids 70–78, helix 3 from amino acids 80–92, helix 4 from amino acids 95–101, and helix 5 from amino acids 127–130. These five helices are on one side of the five-stranded sheet, thus, forming a hydrophobic core-like region between the two secondary structure layers. The interacting pairs of the helices are between helices 1 and 2 (N-terminal to C-terminal), between helices 2 and 3 (C-terminal to N-terminal), between helices 3 and 4 (C-terminal to the middle), and between helices 3 and 5 (the middle to C-terminal).
Figure 2.
Native structure of T581 (3NPDA).
The secondary structure prediction for T581 has a relatively low prediction accuracy (59.8%). This can be attributed to the fact that the protein is categorized as a free modeling target, thus, having a low sequence similarity to the protein database. This would result in varied predictions of secondary structures by multiple methods, thus, resulting in an unsatisfactory consensus result. The predicted secondary structure information is listed in Table 2. As for the helical prediction, predicted helix 1 cannot be evaluated because the first 19 amino acids of T581 do not have coordinates in native structure. The prediction of the two helices at the C-terminal is accurate, whereas the predicted helix 3 contains strand 1 of the native structure, and the predicted helix 4 corresponds to strand 3 of the native structure.
Table 2.
Predicted Secondary Structure Information for T581 by ASTRO-FOLD 2.0
| Helix | Strand |
|---|---|
| 3–12 | 106–111 |
| 15–35 | 120–125 |
| 44–52 | 129–132 |
| 62–77 | |
| 81–89 | |
| 97–102 |
While evaluating the contact prediction results (Table 3), we observe that ASTRO-FOLD 2.0 has an accuracy of 40% for amino acid pairs that are at least six amino acids apart, with average true prediction distance 5.9 Å and average false prediction distance 15 Å. A maximum distance cutoff of 12 Å between two Cα atoms has been used for defining a contact between two amino acids. The distance cutoff of 12 Å has been used to match the distances predicted in the contact prediction model, which uses a high-resolution Cα-Cα distance-dependent force field for its predictions. The lower accuracy of the contact prediction algorithm can be attributed to inconsistencies in the secondary structure prediction algorithm.
Table 3.
Predicted Amino Acid Contacts for T581 of CASP9
| AA1 | AA2 | Distance | AA1 | AA2 | Distance |
|---|---|---|---|---|---|
| 106 | 125 | 5.458 | 107 | 123 | 8.238 |
| 107 | 124 | 5.646 | 108 | 122 | 7.05 |
| 108 | 123 | 5.642 | 109 | 121 | 7.79 |
| 109 | 122 | 5.57 | 110 | 120 | 7.933 |
| 110 | 121 | 6.215 | 108 | 124 | 4.303 |
| 111 | 120 | 5.377 | 106 | 123 | 10.02 |
| 106 | 124 | 6.445 | 107 | 122 | 10.58 |
| 107 | 125 | 5.154 | 108 | 121 | 10.35 |
| 109 | 123 | 5.171 | 109 | 120 | 10.47 |
| 110 | 122 | 4.634 | 124 | 131 | 13.86 |
| 111 | 121 | 5.17 | 123 | 131 | 15.97 |
| 108 | 125 | 6.379 | 124 | 130 | 10.83 |
| 109 | 124 | 6.421 | 125 | 131 | 10.4 |
| 110 | 123 | 6.765 | 122 | 131 | 19.75 |
| 111 | 122 | 6.171 | 123 | 130 | 12.88 |
| 27 | 62 | 10.33 | 27 | 46 | 28.12 |
| 50 | 68 | 4.65 | 30 | 46 | 25.47 |
| 51 | 66 | 5.443 | 31 | 46 | 22.3 |
| 76 | 83 | 6.429 | 27 | 63 | 13.93 |
| 30 | 68 | 28.23 | |||
| 31 | 66 | 17.98 | |||
| 31 | 68 | 24.53 | |||
| 34 | 66 | 16.72 | |||
| 50 | 62 | 18.85 | |||
| 50 | 63 | 15.68 | |||
| 51 | 62 | 17.28 | |||
| 51 | 63 | 14.2 | |||
| 83 | 100 | 21.61 | |||
| 83 | 101 | 19.86 |
Data are shown for amino acid pairs that are at least six amino acids apart. First three columns show the true predicted contacts whose distances fall between the predicted lower and upper distance bounds; whereas the last three columns show the false predicted contacts where the real distance falls outside the predicted distance range.
It is worthy to note that the above accuracy is calculated based on the lower and upper distance bounds used by the contact prediction model in ASTRO-FOLD 2.0. If the real distance falls in the range between lower and upper distance bounds, the contact is taken as a true contact, otherwise it is a false contact. In ASTRO-FOLD 2.0, lower and upper distance bounds are used as constraints for tertiary structure prediction. ASTRO-FOLD 2.0 uses 4.5–6.5 Å for the vertically contacted strand amino acid pairs (if two amino acids on two different interacting strands are closest in space, these two amino acids are denoted as “being vertically contacted”.). If lower and upper bounds are set to 0 and 12 Å for all the predicted contacts, the contact prediction accuracy is 62.5%.
The top submitted structure from ASTRO-FOLD 2.0 predictions has a RMSD value of 12.08 Å, a GDT score of 36%, and a TM score of 37% from the native. The overlay between the top structure of ASTRO-FOLD 2.0 and the native does not fit well between these two structures due to the high RMSD and low GDT, TM scores. However, when compared with all submitted structures to the CASP9 organizers (including predictions by servers and human expert groups), the ranking of the top submitted structure by ASTRO-FOLD 2.0 is 6, 5, and 16 based on TM, GDT, and RMSD, respectively.
A closer analysis shows that for a segment of T581 (amino acids 70 to 128), its RMSD value is 3.9 Å, and its GDT score is 61%. Figure 3 shows the overlay of this segment with the corresponding native segment. The overall fit between the predicted segment and the native is much better than the whole protein. This indicates that ASTRO-FOLD 2.0 is able to predict parts of the protein very well even when the overall topology prediction is incorrect. In a number of cases, there are parts of crystallographic structures that are missing due to inconsistencies in experimental results. The role of ASTRO-FOLD in modeling small subsections accurately could be utilized for identification of these regions. This is particularly relevant for free modeling targets where we observe that most methods which depend on the sequence or structural database (for alignment, threading or fragment assembly) are unable to provide structures of very high quality.
Figure 3.
Native structure of T581 segment (70–128 amino acids) shown in gray. Top 1 model segment (70–128 amino acids) from ASTRO-FOLD 2.0 is colored in rainbow.
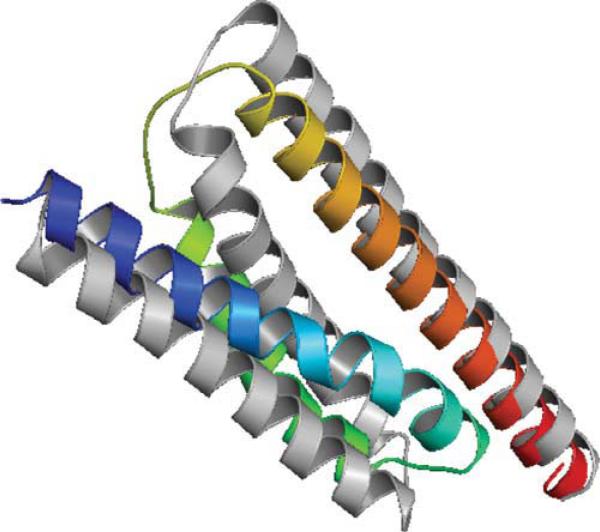
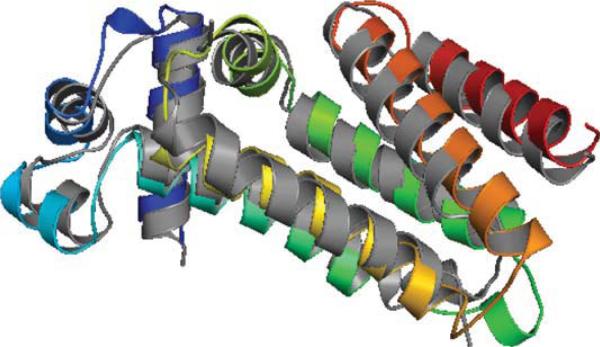
T602:3NKZ
Target T602 of CASP9 corresponds to protein 3NKZ. 3NKZ has four identical chains with three helices on each chain. T602 sequence has 123 amino acids while each chain of protein 3NKZ has only the first 97 amino acids available. Thus, the evaluations of secondary structure prediction, contact prediction, and tertiary structure prediction are based on the 97 amino acids only. The three helices of 3NKZA form a plane with helices 1 and 2 antiparallel, helices 2 and 3 antiparallel (see Figure 4).
Figure 4.
Native structure of T602 (3NKZA) shown in gray. Helix 1: amino acids 3–28; Helix 2: amino acids 35–56; Helix 3: amino acids 61–96. Top 1 model from ASTRO-FOLD 2.0 is colored in rainbow.
The secondary structure prediction resulted in four helices for T602 (123 amino acids), and they are: helix 1 from amino acid 4 to amino acid 30; helix 2 from amino acid 34 to amino acid 51; helix 3 from amino acid 63 to amino acid 96; helix 4 from amino acid 100 to amino acid 110. By excluding the amino acids beyond amino acid 97, the secondary structure prediction has a Q3 prediction accuracy 88.7%.
Contact prediction shows an average accuracy of 42.9% for amino acid pairs that are at least six apart in protein T602. The detailed list of predicted contacts for T602 is presented in Table 4.
Table 4.
Predicted Amino Acid Contacts for T602 of CASP9
| AA1 | AA2 | Distance | AA1 | AA2 | Distance |
|---|---|---|---|---|---|
| 17 | 39 | 10.64 | 17 | 36 | 14.14 |
| 20 | 36 | 9.97 | 18 | 36 | 14.55 |
| 20 | 39 | 7.09 | 18 | 39 | 12.19 |
| 24 | 37 | 8.65 | 25 | 41 | 14.80 |
| 24 | 41 | 11.55 | 27 | 41 | 15.11 |
| 25 | 37 | 11.63 | 43 | 66 | 22.92 |
| 27 | 37 | 9.95 | 43 | 67 | 19.89 |
| 44 | 71 | 11.11 | 43 | 71 | 14.66 |
| 47 | 71 | 10.13 | 44 | 66 | 19.46 |
| 44 | 67 | 16.60 | |||
| 47 | 66 | 17.80 | |||
| 47 | 67 | 14.44 |
Data are shown for amino acid pairs that are at least six amino acids apart. First three columns show the true predicted contacts whose distances fall between the predicted lower and upper distance bounds; whereas the last three columns show the false predicted contacts where the real distance falls outside the predicted distance range.
As can be seen from Table 4, there are five false and seven true predicted contacts between helices 1 and 2, while for helices 2 and 3, there are only two true contact predictions, and seven false predicted contacts. One thing to note from Figure 4 is the three helices of T602 are not compact, and it is an open structure.
The top submitted structure of ASTRO-FOLD 2.0 has a RMSD value of 2.18 Å from the native, a GDT score of 72% from the native, and a TM score of 57% from the native. ASTRO-FOLD 2.0 was able to predict the structure for T602 with 2.18 Å RMSD to the native. The overlay between the top 1 model and the native is shown in Figure 4. In this figure, native structure is presented in gray and top 1 model is colored in rainbow. As can be seen from Figure 4, the overall topology of the first submitted structure is the same as the native, which is also indicated by its above 70% GDT score to the native.
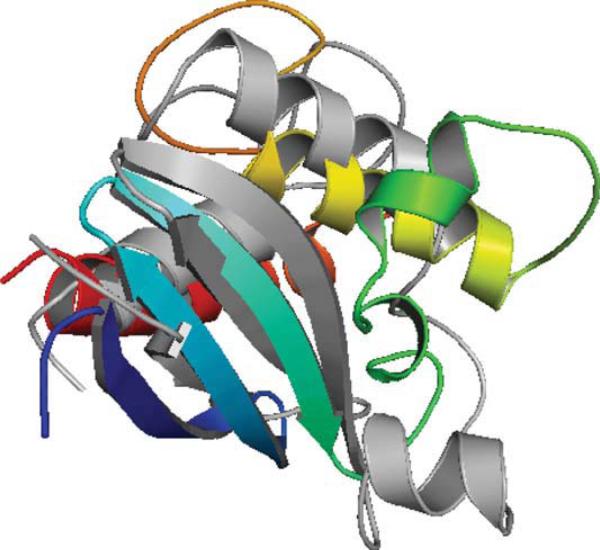
T562:2KZX
Target T562 has 123 amino acids and the corresponding PDB code is 2KZX. 2KZX is a NMR structure and has only 1 chain (A). 2KZXA is a mixed α/ β protein with three strands in the first 45 amino acids forming a beta sheet, and three helices in the rest part of protein. The three helices surround the beta sheet, see the gray structure in Figure 5.
Figure 5.
Native structure of T562 shown in gray. Top 1 model from ASTRO-FOLD 2.0 is colored in rainbow.
The secondary structure prediction has a Q3 prediction accuracy of 70%. The detailed secondary structure prediction, together with the native secondary structure information are listed in Table 5.
Table 5.
Predicted Secondary Structure Information for T562 by ASTRO-FOLD 2.0 and the Native Secondary Structure Information
| Helix (Predicted) | Helix (Native) | Strand (Predicted) | Strand (Native) |
|---|---|---|---|
| 47–53 | 5–10 | 5–9 | |
| 67–81 | 72–82 | 19–26 | 18–27 |
| 85–89 | 30–38 | 30–40 | |
| 107–121 | 108–117 | 56–61 |
As shown in the table, the second and third helices are correctly predicted, while the first helix is mispredicted. For the beta strand prediction, all the three native strands are correctly predicted.
Contact prediction for T562 has an accuracy of 35.7% for predicted contacts of amino acids that are at least six amino acids apart using predicted lower and upper distance bounds as distance cutoff. If 0 and 12 Å are used as lower and upper bounds, the prediction accuracy increases to 62%. A total of 98 contacts are predicted. The anti-parallel beta sheet topology is correctly predicted for T562, as can be seen from the true contacts of Table 6. Strand 1 (amino acids 5–9) and strand 2 (amino acids 18–27) interact in an antiparallel orientation, and the corresponding amino acids pairs from these two strands are predicted to form contacts. For example, amino acids 5 and 26 form a contact with a distance of 6.01 Å; amino acids 9 and 22 form a contact with a distance of 6.92 Å; As the beginning of strand 1 (amino acid 5) contacts with the end of strand 2 (amino acid 26), and the beginning of strand 2 (amino acid 22) contacts with the end of strand 1 (amino acid 9), these two strands form an antiparallel contact. A similar observation can be made to strands 2 and 3 as well.
Table 6.
Predicted Amino Acid Contacts for T562 of CASP9
| AA1 | AA2 | Distance | AA1 | AA2 | Distance | AA1 | AA2 | Distance |
|---|---|---|---|---|---|---|---|---|
| 5 | 26 | 6.01 | 6 | 26 | 7.83 | 30 | 61 | 37.83 |
| 6 | 25 | 6.63 | 7 | 25 | 8.71 | 31 | 60 | 33.43 |
| 7 | 24 | 6.09 | 8 | 24 | 9.01 | 32 | 59 | 32.82 |
| 9 | 22 | 6.92 | 9 | 23 | 8.94 | 33 | 58 | 26.50 |
| 10 | 21 | 6.06 | 10 | 22 | 9.02 | 34 | 57 | 23.27 |
| 5 | 25 | 4.67 | 8 | 23 | 6.90 | 35 | 56 | 17.39 |
| 6 | 24 | 5.05 | 7 | 26 | 10.91 | 32 | 61 | 33.67 |
| 8 | 22 | 5.80 | 8 | 25 | 12.17 | 33 | 60 | 29.69 |
| 10 | 20 | 5.46 | 9 | 24 | 11.86 | 34 | 59 | 25.70 |
| 19 | 38 | 5.17 | 10 | 23 | 11.92 | 35 | 58 | 19.69 |
| 22 | 35 | 6.49 | 7 | 23 | 4.23 | 36 | 57 | 16.69 |
| 23 | 34 | 5.62 | 9 | 21 | 4.26 | 37 | 56 | 12.41 |
| 24 | 33 | 6.36 | 8 | 26 | 14.14 | 30 | 60 | 36.98 |
| 25 | 32 | 6.15 | 9 | 25 | 15.03 | 31 | 59 | 32.81 |
| 25 | 31 | 5.95 | 10 | 24 | 14.72 | 32 | 58 | 30.23 |
| 21 | 37 | 5.34 | 20 | 37 | 6.51 | 33 | 57 | 26.30 |
| 22 | 36 | 5.80 | 21 | 36 | 6.80 | 34 | 56 | 21.16 |
| 23 | 35 | 5.00 | 19 | 37 | 8.68 | 33 | 61 | 29.95 |
| 24 | 34 | 4.59 | 20 | 36 | 8.05 | 34 | 60 | 26.21 |
| 25 | 33 | 4.84 | 21 | 35 | 8.80 | 35 | 59 | 22.36 |
| 26 | 32 | 5.68 | 22 | 34 | 7.40 | 36 | 58 | 16.36 |
| 24 | 31 | 7.01 | 23 | 33 | 8.59 | 37 | 57 | 13.99 |
| 21 | 38 | 5.01 | 24 | 32 | 8.32 | 38 | 56 | 10.97 |
| 22 | 37 | 6.28 | 20 | 38 | 4.39 | 75 | 113 | 13.02 |
| 23 | 36 | 6.41 | 19 | 36 | 11.21 | 79 | 113 | 12.17 |
| 24 | 35 | 6.51 | 20 | 35 | 11.11 | 80 | 107 | 14.50 |
| 25 | 34 | 5.44 | 21 | 34 | 10.75 | 80 | 111 | 12.01 |
| 26 | 33 | 6.74 | 22 | 33 | 10.97 | 80 | 113 | 15.00 |
| 75 | 110 | 7.92 | 23 | 32 | 11.45 | |||
| 75 | 111 | 9.48 | 31 | 61 | 34.16 | |||
| 78 | 107 | 10.74 | 32 | 60 | 33.35 | |||
| 78 | 110 | 10.87 | 33 | 59 | 29.16 | |||
| 78 | 111 | 10.65 | 34 | 58 | 23.20 | |||
| 79 | 107 | 10.87 | 35 | 57 | 19.57 | |||
| 79 | 110 | 9.19 | 36 | 56 | 14.88 |
Data are shown for amino acid pairs that are at least six amino acids apart. First three columns show the true predicted contacts whose distances fall between the predicted lower and upper distance bounds; whereas the last three columns show the false predicted contacts where the real distance falls outside the predicted distance range.
The 3-D structure prediction of ASTRO-FOLD 2.0 generates a top 1 model with a RMSD value of 10.8 Å, a TM score of 40.9%, and a GDT score of 34.8% from the native structure. The corresponding rankings of the top 1 model compared with all other human and server predictions are 19, 3, and 4, respectively. As shown from Figure 5, the overall topology of the prediction is fairly similar to the native but not close enough to generate RMSD values lower than 6 Å. This can be attributed to the inconsistencies in secondary structure prediction, which led to some incorrect contact predictions.
The segment analysis shows that for a segment of T562 (first 43 amino acids), the top 1 predicted model of ASTRO-FOLD 2.0 has a RMSD value of 4.9 Å with a GDT score of 54.7% and a TM score of 37.2%. The overlay structure between the segment of the top 1 model of ASTRO-FOLD 2.0 predictions and the corresponding segment of the native structure is displayed in Figure 6. As shown in this figure, the two structures are well fitted to each other. This segment is a three-strand-beta sheet structure. As described earlier, these three strands form antiparallel contacts with each other and the contact predictions between these three strands are correct. This is why ASTRO-FOLD 2.0 predicted this segment with a low RMSD value (below 5 Å), thus, reflecting the importance of the intermediate contact prediction algorithm in the larger picture of tertiary structure prediction.
Figure 6.
Native structure of T562 segment (first 43 amino acids) shown in gray. Top 1 model from ASTRO-FOLD 2.0 is colored in rainbow.
T580:3NBM
T580 has 105 amino acids, and it is a mixed α/ β protein with four strands and five helices. Its PDB code is 3NBM. 3NBM has only one chain (A). Only the first amino acid does not have coordinates in the PDB structure, thus, total 104 amino acids are used for evaluation. The four strands form one sheet in the center of the protein with all pairs parallel, and five helices lie on both sides of the sheet in an alternative fashion, see Figure 7. The four strands of T580 are: strand 1 from amino acids 4–10; strand 2 from amino acids 34–40; strand 3 from amino acids 53–56; and strand 4 from amino acids 77–80. The five helices are: helix 1 from amino acids 15–30; helix 2 from aminos acid 48–50; helix 3 from amino acids 64–71; helix 4 from amino acids 83–90; and helix 5 from amino acids 93–102.
Figure 7.
Native structure of T580 shown in gray. Top 1 model from ASTRO-FOLD 2.0 is colored in rainbow.
The contact prediction of T580 has an accuracy of 51.4% for amino acid pairs that are at least six amino acids apart. If lower and upper distance bounds are set to 0 and 12 Å, respectively, the contact prediction accuracy for T580 increases to 70.8%. The analysis of the predicted contacts (see Table 7) shows that the parallel sheet topology is correctly predicted.
Table 7.
Predicted Amino Acid Contacts for T580 of CASP9
| AA1 | AA2 | Distance | AA1 | AA2 | Distance |
|---|---|---|---|---|---|
| 5 | 34 | 6.04 | 6 | 34 | 7.38 |
| 6 | 35 | 6.08 | 7 | 35 | 8.57 |
| 7 | 36 | 5.62 | 8 | 36 | 7.12 |
| 8 | 37 | 6.15 | 9 | 37 | 8.63 |
| 4 | 34 | 4.59 | 7 | 34 | 10.81 |
| 5 | 35 | 5.25 | 8 | 35 | 10.75 |
| 7 | 37 | 4.89 | 9 | 36 | 10.60 |
| 6 | 53 | 4.88 | 10 | 37 | 11.35 |
| 7 | 54 | 4.78 | 8 | 34 | 12.90 |
| 8 | 55 | 4.73 | 9 | 35 | 14.24 |
| 9 | 56 | 5.13 | 10 | 36 | 13.47 |
| 7 | 53 | 6.46 | 6 | 36 | 4.46 |
| 8 | 54 | 5.80 | 53 | 79 | 7.70 |
| 9 | 55 | 6.30 | 54 | 80 | 8.60 |
| 10 | 56 | 6.40 | 55 | 81 | 7.40 |
| 5 | 53 | 6.60 | 53 | 80 | 10.90 |
| 6 | 54 | 5.75 | 54 | 81 | 10.94 |
| 7 | 55 | 6.25 | 19 | 47 | 18.84 |
| 8 | 56 | 5.97 | 23 | 45 | 22.44 |
| 8 | 53 | 8.54 | 23 | 47 | 19.54 |
| 9 | 54 | 7.38 | 23 | 48 | 18.17 |
| 10 | 55 | 8.93 | 29 | 45 | 31.16 |
| 4 | 53 | 7.96 | 29 | 48 | 26.37 |
| 5 | 54 | 8.68 | 60 | 99 | 18.25 |
| 6 | 55 | 7.49 | 63 | 97 | 23.39 |
| 7 | 56 | 8.59 | 63 | 99 | 20.18 |
| 53 | 78 | 5.80 | 63 | 101 | 22.33 |
| 54 | 79 | 6.41 | 64 | 99 | 17.57 |
| 55 | 80 | 5.86 | 64 | 100 | 16.96 |
| 56 | 81 | 6.11 | 67 | 97 | 22.31 |
| 53 | 77 | 4.64 | 67 | 100 | 17.75 |
| 54 | 78 | 4.94 | 67 | 101 | 20.00 |
| 55 | 79 | 4.93 | 69 | 97 | 25.58 |
| 56 | 80 | 4.73 | 69 | 100 | 20.61 |
| 54 | 77 | 6.32 | 69 | 101 | 22.10 |
| 55 | 78 | 5.98 | |||
| 56 | 79 | 6.23 |
Data are shown for amino acid pairs that are at least six amino acids apart. First three columns show the true predicted contacts whose distances fall between the predicted lower and upper distance bounds; whereas the last three columns show the false predicted contacts where the real distance falls outside the predicted distance range.
The top 1 prediction of ASTRO-FOLD 2.0 agrees well with the native structure, see Figure 7. This prediction has a RMSD value of 1.37 Å, a TM score of 91%, and a GDT score of 88%. The overall rankings of this structure compared with other methods are 2 according to GDT score, 3 according to TM score, and 3 according to RMSD score.
T596:3NI7
T596 is a pure α protein with 213 amino acids, and its PDB code is 3NI7. Protein 3NI7 has two chains and out of which, only one chain is sequence-unique. 3NI7A has amino acids 6 to 188 in its PDB structure, thus, only 183 amino acids are used for evaluation of structure prediction, secondary structure prediction, and contact prediction. See Figure 8 for the native structure of T596.
Figure 8.
Native structure of T596 (3NI7A) shown in gray (Only amino acids 6–188 are shown). The best models from ASTRO-FOLD 2.0 is colored in rainbow.
The secondary structure prediction of T596 has a Q3 accuracy of 82.7%. The predicted secondary structure of T596 is shown in Table 8. The two small 3–10 helices are not predicted, and helices 6 and 7 are predicted as one helix (helix 5 of the prediction result). All other helices are correctly predicted and a high prediction accuracy indicates the overall secondary structure prediction for T596 is successful.
Table 8.
Predicted Secondary Structure Information for T596 by ASTRO-FOLD 2.0 and the Native Secondary Structure Information
| Helix (Predicted) | Helix (Native) |
|---|---|
| 7–22 | 7–22 |
| 25–37 | 30–36 |
| 41–48 | 41–47 |
| 51–70 | 51–69 |
| 75–77 | |
| 78–109 | 80–96 |
| 99–108 | |
| 119–137 | 115–135 |
| 140–164 | 149–164 |
| 169–171 | |
| 172–188 | 172–187 |
Helixes 5 and 10 of the native structure are 3–10 helices.
The high secondary structure prediction accuracy in part contributes to the high-contact prediction accuracy (60.5%). This contact accuracy is for amino acid pairs that are at least six amino acids apart. The detailed true and false contact predictions are listed in Table 9.
Table 9.
Predicted Amino Acid Contacts for T596 of CASP9
| AA1 | AA2 | Distance | AA1 | AA2 | Distance |
|---|---|---|---|---|---|
| 17 | 25 | 7.79 | 67 | 92 | 13.12 |
| 17 | 28 | 8.70 | 59 | 123 | 12.97 |
| 17 | 30 | 11.49 | 95 | 125 | 14.97 |
| 19 | 25 | 7.80 | 97 | 125 | 20.35 |
| 19 | 30 | 10.46 | 101 | 119 | 20.96 |
| 19 | 31 | 11.58 | 101 | 122 | 20.07 |
| 31 | 41 | 5.39 | 101 | 125 | 19.08 |
| 31 | 44 | 8.13 | 105 | 119 | 15.16 |
| 33 | 41 | 8.12 | 105 | 122 | 15.08 |
| 33 | 44 | 7.83 | 105 | 123 | 17.04 |
| 37 | 44 | 9.46 | 106 | 119 | 13.13 |
| 66 | 88 | 7.60 | 106 | 123 | 14.94 |
| 66 | 89 | 8.61 | 107 | 122 | 14.78 |
| 66 | 92 | 9.41 | 131 | 147 | 13.17 |
| 67 | 87 | 8.35 | 164 | 177 | 12.76 |
| 67 | 88 | 10.90 | |||
| 129 | 147 | 11.08 | |||
| 132 | 147 | 11.36 | |||
| 155 | 178 | 7.52 | |||
| 157 | 178 | 10.57 | |||
| 158 | 177 | 9.60 | |||
| 160 | 177 | 10.46 | |||
| 161 | 178 | 11.59 |
Data are shown for amino acid pairs that are at least six amino acids apart. First three columns show the true predicted contacts whose distances fall between the predicted lower and upper distance bounds; where the last three columns show the false predicted contacts where the real distance falls outside the predicted distance range.
The best tertiary structure of the ASTRO-FOLD 2.0 predictions has a GDT score of 66%, a TM score of 72%, and a RMSD value of 3.3 Å to the native. The overlay between the best model of ASTRO-FOLD 2.0, and the native is displayed in Figure 8. The overall topology as well as the local structures are well fitted to each other. The rankings compared with the best model from other methods of CASP9 are 5, 7, and 7 according to GDT, TM, and RMSD scores, respectively.
Conclusions
This article presented several novel components of ASTRO-FOLD 2.0. A new secondary structure prediction algorithm, based on a MILP approach was introduced. The locations of predicted β strands was used in a new integer linear formulation for the prediction of the number of β sheets and the arrangement of β strands in all sheets. A MILP-based contact prediction model was then introduced, which uses secondary structure and sheet topology information to derive lower and upper bounds on distances between pairs of amino acids. Separately, tight dihedral angle bounds on regions between secondary structures (known as random-coil or loop regions) were derived using an iterative approach based on database sampling, constrained nonlinear optimization, and dihedral angle clustering. All of the aforementioned constraints were introduced into the final three dimensional structure prediction algorithm, which combines deterministic global optimization (αBB), stochastic conformational space annealing (CSA), and torsion angle dynamics (TAD). Predicted structures were clustered using a novel traveling salesman problem based iterative clustering algorithm, ICON. The selected structures from the clustering procedure were used to derive improved structures using chemical shift data. These improved structures were used to derive improved dihedral angle and distance bounds, which were used to run a second iteration of the tertiary structure prediction algorithm. All of the novel components of ASTRO-FOLD 2.0 were integrated into the existing ASTRO-FOLD framework. The performance of the improved ASTRO-FOLD 2.0 framework was demonstrated for a number of blind targets from the recently concluded CASP9 community-wide experiment.
Acknowledgments
CAF gratefully acknowledges financial support from the National Science Foundation, National Institutes of Health (R01 GM52032; R24 GM069736), and U.S. Environmental Protection Agency EPA (GAD R 832721-010). Although the research described in the article has been funded in part by the U.S. Environmental Protection Agency's STAR program through grant (R 832721-010), it has not been subjected to any EPA review and does not necessarily reflect the views of the Agency, and no official endorsement should be inferred.
Literature Cited
- 1.Anfinsen CB, Haber E, Sela M, White FH. The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain. Proc Natl Acad Sci USA. 1961;47:1309–1314. doi: 10.1073/pnas.47.9.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucl Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang Y. Progress and challenges in protein structure prediction. Curr Opin Struct Biol. 2008;18:342–348. doi: 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Floudas CA, Fung HK, McAllister SR, Mönnigmann M, Rajgaria R. Advances in protein structure prediction and de novo protein design: a review. Chem Eng Sci. 2006;61:966–988. [Google Scholar]
- 5.Floudas CA. Computational methods in protein structure prediction. Biotechnol Bioeng. 2007;97:207–213. doi: 10.1002/bit.21411. [DOI] [PubMed] [Google Scholar]
- 6.Altschul SF, Madden TL, Schäffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped Blast and PSI-BLAST: a new generation of protein database search programs. Nucl Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eswar N, Marti-Renom MA, Webb B, Madhusudhan MS, Shen M, Pieper U, Sali A. Comparative protein structure modeling using Modeller. Curr Protoc Bioinformatics. 2006 doi: 10.1002/0471250953.bi0506s15. Chapter 5:Unit 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Krivov GG, Shapovalov MV, Dunbrack RL. Improved prediction of protein side-chain conformations with SCWRL4. Proteins. 2009;77:778–795. doi: 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moult J, Fidelis K, Zemla A, Hubbard T. Critical assessment of methods of protein structure prediction CASP-round 4. Proteins. 2001;S5:2–7. [PubMed] [Google Scholar]
- 10.Lipkowitz KB, Cundari TR, Boyd DB. Reviews in Computational Chemistry. Wiley-VCH; New York: 2007. [Google Scholar]
- 11.Zhang Y, Skolnick J. The protein structure prediction problem could be solved using the current PDB library. Proc Natl Acad Sci USA. 2005;102:1029–1034. doi: 10.1073/pnas.0407152101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jones DT. GenTHREADER: an efficient and reliable protein fold recognition method for genomic sequences. J Mol Biol. 1999;287:797–815. doi: 10.1006/jmbi.1999.2583. [DOI] [PubMed] [Google Scholar]
- 13.Skolnick J, Zhang Y, Arakaki AK, Kolinsi A, Boniecki M, Szilágyi A, Kihara D. TOUCHSTONE: a unified approach to protein structure prediction. Proteins. 2003;53:469–479. doi: 10.1002/prot.10551. [DOI] [PubMed] [Google Scholar]
- 14.Roy A, Kucukural A, Zhang Y. I-TASSER: a unified platform for automated protein structure and function prediction. Nat Protoc. 2010;5:725–738. doi: 10.1038/nprot.2010.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Raman S, Qian B, Baker D, Walker RC. Advances in Rosetta protein structure prediction on massively parallel systems. IBM J Res Dev. 2008;52:7–18. [Google Scholar]
- 16.Simons KT, Kooperberg C, Huang E, Baker D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J Mol Biol. 1997;268:209–225. doi: 10.1006/jmbi.1997.0959. [DOI] [PubMed] [Google Scholar]
- 17.Rohl CA, Strauss CEM, Chivian D, Baker D. Modeling structurally variable regions in homologous proteins with Rosetta. Proteins. 2004;55:656–677. doi: 10.1002/prot.10629. [DOI] [PubMed] [Google Scholar]
- 18.Pandit SB, Zhou H, Skolnick J. Introduction to Protein Structure Prediction: Methods and Algorithms. wiley; Hoboken, New Jersey: 2010. pp. 219–242. chapter 10. [Google Scholar]
- 19.Maisuradze GG, Liwo A, Scheraga HA. Relation between free energy landscapes of protein and dynamics. J Chem Theory Comput. 2010a;6:583–595. doi: 10.1021/ct9005745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ozkan SB, Wu GA, Chodera JD, Dill KA. Protein folding by zipping and assembly. Proc Natl Acad Sci USA. 2007;104:11987–11992. doi: 10.1073/pnas.0703700104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Srinivasan R, Rose GD. LINUS: a hierarchic procedure to predict the fold of a protein. Proteins. 1995;22:81–89. doi: 10.1002/prot.340220202. [DOI] [PubMed] [Google Scholar]
- 22.Srinivasan R, Rose GD. Ab initio prediction of protein structure using LINUS. Proteins. 2002;47:489–495. doi: 10.1002/prot.10103. [DOI] [PubMed] [Google Scholar]
- 23.Zagrovic B, Snow CD, Shirts MR, Pande VS. Simulation of folding of a small alpha-helical protein in atomistic detail using worldwide-distributed computing. J Mol Biol. 2002;323:927–937. doi: 10.1016/s0022-2836(02)00997-x. [DOI] [PubMed] [Google Scholar]
- 24.Liwo A, Arlukowicz P, Czaplewski C, Oldziej S, Pillardy J, Scheraga HA. A method for optimizing potential-energy functions by hierarchical design of the potential-energy landscape. Proc Natl Acad Sci USA. 2002;99:1937–1942. doi: 10.1073/pnas.032675399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liwo A, Oldziej S, Pincus MR, Wawak RJ, Rackovsky S, Scheraga HA. A united-residue force field for off-lattice protein-structure simulations. I. Functional forms and parameters of long-range side-chain interaction potentials from protein crystal data. J Comput Chem. 1997;18:849–873. [Google Scholar]
- 26.Maisuradze GG, Senet P, Czaplewski C, Liwo A, Scheraga HA. Investigation of protein folding by coarse-grained molecular dynamics with the UNRES force field. J Phys Chem A. 2010;114:4471–4485. doi: 10.1021/jp9117776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lee J, Scheraga HA, Rackovsky S. New optimization method for conformational energy calculations on polypeptides: conformational space annealing. J Comput Chem. 1997;18:1222–1232. [Google Scholar]
- 28.Skwierawska A, Rodziewicz-Motowidlo S, Oldziej S, Liwo A, Scheraga HA. Conformational studies of the α-helical 28–43 fragment of the B3 domain of the immunoglobulin binding protein G from Streptococcus. Biopolymers. 2008;89:1032–1044. doi: 10.1002/bip.21056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lewandowska A, Oldziej S, Liwo A, Scheraga HA. β-Hairpin forming peptides: models of early stages of protein folding. Biophys Chem. 2010;151:1–9. doi: 10.1016/j.bpc.2010.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, Wriggers W. Atomic-level characterization of the structural dynamics of proteins. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- 31.Klepeis JL, Floudas CA. ASTRO-FOLD: A combinatorial and global optimization framework for ab initio prediction of three-dimensional structures of proteins from the amino acid sequence. Biophys J. 2003c;85:2119–2146. doi: 10.1016/s0006-3495(03)74640-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Klepeis JL, Floudas CA. A comparative study of global minimum energy conformations of hydrated peptides. J Comput Chem. 1999;20:636–654. [Google Scholar]
- 33.Klepeis JL, Floudas CA, Morikis D, Lambris JD. Predicting peptide structures using NMR data and deterministic global optimization. J Comput Chem. 1999;20:1354–1370. [Google Scholar]
- 34.Klepeis JL, Floudas CA. Ab initio prediction of helical segments of polypeptides. J Comput Chem. 2002;23:246–266. doi: 10.1002/jcc.10002. [DOI] [PubMed] [Google Scholar]
- 35.Klepeis JL, Floudas CA. Prediction of beta-sheet topology and disulfide bridges in polypeptides. J Comput Chem. 2003;24:191–208. doi: 10.1002/jcc.10167. [DOI] [PubMed] [Google Scholar]
- 36.Klepeis JL, Floudas CA. Ab initio tertiary structure prediction of protiens. J Glob Opt. 2003;25:113–140. [Google Scholar]
- 37.McAllister SR, Floudas CA. Enhanced bounding techniques to reduce the protein conformational search space. Optim Meth Soft. 2009;24:837–855. doi: 10.1080/10556780902753486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McAllister SR, Floudas CA. An improved hybrid global optimization method for protein tertiary structure prediction. Comput Optim Appl. 2010;45:377–413. doi: 10.1007/s10589-009-9277-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Némethy G, Gibson KD, Palmer KA, Yoon CN, Paterlini G, Zagari A, Rumsey S, Scheraga HA. Energy parameters in polypeptides. X. Improved geometrical parameters and nonbonded interactions for use in the ECEPP/3 algorithm, with application to proline-containing peptides. J Phys Chem. 1992;96:6472–6484. [Google Scholar]
- 40.Adjiman CS, Androulakis IP, Maranas CD, Floudas CA. A global optimization method, αBB, for process design. Comput Chem Eng. 1996;20:S419–S424. [Google Scholar]
- 41.Adjiman CS, Androulakis IP, Floudas CA. Global optimization of MINLP problems in process synthesis and design. Comput Chem Eng. 1997;21:S445–S450. [Google Scholar]
- 42.Cheng J, Randall AZ, Sweredoski MJ, Baldi P. SCRATCH: a protein structure and structural feature prediction server. Nucl Acids Res. 2005;33:72–76. doi: 10.1093/nar/gki396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.King RD, Sternberg M. Identification and application of the concepts important for accurate and reliable protein secondary structure prediction. Protein Sci. 1996;5:2298–2310. doi: 10.1002/pro.5560051116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ouali M, King RD. Cascaded multiple classifiers for secondary structure prediction. Protein Sci. 2000;9:1162–1176. doi: 10.1110/ps.9.6.1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rost B, Yachdav G, Liu J. The predictProtein Server. Nucl Acids Res. 2004;32:W321–W326. doi: 10.1093/nar/gkh377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. J Mol Biol. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- 47.Frishman D, Argos P. Incorporation of non-local interactions in protein secondary structure prediction from the amino acid sequence. Protein Eng. 1996;9:133–142. doi: 10.1093/protein/9.2.133. [DOI] [PubMed] [Google Scholar]
- 48.Garnier J, Gibrat JF, Robson B. GOR method for predicting protein secondary structure from amino acid sequence. Method Enzymol. 1996;266:540–53. doi: 10.1016/s0076-6879(96)66034-0. [DOI] [PubMed] [Google Scholar]
- 49.noz VM, Thompson PA, Hofrichter J, Eaton WA. Folding dynamics and mechanism of β-hairpin formation. Nature. 1997;390:196–199. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- 50.Bryant Z, Pande VS, Rokhsar DS. Mechanical unfolding of a β-hairpin using molecular dynamics. Biophys J. 2000;78:584–589. doi: 10.1016/S0006-3495(00)76618-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dinner AR, Lazaridis T, Karplus M. Understanding β-hairpin formation. Proc Nat Acad Sci USA. 1999;96:9068–9073. doi: 10.1073/pnas.96.16.9068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pande VS, Rokhsar DS. Molecular dynamics simulations of unfolding and refolding of a β-hairpin fragment of protein g. Proc Natl Acad Sci USA. 1999;96:9062–9067. doi: 10.1073/pnas.96.16.9062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cheng J, Baldi P. Three-stage prediction of protein beta-sheets by neural networks, alignments and graph algorithms. Bioinformatics. 2005;21:75–84. doi: 10.1093/bioinformatics/bti1004. [DOI] [PubMed] [Google Scholar]
- 54.Przytycka T, Srinivasan R, Rose GD. Recursive domains in proteins. Protein Sci. 2002;11:409–417. doi: 10.1110/ps.24701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Fokas AS, Papatheodorou TS, Kister AE, Gelfand IM. A geometric construction determines all permissible strand arrangements of sandwich proteins. Proc Natl Acad Sci USA. 2005;102:15851–15853. doi: 10.1073/pnas.0507335102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kister AE, Fokas AS, Papatheodorou TS, Gelfand IM. Strict rules determine arrangements of strands in sandwich proteins. Proc Natl Acad Sci USA. 2006;103:4107–4110. doi: 10.1073/pnas.0510747103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Papatheodorou TS, Fokas AS. Systematic construction and prediction of the arrangements of the strands of sandwich proteins. J Royal Soc Interface. 2009;6:63–73. doi: 10.1098/rsif.2008.0192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Floudas CA. Nonlinear and Mixed-Integer Optimization. Oxford University Press; New York: 1995. [Google Scholar]
- 59.Rajgaria R, McAllister SR, Floudas CA. Towards accurate residue-residue hydrophobic contact prediction for alpha helical proteins via integer linear optimization. Proteins. 2009;74:929–947. doi: 10.1002/prot.22202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rajgaria R, Wei Y, Floudas C. Contact prediction for beta and alpha-beta proteins using integer linear optimization and its impact on the first principles 3D structure prediction method ASTRO-FOLD. Protein Struct Funct Gen. 2010;78:1825–1846. doi: 10.1002/prot.22696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Cornette JL, Cease KB, Margalit H, Spouge JL, Berzofsky JA, DeList C. Hydrophobicity scales and computational techniques for detecting amphipathic structures in proteins. J Mol Biol. 1987;195:659–685. doi: 10.1016/0022-2836(87)90189-6. [DOI] [PubMed] [Google Scholar]
- 62.de Bakker PIW, DePristo MA, Burke DF, Blundell TL. Ab initio construction of polypeptide fragments: accuracy of loop decoy discrimination by all-atom statistical potential and the AMBER force field with the generalized born solvation model. Proteins. 2003;51:21–40. doi: 10.1002/prot.10235. [DOI] [PubMed] [Google Scholar]
- 63.Jacobson MP, Pincus DL, Rapp CS, Day TJF, Honig B, Shaw DE, Friesner RA. A hierarchical approach to all-atom protein loop prediction. Proteins. 2004;55:351–367. doi: 10.1002/prot.10613. [DOI] [PubMed] [Google Scholar]
- 64.Mönnigmann M, Floudas CA. Protein loop structure prediction with flexible stem geometries. Proteins. 2005;61:748–762. doi: 10.1002/prot.20669. [DOI] [PubMed] [Google Scholar]
- 65.Dunbrack RL. Rotamer libraries in the 21st century. Curr Opin Struct Biol. 2002;12:431–440. doi: 10.1016/s0959-440x(02)00344-5. [DOI] [PubMed] [Google Scholar]
- 66.Lovell SC, Word JM, Richardson JS, Richardson DC. The penultimate rotamer library. Proteins. 2000;40:389–408. [PubMed] [Google Scholar]
- 67.Xiang Z, Honig B. Extending the accuracy limits of prediction for side-chain conformations. J Mol Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
- 68.Desmet J, Spriet J, Lasters I. Fast and accurate side-chain topology and energy refinement as a new method for protein structure optimization. Proteins. 2002;48:31–43. doi: 10.1002/prot.10131. [DOI] [PubMed] [Google Scholar]
- 69.Subramani A, DiMaggio PA, Floudas CA. Selecting high quality structures from diverse conformational ensembles. Biophys J. 2009;97:1728–1736. doi: 10.1016/j.bpj.2009.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Cornell W, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the stimulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 71.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, III, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 72.Momany FA, McGuire RF, Burgess AW, Scheraga HA. Energy parameters in polypeptides. VII. Geometric parameters, partial atomic charges, nonbonded interactions, hydrogen bond interactions, and intrinsic torsional potentials for the naturally occuring amino acids. J Phys Chem. 1975;79:2361–2381. [Google Scholar]
- 73.Arnautova YA, Jagielska A, Scheraga HA. A new force field (ECEPP-05) for peptides, proteins and organic molecules. J Phys Chem B. 2006;110:5025–5044. doi: 10.1021/jp054994x. [DOI] [PubMed] [Google Scholar]
- 74.Adjiman CS, Androulakis IP, Floudas CA. A global optimization method for general twice-differentiable NLPs. II. Implementation and computational results. Comput Chem Eng. 1998a;22:1159–1179. [Google Scholar]
- 75.Adjiman CS, Dallwig S, Floudas CA, Neumaier A. A global optimization method for general twice-differentiable NLPs. I. Theoretical advances. Comput Chem Eng. 1998b;22:1137–1158. [Google Scholar]
- 76.Androulakis IP, Maranas CD, Floudas CA. αBB: a global optimization method for general constrained nonconvex problems. J Glob Opt. 1995;7:337–363. [Google Scholar]
- 77.Floudas CA. Deterministic Global Optimization: Theory, Methods and Applications. Kluwer Academic; Dordrechtl: 2000. [Google Scholar]
- 78.Crippen GM, Havel TF. Distance Geometry and Molecular Conformation. Wiley; New York: 1988. [Google Scholar]
- 79.Moré JJ, Wu Z. Distance geometry optimization for protein structures. J Glob Opt. 1999;15:219–234. [Google Scholar]
- 80.Güntert P, Wüthrich K. Improved efficiency of protein structure calculations from NMR data using the program DYANA with redundant dihedral angle constraints. J Biomol NMR. 1991;1:447–456. doi: 10.1007/BF02192866. [DOI] [PubMed] [Google Scholar]
- 81.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Clarendon Press; Oxford: 1987. [Google Scholar]
- 82.Güntert P. Structure calculation of biological macromolecules from NMR data. Q Rev Biophys. 1998;31:145–237. doi: 10.1017/s0033583598003436. [DOI] [PubMed] [Google Scholar]
- 83.Güntert P, Mumenthaler C, Wüthrich K. Torsion angle dynamics for NMR structure calculation with the new program DYANA. J Mol Biol. 1997;273:283–298. doi: 10.1006/jmbi.1997.1284. [DOI] [PubMed] [Google Scholar]
- 84.Lee J, Scheraga HA. Conformational space annealing by parallel computations: Extensive conformational search of met-enkephalin and the 20-residue membrane-bound portion of melittin. Int J Quantum Chem. 1999;75:255–265. [Google Scholar]
- 85.Czaplewski C, Liwo A, Pillardy J, Oldziej S, Scheraga HA. Improved conformational space annealing method to treat beta-structure with UNRES force-field and to enhance scalability of parallel implementation. Polymer. 2004;45:677–686. [Google Scholar]
- 86.Rajgaria R, McAllister SR, Floudas CA. A novel high resolution C-alpha C-alpha distance dependent force field based on a high quality decoy set. Proteins. 2006;65:726–741. doi: 10.1002/prot.21149. [DOI] [PubMed] [Google Scholar]
- 87.Rajgaria R, McAllister SR, Floudas CA. Distance dependent centroid to centroid force fields using high resolution decoys. Proteins. 2007;70:950–970. doi: 10.1002/prot.21561. [DOI] [PubMed] [Google Scholar]
- 88.Qiu J, Elber R. Atomically detailed potentials to recognize native and approximate protein structures. Proteins. 2005;61:44–55. doi: 10.1002/prot.20585. [DOI] [PubMed] [Google Scholar]
- 89.DiMaggio PA, Subramani A, Judson RS, Floudas CA. A novel framework for predicting in vivo toxicities from in vitro data using optimal methods for dense and sparse matrix reordering and logistic regression. Toxicol Sci. 2010;118:251–265. doi: 10.1093/toxsci/kfq233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.DiMaggio PA, McAllister SR, Floudas CA, Fend XJ, Rabinowitz JD, Rabitz HA. Biclustering via optimal re-ordering of data matrices in systems biology: rigorous methods and comparative studies. BMC Bioinformatics. 2008;97:207–213. doi: 10.1186/1471-2105-9-458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Applegate D, Bixby R, Chvatal V, Cook W. The Traveling Salesman Problem: A Computational Study. Princeton University Press; Princeton, NJ: 2007. [Google Scholar]
- 92.Shen Y, Bax A. Protein backbone chemical shifts predicted from searching a database for torsion angle and sequence homology. J Biomol NMR. 2007;38:289–302. doi: 10.1007/s10858-007-9166-6. [DOI] [PubMed] [Google Scholar]
- 93.Wishart DS, Arndt D, Berjanskii M, Tang P, Zhou J, Lin G. CS23D: a web server for rapid protein structure generation using NMR chemical shifts and sequence data. Nucl Acids Res. 2008;36:W496–W502. doi: 10.1093/nar/gkn305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Shen Y, Vernon R, Baker D, Bax A. De nono protein structure generation from incomplete chemical shift assignments. J Biomol NMR. 2009;43:63–78. doi: 10.1007/s10858-008-9288-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Meiler J, Baker D. Rapid protein fold determination using unassigned NMR data. Proc Natl Acad Sci USA. 2003;100:1540415409. doi: 10.1073/pnas.2434121100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Shen Y, Lange O, Delaglio F, Rossi P, Aramini JM, Liu G, Eletsky A, Wu Y, Singarapu KK, Lemak A, Ignatchenko A, Arrowsmith CH, Szyperski T, Montelione GT, Baker D, Bax A. Consistent blind protein structure generation from NMR chemical shift data. Proc Natl Acad Sci USA. 2008;105:4685–4690. doi: 10.1073/pnas.0800256105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Neal S, Nip AM, Zhang H, Wishart DS. Rapid and accurate calculation of protein 1H, 13C and 15N chemical shifts. J Biomol NMR. 2003;26:215–240. doi: 10.1023/a:1023812930288. [DOI] [PubMed] [Google Scholar]
- 98.Cornilescu G, Delaglio F, Bax A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J Biomol NMR. 1999;13:289–302. doi: 10.1023/a:1008392405740. [DOI] [PubMed] [Google Scholar]
- 99.Li W, Zhang Y, Kihara D, Huang YJ, Zheng D, Montelione GT, Kolinski A, Skolnick J. TOUCHSTONEX: protein structure prediction with sparse NMR data. Proteins. 2003;53:290–306. doi: 10.1002/prot.10499. [DOI] [PubMed] [Google Scholar]