Predicting mortality and length-of-stay for neonatal admissions to private hospital neonatal intensive care units: a Southern African retrospective study

Abstract

Objectives

To predict neonatal mortality and length of stay (LOS) from readily available perinatal data for neonatal intensive care unit (NICU) admissions in Southern African private hospitals.

Methods

Retrospective observational study using perinatal data from a large multicentre sample. Fifteen participating NICU centres in the Medi-Clinic private hospital group in Southern Africa. We used 2376 infants born between 1 January – 31 December 2008 to build the regression models, and a further 1 578 infants born between 1 January – 31 December 2007 to test the models. Outcome measures were mortality and length of hospital stay for NICU admissions.

Results

Of the infants included in the 2008 dataset, ninety-one (3.8%) died after being admitted to NICU centres. The median LOS for non-transferred survivors was 11 days. An analysis of the structural peculiarities of the data showed high correlations between groups of the perinatal variables pertaining to the size and Apgar scores of the newborn infants, respectively. The logistic regression model to predict neonatal mortality had a good fit (AUC: 0.8507, misclassification rate: 13.6%), but the low positive predictive value of this model reduces its usefulness. The poisson log-linear model to predict LOS had a good fit (predicted R²: 0.7027).

Conclusions

Apgar score at one minute, birth weight, and delivery mode significantly influence the odds of neonatal death and are associated with significant effects on LOS.

Introduction

In neonatology, early prediction of neonatal mortality and length of hospital stay may help in decision making^1,2. It is of interest to health care providers and hospital administrators for both economic and organisational reasons. Previous studies^2,3 have shown that there is a close relationship between cost of neonatal care and length of stay (LOS).

Parents also have a strong interest in knowing the anticipated date of discharge of their preterm neonate. Although other authors² have cautioned against the making of predictions about LOS based on perinatal variables alone, the physician caring for the newborn needs to answer questions regarding neonatal LOS shortly after the baby's birth in order to counsel parents⁴.

Furthermore, good predictions of LOS can provide a benchmark for measuring and comparing quality of care between different neonatal units¹. This in turn, can stimulate quality improvement initiatives in neonatal care², as part of an increasing emphasis on quality control in modern medicine.

Although similar studies have been done in the past, hospital policies and clinical practice probably differ enough between hospitals and countries to make a study of the South African experience relevant³. It should be of interest to compare variables influencing neonatal mortality and LOS in South Africa and Namibia with previous findings.

The purpose of this retrospective observational study was to determine models for predicting neonatal mortality and LOS for NICU admissions within the Southern African private hospital setting. Data that are readily available and easily measureable upon the date of admission were used for these purposes. As mortality and length of stay are two separate issues², they were addressed and modelled separately.

Methods

The Vermont Oxford Network (VON) is a non-profit initiative with the purpose of improving the quality and safety of medical care for newborn infants⁵. This is done through research on data collected at over 800 neonatal intensive care unit (NICU) centres around the world, including 34 centres in Southern Africa.

According to the VON database entrance criteria, any infant with a birth weight of between 401 and 1 500 grams, or whose gestational age was between 22 weeks 0 days and 29 weeks 6 days is eligible for entry into the VON database, regardless of where in the hospital the infant receives care. Furthermore, any infant with a birth weight of over 1500 grams, who was admitted to a NICU within the first 28 days of life without first having gone home, is eligible for inclusion. A NICU is defined as any location within the hospital where newborn infants receive continuous positive airway pressure (CPAP) or intermittent mandatory ventilation (IMV)⁵.

A training data set consisting of the VON data on 2 376 infants born between 1 January and 31 December 2008 and admitted to one of fifteen participating NICU centres in the Medi-Clinic private hospital group was used for the analyses and construction of the regression models. The case volumes ranged from 49 infants at the smallest to 297 infants at the largest centre.

To account for possible demographic differences, as well as differences in clinical practice between regions, the centres were divided into four regions named South West, Central, North, and Namibia.

In order to construct the regression models, only perinatal input variables which under normal circumstances are readily available upon admission to a NICU were used, namely: the continuous measures were Apgar scores at one and five minutes after birth, temperature measured within one hour after birth, birth weight, gestational age and birth head circumference. Because the numerical variables were not normally distributed, Spearman's rank-order method^6,7 was used to determine correlations between these variables.

The nominal variables were delivery mode, gender, maternal ethnicity, and hospital region. The response variables were survival to hospital discharge and total hospital length of stay in days. The mortality response variable was coded as a one if the infant died during hospital stay (including delivery room deaths), and as a zero if the infant survived until discharge.

A total of 2 307 cases (neonates born in 2008, excluding transfers and cases with incomplete data) were used in the exploratory analysis. Univariate analyses were performed to gauge the effects of each of the predictor variables on the response variables of interest. For mortality, univariate generalised linear models, using a logit link function, were constructed for each of the predictor variables. The area under the curve (AUC) was calculated for each of these models, indicating the usefulness of each of the variables in predicting neonatal mortality.

In a similar way, univariate generalised linear models, with a log link function, were used to test the effect of each of the predictor variables on LOS. The coefficient of determination (R²) was used to determine the usefulness of each of the variables in predicting LOS.

It is well known that highly correlated variables in multiple linear regression models give rise to the problem of multi-collinearity. Thus, in order to predict log(LOS), a decision on the inclusion or exclusion of variables from the regression model had to be made. Applying traditional variable selection techniques such as stepwise- and Cp-selection failed to correct the problem. We therefore decided to select one numerical variable from each of the three groups obtained from a principal component analysis. Principal components provide a good starting point from which to explore the often more complex correlation structure in the data. In turn, knowledge of the correlation structure guides the model building process at later stages of the analysis. The principal component analysis (PCA)^6,7 was performed on the correlation matrix of the six numerical variables.

A generalised linear model with a logit link function⁸ was used to predict NICU neonatal mortality. The 2 307 cases (i.e. excluding transfers and cases with incomplete data items) from the VON 2008 data were used for building the model.

Welch two-sample t-tests⁸ were used to compare the two groups (infants who died and those who survived), with regard to each of the numeric variables. This method assumes heterogeneity of variances, which is appropriate here. The relationships of the nominal variables with the mortality response (death/survival) were tested using Fisher's exact test of independence⁸.

The full model considered Apgar score at one minute, temperature, birth weight, maternal ethnicity, and delivery mode as possible candidates. Stepwise logistic regression with Akaike's Information Criterion was used as variable selection technique.

The VON 2008 data were also used to build a model for predicting neonatal LOS for NICU admissions. All deaths and transferred cases were removed from the data leaving a total of 2 216 NICU admissions. To decide which of the nominal variables to include in the regression model, one-way ANOVA analyses were performed^6,7 to test the independence of these variables with log(LOS). All four nominal variables had significant associations with log(LOS) and were therefore included in the regression model.

Using all variables selected in the univariate analyses and PCA, a poisson loglinear multiple regression model^8,9 was fitted. Cook's distance¹⁰ was applied to identify six influential observations. These observations were removed from the data before fitting the final model. The model was corrected for overdispersion⁸, and variables not significant at the 95% confidence level were sequentially dropped. The square of birth weight was included to correct the curvature associated with birth weight in the initial fit.

In order to perform diagnostic procedures on the fitted regression models, a test data set of 1578 infants, delivered during 1 January and 31 December 2007 and admitted to nine NICUs, was used. Three cases, with hospital stays exceeding 200 days, were identified as outliers and excluded when the model was tested to predict neonatal LOS.

All analyses were performed using the statistical software packages, R and Statistica, and a significance level of 5% was used for all inferences.

Results

For the infants in the training data set, median Apgar scores at one and five minutes were 8 and 9, respectively. Gestational age ranged from 23 to 42.3 weeks (median: 35.9 weeks), birth weight from 430 to 5345 grams (median: 2350 grams), birth head circumference from 20 to 42 centimetres (median: 33 cm), and temperature from 32 to 40 degrees Celsius (median: 36.3 degrees).

The maternal ethnicity of 44% of the infants in the data set was White, followed by Black (42.1%), other (12.3%), and Asian (1.6%). In the Southern African context, the other category refers mainly to people from the coloured groups.

The majority of infants in the training data set (53%) were admitted to NICUs of hospitals in the Northern region, followed by the Central region (24%), South West (20%), and Namibia (3%). About 54% of the cases were male. A very high proportion of the infants (83%) were delivered by caesarean section.

Ninety-one infants died (mortality rate: 3.8%) before being discharged, and 69 infants (2.9%) were transferred to other hospitals/facilities and therefore lost for follow-up purposes. For infants surviving until discharge, LOS ranged from 1 to 171 days (median: 11 days), with an average of 17.9 days. Of the cases in the 2007 test data set, 49 infants (3.1%) died before being discharged, and 39 (2.5%) were transferred to other facilities. The results from univariate logistic regressions of mortality on each of the predictor variables are shown in table 1.

Table 1.

Univariate analyses to investigate the effects of the perinatal variables on mortality

	Effect on mortality (odds ratio)	p value	AUC
Apgar at 1 min	0.65	<0.0001	0.78
Apgar at 5 mins	0.61	<0.0001	0.79
Temperature	0.49	<0.0001	0.64
Birth head circumference	0.70	<0.0001	0.76
Birth weight	0.9983	<0.0001	0.78
Gestational age	0.73	<0.0001	0.74
Region			0.55
Central	(base)
Namibia	1.66	0.4320
Northern	1.54	0.1270
South West	0.97	0.9250
Maternal ethnicity			0.60
Asian	(base)
Black	1.02	0.9740
Other	0.76	0.7310
White	0.42	0.2510
Delivery mode			0.61
Caesarean	(base)
Vaginal	3.11	<0.0001
Gender			0.51
Female	(base)
Male	1.10	0.6480

When analysed separately, all of the numerical variables had significant effects on neonatal mortality. Delivery mode was the only nominal variable which showed a significant effect on mortality. The other nominal variables (region, maternal ethnicity, and gender) did not have significant predictive power when considered separately.

The results of the univariate regressions of LOS on each of the predictor variables are shown in table 2. All of the numerical variables showed significant effects on LOS, although the Apgar scores and temperature had limited usefulness (as indicated by their low R² values) in explaining the variation in LOS. Region, delivery mode and gender were also significant when considered separately, but their low R² values indicate that these variables add little explanatory power. Maternal ethnicity did not seem to affect LOS significantly when considered separately.

Table 2.

Univariate analyses to investigate the effects of the perinatal variables on LOS

	Effect on LOS	p value	R2
Apgar at 1 min	−9.96%	<0.0001	0.04
Apgar at 5 mins	−11.63%	<0.0001	0.04
Temperature	−22.91%	<0.0001	0.04
Birth head circumference	−18.74%	<0.0001	0.63
Birth weight	−0.09%	<0.0001	0.65
Gestational age	−17.83%	<0.0001	0.65
Region			0.004
Central	(base)
Namibia	40.80%	0.0092
Northern	13.42%	0.0251
South West	15.72%	0.0302
Maternal ethnicity			0.001
Asian	(base)
Black	−10.00%	0.5380
Other	−17.19%	0.2950
White	−7.91%	0.6290
Delivery mode			0.011
Caesarean	(base)
Vaginal	−27.79%	<0.0001
Gender			0.002
Female	(base)
Male	−8.33%	0.0497

The principal component analysis resulted in the eigenvectors shown in table 3.

Table 3.

Principal components of the numeric variables

	Component
	1	2	3
Apgar at 1 min	−0.28	0.63	−0.16
Apgar at 5 mins	−0.28	0.64	−0.09
Temperature	−0.24	0.08	00.96
Birth head circumference	−0.51	−0.25	−0.10
Birth weight	−0.51	−0.26	−0.10
Gestational age	−0.51	−0.23	−0.12
Standard deviation	1.74	1.25	0.93
Proportion of variance	50.2%	26.2%	14.5%
Cumulative proportion	50.2%	76.5%	90.9%

The data varied mainly in three dimensions, with the first three principal components accounting for more than 90% of the total variance. The three dimensions roughly corresponded to size (birth head circumference, birth weight, and gestational age), apgar score (Apgar scores at one and five minutes), and temperature (measured within one hour from birth).

The Spearman rank-order correlations confirmed the grouping of variables obtained in the first three principal components: the two Apgar score variables were highly correlated (r = 0.75), and so were the variables pertaining to size of the neonates (all r > 0.76).

Together with temperature, Apgar score at one minute and birth weight were the respective variables from the first and second groups that showed the highest correlation with log(LOS). These three numerical variables were therefore included in the linear regression model.

Apgar score at one minute (p < 0.0001), temperature (p < 0.0001), and birth weight (p < 0.0001) were found to be the variables most significantly correlated with the two mortality groups.

Of the nominal variables, only maternal ethnicity (p = 0.002) and delivery mode (p < 0.0001) were found to be significantly associated with mortality.

The estimated coefficients of the multiple logistic regression model are given in Table 4. Apgar score at one minute, birth weight, and delivery mode are the variables that emerged as significant.

Table 4.

Multiple logistic regression model to predict neonatal deaths

	Estimate	p-value	Odds ratio	OR 95% confidence interval
Intercept	1.4853	< 0.0001
Apgar at 1 min	−0.3675	< 0.0001	0.69	[0.63 ; 0.76]
Birth weight	−0.0014	< 0.0001	0.9986	[0.9983 ; 0.9989]
Delivery mode	1.4469	< 0.0001	4.25	[2.53 ; 7.08]

Increases in Apgar score and birth weight both had negative effects on the odds of neonatal death. For each unit increase in the Apgar score at one minute, the odds of neonatal death decreases by roughly 30%. With each gram increase in birth weight, the odds of neonatal death decreases by 0.14%: thus on average for each 100g increase in birth weight, the odds of neonatal death decreases by about 13.1%. Vaginal delivery appeared to increase the odds of neonatal death with 325% compared to delivery by caesarean section.

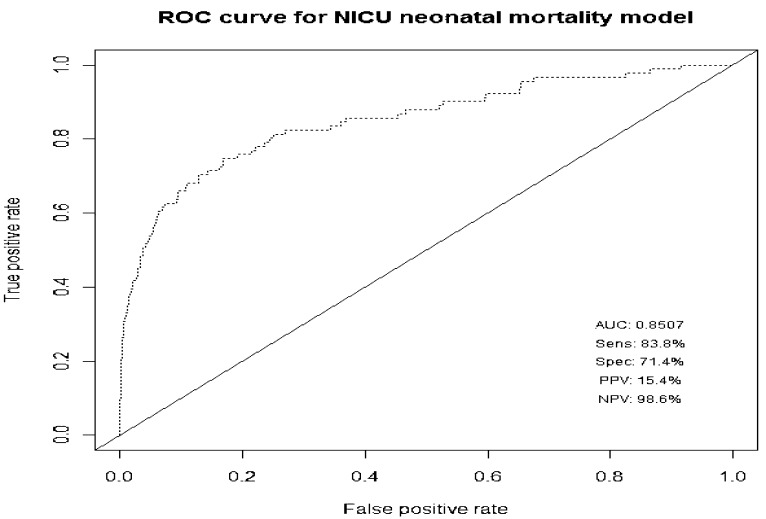
The area under the ROC curve (Figure 1) was 0.8507, which suggests that the model provides an adequate fit. The optimal classification cut-off point equals an expected mortality of 0.04619.

Figure 1.

ROC curve for the NICU neonatal mortality model

This optimal cut-off point was used to classify cases of the training data set. A misclassification rate of 16.6% was obtained. The sensitivity and specificity were relatively good at 83.8% and 71.4% respectively. The fitted model produced satisfying results when predicting survival (negative predictive value¹¹ = 98.6%), but performed poorly with regards to the prediction of NICU neonatal death (the positive predictive value¹¹ was a mere 15.4%).

The results obtained if the fitted model are applied to the VON 2007 data were similar to that of the VON 2008 data: high sensitivity (86.6%), specificity (79.6%), and negative predictive value (99.2%), with a positive predictive value which was still unacceptably poor (16.3%). Overall misclassification rate for the test data was 13.6%.

Although the model did not perform well it has some merit. For a predicted death, the odds of dying are about 24 times higher than for a predicted survival. It can therefore be used as a simple screening test to identify high mortality risk infants upon their admission to the NICU.

The estimated regression coefficients of the model for predicting LOS is given in table 5. The coefficient of determination was 0.7512.

Table 5.

Poisson loglinear regression model to predict neonatal length of stay

	Estimate	p-value	Effect on	Effect 95%
			LOS	confidence interval
Intercept	6.2590	< 0.0001
Apgar at 1 min	−0.0284	< 0.0001	−2.80%	[−3.83% ; −1.74%]
Birth weight	−0.0021	< 0.0001	−0.21%	[−0.22% ; −0.20%]
(Birth weight)2	0.00000028	< 0.0001	0.000028%	[0.000026% ; 0.000031%]
Maternal ethnicity
Black	−0.1994	0.0208	−18.08%	[−30.53% ; −2.56%]
Other	−0.2280	0.0115	−20.38%	[−33.03% ; −4.61%]
White	0.0412	0.6316	4.20%	[−11.57% ; 23.87%]

Temperature (p = 0.3952), region, gender (p = 0.3108), and mode of delivery (p = 0.1545) were excluded from the model. An increase in Apgar score at one minute and a larger birth weight will result in a shorter predicted LOS.

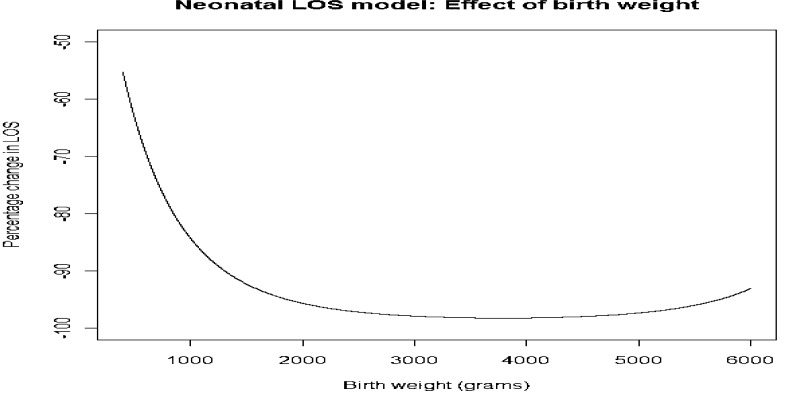
The effect of birth weight, ranging from 400 to 6 000 grams, on LOS is shown in figure 2. The negative effect of birth weight on LOS increases steadily from 4 000 grams, reaching a maximum between 2 500 and 4 500, and decreases again slightly for values larger than 4 500 grams. Infants in the “normal” birth weight range of between 2 500 and 4500 grams therefore tend to have shorter stays in hospital than their very low or very high birth weight counterparts.

Figure 2.

Effect of birth weight on neonatal LOS

Maternal ethnicity also plays a role in LOS: while LOS of white infants did not differ significantly from LOS of Asians (the model base), LOS of black and other (coloured) infants was on average 18.1% and 20.4% shorter than that of Asians.

An analysis of the residuals showed that the model fit is adequate.

There were no influential outliers or distinctive patterns in any of the residual plots.

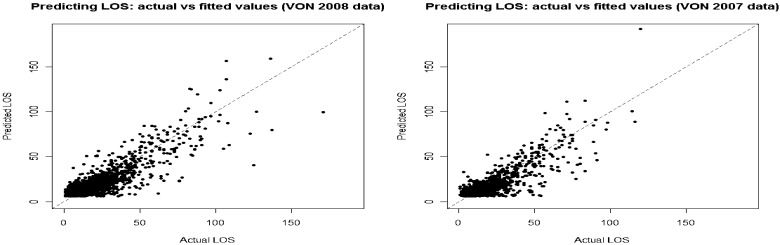
Testing the fitted model on the 1 487 cases of the VON 2007 data set yielded a predicted R² value of 0.7027. This corresponds to a correlation of 0.8383 between the predicted values and actual LOS. Graphs comparing actual LOS to predicted LOS for the training (VON 2008) and test (VON 2007) data sets are given in figure 3.

Figure 3.

Actual versus predicted LOS for the build (VON 2008) and test (VON 2007) data sets

Discussion

Readily available day-of-admission data provide a good source of information to predict neonatal survival and length-of-stay in the South African private hospital setting.

The neonatal mortality model has relatively good sensitivity and specificity, as well as a low misclassification rate, but has an unacceptably high false positive rate. As was expected, a low Apgar score at one minute and low birth weight are associated with an increase in the probability of death.

The more than threefold increase in the probability of death associated with vaginal delivery should be interpreted with caution: This apparent effect is most probably due to differences in the NICU admission protocol for vaginal and caesarean deliveries and not due to any real effect. The infants delivered by caesarean section were on average weaker, sicker, and more premature than their vaginal delivery counterparts and were more readily admitted to NICU for observation only, as also observed in a recent Canadian study by Fallah et al¹². On the other hand, infants born by vaginal delivery were usually less premature and were admitted to NICU only for more serious birth defects or illnesses. Therefore, given that the infants have been admitted to NICU, the pool of infants delivered by caesarean section were on average in better health compared to those born by vaginal delivery, thereby skewing the results.

The predictive value and adequacy of the fitted model may have been diminished to some extent by the difference in size of the two groups (surviving infants compared to non-surviving infants). However, it presents a simple model to indicate high mortality risk neonates: the odds of death for positive predictions are about 24 times higher than for negative predictions.

The fitted model predicting LOS performed well as was illustrated when it was applied to test data. The fitted model is parsimonious yet effective, and it provides a good benchmark indication for the length of hospital stay of NICU admissions. It also provides valuable information for resource planning and funding expenditure by medical aid schemes. Finally, the model can be useful in managing the expectations of anxious parents.

Increases in Apgar score at one minute and birth weight are both associated with a decrease in LOS, with the effect of birth weight reaching a maximum for infants weighing between 2 500 and 4 500 grams. Black and coloured infants seemed to be discharged from hospital earlier than their white and Asian counterparts. The reason for this is unclear and will require further investigation into regional and/or demographic differences between these groups.

Other studies^2,13 found gestational age to be the strongest predictor for LOS. In this retrospective observational study, we found gestational age, birth weight and birth head circumference to be highly correlated, with birth weight emerging as the strongest predictor for LOS.

Note that neither of the two prediction models discussed above is intended to provide admission criteria for NICUs, as only infants that have been admitted to NICU were included in the study. The objective of the study was to develop prediction models on data readily available on the day of admission. The predicted values can then be used as benchmarks from which to evaluate and monitor the performance of specific NICUs in terms of neonatal mortality and length of stay. Ideally this should form part of a greater NICU quality control programme, of which the results may be used by hospital managers for improved direction of resources, hopefully resulting in an improvement in the quality of patient care.

There are several interesting problems for further research. The prediction models can most probably be improved by using knowledge of later-occurring morbidities². The effect of unobserved variables such as congenital malformations and possible early infections should also be discounted. When interpreting the model effects, it should be kept in mind that there may be confounding or proxy effects attributed to the day-of-admission variables¹³. Low birth weight infants may, for example, be more prone to hospital acquired infections (increasing their LOS) and because of the model specification this effect is now attributed to the birth weight variable. Another factor to consider for future research, especially in the Southern African context, is the role of maternal HIV status on mortality and LOS predictions.

Conclusion

Apgar score at one minute, birth weight, and delivery mode significantly influence the odds of neonatal death. Apgar score at one minute, birth weight, and maternal ethnicity are associated with significant effects on LOS. Hospital region, gender, and temperature of the infant did not have significant effects on either mortality or LOS.

Both constructed models can be useful for the resource planning of hospital administrators and funders, and can provide benchmarks for NICU quality control programmes. The models can also be helpful in managing expectations regarding mortality and LOS of neonates admitted to NICU centres.”