Transcriptional regulation by the numbers: applications

Abstract

With the increasing amount of experimental data on gene expression and regulation, there is a growing need for quantitative models to describe the data and relate them to their respective context. Thermodynamic models provide a useful framework for the quantitative analysis of bacterial transcription regulation. This framework can facilitate the quantification of vastly different forms of gene expression from several well-characterized bacterial promoters that are regulated by one or two species of transcription factors; it is useful because it requires only a few parameters. As such, it provides a compact description useful for higher-level studies (e.g. of genetic networks) without the need to invoke the biochemical details of every component. Moreover, it can be used to generate hypotheses on the likely mechanisms of transcriptional control.

Introduction

Biology is undergoing a transformation from a `component-centric' focus on the individual parts toward a `system-level' focus on how a limited number of parts work together to perform complex functions. For gene regulation, this theme has been discussed extensively in the context of simple genetic circuits [1^•,2–4] in addition to complex, developmental networks [5]. The functional properties of a genetic circuit often critically depend on the degree of cooperativity (see Glossary) in the interactions between the molecular components [6]. For gene regulation, this cooperativity is dictated to a large extent by the architecture of the cis-regulatory region (see Glossary), [7] and the specific mechanism of transcriptional activation or repression [8^••], which is mediated through interactions among various transcription factors (TFs) and the RNA polymerase (RNAP) complex. Often, even qualitative features of a gene circuit (e.g. whether a circuit can be bistable or whether it can spontaneously oscillate) cannot be determined without quantitative knowledge of the transcriptional regulation of key genes in the circuit [3].

Predicting the expression level of genes directly from the underlying biochemistry and biophysics is a difficult task. This is due most notably to ignorance of many biochemical parameters, especially their relevant in vivo values. However, the thermodynamic model reviewed in the preceding article [9^••] yields several general mathematical forms for the dependence of the fold-change in gene expression on the concentration(s) of the TF(s) regulating transcription. These general forms contain only a few parameters characterizing the effective interactions between the molecular players. Thus, from a practical standpoint, it is expedient to quantify the transcriptional regulation of a gene by fitting expression data to the appropriate model function in order to obtain effective parameters that best describe the promoter [10,11]. This procedure might be useful even when the simplifying assumptions made by the thermodynamic models are not satisfied [9^••]. By analyzing gene expression data within the thermodynamic framework, one can elucidate whether an assumed set of interactions between TFs and RNAP can consistently explain the data. Failure of the analysis can suggest important missing ingredients, such as unknown mechanisms of cooperativity, whereas success can lead to predictions for new experiments (e.g. how operator deletion would affect gene expression).

There has been much recent progress in understanding the mechanistic aspect of bacterial gene regulation [8^••]. However, the systematic quantification of gene expression is still in its infancy. In this paper, we review several experimentally characterized cis-regulatory systems in bacteria. For each case, we provide what we believe to be the most appropriate form for the dependence of the promoter activity (see Glossary) on the TF concentration(s). For each system, we show graphically how the expected form depends on the effective parameters. We hope to demonstrate how the thermodynamic models can provide a direct link between the arrangements of interactions in a promoter region and the quantitative characteristics of gene expression.

Quantitative characteristics of activation and repression

Our quantitative discussion focuses on several well-characterized bacterial promoters controlled by one or two species of TFs. We use the results of the thermodynamic model listed in Table 1 of the preceding paper [9^••], which we refer to as Table 1 throughout this review. We make the additional simplifying assumption that the in vivo promoters are weak, so that even at full activation the equilibrium gene expression is still small (e.g. <10% of the strongest promoters). Indeed, for a large number of bacterial promoters, the expression is small in the exponential growth phase when compared with the expression of the ribosomal genes, for example, which are fully turned on [12]. In this weak promoter limit, the fold-change in promoter activity (henceforth simply referred to as `fold-change') is given directly by the regulation factor (F_reg) listed in Table 1. We will consider two types of activators: those activators that recruit RNAP to its promoter, and those that stimulate the transition rate of bound RNAP from a closed to an open complex. Even though the latter is a kinetic effect, its impact on the overall promoter activity (e.g. transcription initiation rate) can, nevertheless, be effectively described by the thermodynamic model in the weak promoter limit that we study.

Simple activation

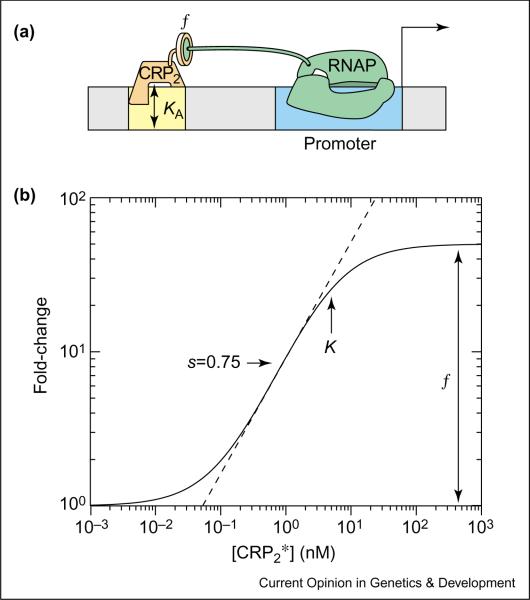
The simplest example of activation involves the binding of an induced TF to a single operator site, and the subsequent recruitment of RNAP. This is the case with the lac promoter of E.coli, shown in Figure 1a (in the absence of the lac repressor). The activating TF is a CRP (cAMP receptor protein) dimer in complex with the inducer cAMP [13,14]. We will denote this complex by CRP₂* and use * to indicate the activated form of a TF. Case 2 in Table 1 gives the mathematical form of the expected fold-change for this situation with [A] = [CRP₂*], and Figure 1b plots its dependence on the induced dimer concentration. The two parameters of the model are the effective in vivo dissociation constant (K_A) between CRP and the operator, and the enhancement factor (f), which characterizes the degree of stimulation in transcription resulting from operator-bound CRP. These are readily revealed in a log–log plot of the relative promoter activity against the cellular concentration of the induced activator, [CRP₂*]. As long as the range of [CRP₂*] probed is sufficiently broad, one can read the enhancement factor (f) from the graph as the maximal fold-change between full activation at saturating levels of [CRP₂*] and basal activity at low levels of [CRP₂*]. One can also read off the effective dissociation constant (K_A) as the value of [CRP₂*] at half-activation. The steepness of the transition region — called the `sensitivity' (or `gain') in the literature (see Glossary) [15^•] — plays an important role in the function of genetic circuits. Here, we quantify transcriptional sensitivity by the log–log slope (s) at the mid-point of the transition region. s ≤ 1 for promoters containing a single operator, and s approaches 1 for only very large values of f. In contrast, functions such as amplification, bistability or spontaneous oscillation all require circuit components to have high sensitivity, with a value of s > 1 [6].

Figure 1.

Simple activation. (a) Cis-regulatory architecture for transcriptional activation involving a single CRP operator, as found in the lac operon. The yellow box denotes the operator site and the blue box corresponds to the promoter. The DNA-binding affinity of the transcription factor for its operator is described by the in vivo dissociation constant K_A, which is the TF concentration at which the operator occupancy is half-maximal. The activator recruits RNAP through protein–protein interactions (schematically drawn as interacting protein subunits). (b) Log–log plot of the fold-change in gene expression as a function of the induced CRP dimer concentration, [CRP₂*]. The maximum log–log slope in the transition region, which is defined as the sensitivity (s), is highlighted with the dashed line and is equal to 0.75. This plot was generated using K_A = 5 nM, f = 50. These parameter values were estimated from experiments similar to those of Setty et al. [10], who measured β-galactosidase activity as a function of extra-cellular cAMP concentration in E. coli MG1655 cells, but with the additional deletion of the cyaA gene which encodes adenyl cyclase (T Kuhlman and T Hwa, unpublished). The enhancement factor obtained is consistent with that of others [41]. The estimated value of the effective dissociation constant K_A is dependent on the literature values for several biochemical parameters concerning cAMP binding and transport, and is not expected to be accurate to within a factor of 2. (For comparison, previous in vitro measurement of the CRP-operator affinity has ranged from 0.001 nM to 50 nM depending on the ionic strength of the assay [42–44].)

Cooperative activation

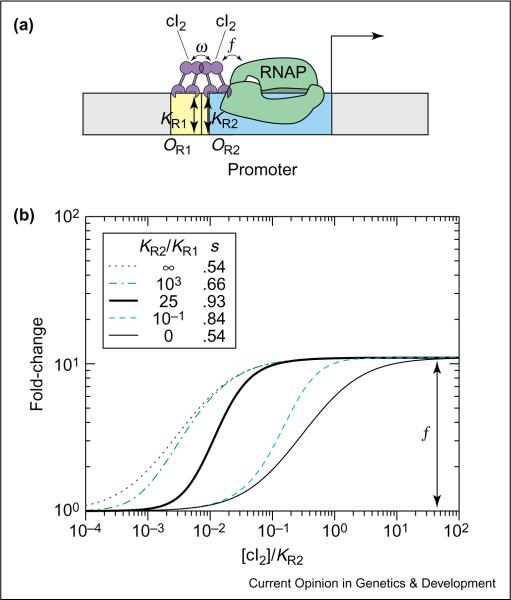
TFs often have domains that enable interaction with one another when bound to adjacent operator sites, and this interaction can result in cooperativity in transcriptional activation. The P_RM promoter of phage lambda, shown in Figure 2a, is such an example [1^•]. Binding of the dimeric lambda repressor cI to the operator O_R2 (the `activator' site) stimulates transcription, and binding of cI to the upstream operator O<sub>R1</sub> (the `helper' site) helps to recruit cI to O_R2. The expected fold-change (Case 3 in Table 1 with [A] = [H] = [cI₂], K_H = K_R1 and K_A = K_R2) depends on the affinities K_R1 and K_R2 of cI to the two operators, the cooperative interaction (ω) between the two operator-bound cI dimers, and the enhancement factor f due to the O_R2-bound cI. It is shown in the log–log plot of Figure 2b (thick solid line) as a function of [cI₂]/K_R2.

Figure 2.

Enhanced sensitivity by cooperative activation. (a) Cis-regulatory architecture for cooperative transcriptional activation in phage lambda P_RM promoter. Here, we are considering P_RM alone without the upstream P_R promoter [1^•] or the upstream P_L region, which affects P_RM activity through DNA looping [45]. We also neglect the operator O_R3, which has very weak affinity to cI in the absence of P_L [45]. The yellow boxes denote the operator sites O_R1, O_R2 and the blue box corresponds to the promoter. The DNA-binding affinity of cI₂ for O_R1 and O_R2 is described by the dissociation constants K_R1 and K_R2, respectively. The activator stimulates transcription and cI dimers interact with one another through intimate, cooperative interactions, both of which are indicated by overlapping protein–protein domains. (b) Log–log plot of the fold-change in gene expression as a function of cI₂ concentration for different ratios of K_R2/K_R1. The maximum log–log slopes (s) for the different curves are listed in the legend. The promoter with K_R2/K_R1 = 0 corresponds to a deletion of O_R1, and the regulation function for this case (thin solid line) is identical to the single operator case shown in Figure 1. If this promoter has a very small K_R1 (i.e. strong O_R1), then the onset of full activation will be shifted to smaller cI concentrations (dotted line). The latter corresponds effectively to a stronger O_R2 site, with dissociation constant K_R2/ω. These plots are generated using f ≈ 11 [46] and ω ≈ 100 [47] as extracted from in vitro biochemical studies. The absolute in vivo values of the K values are not known (which is why the concentration is expressed in terms of [cI₂] / K_R2). However, the ratio K_R2/K_R1 ≈ 25 (thick solid line) can be deduced from the in vitro results [47]. The transition region is steepest when ω ⪢ f and K_R2/K_R1 ≈ f. We note that the parameters for P_RM are nearly optimal for enhanced sensitivity.

To quantify the possible role of the auxiliary operator O_R1, we also plot in Figure 2b the fold-change for different ratios of K_R1 and K_R2. Comparing these curves, it is clear that the auxiliary operator O_R1 does not change the degree of full activation, given by ƒ. The most significant feature of this dual-activator system is perhaps the increase in the log-log slope of the transition region (compared with the extreme cases) for intermediate values of K_R2/K_R1. In fact, for the realistic parameter of K_R2/K_R1 ≈ 25 (thick solid line in Figure 2b), we have a sensitivity of s ≈ 0.93. This is close to the maximum attainable for this system, with its small enhancement factor (ƒ ≈ 11), and is nearly double the maximum sensitivity (s ≈ 0.54) for the promoter with O_R2 only (thin solid line in Figure 2b). For TFs with larger values of ω and ƒ, this cis-regulatory construct can, in principle, provide more sensitivity, with s approaching 2.

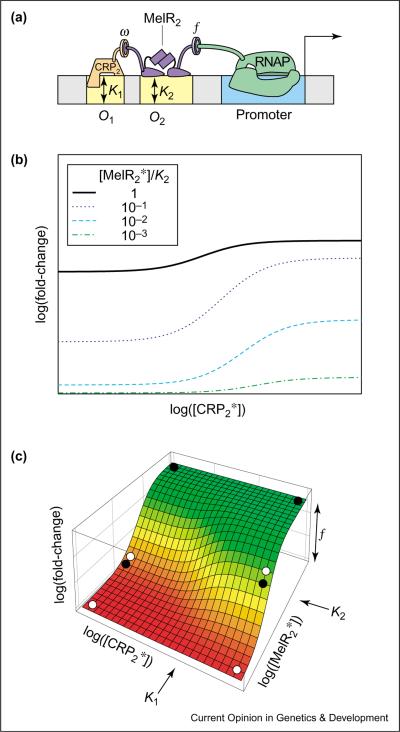
The same cis-regulatory design can be used to implement co-activation — one of the simplest forms of signal integration (see Glossary) — if the two operators are targets of two distinct TF species. A possible example of this is the variant of E. coli's melAB promoter studied by Wade et al. [16] (see Figure 3a), where transcription is stimulated by an induced MelR dimer bound to the weak proximal operator, O₂. Meanwhile, CRP bound to the upstream operator O₁ helps recruit MelR but does not directly participate in activation. Assuming that the induction of MelR by melibiose results in an increase in MelR-operator binding affinity, we expect the form of the co-dependence to be given by Case 3 in Table 1, but with [A] = [MelR₂*], [H] = [CRP₂*] and K_H = K₁, K_A = K₂. The fold-change is plotted against the induced CRP concentration on the log-log plot of Figure 3b for different concentrations of the induced MelR. To better visualize the co-dependence on CRP and MelR, it is useful to plot the fold-change as a three-dimensional plot; see Figure 3c. The transition region (the yellow band) is clearly dependent on both TFs. Consider a simplified situation where CRP and MelR can each take on two possible concentrations — a pair of `low' and `high' values. Then it is possible to choose the pair of concentrations (e.g. those marked by the 4 open circles in Figure 3c) such that the fold-change is large (the green region) only when both concentrations are `high'. This mimics a logical AND function of the two inputs [17<sup>•</sup>]. It is also possible to choose the pair of concentrations as marked by the four solid circles such that the fold-change is large (the green region) unless both concentrations are `low'. The latter choice mimics a logical OR function. The flexibility of this cis-regulatory scheme makes the shape of the fold-change readily evolvable [18] (e.g. between the AND/OR functions) by merely altering the operator sequences that encode the values of K₁ and K₂.

Figure 3.

Cooperative co-activation. (a) Cis-regulatory construct for co-activation by CRP and MelR. The figure shows the truncated JK15 version of melAB promoter studied by Wade et al. [16]. The full melAB promoter is more complicated due to the presence of multiple MelR operators. However, the co-activation pattern is similar to that of JK15 discussed here. The yellow boxes denote the operator sites O₁, O₂ and the blue box corresponds to the promoter. The DNA-binding affinity of CRP₂ for O₁ and MelR₂ for O₂ is described by the dissociation constant K₁ and K₂, respectively. MelR can recruit RNAP (drawn with protein–protein contacts) and cooperative interaction between MelR₂ and CRP₂ is indicated by interacting protein subunits. (b) Log–log plot of the fold-change in gene expression as a function of activated CRP dimer concentration [CRP₂*] for different activated MelR dimer concentrations [MelR₂*]. Since none of the parameters f, ω, and K values have been determined experimentally, the scales of the plot can only be expressed relative to these parameters. Nevertheless, the plot reveals important qualitative predictions by the thermodynamic model (e.g. the dependence of the maximal CRP-dependent fold-change on the MelR concentration). (c) Three-dimensional log–log plot of the fold-change in gene expression as a function of both CRP₂ and MelR₂. For different choices of `high' and `low' concentration (the four combinations of `high/low' for these two TFs form a rectangle), the same melAB promoter can serve as an OR function (solid circles) or an AND function (open circles).

Synergistic activation

An alternative mechanism for co-activation is synergistic or dual activation [19–21], where two operator-bound TFs can simultaneously contact different subunits of RNAP and activate transcription. This mechanism is limited to TFs that can activate transcription at different locations relative to the core promoter. Prominent examples of such synergistic activation in the bacterial literature [19–25] all involve the activator CRP because it can recruit RNAP from multiple locations at varying distances upstream of the promoter [8^••,26].

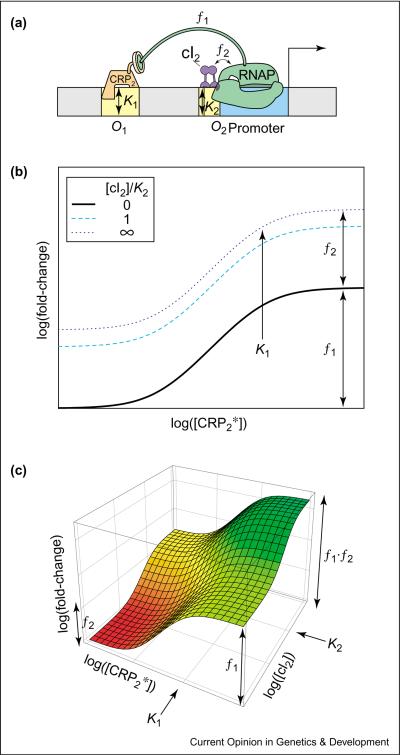
The synthetic promoter studied by Joung et al. [21] contained two operators: one for cI proximal to the core promoter (O₂) and the other for CRP at an upstream operator (O₁) (see Figure 4a). The data from the study by Joung et al. support the model where each operator-bound activator can independently interact with RNAP and enhance transcription [21]. The expected fold-change is given by Case 8 in Table 1 (with [A₁] = [CRP₂*], [A₂] = [cI₂], K_A1 = K₁, K_A2 = K₂ and ω = 1) and shown in the log–log plot of Figure 4b as a function of [CRP₂*] for various cI concentrations. Note that, since ω = 1, the dependence of gene expression on [CRP₂*] is independent of [cI₂], except for an overall vertical shift. This is a reflection of the multiplicative nature of independent synergistic activation. An alternative way of visualizing the same result is the three-dimensional plot of Figure 4c.

Figure 4.

Synergistic co-activation. (a) Cis-regulatory architecture for synergistic co-activation in synthetic promoters [21]. The yellow boxes denote the operator sites O₁, O₂ and the blue box corresponds to the promoter. The DNA-binding affinity of CRP₂ for O₁ and cI₂ for O₂ is described by the dissociation constants K₁ and K₂, respectively. Each activator can independently interact with RNAP and enhance transcription at different strengths f₁, f₂ (as shown with interacting protein–protein subunits). (b) Log–log plot of the fold-change in gene expression as a function of [CRP₂*] for different concentrations of [cI₂]. (c) Three-dimensional log–log plot of the fold-change in gene expression as a function of both CRP₂ and cI₂. Note that on log scale, the product appears as an additive shift.

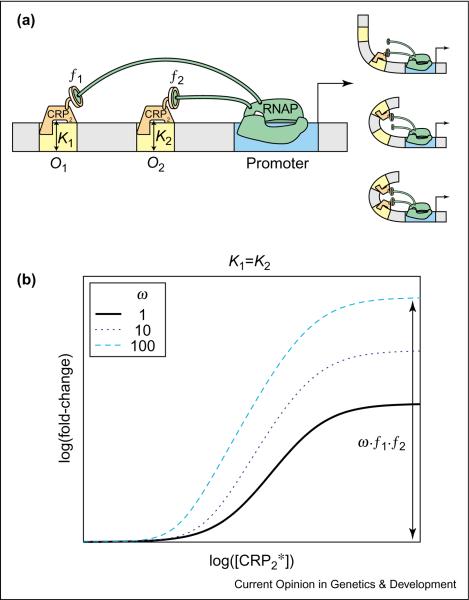
In another experiment by Joung et al. [19], both the proximal site (O₂) and the distal site (O₁) were engineered to bind CRP (see Figure 5a, left). An important result of these experiments was that the fold-change with both CRP operators is larger than the product of the fold-changes with one operator alone. This is not consistent with the independent recruitment assumption and suggests additional cooperativity (ω > 1). A possible mechanism proposed by Joung et al. is that DNA bending (see Figure 5a, right) induced by the CRP bound to the proximal operator O₂ facilitates the upstream CRP interaction with RNAP, without any direct protein–protein interaction between the two TFs. This cooperative effect can be included in the thermodynamic model as shown in Case 8 of Table 1 (with [A₁] = [A₂] = [CRP₂*], K_A1 = K₁, K_A2 = K₂ and w > 1) regardless of the specific molecular mechanism. Similar to the case of activation by cI, the expression level is most sensitive when the K values for the two binding sites are equal. In Figure 5b, we plot the expected fold-change, with K₁ = K₂ and different values of w. The extra cooperativity increases both the enhancement factor (w · f₁ · f₂) and the sensitivity (s) of the transition region.

Figure 5.

Enhances sensitivity by synergistic activation. (a) To the left is the cis-regulatory architecture for synergistic activation by the same TF in synthetic promoters [19]. The yellow boxes denote the operator sites O₁, O₂ and the blue box corresponds to the promoter. The DNA-binding affinity of CRP₂ for O₁ and O₂ is described by the dissociation constants K₁ and K₂, respectively. Activators at each operator can recruit RNAP independently at different strengths f₁, f₂ (as shown with interacting protein–protein subunits). As illustrated to the right, the binding of CRP to proximal O₂ bends DNA and facilitates the `bent' interaction of RNAP to CRP bound at upstream O₁. (b) Log–log plot of the fold-change in gene expression as a function of [CRP₂*] for equal dissociation constants (K₁ = K₂). We have included the additional cooperativity ω that can occur when the binding of CRP to O₁ promotes the interaction of RNAP to CRP bound at O₂. The additional cooperativity simultaneously increases the maximal fold-change to ω · f₁ · f₂ and enhances the transcriptional sensitivity in the transition region.

Simple repression

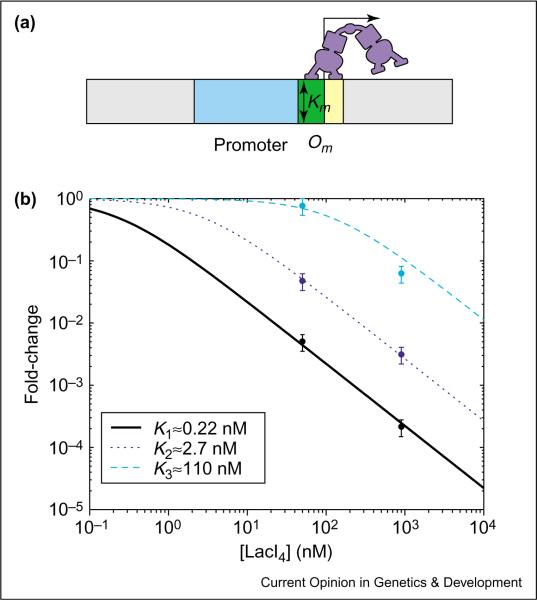
The simplest example of repression involves the binding of a TF to a single operator site that interferes with the binding of RNAP to the core promoter. This is the case in the truncated lac promoter (e.g. lacUV5) which has only the main operator, O_m, of LacI located closely downstream of the core promoter (Figure 6a) [27]. The expected fold-change is given by Case 1 of Table 1, with [R] = [LacI₄], K_R = K_m and only one unknown parameter, K_m, characterizing the effective dissociation constant of the operator O_m. Here, it is possible to compute K_m [28^••] directly from the experimental data of Oehler et al. [27], because the cellular concentration of LacI was quantified. In fact, because Oehler et al. characterized gene expression at two distinct LacI concentrations, the two data points can be used to check the consistency of the thermodynamic model.

Figure 6.

Simple repression. (a) Cis-regulatory structure of the truncated lac promoter, with the main operator O_m (yellow box) located closely downstream of the core promoter (blue box). Repressor bound at O_m will block RNAP binding to the promoter, as denoted by the overlap (green box). The DNA-binding affinity of LacI₄ for O_m is described by the dissociation constant K_m. (b) Log–log plot of the fold-change in gene expression as a function of LacI₄. Here, the repressor concentration shown on the horizontal axis refers to the cellular LacI tetramers in the absence of inducers. The experiments of Oehler et al. [27] used the operator sequences O1, O2, O3 at position O_m and measured fold-repression at two different LacI concentrations (50 nM and 900 nM); the data are shown as circles. The expected form of the fold-changes are plotted as the solid, dotted and dashed lines as indicated in the legend. The value of K_m for each curve (see legend) is determined by fitting one of the two data points. The fact that the other data point lies closely on the curve supports the applicability of the thermodynamic model to this promoter.

This analysis was performed for the three lac operator sequences O1, O2 and O3 studied in [27] (results shown in Figure 6b). We note that the K_m values obtained, K₁ ≈ 0.22 nM, K₂ ≈ 2.7 nM and K₃ 110 nM for the three operators, are significantly different from, for example, the results K₁ ≈ 10⁻³ nM, K₂ ≈ 10⁻² nM and K₃ 0.016 nM to 1 nM obtained from in vitro assays [29–31]. These results underscore the fact that the relevant TF-operator binding constant for the thermodynamic model is not given by the in vitro measurement — even if the appropriate physiological conditions are used — but must be corrected for by considering the interaction of the TF with the genomic background [9^••,32]. Consistent with the theoretical expectation, the ratios of the K values are in reasonable agreement between the in vivo and the in vitro results. We note also that the expected range of promoter activities is much larger than those for the activator-controlled promoters described above. This follows from the strong excluded-volume interaction between the repressor and RNAP, such that more repressor proteins generally lead to stronger repression; whereas in activation more activator protein does not lead to more activation beyond the enhancement factor (f), which is set by the weak activator-RNAP interaction¹. By contrast, the sensitivity is still limited to s ≤ 1 with a single operator site.

Repression by DNA looping

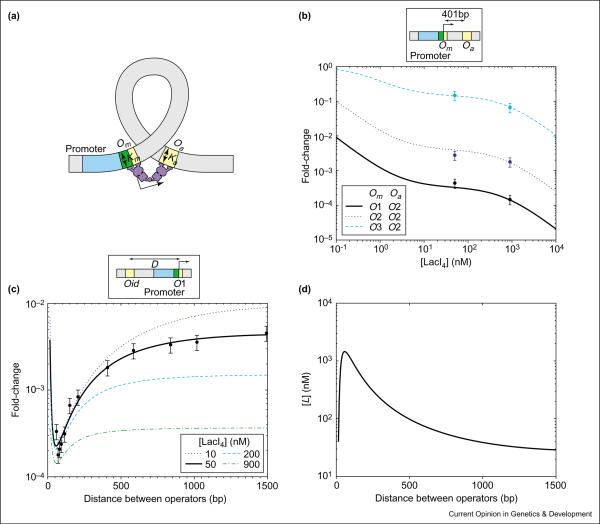
For the wild-type lac promoter, the degree of repression exceeds 1000-fold with only ~10 repressor molecules in a cell [14]. This is substantially larger than the <100-fold repression achievable by the best of the truncated promoters (Figure 6) at the same repressor concentration. The additional repression is facilitated by the stabilization of the O_m-bound Lac tetramer, which can simultaneously bind to an auxiliary operator O_a through DNA looping (see Figure 7a). The wild type lac promoter has two such auxiliary operators: O2 located 401 bases downstream and O3 located 92 bases upstream. We describe the simpler case studied experimentally by Oehler et al. [27], which involves only repression and looping between the main operator, O_m, and the down-stream auxiliary operator, O2. The expected fold-change is given by Case 9 of Table 1, with [R] = [LacI₄].

Figure 7.

Repression by DNA looping. (a) Cis-regulatory layout for looping and repression in the lac promoter experiments of Oehler et al. [27]. Yellow boxes are operators and the blue box is the promoter. LacI tetramer bound at the main operator O_m interferes with RNAP binding to the promoter, and this is indicated by the overlap (green box) between the promoter and the operator. This binding is further stabilized if the other two legs of the tetramer bind at O_a through DNA-looping. (b) Log–log plot of the fold-change in gene expression as a function of LacI₄ concentration for different constructs where O_m is replaced by O1, O2, or O3 and O_a is O2. The curves are generated by plotting Case 9 of Table 1 using the appropriate dissociation constants shown in Figure 6 for each pair of operators involved. Note that the six data points (shown with circles) can all be brought into agreement with the expected form (the lines) by the choice of a single parameter, the available LacI₄ concentration [L] due to looping. The best-fit value obtained is [L] ≈ 660 nM. (c) Log–linear plot of the transcriptional fold-change as a function of distance D between O1 (located at position O_m) and an auxiliary operator Oid located upstream of the promoter, for various repressor concentrations. The data of [34] (filled circles) are fitted to the transcriptional fold-changes expected for looping (solid line) using [LacI₄] = 50 nM and values of K₁ ≈ 0.27 nM and K_id 0.05 nM determined from the data of [27]. The fitting function is the dependence of the available concentration due to looping, [L], on the operator spacing D. We use the form [L] = exp(−a/D − b · ln(D) + c · D + e) motivated by the worm-like chain model of DNA bending [48]. The other lines correspond to the predicted gene expression of the same constructs at different LacI concentrations as indicated in the legend. (d) Log–linear plot of [L] versus D obtained from the fit described in (d), with a = 140.6, b = 2.52, c = 1.4 × 10⁻³, e = 19.9.

Given that the three K values are already determined (see Figure 6b), there is only one unknown parameter in this case in the form for the fold-change (Case 9 of Table 1). This is [L], the effective concentration of repressors that are made available, as a result of DNA-looping, for binding to one of the two operators. This looping is itself caused by the binding of a repressor to the other operator. Oehler et al. [27] did experiments with the main operator, O_m, substituted for one of the three operator sequences (O1, O2 and O3), each for two concentrations of LacI. The results of all six experiments are described consistently by the expected fold-changes according to the thermodynamic model (see Figure 7b), with [L] ≈ 660 nM [28^••].

Quantitatively, the strong repression effect (compare Figure 6b and Figure 7b) results directly from the large value of [L] generated by DNA looping, which amplifies the effective concentration of one operator-bound repressor 660-fold. This enhancement of the local repressor concentration is a result of the linkage between O_m and O_a, as already described qualitatively elsewhere [27,33]. Intuitively, once a LacI tetramer binds to one of the two operators, it is available within a small volume for binding to the other. The actual value of [L] is clearly dependent on the spacing between the two operators, in addition to the energetics of bending the DNA backbone. We have deduced the dependence of [L] on operator spacing (shown in Figure 7d) by analyzing the data of Müller et al. [34], who measured the fold-changes in repression for promoter constructs with different spacing between the main and auxiliary operators (see Figure 7c). In Figure 7c, we also show the predicted transcriptional fold-changes for the same constructs of Müller et al. [34], but at different LacI concentrations.

Cooperative repression

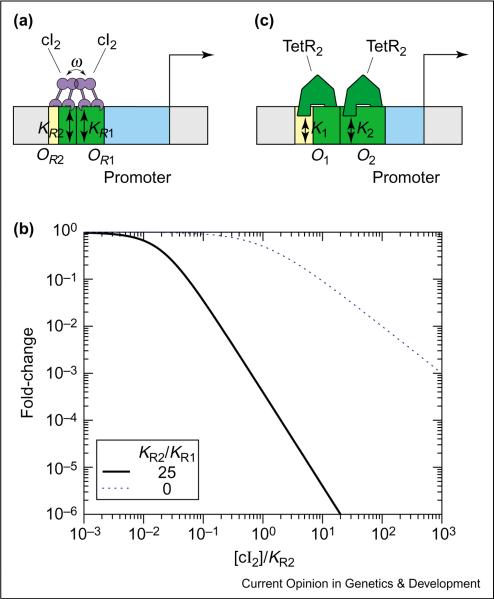
Interaction between the TFs can also enhance the sensitivity in transcriptional repression. The P_R promoter, which controls the expression of cro in phage lambda (illustrated in Figure 8a), is a good example of this mode of repression [1^• ]. When bound to either O_R1 or O_R2, the lambda repressor, cI, blocks the access of RNAP to the core promoter, thereby repressing transcription. The combined effect of two repressive operators, reinforced by the cooperative interaction between the operator-bound cIs, results in both further repression and enhanced sensitivity. The expected form of fold-change is given by Case 6 in Table 1 ([R₁] = [R₂] = [cI₂]) and plotted in Figure 8b. Maximum log-log (i.e. sensitivity) in repression is the largest when K_R1 and K_R2 are equal. Similar schemes have been generalized for co-repression by two species of repressors [35–37], and can be used to mimic the logical NAND function [17^•].

Figure 8.

Enhanced sensitivity by dual repression. (a) Cis-regulatory architecture for cooperative transcriptional repression in phage lambda P_R promoter. The yellow boxes denote the operator sites O_R1, O_R2 and the blue box corresponds to the promoter. Repression is indicated by the overlap (green box) between the promoter and operator. The cooperative interaction between bound cI₂ at operators O_R1 and O_R2 is given by ω (protein–protein contacts). (b) Log–log plot of the fold-change in gene expression as a function of cI₂ concentration for two different values of K_R2/K_R1. At high repressor concentrations, the maximum log–log slope(s) for all the curves is equal to 2 with the exception of K_R2/K_R1 = 0 (i.e. deletion of O_R1) where the maximum log–log slope is equal to 1. The latter case corresponds to a single repressive site, O_R2 (see Figure 6). This plot was generated using ω ≈ 100, and K_R2/K_R1 ≈ 25 extracted from in vitro biochemical studies [47]. The absolute in vivo values of the K values are unknown, which is why our concentration is expressed in terms of [cI₂]/K_R2. (c) Cis-regulatory architecture for transcription repression in P_LtetO-1 promoter engineered by Lutz and Bujard [38]. Note that there is no cooperative interaction between the TetR dimers. The log–log plot of fold-change of P_LtetO-1 promoter is similar to that of phage lambda P_R with a maximum log–log slope equal to 2.

In fact, enhanced sensitivity in repression does not require direct interaction between the repressor molecules. An example is the P_LtetO-1 promoter [38], which contains two operators of TetR; see Figure 8c. The expected form of the fold-change is given by Case 5 in Table 1, with [R] = [R₂ = [TetR₂*], and K_R1 = K₁, K_R2 = K₂. By appropriately decreasing K₁ and K₂, it is possible to make the activity of this promoter (not shown) nearly identical to that represented by the solid line in Figure 8b (i.e. with the steepened slope) even though the TetR dimers do not contact each other physically. The enhanced sensitivity is expected here because of the `collaborative' nature of repression — the occupation of either operator is sufficient to block RNAP from the core promoter, leaving the other operator site available for binding for `free' [39]. We expect that a similar construct where the two operators are targets of different, non-interacting TFs would implement co-repression. Comparing the activating and repressive modes of transcription control, we find repressive control to be advantageous because high sensitivity can be generated by TFs without the need of TF–TF interaction, and fold changes are not limited by the magnitude of the (typically weak) TF–RNAP interaction [40].

Phenomenological model of transcription control

The mathematical description for the different activation and repression mechanisms discussed above can be summarized by very simple forms. For a single TF species with up to two operators in the cis-regulatory region, all of the fold-changes described in Table 1 can be compactly represented by the general form

$$F_{reg}\left(\left[TF\right]\right)=\frac{1+a_1\left[TF\right]+a_2{\left[TF\right]}^2}{1+b_1\left[TF\right]+b_2{\left[TF\right]}^2}$$ (1)

Similarly, for co-regulation by two TFs with cellular concentrations, [TF₁] and [TF₂], and for no more than one operator each in the regulatory region, the fold-change has the form

$$F_{reg}(\left[T{F}_1\right],\left[T{F}_2\right])=\frac{1+a_{1,0}\left[T{F}_1\right]+a_{0,1}\left[T{F}_2\right]+a_{1,1}\left[T{F}_1\right]\cdot \left[T{F}_2\right]}{1+b_{1,0}\left[T{F}_1\right]+b_{0,1}\left[T{F}_2\right]+b_{1,1}\left[T{F}_1\right]\cdot \left[T{F}_2\right]}$$ (2)

The general forms in Equation 1 and Equation 2 include many possible mechanisms of activation and repression not discussed above. If 3 binding sites for the TF are involved in the regulatory process, then Equation 1 or Equation 2 would be generalized to the ratio of third-degree polynomials of the [TF]s.

The above analysis indicates that, by quantitatively measuring the fold-change as a function of the activated TF concentration(s), we can achieve two important goals (i) by fitting experimental results to an expression such as Equation 1 or Equation 2, one would obtain a quantitative characterization of the promoter at all TF concentrations, but with only a few (e.g. four or six) parameters. This can be done regardless of the validity of the thermodynamic model itself. As discussed previously, the compact description will facilitate quantitative higher-level study of gene circuits. (ii) By comparing the values of these parameters to the expected forms according to the thermodynamic model (e.g. Table 1), one can generate hypotheses on the likely mechanisms of transcriptional control for further experiments. Thus, the form of the fold-change in gene expression itself can be an effective diagnostic tool to distinguish subtle mechanisms of transcriptional control.

Conclusions

We have illustrated a variety of promoter activities implemented in different cis-regulatory designs. Also illustrated are important functional differences (e.g. in transcriptional cooperativity, and in the nature of combinatorial control) among promoters characterized by different parameters of the same cis-regulatory construct. These differences often cannot be discriminated by the qualitative characterization of promoter activity predominantly practiced in molecular biology today (e.g. fold-change in gene expression caused by deletion of a regulatory protein). Instead, they call for more quantitative characterization, particularly the quantification of the TF concentrations — or their relative concentrations — controlling promoter activity. The reward of quantitative characterization includes a compact phenomenological description of promoter activity for higher-level analysis and the elucidation of unknown mechanisms of transcriptional control.

Glossary

Cis-regulatory region

Region on the DNA located in the proximity of the promoter of a gene. It contains binding sites for transcription factors that regulate the transcription of that gene.

Cooperativity

In the narrow sense, cooperativity refers to the situation in which two molecules, A and B, bind to a third one, C, with a higher affinity than expected from their individual binding affinities to C alone. In a wider sense, cooperativity may be used to describe any mechanism that increases the sensitivity.

Sensitivity

This term refers generally to the change in gene expression (output) for small changes in the concentration of regulatory proteins (input) controlling the gene (i.e. the derivative). In this review, sensitivity refers specifically to the log-log slope of gene expression as a function of the transcription factor concentration (see Figure 1). Sensitivity is also known as the `gain' [49] or the `control coefficient' [50].

Promoter activity

The rate at which transcription is initiated from a promoter. Assuming that all transcripts are completed, this equals the rate of mRNA synthesis. In the absence of transcription factors, the promoter activity is at a basal level that depends on the promoter strength. The promoter activity can be elevated by activators or reduced by repressors. Throughout this paper we always measure the promoter activity relative to the basal level.

Signal Integration

The process whereby several regulatory signals elicit combinatorial responses as a function of the input levels. In transcriptional regulation, these responses might in some cases be approximately described by logical functions: e.g. AND, OR, NAND. For example, A AND B refers to when gene expression is high only when transcription factor A and B are both present in significant amounts. Conversely, A NAND B denotes the situation where gene expression is high as long as both A and B are not present in significant amounts.