Abstract
Background
The position of the femoral component in a TKA in the axial plane influences patellar tracking and flexion gap symmetry. Errors in femoral component rotation have been implicated in the need for early revision surgery. Methods of guiding femoral component rotation at the time of implantation typically are derived from the mean position of the flexion-extension axis across experimental subjects. The functional flexion axis (FFA) of the knee is kinematically derived and therefore a patient-specific reference axis that can be determined intraoperatively by a computer navigation system as an alternative method of guiding femoral component rotation. However, it is unclear whether the FFA is reliable and how it compares with traditional methods.
Question/purposes
We asked if the FFA could be measured reproducibly at different stages of the operative procedure; (2) where it lies in relation to a CT-derived gold standard; and (3) how it compares with more traditional methods of judging femoral component rotation.
Methods
Thirty-seven patients undergoing elective TKAs were recruited to the study. Preoperative CT scans were obtained and the transepicondylar axis (TEA) was identified. The TKA then was performed using computer navigation. The FFA was derived before incision and again after the surgical approach and osseous registration. The navigation system was used to register the surgical TEA. The FFA and surgical TEA then were compared with the CT-derived TEA.
Results
The mean preincision FFA was similar to the intraoperative FFA and therefore deemed reproducible. We observed no differences in variability between surgical TEA and preincision FFA. The FFA was different from the CT-TEA and judged similar in accuracy to the surgical TEA.
Conclusion
The reliability and accuracy of the FFA were similar to those of other intraoperative methods. Further evaluation is required to ascertain whether the FFA improves on currently available methods for determining the ideal rotation of the femoral component during TKA.
Introduction
Prosthetic loosening and periprosthetic osteolysis remain the most common causes for revision TKAs, with 42% of revision procedures being performed for these reasons according to the 2010 Australian Orthopaedic Association National Joint Replacement Registry Annual Report [3]. Component malpositioning is a major cause of excessive wear and early failure of TKAs [20, 21]. Femoral component rotation influences patellofemoral [27] and tibiofemoral joint kinematics [22] and therefore is important in obtaining durable knee function [22]. Traditionally, four methods have been available to the surgeon to guide femoral component rotation at implantation: matching rotation to the transepicondylar axis (TEA) [4], the AP axis [26], the posterior condylar axis (PCA) [19], or balancing the medial and lateral flexion gaps [14].
Churchill et al. suggested matching femoral rotation to the TEA most closely matched the mean flexion axis of the knee in 15 cadaveric specimens [6]. Kurosawa et al. [18] observed the spherical nature of the posterior condyles and identified the location of the centers of these spheres, which coincided with the center of the condyles on lateral radiographs. Elias et al. [11] divided the femoral condyles into three distinct regions, each with its own radius and center. From 10° to 150° tibiofemoral flexion, the centers of rotation were found to lie on a line connecting the area of attachment of the medial collateral ligament and the lateral collateral ligament [11]. However, this model included out-of-plane movement of both centers, which could not be explained through a single, fixed axis of rotation [6]. Hollister et al. [13] used a mechanical device, the “axis finder”, to locate a flexion-extension axis and a longitudinal rotation axis, with all positions of knee flexion occurring through movement about these two axes in a compound hinge model. The flexion-extension axis passed through the origins of the medial and lateral collateral ligaments, while the longitudinal rotation axis passed through the insertion of the ACL on the tibia and the insertion of the PCL on the femur [13]. The helical axis model [23–25, 27] has a moving axis of rotation about which all tibiofemoral motion takes place. This can be viewed as a combination of the two axes suggested by the compound hinge model [6]. This helical model was used in our study to locate the functional flexion axis (FFA).
Computer-aided navigation reportedly improves the precision of component positioning [5, 16]. This relies on kinematic registration and accurate identification of bony landmarks to generate reference axes. However, palpation of the femoral epicondyles has been prone to error [15, 17], leading to inaccuracy in the calculation of femoral rotation. The use of navigation has allowed the development of a method of determining the FFA from intraoperative kinematic data [8], thus matching its location to the subject’s specific knee kinematics. The FFA, also known as the navigated knee axis, reportedly has better reliability compared with surgeon-determined TEA in determining femoral component rotation in a cadaveric model [8]. However, the validity and reliability of the FFA in vivo are unknown.
Therefore, we asked (1) whether the FFA can be measured reproducibly, (2) where it lies in relation to a CT-derived gold standard, and (3) how it compares with more traditional methods of judging femoral component rotation during TKA in vivo.
Patients and Methods
We enrolled 37 patients undergoing 50 TKAs from January 2010 to March 2010; 13 patients had simultaneous bilateral surgeries. During that same time, we treated 51 patients with TKAs. Patients with a diagnosis of osteoarthritis of the knee requiring TKA under the care of either of two of the authors (DP and JR) were recruited for the study. One of the authors (DP) performed 17 TKAs in 14 patients (five men, nine women) with a mean age of 70 years (range, 57–82 years) and a mean BMI of 31.8 kg/m2 (range, 21.7–41.7 kg/m2), and another author (JR) performed 33 TKAs in 23 patients (15 men, 19 women) with a mean age of 65 years (range, 54–89 years) and a mean BMI of 30.6 kg/m2 (range, 24–38 kg/m2). Ethical approval for the study was obtained from the local human research ethical committee (HREC/09/HARBR/39).
Preoperative assessment was performed with a CT scan using a reduced radiation protocol. These images were imported into custom surface-matching software. Two observers (DF, SL) manually identified medial and lateral epicondyles for each patient as described by Berger et al. [4]. These manually digitized points then were used to generate the TEA (CT-TEA). The observers then repeated the measurements for each patient. The interobserver and intraobserver reliabilities of the CT-TEA relative to the PCA were calculated and revealed a typical error of 0.9°–1.4° and an intraclass correlation coefficient (ICC) of 0.77 (95% CI, 0.62–0.86) for the average CT-TEA of the two observers.
Custom-derived algorithms developed in MATLAB (Mathworks Inc, Natick, MA, USA) were used to create cylindrical models of the condyles from the CT data. The first applied a cylinder of best fit to the medial femoral condyle and a second, concentric cylinder to the lateral femoral condyle in a similar approach as a previously described method [10]. The second algorithm modified this approach by applying a single cylinder of best fit to both condyles. The PCA was generated from the point cloud (the cloud of digitized points generated during the registration process) digitized intraoperatively, and matched to the CT data with surface-matching software. For comparison to the other axes, the PCA was externally rotated by 3° (PCA-3) [27]. The PCA is internally rotated by a mean of 3° to the surgical TEA [1] and this corresponds to the built-in correction of manual posterior referencing jigs [1].
Each surgeon performed TKA according to his normal protocol. The surgically treated limb was prepared and isolation drapes applied. Data were collected using the Stryker Precision navigation system (Stryker Corporation, Kalamazoo, MI, USA) as previously described [8]. The hip was taken through a ROM, and a digital hip center was generated by the software package. The position of the malleoli was registered and the knee was taken through another ROM with neutral loading, cupping the heel with the hip in neutral rotation. The navigation software generated a preincision FFA (FFA1) from the knee motion. The surgeons then made a midline incision, before a medial parapatellar arthrotomy. The medial collateral ligament was elevated from the tibia sufficient to gain access to the joint. The epicondyles, femoral center, AP axis, and femoral condyles were recorded, followed by registration of tibial landmarks. We defined the lateral epicondyle as the most lateral prominence of the lateral femoral condyle, whereas the medial landmark was registered from the medial sulcus of the medial epicondyle [2, 4]. The navigation software then generated the surgical TEA, a line connecting these two landmarks. The knee was taken through another ROM with neutral loading, and the postincision FFA (FFA2) was measured. The surgeon prepared the femur, tibia, and patella in the standard fashion before implantation of prostheses, then performed closure in a standard fashion. We used the femoral landmarks digitized during surgery to create a local anatomic coordinate system. Each ROM the knee was taken through generated more than 100 measurements between 20° and 80° flexion. We superimposed these navigation-derived positions of the tibia and femur on the local anatomic coordinate system and exported these data from the navigation software into MATLAB (Version 9, Mathworks® Inc) for further analysis. We then processed the point cloud through an algorithm to calculate a helical axis of motion for each data point. We calculated the FFA as the mean of the result of the more than 100 helical axes.
We merged the CT images of the distal femur on the navigation-generated images using surface matching. This process involved matching the point clouds generated by intraoperative registration of the femoral condyles and anterior femoral cortex with the CT images. We confirmed the accuracy of the surface-matching technique by inserting radiopaque markers into five cadaveric knees, which then underwent CT scans and digitization of the markers’ locations using the navigation package. After superimposition of the images produced by each technique, the markers’ locations were analyzed to reveal a mean deviation of 2.4° introduced by the surface matching. The mean error in axial rotation was 0.9°.
FFA1 and FFA2 were expressed as an angular deviation from the CT-derived TEA (CT-TEA). The within-patient reliability of the FFA was assessed by determining if the arthrotomy altered angular deviation of the FFA relative to the CT-TEA. The absolute reliability of the average angular deviation, that is, whether the average deviation changed as a result of the arthrotomy, was assessed using a paired t-test, with Cohen’s d used to express the size of the effect [7]. Additionally, a predicted difference between the angular deviations of FFA1 and FFA2, based on the observed data, was calculated with 99% confidence intervals [7]. The validity of the FFA was assessed by comparing the angular deviation between FFA1 and the gold standard CT-TEA. The frequency with which FFA1 fell within a clinical threshold of ± 3° [14] from the CT-TEA as a proportion of the total number of observations was calculated. The angular deviations were compared using a one-way ANOVA test, following assessment of the data for normality and equality of variance. Tukey’s HSD post hoc comparison was performed to identify the location of differences between methods. The size of the effect between methods was expressed using the R2 statistic.
FFA1 was compared with other methods of axis generation by repeating this process for the angular deviations of the surgical TEA, the cylindrical models (one cylinder and two cylinders) and the posterior condylar axis with 3° internal rotation (PCA-3). The angular deviations of the axes generated intraoperatively also were averaged to assess whether combined axes offered better agreement with the CT-TEA. The FFA1 and surgical TEA axes were averaged (FFA1 + surgical TEA) in addition to the FFA1, surgical TEA and PCA axes (combined). Further comparison was done by analyzing the between-patient variability of the angular deviations for each rotational axis. These were calculated by determining the absolute difference between each measurement and the mean of the sample for each axis. Between-patient variability of the angular deviations for each rotational axis was compared using a second one-way ANOVA as described above, including post hoc comparisons. In addition, the predicted range of values for a single future measurement, the prediction interval, was calculated for each method. The prediction interval indicates the most likely range of values within which the angular deviation for each method will fall for the next future patient and provides an indication of between-patient variability. Alpha and confidence interval were set a priori at 5% and 95% respectively for the t-tests, correlation, and ANOVAs, and a 99% confidence interval was set for the prediction interval [12, 29]. All statistical analyses were conducted in Minitab® statistical software (Version 16, Minitab® Inc, State College, PA, USA).
Results
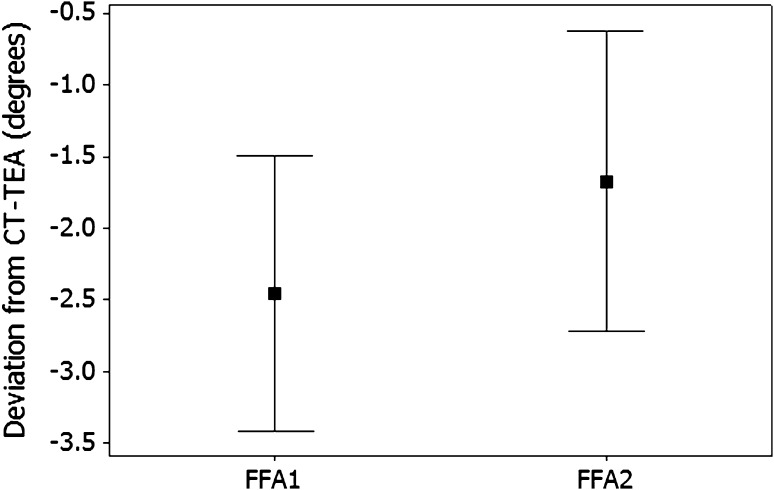
Generating the FFA was reproducible, with FFA1 correlated (r = 0.89; p < 0.01) with FFA2 values. However, the mean FFA2 value was internally rotated relative to FFA1 (p < 0.01) (Fig. 1).
Fig. 1.
The graph shows the angular deviation between the preincision FFA (FFA1) and postincision FFA (FFA2). The error bars represent the 95% confidence intervals around the mean. FFA = functional flexion axis.
Comparing the FFA1 with the CT-TEA revealed these two axes were within 3° of each other for 48% of the sample. The predicted value for a single future measurement using the FFA1 was externally rotated relative to the CT-TEA.
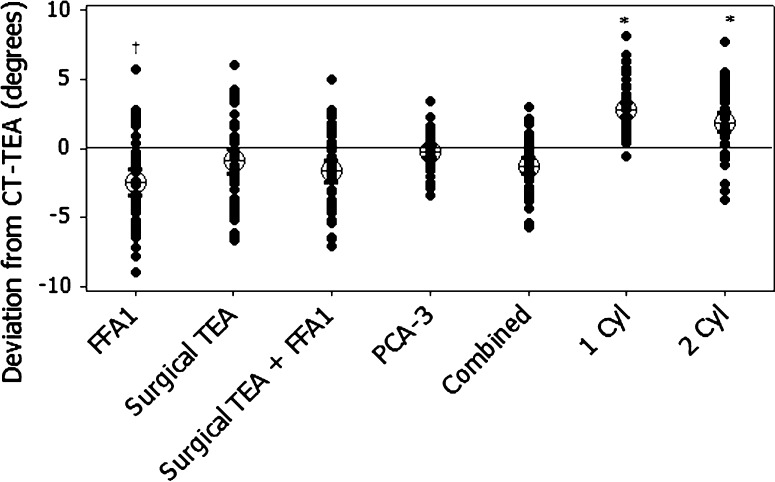
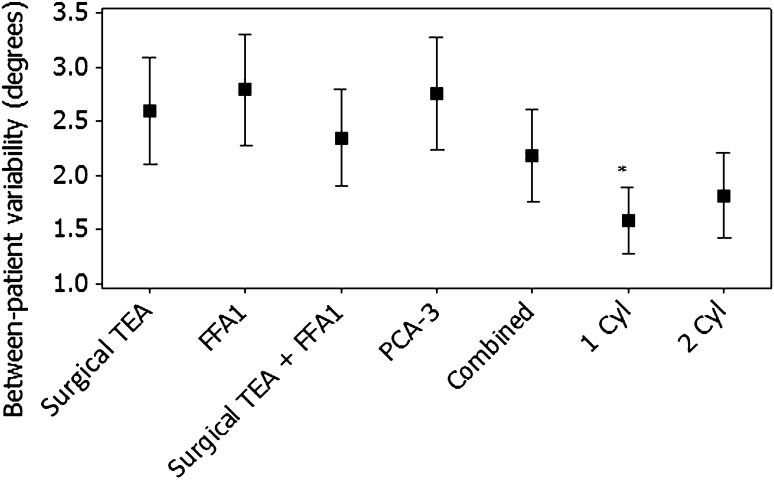
The accuracy of FFA1 compared with the CT-TEA was less than the other axes compared with the CT-TEA, with the surgical PCA-3 falling within the 3° threshold in 56% of cases, the one-cylinder axis 56%, surgical TEA 58%, surgical TEA plus FFA1 60%, the combined axis 60%, and the two-cylinder axis 66%. FFA1 and surgical TEA were similar (p = 0.195); however, both were externally rotated relative to the one-cylinder and two-cylinder axes (Fig. 2). The confidence limits bounding the predicted angular deviations for FFA1 were also wider than other methods (Table 1). Although the surgical TEA’s predicted value was in closer agreement with the CT-TEA, the total width of the interval was similar to the FFA1. The combined axis reduced the external rotation of FFA1 and decreased the width of the prediction interval (Table 1). A small difference was observed between methods for between-patient variability of the rotational axes (R2 = 0.06; p < 0.01). Less variability was observed for the one-cylinder axis compared with the FFA1 and PCA-3 axes (Fig. 3). We detected no differences between the surgical TEA and FFA1 with the remaining methods, or between the surgical TEA and FFA1.
Fig. 2.
The graph shows angular deviation between each knee flexion axis and the CT-TEA, denoted by the solid line at zero. The error bars represent 95% confidence intervals about the mean. FFA = functional flexion axis; TEA = transepicondylar axis; FFA1 = preincision FFA; FFA2 = postincision FFA; PCA-3 = posterior condylar axis externally rotated by 3°; Cyl = cylinder.
Table 1.
Predicted values for a single future measurement with 99% CI and total interval width*
| Rotation axis | Predicted value | Lower limit | Upper limit | Total |
|---|---|---|---|---|
| Preincision FFA1 | −2.5 | −11.5 | 6.6 | 18.1 |
| PCA-3 | −1.3 | −10.2 | 7.6 | 17.8 |
| Surgical TEA | −0.91 | −9.4 | 7.6 | 17 |
| Surgical TEA + preincision FFA1 | −1.7 | −9.3 | 6 | 15.3 |
| Combined | −1.6 | −8.8 | 5.6 | 14.4 |
| 2 cylinder | 1.9 | −4.3 | 8.1 | 12.4 |
| 1 cylinder | 2.8 | −2.4 | 8 | 10.4 |
* All values are in degrees; FFA1 = preincision functional flexion axis; PCA = posterior condylar axis externally rotated by 3°; TEA = transepicondylar axis.
Fig. 3.
The graph shows between-patient variability of knee flexion axes. The error bars represent the 95% confidence intervals about the mean. FFA = functional flexion axis; TEA = transepicondylar axis; FFA1 = preincision FFA; PCA-3 = posterior condylar axis externally rotated by 3°; Cyl = cylinder.
Discussion
The improved accuracy in component positioning afforded by computer navigation has focused attention on defining the ideal component position. Axial rotation of the femoral component is crucial for obtaining well-balanced flexion gaps and tibiofemoral and patellofemoral congruency through flexion [22, 27]. However it has been difficult to define the ideal rotational target with variations in its described location. A robust kinematically derived target therefore is an attractive proposition. We sought to evaluate the accuracy and validity of the FFA by (1) analyzing its reproducibility at two different stages in the surgical procedure, (2) comparing it with a CT-derived gold standard, and (3) comparing it with other methods of choosing a rotational target available to the operating surgeon.
We acknowledge limitations of our study. First, calculation of the CT-TEA involves manual identification of the appropriate landmarks from axial CT slices. This is prone to error and is unreliable [26, 28]. However no better gold standard has been described. Second, the data from computer navigation and CT data were combined to allow comparison of the different axes. The mean error in surface matching axial rotation of 0.9° seen in our series suggested meaningful comparisons could be drawn between the CT data and the navigation data for measurements in the axial plane. Third, the FFA is generated by flexing and extending the anesthetized patient’s knee thus eliminating active muscle contraction and perhaps affecting knee kinematics. Finally, the effects of a tourniquet also must be considered with possible quadriceps tethering and resultant alteration in tibiofemoral rotation as the knee is flexed.
The reproducibility of generating the FFA was evaluated by comparing the FFA1 with FFA2 and these correlated (R2 = 0.89). The mean difference between the two axes was 1.5° (± 1.2°) internal rotation. Further analysis revealed this difference was only in the results of one operating surgeon (JR) and could be attributed to the way he sectioned the ACL as part of the surgical approach. The second operating surgeon (DP) did not routinely section the ACL before registering the FFA2 and a comparison of his axes in isolation showed better correlation. Doro et al. [8] also found the FFA was reproducible in their cadaveric study.
The validity of the FFA was evaluated through comparison of the FFA1 to the CT-TEA. These were within a clinical threshold of ± 3° in only 48% of cases. This compared poorly with the other rotational targets evaluated and suggests a limited clinical role for the FFA. The relationship between the CT-TEA and the kinematically derived, nonfixed helical FFA is difficult to predict. We showed these to be discrete axes; therefore, using a mean of the helical axes as the best guide to femoral component rotation appeared to be a flawed concept since the position of the axis in the femur was dependent on the tibiofemoral flexion angle at any point. In turn, attempting to recreate the native helical flexion axis with a symmetric femoral prosthesis with either cruciate retaining or posterior stabilized geometry has the same potential flaws [17].
The validity of alternative rotational targets has previously been investigated. Churchill et al. [6] found, in their study of 15 cadaveric specimens, that the TEA approximated the optimal flexion axis of the knee as defined by a compound hinge mathematical model. However, we found these two axes to be nonparallel, with a mean difference of 2.9°, which might be accounted for by their use of the TEA rather than the surgical TEA. Asano et al. [2] reported the surgical TEA coincided with the fixed axis of flexion-extension generated by a two-cylinder model within the 0° to 90° range and we found good agreement between these two axes. Eckhoff et al. [9] suggested that the two-cylinder axis is the true flexion extension axis of the knee, substantially differing from the TEA when viewed in three dimensions. No comparison was drawn in their study with the surgical TEA. Assuming correct identification of the epicondyles, the CT-TEA we used, a line connecting the medial epicondylar sulcus to the lateral epicondyle, would appear to be a reasonable gold standard with which other fixed axes may be compared.
Intraoperative detection of the epicondyles is reportedly unreliable [4, 8, 15], suggesting limits to its clinical usefulness. In our series it was more reproducible (SD, 1.4°; ICC, 0.83) than in previous studies [4, 8]. For example, Berger et al. [4], in a series of 75 cadaveric measurements, reported intraobserver and interobserver variations of 1.5° and 4°, respectively. Furthermore, Jenny and Boeri [15] described 6° and 9° for intraobserver and interobserver variations, respectively, in a series of 20 TKAs. The improvement we saw may reflect the operating surgeons’ greater familiarity with the navigation system, requiring routine identification of the epicondyles and the high-volume nature of their practices.
Component rotation is a critical factor in the outcome of TKA [20–22], and to date there is no specific measure that has been reliable for all surgeons and clinical scenarios to achieve this. Kinematic registration therefore is attractive as a potentially simple method to generate a functional axis based on the individual patient’s knee motion. This might represent a truly patient-specific rotational target, which could be attained without the expense and potential measurement errors of image-based methods. The reproducibility of the FFA1 and surgical TEA was similar; however, the greater between-patient variability in the FFA1 meant that general clinical use could not be recommended at this stage of development. The differences seen between the FFA and the other axes examined do not refute its validity, and further development to improve its reliability and better understand its applicability to clinical practice is warranted.
Acknowledgments
We thank Michael Theodor Dipl-Ing for invaluable assistance in the technical aspects of the data analysis and Sean Leo MD for assistance with data collection and analysis.
Footnotes
Two authors certify that he (DP, JR), or a member of his immediate family, has or may receive payments or benefits, in any one year, an amount in excess of $10,000 from a commercial entity (Stryker South Pacific, St Leonards, Australia) related to this work.
All ICMJE Conflict of Interest Forms for authors and Clinical Orthopaedics and Related Research editors and board members are on file with the publication and can be viewed on request.
Clinical Orthopaedics and Related Research neither advocates nor endorses the use of any treatment, drug, or device. Readers are encouraged to always seek additional information, including FDA-approval status, of any drug or device prior to clinical use.
Each author certifies that his institution has approved the human protocol for this investigation that all investigations were conducted in conformity with ethical principles of research, and that informed consent for participation in the study was obtained.
This work was performed at the Sydney Orthopaedic Research Institute and the North Sydney Orthopaedic and Sports Medicine Centre
References
- 1.Akagi M, Yamashita E, Nakagawa T, Asano T, Nakamura T. Relationship between frontal knee alignment and reference axes in the distal femur. Clin Orthop Relat Res. 2001;388:147–156. doi: 10.1097/00003086-200107000-00022. [DOI] [PubMed] [Google Scholar]
- 2.Asano T, Akagi M, Nakamura T. The functional flexion-extension axis of the knee corresponds to the surgical epicondylar axis: in vivo analysis using a biplanar image-matching technique. J Arthroplasty. 2005;20:1060–1067. doi: 10.1016/j.arth.2004.08.005. [DOI] [PubMed] [Google Scholar]
- 3.Australian Orthopaedic Association. National Joint Replacement Registry Annual Report. 2010. Australian Orthopaedic Association. Available at: http://www.dmac.adelaide.edu.au/aoanjrr/documents/AnnualReports2011/AnnualReport_2011_WebVersion.pdf. Accessed July 14, 2011.
- 4.Berger RA, Rubash HE, Seel MJ, Thompson WH, Crossett LS. Determining the rotational alignment of the femoral component in total knee arthroplasty using the epicondylar axis. Clin Orthop Relat Res. 1993;286:40–47. [PubMed] [Google Scholar]
- 5.Chauhan SK, Clark GW, Lloyd S, Scott RG, Breidhal W, Sikorski JM. Computer-assisted total knee replacement: a controlled cadaver study using a multi-parameter quantitative CT assessment of alignment (The Perth CT Protocol) J Bone Joint Surg Br. 2004;86:818–823. doi: 10.1302/0301-620X.86B6.15456. [DOI] [PubMed] [Google Scholar]
- 6.Churchill DL, Incavo SJ, Johnson CC, Beynnon BD. The transepicondylar axis approximates the optimal flexion axis of the knee. Clin Orthop Relat Res. 1998;356:111–118. doi: 10.1097/00003086-199811000-00016. [DOI] [PubMed] [Google Scholar]
- 7.Cohen J. The earth is round. Am Psych. 1994;49:997–1003. doi: 10.1037/0003-066X.49.12.997. [DOI] [Google Scholar]
- 8.Doro LC, Hughes RE, Miller JD, Schultz KF, Hallstrom B, Urquhart AG. The reproducibility of a kinematically-derived axis of the knee versus digitized anatomical landmarks using a knee navigation system. Open Biomed Eng J. 2008;2:52–56. doi: 10.2174/1874120700802010052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Eckhoff D, Hogan C, DiMatteo L, Robinson M, Bach J. Difference between the epicondylar and cylindrical axis of the knee. Clin Orthop Relat Res. 2007;461:238–244. doi: 10.1097/BLO.0b013e318112416b. [DOI] [PubMed] [Google Scholar]
- 10.Eckhoff DG, Bach JM, Spitzer VM, Reinig KD, Bagur MM, Baldini TH, Rubinstein D, Humphries S. Three-dimensional morphology and kinematics of the distal part of the femur viewed in virtual reality: Part II. J Bone Joint Surg Am. 2003;85(suppl 4):97–104. doi: 10.2106/00004623-200300004-00012. [DOI] [PubMed] [Google Scholar]
- 11.Elias SG, Freeman MA, Gokcay EI. A correlative study of the geometry and anatomy of the distal femur. Clin Orthop Relat Res. 1990;260:98–103. [PubMed] [Google Scholar]
- 12.Escobar LA, Meeker WQ. Statistical prediction based on censored life data. Technometrics. 1999;41:113–124. doi: 10.1080/00401706.1999.10485632. [DOI] [Google Scholar]
- 13.Hollister AM, Jatana S, Singh AK, Sullivan WW, Lupichuk AG. The axes of rotation of the knee. Clin Orthop Relat Res. 1993;290:259–268. [PubMed] [Google Scholar]
- 14.Insall JN, Binazzi R, Soudry M, Mestriner LA. Total knee arthroplasty. Clin Orthop Relat Res. 1985;192:573–576. [PubMed] [Google Scholar]
- 15.Jenny JY, Boeri C. Low reproducibility of the intra-operative measurement of the transepicondylar axis during total knee replacement. Acta Orthop Scand. 2004;75:74–77. doi: 10.1080/00016470410001708150. [DOI] [PubMed] [Google Scholar]
- 16.Jenny JY, Clemens U, Kohler S, Kiefer H, Konermann W, Miehlke RK. Consistency of implantation of a total knee arthroplasty with a non-image-based navigation system: a case-control study of 235 cases compared with 235 conventionally implanted prostheses. J Arthroplasty. 2005;20:832–839. doi: 10.1016/j.arth.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 17.Katz MA, Beck TD, Silber JS, Seldes RM, Lotke PA. Determining femoral rotational alignment in total knee arthroplasty: reliability of techniques. J Arthroplasty. 2001;16:301–305. doi: 10.1054/arth.2001.21456. [DOI] [PubMed] [Google Scholar]
- 18.Kurosawa H, Walker PS, Abe S, Garg A, Hunter T. Geometry and motion of the knee for implant and orthotic design. J Biomech. 1985;18:487–499. doi: 10.1016/0021-9290(85)90663-3. [DOI] [PubMed] [Google Scholar]
- 19.Laskin RS. Flexion space configuration in total knee arthroplasty. J Arthroplasty. 1995;10:657–660. doi: 10.1016/S0883-5403(05)80211-6. [DOI] [PubMed] [Google Scholar]
- 20.Moreland JR. Mechanisms of failure in total knee arthroplasty. Clin Orthop Relat Res. 1988;226:49–64. [PubMed] [Google Scholar]
- 21.Ritter MA, Faris PM, Keating EM, Meding JB. Postoperative alignment of total knee replacement: its effect on survival. Clin Orthop Relat Res. 1994;299:153–156. [PubMed] [Google Scholar]
- 22.Romero J, Stahelin T, Binkert C, Pfirrmann C, Hodler J, Kessler O. The clinical consequences of flexion gap asymmetry in total knee arthroplasty. J Arthroplasty. 2007;22:235–240. doi: 10.1016/j.arth.2006.04.024. [DOI] [PubMed] [Google Scholar]
- 23.Shiavi R, Limbird T, Frazer M, Stivers K, Strauss A, Abramovtiz J. Helical motion analysis of the knee: I. Methodology for studying kinematics during locomotion. J Biomech. 1987;20:459–469. doi: 10.1016/0021-9290(87)90247-8. [DOI] [PubMed] [Google Scholar]
- 24.Shiavi R, Limbird T, Frazer M, Stivers K, Strauss A, Abramovtiz J. Helical motion analysis of the knee: II. Kinematics of uninjured and injured knees during walking and pivoting. J Biomech. 1987;20:653–655. doi: 10.1016/0021-9290(87)90032-7. [DOI] [PubMed] [Google Scholar]
- 25.Soudan K, Audekercke R, Martens M. Methods, difficulties and inaccuracies in the study of human joint kinematics and pathokinematics by the instant axis concept: example: the knee joint. J Biomech. 1979;12:27–33. doi: 10.1016/0021-9290(79)90006-X. [DOI] [PubMed] [Google Scholar]
- 26.Suter T, Zanetti M, Schmid M, Romero J. Reproducibility of measurement of femoral component rotation after total knee arthroplasty using computer tomography. J Arthroplasty. 2006;21:744–748. doi: 10.1016/j.arth.2005.09.012. [DOI] [PubMed] [Google Scholar]
- 27.Verlinden C, Uvin P, Labey L, Luyckx J, Bellemans J, Vandenneucker H. The influence of malrotation of the femoral component in total knee replacement on the mechanics of patellofemoral contact during gait: an in vitro biomechanical study. J Bone Joint Surg Br. 2010;92:737–742. doi: 10.1302/0301-620X.92B5.22603. [DOI] [PubMed] [Google Scholar]
- 28.Yoshino N, Takai S, Ohtsuki Y, Hirasawa Y. Computed tomography measurement of the surgical and clinical transepicondylar axis of the distal femur in osteoarthritic knees. J Arthroplasty. 2001;16:493–497. doi: 10.1054/arth.2001.23621. [DOI] [PubMed] [Google Scholar]
- 29.Yu K, Ally A. Improving prediction intervals: some elementary methods. Am Stat. 2009;63:17–19. doi: 10.1198/tast.2009.0003. [DOI] [Google Scholar]