Sexual Dimorphism and Sexual Selection: A Unified Economic Analysis

Abstract

We develop a life history model with two sexes, and study the optimal energy allocation strategy of males and females. We join Darwin and others in suggesting that the origin of sexual dimorphism and sexual selection is the difference between male and female reproduction costs. Due to this assumed cost difference, the resulting Bellman equations of gene dynamics in our two-sex life history model imply a large “energy surplus” on the part of males. This allows the male form to devote energy to the development of some costly male traits that help the males to compete for access to females. These costly male traits are sexually dimorphic. Using this life history model, we are able to explain important features of sexual dimorphism, as well as why males often transfer less to their offspring than do females, and why only females have menopause.

1 Introduction

Over the past two decades a number of researchers (e.g. Bergstrom [1995], Rogers [1994], Robson and Kaplan [2003], Chu and Lee [2006], Chu and Lee [2008a,b]) have applied economic approaches to the evolutionary processes leading to particular characteristics in various species. A recent survey can be found in Cox (2007). A topic mentioned but not seriously studied in the economics literature is sexual dimorphism, the phenomenon that male and female adults possess significantly different biological traits, whereas juveniles are more similar (see the classic paper by Trivers, 1972). A related topic is sexual selection, in which either direct male-male competition for access to females or females’ preferences for certain male traits shape the evolution of those traits. It is well known from evolutionary research that sexual dimorphism across species is highly correlated with the intensity of competition for mating partners. In practice, this competition is usually between males, although it is increasingly recognized that female competition is pervasive (Clutton-Brock, 2007). In this paper we propose a unified economic theory that can explain the core features of sexual dimorphism and sexual selection, although not all the nuances such as female competition for mates.

1.1 Previous Literature

A brief introduction to the abundant biological literature should be helpful to general readers. According to Maynard Smith (1991), there are two broad types of sexual interactions: intrasexual competition and intersexual selection. The latter involves both male traits and female preferences; and the former does not consider the preference side of females, but emphasizes the male-male competition.

For intrasexual competition, the classic article is a contribution by Trivers (1972), who argued that relative parental investment is the key to understanding sexual competition. By parental investment, Trivers meant “any investment by the parent in an individual offspring that increases the off-spring’s chance of surviving (and hence reproductive success) at the cost of the parent’s ability to invest in other offspring” (p.139, italics added). From the italicized words and the discussion in his paper, we know that the resources Trivers refers to are mostly parental transfers after the offspring is born. From the perspective of life history theory, however, parental transfers are part of the evolved life history strategy that is to be explained. We believe that sexual dimorphism can be explained based on more fundamental characteristics of a species such as the difference between the sexes in the size of investment in gametes.

Other than Trivers (1972), Emlen and Oring (1977) emphasized the importance of operational sex ratio (OSR) on sexual selection, where the OSR is defined as the ratio of active males to fertilizable females. In practice, the OSR is evidently related to ecological, geographical, and spatial factors that may influence the environment of male-female interactions. Kokko and Johnstone (2002) considered the joint influence of parental investment, mortality, mate-encounter rate and OSR, and concluded that the importance of parental investment outweighs that of OSR. In this paper, we leave most environmental factors to the background, and concentrate on the role of parental investment decisions.

In the analysis of sexual interaction, the literature sometimes addresses the correlation of dimorphic traits with other characteristics of a species, and the interpretation or any correlation. For instance, in studies of primates, Leutenegger and Choverud (1982) found and analyzed a correlation between sexual dimorphism and body size; however, Gaulin and Sailer (1984) suggested a very different interpretation of the same correlation. Partly because of such difficulties of interpretation, we set up a life history model to study the problem of sexual dimorphism. In the framework of an optimal life history, species’ traits such as body size and tooth size are control variables chosen by species, and the interpretation follows naturally from the model. Basically, the only fundamentals in a life history model are the energetic costs of various control variables, and we shall interpret most observations by sex-specific differences of these fundamentals, thereby avoiding paradoxical interpretations of correlations.

In our analysis, we go beyond Trivers (1972) and differentiate afterbirth parental transfers from fertility costs, which were bundled together as “parental investments” by Trivers. We will take sex-specific fertility costs as given for each species, whereas parental transfers are something each species “chooses” in their life history. This distinction is important to the understanding of evolutionary dynamics. For example, our theory suggests that viviparous species are likely to have sexual dimorphism, for viviparous males and females have drastically different reproduction costs.

For intersexual selection, Zahavi (1975) argued that males may have some advantageous traits which are unobservable to females. In this case, males may employ a seemingly useless trait (a handicap), such as the plumage of some birds, to signal their superior quality to females. However, Fisher (1958) and Lande and Arnold (1985) all pointed out that the evolution of such trait-preference may be selectively neutral. Using a simple 2-trait 2-allele model, Kirkpatrick (1982) showed that even the initial selective advantages of evolution are not necessary. This pretty much makes the evolutionary outcome of intersexual selection indeterminate. Later, Iwasa et al. (1991) showed that this neutrality result breaks down if there is a small cost of female searching. They also demonstrated that the handicap hypothesis is valid only if there exists a connection between the male trait and viability parameters. Using our model we are able to provide a neat economic interpretation for this connection.

1.2 Contribution of this Paper

The existing literature explains various features of sexual dimorphism and sexual selection using different models, including quantitative genetics (Iwasa et al. [1991]), Malthusian competition (Hausken and Hirshleifer [2008]), and a very insightful verbal analysis (Trivers [1972]). In this paper, we propose a unified framework of two-sex life history, along the lines of Stearns (1972), that can explain many of the core features of sexual selection and its consequences.

The origin of sexual dimorphism and sexual selection as proposed by (Darwin 1871) is the difference between male and female reproduction costs: the cost of producing sperm is trivial for males and that of producing eggs by females is significantly larger, not to mention the cost of pregnancy and delivery for many viviparous species. This leads to a higher potential rate of reproduction (PRR) for males than females, so that the female costs and PRR constrain the male possibilities, leaving them with surplus energy that can be devoted to costly traits that may increase their access to female mates. Our formal analysis of the optimal energy allocation strategy of males and females over the course of a life history incorporates these features.

The fact that males have an energy surplus implies that their overall reproductive output is constrained by females. This constraint greatly simplifies the analysis, and helps us derive clear-cut sex-dimorphism results. Furthermore, this constraint also implies that the analyses of female fitness and male traits can be done recursively. As a result, we find that the analytics of inter-sexual interactions is not very different from that of male-male intra-sexual competition.

Consider the scenario that many males compete to become an alpha male, who alone can mate. Since there is only a small chance for a male to become an alpha male, ex ante each male child can be seen as a risky lottery with a small probability to mate many females and a large probability to mate none. Female children almost surely can mate with the alpha male, and hence the corresponding lottery is degenerate. From the parents’ point of view, their children are assets for the proliferation of their genes. Just as an investor’s portfolio of assets may include some risky ones which may yield a high rate of return, and some safe ones that will likely yield a low rate of return, so we can view the parents’ portfolio of children. The parents have a sex-specific portfolio, with male children who are high-risk high-return, and females who are low-risk and low-return. We shall explain why this particular phenomenon arises from a life history model.

Male competition favors the evolution of some particular male traits, and eventually to the phenomenon of sexual dimorphism. Using this two-sex life history model we are also able to explain, for instance, why for most species males provide smaller intergenerational transfers than females, and why menopause occurs occasionally in females but never in males. Thus, we elaborate the discussion of Trivers (1972), and extend it to some other sex-specific differences that have not been analyzed in the literature. In his review article, Clutton-Brock (2007) concludes that “…the theory of sexual selection still provides a robust framework that explains much of the variation in the development of secondary sexual characters in males….” He discusses the increasing evidence of the prevalence and importance of sexual selection in females, but finds that the recognition of these complexities “does not undermine its basic structure”. It is this basic structure of the classic theory that we model, analyze and interpret in the following.

1.3 Paper Structure

The rest of this paper is arranged as follows. Section 2 introduces the model of life history and energy constraints, and derives the two-sex Bellman equation for maximizing fitness. Section 3 discusses intrasexual competition, and relates various phenomena of sexual dimorphism to the difference of distinct sex-specific reproduction costs. Section 4 discusses intersexual selection. The fifth and sixth sections are about differences in male-female transfers and menopause. The final section summarizes and concludes.

2 A Two-sex Model of Selfish Genes

In all but one section of this paper we adopt a 1-age or 2-age setting. The two ages are denoted as (0, 1). The principle of our modelling is to choose the simplest setting to the extent that the key message can be delivered.

There are two sexes, male and female. Let M_a,t be the value of a genome carried by a male at age-a and time-t, and F_a,t be the value of a genome carried by a female at age-a and time-t. The value of a genome is the maximum reproductive fitness that could be achieved starting at some particular age and time given all the prior life history strategic allocations (e.g. allocations of energy to survival, fertility, or somatic growth at earlier ages). Let m(f ) be the reproductive effort by males (females), and p_a,m (p_a,f ) be the survival probability for males (females) aged-a. In practical context, m refers to the male effort of producing sperm and successful insemination (not including the costs of gaining access to a female through competition based on costly traits and not including post-birth parental investments), and f refers to the female effort of producing ova and conducting a successful pregnancy and delivery, but not including costs of mate selection. At each age, energy is assumed to be allocated among four uses: maintenance, reproduction, somatic growth and parental downward transfers.

2.1 Event Order and Preliminaries

Life begins with a juvenile stage of growth and survival but no reproduction (age-0), followed by an adult stage of reproduction and survival but no growth (age-1), that is, a “determinate” life history.³ The juvenile at age-0 allocates energy between maintenance and growth. However, we must specify he order of events for an age-1 adult. We assume that at the beginning of age-1, each adult first hunts or forages, generating the energy to be used throughout this life cycle stage. Then, each adult decides how to allocate this energy between reproduction and maintenance. This event order is somewhat arbitrary, but some order must be specified in this discrete-time model. None of our results will be affected qualitatively if this order is changed.

In some parts of our analysis, we consider reproductive access as a lottery. For instance, monogamy and polygamy are two different marriage-fertility lotteries for males: the former has a high probability of mating one partner and a low probability of mating none, and the latter has a low probability of mating many partners and a high probability of mating none. When the random outcome of the lottery is realized, each adult allocates the available energy to maintenance, transfers and reproduction. Nature then determines whether an adult survives, and only survivors can reproduce.

In this 2-sex model, individuals of opposite sexes combine their reproductive efforts to successfully produce an offspring. However, only one sex actually bears the child, and we call this sex “female”. There are two unique features associated with the female sex. First, as Trivers (1972 p. 138) pointed out, for almost all two-sex species (and especially for viviparous ones), the metabolic energy of reproduction is particularly large for females, but is very small for males. Second, the number of male impregnations by males can never exceed the number of female pregnancies, whereas it is the female’s pregnancies that determine the final births. The first property specifies a difference in energy coefficient associated with reproduction, and the second property suggests an aggregation constraint on male/female reproduction.

2.2 The Two-sex Bellman Equations

We shall first write down Bellman’s principle of optimality for the maximal replication of genes (Bellman 1957), and then explain its meaning. Following Chu and Lee (2006), we see that the Bellman equations for selfish genes in this 2-sex model look like

$$\begin{array}{l}{F}_{0,t}=max\left\{p_{0,f}{F}_{1,t-1}\right\}\\ M_{0,t}=max\left\{p_{0,m}{M}_{1,t-1}\right\}\\ F_{1,t-1}=max\left\{p_{1,f_j}{f}_j\left(\frac{M_{0,t-1}}{4}+\frac{F_{0,t-1}}{4}\right)\right\}\\ M_{1,t-1}=max\left\{p_{1,m_i}{m}_i\left(\frac{M_{0,t-1}}{4}+\frac{F_{0,t-1}}{4}\right)\right\}\end{array}$$ (B)

In the above expression, the fitness maximization is over age-specific controls including (p_a,mi, p_a,fj, m_i, f_j ), a = 0, 1 and some others to be described shortly, where m_i refers to the individual’s i^th fertility choice, and p(a, m_i) refers to the individual’s survival probability at age-a, when the i^th fertility option is chosen.

2.3 Interpreting the Bellman Equations

Individuals at age-0 only grow and survive but do not give birth, so the value of the genes they carry derives from successful survival to age 1 one period later. This explains the first two equations. For genes of females at age 1, the F_1,t equation is straightforward. If a female lioness has f_j pregnancies, we assume, as in Trivers (1972 p.140), that the probability is 1/2 of having a newborn of either sex.⁴ The values in the next generation of genes carried by males and females at age-0 are denoted respectively M_0,t−1 and F_0,t−1. Because each birth only carries 1/2 of the original genes, and because there is a 1/2 probability that a given birth will be male or female, we divide the M_0,t−1 and F_0,t−1 by 4 on the right hand side of the third equation. This explains the F_1,t−1 equation.

Because the expected number of impregnations, which is p_1,mim_i, times the number of age-1 males, must be equal to the expected number of pregnancies, which is p_1,fjf_j times the number of age-1 females, an aggregation constraint must be taken into account as we solve the Bellman equation. If the numbers of surviving male and female adults are roughly equal, and if the unconstrained p_1,mim_i is expected to be larger than the unconstrained p_1,fjf_j, then the male’s choices will be suppressed. We shall come back to this point later.

Some choice of the control variables, designated by an asterisk, will maximize the Euler-Lotka growth rate λ that is implied by the Bellman equations above. Replacing the controls by these optimal values, we can iterate the Bellman equations (B) to obtain the dynamic equations for (M_0,t, F_0,t), as in Chu and Lee (2006). The dimension of the state variables can be further reduced, once we observe that we can define x_t = (M_0,t + F_0,t)/2, and re-write everything in terms of x_t. The Bellman equations (B) can now be expressed compactly as

$$x_t=\frac{1}{4}\left[p_{0,m}(p_{1,m_{i^{\ast }}}{m}_{i^{\ast }})+p_{0,f}(p_{1,f_{j^{\ast }}}{f}_{j^{\ast }})\right]x_{t-1}$$ (1)

From demographic theory it is well known that as long as the controls (m_i^*, f_j^*, p_a,s) are time invariant, the dynamics of (1) will guarantee the convergence of x_t to an exponential growth path, growing at a rate called the Euler-Lotka parameter. Suppose λ is this steady state growth rate of x_t. Then the above discussion suggests a simple characterization of the Euler-Lotka parameter λ for the two-sex model:

$$\lambda =\underset{i,j}{max}\frac{1}{4}\left[p_{0,m}(p_{1,m_i}{m}_i)+p_{0,f}(p_{1,f_j}{f}_j)\right]$$ (2)

On the right hand side of (2), terms in the square brackets are the expected number of replications of each gene over the lifetime of its carrier, similar to the lifetime birth criterion or Net Reproduction Ratio (R₀) adopted in many of the one-sex (female) models (see e.g. Sozou and Seymour [2003]). Note that in a one-age setting, we can simply assume p_0,m = p_0,f = 1, drop the age subscript of p_m and p_f, and re-write the Euler-Lotka parameter as

$$\lambda =\underset{i,j}{max}\frac{1}{4}\left[p_{m_i}{m}_i+p_{f_j}{f}_j\right]1-\text{age}\text{setting}$$

2.4 Energy Constraints and Assumptions

Consider the energy constraint in adulthood (at age 1). Let the unit cost of m and f be respectively c_m and c_f. Similarly, the unit cost of p_1,s is assumed to be b_1,s. These are the energetic costs per unit of survival and fertility. These fertility costs exclude post birth transfers which we denote separately as T_m and T_f. The fertility costs also exclude pre-impregnation costs of competition or searching for mates. Then, if a male and a female choose i and j respectively, we have the following adult energy constraints:

$$\begin{array}{r}{b}_{1,m}{p}_{1,m_i}+c_m{m}_i+T_m\le g(z_m)\\ b_{1,f}{p}_{1,f_j}+c_f{f}_j+T_f\le g(z_f),\end{array}$$

where z_f (z_m) is the initial somatic state of female (male) adults, most simply size, for example. We assume that the energy generated is increasing in z, given by g(z_s). In Trivers (1972), c_f f_j and T_f are combined under the heading “female investment”, and similarly for males. Here we separate them and shall provide respective interpretations later. In a one-age setting, we simply assume that T_s is zero. Later in a two-age setting we shall study how T_m and T_f are determined.

3 How Does Sexual Dimorphism Arise?

Since juvenile growth is not important for the discussion of sexual dimorphism, we shall consider a one-age scenario in this section, set p_0,s = 1 and T_s = 0 (s = m, f ), and drop the age subscripts of (p_m, p_f ). We will return to the two age group model later. When m_i is chosen by a male, using the energy constraint (C), p_mi can be written as p_mi = (g(z_m) − c_mm_i)/b_m. Similarly, p_fj can be written as p_fj = (g(z_f ) − c_f f_j )/b_f. Substituting these into (2′), we can rewrite the fitness-maximizing problem as solving

$$\underset{i,j}{max}\frac{1}{4}\left[p_{m_i}{m}_i+p_{f_j}{f}_j\right]=\frac{1}{4}\left[\underset{i}{max}[m_i(g(z_m)-c_m{m}_i)/b_m]+\underset{j}{max}[f_j(g(z_f)-c_f{f}_j)/b_f]\right].$$ (3)

There is actually one more constraint for the male’s maximization, which we shall soon add.

We first look at the female problem, because the male’s choice does not affect the female reproduction solution (whatever the male impregnation effort, the female’s gene is passed on in each of her pregnancies). Let f_j^* be the value of f that maximizes the expected number of pregancies u (f ) given by the quadratic formula f_j (g(z_f )− c_f f_j )/b_f. The optimal policy for femalesis certainly to choose $f_j^{\ast }$. Considering the simplifying approximation that f is a continuous variable, then the optimal f from maximizing the quadratic objective function can be written as

$$f^{\ast }=g(z_f)/(2c_f).$$

3.1 A Male-Female Interacting Constraint

Now we look at the male’s choice. Let u (m) = p_mim_i be the expected number of impregnations by a male. Since this must be equal to the expected number of pregnancies, u (f ) = p_fjf_j, the following constraint should hold

$$p_{m_i}{m}_i=p_{f_j}{f}_j=p_{f^{\ast }}{f}^{\ast }\equiv F^{\ast }.$$ (4)

If the male’s outcome is constrained by the female’s optimum, then the male’s choice of reproduction is redundant. Thus, in view of (3), we see that the constraint in (4) makes the Euler-Lotka parameter in (2′) simply λ = F^*/2.

But intuitively, why is the male the constrained sex? For the time being we ignore the constraint in (4), and seek the male’s “ideal” solution, similar to the concept of the potential rate of reproduction or PRR. If males are not constrained by (4), their optimal choice of m (when it can be chosen continuously) could be solved from the maximization m_i[g(z_m) − c_mm_i]/b_m. Since m_ip_mi is quadratic in m_i, it is easy to see that under a continuous approximation,

$$m^{\ast }=g(z_m)/(2c_m).$$

Suppose that the energy available to the adult male and female does not differ much, so that the difference between g(z_m) and g(z_f ) is not significant. Then, comparing p_m^*m^* = [g(z_m)]²/(4c_mb_m) with p_f^*f^* = [g(z_f )]²/(4c_f b_f ), we see that p_m^*m^* would be significantly larger than p_f^*f^*, because c_m is significantly smaller than c_f. Thus, the male is likely to be the constrained sex.

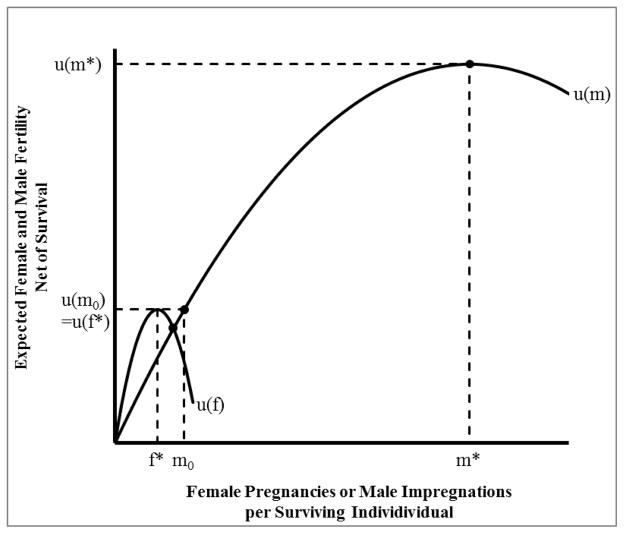
When males’ choice is constrained by (4), the ideal m^* is out of the question. From (4), for instance, the male can choose a certain m₀ such that u (m₀) = m₀p_m0 = m₀[g(z_m) − c_mm₀]/b_m = p_f^*f^*. This m₀ is the male reproduction sufficient to match the female’s f^*. The fact that p_f^*f^* and p_m^*m^* differ a lot indicates that males have much lower fertility at their compromised choice of m₀ than their potential maximum.⁵ Letting u(m) = [g(z_m) − c_mm]m/b_m, we see from Figure 1 that monogamous males are very inefficient in using their energy, producing an expected number of impregnations, u(m₀) = u (f^*), that is much lower than u(m^*).

Figure 1.

There is a large difference between the fitness-maximizing fertility of females (f*) and males (m*) abstracting from their interdependence. u(m) and u(f) are the expected number of female and male births taking into account the relation of fertility to survival through the energy constraint. Taking into account the interdependence of the sexes, the male level of expected births, u(m), is constrained to equal the female level, u(f). The hypothetical separate male optimum u(m*) violates this constraint and cannot be attained. Instead at the optimum male expected fertility is u(m₀).

3.2 The Male’s Motivation for Competition

Because male energy is used “inefficiently” due to the female constraint, there is room for an invading mutation to exploit the unused potential energy in order to improve a male’s competitive access to females. Specifically, a mutation may shift some of the male’s energy to somatic investment I which may improve the spread of his gene. The somatic investment may be enlarging canine teeth, improving muscle strength, growing bigger antlers, or larger body size, and so on. These somatic investments increase the probability of his successful impregnation of a female either by being more attractive to females, or by fighting and driving away other competitors. But of course, all investments are at the cost of reducing survival probability or gamete production (see Section 2.4).⁶

For exposition purposes, we assume that females always live in a pride of size n, and that the male faces a lottery for mating opportunity which is specified as having probability q of mating all n females in this pride, and probability 1 − q of mating none of them. In the latter case, we can think of it as a scenario in which the male in question loses the competition and is driven away. Formally, for a male indexed k, let the probability of winning these n females be written as q(I^k, I^~k), where I^k is k’s somatic investment and I^~k is the vector of investment for all other competitors. We shall consider a mutation of the male-k gene that increases I^k, and see if this will help k win over other gene lines.

Given our specification, once k becomes an alpha lion, he can impregnate all n females. The constraint in (4) now becomes

$$q(I^k,I^{~k}){np}_{f^{\ast }}{f}^{\ast }=p_{f^{\ast }}{f}^{\ast }$$ (5)

First, we check whether a mutation of male investment could invade the original gene line in which there was no sexual competition, or all males were equal. To simplify our discussion we shall consider the symmetric case. Suppose the original investment for all relevant males is the same, and is equal to $I_0^k$, which may well be zero. In such a symmetric equilibrium, each male is equally efficient in mate competition, and we know that q(I^k, I^k) = 1/n must hold at any symmetric equilibrium. If a mutation now leads male k to increases his investment slightly, while all other males make the original investment, the impact of this change on q can be written as⁷

$${\frac{\partial q(I^k,I^{~k})}{\partial I^k}|}_{I^k=I^{~k}=I_0^k}\equiv \phi (I_0^k)>0.$$ (6)

We assume φ(I^k) > 0 because more unilateral investment by k usually implies higher likelihood of winning the competition.

Noting that q(I^k, I^k) = 1/n in any symmetric equilibrium, by differentiating the left hand side of (5) we see that the mutation will invade successfully as long as (6) holds (note that in (6), b_m and c_m are parameters).

3.3 Relating Sexual Dimorphism to Reproduction Costs

How would this arms race in I^k and I^~k end? Recall from (5) that in any symmetric equilibrium the following constraint must hold:

$$\frac{g{(z_f)}^2}{4c_f{b}_f}=p_{f^{\ast }}{f}^{\ast }=\frac{{[g(z_m)-I^k]}^2}{4n{c}_m{b}_m}$$

or equivalently

$$g{(z_f)}^2=\frac{c_f{b}_f{[g(z_m)-I^k]}^2}{n{c}_m{b}_m}\equiv h(I^k,c_f,c_m),$$ (7)

where we have used the formulae f^* = g(z)/(2c_f ), and p_f^* = [g(z)− c_f f^*]/b_f. This is the equation that determines the equilibrium I^k. Since g(z_m) − I^k must be positive by the energy constraint, we see that ∂h/∂I^k < 0 in the equilibrium. Furthermore, ∂h/∂c_m (∂h/∂c_f ) is obviously negative (positive). Thus, we know that I^k and c_m/c_f move in opposite directions along the equilibrium. In fact, we have shown from (7) that when c_m (c_f ) is smaller (larger), the equilibrium I^k* is larger. Therefore, we directly relate the degree of equilibrium male competition (I^k*) in sexual competition to the relative size of male/female reproduction costs.

This is intuitively appealing, for male species with smaller c_m can produce a relatively large m costlessly, and hence they feel particularly depressed by the constraint in (4). Their excess energy, therefore, is more likely to be directed to investment on I^*.

3.4 Other Factors

In the above analysis, we put most of our emphasis on the difference in reproduction costs. But what about the ecological and territorial costs emphasized by Brown (1964) and Emlen and Oring (1977) as key factors explaining sexual dimorphism? In our setup, these environmental factors are implicitly embodied in the q(I^k, I^~k) function. For instance, in an environment where potential mates are not defendable, it is even difficult for a strong male to maintain his control over females. In our model, this implies that f is almost zero, and hence a mutation that raises investment in I^k does not pay off. Thus, sexual dimorphism in this dimension cannot arise. For life history specification of genes, environmental factors are taken as given, but our model is consistent with the resource-environment argument of Brown, and Emlen and Oring.

Our theory is also consistent with models of intersexual selection with female preferences. Conceptually, the q function in (5) may be determined, not by nature, but by female preferences, and hence only investments that appeal to females can possibly have a rewarding φ. We shall come back to this discussion later in section 4.

3.5 The Sex-specific “Portfolio”

When a competition equilibrium is reached, each male devotes I^*; but since all individuals in the new symmetric equilibrium have the same I^*, the resulting probability of winning the mating privilege must still be 1/n. Thus, what we observe is that the female faces a degenerate lottery of f = f^*, whereas the male faces a risky lottery: [m = m^* with probability 1/n and m = 0 with probability 1 − (1/n)]. Because realizing a small f^* is certain, the female strategy is low-risk and low-return. The male strategy on the other hand is high-risk and high-return, for m^* is large and its probability of realization is small (1/n). Treating the male and female children as assets, we observe that a parent has a reproductive portfolio of some lotteries with high-risk high-return and some lotteries with low-risk low-return. It is well-known from the finance literature that it is efficient to combine low-risk low-return assets with high-risk high-return ones. But can we claim any efficiency here in the case of the portfolio of children?

We first should note that the male and female lotteries appear for different reasons. The female chooses a degenerated birth strategy because her p_f ·f = [g(z_f )− c_f f]f/b_f is a concave function of f, and therefore it does not pay to randomize over f. For males, it is not that they “choose” a randomized strategy; rather, it is that they compete with one another, and each has a small probability of winning a pack of females. In fact, their competition has nothing to do with the equilibrium λ, which is solely determined by females.

As one can see, when (6) is positive, a mutation leading to more trait investment will successfully invade. However, all competitive outcomes will end up with the same success fitness index, given the constraint in (4). Whatever lottery a male gene mutates into, the fate of having fitness λ = p_f^*f^*/2 is simply preordained. Therefore, in a symmetric evolutionary equilibrium, the male competition is like an arms race, in which a unilateral mutation of increasing I may be a dominant strategy when (6) is positive, although the eventual equilibrium result actually provides exactly the same evolutionary equilibrium. This “fight-for-nothing” property actually implies some kind of inefficiency from intrasexual competition. However, those gene lines that do not invest in I^k were out-competed and went extinct.

4 Inter-Sexual Selection

The typical description of inter-sexual selection is that the male has a gene controlling the size of some trait (such as the plumage of a peacock), and the female has a gene controlling her preference for mating males that excel tin his trait. The question is: if such traits appear to be useless or even harmful (e.g. the excessively large plumage of male peacocks which reduce their agility), why and how would this trait-preference interaction arise from evolution?

There are two strands of theories that try to explain this evolution. The first was proposed by Fisher (1930) who suggested that the advantage of preferences lies in the choice of mates who will father attractive sons. If females on average prefer a particular male trait, then males having that trait will have a mating advantage. If this trait is heritable, then females would also prefer to mate with males with this trait. Fisher argued that this evolution may lead to a runaway process, leading to an inefficient trait size, such as the excessively large plumage of peacocks. However, as pointed out by Pomiankowski et al. (1991), this runaway argument is valid only when there is no cost associated with female preferences. If there is some cost (say of searching), no matter how small, Fisher’s argument cannot go through.

The second hypothesis suggests that the benefit of female preferences hinges upon the improved survival of offspring. Zahari (1975) argued in his well-known “handicap” theory that the male trait provides the female with information about heritable male quality, very much like the idea of signaling in economics. Iwasa et al. (1991) showed that a correlation between male trait and viability is necessary to create an equilibrium with female preferences. With respect to this handicap theory, most existing literature uses quantitative genetic theories to present their arguments. In this section, we shall use our life history model to demonstrate this theory in a very neat way. The key, as we shall see, is the dominance of the female reproduction constraint in (4).

4.1 The Correlation Between Viability and Female Search

Again, consider a species that has polygamous marriages of one-male mating n females, and each surviving female bears f^* children. However, there is some probability 1 − q that a male cannot find a female willing to mate with him, and hence has zero impregnations. The chance that a male can find a mate is determined by competition with other males to attract females, based on their trait value Y. We assume that females like to mate with males with larger Y, and we shall justify this assumption later.

For females, they have to spend some search energy S in order to find a male with larger Y. Both Y and S are controlled by sex-specific genes. Other than S and Y, there is a viability gene v that affects both males and females. We assume that v affects b_m and b_f, the efficiency coefficients of maintenance, with $b_f^{\prime }(v)<0$ and $b_m^{\prime }(v)<0$. The gene affects adult maintenance efficiency but of course it is carried by offspring (see Iwasa et al. (1991)).

From our discussion in section 3, we know that the intrinsic growth rate of the species is dominated by females. Assuming that there is no investment or transfer by females, her available energy net of her search cost is g(z_f )− S. Thus, maximizing F = p_f · f subject to b_f (v)p_f + c_f f ≤ g(z_f ) − S yields

$$F^{\ast }(S,v)\equiv {[g(z_f)-S]}^2/[4b_f(v)c_f].$$

Note that F^* is the equilibrium intrinsic growth rate irrespective of the trait competition among males.

Since ∂F^*/∂S < 0, meaning that searching costs some female energy, in order for us to observe an evolutionary equilibrium that involves female search, it must be the case that there is some connection between S and v. Specifically, since

$$\frac{{dF}^{\ast }}{dS}=\frac{\partial F^{\ast }}{\partial S}+\frac{\partial F^{\ast }}{\partial v}\frac{dv}{dS},$$

and since ∂F^*/∂v > 0,⁸ we must have a positive correlation between S and v (dv/dS > 0) in order to have dF^*/dS > 0. Thus, we have used a very simple argument to establish the result in Iwasa (1991). The key reason we have this neat derivation is that female dominance is always true, even when the species in question has inter-sexual interactions. Note that this analysis is based on maximization of F* across gene lines that have different amounts of energy devoted to search.

4.2 The Correlation Between Viability and Male Trait

What about the male competition based on trait size Y ? The fact of female dominance in reproduction shows that Y does not affect the equilibrium λ= F^*/2 at all. Suppose the probability q̃ for a male k to be selected by females is a function of his trait Y ^k relative to others’ Y^~k. Then we have q̃ = q̃(Y^k, Y^~k). For any given amount of energy spent on trait Y, the male chooses m to maximize his q̃ ·(nF^*). We also note that in a symmetric equilibrium, q(Y ^k, Y ^k) = 1/n must hold. Thus, as in (7), the evolutionary result must be constrained by the following equation in a symmetric equilibrium:

$$\frac{1}{n}\frac{{[g(z_m)-Y^k]}^2}{4c_m{b}_m(v)}=p_{f^{\ast }}{f}^{\ast }$$ (8)

Evidently, since $b_m^{\prime }(v)<0$, from (8) we see that Y ^k and v move in the same direction for any constrained p_f^*f^*, meaning that only viable males are capable of growing larger Y: cov(Y, v) > 0. This is the essence of the handicap theory. And this is also what is needed to justify the search of larger Y on the female side. By searching, the female finds males with larger Y. These males happen to be more viable ones because cov(Y, v) > 0, and their gene controlling larger Y helps the energy efficiency of their offspring. This justifies the female expenditure of energy-on search.

Note that our analysis of Y is not different from our analysis of male investment (I) on canine teeth in section 3. The model in this section is one with inter-sexual selection, whereas the one in section 3 is of intra-sexual competition. However, the fact of female dominance makes the superficial sexual interaction between females and males degenerate. It turns out that we can still solve the female problem first, and then work on the male problem afterwards. Intra-sexual male competition or male-female interaction turn out to be technically the same.

5 Why Do Males Transfer Less than Females?

Now we take into account the role of parental transfers, a variable we distinguished from the cost of fertility in section 1. This discussion is also related to the endogeneity of z_s, s = m, f, which was assumed to be exogenous (that is, a given in the analysis) in a previous analysis but will be derived here as part of the life history strategy. In Trivers (1972), parental transfers and reproduction costs were bundled together as a single variable. When male (female) adults provide T_m (T_f ) transfers to their children, from the energy budget constraint we see that survival at age-1 should be revised to p_1,m = [g(z_m) − c_mm − T_m]/b_1,m for males and p_1,f = [g(z_f ) − c_f f − T_f ]/b_1,f for females. From the previous discussion, we know that the female should choose f^* = [g(z_f ) − T_f ]/(2c_f ).

In a setting with 2-ages, parental transfers are an energy endowment for juveniles age 0. In general, such energy is used by the young for maintenance and somatic growth. To simplify the analysis, we assume that juvenile survival p_0,s is mostly determined by parental guarding and watching, and therefore that parental transfers are all used for somatic growth z_s.

5.1 Male Transfers in Monogamy and Polygyny

Given any planned transfer T_f we have shown that the female’s expected fertility is

$$F^{\ast }=p_{1,f^{\ast }}{f}^{\ast }=\frac{{[g(z_f)-T_f]}^2}{4c_f{b}_{1,f}}.$$ (9)

Now consider the case of polygyny where each alpha male mates n females. In a more general interpretation, the case of monogamy is approximated when n → 1. In this way, n characterizes the mating scenario. The mate-competition that has occurred before the actual mating is not important here for the discussion of transfers, because transfers happen only after a male achieved the privilege to impregnate a female.

Consider a pride of lions with one male and n female lionesses. Suppose for simplicity that male and female juveniles share parental transfers equally.⁹ Then, given that there are p_0,s age-1 adults of sex s, the average energy shared by each of the f^* newborns in an n-female cooperative breeding group would be

$$z_m=z_f=z=\frac{p_{0,m}{T}_m+p_{0,f}{nT}_f}{{nf}^{\ast }}=\frac{p_{0,m}{T}_m+p_{0,f}{nT}_f}{n[g(z)-T_f]/(2c_f)}.$$ (10)

For any given T_m, the female should choose a T_f to maximize F^* in (9) subject to the constraint in (10).

The male lion, after becoming the king, may use his energy in different ways. Because his total number of impregnations is constrained by the females, there is not much choice in that direction. The lion king, of course, has an incentive to make a transfer T_m which increases the starting z of his offspring and raises λ. But there are also other uses for his energy, such as roaring, patrolling, killing hyaenas, etc. Suppose the opportunity cost of other uses of energy is a constant C. We shall investigate the marginal benefit he derives from devoting energy to transfers.

Note that z_f = z is a function of T_m by (10). Differentiating nF^* with respect to T_m, we have

$${\text{MB}}_{T_m}=\frac{{\mathit{dnF}}^{\ast }}{{dz}_f}\frac{{dz}_f}{{dT}_m}=\frac{2[g(z)-T_f]}{4c_f{b}_{1,f}}{g}^{\prime }(z)n·\frac{dz}{{dT}_m}.$$

The formula of z in (10) tells us that

$$n·\frac{dz}{{dT}_m}=\frac{p_{0,m}}{f^{\ast }}.$$

Since f^* is determined solely by females, we see that the marginal benefit of T_m is independent of n. However, the larger the female pride size (n), the more costly it is for the alpha male to lose control of the females in his pride, hence the higher the opportunity cost of diverting energy away from patroling-roaring to transfers to his offspring. In other words, the marginal cost of T_m for larger n is likely to be higher. This means that other things being equal, fathers of polygamous species have less incentive to transfer to offspring. This is mainly because a single father’s contribution is diluted by the group of mothers in a cooperative breeding species. We can look at the this finding from another angle: Consider a mutation that shifts male energy from maintenance to investment in trait-competition to increase the chances of becoming a polygynous alpha male. If this mutation is selected, then a mutation that reduces total transfers by the alpha male to the young would also be selected.

Concerning the relationship between transfers and investment in a mate-competition trait, equations (7) and (8) can be combined and re-written as

$$\frac{g(z_m)-I_k-T_m)}{4n{c}_m{b}_m}=p_{f^{\ast }}{f}^{\ast }.$$ (11)

It is evident from (11) that I^k and T_m must move in opposite directions. Thus, the more energy that males invest in I^k, other things being equal, the less energy that males transfer to their offspring. We therefore expect to have a negative correlation between male investment in mate-competition traits and male transfers. This seems to be consistent with what we observe in nature.

5.2 Transfers and the Risk of Cuckoldry

Now consider the case when the pride includes other males. This will happen when male competition generates an alpha male but he cannot drive away other males. Well-known examples include baboons, wolves, and sea lions. Then, the alpha male has the privilege of priority in mating, but he cannot completely prevent access to females by the other males and consequently he is never sure whether a pregnant female actually carries his genes. In other words, we have paternal uncertainty, or the possibility of cuckoldry for the alpha male. Facing such a cuckoldry risk, how would the alpha male change his transfers?

Suppose each female still has a certain number of births, but that now on average f^* of them are with the alpha male and f′ of them are with other males. The female does not care because in either case the baby carries her genes. Since a female seeks to maximize f · [g(z_f ) − c_f f − T_f ], her optimal fertility is f^* + f′ = [g(z_f ) − T_f ]/(2c_f ). However, because only f^* births are from the alpha male, his transfers are even more diluted in this cooperative breeding group. This result is further strengthened if the non-alpha males also make some transfers to the young. It is easy to see that his marginal benefit from providing a transfer is further reduced by the risk of cuckoldry, not to mention the dilution effect of male transfers as in the case of subsection 5.1.

In short, Cuckoldry dilutes the probability that a particular child is the descendant of the alpha male, and therefore reduces his incentive to transfer.

6 The Sex Asymmetry of Menopause

Very few species in the world have menopause. According to Carey and Gruenfelder (1997), only human beings, killer whales, and dolphins have adaptive menopause. In terms of life history, an adaptive menopause means that the species has an optimal life history path that corresponds to a corner solution of zero fertility for an old female. In the traditional evolutionary framework of maximizing gene proliferation, the life history of a species should not include survival to ages in which fertility is zero. However, for species that make intergenerational transfers, even post-reproductive old age can still contribute to gene proliferation so long as these old individuals provide net transfers to the young (Lee, 2003). Most researchers, for instance Hawkes et al. (1997), Carey and Gruenfelder (1997),b and Chu and Lee (2008b), explain menopause as a special kind of division of labor between a grandmother and mothers, where the grandmother specializes in non-reproductive tasks such as food gathering and care of young, while the mothers do all these tasks plus bearing children. However, all these papers implicitly consider a model of females, and therefore don’t address the logical question of why males never have menopause. In this section we shall provide an answer to this question.

To consider menopause in our framework, we must extend our model to two mature ages, so that a choice of zero fertility in old age is meaningful. However, with two mature ages, we have the possibility of a female age 1 or 2 mating with a male age 2 or 1, and also the possibility of pairings lasting 1 period or two periods. To avoid all these technical complications, we make the following assumptions. We consider a polygamous mating system where the females living together have a size of n₁ age-1 adults and n₂ age-2 adults. Only males at age-1 can compete for the alpha status, and the probability of victory is q₁. If a male wins, he will impregnate all the females in his pride. He will be the alpha male for two consecutive periods if he survives to old age. When he dies, either at age 1 or age 2, another alpha male arises from a new round of competition. None of these assumptions is crucial to our results, but they do make it easier to derive insights. As in our 2-age model of the previous sections, adult females determine their optimal fertility independent of the male decisions. We denote females’ optimal decisions at age-1 and age-2 by f₁ and f₂ respectively.

Given these assumptions, we can write down the expanded Bellman equation for our 3-age setup. Details are given in the Appendix, and the interpretation is the same as in section 2, and is therefore omitted.

Chu and Lee (2008b) showed that a key reason for menopause to appear is the division of labor between grandmothers and mothers. To specialize in care of the young, grandmothers have to give up their foraging time, which in turn reduces their available energy. As the grandmothers move closer and closer to complete specialization care of the young, their energy constraint pushes them toward a corner solution for fertility, to conserve energy, ultimately leading to menopause. From our model we can provide three reasons for males not to have menopause:

• Female menopause corresponds to a life history with f₂ = 0, a particular corner solution. This would be a reasonable choice only if the opportunity cost of f₂ (which is c_f ) is high, so that avoiding fertility at age-2 saves substantial energy on the part of the potential mothers. But for males, since c_m is trivially small, it does not pay to avoid m₂. Even if males do have m₂ = 0, they cannot save much energy thereby in any case. Thus, an efficient division of labor is unlikely to involve a corner solution of m₂ = 0 for old males.

• We see from Chu and Lee (2008b) that the division of labor is the key feature of menopausal species. However, we have shown in the previous sections that the alpha male has little incentive to transfer to the young, due to the dilution effect and paternity uncertainty in a cooperative breeding group. Even if the male does save some energy by choosing m₂ = 0 he is likely to move it to investment in competitive traits or somatic maintenance. Thus, because the male does not tend to transfer energy anyway, it is difficult to form a division of labor involving the male. However, this reason is diminished when the male can make public good type transfers that are not subject to dilution, such as defense of all offspring from a single infanticidal competitor.

• In a polygynous pride, if an old male were to stop producing sperm, then all females in the pride would be unable to reproduce. There would be a high fitness cost if the alpha male were to have m₂ = 0, while still maintaining his alpha status.

7 Conclusion

In this paper, we provide a unified approach to explain sexual dimorphism, intrasexual competition, and intersexual selection in biology. In terms of analytical structure, we adopt a model of two-sex life history. We suggest that the fundamental driving force is the male-female difference in direct costs of reproduction (as opposed to mating costs and post-birth investments). Using our model we are able to explain why males are motivated to grow canine teeth, why fathers provide smaller transfers to children, why there is a positive correlation between polygyny and sex-specific size dimorphism, how environmental factors influence sex competition, why males can sometimes mate only through a risky lottery for access to females, and why only females are likely to have menopause. Finally, we explain the negative correlation between male traits and viability using our framework of optimal life history.

Not surprisingly, the richness of nature does not always conform to our predictions. For instance, hyenas have a matriarch instead of an alpha male, and among wolves and African hunting dogs there are both alpha males and alpha females, with only the alpha female permitted to breed. Indeed, we believe the hyena and wolf cases indicate scenarios not covered by our model. For instance, wolves and African wild dogs are pack hunters who need agile individuals to join the hunt, including non-pregnant females. Efficiency is gained by exploiting economies of scale in breeding and lactation. In terms of our model, the energy-generating function g would have to be specified differently. Hyenas have many predators such as lions, and they cannot provide effective protection for too many juveniles. This implies that few or even one pregnant female might be enough. In either case, these examples fall into the broad-sense category of Emlen and Oring (1977) that some resources are “undefendable”, and hence certain sexual interaction phenomena do not arise. In fact, this is also why there is not much sexual dimorphism in species such as hyenas and wolves.

Appendix: The 3-age Model for Analyzing Menopause

The Bellman equation for the 3-age model described in the text can be written as follows.

$$\begin{array}{l}{F}_{0,t}=max\left\{p_{0,f}{F}_{1,t-1}\right\}\\ M_{0,t}=max\left\{p_{0,m}{M}_{1,t-1}\right\}\\ F_{1,t}=max\left\{p_{1,f}{f}_1\left(\frac{M_{0,t}}{4}+\frac{F_{0,t}}{4}\right)\right\}+p_{1,f}{F}_{2,t-1}\\ M_{1,t}=max\left\{p_{1,m}{q}_1{m}_1\left(\frac{M_{0,t}}{4}+\frac{F_{0,t}}{4}\right)\right\}+p_{1,m}{M}_{2,t-1}\\ F_{2,t}=max\left\{p_{2,f}{f}_2\left(\frac{M_{0,t}}{4}+\frac{F_{0,t}}{4}\right)\right\}\\ M_{2,t}=max\left\{p_{2,m}{q}_1{m}_2\left(\frac{M_{0,t}}{4}+\frac{F_{0,t}}{4}\right)\right\},\end{array}$$

where there is also a reproduction constraint on the alpha male. Males compete to become the alpha male, and the probability of success depends on their respective investments in a competitive trait. Let the age of the alpha male be α. The energy budget constraint for this cooperative breeding pride is

$$n_1{g}_1(z_f)+n_2{g}_2(z_f)+p_{\alpha ,m}g(z_m)\ge n_1(b_{1,f}{p}_{1,f}+c_f{f}_1+T_{1,f})+n_2(b_{2,f}{p}_{2,f}+c_f{f}_2+T_{2,f})+[b_{\alpha ,m}{p}_{\alpha ,m}+c_m{m}_{\alpha }+T_{\alpha ,m}+I_{\alpha ,m}].$$

In the above expression, the left hand side adds up the energy output by all members in the pride. The first and second terms on the right hand side are the female’s energy expense on her age-1 and age-2, and the third term is the energy expense of the alpha male. Other than this constraint, the somatic investment for each youth is determined by

$$z_f=z_m=z=\frac{n_1{T}_{1,f}+n_2{T}_{2,f}+T_{\alpha ,m}}{n_1{f}_1+n_2{f}_2}A2$$ (*)

The stationary state of the pride can be solved from the above expressions, with the understanding that the constancy of n₁ and n₂ holds only in a density-dependent equilibrium. In a stationary state equilibrium, the population age structure will appear, and the size of females aged a will be determined by the environmental density. We do not want to go into details here, for that is not the purpose of our research.