Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Oct 3;2:702. doi: 10.1038/srep00702

Rainfall reductions over Southern Hemisphere semi-arid regions: the role of subtropical dry zone expansion

Wenju Cai 1,a, Tim Cowan 1, Marcus Thatcher 1
PMCID: PMC3463003  PMID: 23050086

Abstract

Since the late 1970s, Southern Hemisphere semi-arid regions such as southern-coastal Chile, southern Africa, and southeastern Australia have experienced a drying trend in austral autumn, predominantly during April and May. The rainfall reduction coincides with a poleward expansion of the tropical belt and subtropical dry zone by around 2°–3° in the same season. This has raised questions as to whether the regional rainfall reductions are attributable to this poleward expansion. Here we show that the impact of the poleward subtropical dry-zone shift is not longitudinally uniform: a clear shift occurs south of Africa and across southern Australia, but there is no evidence of a poleward shift in the southern Chilean sector. As such, a poleward shift of climatological April-May rainfall can explain most of the southeastern Australia rainfall decline, a small portion of the southern Africa rainfall trend, but not the autumn drying over southern Chile.

Climatological rainfall patterns in the subtropics are known to be influenced by the Hadley cell, which describes an east-west average of the large-scale atmospheric vertical circulation that carries rising tropical heat and moisture polewards to the extratropics. The regions where the descending branch of the Hadley cell lies are marked by the subtropical dry zones that separate the tropics and extratropics. Based on various metrics from independent datasets, the width of the tropical circulation and subtropical dry zone in each hemisphere has been found to be expanding polewards, with an annual-mean expansion in the range of 1°–2.5° over the 1979–2005 period1,2,3,4,5 using a zonal mean definition (see Methods). A maximum expansion of over 2° latitude has occurred in each hemisphere's summer and autumn since the late 1950s6 or later3, although the expansion rates are dataset and metric dependent7.

It has been speculated that the observed expansion has influenced the climate in semi-arid regions, affecting ecosystems, agriculture and water availability4. During the period of tropical expansion, semi-arid regions across the Southern Hemisphere (SH) have experienced a marked decline in autumn rainfall8,9, predominantly in April and May. For semi-arid regions like southern Chile and southern Australia, a poleward shift in the storm tracks is thought to be a prominent driver of substantial reductions in rainfall during the late 20th century8,10,11. However, to date, the extent to which these regional rainfall reductions are attributable to the poleward expansion has not been clarified. Here, we examine whether: (1) the April-May rainfall variability in these semi-arid regions is influenced by interannual variability of the Hadley cell edge; and (2) if the rainfall reductions can be explained by a poleward shift of the climatological mean April-May rainfall using the extent of the poleward shift in the zonal mean Hadley cell edge.

Results

Variability of zonal mean SH Hadley cell edge

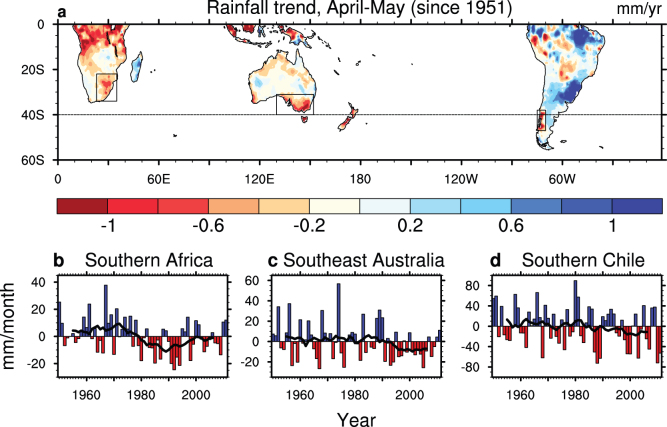
Extended to 2010 (see Methods), the strongest expansion in the SH zonal mean Hadley cell edge occurs in austral autumn (Fig. 1a), ranging from 2°–4.5° since 1979, with a comparable rate if just the April-May averages are considered. The four reanalysis products used here each show similar variability in their Hadley-cell edge since 1979 and display statistically indistinguishable trends. The relatively large error of each individual trend (Fig. 1b) could be a consequence of the reanalysis products' inability to simulate specific cloud types12. During this period of strong subtropical dry zone expansion, substantial mid-to-late autumn drying trends have been observed over SH semi-arid regions such as southern-coastal Chile, southeastern Africa, and southeastern Australia (Fig. 2a). Based on a multi-product ensemble average, reductions in the order of 1 mm/autumn since 1951 have been recorded across these three regions in April-May (Figs. 2b–2d). Although the timing and length of regional droughts can vary, the commencement of rainfall declines approximately coincided with the start of the zonal mean Hadley cell widening around the early 1980s (Fig. 1b).

Figure 1. Poleward shifts in the southern branch of the zonal mean Hadley cell edge.

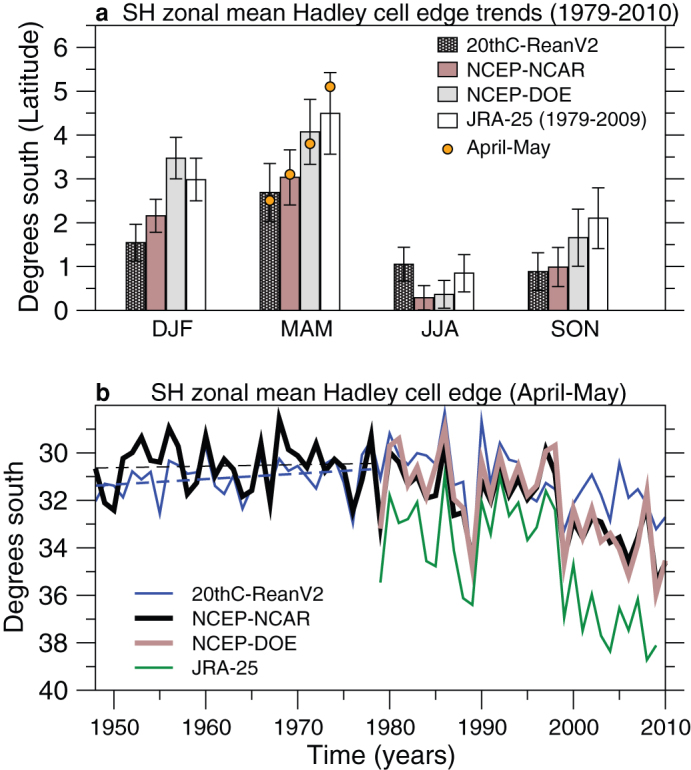
Figure 1

Open in a new tab

(a) Seasonal shifts of the southern branch of the zonal mean Hadley cell edge from four reanalyses products over 1979–2010: 20thC-ReanV2, NCEP-NCAR, NCEP-DOE and JRA-25 (data only available up to 2009 at time of writing), based on linear trends; (b) the corresponding time series for April-May with linear trend lines (dashed) for 20thC-ReanV2 and NCEP-NCAR from 1948–1978. Error bars in (a) signify the standard error of the trends.

Figure 2. Mid-to-late autumn (April-May) rainfall linear trends across the Southern Hemisphere since 1951.

Figure 2

Open in a new tab

Rainfall linear trend for: (a) April-May using a four-rainfall product average (mm/year). The datasets used to calculate trends are CPC (1951–2010), GPCC (1951–2010), CRU (1951–2009), and UDel (1951–2010). The four rain gauges datasets are averaged to generate time series of rainfall (in mm/month) for: (b) southern Africa (average over 23°–35°E, 22°–34°S); (c) southeast Australia (130°–152°E, 31°–40°S); and (d) southern Chile (285°–290°E, 38°–47°S). The thick black lines in (b)–(d) denote 11-year (season) running averages. In (a), the semi-arid regions are shown in boxes and the 40°S midlatitude line is shown.

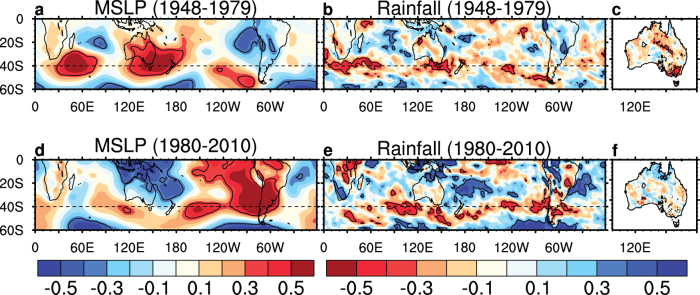
Given that the regional influence of the Hadley cell edge variability resides near its mean position, by comparing the regional “position of influence” between the wet (pre-1980) and dry (post-1980) periods, we are able to gauge the longitudinal distribution of the regional mean position between the two periods. This generates spatially varying edges and allows an assessment of whether the subtropical dry zone expansion is experienced equally across the SH semi-arid regions. This is essential because the zonal mean edge does not provide regional information on the poleward shift or regional impact. Prior to 1980, the influence of the zonal mean Hadley cell edge is observed through significant positive correlations with mean sea level pressure (MSLP) over southeast Australia and the southwest Indian Ocean (indicated by red regions in Fig. 3a). The zonal mean Hadley cell edge is coherent with subsidence, and hence anomalously high MSLP and low rainfall (indicated by red regions in Fig. 3b), particularly across southeast Australia (Fig. 3c). Moving eastward from the region of strong correlation over southeast Australia, the region of subsidence veers southward toward the southern tip of South America and away from the southern Chilean region (Fig. 3b). As such, the influence from variability of the zonal mean Hadley cell edge is situated too far from the southern African and Chilean regions (indicated by the rectangular boxes in Fig. 2a) to affect rainfall in these locations.

Figure 3. Coherence of SH zonal mean Hadley cell edge with MSLP and rainfall in pre- and post-drought periods for April-May.

Figure 3

Open in a new tab

Spatial correlation maps of the SH zonal mean Hadley cell edge, based on MMS500 = 0 kg s−1, with April-May MSLP, SH rainfall, and Australian rainfall for: (a)–(c) 1948–1979; and (d)–(f) 1980–2010. The SH patterns are based on NCEP-NCAR reanalysis, while the Australian maps use high-quality station-based rainfall observations. Significant correlations at the 95 % confidence level (N = 32, 31 in (a) and (b), respectively) are shown in areas within the black contours, and the 40°S midlatitude line is also shown to highlight the shift. Note that MSLP and rainfall correlation panels have opposite colour bars.

In the dry period (post-1980), trends in both rainfall and the zonal mean Hadley cell edge contribute to the correlations. It is expected that the correlation ridge will move poleward at all longitudes. There is indeed an indication of a poleward shift (from the pre-1980 position) in the southern Australian sector, and to a lesser extent, the ocean to the south of Africa (Figs 3d and 3e). Focusing on southeast Australia, variability of MSLP and rainfall is no longer influenced by variability of the edge, as the regional edge appears to have passed a threshold latitude, beyond which its variability no longer influences southern Australia (Fig. 3f). However, the shift of the ridge of significant correlations (and by inference, the edge as represented by the zonal mean Hadley cell) is not longitudinally uniform. Over the southern Chile sector, the correlation ridge has moved northward, at odds with what is expected. This may be an indication that the zonal mean Hadley cell is comprised of individual branches13, each of which is subject to hemispheric trends as well as being additionally influenced by climate variability that varies at regional scales. Thus, we cannot attribute the rainfall reduction over southern Chile to the Hadley cell expansion as indicated by the zonal mean Hadley cell edge, because there is no evidence of (and in fact, evidence against) a concurrent local poleward expansion.

A conspicuous feature in the post-1980 MSLP correlations (Fig. 3d) is the emergence of a Southern Oscillation (SO)-like pattern in the tropical Pacific, reflecting a stronger relationship of the zonal mean Hadley cell with the El Niño Southern Oscillation, as observed for the boreal winter season cell12. This SO-like pattern means that, statistically, during La Niña (El Niño) conditions, the zonal mean Hadley cell edge is anomalously poleward (equatorward) when enhanced (reduced) convection over the western (eastern) Pacific occurs. This relative widening of the Hadley cell during La Niña compared to El Niño is a feature seen in other reanalysis products12. Prior to the 1980–2010 period, the existence of a SO-like pattern is not observed, which suggests that the association of the Hadley cell with the El Niño-Southern Oscillation before and after the mid-1970s climate shift is quite different14; that is, there is a strong influence from multidecadal variability.

Our analysis suggests that April-May rainfall variability over southern Africa is not directly affected by variability of the Hadley cell edge in either period, although there is a poleward shift in the associated rainfall pattern to the south of the African landmass (Fig. 3e). Further, we cannot attribute the southern Chile rainfall reduction to a poleward expansion in the Hadley cell edge, because there is no evidence of a local poleward shift. Only across the southeast Australia sector is there a systematic poleward shift in the influence of the SH Hadley cell edge, and this is confirmed using high-quality rainfall data (Figs. 3c and 3f).

Poleward shift of mean rainfall

During the expansion period, the regional or zonal mean Hadley cell edge has no direct influence on southeast Australia. Therefore, we cannot calculate the sensitivity of regional rainfall to variability of the edge, or use such sensitivities to quantify the rainfall change induced by a poleward shift in the edge. Instead, we next investigate whether the poleward expansion of the subtropical dry zone is able to account for some of the regional rainfall reduction, as expected by previous studies4,7. We use the long-term shift of the zonal mean Hadley cell as an indication of the extent of the dry-zone expansion and calculate changes arising from a poleward shift in the mean climatological April-May rainfall assuming a hemispheric-wide expansion. This approach is similar to using a poleward shift in the mean ocean state to explain recent observed ocean warming15. In the SH extratropical latitudes, average April-May rainfall over southeastern Africa, southeastern Australia and southern-coastal Chile is higher than over latitudes immediately to the north (Fig. 4b). A poleward shift of a climatologically drier climate from the north could potentially explain the observed rainfall decline. We calculate the latitudinal gradient of the climatological April-May rainfall for the four-rainfall product climatology ensemble (arithmetic mean), for the land points (all datasets are on a 0.5° by 0.5° grid). The resultant derivative pattern indicates where a rainfall reduction is potentially attributable to a poleward shift in the mean climate (Fig. 4a). Given the low resolution of the rainfall ensemble, the derivative pattern is not used to quantify the associated rainfall change.

Figure 4. April-May rainfall change pattern from a poleward mean climate shift, and comparison between observed climatology and simulated climatology without orography.

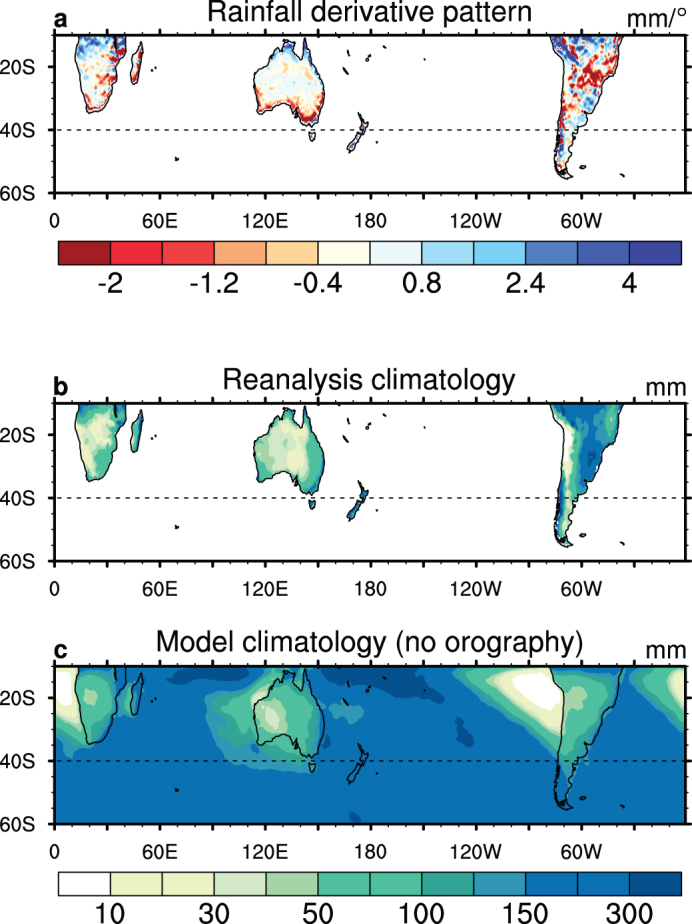
Figure 4

Open in a new tab

(a) Pattern of the latitudinal gradients of climatological April-May rainfall for identifying regions where a rainfall reduction is potentially attributable to a poleward shift of the mean climate; (b) April-May rainfall climatology for observations (four-rainfall product average for 1951–2010); and (c) a model simulation with “no orography” (1980–2000). The units in (a) are mm/degree of shift; and (b) and (c) are mm. The datasets used to calculate the derivatives and climatology are the same as in Fig. 2. The 40°S midlatitude line is also shown.

Immediately clear in the derivative pattern is a band of rainfall reduction in the subtropical to extratropical latitudes (25°–40°S), with southern Australia exhibiting a clear decline, and the pattern of the change matching the observed trend (Fig. 2a). There is a broad agreement across southern Africa, despite the reduction implied in the derivative pattern being more dominant along the coast. Over southern Chile, a maximum reduction is generated north of 40°S; this pattern of change does not match with the observed trend, as most of the observed rainfall reduction for Chile occurs south of 40°S. Thus a poleward shift in climatological April-May rainfall, as described through the rainfall derivative pattern, also fails to explain the rainfall reduction over southern Chile. Thus it is likely that other factors, such as multidecadal variability and/or shifts in the extratropical storm tracks dominate rainfall trends in this sector, as found using annual data10.

To provide an accurate quantification for the southeast Australia region, high-quality climatological April-May rainfall (from Australian rainfall observations) is shifted poleward between 1° and 4° (Table 1). The total observed reduction over the 1951–2010 period is approximately 38% of the long-term climatological rainfall. Table 1 shows that the declining rainfall trend increases with the amplitude of the poleward shift, with a 3° shift potentially explaining more than 65% of the entire long-term April-May trend for southeast Australia.

Table 1. Trend in southeast Australian rainfall in April-May from 1951–2010, and changes due to different magnitude poleward shifts in rainfall climatology. Shown are total changes and changes in terms of % of climatology. A poleward shift of 4° latitude would explain more than 85% of the observed reduction.

Climate shift (° poleward) Total change in mm (% of climatology)
Actual trend −31.5 (−38.0%)
0.5 −7.8 (−7.6%)
1 −13.5 (−13.6%)
2 −19.1 (−19.7%)
3 −23.7 (−24.8%)
4 −27.3 (−29.0%)
Open in a new tab

The success of the above explanation relies on the feature that climatological April-May rainfall over regions such as southern Africa and southeast Australia is higher than that over latitudes immediately to the north, as seen in observations (Fig. 4b). A common feature between these two regions is their coastal mountain ranges, which can lead to an orographic uplift amplifying the rainfall signal16. We make use of a model simulation17 that removes SH orography to test the extent to which the April-May meridional rainfall gradient is amplified by these features. The climatological April-May rainfall averaged over the last 20 years of integration (1980–2000) in the no-orography experiment (Fig. 4c) broadly captures the observed seasonal features (Fig. 4b): regions such as southern Africa, southern Australia and southern Chile latitudes are generally wetter than regions to their north, even without orography. Therefore a hemispheric-wide poleward shift leads to a rainfall reduction over these regions, regardless of the presence of mountains, suggesting that the orographic amplification effect is small.

Discussion

Using the southern edges of the zonal mean Hadley cell to represent the subtropical dry zone edges, we show that prior to the commencement of the poleward shift, rainfall over southeast Australia is influenced by the Hadley cell edge, but rainfall over southern Chile and southern Africa are not. The poleward shift in the Hadley cell does not mean that there is a regionally uniform shift: while a clear shift occurs in the Australian sector, and a weaker shift occurs in the sector to the south of the African landmass, there is no evidence of a poleward shift in the southern Chilean sector, discounting a shift as a cause for the rainfall decline there. A poleward shift of the April-May climatological rainfall is able to explain a small portion of the southern African rainfall trend, and most of the southeast Australia rainfall decline, but not the reduction over southern Chile. Out of the three semi-arid regions, the southeast Australia rainfall reduction is best attributable to an expansion of the subtropical dry zone. As the poleward expansion proceeds, one could expect an increasing coherence between the near tropical circulation and the semi-arid climate of southeast Australia. Using a 30-year moving window, one study showed an unprecedented high coherence between the tropical circulation north of Australia and MSLP averaged over southeast Australia in mid-to-late autumn8, only observed in the most recent decades.

However, an important issue remains as to why the poleward expansion is largest in autumn. In austral summer, according to modeling studies18,19, the expansion is largely driven by Antarctic stratospheric ozone depletion, although increasing greenhouse gases also play a key role6. This raises questions as to whether the large autumn expansion is a delayed effect from ozone depletion that climate models fail to capture, or due entirely to greenhouse gases, the impact of which Coupled Model Intercomparison Project Phase 3 models under-estimate, unless forced with observed sea surface temperatures7. Despite this uncertainty we show that a direct impact of a poleward expansion may have already contributed to the long-term autumn rainfall reduction over southern Australia.

Methods

Data

Reanalysis and station observations

The zonal mean Hadley cell edge is defined as the subtropical latitude where the meridional mass streamfunction at 500 hPa (MMS500) is zero. The MMS500 is defined as:

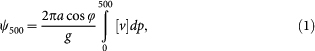graphic file with name srep00702-m1.jpg

where [v] is the zonal mean meridional wind, a is the earth's radius, 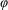Inline graphic is latitude, and 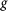Inline graphic is gravity5. Figure 1 is constructed using data from Twentieth Century Reanalysis Project (20thC-ReanV2)20, National Centers for Environmental Prediction-National Center for Atmospheric Research (NCEP-NCAR) reanalysis21, NCEP/Department of Energy (NCEP-DOE) reanalysis22 and the Japanese 25-year Reanalysis Project (JRA-25)23. It updates the time series and trends of the SH Hadley cell edge since 1979 shown in a previous study3. Four rain-gauge precipitation datasets are used to calculate rainfall trends (Fig. 2) and climatology (Fig. 4b): (1) Delaware University (UDel) interpolated product (Version 3.01)24 for the period 1951–2010; (2) Climate Prediction Center (CPC) Global Land Precipitation25 over land for 1951–2010; (3) Global Precipitation Climatology Centre (GPCC) within the project “Variability Analysis of Surface Climate Observations” (Version 6)26 for 1951–2010; and (4) University of East Anglia Climatic Research Unit (CRU) precipitation27 (Version 3.1) for 1951–2009. The spatial resolution of the four rain-gauge precipitation datasets is 0.5° by 0.5°. The results for Table 1 and Figs. 3c and 3f were calculated using high-quality gridded (0.05° by 0.05°) Australian rainfall data28.

Model simulations

The experiments from a Cubic Conformal Atmospheric Model (CCAM)17 are run with and without orography. This CCAM version contains a C96 grid with 18 vertical levels and an approximate 100 km quasi-uniform horizontal resolution. It is forced by ECMWF 40-year reanalysis (ERA40) sea surface temperatures from 1971–2000. For the no-orography experiment, the orographic height of the SH landmasses of interest here (Africa, Australia and South America) are set to zero. Where the orography is set to zero, a constant roughness length, albedo, stomatal resistance and soil texture over land surfaces are employed (i.e., land-surface parameters are set to the same values).

Statistical analysis

The influence of the SH zonal mean Hadley cell edge on rainfall is examined through correlation analysis. Usually, detrending is conducted prior to correlating fields to ensure that any coherence is not due to unrelated long-term trends. However, detrending a position index, such as the zonal mean Hadley cell edge location, does not make physical sense as it has the effect of moving the cell edge back to a position prior to its shift, and therefore inducing an unrealistic teleconnection in regions where it may no longer have an influence. As such, detrending of the position index is not carried out here. To test significance a two-sided Student's t-test is used to determine whether correlation coefficients are statistically significant above the 95% confidence level.

Author Contributions

W.C. and T.C. designed the study, and collated the data. M.T. ran the CCAM simulations. T.C. analysed the data. All authors discussed the results and reviewed the manuscript.

Acknowledgments

We thank Qiang Fu for stimulating discussion, Bertrand Timbal and Hanh Nguyen for their comments prior to submission, and Ariaan Purich for her many suggested improvements. This work is supported by the Goyder Institute and the Australian Climate Change Science Programme.

References

  1. Hudson R. D., Andrade M. F., Follette M. B. & Frolov A. D. The total ozone field separated into meteorological regimes, Part II: Northern Hemisphere mid-latitude total ozone trends. Atmos. Chem. Phys. 6, 5183–5191 (2006). [Google Scholar]
  2. Fu Q., Johanson C. M., Wallace J. M. & Reichler T. Enhanced mid-latitude tropospheric warming in satellite measurements. Science 312, 1179 (2006). [DOI] [PubMed] [Google Scholar]
  3. Hu Y. & Fu Q. Observed poleward expansion of the Hadley circulation since 1979. Atmos. Chem. Phys. 7, 5229–5236 (2007). [Google Scholar]
  4. Seidel D. J., Fu Q., Randel W. J. & Reichler T. J. Widening of the tropical belt in a changing climate. Nature Geoscience 1, 21–24 (2008). [Google Scholar]
  5. Johanson C. M. & Fu Q. Hadley cell widening: Model simulations versus observations. J. Climate. 22, 2713–2725 (2009). [Google Scholar]
  6. Lu J., Deser C. & Reichler T. Cause of the widening of the tropical belt since 1958. Geophys. Res. Lett. 36, L03803, 10.1029/2008GL036076 (2009). [Google Scholar]
  7. Hu Y. Y., Zhou C. & Liu J. P. Observational evidence for poleward expansion of the Hadley circulation. Adv. Atmos. Sci. 28(1), 33–44 (2011). [Google Scholar]
  8. Cai W. & Cowan T. Southeast Australia autumn rainfall reduction: A Climate-Change-Induced Poleward Shift of Ocean-Atmosphere Circulation. .J. Climate. In press. [Google Scholar]
  9. Hoerling M., Hurrell J., Eischeid J. & Phillips A. Detection and Attribution of Twentieth-Century Northern and Southern African Rainfall Change. J. Climate. 19, 3989–4008 (2006). [Google Scholar]
  10. Haylock M. R. et al. Trends in Total and Extreme South American Rainfall in 1960–2000 and Links with Sea Surface Temperature. J. Climate. 19, 1490–1512 (2006). [Google Scholar]
  11. Frederiksen J. S., Frederiksen C. S., Osbrough S. L. & Sisson J. M. Changes in Southern Hemisphere Rainfall, Circulation and Weather Systems. .19th International Congress on Modelling and Simulation (2011). [Google Scholar]
  12. Stachnik J. P. & Schumacher C. A comparison of the Hadley circulation in modern reanalyses. J. Geophys. Res. 116, D22102, 10.1029/2011JD016677 (2011). [Google Scholar]
  13. Oort A. H. & Yienger J. J. Observed Interannual Variability in the Hadley Circulation and Its Connection to ENSO. J. Climate 9, 2751–2767 (1996). [Google Scholar]
  14. Quan X.-W., Diaz H. F. & Hoerling M. P. Change in the tropical Hadley cell since 1950, .in The Hadley Circulation: Past, Present, and Future. Edited by H. F. Diaz, and R. S. Bradley, Cambridge Univ. Press, New York (2004). [Google Scholar]
  15. Gille S. Decadal-Scale Temperature Trends in the Southern Hemisphere Ocean. J. Climate 21, 4749–4765 (2008). [Google Scholar]
  16. Cai W., van Rensch P., Cowan T. & Hendon H. H. Teleconnection Pathways of ENSO and the IOD and the Mechanisms for Impacts on Australian Rainfall. J. Climate 24, 3910–3923 (2011). [Google Scholar]
  17. McGregor J. & Dix M. An updated description of the Conformal Cubic Atmospheric Model, in High-Resolution Simulation of the Atmosphere and Ocean, .edited by K. Hamilton, and W. Ohfuchi, pp. 51–76, Springer (2008).
  18. Son S.-W. et al. The impact of stratospheric ozone on Southern Hemisphere circulation changes: A multi-model assessment. J. Geophys. Res. 115, D00M07, 10.1029/2010JD014271 (2010). [Google Scholar]
  19. Kang S., Polvani L. M., Fyfe J. C. & Sigmond M. Impact of Polar Ozone Depletion on Subtropical Precipitation. Science 332, 951–954 (2011). [DOI] [PubMed] [Google Scholar]
  20. Compo G. P. et al. The Twentieth Century Reanalysis Project. Quarterly J. Roy. Meteorol. Soc. 137, 1–28. 10.1002/qj.776 (2011). [Google Scholar]
  21. Kalnay E. et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteorol. Soc. 77, 437–471, 10.1175/1520-0477 (1996). [Google Scholar]
  22. Kanamitsu M. et al. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Amer. Meteorol. Soc. 83, 1631–1643 (2002). [Google Scholar]
  23. Onogi K. et al. The JRA-25 reanalysis. J. Meteorol. Soc. Jpn. 85, 369–432, 10.2151/jmsj.85.369 (2007). [Google Scholar]
  24. Legates D. R. & Willmott C. J. Mean seasonal and spatial variability in gauge-corrected, global precipitation. Int. J. Climatol. 10, 111–127 (1990). [Google Scholar]
  25. Chen M., Xie P., Janowiak J. E. & Arkin P. A. Global Land Precipitation: A 50-yr Monthly Analysis Based on Gauge Observations. J. Hydrometeorology 3, 249–266 (2002). [Google Scholar]
  26. Beck C., Grieser J. & Rudolf B. A New Monthly Precipitation Climatology for the Global Land Areas for the Period 1951 to 2000. .Climate Status Report 2004, pp. 181–190 (2005). [Google Scholar]
  27. Mitchell T. D. & Jones P. D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Climatol. 25, 693–712. 10.1002/joc.1181 (2005). [Google Scholar]
  28. Jones D. A., Wang W. & Fawcett R. High-quality spatial climate data-sets for Australia. Aust. Meteor. Oceanogr. 58, 233–248 (2009). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES