Abstract
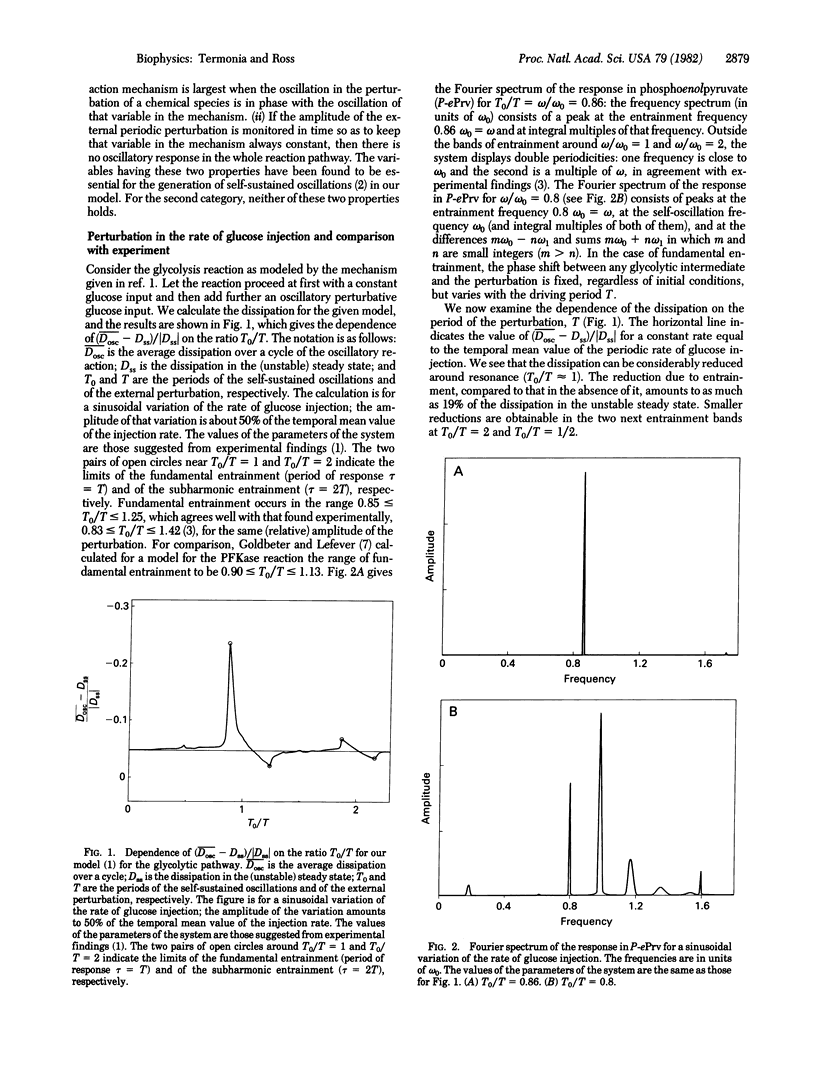
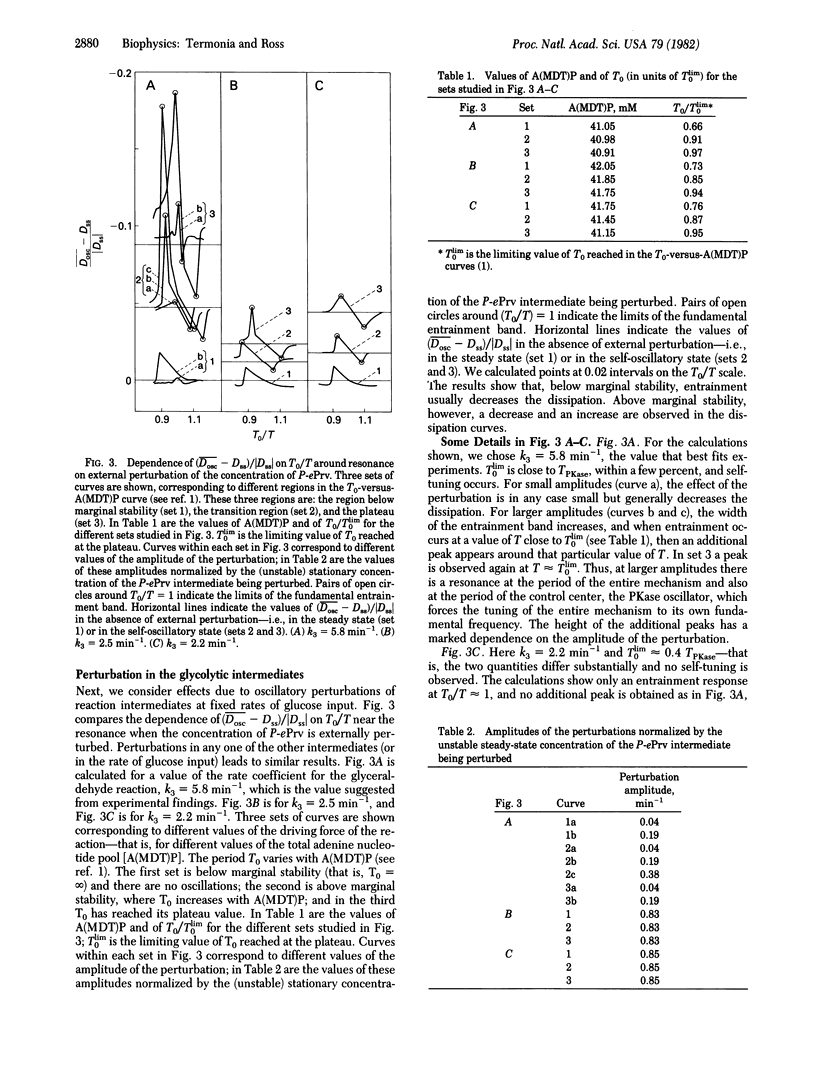
We have proposed a comprehensive model for the glycolytic reaction mechanism and have shown the possibility of self-tuning to resonance, with consequent increase in efficiency of energy transduction by separating the model into two subsystems: one for the phosphofructokinase (PFKase; ATP:D-fructose-6-phosphate 1-phosphotransferase, EC 2.7.1.11) reaction and the other for the pyruvate kinase (PKase; ATP:pyruvate 2-O-phosphotransferase, EC 2.7.1.40) reaction. The purpose of this article is to present an alternative theoretical approach—one more directly applicable to experimental situations—for the detection of these effects without the need for any decomposition. The approach consists in studying the response of such systems to externally applied periodic perturbations inside the fundamental entrainment band by computation. We show, in agreement with previous results obtained for simpler reaction schemes, that large increases and decreases in dissipation may occur in a narrow range of the period of entrainment of the entire mechanism. If the period of the autonomous glycolytic oscillation past marginal stability approaches a value, T0lim, that is close to the period of relaxation oscillation of the PKase subsystem, TPKase, then tuning of the primary oscillophor, the PFKase system, has been effected by the PKase system; in such cases we predict, for larger values of the amplitude of perturbation, two peaks in the response spectrum: one near the period of the autonomous oscillation and the other at the period of the PKase system. For small amplitudes of perturbation, there is only one resonance peak near the period of the autonomous oscillation. If T0lim is not close to TPKase, then there is only one resonance peak for small and large amplitudes of external perturbations. Our computer results lead to a classification of the chemical species in the reaction mechanism into two categories. The first category has the following two properties. (i) When fundamental entrainment occurs, the amplitude of the response in all species in the reaction mechanism is largest when the oscillation in the perturbation of a chemical species is in phase with the oscillation of that variable in the mechanism. (ii) If the amplitude of the external periodic perturbation is monitored in time so as to keep that variable in the mechanism always constant, then there is no oscillatory response in the whole reaction pathway. The variables having these two properties have been found to be essential for the generation of self-sustained oscillations in our model. For the second category neither of these two properties holds.
Keywords: oscillations, periodic perturbations, resonances, self-tuning
Full text
PDF

Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Boiteux A., Goldbeter A., Hess B. Control of oscillating glycolysis of yeast by stochastic, periodic, and steady source of substrate: a model and experimental study. Proc Natl Acad Sci U S A. 1975 Oct;72(10):3829–3833. doi: 10.1073/pnas.72.10.3829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbeter A., Lefever R. Dissipative structures for an allosteric model. Application to glycolytic oscillations. Biophys J. 1972 Oct;12(10):1302–1315. doi: 10.1016/S0006-3495(72)86164-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter P. H., Ross J. Oscillations and efficiency in glycolysis. Biophys Chem. 1980 Dec;12(3-4):285–297. doi: 10.1016/0301-4622(80)80006-8. [DOI] [PubMed] [Google Scholar]
- Termonia Y., Ross J. Oscillations and control features in glycolysis: analysis of resonance effects. Proc Natl Acad Sci U S A. 1981 Jun;78(6):3563–3566. doi: 10.1073/pnas.78.6.3563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Termonia Y., Ross J. Oscillations and control features in glycolysis: numerical analysis of a comprehensive model. Proc Natl Acad Sci U S A. 1981 May;78(5):2952–2956. doi: 10.1073/pnas.78.5.2952. [DOI] [PMC free article] [PubMed] [Google Scholar]



