Bayesian ontology querying for accurate and noise-tolerant semantic searches

Abstract

Motivation: Ontologies provide a structured representation of the concepts of a domain of knowledge as well as the relations between them. Attribute ontologies are used to describe the characteristics of the items of a domain, such as the functions of proteins or the signs and symptoms of disease, which opens the possibility of searching a database of items for the best match to a list of observed or desired attributes. However, naive search methods do not perform well on realistic data because of noise in the data, imprecision in typical queries and because individual items may not display all attributes of the category they belong to.

Results:: We present a method for combining ontological analysis with Bayesian networks to deal with noise, imprecision and attribute frequencies and demonstrate an application of our method as a differential diagnostic support system for human genetics.

Availability: We provide an implementation for the algorithm and the benchmark at http://compbio.charite.de/boqa/.

Contact: Sebastian.Bauer@charite.de or Peter.Robinson@charite.de

Supplementary Information: Supplementary Material for this article is available at Bioinformatics online.

1 INTRODUCTION

Ontologies are knowledge representations using controlled vocabularies that are designed to help knowledge sharing and computer reasoning (Robinson and Bauer, 2011). An ontology can be defined as a specification of a conceptualization (Gruber, 1993), meaning that the ontology provides a computational representation of the concepts of a domain together with the semantic relations between them. Concepts are often represented as nodes and the relations between them as edges in a directed graph. Ontologies have become essential components of search engines for the world-wide web, e-commerce and medicine (Köhler et al., 2009; Labrou and Finin, 1999; McGuinness, 2003). They are used to represent items of a domain of knowledge, e.g. the ChEBI ontology not only provides a comprehensive representation of biologically relevant small molecules (Degtyarenko et al., 2008) but also to represent the attributes of the items of a domain; for instance, the Gene Ontology (GO) provides a comprehensive representation of gene functions (Ashburner et al., 2000), i.e. the attributes of items of the domain of molecular biology.

Terms that describe only attributes of items are the base of ontologies to which we refer as attribute ontologies. There is a special annotation relation by which items are linked to the terms in order to express the fact that an item possesses the attribute described by the term. The annotation propagation rule implies that the annotation relation is propagated along other relations to parent terms and thus to all ancestor terms (Robinson and Bauer, 2011). For instance, in GO, annotation propagation is defined over is a and part of relations. Hence, if a gene is annotated to the GO term ATP binding, it is implicitly annotated to all ancestors of the term including nucleotide binding. This leads to statistical dependencies between ontology terms that can substantially degrade the performance of ontology analysis methods (Alexa et al., 2006; Bauer et al., 2010; Grossmann et al., 2007; Lu et al., 2008).

In addition, semantic similarity measures have been developed that exploit information content or graph structure to compare different items based on their annotations (Pesquita et al., 2009). On the basis of these measures, we have previously developed an algorithm for querying a database with ontology terms and ranking the results (Köhler et al., 2009; Schulz et al., 2011). However, none of the presently available ontology search algorithms has been explicitly designed to deal with the kinds of noise to be expected in real-life queries. For instance, in the setting of a clinical differential diagnosis decision support system, false-positive queries may ensue if a patient has signs or symptoms unrelated to the underlying diagnosis. Consider phenylketonuria (PKU), which is a hereditary metabolic disease that is characterized by numerous phenotypic abnormalities in untreated patients. A person with PKU may additionally develop an unrelated disease such as rheumatoid arthritis (RA), but the physician may not recognize the fact that the joint manifestations of RA are unrelated to the manifestations caused by PKU. On the other hand, not every person with a given disease necessarily has all of the signs and symptoms that are associated with the disease. For instance, most patients with Marfan syndrome have aortic dilatation, i.e. an expansion of the ascending aorta, but only about half have ectopia lentis, which is a displacement of the lens of the eye. If a feature occurs more frequently in one disease than in another, then, all else equal, we would tend to believe that the former disease explains the presence of that feature better than the latter disease and therefore can be considered as the more likely candidate.

Medical diagnostic decision support systems have been under development for decades, making use of algorithms based on Bayes’ theorem, fuzzy set theory, Bayesian networks and artificial neural networks. Many of these systems were designed for the diagnosis of individual diseases such as appendicitis. Several Bayesian network algorithms have modeled relations between diseases, findings and probabilistic links between the findings, but such Bayesian networks can be complex and intractable for large-scale problems (Wagholikar et al., 2011).

In this work, we develop the Bayesian Ontology Query Algorithm (BOQA), which, in contrast to previous approaches, integrates the knowledge stored in an ontology and the accompanying annotations into a Bayesian network (Neapolitan, 2003) in order to implement a search system in which users enter one or more terms of the ontology to get a list of the best matching domain items. For this purpose, we propose a graphical model that both reflects the hierarchical structure of the underlying attribute ontology and the propagation of errors of queries. We derive an efficient algorithm to apply probabilistic inference on this model given the queries and perform simulation studies to assess the performance. We conclude that embedding the ontology search into a Bayesian framework naturally enables a general framework for searching that deals with false-negative and false-positive query items, statistical dependencies in the attribute ontology and annotation frequencies.

We demonstrate our method with an application as a decision support system for differential diagnosis in human genetics. The model is built using the Human Phenotype Ontology (HPO; Robinson et al., 2008), Online Mendelian Inheritance in Man (OMIM; Amberger et al., 2009) and Orphanet (Aymé, 2003). Figure 1A shows an excerpt of the human ontology with annotated diseases, whereas Figure 1B shows a high-level overview for the problem. We note that a preliminary version of this application has been published in Robinson and Bauer (2011).

Fig. 1.

Principle idea of the approach in the context of clinical diagnosis. BOQA takes the data model derived from an attribute ontology and annotations together with a set of query terms to produce a ranked list of items. (A) A portion of the HPO with frequency-enhanced annotations to OMIM diseases. This information is used to define the data model of our application. (B) The high-level specification of the approach in the context of the diagnostic setting

2 METHODS

2.1 Modeling queries

We model the queries using a three-layered Bayesian network of Boolean variables. A variable represents either a state of an item or a state of a term (Fig. 2).

Fig. 2.

A Bayesian network with two items annotated using an ontology with seven terms. Item 1 is annotated to term 3, and item 2 is annotated to terms 4 and 7. The annotations are modeled by edges from the item to the hidden layer. The edges within the hidden layer are directed from child to parent terms in the ontology and implement the annotation propagation rule. The edges within the query layer are directed in the opposite direction, and together with the one-to-one edges from hidden to query layer are used to model false-positive and false-negative queries. We also depict a particular configuration of the network, in which item 1 is active and term 6 forms the query. Thus, there is a false-negative event for term 3 and a false-positive event for term 6. Probabilities of involved non-trivial events are shown associated with the nodes of the query layer

The first layer is referred to as the item layer I, and contains n Boolean variables . Each variable stands for the state of one of the n items of the domain. If 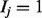, then item j is active, and if 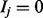, then item j is inactive.

The variables of I are connected only to variables of the second layer, which contains Boolean variables representing the hidden states of the m ontology terms. If , then term i is on in the hidden layer, and if , term i is off. For every annotation between an item j and an term i, there is an edge from to . That is, the connections between I and H reflect the explicit annotations of domain items to ontology terms. Annotations implied by the annotation propagation rule are modeled using edges in the hidden layer H that correspond to the structure of the ontology.

Finally, the hidden states of the terms are connected to the query states of the terms denoted as . They form the third layer Q. If 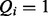, then term i is part of the query, whereas 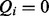means that i is not part of the query. The query state of a term depends on the corresponding state of the hidden layer, so there are links between elements of H and Q, i.e. for each i there is an edge from 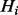to . The propagation between H and Q is probabilistic and thus is used to model false negatives (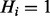 but 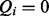) and false positives ( but ).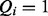

According to the annotation propagation rule for ontologies, if an item j is annotated to term i then it is also annotated to all ancestors of i. We assume that queries follow a similar rule. That is, if a term i is explicitly used in the query, i.e. 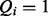, then it is assumed that all of the ancestors of this term are also part of the query. This has implications for classifying the query states, which we reflect using edges within the query layer that are directed in the opposite orientation to the edges of the hidden layer.

2.2 Application

In our clinical diagnostics application, the domain items correspond to diseases, and HPO terms describe the attributes (i.e. signs, symptoms or other phenotypic abnormalities, all referred to as ‘symptom’ in the following) of the diseases. If 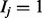, then the patient has disease j, and if 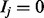, the patient does not have the disease. If , then feature i is present in the patient, whereas it is not present if . 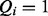expresses that symptom i was identified as present in the patient, whereas if 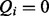, then symptom i was not observed by the physician making the diagnostic query. A false positive occurs if the physician diagnosed a symptom even though it is not truly present. A false negative occurs if the patient has a symptom, which is not observed by the physician.

2.3 Notation

The joint probability distribution (JPD) of the model is denoted as P(I, H, Q). In order to specify the local probability distribution (LPD) for each type of variable, we use subscripts to refer to a set of indices, e.g. 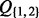refers to 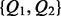. Expression pa(i) denotes the set that contains the parent or parents of term i and ch(i) refers to the children of i. Note that parent and children refer to relations of the ontology and not to edges of the Bayesian network. Finally, ea(i) denotes the set of all items that are explicitly annotated to term i. In the example shown in Figure 2, we have

If X denotes a set of random variables , then defines another Boolean random variable, such that 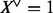, if and only if (iff) there is any 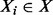with , otherwise 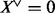. In other words, is the logical disjunction defined by . Similarly, we define as the logical conjunction of all variables of X. That is, 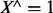iff all members of X are 1, otherwise .

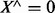2.4 LPDs of hidden term variables

For didactic purposes, we will first present a simplified version of the BOQA network in which the frequency of each annotation is 1. Therefore, if an item j is active, then all terms to which j is explicitly annotated are on in the hidden layer. If a term i in the hidden layer is not annotated to an active item, then it is off if all of the children of term i are off in the hidden layer, otherwise it is on. Thus, the state propagation from the item layer to the hidden layer, i.e. the explicit annotations, as well as the propagation within the hidden layer, i.e. implied annotations, is a deterministic function. Formally, the LPD of a single 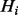is specified as:

If we denote the set of items that are explicitly or implicitly annotated to term i as 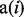, it follows that, for a given configuration and

(1)

Equation (1) merely states that there is only one valid configuration of states of H for a given configuration of states of I, namely that in which only the hidden states for the terms are on to which any active item is explicitly or implicitly annotated.

2.5 LPDs of query term variables

State propagation between the hidden layer and the query layer is modeled probabilistically, whereby the global parameters α and β represent the probability of a false-positive and false-negative event. Edges between nodes within the query layer are used to model the propagation of false positives and false negatives within the query layer.

A false-negative query occurs if . Q_i is off with probability β, if the query state of at least one parent of i is on and the hidden state of term i is also on. By assumption, if the query state of the parents of term i is off, then the query state of term i must also be off. Formally, we have

Thus, the off-case is propagated in a top-down fashion, in which a false negative is only counted once per branch, when it is first encountered.

A false-positive observation occurs if 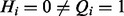. We assign this event a probability of α. Note that by assumption, the query state of parents of i have to be on as well. The probability that the query state of a term is correctly off given that the query state of all of its more general terms are on is 1 – α. Formally, we have

2.6 JPD for the basic network

Letting m represent the number of terms in the ontology and using the LPDs of the last paragraphs, we can now specify P(I, H, Q):

(2)

Given a particular configuration (H, Q) for the variables of the hidden and query layers, we define

to represent the number of all pairs of nodes (H_i, Q_i) with the given configuration. Note that

We will assume that the probability of an invalid configuration is zero, i.e. . Furthermore, observe that the conditional probabilities for cases 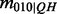and 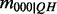do not contribute to the product as they are 1. Therefore, only four of the eight possible values contribute to the conditional probabilities of , so that we have

(3)

2.7 Searching for items using probabilistic inference over annotations

BOQA is designed to provide a query system by which users enter a list of terms representing attributes of items in a database and get back a list of the items ranked according to how well the attributes of the item match the attributes in the query. In our model, this is captured by the probability distribution of the activity state of the items given the observation or 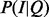. After applying the definition of conditional probability and demarginalizing P(I, Q) for H, we have

By using Equation (2), we get for the numerator:

(4)

Note that although there are distinct configurations of H, only one is valid because of Equation (1). That is, for H, we only need to consider a single configuration , in which 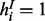, iff term i is explicitly or implicitly annotated to the active items of i. The probability of other possible assignments of H is 0. Thus, we have

(5)

Finding the configuration of items that best explain the observed data is equivalent to maximizing 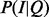for I. For this purpose, it is enough to maximize the product of the likelihood and the prior P(I), since P(Q) is the normalization constant. In general, the optimization problem to maximize this product is NP-hard (Neapolitan, 2003). However, if we limit to possible configurations of active items to ones in which only a single item is active (e.g. a situation in which a patient only has one disease), then we are able to find the best item more efficiently. We implement this restriction by defining the prior P(I) to have a probability of one only for such configurations, and zero otherwise:

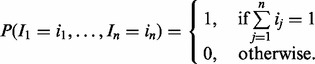We are also able to determine the marginals exactly without increasing complexity, as

where the sum is taken over the n valid models. The procedure is summarized in Algorithm1.

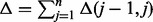Assuming that all involved mathematical calculations can be done in O(1), the inference procedure as specified in Algorithm 1 has a complexity of O(nm). However, it is easily possible to conceive an algorithm with running time time steps, where and 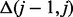is the Hamming distance between the annotation bit vectors for item j – 1 and j, by updating rather than calculating the counts for subsequent items. For an optimal running time, the items are renumbered in a preprocessing step such that is minimal. Although this optimization problem is NP-hard, efficient algorithms such as the one by Christofides (1976) can be used to get a constant factor approximation of the optimal solution due to the relatedness of this problem with the traveling salesman problem.

2.8 Parameter-augmented network

Up to now, we have treated the false-positive rate α and the false-negative rate β as constants. Since the true value of these parameters is unknown, we choose to integrate over a range of values for α and β. Since the integral is not tractable, we integrate over a grid of suitable range of different combinations of α and β.

Formally, we augment the Bayesian network with two nodes A and B that represent these parameter values, i.e. the realization of A is α and the realization of B is β and which have links to the nodes within the query layer. Letting 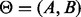, then the LPD is parameterized as . The JPD of the augmented network is factored as

The likelihood 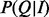becomes

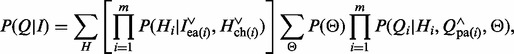while we assume that A and B and thus Θ are discrete random variables. A simple choice for values is an equal-sized grid over the range (0, 1). However, assuming that only few false positives are entered, it is appropriate to limit α. We choose and 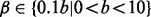with uniform prior.

2.9 Frequency awareness

In many diseases, any given symptom may not occur in all patients but only in a certain proportion of the patients. We will refer to this quantity as the frequency of a disease feature. The HPO project provides feature frequencies for an increasing number of diseases based on original publications and data extracted from OMIM (Amberger et al., 2009) and Orphanet (Aymé, 2003). We will now show how our framework can be extended to exploit frequency information.

We define the frequency of an attribute represented by term i associated to an item j as 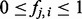. We assume that 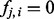, iff an item j is not annotated to a term i. Using this convention, we reformulate the LPDs of the hidden nodes as follows:

(6)

(7)

Thus, the state propagation, which is exemplified in Figure 3, is no longer deterministic. By definition, represents the probability that term i is on if item j is active, and thus the probability that the hidden state of i is off if item j is active is . If we additionally incorporate the activity state of the item, we get that is, if item j is inactive, then term j is off with probability of 1. Therefore, the hidden state of term i given all items is off, if the propagation of each active item independently lead to an off state. The probability of this event is the product of for each item j. Note that if only one item is active, then Equation (6) can be simplified to .

Fig. 3.

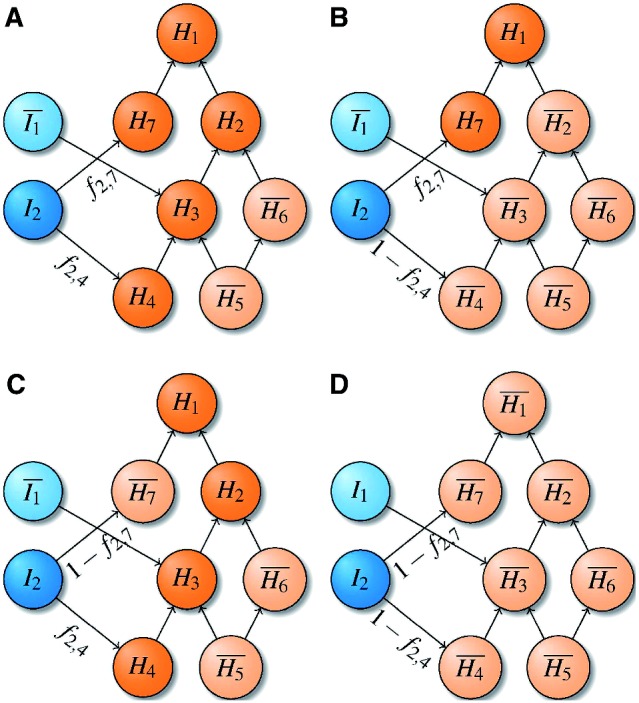
Frequency-aware propagation. Here, I₂ is active, whereas I₁ is inactive. Given that, the probability that H₄ is on is f_2,4. The probability that H₇ is on is f_2,7. In addition, the frequencies between the diseases and all other terms are 0 so they can be omitted. Thus, there are four possible configurations of the model. The probability of configuration (A) is 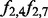, (B) is , (C) is , whereas for (D) it is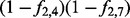

Using this definition, the calculation for the likelihood becomes more complex the more annotations with frequencies are available, i.e. the more non-deterministic state propagations are included in the model, because the number of possibilities that needs to be explored grows exponentially in the number of such annotations. In the search procedure, we therefore restrict the search space to the k least frequent annotations which are not 0, all other annotations always considered as present. As we will see in the benchmarks, even though this is a simple heuristic, we are able maintain highly precise predictions for a greater recall.

2.10 Benchmarks

We performed a systematic benchmark of five search methods using data from the HPO project supplemented by frequency information from Orphanet. The HPO ontology file and phenotype annotation file were downloaded at June 1, 2011. In total, there were n = 2368 diseases with frequency information annotated to a total of 6584 HPO terms, with on average for any disease j.

We simulated five patients for each of the n diseases. For any one simulated patient, phenotypic features were assigned according to the frequency data, and it was assumed that features without any frequency information are always present. The features of the simulated patient were then used to generate a diagnostic query. We additionally simulated the uncertainties of the diagnostic process by randomly adding assigned unrelated features, i.e. false positives, with a probability α to the query. Note that by this event, also terms that are the ancestors will be part of the query. In order to simulate false-negative observations, we removed disease features from the query with a probability of β. If a term is removed from the query, then by assumption, all of its descendants were also removed. These arrangements represent a kind of noise intended to represent realistic clinical situations in which not all patients have textbook presentations of disease, and not all physicians have the same expertise. Finally, from the set of most specific terms, we randomly drew s terms to simulate the fact that physicians, as well as users of other search systems, are unlikely to enter more than a relatively small number of search terms. Note that this has an impact on the true β.

For each set of simulated query terms, we applied one of following search procedures: (i) Res: ranking according to Resnik-based semantic similarity score as done in Köhler et al. (2009); (ii) Lin: similar to Res but using term similarity measure defined in Lin (1998); (iii) JC: similar to Res but using term similarity measure defined in Jiang and Conrath (1997); (iv) ResP: ranking according to the P-value approach as in Köhler et al. (2009). We use 250 000 random queries to approximate the score distribution. Ties are resolved using the semantic similarity score. A Bonferroni correction based on the number of diseases tested for was applied. Although this has no influence on the ranking, this affects how items are classified at a fixed threshold; (v) BOQA: the Bayesian approach without taking frequency into account; (vi) BOQA: the frequency-aware Bayesian approach with k = 10 and (vii) BOQA′: the frequency-aware Bayesian approach with k = 10 and without integrating over parameters, i.e. with the parameters α and β set to the correct values. This gives an upper bound for the performance of the algorithm.

Each method returns a result vector of length n, in which entry j represents either a score or a probability value for disease j. The concatenation of all five n result vectors and the true labels are used to evaluate the performance of the method by receiver operating characteristic (ROC) and precision/recall analysis.

3 RESULTS

The result of this work is an efficient search procedure called BOQA that embeds an attribute ontology, items of a domain and their annotations into a Bayesian network. Figure 2 depicts a graphical representation of the network for an example ontology. The objective of the method is to find appropriate items given a set of user query terms, which we handle by applying probabilistic inference on the Bayesian network instance. Formulating the task as a Bayesian network problem allows one to take false-positive and false-negative user queries as well as the attribute frequencies into account. Details are given in Section 2.

We test BOQA by using it as a differential diagnostic tool for clinicians by simulating 11 840 patients with 2368 diseases annotated using information from the HPO, OMIM and Orphanet. ROC and precision/recall analysis were used to compare the performance of BOQA with two other ontology-based search procedures. We report the results for different settings for the false-positive rate α, the false-negative rate β as well the number of terms that are used to form a query of size s.

The upper part of Figure 4 shows the evaluation of simulations through ROC curves. The Res, Lin and JC approaches, which are all based on variants of raw semantic similarity scores, have the worst performance. The P-value method, ResP, shows better performance, as has been previously reported (Köhler et al., 2009; Schulz et al., 2011). The Bayesian approaches presented here shows the best performance at all tested noise levels. In particular, the BOQA performs better than the simpler BOQA approach, which lacks the inclusion of frequency information. BOQA is only beaten by the BOQA′ approach, in which the true values of α and β are known.

Fig. 4.

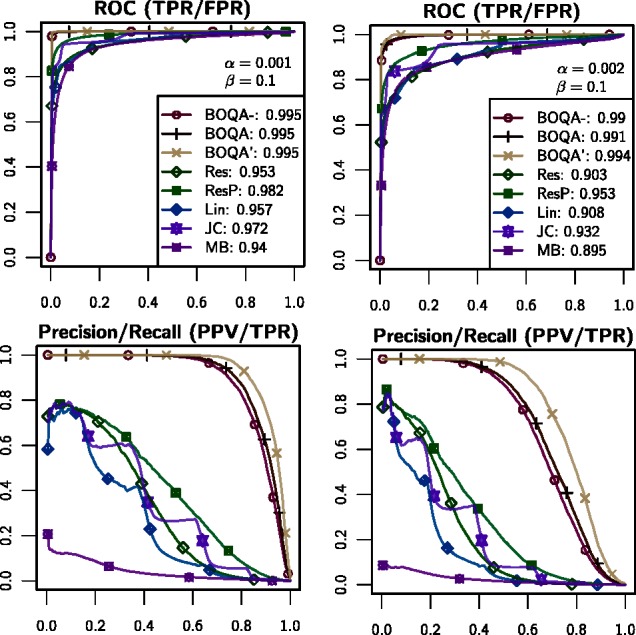
Performance comparison using ROC and precision/recall analysis. The analysis was performed on 2368 diseases. For each disease, five patients were generated according to available frequency information. The true features of each patient were then obfuscated according to different levels of noise (α,β) as indicated. The maximum query size s was set to 6

Due to the large disproportion between the positive and negative classes, the difference between the methods is noticeable but not very large in the ROC analysis. The difference becomes clearer, if one looks at the positive prediction value (PPV) at a fixed threshold. For instance, for the setting in which α = 0.002, β = 0.002 and s = 6, from the data generated for the 11 840 patients, BOQA assigns 6933 items a marginal probability >0.5, of which 5626 were true positives. This gives a PPV of 80%. In contrast, the P-value approach flagged 8636 items with a P-value <0.05, of which 3761 items were true positives, yielding a PPV of only 44%. As reported in Table 1, the same conclusion holds for other parameter settings.

Table 1.

Performance according to the positive predictive value TP/(TP + FP) at a fixed classification threshold

	BOQA (>0.5)			P-value (<0.05)
α/β/s	TP	TP + FP	PPV (%)	TP	TP + FP	PPV (%)
0.001/0.1/6	8479	9448	90	6129	14 913	41
0.002/0.1/6	5725	7139	80	3761	8636	44
0.001/0.1/3	3456	4648	74	2035	4721	43
0.002/0.1/3	1903	2988	64	1210	2753	44

The PPV and the precision of a classifier refer to the same quantity. In general, the so-called precision/recall analysis represents a complementary way of evaluating the results of prediction methods in which a range of recall, i.e. sensitivity, thresholds are analyzed. As shown in the lower part of Figure 4, the Bayesian approaches indeed yield a higher precision over the entire range of recall thresholds with all noise configurations tested.

4 DISCUSSION

We have demonstrated the use of BOQA as a decision support tool in human genetics, in which physicians enter the phenotypic abnormalities observed in a patient to search among 2368 Mendelian diseases for the most likely diagnosis to explain the symptoms of the patient. In this setting, BOQA models a generative process, in which a disease causes observable phenotypic abnormalities that are structured according to the HPO. After the physician has entered the observations, probabilistic inference is applied in order to rank each disease according to the probability that it explains the observed phenotypic abnormalities.

We showed with simulations that a marginal probability of an item being >0.5 of items as calculated by our model is a more precise indicator for finding the true item as a P-value <0.05 (Table 1). This holds true for the entire range of recalls (Fig. 4). One obvious reason for this improvement is that BOQA directly models false-positive and false-negative observations and seamlessly integrates available frequency information. Another important reason is that BOQA is a global approach. It models the generation of search queries and applies probabilistic inference by which the result of each item depends on the result of all other items: the marginal probabilities add up to 1.

In order to derive an efficient inference algorithm, we assume that exactly one item is responsible for the terms part of the query. This simplification is often realistic in the field of medical genetics, which we used as a demonstration. Clearly, BOQA can also find combinations of items that best explain a given set of query terms by defining appropriate prior distribution P(I) in Equation (6), which may be useful for certain applications. Note that this generalization has consequences on the tractability of the inference problem as combinations of items being active may have to be considered. Furthermore, for reasons of efficiency, we considered merely the frequency information for k-lowest probable features. In order to generalize the algorithm with respect to these simplifications, it may be worthwhile to apply more sophisticated probabilistic inference procedures such as sampling based or approximative ones. These may also help to reduce the still relative large gap between BOQA′ and BOQA.

Our Bayesian approach to ontology-based searching allows a wide range of extensions that may be useful in specific situations. For instance, if a physician is absolutely sure that a certain observed feature is present, then one could assign a very small α-value (probability of false positives) to that feature. Analogously, a very small β range value can be asserted for a particular feature, if the physician is sure that the feature is not present in the patient, say because it has been ruled out by a targeted laboratory investigation. On the other hand, if the physician is unsure, this could be encoded by larger values for these parameters. This additional knowledge could help to distinguish between different search results if no disease attains a probability >0.5. Another conceivable enhancement is the inclusion of knowledge about possible co-occurrences of features. As this requires a more complex annotation model, a simulation experiment similar to the proposed one could be used to verify the usefulness of the approach.

Although we have presented an application of BOQA in the medical domain, the search algorithm is by no means limited to medicine. Applications for searching archives of documents in order to find documents belonging to categories that have been annotated to certain concepts based on word usage may profit from BOQA. For instance, if a word such as semiconductor occurs in 35 of 70 documents in the category computer hardware, then the frequency of this term would be 0.5; categories such as computer hardware would play the role of diseases in our example, and documents would play the role of patients.

Funding: Deutsche Forschungsgemeinschaft (DFG RO 2005/4-2) and the NIH (R01 HG004838-02).

Conflict of Interest: none declared.