Deep architectures for protein contact map prediction

Abstract

Motivation: Residue–residue contact prediction is important for protein structure prediction and other applications. However, the accuracy of current contact predictors often barely exceeds 20% on long-range contacts, falling short of the level required for ab initio structure prediction.

Results: Here, we develop a novel machine learning approach for contact map prediction using three steps of increasing resolution. First, we use 2D recursive neural networks to predict coarse contacts and orientations between secondary structure elements. Second, we use an energy-based method to align secondary structure elements and predict contact probabilities between residues in contacting alpha-helices or strands. Third, we use a deep neural network architecture to organize and progressively refine the prediction of contacts, integrating information over both space and time. We train the architecture on a large set of non-redundant proteins and test it on a large set of non-homologous domains, as well as on the set of protein domains used for contact prediction in the two most recent CASP8 and CASP9 experiments. For long-range contacts, the accuracy of the new CMAPpro predictor is close to 30%, a significant increase over existing approaches.

Availability: CMAPpro is available as part of the SCRATCH suite at http://scratch.proteomics.ics.uci.edu/.

Contact: pfbaldi@uci.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Protein residue–residue contact prediction is the problem of predicting whether any two residues in a protein sequence are spatially close to each other in the folded 3D structure. Contacts occurring between sequentially distant residues, i.e. long-range contacts, impose strong constraints on the 3D structure of a protein and are particularly important for structural analyses, understanding the folding process and predicting the 3D structure. Even a small set of correctly predicted long-range contacts can be useful for improving ab initio structure prediction for proteins without known templates (Tress and Valencia, 2010).

The performance of many contact predictors has been assessed every 2 years during the Critical Assessment of protein Structure Prediction (CASP) experiments since CASP2 in 1996. Unfortunately, the ~20% accuracy for long-range contacts, routinely reported at CASP for the best predictors (Ezkurdia et al., 2009; Kryshtafovych et al., 2011), suggests that contact prediction is not yet accurate enough to be systematically useful for ab initio protein structure prediction or engineering.

In broad terms, there are four main approaches for residue–residue contact prediction. Machine learning approaches use methods such as neural networks (Fariselli et al., 2001; Punta and Rost, 2005; Shackelford and Karplus, 2007), recursive neural networks (Baldi and Pollastri, 2003; Vullo et al., 2006), support vector machines (Cheng and Baldi, 2007) and hidden Markov models (Björkholm et al., 2009) to learn how to predict contact probabilities from a training set of experimentally determined protein structures. Inputs to these approaches typically include predicted secondary structure, predicted solvent accessibility as well as evolutionary information in the form of profiles. Template-based approaches use homology or threading methods to identify structurally similar templates from which residue–residue contacts are then inferred (Misura et al., 2006; Skolnick et al., 2004). Correlated mutations approaches apply statistical measures, such as Pearson correlation (Göbel et al., 1994; Olmea and Valencia, 1997) and mutual information (Burger and van Nimwegen, 2010; Dunn et al., 2008), to multiple alignments in order to identify pairs of residues that co-evolve and thus are likely to be in contact. Recently, a new elegant mutual information-based measure for correlated mutations, PSICOV, has been proposed in Jones et al. (2011) and used for fold recognition (Taylor et al., 2011). Although this method has been reported to yield significant accuracy improvements, its performance is very dependent on the availability and quality of multiple alignments. Finally, 3D model-based approaches rely on predicted 3D structures for deriving distance constraints through a consensus strategy. Although 3D model-based approaches have been reported to be the most accurate at CASP (Kryshtafovych et al., 2011), in practice, their applicability remain somewhat limited since the main goal of contact prediction is to improve ab initio structure prediction and not the converse.

Here, we introduce several new ideas for contact prediction using primarily a multi-stage machine learning approach, with increasingly refined levels of resolution. First, we predict coarse contact maps corresponding to contacts between secondary structure elements. By itself, the idea of coarse contact maps is not new, and several useful methods have been developed (Baldi and Pollastri, 2003; Pollastri et al., 2006; Vullo and Frasconi, 2003). Yet, none of these approaches has been able to convincingly demonstrate that coarse prediction is useful for residue–residue contact prediction. Here, we both refine the previous coarse prediction methods, in part, by extending the notion of coarse contact beyond a simple binary value to include information about orientation (parallel versus anti-parallel) between contacting segments and demonstrate that coarse-grained prediction can be used to improve fine-grained prediction of contact maps. Second, we use a novel energy-based neural network approach to refine the prediction of the alignment and orientation of contacting secondary structure elements and predict residue–residue contact probabilities for residues in contacting pairs of alpha-helices or beta-strands. Finally, we introduce a deep neural network architecture in the form of a deep stack of neural networks, with the same topology but different parameters, to predict all the residue–residue contact probabilities by integrating information both spatially and temporally. Spatial integration refers to the idea that contacts are spatially correlated; for instance, long-range contacts often include other long-range contacts in their neighborhood. Temporal integration refers to the idea that protein folding is not an instantaneous physical process. Although the stack is not necessarily meant to mimic the actual physical process, the stack is used to organize the prediction in such a way that each level in the stack is meant to refine the prediction produced by the previous level. Inputs at a given level of the stack include both information coming from the previous level in the stack as well as static information produced by the previous coarse prediction stages, as well as predicted secondary structure and solvent accessibility, and evolutionary profiles. Thus, these dynamic and static inputs are used to iteratively refine the contact prediction. We next describe these methods in detail together with the data used for rigorous training and assessment results.

2 MATERIALS AND METHODS

2.1 Contact definition and evaluation criteria

We adopted the same intra-molecular contact definition and the same evaluation criteria as in the most recent CASP experiments. Two residues are defined to be in contact if the Euclidean distance between their 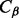atoms ( 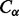for glycines) is <8 Å. Three distinct classes of contacts are defined depending on the linear sequence separation between the residues: (i) long-range contacts, with separation ≥24 residues; (ii) medium-range contacts, with separation between 12 and 23 residues and (iii) short-range contacts, with separation between 6 and 11 residues. Contacts between residues separated by <6 residues are dense and can be easily predicted from the secondary structure. Conversely, the sparse long-range contacts are the most informative and also the most difficult to predict. Thus, as in the CASP experiments, we focus primarily on long-range contact prediction.

The performance is evaluated using two main measures: the accuracy (Acc) and the distance distribution (X_d). The accuracy is defined as the fraction of correctly predicted contacts with respect to the total number of contacts evaluated:

where TP and FP are the true-positive and false-positive predicted contacts, respectively. The distance distribution score measures the weighted harmonic average difference between the predicted contacts distance distribution and the all-pairs distance distribution. The X_d is defined by

where 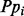is the fraction of predicted pairs whose distance is in the bin 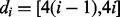and 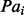is the fraction of all pair of targets in the bin 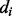. The higher X_d is, the better the performance (a random predictor corresponds to X_d = 0). Contact predictors usually assign a probability score to every possible pair of residues or to a subset of the possible pairs. The Acc and X_d measures are computed for the sets of L/5, L/10 and five top-scored predicted pairs, where L is the length of the domain sequence. Although predictions are evaluated on all three sets, the most widely used performance measure is Acc for L/5 pairs and sequence separation ≥24.

2.2 Training and test sets

The training set is derived from the ASTRAL database (Chandonia et al., 2004). We extract from the ASTRAL release 1.73 the (pre-compiled) set of protein domains with <20% pairwise sequence identity, removing domains of length <50 residues, domains with multiple 3D structures, as well as non-contiguous domains (including those with missing backbone atoms). We further filter this list by selecting just one representative domain—the shortest one—per structural classification of proteins (SCOP) family (Murzin et al., 1995) ending up with a final set of 2356 structures. For cross-validation purposes, this set is then partitioned into 10 disjoint groups of roughly the same size and average domain lengths so that no domains from two distinct groups belong to the same SCOP fold. In this way, training and validation sets share neither sequence nor structural similarities.

For performance assessment, a non-redundant test set is derived from ASTRAL release 1.75, by selecting all the new folds, with respect to version 1.73, belonging to the main SCOP classes (all-alpha, all-beta, alpha/beta and alpha + beta). From this set (256 new folds and 287 new families), we remove all the domains of length <50 residues and those with <L/5 long-range contacts (239 new folds and 268 new families). Redundancy is filtered out by clustering each group of domains belonging to the same SCOP family at 40% of sequence similarity. The final set of 364 domains contains at least one representative for each one of the 268 new families. A BLAST (Altschul et al., 1990) search with E-value cutoff 0.01 of the test domain sequences against the set of training domain sequences returns no hit.

For comparison with the current state-of-art contact predictors, the performance is tested on the template-based/free-modeling (TBM/FM) domain targets used in the last two CASP experiments, CASP8 (Ezkurdia et al., 2009) and CASP9 (Monastyrskyy et al., 2011) for contact prediction assessment. Note that ASTRAL 1.73 was released in 2007, before the CASP8 experiment held in 2008, thus no structural similarities exist between the domains in the training set and those from CASP8 (12 domains) and CASP9 (28 domains). An additional test is performed with BLAST to detect sequence similarities between the CASP and the training target sequences. A BLAST search with an E-value cutoff of 0.01 returns no similar domain pairs. The predictions for the groups participating at the CASP8 and CASP9 meetings are obtained from the CASP website http://predictioncenter.org/. As in CASP, performance is assessed here only at the domain level, although predictions are available for the entire protein targets. To simplify the comparison, we select only those groups that submitted a prediction for all the targets in the respective CASP8 and CASP9 sets. Furthermore, we considered all the domain targets for each group, regardless of the number of predicted contacts per domain. CASP assessors typically exclude from the analysis the results of a predictor on any domain where the number of predicted contacts is not high enough. This filtering step is not used here since it does not affect the performance of the top-scoring predictors.

2.3 Coarse contact and orientation prediction (bidirectional recurrent neural network)

We use 2D bidirectional recurrent neural networks (2D-BRNNs; Baldi and Pollastri, 2003) to predict coarse contact probabilities and orientations between secondary structure elements. Specifically, ignoring for robustness coils, short strands (≥3 residues) and short helices (≥6 residues), we predict the probability of whether two elements are in parallel contact, anti-parallel contact or no-contact. The distance between two secondary structure elements is defined to be the minimum Euclidean distance among all the possible pairs of 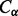atoms, one from each element. A pair of elements is defined to be in contact if and only if their distance is <8 Å. The orientation angle of two elements is defined as the angle between their orientation vectors. The orientation vector is computed by joining the centers of gravity ( 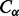coordinates) of the first and second half of the element. Two elements are in parallel contact if their distance is <8 Å and their orientation angle is <90°, anti-parallel contact if their distance is <8 Å and their orientation angle is >90° and no-contact if their distance is >8 Å.

For each pair, 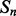and 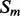, of secondary structure elements, the output of the 2D-BRNN is a probability vector corresponding to the probability of parallel contact, anti-parallel contact or no-contact. The input of the 2D-BRNN for the pair S_n and S_m consists of two feature vectors 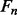and 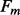as well as the number of elements between 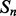and 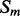. The feature vector 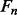for segment 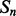has the following components:

1. Three vectors (20 entries each) representing the average amino acid distribution computed over the profiles of S_{n – 1}, S_n and S_{n + 1}.

2. The lengths (three entries) in residues of S_{n – 1}, S_n and S_{n + 1}.

3. The lengths (two entries) in residues of the intervals between S_{n – 1} and S_n and S_n and S_{n + 1}. These intervals correspond to the sum of the lengths of the coils and short elements that are ignored between the elements under consideration. This length is 0 for adjacent elements (Supplementary Fig. S1).

4. A vector of flags (four binary entries) to identify the first, second, second-to-last and last elements in the sequence.

5. Two vectors (20 entries each) containing the average amino acid distribution for alternate even- and odd-numbered columns in the profile of S_n. Specifically, if S_n consists of residues s₁, s₂, s₃, … , the first vector contains the average sequence profile over residues (s₁, s₃, s₅, …) and the second vector over (s₂, s₄, s₆, …). This feature is designed explicitly for strands, since these two sets of positions tend to have similar properties when the two strands are paired in a beta-sheet.

The 2D-BRNN is trained using 10-fold cross-validation.

2.4 Element alignment prediction (energy)

We use an energy-based method (Nagata et al., 2011) to assign energies then probabilities to the alignment between contacting secondary structure elements and derive approximate probabilities of contact for their residue pairs. This approach is used only for helix–helix and strand–strand contacting elements, since these are by far the most frequent among well-defined secondary structure elements (i.e. strand–helix contacts are relatively rare). Furthermore, it is generally hard to align strand and helix elements at the residue-level because helices are more compact when compared with strands.

Alignments between secondary structure elements are described by two components: the relative shift and the phase. The relative shift is an integer representing how the residues in the first element are shifted with respect to the second element. For instance, the shift between two strands of length 5 can have any integer value from 0 to 9. The phase is an integer assigned to pairs of residues, one from each contacting element, which is meant to capture in approximate fashion the periodic component of strand–strand and helix–helix contacts with some partial correlation to physical distance. Since the side chains of contacting strands are alternatively distributed on each side of the corresponding beta-sheet, and alpha-helices make approximately two turns every seven residues, it is reasonable to view strands and helices as periodic structures with periods 2 and 7, respectively. The phase value is assigned periodically by starting from the two residues with the closest 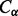s and moving away from it in both directions. For strand–strand contacts, the phase values alternate between 0 and 1, whereas for helix–helix contacts, the phase values cycle periodically from 0 to 6 (Supplementary Fig. S2a and b).

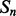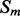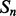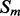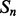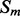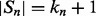Given a pair of contacting elements, and , we need to evaluate the energy of all the possible alignments obtained by shifting over (which is kept fixed), such that at least one residue in is paired with one residue in . If and 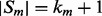are the lengths of 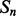and 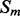, respectively, there are exactly 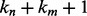possible shifts numbered 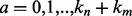. Each one of these shifts can be in O different phases numbered 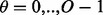with O = 2 for strands and O = 7 for helices. Thus, we need to evaluate the energy of 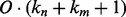alignments. Assume that the segment 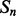consists of residues 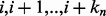and 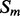of residues . Then, the energy for the ath shift with phase of segment 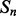versus segment 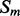is given by

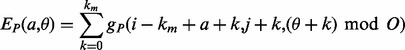(1)

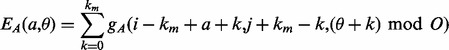(2)

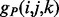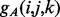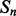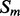where the function (respectively, ) returns the estimated energy for the residue pair i, j, under the assumption that and are parallel contacting (respectively, anti-parallel contacting) and that the phase of i, j is k (Supplementary Fig. S2c). As a manageable example, Figure S3a in the Supplementary Material shows all the alignment positions and the corresponding energies for two anti-parallel strands of hypothetical length 3. The alignment energies 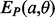and 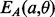are normalized into probabilities by

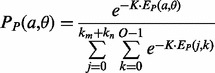(3)

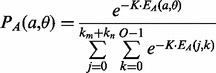(4)

where K is a fixed constant.

In order to compute the alignment energies (1) and (2) and the corresponding normalized probabilities (3) and (4), we need to define the residue–residue energy functions 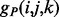and 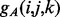. We model these functions by using two-layer feedforward Neural Networks (NN). There are four NNs: two for the strand–strand parallel and anti-parallel cases and two for the helix–helix parallel and anti-parallel cases. In all four cases, the NN input simply encodes the two sequence profile vectors (20 entries each) for the residue pair (i and j). The output size of the NNs is O = 2 for the strand-related predictors and O = 7 for the helix-related predictors and represents the phases. The function 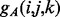thus represents the kth output of the (anti-parallel) NN for the residue pair (i and j). The network weights for the anti-parallel case are trained by gradient-descent minimization of the log-likelihood objective function

(5)

where n is the number of anti-parallel contacting element pairs used in training and 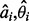are the true shift and phase for the ith example (the objective function is similar for the parallel case). Thus, we can train the NN weights by gradient descent, back-propagating the partial derivatives:

(6)

The four alignment predictors are also trained using 10-fold cross-validation on the data described in Section 2.2.

The alignment probabilities provide an estimation of the possible spatial arrangement of two secondary structure elements. These probabilities can easily be mapped to residue–residue contact probabilities. The mapping is obtained by choosing the probability score of the unique alignment in which the two residues are paired together and are close (i.e. their phase is 0). For instance, assume that i and j belong to two anti-parallel elements 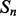and 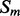. Then, there is a unique shift a of 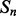over 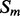in which i and j are paired together. For this shift, there is a unique overall phase 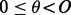such that i and j are given phase 0. Then, the probability 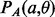represents the probability of contact for the pair (i and j; Supplementary Fig. S3b).

2.5 Residue–residue contact prediction (deep NN)

The deep neural network architecture for residue–residue contact prediction consists of a 3D stack of neural networks 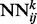. Each network 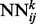in the stack is a standard three-layer feedforward network trainable by back propagation, and all the networks share the same topology: same input size, same hidden layer size, with one single output, which represents the residue–residue contact probability computed at position i, j and level k. Thus, i and j are spatial indexes over the contact map, whereas k is a ‘temporal’ index. Each layer k of NNs in the stack produces a contact map prediction, which is then refined in the subsequent layers. The range of k is determined during the training phase, as described below. Each 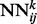has two different kinds of input features: purely spatial features and temporal features. For fixed i and j, the purely spatial features are identical for all the 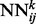as k varies and consist of typical features used in contact map prediction. The temporal input features for 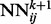consist of the predicted contact map around i and j at the previous level of the stack, i.e. the outputs of the networks 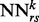, where r, s ranges over a ‘receptive field’ neighborhood of i and j. The receptive fields used in the simulations results are essentially 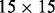square patches (Supplementary Fig. S4). The integration over time provided by the different levels in the stack corresponds to the intuition that folding is a somewhat organized, non-instantaneous, process which proceeds through successive stages of refinement. The integration over space provided by the receptive fields of the temporal features captures the idea that residue–residue contacts in native protein structures are generally not isolated: a contacting residue pair is very likely to be in the proximity of a different pair of contacting residues. Over 98% of long-range contacting residues are in close proximity of another contact, compared with 30% for non-contacting pairs. Furthermore, over 60% of contacting pairs are in the proximity of at least 10 different contacts, compared with 2.5% for non-contacting pairs (Supplementary Fig. S5). In other words, for a residue pair (i and j), the higher the number of its neighboring contact pairs, the higher the probability that i and j are in contact. Most previous machine learning-based contact predictors learn the contact probabilities of residue pairs independently of the contact probabilities in their neighborhoods. Thus, one of the aims of the deep-NN architecture (DNN) is to leverage this important information during the learning phase. Note that even if the individual contact predictions at a given stage are inaccurate, the contact probabilities can still provide a rough estimate of the number of contacts in a given neighborhood. (Fig. 1)

Fig. 1.

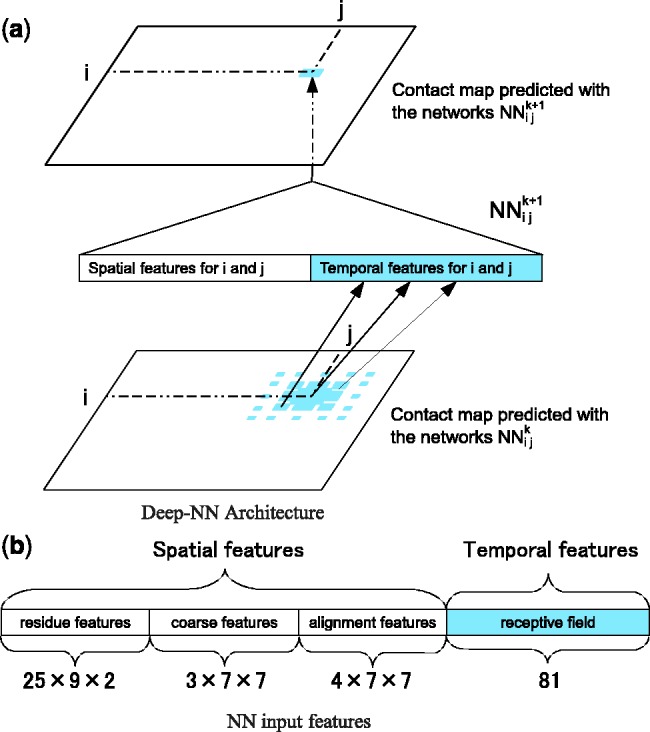
(a) The deep-NN architecture consists of a 3D stack of neural networks 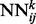with identical architecture but different weights. When i and y vary, the outputs of the 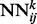correspond to the predicted contact map at level k of the stack. A neural network 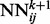purely spatial input features that depend only on i and j and are identical at all levels of the stack, and temporal input features associated with the contact probabilities predicted in the previous layer over a receptive field neighborhood of ij. (b) Input feature vector of each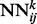

There are three types of purely spatial input features: residue–residue features coarse features and alignment features.

Residue–residue features encodes three kinds of information (for a total of 25 values): evolutionary information (20 values, one for each amino acid type), predicted secondary structure (three binary values: 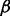-sheet, 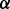-helix or coil) and predicted solvent accessibility (two binary values: buried or exposed). The evolutionary information is encoded in the standard way, as residue frequency profiles extracted from multiple sequence alignments. Frequency profiles are obtained by running PSI-BLAST (Altschul et al., 1997) with E-value cutoff equal to 0.001 and up to 10 iterations against NCBI’s non-redundant protein sequence database NR. The secondary structure is predicted with SSpro (Pollastri et al., 2002a) and the solvent accessibility with ACCpro (Pollastri et al., 2002b). We used two previously published versions of SSpro (Pollastri et al., 2002a) and ACCpro (Pollastri et al., 2002b), derived before 2008 (Cheng et al., 2005), without retraining them. The residue–residue features for the pair (i and j) are included in the network input by taking a fixed-size window centered at each residue. That is, for the pair (i and j), the network input includes the residue–residue feature vectors for residues 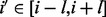and 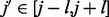, where 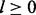is the radius of the window. After some experimentation, we use l = 4 since larger radiuses lead to slower training with no significant performance improvement.

Coarse features (three values) contain the predictions obtained with the coarse contact and orientation predictor (see Section 2.3). If residues i, j are in elements 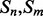, the feature vector is setup with the predicted contact orientation probabilities (parallel, anti-parallel and non-contact) for 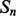and 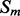(Supplementary Fig. S1). If eithe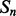r or 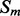is an ignored element (i.e. coil element or short helix/strand element), the three values in the feature vector are set by default to zero. The coarse contact features are included in the network input by taking a fixed-size window (of radius 3) centered at the element pair.

Alignment features (four values) contain the predictions obtained with the element alignment predictor (see Section 2.4). If residues i, j are in elements 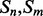and 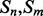are both helix elements, the first and second entries of the vector contain the alignment probability score between i and j for the cases parallel and anti-parallel contact, respectively. The remaining two entries are set to zero. The encoding is symmetrical for the strand–strand case. If 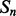and 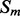are not both helix or both strand elements, the four entries of the feature vector are set by default to zero. As for the coarse contact features, the alignment features are included in the network input by taking a fixed-size window (of radius 3) centered at the residue–residue pair.

2.5.1 Deep-NN training

Training deep multi-layered neural networks is generally hard, since the backpropagated gradient tends to vanish or explode with a high number of layers (Larochelle et al., 2009). Here, we use an incremental approach to overcome this problem. The weights of the first level networks, 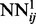, are randomly initialized and their temporal input features set to 0. These networks are then trained by on-line backpropagation for one epoch. The weights of 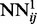are then used to initialize the weights of 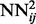, and all the outputs of the 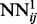networks on the training set are stored and used to compute the temporal input features of the networks 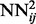, which are then trained by back-propagation during one epoch. Then, the weights of the networks 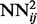are used to initialize the weights of the networks 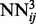and so forth all the way to the top of the stack. This progressive initialization is critical: initialization with random weights at each level of the stack results in poor performance, from unstable learning to getting stuck in poor local minima. Likewise, more stable training is obtained by using the same training set at each level of the stack, as opposed to randomizing the training data. Thus, in practice, at each training epoch, we append a new neural network to the growing DNN, initialize it with the weights of the previous level and train it by back-propagation using the true contacts as the targets (or softer targets could be derived from folding data). We have experimented with many variations such as growing the stack up to a maximum of 100 networks or growing it to a smaller depth but then repeating the training procedure through one or more epochs. The approach described earlier in the text provides a good compromise between training time and average cross-validation accuracy. Note that, although a deep-NN with n levels comprises 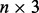layers, the number of free training parameters is rather small. Only the parameters of the first level are free, all other parameters are initialized in succession using the parameters from the previous level after one training epoch.

Since the non-contact pairs are considerably more abundant than the contact pairs, a standard approach to deal with unbalanced training set is to rebalance the data. For contact map prediction, this is often done randomly selecting only 5% of the negative examples, while keeping all the positive examples. In our experiments, we obtain considerable better overall performance by increasing this percentage to 20% (data not shown).

We train 10 different deep-NN predictors by cycling through the 10 training subsets (Section 2.2), each time holding one subset for early stopping or validation purposes. Furthermore, we synchronize the early stopping across the 10 DNNs, so that they all have the same depth n, retaining the depth providing the best prediction performance (Supplementary Fig. S7).

3 RESULTS AND DISCUSSION

3.1 Coarse contact and orientation prediction

We evaluate the average classification performance of the coarse contact and orientation predictor on the three classes Parallel contact (P), Anti-parallel contact (A) and No-contact (N) on the 364 test domains (Section 2.2). We evaluate the performance using the percentage of correctly predicted pairs

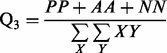(7)

the positive predictive value (or precision)

(8)

and the true-positive rate (or recall)

(9)

where XY denotes the number of segment pairs in class 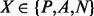predicted to be in class 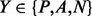. Table 1 reports the cross-validation average performance on the full set of protein domains (All) and as a function of the main structural domain classes: all-alpha (mainly alpha-helices), all-beta (mainly beta-sheets), alpha/beta (alpha-helices and beta-sheets, mainly parallel beta sheets) and alpha + beta (alpha-helices and beta-sheets, mainly anti-parallel beta sheets). As shown in Table 1, the performance of the coarse predictor on the Parallel (P) class is highly affected by the protein structural domain; in particular, the prediction precision and recall are higher for the alpha/beta proteins and are quite low for the all-beta proteins. Conversely, the performance on the Anti-parallel class (A) is nearly uniform, regardless of the domain structural classification. The anti-parallel contacts seem to be easier to predict than the parallel contacts, even within the alpha + beta class. Although not directly comparable (due to a different definition of segment–segment contact), the coarse contact predictor has higher precision and lower recall than the 2D-BRNN developed for the same classification problem in Pollastri et al. (2006).

Table 1.

Average performance for the coarse contact and orientation predictor

	Parallel (P)			Anti-parallel (A)		No-contact (N)
Class		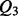PPV	TPR	PPV	TPR	PPV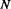	TPR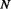
All	0.80	0.45	0.15	0.65	0.39	0.82	0.95
All-alpha	0.73	0.40	0.13	0.63	0.47	0.77	0.92
All-beta	0.86	0.29	0.06	0.69	0.35	0.88	0.97
Alpha/beta	0.81	0.57	0.25	0.67	0.36	0.83	0.96
Alpha + beta	0.79	0.38	0.09	0.64	0.38	0.82	0.95

Parallel contact (P), Anti-parallel contact (A) and No-contact (N) are the three classes considered by the coarse contact and orientation predictor. 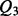is the percentage of correctly predicted pairs in equation (7), PPV 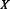is the Positive Predictive Value on class X in equation (8) and TPR 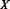is the True Positive Rate on class X in Equation (9).

3.2 Element alignment prediction

We evaluate the contact prediction performance of the element alignment predictor at the residue level on the (predicted) strand–strand and helix–helix regions of the contact map. We use the same accuracy measure adopted for the evaluation of contact prediction performance on the entire contact map (Section 2.1).

Recall that the element alignment predictor can be used to derive approximate probabilities of contacts for residue pairs in helix–helix and strand–strand elements, under the assumption that the elements are contacting (Section 2.4). A probability of parallel or anti-parallel contact between two elements is provided by the coarse contact and orientation predictor (Section 2.3). One can thus evaluate two different probability measures of contact at the residue level for the alignment predictor: a naive measure that uses only the alignment scores, and a more refined measure that combines alignment and coarse scores. 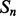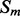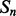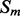Specifically, consider two residues i and j in secondary structure elements and , where and are both helices or strands. A naive probability of contact between i and j can be derived from the alignment scores only by

(10)

(11)

where 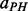(helix–helix parallel contact), 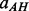(helix–helix anti-parallel contact), 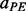(strand–strand parallel contact) and 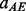(strand–strand anti-parallel contact) are the contact probabilities obtained with the alignment predictor for residues i and j. A more refined probability of contact can be defined by combining the alignment scores with the coarse predictor scores

(12)

(13)

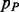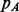where and are the probability of parallel and anti-parallel contact, obtained with the coarse contact predictor, between the secondary structure elements 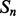and .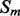

The average accuracy on the 364 test domains for these two probability measures and for long-range residue pairs is reported in Table 2. The prediction accuracy is reported on the full set of protein domains (All) as well as on the main structural classes (all-alpha, all-beta, alpha/beta and alpha + beta). Overall, the prediction performance obtained by combining alignment and coarse probabilities (H–H and E–E) is higher than the one obtained by considering the alignment probabilities alone (H–H and E–E). Thus the coarse contact and alignment features alone contain relevant information on long-range residue–residue contacts, although the accuracy of this information is unevenly distributed with respect to the different structural classes and secondary structure elements. In particular, the prediction accuracy for beta-residues is much higher than for helix-residues, regardless of the structural class. This uneven distribution of performance is consistent with the native distribution of contacts between the respective classes of secondary structure elements: the strand–strand contacts are more dense than the helix-helix contacts and thus also easier to predict.

Table 2.

Average accuracy on long-range contacts for the element alignment predictor

	E–E			H–H			E–E			H–H
Class	L/5	L/10	Best 5	L/5	L/10	Best 5	L/5	L/10	Best 5	L/5	L/10	Best 5
All	0.24	0.25	0.25	0.09	0.10	0.10	0.35	0.36	0.37	0.11	0.12	0.13
All-alpha	—	—	—	0.09	0.10	0.11	—	—	—	0.10	0.11	0.11
All-beta	0.19	0.21	0.20	—	—	—	0.19	0.17	0.17	—	—	—
Alpha/beta	0.22	0.19	0.21	0.07	0.07	0.07	0.52	0.55	0.54	0.11	0.14	0.12
Alpha + beta	0.26	0.27	0.27	0.08	0.08	0.08	0.34	0.37	0.35	0.09	0.11	0.10

Contact prediction accuracy (Acc, see Section 2.1) of the element alignment predictor for long-range residue pairs. The length L refers to the sum of the lengths of helix/strand elements in the protein sequence. The protein domains having <5 contacts in the strand–strand and helix–helix regions have been excluded from the evaluation. The strand–strand predictions on the All-alpha class, as well as the helix-helix predictions on the All-beta class, are not included. The performance on the strand–strand regions, E–E, E–E and helix–helix regions, H–H, H–H, are obtained by using the contact probabilities in Equations (10), (12), (11) and (13), respectively.

3.3 Residue–residue contact prediction: test set

We compare the performance on the 364 test domains of different contact predictors in order to separate the contribution of the DNN from the contribution of the features obtained with the coarse contact/orientation and alignment predictors (CA-features). Table 3 reports the performances of the full predictor (CMAPpro), a single-hidden-layer back-propagation neural network with CA-features (NN + CA) and without CA-features (NN), and a DNN that does not incorporate CA-features. In order to consider separately the contribution of coarse and alignment features, we also train a single-hidden-layer neural network that incorporates only coarse (NN + C) and only alignment (NN + A) features. For all such predictors, we build a corresponding ensemble by averaging the 10 cross-validation models. In Table 3, note that the performance of the basic neural network NN reflects the state-of-the-art in contact prediction, as assessed by all previous CASP experiments. Both the CA-features and the DNN help improve the contact prediction accuracy in comparison with the performance of the plain neural network NN. The performance of the NN incorporating the CA-features (NN + CA) is indistinguishable from the performance of the deep-NN without CA-features (DNN). CMAPpro (deep-NN with CA-features) achieves the best performance among the predictors, indicating that both CA features and deep architecture play a role in improving contact prediction. Furthermore, in Table 3, the coarse features (NN + C) seem to be more informative than the alignment features (NN + A). On the other end, the performance comparison on the CASP datasets (Section 3.4) shows that in specific cases the alignment features are more informative than the coarse features (NN + A versus NN + C in Tables 5 and 6).

Table 3.

Average accuracy and X_d comparison on long-range contacts

Method	Acc			Xd
	L/5	L/10	Best 5	L/5	L/10	Best 5
CMAPpro	0.28	0.32	0.36	0.14	0.15	0.16
NN + CA	0.25	0.29	0.32	0.13	0.14	0.15
DNN	0.25	0.28	0.32	0.13	0.14	0.15
NN + C	0.23	0.27	0.30	0.12	0.13	0.14
NN + A	0.21	0.23	0.26	0.11	0.12	0.13
NN	0.20	0.24	0.26	0.10	0.12	0.13

Table 5.

Average Acc and 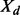for seq. sep. 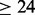on CASP8 set

Method	Acc			Xd
	L/5	L/10	Best 5	L/5	L/10	Best 5
CMAPpro	0.32	0.41	0.42	0.13	0.15	0.15
NN + CA	0.28	0.38	0.40	0.12	0.15	0.15
NN + A	0.26	0.33	0.32	0.11	0.12	0.14
DNN	0.25	0.35	0.37	0.11	0.13	0.14
RR157	0.24	0.30	0.32	0.09	0.10	0.11
RR072	0.24	0.30	0.28	0.11	0.13	0.13
NN + C	0.23	0.32	0.30	0.10	0.12	0.11
RR453	0.23	0.30	0.38	0.11	0.13	0.15
RR477	0.23	0.28	0.28	0.10	0.12	0.11
RR197	0.22	0.22	0.22	0.09	0.09	0.11
RR131	0.21	0.24	0.22	0.10	0.09	0.08
PSICOV	0.21	0.20	0.20	0.07	0.08	0.08
RR249	0.20	0.25	0.28	0.12	0.14	0.15
RR413	0.20	0.24	0.20	0.10	0.12	0.11
NN	0.20	0.25	0.27	0.09	0.10	0.10

Table 6.

Average Acc and 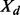for seq. sep. 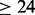on CASP9 set

Method	Acc			Xd
	L/5	L/10	Best 5	L/5	L/10	Best 5
RR490	0.32	0.37	0.44	0.15	0.17	0.20
CMAPpro	0.31	0.35	0.34	0.13	0.15	0.15
DNN	0.27	0.31	0.41	0.12	0.14	0.16
NN + CA	0.23	0.27	0.29	0.11	0.12	0.13
RR051	0.22	0.24	0.24	0.11	0.12	0.12
RR103	0.21	0.27	0.31	0.10	0.12	0.12
NN + C	0.21	0.27	0.25	0.10	0.11	0.11
RR002	0.21	0.23	0.23	0.11	0.12	0.12
PSICOV	0.20	0.28	0.33	0.08	0.10	0.11
NN + A	0.20	0.20	0.21	0.09	0.09	0.09
RR138	0.19	0.23	0.26	0.09	0.11	0.11
NN	0.19	0.19	0.19	0.09	0.09	0.09
RR375	0.18	0.21	0.24	0.08	0.09	0.10
RR204	0.18	0.20	0.22	0.09	0.10	0.11
RR422	0.17	0.20	0.21	0.09	0.10	0.09

Table 4 shows the cross-validation performance of CMAPpro as a function of the main protein structural classes. These performances are somewhat consistent with what has been reported in literature: the residue contacts in the alpha/beta class are relatively easy to predict, whereas the contacts in the all-alpha class are more difficult (Fariselli et al., 2008). The 20% accuracy of CMAPpro on the all-alpha class still represents some improvement with respect to the state-of-the-art for long-range contact prediction (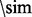15%) on this class of proteins (Fariselli et al., 2008).

Table 4.

Average accuracy and xd on long-range contacts for CMAPpro

Set	Acc			Xd
	L/5	L/10	Best 5	L/5	L/10	Best 5
All	0.28	0.32	0.36	0.14	0.15	0.16
All-alpha	0.20	0.22	0.25	0.12	0.13	0.13
All-beta	0.28	0.31	0.36	0.12	0.13	0.15
Alpha/beta	0.50	0.59	0.68	0.22	0.24	0.27
Alpha + beta	0.27	0.32	0.36	0.14	0.15	0.16

The prediction performance of CMAPpro as a function of architecture depth is shown in Figure 2 for the full set of test domains (All), as well as for different subsets organized by domain lengths. Overall, the contact prediction accuracy improves up to depth 50 and then remains roughly constant for depths in the range of 50–100. Even for architectures with depth as large as 100, CMAPpro does not show any sign of overfitting. The apparent weaker performance on domains of length 100–150 is artificially due to an uneven distribution of the easiest targets across the different sets.

Fig. 2.

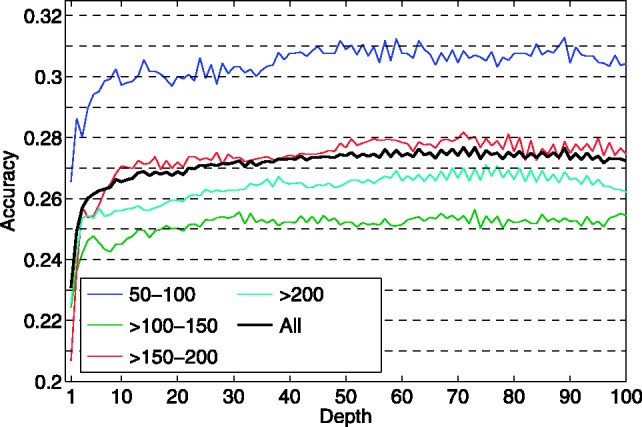
Accuracy (L/5 long range contacts) versus network depth for the set of test domains (All), the test domains of length between 50 and 100 residues (50–100, 87 domains), between 101 and 150 (100–150 and 111 domains), between 151 and 200 (150–200 and 76 domains) and longer than 200 (200, 90 domains)

3.4 Residue–residue contact prediction: CASP sets

In addition to the top 8 (top 16 in Supplementary Material) CASP predictors, we include in the comparison also the recent mutual information-based approach, PSICOV, using multiple alignments obtained by running jackhammer (http://hmmer.org) for three iterations on the NR database (Jones et al., 2011). The performance comparison on the CASP8 and CASP9 datasets are shown in Tables 5 and 6, respectively.

On the CASP datasets, the performance improvements obtained by considering separately the coarse/orientation and alignment features (NN + CA) and the DNN are somewhat different from those in Table 3. NN + CA performs better on the CASP8 dataset, whereas DNN performs better on the CASP9 dataset. CMAPpro combines and refines the qualities of these two predictors achieving higher accuracy on both the CASP8 and CASP9 datasets. This behavior can be explained by considering an example. Figures 3 and 4 show the predicted contacts for the CASP9 domain T0604-D1. The red and blue dots in the picture represent the L top-scored true positive and false positive contacts, respectively. The predictions obtained by DNN and NN + CA are compared in Figure 4. Globally, the two predictors assign a high probability of contact (grey dots) to approximately the same regions. Locally, however, they assign different contact probabilities to the individual pairs of residues, leading to different sets of correctly predicted contacts (blue dots). CMAPpro combines and refines the characteristics of these two predictors (Fig. 3): the segment–segment features improve the identification of contacting regions between secondary structure elements and the DNN is able to refine the prediction scores.

Fig. 3.

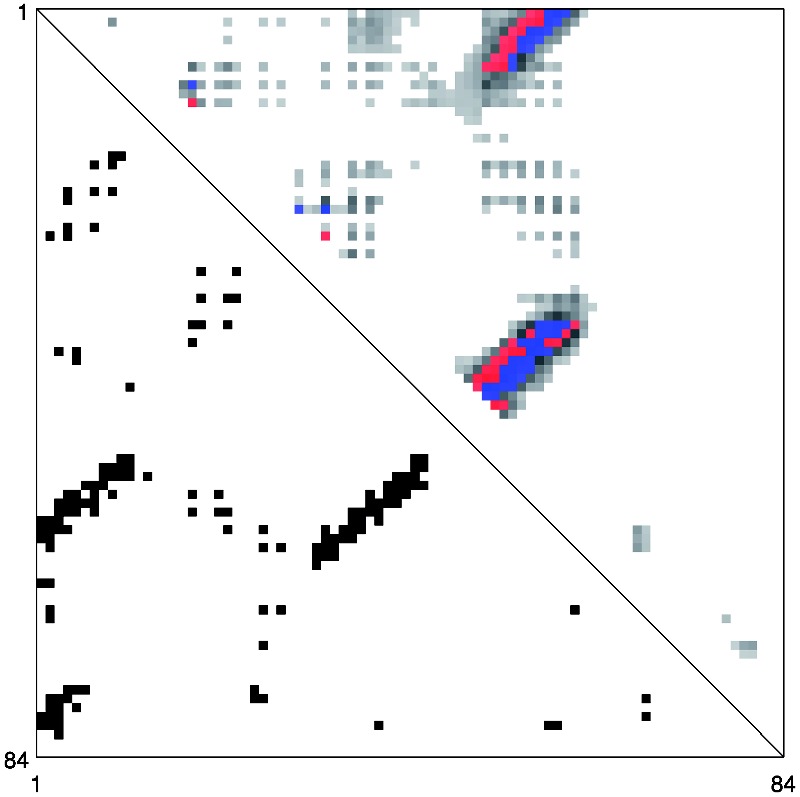
Native and predicted contact map for the T0604-D1 target from CASP9 set. The lower triangle shows the native contacts. The upper triangle shows contacts predicted by CMAPpro. The blue and red dots represent the correctly and incorrectly predicted contacts, respectively, among the L top-scored residue pairs

Fig. 4.

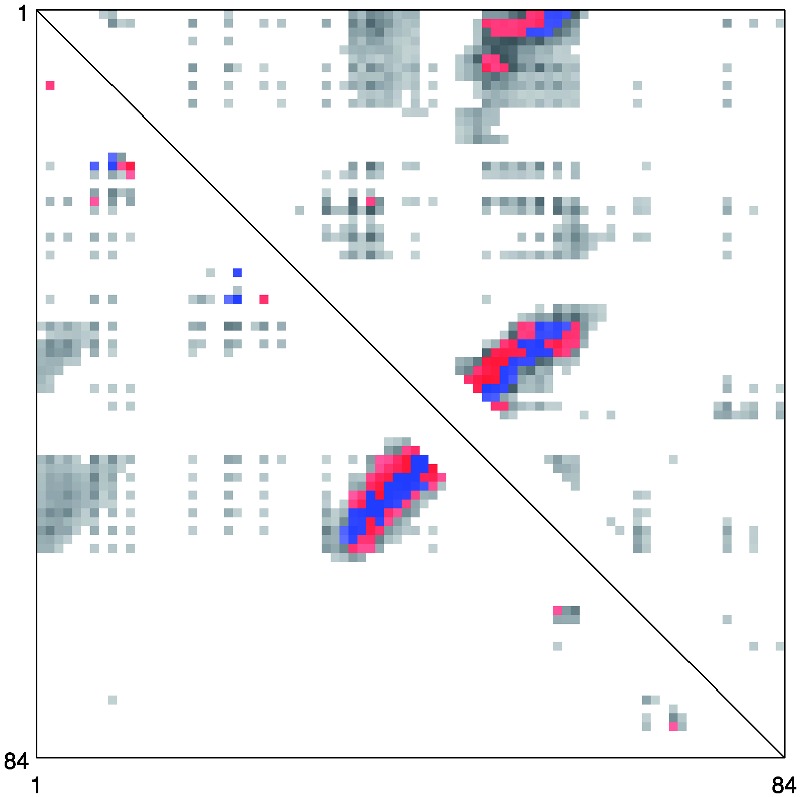
Predicted contact map for the T0604-D1 target from CASP9 dataset. The lower triangle shows the predictions obtained with DNN and the upper triangle those obtained with NN + CA. The blue and red dots represent the correctly and incorrectly predicted contacts, respectively, among the L top-scored residue pairs

Compared with other methods, CMAPpro is considerably more accurate on both CASP datasets. In particular, on the CASP8 dataset, CMAPpro achieves the best ranking both in terms of Acc and X_d. The only method (Wang et al., 2010) outperforming CMAPpro on the CASP9 dataset by a small margin relies on 3D structure models for deriving contact predictions through consensus, which defeats the purpose of predicting contact maps from scratch. Indeed, if we remove the only three TBM domains from the CASP9 dataset and focus exclusively on the FM targets, which are harder to predict, then RR490’s accuracy (L/5) drops down from 0.32 to 0.28, whereas CMAPpro’s accuracy increases from 0.31 to 0.32.

Due to the small number of targets, the average performances on the CASP8 and CASP9 are consistently affected by the network depth (Supplementary Fig. S6). In particular, on the CASP8 set, for architectures depths in the range of 10–100, the average accuracy on L/5 long range contacts varies from 0.30 to 0.35. On the CASP9 set, the average accuracy varies from 0.28 to 0.31. Notwithstanding such variability, on both CASP datasets, the performance of CMAPpro remains above the performance of the other methods at all depth values. As a general trend, on both CASP8 and CASP9 datasets, the improvement obtained in contact prediction with CMAPpro is ~10% or higher with respect to methods that do not use 3D structures. In Tables 5 and 6, we also note that the performance of the plain neural network predictor NN is comparable with the average performance across all groups. This confirms that the overall good performance of CMAPpro is not due to the particular set of protein domains used for training.

The accuracy of PSICOV (20%) is lower than previously reported (>50%; Jones et al., 2011). The performance of PSICOV is considerably affected by the quality of the multiple alignments. Since TBM/FM targets for contact prediction at CASP usually have few homologs in the protein sequence databases, this considerably lowers the prediction accuracy of PSICOV. The performance of PSICOV may suggest that even the most updated database of protein sequences (i.e. the NR database used to extract sequence profiles) does not contain enough information to derive rich evolutionary profiles for the CASP hardest targets. On the other hand, PSICOV relies only on multiple alignments and thus a direct comparison with methods that make use of predicted secondary structure or solvent accessibility is somewhat unfair.

Finally, Tables 3 and 4 in Supplementary Materials report the head-to-head comparison of the 10 top predictors on the CASP data. These results show that the average accuracies of the best performing methods are not biased by just a few very good predictions. With very few exceptions, in head-to-head comparisons, CMAPpro achieves a better accuracy for over 60% of the targets and worse accuracy for <30% of the targets.

4 CONCLUSION

Here, we have introduced a new approach for the prediction of protein contact maps. In particular, partly inspired by the observation that nature uses an iterative refinement approach to ‘compute’ the structure of proteins, we have developed modular deep architectures that can integrate information over multiple temporal and spatial scales. In rigorous tests, these architectures have been shown to predict contact maps with an accuracy close to 30%, a significant improvement. Although further improvements are necessary, it should be obvious that there are many generalizations and variations on the architectures and training methods we have described that remain to be explored, giving us hope that further progress lies ahead.

Funding: NSF IIS-0513376, NIH LM010235 and T15 LM07443 (to P.B.).

Conflict of Interest: none declared.