Estimation of pleiotropy between complex diseases using single-nucleotide polymorphism-derived genomic relationships and restricted maximum likelihood

Abstract

Summary: Genetic correlations are the genome-wide aggregate effects of causal variants affecting multiple traits. Traditionally, genetic correlations between complex traits are estimated from pedigree studies, but such estimates can be confounded by shared environmental factors. Moreover, for diseases, low prevalence rates imply that even if the true genetic correlation between disorders was high, co-aggregation of disorders in families might not occur or could not be distinguished from chance. We have developed and implemented statistical methods based on linear mixed models to obtain unbiased estimates of the genetic correlation between pairs of quantitative traits or pairs of binary traits of complex diseases using population-based case–control studies with genome-wide single-nucleotide polymorphism data. The method is validated in a simulation study and applied to estimate genetic correlation between various diseases from Wellcome Trust Case Control Consortium data in a series of bivariate analyses. We estimate a significant positive genetic correlation between risk of Type 2 diabetes and hypertension of ~0.31 (SE 0.14, P = 0.024).

Availability: Our methods, appropriate for both quantitative and binary traits, are implemented in the freely available software GCTA (http://www.complextraitgenomics.com/software/gcta/reml_bivar.html).

Contact: hong.lee@uq.edu.au

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recently, we have developed new methods to estimate the proportion of variation in quantitative traits (Yang et al., 2010, 2011) or in liability to disease that is associated with single-nucleotide polymorphisms (SNPs) (Lee et al., 2012, 2011). The methods use very distant relationships between individuals so that estimates are unlikely to be confounded with shared family environment effects. The methodology can be extended to estimation of the genetic covariance and hence genetic correlation between different disorders that is tagged by SNPs to provide estimates of genome-wide pleiotropy. Evidence for a genetic correlation between disorders estimated directly by interrogation of the genome could have an important impact on the design of future genetic and functional studies for medical nosology and may provide new insights for novel treatments across disorders.

The aim of this study is to estimate genome-wide pleiotropy using genome-wide association studies (GWAS) case–control data for different diseases or disorders. For binary disease traits, we derive valid statistical approaches to obtain unbiased estimates of comorbidity interpretable on the scale of liability to disease. We develop computationally efficient algorithms for estimation. The method is applied to estimate the genetic correlation between hypertension (HT) and type 2 diabetes (T2D), bipolar disorder (BD) and rheumatoid arthritis (RA), BD and T2D or HT and RA from Wellcome Trust Case Control Consortium (WTCCC) GWAS data.

2 METHODS

2.1. Bivariate linear mixed model and efficient AIREML

We used a standard bivariate linear mixed model (Thompson, 1973). The models can be written as

where y is a vector of observations for trait, b₁ and b₂ are vectors of fixed effects, g₁ and g₂ are vectors of random polygenic effects for each individual in both trait 1 and 2 and e₁ and e₂ are residuals for trait 1 and 2, respectively. X and Z are incidence matrices for the effects b and g, respectively. The variance covariance matrix (V) is defined as

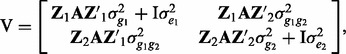where A is the genomic similarity relationship matrix based on SNP information (Yang et al., 2010) and I is an identity matrix, 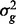, 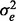and 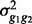, which are genetic variance, residual variance and covariance between g₁ and g₂. Lee and Van der Werf (2006) showed that the method of average information (AI) matrices derived directly from the V is much more efficient computationally than the original AI algorithms (Gilmour et al., 1995; Johnson and Thompson, 1995). Following equation (8) in Lee and Van der Werf (2006) , the AI matrix for the bivariate model can be derived as

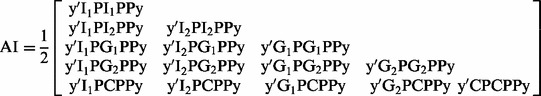where 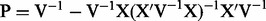, , 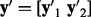, , 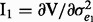, 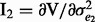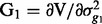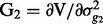and .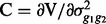

2.2. Correlation on the scale of liability is approximately the same as that on the observed risk scale

For disease traits when the y phenotype vectors contain only 1 for cases and 0 for controls, a liability threshold model can be written to link unobserved continuous liability to the observed discrete scale of disease (Falconer, 1965)

(1)

where l is a vector of liability phenotypes which are distributed as N(0, 1) in the population, g* is a vector of random additive genetic effects on the liability scale which are distributed N (0, 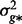) and e* is a vector of random residuals on the liability scale distributed with N(0, 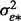). The probit link function links liability to the probability of y = 1, and g* on the scale of liability can be approximated by a linear function of g on the observed 0–1 scale (Dempster and Lerner, 1950). Using this linear approximation, the correlation between two diseases is the same on both the observed and liability scale (Gianola, 1982; Höschele et al., 1987). When samples are ascertained (typical in case–control studies), the genetic value on the observed scale can be defined with an ascertainment correcting factor as (Lee et al., 2011)

(2)

where g_cc is genetic values on the observed scale in a case–control study, c is a constant, K is the disease prevalence in the population, P is the proportion of the sample that are cases and z is the height of the standard normal probability density function that truncates the proportion K. From equation (2), the covariance between genetic values on the observed scale with ascertained samples can be written as

(3)

From equation (3) it is clear that that even when samples are ascertained, the correlation is the same on both observed and liability scales, because an approximate linear relationship exists between the genetic values on the different scales.

2.3. Simulation study

In order to confirm the derivation that the genetic correlation is approximately the same on both observed and liability scales when samples are ascertained, we performed a simulation study. The simulation procedure was similar to that in Lee et al. (2011) except that two traits were simulated with a genetic correlation between them (described in the Supplementary material).

2.4. Application to genome-wide genotype data

We applied our method to estimate genetic correlation between HT and T2D, BD and RA, BD and T2D, or HT and RA using WTCCC GWAS data (WTCCC, 2007) , following stringent quality control (QC) as described in the supplementary material. Since there are two control groups in the WTCCC data, i.e. 1958 cohort controls and NBS controls, we used 1958 cohort controls for the first trait, and NBS controls for the second trait. In a confirmation study, we swapped the control groups i.e. NBS for the first trait and 1958 cohort for the second trait.

We estimated a test statistic by dividing the square of the estimated genetic correlation coefficient by its approximate sampling variance and calculated a p-value from this test statistic assuming that it is distributed as a chi-square with 1 degree of freedom.

3 RESULTS

In simulations the estimated genetic correlation on the observed scale was close to the true values when using various combinations of true heritability and population prevalence (Supplementary Table S1). This confirms that the estimated genetic correlation is approximately the same on both observed and liability scales [Equation (3)]. Previously we have shown that if misdiagnosis occurs between the two disorders, then the expectation of the estimate of the genetic correlation coefficient can be non-zero even when the true genetic correlation is zero (Wray et al., 2012).

The estimated genetic correlation between HT and T2D was 0.31 (SE = 0.14 and p-value = 0.023) (Supplementary Table S2), indicating that genetic factors for HT and T2D are positively correlated. However, estimates for genetic correlation between BD and RA, BD and T2D, or HT and RA were not significantly different from zero (Supplementary Table S2). In a confirmation study switching control groups between the first and second trait (Supplementary Table S2), the genetic correlation between HT and T2D was 0.32 (SE = 0.14 and P = 0.024). Again, none of other analyses had significant genetic correlations (Supplementary Table S2). None of the parameter estimates differed significantly between our original and confirmation analyses. We previously demonstrated that the application of our stringent QC process resulted in estimated genetic variance not significantly different from zero if we conduct a dummy case-control analysis using these two control sets but treating one set as a cases (Lee et al., 2011) (h² = 0.06, SE 0.11).