Large-scale dynamics of horizontal transfers

Abstract

The widespread exchange of genes between bacteria must have consequences on the global architecture of their genomes, which are being found in the abundant genomic data available today. Most of the expansion of bacterial protein families can be attributed to transfer events, which are positively biased for smaller evolutionary distances between genomes, and more frequent for classes that are larger, when summed over all known bacteria. Moreover, “innovation” events where horizontal transfers carry exogenous evolutionary families appear to be less frequent for larger genomes. This dynamic expansion of evolutionary families is interconnected with the acquisition of new biological functions and thus with the size and distribution of the genes’ functional categories found on a genome. This commentary presents our recent contributions to this line of work and possible future directions.

The current era of fully sequenced genomes and metagenomes confronts us with the challenge and the opportunity of integrating unprecedented amounts of biological data. With such an abundance of data, simplifying views are often useful for figuring out relevant biological phenomena. For example, one can characterize the content of a genome by partitioning it into classes of functional and evolutionary levels. In other words, a genome can be divided in subsets describing its different operative elements, such as genes and their functional and evolutionary, families, transposons and their families, noncoding RNAs, etc. Notably, studies following this approach revealed that some of these elementary features of the functional and evolutionary composition of a genome are often governed by simple quantitative laws.¹

Considering the protein-coding part of genomes, it is often an advantage to focus on protein domains, rather than full proteins, because they are the building blocks of proteins and they follow similar trends.² The sizes of protein/protein-domain families have a fat-tailed distribution^2-7 whose “slope” depends on genome size.⁸ The overall number of families represented by at least one member exhibits a slower-than-linear scaling with the total number of genes in a genome.⁸

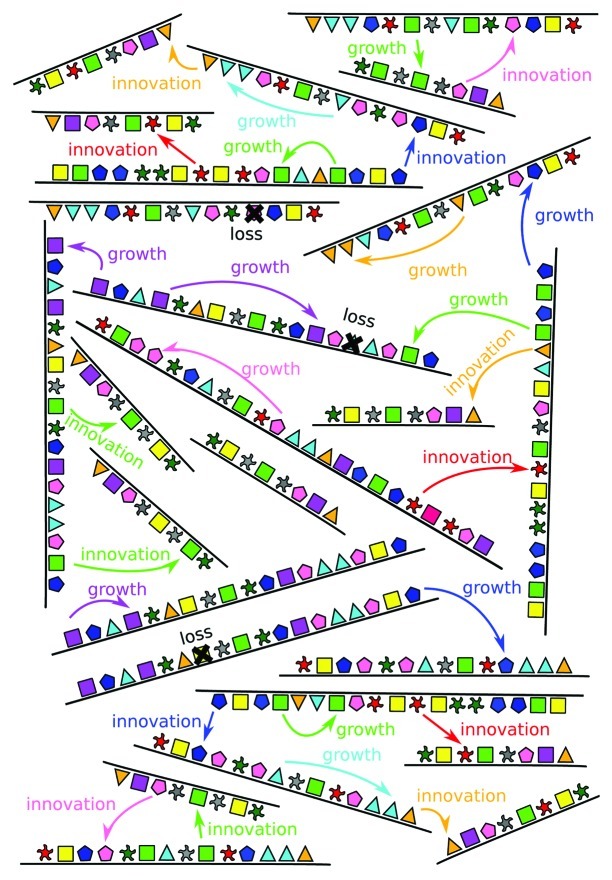
Biologically, the growth of evolutionary families derives from combined processes of horizontal gene transfer, gene duplication, gene genesis and gene loss (Figs. 1 and 2). For prokaryotes, horizontal gene transfer (HGT), the acquisition of genetic material in a non-hereditary manner, is probably the main innovative force,^9-13 and there are systematic indications that HGT dominates gene family expansion.¹⁴ The same process is presumably very important for the introduction of a new evolutionary family into an extant genome. Accordingly, theoretical models have been proposed that account for the observed power-law distribution of family sizes,^5,6,15-17 mostly using class-expansion/innovation/loss moves, abstractly mimicking basic evolutionary moves such as horizontal transfer, gene duplication and gene loss. A related model, in addition to family size distributions, also explains and successfully fits the scaling of the number of distinct gene families represented in a genome as a function of genome size.^18,19

Figure 1. Reports a hypothetical model describing the evolutionary dynamics of protein domains. In this model, horizontal gene transfer can play a double role, on one hand causing the expansion of existing families, and on the other determining innovation through the foundation of new families for a specific lineage which did not possess it.

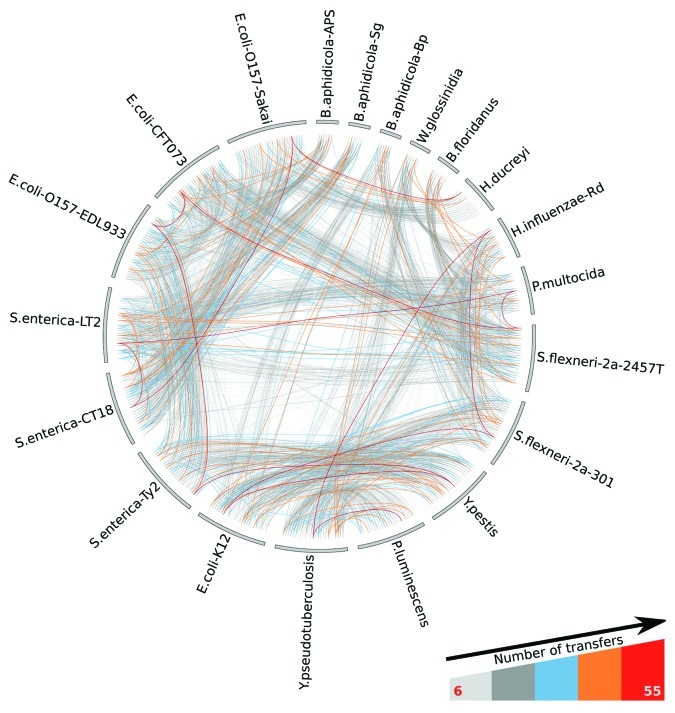
Figure 2. A representation of all species examined in reference 21. Each bar on the outer circle represents a studied genome and links represent protein domains. Different genomes are connected if they share a domain subject to HGT (in the cross-genomic gene pool formed by the union of the analyzed genomes). The color of the links reflects the number of transfers as shown in the legend.

A related important observation is that horizontal gene transfer is reported to be generally biased toward a closer evolutionary lineage with respect to distantly related lineages.²⁰ This bias in transfer partners can create phylogenetic signals that are similar to shared ancestry but are not due to vertical inheritance. In other words, there exist HGT “exchange groups” of genomes, which are analogous to populations able to exchange alleles by recombination.

Data and models, taken together confronted us with two puzzles. First, the growth of the number of families with proteome size is sublinear, indicating that introduction of new families becomes relatively less likely than class expansion with genome size (both processes being presumably driven by HGT). Second, in order to reproduce the correct tails of the evolutionary family histograms, the models need to introduce a rich-get-richer principle for class expansion, where the probability of adding a new member to the class is proportional to the class size.

Motivated by these questions, we recently performed a detailed analysis²¹ of 20 genomes of Proteobacterial species,²² evaluating the extent to which HGTs expand the genomes’ domain repertoires (Fig. 2). As a control, we compared our results with those obtained with a database containing HGTs for hundreds of genomes.²³ We used these data to address the two main questions: (1) does a “rich-get-richer” principle hold for genome growth by HGT? And, (2) do horizontally transferred genes carry novel domains more than expected by chance?

Currently, there is no systematic quantification of how HGT success is correlated with the existing pool of gene classes in a genome. One possibility is that HGT could act effectively as a duplication move in a larger cross-genomic gene family pool (affected by the ecosystems where genes can be exchanged). In some cases, this pool may resemble the genome in question in terms of frequency of gene families, thereby causing a larger class-expansion rate for larger families, but in general this is not necessarily true. Furthermore, HGT may be more likely to be successful for domains that are rare (in the “metagenome” creating the community gene pool or in the receiving genome).

We found that horizontally transferred genes carry domains of exogenous families less frequently for larger genomes, although they might do it more than expected by chance. Additionally, protein domains that are more common in the total pool of genomes appear to have a proportionally higher chance to be transferred. Both features suggest that transfer events behave as if they were drawn randomly from a “ross-genomic” or metagenomic community gene pool, much like gene duplicates are drawn from a genomic gene pool. Since larger genomes will possess more domain classes, the first finding is also in agreement with the observation that the probability of true innovations will be smaller.⁸

Clearly, it is not obvious that the amount of transfers should behave as if they were drawn randomly from a common pool. Other scenarios are possible in which either a decrease of novelty in larger genomes or a rich-gets-richer class-expansion by horizontal transfer, or both, are not trivially expected. For example, gene gains could be sampled from a very large effective pool of families, or horizontal transfers could be dominated by specific ecological or functional mechanisms. We know that transfers are not random; protein length plays a role, for example,²⁴ and it is natural to expect that selective pressure favors the acquisition of specific traits.

However, our results suggest that, when averaging over many transfer events there is a large contribution of purely combinatorial and statistical aspects to the “emergent” overall distributions of HGTs and their contribution to protein families, as typically happens in systems of many agents (such as crowds, the stock exchange, species in ecosystems^25-28). In these cases the analysis tools and the modeling frameworks of statistical physics may prove useful, as they were developed having in mind closely related phenomenologies in physical and chemical systems.

Notably, since the class sizes within a single genome are similar to the corresponding sizes in the cross-genome gene pool, this also has the consequence that classes should grow according to a rich-get-richer principle. The latter has often been assumed, but is not justified in current models.^2,14,29 For gene duplications, a rich-get-richer principle follows from the null assumption that all genes of a given class are a priori equally likely to get duplicated. However, as we discussed, prokaryotes tend to add genes by HGT rather than by gene duplication.^11,12,14 This behavior also affects the statistics of (domain) functional categories, which in the case of domains are typically made of the sum of a number of evolutionary classes, and empirically grow as power laws³⁰ with genome size at a specific rate, termed “evolutionary potential”.²

The joint partitioning of genes into functional and evolutionary classes also shows relevant universal quantitative trends,²⁹ and is connected to genome innovation by horizontal transfer. Presumably, addition of new genes needs to follow correlated functional “recipes” where genes whose functions are related are added together. For example having in mind the classic “operon model”³¹ (the general model of bacterial transcription control that partitions genes into specific regulatory genes and responding to metabolic cues, environment, and “structural” target genes performing specific tasks) it can be stated that addition of transcription factors needs to be related to the addition of a set of metabolic enzymes that are related by common metabolic pathways. The consequences of these statements have been explored recently using an integrated approach of data analysis and models,^32,33 and appear to explain very well the observed quantitative relationship between transcription factors and metabolic pathways, despite the fact that this might be subject to other constraints.³⁴ However, we still know very little about the nature and the very existence of these recipes, and gathering new insight into the process of how a prokaryotic genome builds new functions will be important for future studies, with evident implications for the applicability of synthetic biology.

The approach followed in our study disregarded relevant ecological aspects, which will be important to explore in future studies, such as population sizes, by assuming that a given domain has a certain occurrence just based on genomic sequences. For a specific ecosystem, total domain occurrence should ideally be derived from a weighted average, where weights are empirical population sizes. Results from individual ecosystems should then be averaged over all the ecosystems concerning the considered set of species, weighted by their relevance in evolutionary terms. We believe this can be addressed in future studies, as data of this kind starts to become available.³⁵ Overall, we believe there are great potentials and great unmet challenges in genomics and metagenomics studies addressing the reciprocal roles of ecology and evolution.³⁶