Ultrashort Echo Time (UTE) Imaging with Bi-Component Analysis: Bound and Free Water Evaluation of Bovine Cortical Bone Subject to Sequential Drying

Abstract

Recent proton magnetic resonance (MR) spectroscopy studies have shown that cortical bone exists as different components which have distinct transverse relaxation times (T2s). However, cortical bone shows zero or near zero signal with all conventional MR sequences on clinical scanners and the different water components cannot be assessed with this approach. In order to detect signal in this situation a two-dimensional (2D) non-slice selective ultrashort echo time (UTE) pulse sequence with a nominal TE of 8 μs was used together with bi-component analysis to quantify bound and free water in bovine cortical bone at 3T. Total water concentration was quantified using a 3D UTE sequence together with a reference water phantom. 2D and 3D UTE imaging were performed on 14 bovine bone samples which were subjected to sequential air-drying to evaluate free water loss, followed by oven-drying to evaluate bound water loss. Sequential bone weight loss was measured concurrently using a precision balance. Bone porosity was measured with micro computed tomography (μCT) imaging. UTE measured free water loss was higher than the volume of cortical pores measured with μCT, but lower than the gravimetric bone water loss measured during air-drying. UTE assessed bound water loss was about 82% of gravimetric bone water loss during oven-drying. On average bovine cortical bone showed about 13% free water and 87% bound water. There was a high correlation (R = 0.91; P < 0.0001) between UTE MR measured free water loss and gravimetric bone weight loss during sequential air-drying, and a significant correlation (R = 0.69; P < 0.01) between UTE bound water loss and gravimetric bone weight loss during oven-drying. These results show that UTE bi-component analysis can reliably quantify bound and free water in cortical bone. The technique has potential applications for the in vivo evaluation of bone porosity and organic matrix.

Introduction

Bone is a composite material consisting of mineral (~45% by volume), organic matrix (~30%) and water (~25%) [1, 2]. The nature and role of water in bone has been studied extensively [3–8]. It occurs at various locations and in different states, and is associated with the mineral phase, bound to the organic matrix, and present in ‘free’ form within the microscopic pores of the Haversian and the lacunar-canalicular systems [9–11]. Any change in the mineral fraction typically results in a reciprocal change in the water fraction [12, 13]. The free water concentration in bone can potentially provide a surrogate measure of bone porosity [13–16], while the bound water concentration reflects organic matrix density [17–19].

Recently proton magnetic resonance (MR) spectroscopy has been used to measure water distribution in cortical bone [20–22]. Nyman et al. used an inversion relaxation technique to convert free induction decay (FID) data into a distribution of T2 relaxation rates, with fast decay indicating solid protons associated with the mineral phase, intermediate decay indicating bound water, and slow decay indicating free water [21]. They found that bound water was directly related to bone strength and toughness, while free water was inversely related to bone modulus of elasticity. Fernandez-Seara et al. measured bone water content using MR-derived diffusion characteristics of exchangeable water, and found an inverse relationship between water content and mineral content [23]. Horch et al. investigated the origin of NMR signal relaxation components in human cortical bone using multi-component analysis of the FID and Carr-Purcell-Meiboon-Gill (CPMG) signal, and found four distinct proton populations from five microanatomical sources: collagen-bound water, free water, collagen and mineral hydroxides, collagen methylene and lipid methylene [24].

However, the techniques used in these studies can only be applied to small samples and requires high performance NMR spectrometers. They are not applicable in vivo. Conventional clinical MR sequences produce a signal void from bone, which has a short T2* of 250 to 500 μs [14–19]. Its MR signal decays to zero or near zero before it can be detected and encoded with conventional clinical MR pulse sequences with TEs of 1–2 ms or greater [25]. Current clinical research therefore tends to focus on indirect imaging of either the fatty or red bone marrow and not direct imaging of bone itself [12]. The lack of direct signal from bone with conventional clinical sequences makes it impossible to quantify transverse (T2) and longitudinal (T1) relaxation times, tissue perfusion, and bone water content [14–19, 26].

In recent years both two-dimensional (2D) and 3D ultrashort echo time (UTE) sequences with nominal TEs of less than 100 μs have been developed to image short T2 tissues such as the Achilles tendon [27], menisci [28], ligaments [25], calcification in soft tissues [29], and cortical bone [14–19]. These techniques make it possible to image and quantify water within cortical bone in vivo [14–19]. Previous studies have shown that water associated with bone mineral has an extremely short T2 (T2* < 12 μs) and is undetectable with MRI including UTE sequences [24]. The MR signal detected with UTE sequences has the potential to provide information on organic matrix density and mineralization assuming that water bound to organic matrix is detected [17–19], or porosity assuming that free water is detected [14–16]. It is therefore important to establish the signal source for UTE imaging of cortical bone on a clinical MR scanner, i.e., whether bound water, free water, or both contribute to the UTE MR signal, and to ascertain whether or not these components can be quantified using a clinical MR scanner.

In this study a 2D UTE pulse sequence with a minimum nominal TE of 8 μs was used together with bi-component analysis to quantify both short T2* (predictive of bound water) and long T2* (predictive of free water) components of bovine cortical bone using a clinical whole body 3T scanner. Sequential drying experiments were performed to determine the source of the signal detected with UTE imaging as well as the accuracy of bound and free water quantification.

Materials and Methods

Sample Preparation and Dehydration Technique

Four mature bovine femoral and tibial midshafts from freshly slaughtered animals were obtained from a local slaughterhouse and cleaned of external muscle and soft tissue. Fourteen bovine fragments with approximate dimensions of 20×15×4 mm³ were cut from the specimens using a low-speed diamond saw (Isomet 1000, Buehler) with constant water irrigation, and stored in phosphate buffered saline (PBS) solution for 24 hours prior to use. At the beginning of the dehydration process, each specimen was removed from PBS solution, wiped free of surface water and weighed using a digital precision balance (Mettler Toledo AL104, precision of 0.1 mg) to provide the weight of each sample (wet weight). All fourteen samples then underwent another five stages of sequential dehydration in a laboratory oven at room temperature (21 °C) for approximate times of 30 min, 60 min, 90 min and 3 days. Following this the samples were dried for 24 hours at 100 °C (13, 30) in an iso-temperature oven (Precision compact gravity oven, Fisher Scientific). The percent water loss by weight was calculated at each step using the following formula:

$$\%\text{Water}\text{loss}\text{by}\text{weight}=({\text{W}}_0-\text{W})/{\text{W}}_0$$ [1]

where W₀ was the initial bone wet weight, and W was the weight at the end of each drying step.

Before and after every drying step, each sample was imaged using the MR sequences and protocols described below. To prevent dehydration during MR imaging, every sample was sealed using a plastic wrapper. The weight of each sample was measured before and after each imaging step. The changes between these two measurements were consistently less than 0.05%.

Pulse Sequences

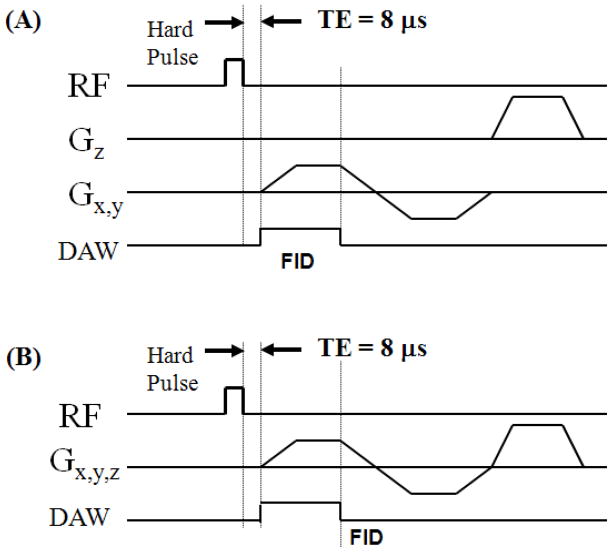
Both 2D and 3D UTE sequences (Figure 1) were implemented on a 3T Signa TwinSpeed scanner (GE Healthcare Technologies, Milwaukee, WI) which had a maximum gradient strength of 40 mT/m and a maximum slew rate of 150 mT/m/ms. The non-slice selective 2D UTE sequence employed a short rectangular pulse (duration = 32 μs) for signal excitation, which together with radial ramp sampling and fast transmit/receive switching allowed the use of a very short nominal TE of 8 μs defined as the time between the end of RF excitation and start of free induction decay (FID) data acquisition (16). We used a short rectangular pulse for the non-slice selective 2D excitation in order to enhance signal to noise ratio (SNR), and to eliminate errors due to eddy currents associated with conventional half-pulse excitation. The 3D UTE sequence employed a short rectangular pulse (duration = 32 μs) for non-slice selective excitation followed by 3D radial ramp sampling. In addition, a home-made 1-inch diameter birdcage T/R coil was used for signal excitation and reception for both 2D and 3D imaging.

Figure 1.

UTE pulse sequence diagrams: (A) non-slice selective 2D UTE with rectangular hard pulse excitation followed by 2D radial ramp sampling; (B) 3D UTE with rectangular hard pulse excitation followed by 3D radial ramp sampling.

MR Data Acquisition

Data acquisition parameters for the 2D and 3D UTE imaging are listed in Table 1. Since a short rectangular pulse was used for signal excitation, only one excitation (NEX=1) was needed for both the 2D and 3D UTE sequences. For more accurate measurement, the 2D UTE imaging protocol was applied to a single sample at a time. Each sample was placed near the center of the birdcage coil to minimize effects due to coil radiofrequency field inhomogeneity. The 2D non-selective axial imaging plane was centered in the middle of each sample so that the UTE signal intensity represented the integrated signal across the whole bone axial thickness. The 3D UTE imaging protocol took more time. To save scan time, the 14 bone samples were studied in three groups of 5, 5 and 4 samples. For each group the bone samples were stacked and placed in a 20 ml syringe for volumetric 3D UTE imaging.

Table 1.

Data acquisition parameters for non-slice selective 2D and 3D UTE imaging protocols.

Imaging Protocol	FOV [cm2]	Reconstructed Matrix	Bandwidth [kHz]	Flip Angle	TE [ms]	TR [ms]	Number of Projections	Undersampling Factor	Total Scan Time [min]
2D UTE	8×8	256×256	125	10°	0.008, 0.1, 0.2, 0.3, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.7, 2, 2.5, 3, 3.5, 4, 5, 6, 7, 8	100	411	1	14
3D UTE	15×15	256×256×256	250	10°	0.008	300	50000	4	250

Bone water concentration was quantified by comparison of 3D UTE image signal intensity from cortical bone with that from an external reference standard ^(14–16). The reference standard was distilled water doped with MnCl₂ to reduce its T2* to close to that of cortical bone (~400 μs). The reference tube was placed close to the bone samples and both were near the coil isocenter. Accurate estimation of bone water requires consideration of relaxation times and coil sensitivity effects. Variation in coil sensitivity was corrected by dividing the 3D UTE signal from bone or the reference phantom by the 3D UTE signal obtained from a separate scan of a 20 ml syringe filled with distilled water doped with Gadolinium (T2* ~ 50 ms). This was large enough to cover the region occupied by both the bone sample and the water reference phantom. To further minimize errors, the 3D UTE sequence employed a high bandwidth of 250 kHz, low flip angle of 10° and relatively long TR of 300 ms. Relaxation during RF excitation could be ignored since the rectangular pulse was significantly shorter than both the T1 and T2* of cortical bone. T1 effects could be ignored since the long TR of 300 ms guaranteed virtually full recovery of bone longitudinal magnetization (T1 of around 200 ms at 3T) when using a low flip angle of 10°. T2 effects could also be ignored because the UTE sequence had a nominal TE of 8 μs and the T2* of the water phantom was close to the 250–500 μs of bone.

MR Imaging Analysis

Multi-component fitting is very sensitive to SNR, the number of fitting components, the distribution of TEs, and the differences between T2 values of the different components [31–33]. The sensitivity to SNR was reduced by limiting the fitting components to two, the use of normalized UTE signal decay as well as automated background noise estimation based on the maximum likelihood estimation model [34]. These procedures reduced the number of fitting parameters to three, namely short T2*, long T2* and the short or long T2* fraction. As a result, robust bi-component fitting could be achieved with clinical achievable SNRs of around 50 using only 12 different TE images [35].

The UTE bi-component analysis algorithm was written in MATLAB (The Mathworks Inc. Natick, MA, USA). The mean intensity within each of the ROIs was used for subsequent curve fitting. Bi-exponential signal decay fitting was performed on UTE images to assess the short and long T2* water components. Goodness of fit statistics including the R-squared value and standard error or fitting confidence level were computed. Fit curves along with their 95% confidence intervals (CI) and residual signal curves were created.

Since both T1 and T2 effects can be ignored with the above 3D UTE imaging protocol, the expression for total bone water concentration (BWC) is as follows ⁽¹⁶⁾:

$$\mathit{BWC}\approx (I_{\mathit{bone}}/I_{\mathit{ref}})\times 100\%$$ [2]

where I_bone is the signal intensity of the bone sample, and I_ref is that of the reference phantom. Bound and free water concentrations were calculated by integrating water fractions determined by bi-exponential fitting with total water concentration using the above equation.

Micro Computed Tomography (μCT) Imaging Analysis

The bovine samples were imaged using a μCT scanner (1076, Skyscan, Kontich, Belgium) with the following parameters: 0.5 mm Aluminum filter, 72 kV, 140 μA, 720 views collected at 0.5° increments corresponding to one full rotation of each bone specimen, field of view (FOV) 25 mm, isotropic 9 μm voxels. For each sample, bone volume was calculated as bone voxel size multiplied by the number of voxels within the outer boundary of the sample. To determine bone porosity, 14 to 19 images, every 0.2 mm along the thickness of each sample, were selected and imported into Matlab. A custom program was used to determine the global histogram of all images and to determine a local signal minimum value for thresholding. Binarized images were despeckled to remove noise, and regions of interest corresponding to the outer boundary of each bone sample were automatically generated. Porosity was determined as one minus the ratio of the area of bone to that of the outer boundary of the sample.

Statistical Analysis

Wet bone density was calculated by dividing wet bone weight by bone volume determined by μCT. Bone weight loss during sequential drying was converted to bone water loss by volume, which was calculated by dividing bone weight loss at each stage by wet bone density for each sample. UTE assessed free water loss during the first four drying stages was correlated with gravimetric measures. UTE assessed bound water loss was correlated with bone water loss during oven-drying. Finally, the following comparisons were made for all 14 bone samples: (1) μCT porosity and UTE assessed free water loss with gravimetric bone water loss during air-drying; (2) UTE assessed bound water loss with gravimetric bone water loss during oven-drying; (3) total bone water determined by 3D UTE with the gravimetric method. Spearman correlation was used, and its significance assessed. A P value of less than 0.01 was considered statistically significant.

Results

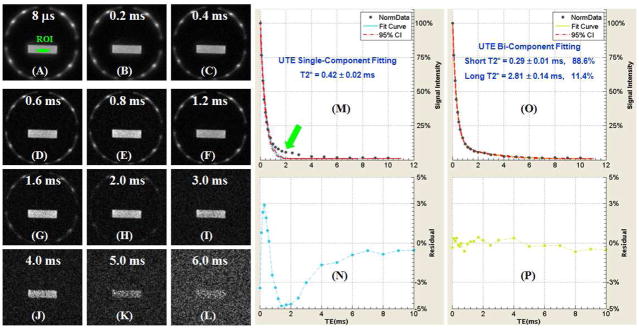
Figure 2 shows selected UTE images of a bovine sample with progressively increasing TEs ranging from 8 μs to 6 ms. A SNR (~68) and in-plane spatial resolution (0.3×0.3 mm²) was achieved in under 41 seconds scan time. Single-component fitting of the UTE T2* decay curve from an ROI drawn in central bovine bone shows a short T2* of 0.42 ± 0.02 ms. However, there is systematic residual signal with errors up to 5% around TE of 2 ms, suggesting the existence of another water component with a longer T2*. Bi-component fitting shows two distinct components one with a short T2* of 0.29 ms and the other with a long T2* of 2.81 ms. The short T2* component accounts for 88.6% of the total UTE MR signal decay, and the long T2* component accounts for the other 11.4% signal decay. The residual signal is less than 0.3%, showing that the bi-component model accounts well for the UTE T2* decay behavior.

Figure 2.

Selected 2D UTE imaging of a bovine cortical bone sample with TEs of 8 μs (A), 0.2 ms (B), 0.4 ms (C), 0.6 ms (D), 0.8 ms (E), 1.2 ms (F), 1.6 ms (G), 2.0 ms (H), 3.0 ms (I), 4.0 ms (J), 5 ms (K), and 6 ms (L), single-component fitting (M) and corresponding fitting residuals (N), and bi-component fitting (O) and corresponding fitting residuals (P). Single-component fitting shows significant residual signal (up to 5%). The residual signal is reduced to 0.3% by bi-component fitting, which shows a short T2* of 0.29 ms and a long T2* of 2.81 ms with respective fractions of 88.6% and 11.4% by volume.

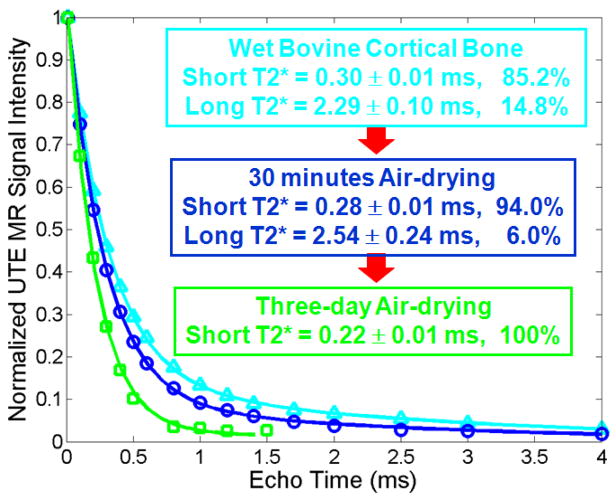
Figure 3 shows UTE images and bi-component analysis of a wet bovine bone, 30 minutes and three days after air-drying, respectively. The signal levels remained high at both of these times, suggesting that bound water contributes significantly to the UTE signal. Following three days of air-drying, only a single short T2* component remained, suggesting that only bound water was left.

Figure 3.

Bi-component fitting of a bovine cortical bone at three drying stages: wet bone, air-drying for 30 minutes and three days. Web bovine cortical bone has a short T2* of 0.30 ms and long T2* of 2.29 ms, with respective fractions of 85.2% and 14.8%. After 30 minutes air-frying, the free water fraction dropped to 6.0%, with respective short and long T2*s of 0.28 and 2.54 ms. A single component with a short T2* of 0.22 ms was observed for the bovine cortical bone after three days air-drying.

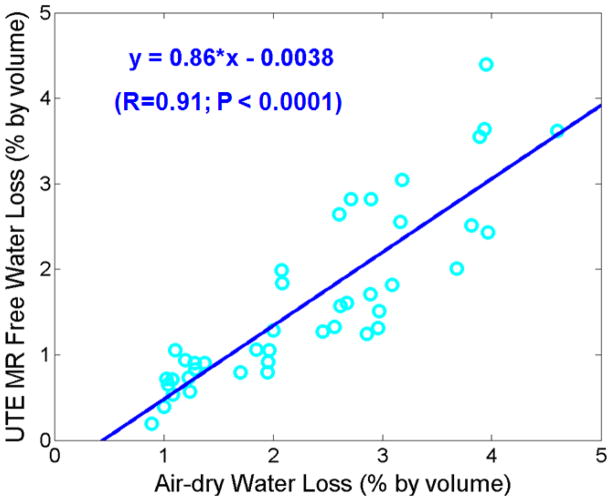
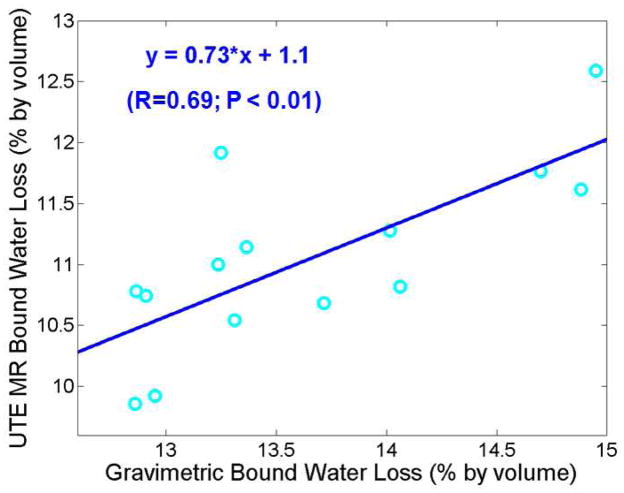
Figure 4 shows the correlation between UTE assessed free water loss and gravimetric bone water loss during air-drying. There was a high correlation (R = 0.91; P < 0.0001) between these two measures, suggesting that UTE bi-component analysis together with 3D UTE bone water measurements reliably estimate free water in bovine samples. The UTE assessed free water was consistently lower than gravimetric measures of bone water loss during air-drying. Figure 5 shows the correlation between UTE assessed bound water loss and gravimetric bone water loss during oven-drying. There was a significant correlation (R = 0.69; P < 0.01) between these two measures. The UTE assessed bound water was consistently lower than gravimetric measures of bone water loss during oven-drying.

Figure 4.

Correlation between UTE assessed free water loss and gravimetric water loss during air-drying. There is a high positive correlation between UTE assessed free water loss and air-drying water loss (R = 0.91; P < 0.0001). UTE assessed free water loss is lower than gravimetric air-drying water loss. This may be in part due to residual surface water which contributes to the latter but not the former.

Figure 5.

Correlation between UTE assessed bound water loss and gravimetric bound water loss during oven-drying. There is a significant correlation between these two measures (R = 0.69; P < 0.01). UTE assessed bound water loss is consistently lower than gravimetric bound water loss.

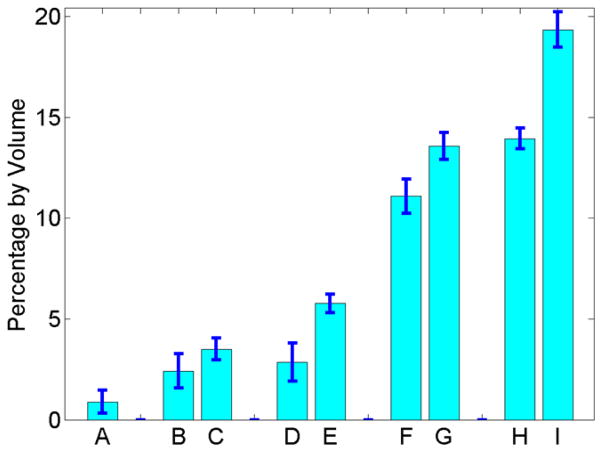
Figure 6 shows the average cortical porosity determined by μCT, UTE assessed free water loss and gravimetric water loss during air-drying after 30 min and 90 min, respectively, UTE assessed bound water loss and gravimetric water loss during oven-drying, as well as the total UTE measured bone water concentration and total gravimetric bone water loss by volume. On average, the 14 bovine samples had a cortical porosity of 0.89 ± 0.57%. After 30 minutes air-drying, UTE measured free water loss was 2.24 ± 0.94%, which was about 31% lower than the corresponding gravimetric bone water loss of 3.50 ± 0.54%. After three days air-drying, UTE measured free water loss was 2.86 ± 0.91%, which was 50% lower than the corresponding gravimetric bone water loss of 5.77 ± 0.46%. The increased discrepancy between UTE measured free water loss and gravimetric bone water loss suggests that significant bound water was lost during air-drying. The UTE measured bound water of 11.08 ± 0.84% was 21% lower than the corresponding gravimetric bone water loss of 13.57 ± 0.66% during oven-drying. The total bone water concentration determined by UTE measurement was 13.94 ± 0.51%, which was significantly lower than that of 19.34 ± 0.88% determined by gravimetric measurement.

Figure 6.

Average of fourteen bovine samples for cortical porosity measured by μCT (A), UTE assessed free water loss (B) and gravimetric bone water loss (C) after 30 minutes air-drying, UTE assessed free water loss (D) and gravimetric bone water loss (E) after three days air-drying, UTE assessed bound water loss (F) and gravimetric bone water loss (G) after oven-drying, as well as UTE assessed total bone water concentration (H) and total gravimetric bone water loss after oven-drying (I). μCT porosity is significantly lower than free bone water loss measured by either UTE or gravimetry. UTE assessed bound and free water concentrations are consistently lower than gravimetric measures.

Discussion

Our data indicate that UTE sequences detect both bound and free water in bovine cortical bone when using a clinical 3T scanner. The high residual signal from bovine cortical bone after three days air-drying directly confirmed that bound water signal is detectable with UTE sequences. The excellent bi-component fitting suggests that no more than two components are needed to explain the UTE signal decay behavior. The UTE measured long T2* water loss is highly correlated (R = 0.9084) with gravimetric bone weight loss during air-drying, suggesting that the long T2* component corresponds to free water. The UTE measured short T2* water loss is significantly correlated (R = 0.6853) with gravimetric bone weight loss during oven-drying, suggesting that the short T2* component corresponds to bound water. The UTE bi-component analysis technique together with 3D UTE imaging, which provides quantitative evaluation of total bone water concentration, allows us the potential to assess organic matrix (bound water) and bone porosity (free water) clinically.

In multi-component fitting accuracy depends on the quality of the data including its SNR, minimal TE, the number of echoes, the number of components, and separation of their relaxation times [31–33]. Anastasiou et al employed the Cramer Rao lower bound theory to show that fitting errors are linearly dependent on TE, inversely proportional to SNR and exponentially reduced by increasing the number of echoes [33]. The lower bounds increase dramatically when T2 values of the two components approach each other. The required SNR is also dramatically increased when more than two components are fitted. Reiter et al demonstrated that an SNR of more than 8000 is required to reduce the fitting error to less than 3% when no a priori information on the number of components is assumed [36]. With our simplified bi-component model the required SNR is greatly reduced.

The success of our UTE bi-component T2* approach in quantifying free and bound water components relies on the following four factors. Firstly, the minimum TE of 8 μs allows detection of proton signal from water bound to the collagen matrix, which typically has a T2* of the order of hundreds of microseconds. Secondly, free water and bound water have quite different T2* values, with about an order of magnitude difference which significantly helps separation of the two components. Thirdly, the assumption of only two components, instead of making no a priori assumptions about the number of relaxation components, greatly reduces the requirement for SNR and number of echoes. Fourthly, the automatic estimation of background noise and normalization of UTE MR signal reduces the fitting parameters down to three, allowing clinical evaluation in realistic times. Our previous simulation study showed that with an SNR of around 50 or higher, accuracy can be reduced to better than 3% with 12 or more echoes [35]. In this study, we acquired 20 echoes with a SNR of around 68 for the first echo.

The free and bound water T2* and fraction values are broadly consistent with published values. For example, single component analysis of cortical bone showed T2* values of 1 ms at 0.47 T, 420 to 500 μs at 1.5 T, and 250 μs at 4.7 T [37, 38]. Inversion FID T2 relaxation spectral analysis of human cortical bone showed 11 μs for mineral bound water, 210 μs for collagen bound water and 2.7 ms for free water at 0.6 T [21]. Our bi-component analysis of UTE bovine bone data showed a mean bound water T2* of 320 μs and a free water T2* of 2.28 ms at 3 T. A recent study by Horch et al showed that collagen bound water and free water account for up to 57.7% of the FID signal of human cortical bone, with 80% from collagen bound water and 20% from free water [24]. Collagen and mineral hydroxides as well as collagen methylene constitute up to 33.7% of the FID signal, with fat making up the rest (~4.6%). Tightly bound water with a T2* of 11.7 μs is undetectable with UTE sequences. We did not observe fat signal in any of the fourteen bovine bone samples. Our bi-component analysis showed a mean free water fraction of ~13% and bound water fraction of ~87%. Bovine cortical bone is denser than human cortical bone, which may help account for the difference in free water fraction (13 vs. 20%). The much lower RF power and weaker gradient strength on clinical MR systems compared with high performance NMR spectrometers may also contribute to the difference.

Based on μCT at 9 μm isotropic resolution, Haversian canal (typical diameter 30~200 μm) porosity of the bovine bone samples in this study was 0.89 ± 0.57%. Considering that the sum of lacunar (typical diameter ~ 10 μm) and canalicular (typical diameter ~0.5 μm) porosity roughly equals Haversian porosity [9], the total average porosity of all fourteen bovine samples was ~1.8%. The UTE MR measured free water loss of 2.42 ± 0.94% after 90 minutes air-drying and 2.86 ± 0.94% after three days air-drying are overestimated relative to twice the μCT values taking into account the fact that μCT does not detect small pores. This result also suggests that long T2* water component corresponds to free water residing in the Haversian and lacunar-canalicular systems.

The sequential drying experiments supported the validity of this technique for separating free and bound water components. It is expected that air-drying mainly results in loss of free water [10], while subsequent oven-drying at 100 °C for 24 hours mainly results in loss of water bound to the collagen matrix. Our recent study (unpublished) shows that the bone weight reached a steady state after about 10 hours air-drying at 21 °C. Little additional bone weight loss was observed after 10 hours air-drying, suggesting that bound water loss was minimal. There was more bone water loss after oven-drying at 100°C for 24 hours, suggesting that higher energy is needed to remove bound water. There was significant UTE signal from bovine cortical bone after three days of air-drying, suggesting that both bound and free bone water contribute to the UTE signal. The high correlation between UTE measured free water loss with gravimetric measurement of bone water loss during air-drying, and the significant correlation between UTE measured bound water loss with bone water loss during oven-drying both support the effectiveness of the UTE bi-component approach.

Free bone water measured by UTE bi-component analysis is consistently lower than gravimetric bone water loss during air-drying while UTE measured bound water is consistently lower than gravimetric measures of bone water loss during oven-drying. There are four possible reasons for this difference. Firstly, residual surface water contributes to gravimetric bone water loss during air-drying, but not UTE measured free bone water concentration. Secondly, bone water may be removed from certain phases of extracellular matrix even at room temperature [10], and this may lead to overestimation of free water loss using the gravimetric method. Timmins et al suggested that removal of bone water by thermal dehydration is a gradual process [6]. As the surfaces of Haversian and lacula-cananicular system dried, water loosely bound to the nearby extracellular matrix could diffuse into newly opened spaces, leading to gradual loss of bound water [10]. Thirdly, free water in small pores may behave to some extent like bound water due to surface relaxation mechanisms [39, 40], leading to underestimation of the free water fraction. Fourthly, oven-drying at 100°C for 24 hours may result in more than just bound water loss.

The ability to quantify free and bound water T2* and their fractions may play an important role in diagnosing osteoporosis (OP) as well as monitoring the effects of drug intervention. For example, free water fraction may be used as a biomarker for OP, which shows significantly increased porosity compared to normal bone [41–45]. It is expected that the ratio of free to bound water would increase significantly with progression of OP.

There are several limitations of this study. Firstly, T2* is known to be sensitive to local field inhomogeneity, including effects due to the B₀ field and local susceptibility differences. The robustness of T2* measurements is less than that of CPMG T2 measurements, where both field inhomogeneity and local susceptibility effects are compensated by use of the spin echo sequence. However, on clinical whole-body scanners CPMG sequences typically have a minimum TE of about 10 ms which is too long to detect signal from bound water in cortical bone. Furthermore, T2* is related to T2 by 1/T2* = 1/T2 + γΔB₀. For short T2 species like cortical bone, T2* approaches T2, therefore the sensitivity to local field inhomogeneity and susceptibility is significantly reduced. The robustness of bi-component analysis is expected to be much higher for short T2 species such as cortical bone than for long T2 species like muscle.

The second limitation is that the drying experiments were performed in a laboratory environment that lacks rigorous temperature and humidity controls. Absorption of water from air during drying and weighing processes may have occurred [23]. Dehydration in a vacuum oven may provide more accurate estimation of bound and free water in bovine cortical bone [20–22].

Thirdly, bound and free water have quite different T2* values, resulting in different levels of signal loss during RF excitation as well as signal blurring during radial ramp sampling [46], which may lead to different levels of signal loss. These errors were minimized by using a short excitation pulse (32 μs) and a short sampling window, but may still be higher than those found with high performance NMR spectrometers.

Fourthly, air-drying and oven-drying experiments may not be ideal for accurate estimation of free water, bound water and total water in cortical bone. D2O/H2O exchange experiments may be better for total bone water estimation [23]. Another approach is to use tritiated water to allow H2O in bone to exchange with tritiated water until a steady state is reached [47]. A measure of the change of radioactivity of the solution can then provide accurate measurement of the total exchangeable water in cortical bone.

In summary the 2D UTE bi-component T2* analysis is able to quantify T2* and fractions of the free and bound water components in bovine cortical bone. UTE MR measured free water loss is highly correlated with gravimetric measured bone water loss during air-drying. UTE MR measured bound water loss is significantly correlated with gravimetric measured bone water loss during oven drying. The UTE bi-component analysis technique has potential for clinical evaluation of bone porosity (free water) and collagen matrix (bound water).

Highlights.

UTE MR techniques measure bound and free water loss in bone after sequential drying. UTE assessed free water loss correlates with gravimetric water loss in air-drying. UTE measured bound water loss correlates with gravimetric water loss in oven-drying. The techniques have potential evaluating bone porosity and organic matrix in vivo.