Quantifying utricular stimulation during natural behavior

Abstract

The use of natural stimuli in neurophysiological studies has led to significant insights into the encoding strategies used by sensory neurons. To investigate these encoding strategies in vestibular receptors and neurons, we have developed a method for calculating the stimuli delivered to a vestibular organ, the utricle, during natural (unrestrained) behaviors, using the turtle as our experimental preparation. High-speed digital video sequences are used to calculate the dynamic gravito-inertial (GI) vector acting on the head during behavior. X-ray computed tomography (CT) scans are used to determine the orientation of the otoconial layer (OL) of the utricle within the head, and the calculated GI vectors are then rotated into the plane of the OL. Thus, the method allows us to quantify the spatio-temporal structure of stimuli to the OL during natural behaviors. In the future, these waveforms can be used as stimuli in neurophysiological experiments to understand how natural signals are encoded by vestibular receptors and neurons. We provide one example of the method which shows that turtle feeding behaviors can stimulate the utricle at frequencies higher than those typically used in vestibular studies. This method can be adapted to other species, to other vestibular end organs, and to other methods of quantifying head movements.

INTRODUCTION

The sensory signals that animals encounter in their natural environments tend to be highly structured (Simoncelli and Olshausen 2001; Schwartz and Simoncelli 2001). It has been recognized for decades (Barlow ‘61) that sensory neurons could exploit this structure to develop encoding strategies that are optimized for natural stimuli. Indeed, recent work in visual and auditory sensory systems has confirmed that sensory neurons encode natural stimuli much more efficiently than artificial stimuli (Borst and Theunissen ‘99; David et al. 2004; Passaglia and Troy 2004; Felsen and Dan 2005; Gil et al. 2008; Kording et al. 2004; Lesica and Stanley 2004; Mante et al. 2005; Smith and Lewicki 2006; Touryan et al. 2005; Vinje and Gallant 2000, 2002). For example, auditory afferents in the frog have been shown to transmit information about natural sounds at rates 2–6 times higher than for broad-band sounds (Rieke et al. ‘95). Thus, the availability of a set of well-characterized natural stimuli is an important prerequisite for understanding the coding strategies used by sensory neurons. While such stimuli are available for auditory and visual sensory modalities, the vestibular stimuli that are generated during natural behaviors have never been characterized.

The development of natural stimulus protocols for vestibular end organs presents a challenging task. The vestibular labyrinth is located in the inner ear . It’s major components are three semicircular canals, which monitor angular head accelerations, and two otoconial organs, the saccule and the utricle, which monitor linear head accelerations as well as the orientation of the head with respect to gravity. Collectively, these organs provide information to the central nervous system about head movements, so that it can initiate compensatory eye and body reflexes that ensure stable balance and clear vision. The precise form of these head movements is species dependent. For any organism, the head movements that occur during natural behavior are constrained by various physical factors such as mode of locomotion (e.g., quadrapedal vs. bipedal), mass of the head, or the arrangement of neck muscles and joints. As a result, the vestibular signals generated by a particular species during particular behaviors will have distinctive spatio-temporal structures. In order to determine whether vestibular neurons use encoding strategies that are optimized for these naturally occurring stimulus patterns, it is necessary to quantify the actual stimulus waveforms delivered to vestibular end organs during unrestrained, natural¹ behaviors so that they can be used in neurophysiological experiments and computational models of vestibular organs. This requires precise measurements of linear and angular motion of the head in freely moving animals and knowledge of the orientation of each end organ within the skull. We have developed a method to quantify stimulus patterns on the surface of one vestibular organ, the utricle, during unrestrained behavior in turtles, as part of a larger project designed to understand mechanisms of signaling in this otoconial organ.

The utricle consists of a sensory epithelium containing receptors (hair cells), which extend mechanoreceptive organelles (hair bundles) from their apical surfaces, and a disc-shaped otoconial membrane (OM), which is suspended above the hair bundles, parallel to the sensory epithelium (reviews: Lysakowski and Goldberg 2004; Rabbitt et al. 2004). The OM comprises three layers: (from superficial to deep) an approximately planar mass of calcium carbonate crystals (otoconia) called the otoconial layer (OL), a densely crossed-linked layer of extracellular material called the gel layer (GL), and a column filament layer (CFL) that spans the space between the underside of the gel layer and the surface of the sensory epithelium (Kachar et al. 1990; Davis et al. 2007). Hair bundles insert into the underside of the gel layer. When the head moves, the inertia of the otoconia causes them to lag behind, and this relative motion of the OL initiates the sensory cascade. It produces a shearing motion of the GL and CFL and deflection of the hair bundles that are attached to the GL. This hair bundle deflection modulates hair cell transmitter release onto postsynaptic neurons (afferents), causing them to modify their firing and thus their signal to the central nervous system.

We chose turtles as our experimental preparation for three reasons. First, more is known about utricular structure and mechanics in turtles than for any other vertebrate (Davis et al. 2007; Moravec and Peterson 2004; Nam et al. 2005, 2006, 2007a,b; Rowe and Peterson 2006; Severinson et al. 2003; Silber et al. 2004; Spoon and Grant 2011; Spoon et al. 2011; Xue and Peterson 2006). Second, the turtle in vitro preparation has become a significant model for neurophysiological analysis of vestibular receptors and afferents (Brichta & Goldberg ‘98, 2000a, b; Brichta et al. 2002, Goldberg & Brichta 2002; Rennie & Ricci, 2004; Rennie et al. 2004; Holt et al., 2006a, b, 2007). Consequently, behavioral data from turtles can be incorporated into a well developed body of knowledge where it can be effectively used to increase our understanding of utricular function. Finally, the utricle is evolutionarily conserved (Lewis et al. 1985), so information about turtle utricle is likely to be generalizable to other vertebrates.

The method we have developed utilizes a combination of high speed digital videography of freely behaving turtles, high resolution imaging of the orientation of the utricle in the skull, and computational methods to quantify patterns of utricular stimulation that occur during a variety of unrestrained behaviors. Here, we demonstrate the application of our method using the turtle feeding strike as an example. The method can be generalized to quantify the stimuli delivered to vestibular organs in a wide range of vertebrates.

MATERIALS AND METHODS

The utricle is essentially a two-dimensional accelerometer that monitors linear head acceleration and head orientation relative to gravity. Head acceleration and orientation in an inertial, earth-fixed reference frame (E-frame) during natural behavior can be readily determined from videos of the moving animal. However, hair cells in the utricle are stimulated by planar movement of theOL (Rabbitt et al. 2004), i.e., by forces acting in the plane of the OL (U-frame), and calculating these forces is complicated by the fact that the OL is not directly observable in videos of behaving animals. Thus, an intermediate reference frame is needed that has a fixed relationship to the U-frame and is defined by landmarks on the head that are visible in videos of behaving animals. We refer to this intermediate, body-fixed reference frame as the B-frame. Thus, calculating the components of acceleration in the U-frame during natural behavior involves six steps.

1. Use three landmarks on the head, visible in multiple camera views, to construct a body-fixed Cartesian coordinate system, the B-frame.

2. Determine the location and orientation of the OL within the B-frame and construct a second Cartesian coordinate system, called the U-frame, whose x-y plane represents the plane of the utricular OL.

3. Use high speed digital video to quantify motion of the B-frame (i.e., of landmarks on the head) during natural behaviors in the inertial, earth-fixed reference frame (E-frame).

4. Calculate the total gravito-inertial (GI) vector acting on the OL in E-frame coordinates.

5. Calculate the components of this GI vector acting in the x-y plane of the U-frame (i.e., in the plane of the OL).

6. Analyze the amplitude and frequency composition of these accelerations for different directions of head movement in the plane of the U-frame.

Step 1. Constructing the B-frame

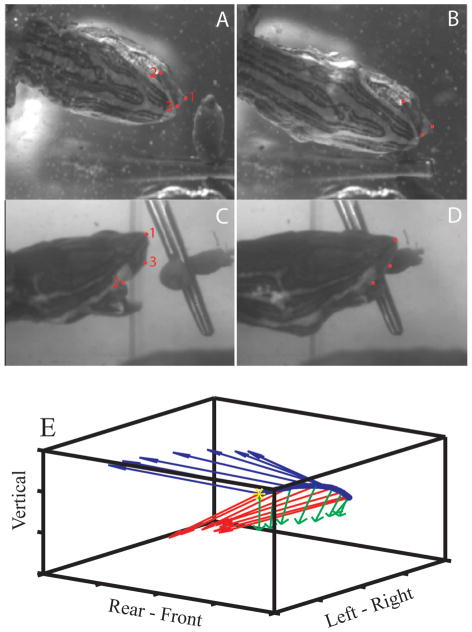
We used three visible landmarks on the head to create a Cartesian body frame of reference (B-frame): the tip of the nose (point 1), the posterior angle of the jaw (point 2), and the tip of the upper jaw (point 3) (Figure 1). The axes of the B-frame were constructed as unit vectors based on these coordinates, following a right-hand rule, as follows. The three visible landmarks form a plane; thus, the vector from point 1 to point 3 (red vector, Figure 1C) and the vector from point 1 to point 2 (black, dashed line, Figure 1C) are both in this plane. We used the vector from point 1 to point 3 as the first axis of the B-frame. Next, a vector cross product of the two in-plane vectors was used to form the second axis of the B-frame. This axis is normal to the plane defined by the three points (blue vector, Figure 1C).The third axis of the B-frame was then calculated as the vector cross product of the first two axes (green vector, Figure 1C). This axis is also in the plane defined by the three skull landmarks.

Fig. 1.

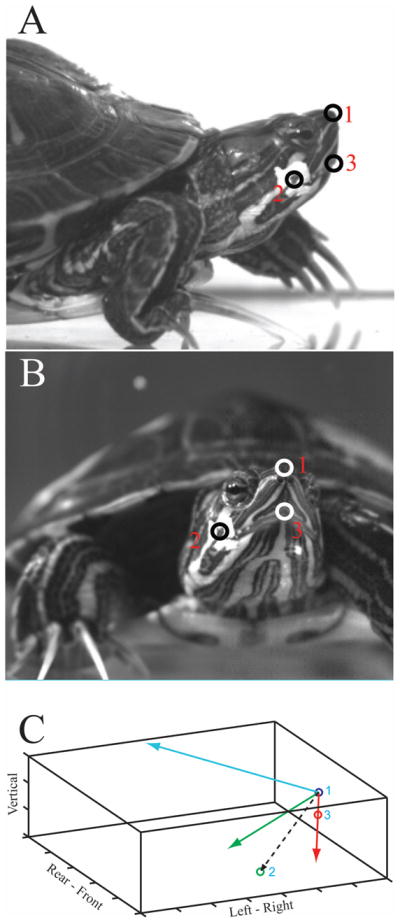
The three visible head landmarks that were tracked in the video sequences are seen in lateral (A) and frontal (B) views: the tip of the nose (1), the angle of the jaw (2), and the tip of the upper jaw (3). C. Construction of the body centered reference frame (B-frame) within the E-frame. The E-frame is represented by the tank in which the animal was filmed (solid black lines). Axis labels indicate direction when viewing the tank from the side; each division is 5mm. The B-frame is constructed from the plane containing the three skull landmarks. Point 1 is used as the origin of the B-frame, and a vector from point 1 to point 3 (red line) is the first in-plane axis. The vector cross-product between this axis and a vector from point 1 to point 2 (dashed black line) yields the B-frame axis (blue line) that is normal to the plane defined by the three skull landmarks. A vector cross-product between these two axes is used to form the second in-plane axis of the B-frame (green line).

Step 2. Position and orientation of the U-frame in the B-frame

Utricular hair cells are stimulated by the planar motion of the OL produced by head accelerations. To establish the position and orientation of the OL plane within the B-frame, we took advantage of the fact that otoconia are electron dense, making the OL readily visible in tomographic images.

TISSUE PREPARATION

Turtles (Trachemys scripta; 9.5–13.2 cm carapace length) were obtained from a commercial supplier (Concordia Turtle Farm, Wildsville, LA). After behavioral testing (see Step 3, below) we killed animals by injection of 0.8–1.0 ml of Fatal Plus (390 mg/ml pentobarbital sodium), in compliance with guidelines of the Clemson University Institutional Animal Care and Use Committee. We then perfused specimens trans-cardially with 0.1 M phosphate buffer followed by 10% formalin, decapitated them at approximately the C4-C5 junction using small scissors, and stored the heads in 10% formalin. Next we placed small barium dots on the three external skull landmarks used in our analysis so that we could locate these landmarks in our μ-CT images. A fourth dot was placed on the dorsal midline of the head at the intersection of the coronal plane containing the inter-aural line with the mid-sagittal plane, when the head is in stereotaxic position (identified by placing the skull in a turtle stereotaxic head holder (Powers and Reiner ‘80)). We used this barium dot to help identify stereotaxic planes in the CT data set so that we could express coordinates for skull and OL in terms of a standardized (stereotaxic) head orientation.

IMAGE ACQUISITION

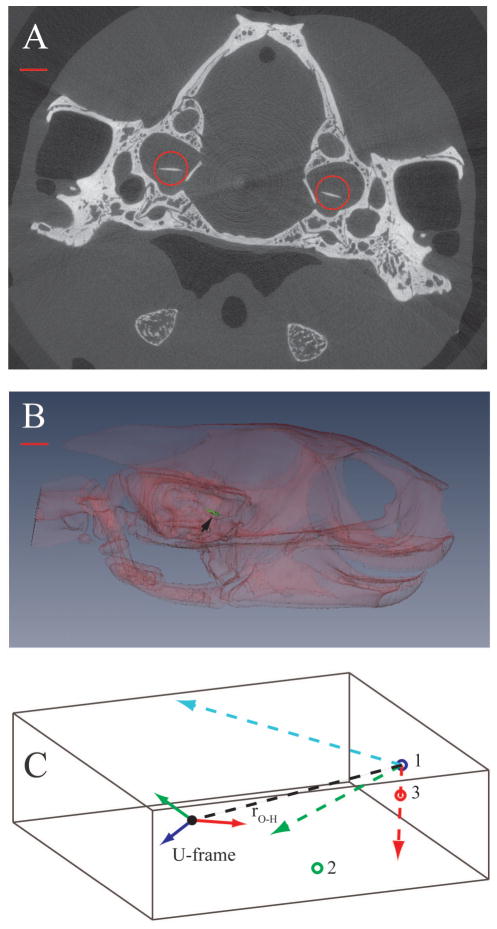
We used micro-tomography to visualize the OL and its position and orientation relative to the B-frame. Micro-CT scans were performed at Virginia Tech using a Scanco VivaCT 40 (1000 projections, 45kV@177 μA, Conebeam reconstruction). Individual images were 2048 × 2048 pixels, and voxel size was 19 μm. Figure 2A shows a sample slice with the right and left OLs circled.

Fig. 2.

A. One slice of a CT series showing the position of the otoconial layer (OL) of the utricle (red circles) within the skull. Dorsal is towards the top of the image. Note that OLs are not horizontal: each one is rolled slightly outward towards the ipsilateral ear. B. Transparent lateral view of a 3D reconstruction showing the right OL (green), indicated by the black arrowhead. In this example, each OL is pitched anterior down ~24° and rotated outward ~6° C. Position and orientation of the right U-frame in the B-frame. The x, y, and z axes of the B-frame are shown as red, green and blue dashed vectors, respectively, originating from point 1. The center of mass of the right OL is represented by a solid black circle. The red, green and blue vectors originating from the center of the OL are the x, y, and z axes, respectively of the U-frame. The vector, r_O-H, connecting the center of mass of the OL to the origin of the B-frame is shown as a black dashed line. Note that the gray box in this figure represents the 3D μ-CT data set in which the measurements were taken. Scale bars represent 1 mm in A and 1.75 mm in B.

STANDARDIZE HEAD ORIENTATION

In order to present our results in a standard format, we rotated all CT data into a stereotaxic reference frame defined by 3 orthogonal planes: coronal, horizontal and mid-sagittal. The mid-sagittal plane is vertical and passes through the skull sutures on the dorsal midline. The coronal plane is also vertical, perpendicular to the mid-sagittal plane, and passes through the inter-aural line. The horizontal plane is perpendicular to both the coronal and mid-sagittal planes and also passes through the inter-aural line. The origin of the stereotaxic reference frame is the point of intersection between the inter-aural line and the mid-sagittal plane. Thus, the stereotaxic reference frame has x- and y-axes in the horizontal plane, with positive x-axis pointing anteriorly and positive y-axis pointing to the left, and a vertical z-axis with positive corresponding to dorsal. A rotation matrix between the CT axes and the stereotaxic axes was constructed and used to rotate all points in the CT data set into this stereotaxic reference frame so that the orientation of the skull and the OL could be specified with reference to this standard head orientation. The next two steps were conducted on this rotated CT data set (i.e., with the head in stereotaxic orientation).

ESTABLISH U-FRAME

Using customized software developed in Matlab , we marked the 3-dimensional perimeters of the right and left OL through the series of slices in which they were visible, and we calculated the center of mass for each OL as the geometric center of its outline. Figure 2B shows a 3-dimensional reconstruction of the right OL in lateral view created with Amira . The orientation of each OL was calculated as a best fitting plane equation (z = ax + by + c) through its outline, and a vector normal to the plane and passing through the OL’s center of mass constituted the z-axis of each U-frame (Fig. 2C, dark blue solid vector). The x-axis of the U-frame (Fig. 2C, red solid vector) was a vector normal to the z-axis and oriented in a parasagittal stereotaxic plane. The y-axis of the U-frame was a vector normal to the x- and z-axes and therefore oriented in the medio-lateral direction (coronal stereotaxic plane; Fig. 2C, green solid vector).

PLACE U-FRAME WITHIN B-FRAME

We identified the coordinates of the three points used to track head motion in the video sequences in the μ-CT images (the tip of the nose, the tip of the upper jaw, and the angle of the jaw) using the small dot of barium paste previously applied to each point. Next we used these 3 points to construct a B-frame within the μ-CT data set, using the same procedure as in Step 1 (colored dashed lines in Figure 2C). We then calculated a rotation matrix, B, that allowed rotation of vectors from the B-frame into the U-frame. The elements of the rotation matrix B are directional cosines between the axes of the B-r⃗_O-H , (dashed black line, Figure 2C) from the tip and U-frames. Finally, we constructed a vector, of the nose to the center of mass of each OL, which represented the distance from the origin of the B-frame to the origin of the U-frame. We used this vector to calculate the tangential and normal accelerations of the OL resulting from rotation of the B-frame during head motion (see Step 4 below).

Step 3. Motion of the B-frame during natural behavior

We used two synchronized digital video cameras (Phantom V 5.1, Vision Research, Inc., Wayne, NJ) to record underwater feeding strikes of unrestrained turtles. The turtles were in a glass tank (91 cm long, 31 cm wide, 42 cm high, with a water depth of 15 cm) that constituted the inertial fixed reference frame (E-frame). One camera viewed the x (left-right in Figure 3C) and z (vertical) axes of the frame, i.e., a side view of the turtle (Fig. 3C, D); the other viewed the x and the y (left-right in Figure 3A) axes through a mirror oriented at 45° and positioned beneath the tank, i.e., a ventral view of the turtle (Fig. 3A, B). Both cameras produced 1024x768 pixel images at a frame rate of 1000 Hz. The spatial resolution was 128 μm/pixel for the x-y view and 142 μm/pixel for the x-z view (the difference being due to the difference in viewing distance between the two cameras). We digitized the skull landmarks that define the B-frame 3 times (Wöhl and Schuster, 2007), frame by frame, in video sequences from each camera using the DLTdataviewer2 Matlab^TM (Mathworks) routine (Hedrick, 2008). Sample images are shown in Figure 3A-D. We used custom Matlab routines to average the three sets of digitized coordinates for each frame and to compensate for differences in magnification between camera views (Rivera and Blob, 2010), producing a single set of three dimensional coordinate data for each frame. After behavioral data collection was complete, we sacrificed the animals, placed each turtle head in a stereotaxic instrument, and measured distances between all pairs of skull landmarks (1–2, 1–3, 2–3) using stereotaxic coordinates. We also measured distances between all pairs of skull landmarks in all video frames, and the scaling of the video images was adjusted so the distances between landmarks matched the stereotaxic measurements. For each pair of skull landmarks, we also constructed a distribution of the inter-landmark distances measured from successive video frames to quantify digitizing error in the video analysis, and we used the variance of these distributions to set the tolerance for quintic spline fitting (see below).

Fig. 3.

Ventral and lateral views of a turtle head during a feeding strike on an earthworm suspended by thread from a hex nut weight. (A,C) Near the beginning of the strike. (B,D) Corresponding views near the end of the feeding strike. (E) Linear motion of the origin of the B-frame in the left-to-right direction during a feeding strike is indicated by the changing position of the blue dots. The beginning of the movement is indicated by the yellow asterisk. Red, green, and blue vectors indicate the angular motion of the B-frame during the strike.

We calculated linear accelerations of all three points in the E-frame by double differentiation of the position data. The differentiation was done by fitting a quintic spline to sequential data segments (Walker, ‘98) and differentiating the spline analytically to minimize noise amplification produced by numerical differentiation. Spline tolerance was matched to the calculated estimates of digitizing error for each data set.

Figure 3E illustrates the components of motion during a feeding strike. Linear components are shown as movement of the nose (blue dots) from left to right, with time zero corresponding to the left-most point (yellow asterisk). Angular components are illustrated by rotation of the three axes of the B-frame (red, green, and blue vectors) at successive points during the strike.

Step 4. Calculating the total GI vector acting on the OL in the E-frame

The total GI vector acting on the OL in the E-frame is calculated as the sum of three components: 1) the linear acceleration of the B-frame from Step 2 (including a gravity component added to the Z-axis); 2) the tangential and normal accelerations resulting from rotation of the B-frame; and 3) the velocity and acceleration of the OL within the B-frame. Thus,

$${\overrightarrow{a}}_O={\overrightarrow{a}}_H+\overrightarrow{\alpha }\times {\overrightarrow{r}}_{O-H}+\overrightarrow{\omega }\times \overrightarrow{\omega }\times {\overrightarrow{r}}_{O-H}+2\overrightarrow{\omega }\times {\overrightarrow{v}}_{O-H}+{\overrightarrow{a}}_{O-H},$$ (1)

where a⃗_H is the linear acceleration of the origin of the B-frame, α⃗ is the angular acceleration of the B-frame, r⃗_O-H is a vector from the origin of the B-frame (tip of nose) to the origin of the U- frame (center of mass of the OL), ω⃗ is the angular velocity of the B-frame, v⃗_O–H is the velocity of the OL relative to the B-frame, a⃗_O–H is the acceleration of the OL relative to the B-frame, and × represents a vector cross-product. The second and third terms on the right hand side are the tangential and normal accelerations, respectively, of the OL resulting from rotation of the B-frame. Since motion of the OL within the B-frame is very small, the magnitudes of v⃗_O–H and a⃗_O–H are negligible relative to the other terms.

The angular velocity of the B-frame within the E-frame, ω⃗ in equation 1, is defined $\overrightarrow{\omega }=\left(\overrightarrow{r}\times \stackrel{.}{\overrightarrow{r}}\right)/{\mid \overrightarrow{r}\mid }^2$, where r⃗ is a vector in the B-frame and the upper dot represents the time derivative. It is calculated in two steps (Schaub and Junkins, 2003). First, the derivatives of the rotation matrix relating the E-frame to the B-frame (A in Step 5 below) are determined and arranged in a 9x1 matrix. This matrix is then multiplied by the inverse of a 9x3 matrix composed of the elements of A to give the instantaneous angular velocity ω⃗ of the B-frame:

$$\left\{\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\end{array}\right\}={\left[\begin{array}{ccc}0& -A_{31}& A_{21}\\ 0& -A_{32}& A_{22}\\ 0& -A_{33}& A_{23}\\ A_{31}& 0& -A_{11}\\ A_{32}& 0& -A_{12}\\ A_{33}& 0& -A_{13}\\ -A_{21}& A_{11}& 0\\ -A_{22}& A_{12}& 0\\ -A_{23}& A_{13}& 0\end{array}\right]}^{-1}\left[\begin{array}{c}{\stackrel{•}{A}}_{11}\\ {\stackrel{•}{A}}_{12}\\ {\stackrel{•}{A}}_{13}\\ {\stackrel{•}{A}}_{21}\\ {\stackrel{•}{A}}_{22}\\ {\stackrel{•}{A}}_{23}\\ {\stackrel{•}{A}}_{31}\\ {\stackrel{•}{A}}_{32}\\ {\stackrel{•}{A}}_{33}\end{array}\right].$$

The subscripts 1, 2 and 3 represent, respectively, the x, y and z vector components. This process is repeated for each video frame to yield a time series of angular velocities. Angular acceleration, α⃗ in equation 1, is then calculated as the time derivatives of the ω⃗ components.

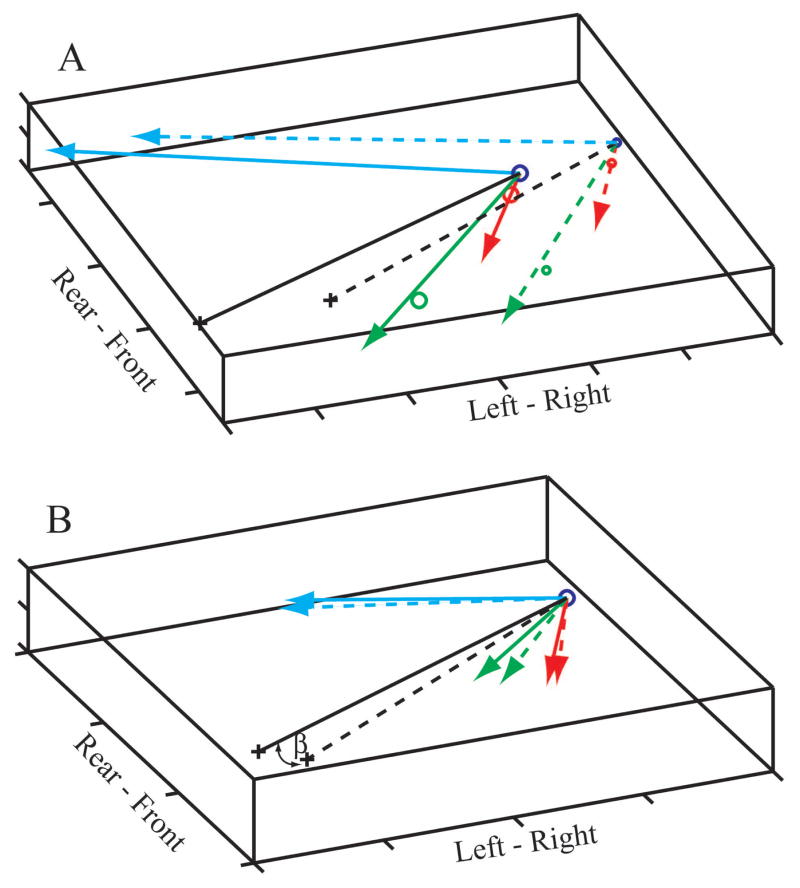
Figure 4 illustrates the linear displacement (Fig. 4A) as well as the rotation (Fig. 4B) of the B-frame at two points in time during a feeding strike. In Figure 4B, the origins of the vectors are superimposed to emphasize rotations. The red, green and blue lines are the axes of the B-frame at two times (t1 = solid, t2 = dashed) during a feeding strike. The black lines are the r⃗ _O-H vectors for the right utricle, β is the angle between them (Fig. 4B), and + represents the location of the OL center.

Fig. 4.

Linear displacement (A) and rotation (B) of the B-frame at two points in time during a feeding strike. (A) Large circles and solid lines show the location of the B-frame early in the strike; small circles and dashed lines show the location late in the strike. (B) The origins of the B-frame at the two points in time (t1 = solid, t2 = dashed) have been superimposed to emphasize the rotation. The OL centers are represented by + signs, black lines are the corresponding r⃗_O-H vectors, and β is the angle between them.

Step 5. Calculate the components of the GI vector in the plane of the U-frame

For each frame, a rotation matrix, A, is calculated and used to rotate the total GI vector from the E-frame into the B-frame:

$$\left\{\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right\}=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right]\left\{\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}\right\},$$

where the b⃗ and e⃗ columns contain vectors corresponding to the 3 axes of the B-frame and E- frame, respectively, and the elements of A are directional cosines between the axes of the E- and B-frames.

A second rotation matrix, B, which was established in Step 2 and used for all frames, is then used to complete the rotation of the GI vector into the plane of OL (U-frame):

$$\left\{\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right\}=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{21}& B_{22}& B_{23}\\ B_{31}& B_{32}& B_{33}\end{array}\right]\left\{\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right\},$$

where the u⃗ column contains vectors corresponding to the 3 axes of the U-frame.

Only the x and y components (subscripts 1 and 2) of the GI vector in the U-frame are considered further, since the z component, normal to the plane of the OL, does not affect hair cell bundles.

Step 6. Waveform calculation and frequency analysis

The x-y components of the GI vector in the U-frame are used to calculate an acceleration vector in the plane of the OL whose magnitude is $a(t)={\left[u_x^2(t)+u_y^2\right]}^{1/2}$, and whose direction is $\phi (t)={tan}^{-1}\left[\frac{u_y(t)}{u_x(t)}\right]$. The projection (component) of this vector on the plane of the utricle in any specified direction, θ, can be expressed as aφ= a(t)cos(φ (t)–θ) . To assess the frequency content of the stimulus to the utricle, we applied a continuous wavelet transform (CWT) to the x and y components of acceleration in the plane of the OL, u_x,y(t): $W_{x,y}(s,t)=\frac{1}{\sqrt{s}}\underset{0}{\overset{T}{\int }}{u}_{x,y}(t^{\prime })g^{\ast }\left(\frac{t^{\prime }-t}{s}\right){dt}^{\prime }$, where g is the wavelet kernel, s is the scale parameter, t, is the position parameter and the asterisk (*) denotes a complex conjugate. We used the Morlet wavelet kernel defined as: $g(\tau )={\pi }^{-1/4}exp\left(i{\omega }_0\tau -\frac{{\tau }^2}{2}\right)$, where ω₀ is set at 6 radians, resulting in the Fourier frequency being equal to 1.03/s. We calculated the CWT power as |W_{x, y} (s,t)|², and we obtained the full frequency spectrum by averaging CWT power over time.

Validation of the Procedure

To validate the calculations of acceleration from video sequences, we filmed a 3-axis accelerometer mounted on a circuit board on which 3 points were marked. We then compared the calculated accelerations with the measured output of the accelerometer and used Monte Carlo simulations to estimate confidence limits for the video-based calculations. See Supplemental Methods.

RESULTS

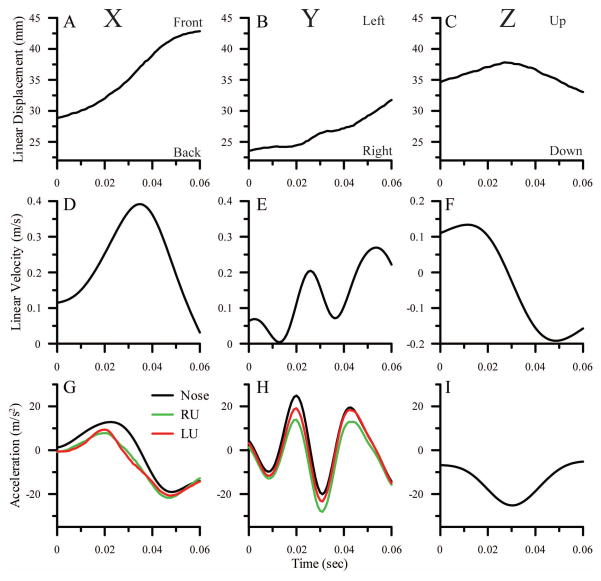
A complete kinematic analysis for one feeding strike is shown in Figure 5. Data for the x, y and z axes of the E-frame (A-I) and the U-frame (G, H) are shown in the left, middle and right columns, respectively. Linear displacements of the nose along the x, y and z axes of the E-frame are shown in panels A, B and C, respectively. For the x-axis, positive displacement is towards the front of the animal. For the y-axis, positive displacement is towards the animal’s left. For the z-axis, positive displacement is up. Calculated linear velocities of the nose along the 3 axes of the E-frame are shown in panels D-F, and corresponding linear accelerations of the nose are shown by the black lines in panels G-I. Panels G and H also show the total accelerations for the x and y axes, calculated from equation 1, in the planes of the left (red lines) and right (green lines) OLs (U-frames). Z axis acceleration for the U-frames are not calculated because accelerations perpendicular to the plane of the utricle do not stimulate hair cells under physiological conditions. Video sequences of lateral (x, z) and ventral (x, y) views of this feeding strike, along with plots of displacements, velocities and accelerations of the head (black lines) and accelerations along the x and y axes of left and right U-frames (red and green lines), can be seen in Supplemental Videos 1 and 2.

Fig. 5.

Displacement (A–C), velocity (D–F) and acceleration (G–I, black lines) of the nose calculated for the X (left column), Y (middle column) and Z (right column) axes of the E-frame during a feeding strike. For the x-axis, positive is towards the front of the animal. For the y-axis, positive is towards the animal’s left. For the z-axis, positive is up. Accelerations calculated for the X and Y axes in the planes of the left (red lines) and right (green lines) utricles, i.e., the left and right U-frames, are also shown in G and H. Data for the left OL are the same as those shown in Figures 7A and 6C. The accelerations in the E-frame do not include any contribution from gravity. The differences between the E-frame accelerations and the left and right U frame accelerations are largely due to gravity components in the U-frame resulting from the orientation of the OL within the head, the orientation of the head within the E-frame, and the Z-axis acceleration of the head in the E-frame. For the X-axis, the accelerations are reduced by the 24° downward pitch of the OL (see Figure 2), which reduces the accelerations produced by forward motion of the head in the E-frame and adds a negative gravity component. These effects are essentially identical for the left and right U-frames. For the y-axis, the reductions are largely due to the negative z-axis acceleration (I) which has a component in the plane of the U-frames due to the 6° outward roll of the OLs (Fig. 2) and the right-ear-down tilt of the head (see supplemental video 2). The right ear down tilt of the head causes the y axis of the right U-frame to be closer to the z-axis of the E-frame than is the y-axis of the left U-frame, resulting in a greater deviation of the right OL profile (compared to the left OL profile) from the E-frame profile in H.

Along the x axis, the head is moving forward (positive x in Fig. 5A) and beginning to accelerate (Fig. 5D, G) at the beginning of the sequence. It reaches a peak acceleration at about 25 msec (Fig. 5G) and a peak velocity at about 33 msec (Fig. 5D), and then decelerates as the mouth closes on the target (Fig. 5G). For the y-axis, the slight left-right oscillation in the displacement profile (Fig. 5B) results in relatively large calculated oscillations in the y axis velocity (Fig. 5E) and acceleration (Fig. 5H, black lines) profiles. On the z-axis, the head is moving upward (positive z in Fig. 5C) early in the strike and reverses direction at about 30 msec, resulting in a negative acceleration profile with a peak at 30 msec (Fig. 5I).

In the U-frames, the x-axis accelerations (Fig. 5G, red and green lines) are reduced relative to the head by the 24° downward pitch of the utricle (see Figure 2); this pitch reduces the accelerations produced by forward motion of the head in the E-frame and adds a negative gravity component. These effects are essentially identical for the left and right U-frames. For the y-axes (Fig. 5H), the accelerations in the y-axis of the E-frame (black lines) are clearly reflected in both left (red) and right (green) U-frames. Four factors combine to cause the U-frame profiles to deviate from the E-frame profile. First, each OL is rolled outwards ~6° (Figure 2) which reduces accelerations in the OL planes caused by left-right (y axis) motion of the head. Second, there is a slight rolling motion as the animal orients its head to match the target. Third, there is a right ear downward tilt of the head throughout the sequence that results in the y-axis of the right OL being closer to the z-axis of the E-frame than the y-axis of the left OL. Fourth, there is an acceleration in the z-axis of the E-frame (Fig. 5I) that is more strongly reflected in the right U-frame profile (Fig. 5H, green line) than the in the left (Fig. 5H, red line), because the right OL is closer to vertical.

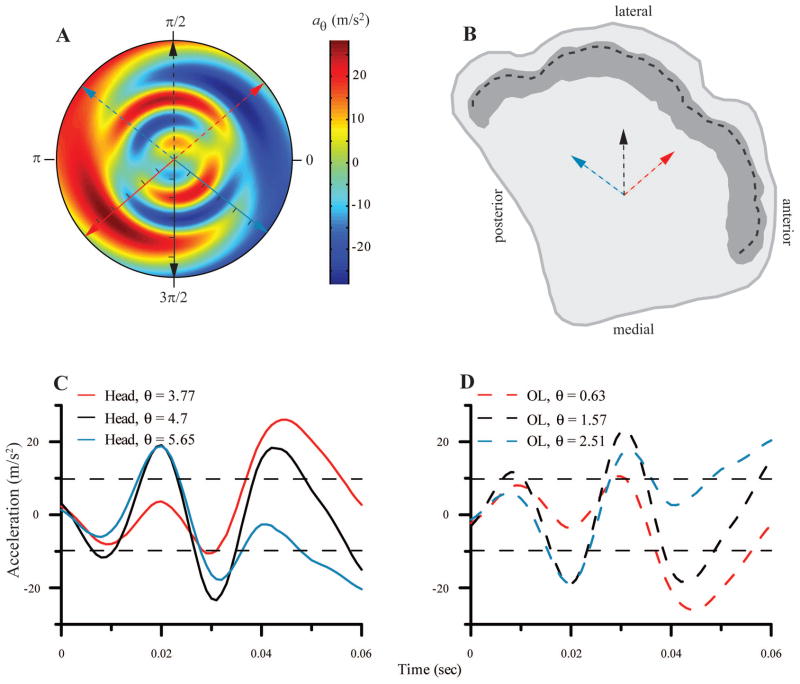
The components of the acceleration vector in the plane of the left OL from the feeding strike of Figure 5 are shown in a polar format in Figure 6A. The radial axis is time (tic marks on the solid arrows represent 10 msec intervals) and the angular axis is direction (in radians) relative to the x-axis of the U-frame. Since the x-axis of the OL lies in a parasagittal plane, 0 on the angular axis of the polar plot corresponds to anterior in anatomical planes (Figure 6B). The solid arrows represent three different directions for which acceleration profiles in the plane of the OL have been extracted. These acceleration profiles are shown as correspondingly colored lines in Figure 6C. For example, the black line in Figure 6C represents acceleration over the time course of the feeding strike time along the y-axis of the left U-frame (left-right motion of the head; same trace as in Fig. 5H). It corresponds to the solid black line in Figure 6A. The two acceleration peaks (at ~ 20 msec and 45 msec) in Figure 6C correspond to the two areas of red shading along the solid black arrow in Figure 6A.

Fig. 6.

A. Composite view of the acceleration profile in the plane of the OL in polar form. The radial axis is time and the angular axis is θ (in radians), the direction relative to x-axis of the U- frame, where 0 corresponds to anterior in anatomical coordinates, and positive is counterclockwise. Solid arrows represent 3 direction vectors for which the time course of head acceleration components in the plane of the OL is calculated (tic marks on solid arrows at 10 msec intervals). The dashed arrows represent the direction of forces applied to the OL for the same movements. B. A schematic view of the surface of the left utricle. The dark shading represents the striola, and the heavy dashed line indicates the line of polarity reversal. The dashed arrows represent hair cells whose excitatory bundle orientation matches the correspondingly colored dashed arrows in A. C. The time course of the head acceleration components in the plane of the OL is shown for the three directions indicated by the correspondingly colored solid arrows in A. D. The time course of the acceleration components applied to the OL for the three directions indicated by the correspondingly colored dashed arrows in A and B. Horizontal dashed lines in C and D represent + and −1g. Legend values in C and D indicate direction in radians.

Because the polar plot exhibits odd symmetry about the origin, the negative reflections of the head acceleration vectors (dashed arrows, Figure 6A) represent the direction and magnitude of the force applied to the OL. Thus, the correspondingly colored dashed lines in Figure 6D represent the forces acting on the OL during the movement. Specifically, each profile represents the stimulus delivered along the correspondingly colored vector in Figure 6B, where positive corresponds to excitation for a hair cell with that orientation. For example, at about 30 msec, the turtle’s head accelerates to the right, and there is a corresponding acceleration of the OL to the left.

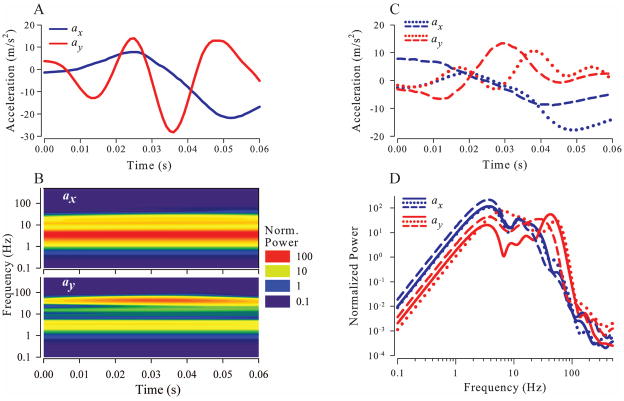
A wavelet analysis of this same feeding strike is illustrated in Figure 7. The separate x and y components (same data as black lines in Fig. 5G and H) of total acceleration of the OL center of mass in the plane of the right OL for are shown in Figure 7A. The wavelet transforms of these components are illustrated in Figure 7B. Normalized wavelet power is color coded according to the scale on the right. For both axes, most of the power is concentrated in a band about 3–5 Hz, although there is power at higher frequencies, especially for the y component, corresponding to the y-axis oscillations seen in Figures 5H and 7A. Figure 7C shows total x and y acceleration components for 2 additional feeding strikes from the same animal. Frequency spectra, obtained by averaging wavelet transforms over time, for all 3 feeding strikes are shown in Figure 7D. Significant power is present at frequencies at least as high as 50 Hz.

Fig. 7.

A. x (blue) and y (red) components of the acceleration vector in the plane of the right OL during a feeding strike. B. Wavelet transforms showing normalized power of the x and y profiles from A. Wavelet power was normalized to the variance of the acceleration magnitude. C. x and y acceleration components in the plane of the right OL are shown for two additional feeding strikes of the same animal. D. Time averaged power for x and y acceleration components of all three feeding strikes shown in A and C.

Validation of the Procedure

The measured accelerometer voltage signals were well within the 95% confidence limits for the video based calculations, indicating that head accelerations calculated from video sequences of the moving head do accurately reflect the accelerations generated by the behavior. (See supplemental Methods.)

DISCUSSION

We have developed a method for calculating, for the first time in any species, the magnitude and frequency content of the accelerations experienced by a utricle during natural head movements, based on digital video recordings of unrestrained behaviors.

The method we have developed makes it possible to develop a library of naturally occurring stimulus waveforms that can be used in neurophysiological experiments to explore how natural utricular stimuli are encoded by utricular receptors, primary afferents, and central neurons. The principles underlying the calculations are straightforward, but the implementation is complicated by a number of factors. Our use of an accelerometer to validate the method allowed us to determine that the major sources of error were digitizing noise and inaccurate image scaling and also allowed us to develop ways of correcting for these issues.

Sources of Error

Fitting the position data from the video sequences with a quintic spline, and then analytically differentiating the spline to calculate acceleration, helped us avoid problems associated with simple numerical differentiation of noisy data, but noise was still a major concern. The major source of noise in our data was digitizing error, and our procedure included a number of steps designed to minimize the effects of that noise.

First, it was important to assess the magnitude of that error accurately in order to optimize the fitting tolerance for the spline procedure. We did this by measuring the distances between the digitized points in each frame. Since the physical distances between landmarks on the skull are constant, any variation in the measured distances between landmarks is a result of digitizing error. The average difference between individual distance measurements and the mean distance for all frames in the video sequence was ~190μm, which is a little more than one video pixel. We then used the variance of the distribution of measured distances to set the tolerance level for the spline fitting procedure. These variances were quite small relative to the actual distance between video frames (0.17%, 0.72% and 1.21% for the x-, y-, and z-axes, respectively, for the example illustrated here). However, they do depend on other experimental parameters such as head velocity and video frame rate. As head velocity along any axis increases, or frame rate decreases, the distance between frames will increase, and digitizing error as a percentage of those distances will decrease. Thus, the smaller relative error along the x-axis is due to the fact that the dominant head motion was along this axis.

Second, we used the known distances between the 3 digitized points to adjust the scaling of each set of video frames and thus improve the accuracy of the displacement measurements, so as to minimize over- or underestimation of velocities and accelerations. Third, the rotation matrices between the E-frame and the B-frame, as well as the vector from the origin of the B-frame to the center of the OL, were calculated from fitted splines rather than raw position data to minimize contamination by digitizing noise. Collectively, these procedures produced kinematic estimates of accelerations that were closely matched to measured accelerations in both amplitude and frequency content, as verified by our accelerometer validation procedures.

Behavioral Results

To illustrate the method, we analyzed data from feeding strikes, which are among the fastest and most forceful movements that turtles make with their heads (Lauder and Prendergast, ‘92; Herrel et al., 2002). The results in Figure 7 indicate that these movements contain significant power at frequencies as high as 50 Hz. This is above the frequency range at which vestibular neurons are typically studied (reviews: Goldberg 2000, Lysakowski and Goldberg 2004). However, it has recently been shown that the otoconial membrane of the turtle utricle can respond to frequencies above 50 Hz (Dunlap et al. 2011), and that bundle deflections at these frequencies result in strong transduction currents and receptor potentials (Meyer and Eatock, 2011). Whether or not utricular afferents carry information at these frequencies has yet to be determined, but it is worth noting that posterior canal afferents in turtles have robust responses to stimulus frequencies at least as high as 100 Hz (Rowe and Neiman, 2012). Our analysis confirms that at least one subset of natural behaviors includes components at frequencies as high as 50 Hz, and the recent results cited above indicate that information about these components may be transmitted to central vestibular neurons. How common such frequencies are across the range of natural behaviors in turtles and other vertebrates remains to be determined, but increasing evidence suggests that such high frequency head transients may be more common than previously supposed. For example, Armand and Minor (2001) report transient head movement components as high as 80 Hz in lightly restrained squirrel monkeys and noted that even higher frequencies could be present in unrestrained animals.

Neurophysiological and Computational Applications

Our method calculates waveforms (Fig. 6) that represent the forces acting in the plane of the OL during natural behaviors. For neurophysiological studies, the direct applicability of these waveforms depends on the experimental protocol. Applicability is most direct for studies of vestibular afferents where stimuli are delivered via an intact labyrinth (e.g., using a linear sled; Angelaki and Dickman, 2000; Jamali, et al. 2009) because the natural coupling between the delivered waveforms and the resulting hair bundle deflections is intact. In these cases, the waveforms should be accurate representations of stimuli delivered to afferents during behaviors. For studies in which hair bundles are deflected by probes or fluid jets (reviewed by Eatock and Lysakowski, 2006), use of our waveforms is complicated by the fact that natural coupling between OL displacement and bundle deflection has been destroyed by removal of the OM. A similar caveat applies to studies in which forces are delivered to intact OMs by probes (e.g., Benser et al. 1993; Strimbu et al. 2009), because OM responses to such point loads may not be identical to OM responses in an intact preparation. Under both these experimental conditions, the waveforms calculated by our method would have to be passed through one or more filters representing the mechanical coupling between the applied stimulus and bundle deflection in order to exactly mimic the effect of stimuli delivered to hair cells in intact organisms. Finally, we note that the availability of natural waveforms is essential for any effort to model the mechanics of vestibular organs and the activity of their receptors and neurons during natural behaviors.

Alternative Behavioral Methods

We used high-speed digital videography of freely moving turtles to quantify head motion because we wanted to avoid any loads on the small turtle head or physical restraints on the body that might limit the range of head accelerations or frequencies expressed by the animal. However, our method for calculating forces in the plane of the utricle can easily be adapted to situations where head movements are directly recorded by sensing devices, e.g., search coils or accelerometers, attached directly to a larger head, where the device would represent a negligible load. In such cases, the B-frame would be replaced by a reference frame defined in terms of the attached sensor, and the location and orientation of the utricle within this reference frame would need to be determined. The total GI vector would be calculated directly in the sensor reference frame and then rotated in the x-y plane of the utricle as in step 5.