Automated quantification of carotid artery stenosis on contrast-enhanced MRA data using a deformable vascular tube model

Abstract

The purpose of this study was to develop and validate a method for automated segmentation of the carotid artery lumen from volumetric MR Angiographic (MRA) images using a deformable tubular 3D Non-Uniform Rational B-Splines (NURBS) model. A flexible 3D tubular NURBS model was designed to delineate the carotid arterial lumen. User interaction was allowed to guide the model by placement of forbidden areas. Contrast-enhanced MRA (CE-MRA) from 21 patients with carotid atherosclerotic disease were included in this study. The validation was performed against expert drawn contours on multi-planar reformatted image slices perpendicular to the artery. Excellent linear correlations were found on cross-sectional area measurement (r = 0.98, P < 0.05) and on luminal diameter (r = 0.98, P < 0.05). Strong match in terms of the Dice similarity indices were achieved: 0.95 ± 0.02 (common carotid artery), 0.90 ± 0.07 (internal carotid artery), 0.87 ± 0.07 (external carotid artery), 0.88 ± 0.09 (carotid bifurcation) and 0.75 ± 0.20 (stenosed segments). Slight overestimation of stenosis grading by the automated method was observed. The mean differences was 7.20% (SD = 21.00%) and 5.2% (SD = 21.96%) when validated against two observers. Reproducibility in stenosis grade calculation by the automated method was high; the mean difference between two repeated analyses was 1.9 ± 7.3%. In conclusion, the automated method shows high potential for clinical application in the analysis of CE-MRA of carotid arteries.

Introduction

MR Angiography (MRA) is a non-invasive imaging modality which is routinely used for assessment of carotid artery (CA) stenosis. Accurate quantification of CA stenosis is clinically relevant as the decision for the type of proper treatment for the patient is highly dependent on the degree of stenosis. The current clinical guidelines have been established based on the results of clinical trials such as NASCET [1] and ECST [2]. Although carotid MRA provides 3D volumetric data, CA stenosis grading is generally evaluated on 2D Maximum Intensity Projections (MIP) followed by visual caliper measurement. Such measurements are highly subjective and potentially inaccurate since MIP projections suffer from loss of 3D anatomical information, including vessel foreshortening over projection and loss of signal to noise. However, 3D quantification of vessel dimensions based on manual delineation of the vessel lumen is a tedious task and prone to subjectivity due to the complex vessel structures, narrowing segments, significant intensity signal losses and irregularities. An automated quantitative measurement is therefore desirable to improve and to support CA assessment from MRA images.

Different approaches have been proposed for automated arterial lumen segmentation. A common approach to segment a complete vasculature is by applying a curve evolution method, better known as the level set method or the active contour model. Lorigo et al. [3] evolved a curve in 3D space, but the calculations consumed a lot of time and the segmentation results often included artifacts around the vessel. Li and Yezzi [4] applied a 4D curve evolution (the fourth dimension is the varying radii) to generate a lumen surface, which resulted in a 3D sphere fitting along a vessel. Consequently, the segmentation results became too restricted for irregular vessel structures, such as stenoses or aneurysms. Frangi et al. [5] used a B-spline model to define a tubular geometry. A center vessel axis was first determined after enhancing vessel structures with the ‘vesselness’ filter and the fitting was performed to the direction of full-width half or 10% maximum intensity between the surface and the center vessel axis. The vesselness filter, however, often produces false responses. A more extensive and recent survey of other vessel segmentation techniques is available in Lesage et al. [7].

We developed a deformable tubular model based on Non-Uniform Rational B-Splines (NURBS) surface modeling to segment vascular structures. To avoid non-vessel artifacts and background noise, the tubular model was initially positioned inside a lumen, centered at a pathline that was automatically detected by using a front propagation method [6]. A gradient-based energy minimization iteration scheme was applied to deform the tubular model towards the lumen. Since the surface was constructed with a tubular shape model, the segmentation result was constrained to the shape of a vessel. Several pilot studies [8–10] have indicated promising results with this approach. We also allowed a minimum but intuitive user intervention particularly on difficult cases by marking forbidden areas for selecting the vessel of interest. We applied our method to delineate carotid arteries from MRA images from patients suffering severe atherosclerotic disease. Clinical findings in terms of the degree of stenosis and correlation analyses of cross-sectional areas and luminal diameter validated with expert observers are presented.

Methods

Pathline definition

The automated detection of a trajectory curve inside a vessel was developed based on the fast level marching set method [11]. A minimum of two seed points (proximal and distal) are required to define the vessel of interest. These seed points are manually placed on one of the three orthogonal MIP images. A depth buffer is created to track the position of a point in 3D space.

Using image as a medium, a front propagation was performed starting from the proximal point to all directions. The method computes the arrival time t _α of the front at each image element, i.e.,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ t_{\alpha } (x_{1} ) = t_{\alpha } (x_{2} ) + \frac{{d(x_{1} ,x_{2} )}}{{f(x_{1} ,x_{2} )}}, $$\end{document} 1

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ x_{1} ,x_{2} \in \Re^{3} $$\end{document} are two adjacent points, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ d:\Re^{3} \times \Re^{3} \to \Re_{ + } $$\end{document} is an Euclidean distance function and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ f:\Re^{3} \times \Re^{3} \to \Re $$\end{document}$ is a speed function. For MRA, we used a sigmoid speed function (see details in de Koning et al. [6]), which depends on the maximum, minimum and background intensities, calculated from the histogram of the whole MRA data.

As soon as the front reaches the distal point, the front propagation process is terminated. The result is a set of accepted points, i.e. points that the front has propagated through. The arrival times on each accepted point are stored in an image (the T-surface image). The pathline is then extracted by finding the fastest route from the distal to the proximal points using a backtracking algorithm. By using the steepest-descent approach, the fastest route is given by a curve \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ C:\Re \subset [0,1] \to \Re^{3} $$\end{document} that satisfies

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{\partial C}{\partial x} = - \nabla T,\quad x \in [0,1] $$\end{document} 2

where T is the T-surface image, C(0) is the distal point, and C(1) is the proximal point. The computed pathline does not follow the center of the vessel since it is a minimal path. A vessel path refinement step is used to move the pathline to the center of the vessel (see details in de Koning et al. [6]). This refinement uses a distance image created from the accepted points and moves the points of the path along the gradient of the distance image until the points reaches the maximum distance.

Intermediate points and forbidden planes

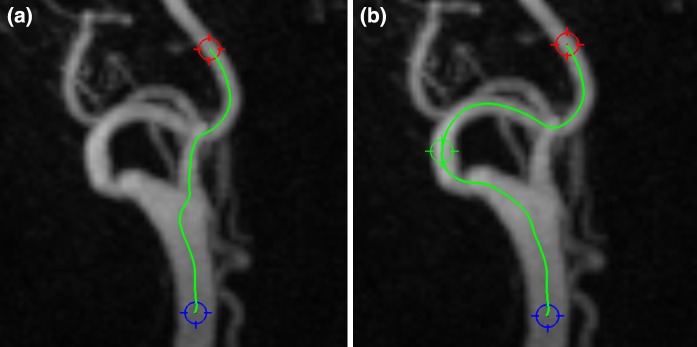
The front propagation method has been previously applied to the extraction of vessel pathlines in non-carotid arteries, e.g., in coronary arteries [12, 13], in peripheral arteries [6] and in cerebral arteries [14]. Although the front propagation method has shown good consistent results irrespective of varied positions of proximal and distal points, there are some drawbacks when applying it in carotid arteries. The distance between vessels in the neck area can be very small. They can be intertwined and sometimes they seem to touch each other due to the image resolution, which can create an easy pass to jump from one vessel to the other (Fig. 1a). To solve this problem, we introduced optional intermediate points that are placed manually by the user upon seeing this mistake; a similar approach was introduced by Benmansour et al. [26] The front should propagate through all intermediate points before terminating at the distal point (Fig. 1b).

Fig. 1.

Failed pathline detection case (a) and the correct pathline through one intermediate point (green marker) (b)

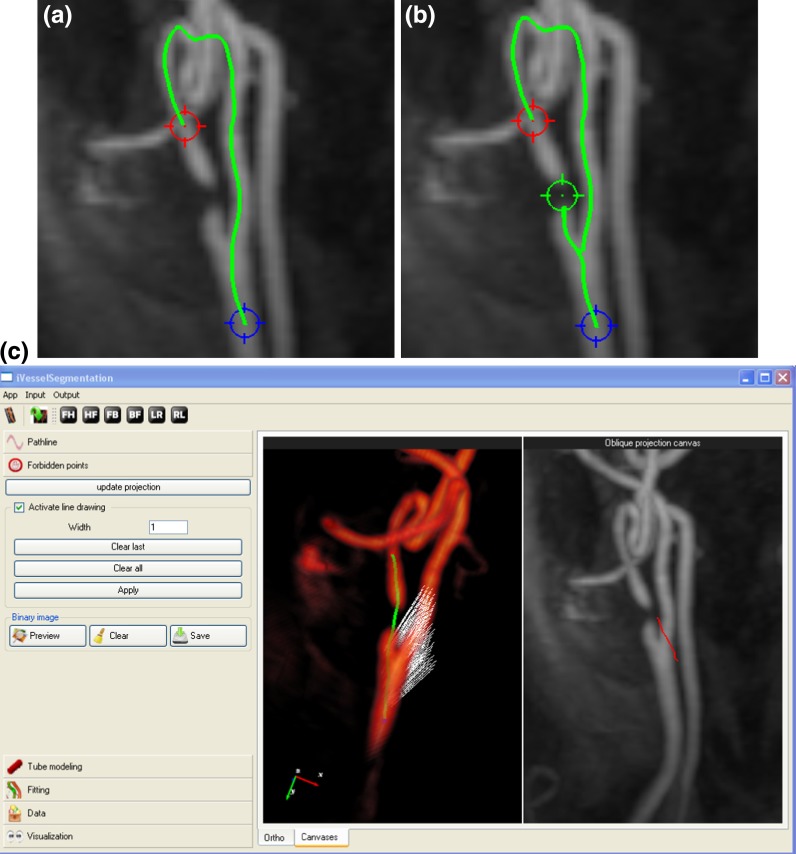
In the presence of a severe stenosis, adding intermediate points does not always solve the problem (Fig. 2b), because the lumen intensity values at the stenosed segment drop significantly almost to the same level as the background. In this case, we introduced another type of user intervention to block the front propagation. Initially, the user selects the best viewing angle of the stenosis in the maximum intensity projection (MIP) image. Subsequently, a curve is drawn on the MIP image to mark a forbidden pathway (Fig. 2c in the right panel). The curve defines a curved plane parallel to the viewing angle. The speed function values on this curved plane are modified to a constant zero, which consequently block the front passing through the plane (see the left panel of the application in Fig. 2c).

Fig. 2.

Failed pathline detection in a stenotic case (a) and even after an intermediate point (green marker) was added to help the pathline detection (b). Allowing user to draw a freehand curve on the projection image (the red curve in the right panel at figure c), a forbidden plane (white dots) does not allow the front propagation to pass through, resulting in the correct pathline inside the stenosis

Vascular tube model

The initial tube model is constructed by using a Non-Uniform Rational B-Spline (NURBS) model. A NURBS surface is defined by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ S(u,v) = \sum\nolimits_{i = 0}^{n} {\sum\nolimits_{j = 0}^{m} {R{}_{i,j}(u,v)\;P_{i,j} } } $$\end{document} 3

where 0 ≤ u, v ∈ R < 1 and P _i,j ∈ R ³ is a set of control points. The function R _i,j (u, v) is the piecewise rational basis function

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R_{i,j} (u,v) = \frac{{N_{i,p} (u)\;N_{j,q} (v)\;w_{i,j} }}{{\sum\nolimits_{k = 0}^{n} {\sum\nolimits_{l = 0}^{m} {N_{k,p} (u)\;N_{l,q} (v)\;w_{k,l} } } }} $$\end{document} 4

where N _i,p (u) is the ith B-spline basis function of p-degree and {w _k,l} are the weights.

NURBS can model any type of 3D surfaces and it has properties that are suitable for segmenting vascular structures. The NURBS surface is smooth and derivable, allowing non-rigid deformation of the model that keeps the smoothness of the surface. Another important property is the local support of the model in which R _i,j (u, v) is non-zero only within [u _i, u _i+p−1] and [v, v _j+q−1] interval. This means that changing the position of one control point P _i,j only affects the local surface S(u, v) on that particular interval. Consequently, it allows local adjustment of the surface to fit onto an irregular vasculature.

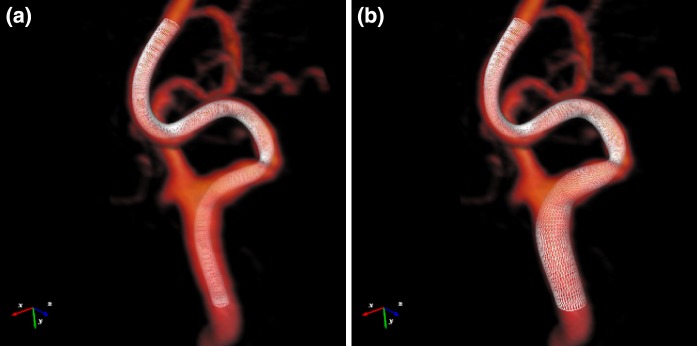
To construct a tube model, a sweep surface technique is performed. A number of circular rings are positioned along the pathline. The u and v components in Eq. 3 are directions along ring circumferential and centerline longitudinal, respectively. The initial diameter of the tube can be set as a constant (Fig. 3a) or automatically estimated from the front propagation method (Fig. 3b). For the automated estimation, the skeletonization process is applied on the accepted points. By using the estimated diameter, the initial tube surface is already in the proximity of the lumen, allowing faster convergence of the fitting iteration process.

Fig. 3.

Two examples of initial tube models prior fitting: a constant radii, and b waveprop estimated radii

Tube fitting

The surface fitting process is a deformation of the NURBS surface \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ S(u,v):\Re^{2} \to \Re^{3} $$\end{document} by a set of forces acting on the control points to reach the dynamic force equilibrium. The energy function to deform the NURBS surface is defined as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ E(u,v) = \int {F(S(u,v))dudv} , $$\end{document} 5

where the potential surface \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ F:\Re^{3} \to \Re $$\end{document} is given by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ F(x,y,z) = - \left| {\nabla I(x,y,z)} \right|. $$\end{document} 6

An intuitive way is to imagine the NURBS surface living on the potential surface F(x, y, z) determined by the opposite direction of the gradient of the image function I(x, y, z).

Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ p(t) \in \Re^{3} $$\end{document} be a vector on a control point that depends on the time t. Minimizing the energy function E(u, v) along time is performed by applying the following Euler–Lagrange differential equation

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \gamma \frac{dp}{dt} + \frac{\partial E}{\partial p} = \gamma \frac{dp}{dt} + \sum\limits_{i = 0}^{L} {\left( {\frac{\partial F}{\partial x}\frac{{\partial S_{x} }}{\partial p} + \frac{\partial F}{\partial y}\frac{{\partial S_{y} }}{\partial p} + \frac{\partial F}{\partial z}\frac{{\partial S_{z} }}{\partial p}} \right)} = 0 $$\end{document} 7

where L is the number of surface tessellations, γ is a weighting factor and S _x, S _y and S _z are the derivatives of Eq. 3 with respect to x, y and z. Note that ∂E/∂p is the image force that applies to the surface nodes. Solving Eq. 7 will define a set of vectors (image force vectors) that act on each control point.

Image acquisition

All MR images were acquired by a 1.5T MRI scanner equipped with a gradient overdrive (Magnetom Vision, Siemens Medical System, Erlangen, Germany). Spoiled 3D FLASH (fast low-angle shot) MR angiography was performed using a 4 × 2 circularly polarized phased-array neck coil. The sequence was performed with 32–36 coronal partitions. The typical image slice parameters were 1.94–2.5 mm thickness, 2.84–3.15 ms repetition time, 1.03–1.11 ms echo time, 35–40° flip angle, 70 × 140 × 280 mm³ field of view and a scan time of 9–9.5 s. The typical image slice resolution was 256 × 256 pixels with 1.09 × 1.09 mm pixel spacing. Four consecutive 3D images were taken, starting at approximately 3 s after the administration of 0.1 mmoL/kg gadolinium (Omniscan, Hafslun Nycomed, Oslo, Norway). Digital subtraction MR images were generated in several cases to improve vessel-to-background contrast.

Patient study

Contrast-enhanced MRA studies from 21 patients suffering carotid atherosclerotic disease were included for this study. Vessel segments of interest were defined from proximal common artery to the distal either internal or external arteries, depending on the stenosis location. For assessing the reproducibility of the automated method, two groups of pathlines were generated: (1) starting from the common artery proximal to the main bifurcation to both internal and external arteries, and (2) using a reversed direction from internal/external artery to the common carotid. Although the two groups of pathlines were similar, they were different in terms of the estimated initial radius.

Image analysis

The detected pathline was used to create curved multiplanar reformatted (CMPR) images for manual luminal contour tracing by an independent expert. CMPR image slices were generated every 1.0 mm (non-stenosed segments) and 0.5 mm (stenosed segments) with the typical size of 64 × 64 pixels of 0.5 × 0.5 mm pixel spacing. An expert drew luminal contours on these images to define the reference by using a dedicated quantitative Vessel Wall MR Analytical Software (VesselMASS, Leiden University Medical Center, the Netherlands) [15].

To maintain the objectiveness and consistency of manual contouring, full-width half-maximum criteria was applied to improve the vessel boundary visualization [16]. Let I _max and I _out be the maximum intensity response at the center of the lumen and the background intensity, respectively. The 50% threshold value was set as follows

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ T = \frac{1}{2}\left( {I_{max} - I_{out} } \right). $$\end{document} 8

The thresholded binary image was used as a soft guideline to delineate the lumen. Comparisons were made with the adjacent slice planes if there were some doubts about the shape of the lumen boundary.

Stenosis grading

Stenoses were graded based on NASCET criteria [1]:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ G = \left( {1 - \frac{{d_{r} }}{{d_{s} }}} \right) \times 100\% $$\end{document} 9

where d _r is the narrowest diameter of the residual lumen and d _s is the luminal diameter of the distal vessel, i.e., the segment of the same artery that is located well beyond the stenosed bulb [17]. The luminal diameter was defined as the minimum diameter of a circle that can still be fitted inside the lumen cross-section.

Statistical analys

Statistical analysis was performed by using R statistical computing environment [18]. Linear regression was applied to analyze correlation of cross-sectional area and luminal diameter measurements derived from the automated method and the expert. Pearson correlation coefficient (r) was used to indicate the degree of linear relationship between the two methods. The statistical significance level was set at P < 0.05 with confidence interval of 95%. The correlation analysis was performed on different vessel segment categories: common carotid arteries (CCA), internal carotid arteries (ICA), external carotid arteries (ECA), bifurcation slices (BA) and stenosed slices (SA).

To measure the degree of similarity between two contours, Dice similarity index was applied [19], i.e.,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ D(C_{1} ,C_{2} ) = \frac{{2\;A(C_{1} \cup C_{2} )}}{{A(C_{1} ) + A(C_{2} )}} $$\end{document} 10

where C ₁, C ₂ are two different contours and A(C) is the area defined by contour C. The same vessel group division was applied for this measurement.

Bland–Altman analysis was performed to study the agreement of stenosis grading between the automated method and the observer [20]. The same analysis was also applied for measuring reproducibility of the method for two repeated trials. Only SA group was included in both analyses.

Results

The automated method was performed on a PC Intel Quad Core Q6600 2.40 GHz 2.00 GB RAM workstation running Microsoft Windows XP in a single thread mode. The maximum number of iterations was set to 200 and the iteration was terminated earlier when the average size of image forces was less than or equal to 10⁻⁵. The distance between control point rings was fixed to 3 mm with 7 control points per ring and 5 mesh patches between rings.

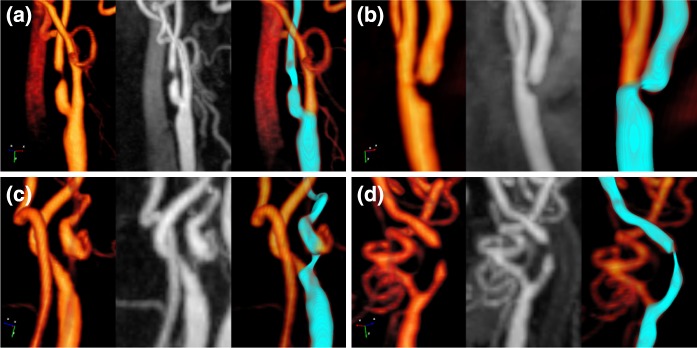
The average iteration time was 15.0 ± 7.0 s or 0.14 ± 0.05 s/mm with the average pathline length of 100.8 ± 21.7 mm. Four cases reached the maximum number of iteration. Examples of four segmentation results on CA stenoses are shown in Fig. 4.

Fig. 4.

Some segmentation results. Left: volume rendering, middle: maximum intensity projection, right: the segmentation mesh result (blue surface)

Correlation analysis

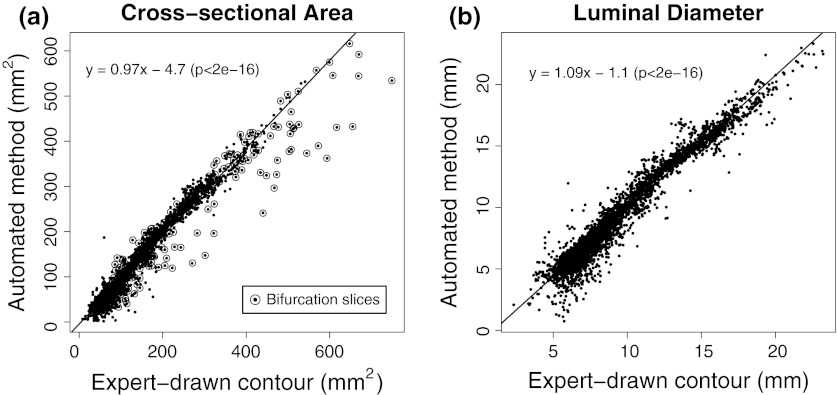
The automated method demonstrated excellent linear correlation with expert contours for both cross-sectional area and luminal diameter measurements (Fig. 5). Pearson correlation coefficients for measuring the cross-sectional area and the luminal diameter, which were calculated from the automated and expert-drawn contours, were both r = 0.98 (P < 0.05).

Fig. 5.

Linear regression analysis for cross-sectional areas (a) and luminal diameter calculations (b) comparing automatically derived with manually traced contours

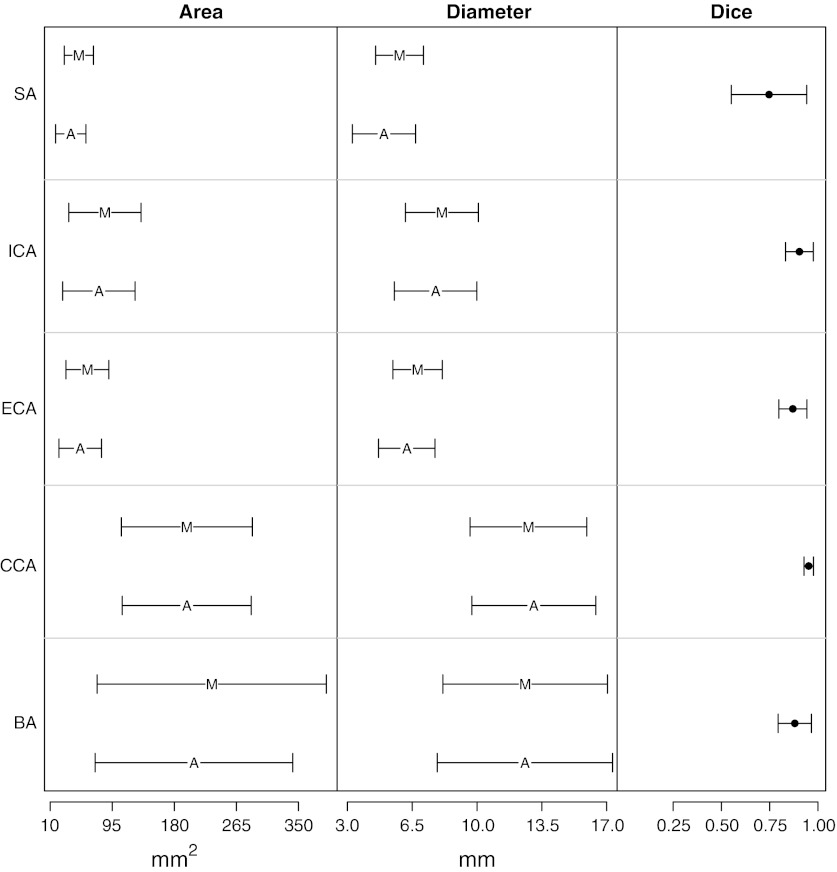
Excellent linear correlation was also achieved in each vessel type. Table 1 shows correlation coefficients for each vessel type. Strong correlations for both cross-sectional area and luminal diameter measurements were found for CCA, ICA, ECA and BA. For stenosed areas (SA), moderate correlation was found. The correlation coefficient to measure area and luminal diameter for SA were r = 0.70 (P < 0.05) and r = 0.58 (P < 0.05), respectively. The mean luminal diameter for SA slices was 8.8 mm (range: 0.75 mm to 23.3 mm) compared to expert mean diameter of 9.05 mm (range: 2.34 mm to 23.23 mm). Figure 6 shows the comparison of measuring area and luminal diameter between the automated method and the expert in a graphical form of standard error bars.

Table 1.

Pearson correlation coefficients for individual categorical slices measuring cross-sectional areas and luminal diameter between the automated method and the expert

Cross-sectional	Area luminal [r(P)]	Diameter [r(P)]
CCA	0.99 (<0.05)	0.98 (<0.05)
ICA	0.96 (<0.05)	0.93 (<0.05)
ECA	0.92 (<0.05)	0.89 (<0.05)
BA	0.91 (<0.05)	0.97 (<0.05)
SA	0.70 (<0.05)	0.58 (<0.05)

CCA common carotid artery, ICA internal carotid artery, ECA external carotid artery, BA bifurcartion, SA stenosed slices

Fig. 6.

Comparison plot of different mean values between automated method (A) and expert drawn contours (M). Horizontal bars denote SE

Degree of similarity

Dice similarity coefficients were excellent for CCA and ICA, i.e., the mean values were 0.95 ± 0.02 and 0.90 ± 0.07, respectively. The lumen similarities were still very high for branching arteries; the mean Dice coefficient for BA was 0.88 ± 0.09 and for ECA was 0.87 ± 0.07. The similarity was however the lowest for the stenosed vessel and had a wider variance (see Fig. 6). The mean Dice coefficient for SA was 0.75 ± 0.2.

Agreement in stenosis grading

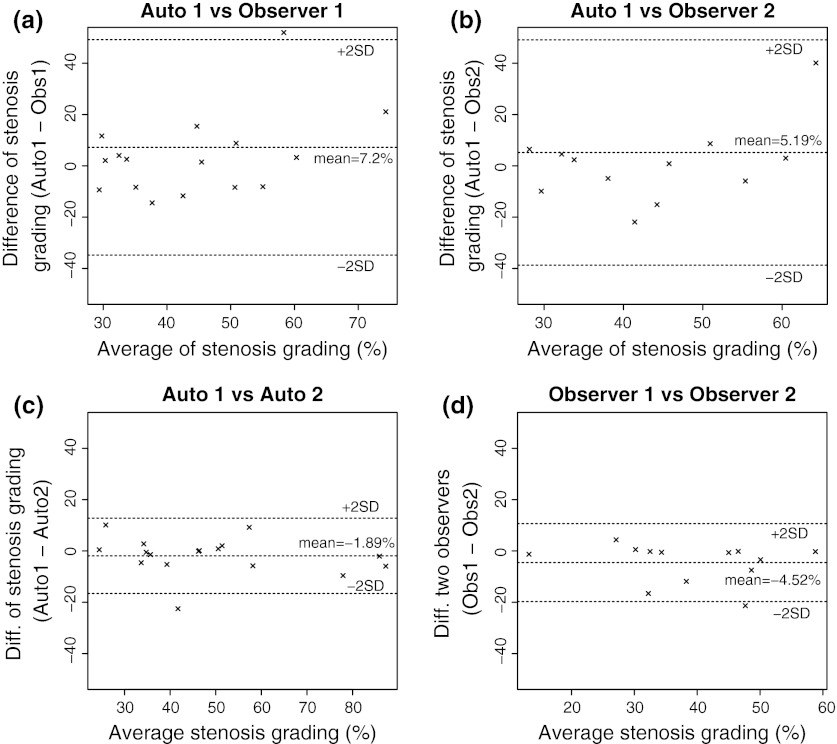
Table 2 shows the agreement results between the automated method and two observers for measuring stenosis grades. The presented method achieved good agreements with the observers, i.e., the mean difference was 7.20% (SD = 21.00%) and 5.19% (SD = 21.96%) with Observer 1 and Observer 2, respectively. The large spread in the statistical results in both validations was mainly caused by one case (see Fig. 7a and b). In this particular case, the loss of signal intensity was so apparent that it caused unreliable lumen contour assessment both by the observers and the automated method. However, the differences between the automated method with both observers were uniformly distributed as shown in Fig. 7a and b.

Table 2.

Stenosis grading assessment results between the automated method and two observers

	Mean difference (%)	Min difference (%)	Max difference (%)	SD (%)
Auto versus Obs1	7.20	−14.44	60.52	21.00
Auto versus Obs2	5.19	−21.91	59.24	21.96
Obs1 versus Obs2	−4.52	−21.34	4.36	7.60
Auto1 versus Auto2	−1.89	−22.51	10.13	7.34

Fig. 7.

Stenosis grading assessments: a automated method (Auto1) versus Observer 1, b automated method (Auto1) versus Observer 2, c between two repeated automated methods with different pathlines (Auto1 vs. Auto2), and d Observer 1 versus Observer 2

To measure the ground truth reliability, we also measured intra observer variability. When both observers were compared, the inter-observer variation was relatively small. The mean difference was 4.52% (SD = 7.60%). Figure 7d also confirms this finding.

Reproducibility of the automated method was measured by switching the position of proximal and distal points. The pathline for the first trial ran from common carotid to either external or internal artery. The second trial used internal/external to common artery pathlines. Given different seed point positions, the automated method generated consistent results. The mean difference was 1.89% (SD = 7.34%). There was no systematic error found as shown in Fig. 7c.

Discussion

We have presented an automated lumen segmentation method for carotid arteries based on a deformable NURBS model. The method showed good agreement with the expert in terms of lumen diameter, cross-sectional area measurement and stenosis grading. This result suggests high potential for clinical applicability of the automated method in the analysis of CE-MRA of carotid arteries. To apply the automated lumen detection method, limited user-interaction is required for indicating the start and end position of the vessel segment of interest. In particular complex cases, such as cases with highly curved vessel segments or cases where different vessels run very close to each other, some additional interaction was needed to obtain a valid lumen pathline. The high reproducibility of the method indicates that these manual initialization steps have negligible influence on the obtained diameter measurements.

We compared our method with a similar study performed by Guzman et al. [21], which segmented carotid arteries by applying the 2D cross-sectional threshold mechanism during the fitting process [6]. Guzman study measured the diameter of common carotid artery (CCA) and internal carotid artery (ICA) with two measurements: caliper and digital subtracted angiography (DSA). Table 3 compares the cross correlation coefficient of the luminal diameter between our method, the Guzman study with caliper and the Guzman study with DSA measurement. In both cases, our method shows better correlation coefficients compared to the Guzman study.

Table 3.

Luminal diameter measurement comparisons

	This study (r)	Guzman et al. [19] with caliper measurement (r)	Guzman et al. [19] with DSA measurement (r)
CCA diameter	0.98	0.75	0.81
ICA diameter	0.93	0.81	0.78

In terms of the stenosis grading, the method achieved good reproducibility. There was one particular case that both observers disagreed with the automated method (one of which the segmentation result is shown in Fig. 4d). The tube model shrank substantially because of significant intensity drop-out in the signal intensity at the stenosed area. The presence of signal intensity drop-out at the stenosis and distal intensity reduction have been associated with severe (≥70%) stenosis [22]. This caused an overestimation of the stenosis grading compared to the observers. This limits the automated method, because the fitting process relies heavily on the image gradient. When the contrast between lumen and the background becomes so low, the image forces cannot stop the iteration process at the correct edge and subsequently the mesh keeps shrinking (Fig. 8).

Fig. 8.

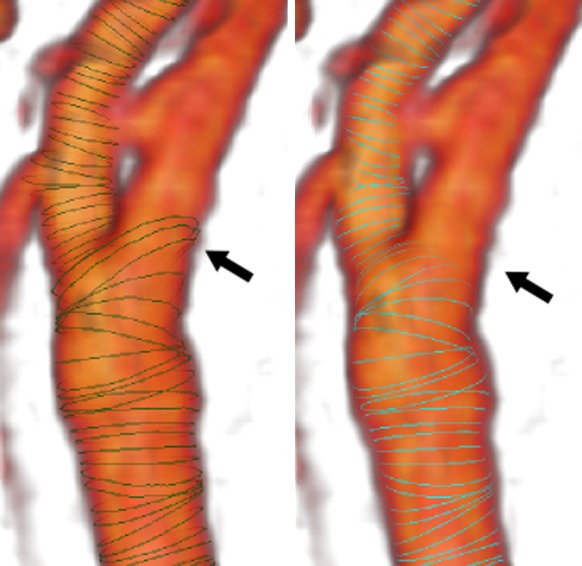
An example of vessel segmentation on carotid bifurcation area showing disagreement (pointed by black arrows) between the automated method with expert drawn contours. The left Figure shows the expert drawn contours (green curves), while the right Figure shows the contours generated by the automated method (cyan curves). Volumetric rendering of the vessel structure is shown in the background

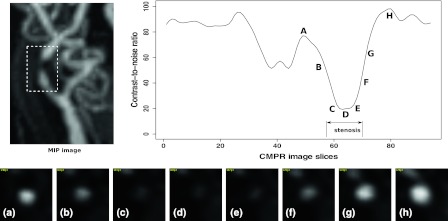
Similarly due to the low tissue contrast, it is difficult to delineate the lumen at the stenosed area, because the lumen is hardly visible (Fig. 9). The only objective guidance for the manual contouring is by taking the full-width half-maximum criteria into account. Accurate stenosis grading therefore highly depends on the quality and spatial resolution of the imaging technique. The use of high-field and parallel imaging MR systems might solve this problem in the future [23–25].

Fig. 9.

Low contrast and signal intensity drop problem when assessing severe stenosis. CMPR image slices show low contrast of the stenosed lumen, making it difficult for an observer to draw the luminal area. The signal intensity drop also causes the automated method to segment less reliably in the stenosed area

Underestimation of luminal area segmentations was present mostly at the bifurcation areas (circle marks in Fig. 5a). Bifurcations are still problematic in the current implementation, because the tube model is still designed to fit onto a single vessel segment. The tube model followed straight to one artery branch inside the main bifurcation, while the observer drew luminal contours of the whole main bifurcation area (see an illustration in Fig. 8). For assessing the degree of stenosis, this limitation might become a problem if the stenosis occurs in the bifurcation area. In this case, the deformable mesh model should be extended to fit onto bifurcation area.

Conclusions

An automated method for quantification of carotid artery stenosis from MRA data based on a deformable mesh model has been presented. The method achieved excellent correlation on area and luminal diameter measurements. The processing time was reasonably fast to segment the vessel of interest. Prior to segmentation, some user interventions were needed in the presence of stenosis but the interaction mechanism was designed to be as easy and as intuitive as possible. When image quality is fairly good, the presented automated MRA analysis method provides very accurate and reproducible quantitative assessment of vessel dimensions and the degree of stenosis.