Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2012 Jul 18;109(4):254–260. doi: 10.1038/hdy.2012.39

Effective size of a wild salmonid population is greatly reduced by hatchery supplementation

M R Christie 1,*, M L Marine 1, R A French 2, R S Waples 3, M S Blouin 1
PMCID: PMC3464026  PMID: 22805657

Abstract

Many declining and commercially important populations are supplemented with captive-born individuals that are intentionally released into the wild. These supplementation programs often create large numbers of offspring from relatively few breeding adults, which can have substantial population-level effects. We examined the genetic effects of supplementation on a wild population of steelhead (Oncorhynchus mykiss) from the Hood River, Oregon, by matching 12 run-years of hatchery steelhead back to their broodstock parents. We show that the effective number of breeders producing the hatchery fish (broodstock parents; Nb) was quite small (harmonic mean Nb=25 fish per brood-year vs 373 for wild fish), and was exacerbated by a high variance in broodstock reproductive success among individuals within years. The low Nb caused hatchery fish to have decreased allelic richness, increased average relatedness, more loci in linkage disequilibrium and substantial levels of genetic drift in comparison with their wild-born counterparts. We also documented a substantial Ryman–Laikre effect whereby the additional hatchery fish doubled the total number of adult fish on the spawning grounds each year, but cut the effective population size of the total population (wild and hatchery fish combined) by nearly two-thirds. We further demonstrate that the Ryman–Laikre effect is most severe in this population when (1) >10% of fish allowed onto spawning grounds are from hatcheries and (2) the hatchery fish have high reproductive success in the wild. These results emphasize the trade-offs that arise when supplementation programs attempt to balance disparate goals (increasing production while maintaining genetic diversity and fitness).

Keywords: bottleneck, genetic diversity, fisheries, parentage, relatedness, salmon

Introduction

The large-scale release of plants and animals into the wild can have unintentional negative effects on the genetic diversity of the recipient populations (Laikre et al., 2010). One widely-used strategy for creating large numbers of individuals suitable for release into the wild is to implement captive-breeding programs. Despite the large numbers of such programs, there remains a distinct lack of appropriate and effective monitoring of individuals released into the wild (Waples, 1999, Laikre et al., 2010). Ideally, the genetic monitoring of populations would consist of sampling before and after the release of individuals into the wild. In practice, however, these comparisons are not feasible for many populations due to the lengthy history of anthropogenic intervention. Nevertheless, a long-term evaluation of the individual- and population-level effects of large-scale releases, particularly when combined with detailed pedigree analyses (Pemberton, 2008), can yield valuable insights into the demographic and genetic effects of population supplementation.

Wild populations of Pacific salmonids have declined sharply over the past century due to a combination of habitat destruction, hydropower and overfishing (McClure et al., 2003; Quinn, 2005; Naish et al., 2008). Consequently, 23% of Pacific salmon stocks are at moderate to high risk (Augerot and Foley, 2005) and 54% of evolutionarily significant units are currently listed as threatened or endangered under the US Endangered Species Act (Gustafson et al., 2007; ESA salmon listings, 2009). In order to alleviate the continued population declines, supplementation programs have been commonly implemented throughout the Northern Pacific. The term ‘supplementation' is used by programs where the main objective is to help wild populations recover, but sometimes the term is used for programs that also have a goal of harvest augmentation. Here we are considering the former. Supplementation programs generally use either hatchery fish (of various backgrounds) or returning wild fish as broodstock and release the hatchery-raised smolts at or near the wild spawning grounds. After returning from the ocean, a portion (or in many cases all) of the returning adult hatchery fish are allowed onto the spawning grounds with the wild-born fish. Wild broodstock are preferred in some supplementation programs because they can produce offspring that have much higher fitness in the wild than offspring from older, domesticated hatchery stocks (though even first generation hatchery fish can have reduced fitness in the wild; Araki et al., 2007a; Araki et al., 2009; Williamson et al., 2010; Berntson et al., 2011; Theriault et al., 2011; Christie et al., 2012).

Aside from creating differences in reproductive success between wild and captive-born individuals, supplementation programs may also affect important population genetic parameters (Waples and Teel, 1990). For example, genetic diversity, allelic richness and patterns of genetic drift may be altered by population supplementation. Furthermore, the effective population size for individuals produced in captive breeding programs can be reduced relative to their wild-born counterparts because (1) typically small numbers of individuals are used as broodstock (especially for populations or species of concern) and (2) there can be substantial variance in reproductive success among the individuals chosen as broodstock (for example, a small portion of the broodstock produce a high percentage of the surviving offspring). Supplementation practices can thus create a ‘Ryman–Laikre effect', where the inbreeding effective population size of the entire population is reduced relative to that of the original wild population (Ryman and Laikre, 1991; Ryman et al., 1995). Even though this effect was pointed out over 20 years ago, the problems associated with inundating a wild population with the offspring of a handful of founders have been largely ignored in current practice. In fact, the recent trend toward producing first-generation hatchery fish could exacerbate the problem because their reproductive success is usually much higher in the wild than that of domesticated stocks.

Steelhead trout, Oncorhynchus mykiss, are typical of most Pacific salmonids in that their declining populations have led to the creation of numerous supplementation programs (Kostow, 2009). In this study, we examined 12 run-years of steelhead from Hood River, Oregon for which all anadromous fish were genotyped at eight highly polymorphic microsatellite loci. We first used pedigree data to calculate the effective number of broodstock breeders represented in the returning hatchery offspring. Owing to the small effective number of breeders we predicted that, in comparison to wild fish, hatchery fish would have (i) high genetic drift among years, (ii) reduced genetic diversity, (iii) increased relatedness, and (iv) substantial linkage disequilibrium (LD) among loci. We further tested for a Ryman–Laikre effect and examined how the strength of the Ryman–Laikre effect is affected by (i) the proportion of hatchery fish allowed onto spawning grounds and (ii) the reproductive success of those hatchery fish in the wild (relative to wild-born fish).

Materials and methods

Sample collection and typing

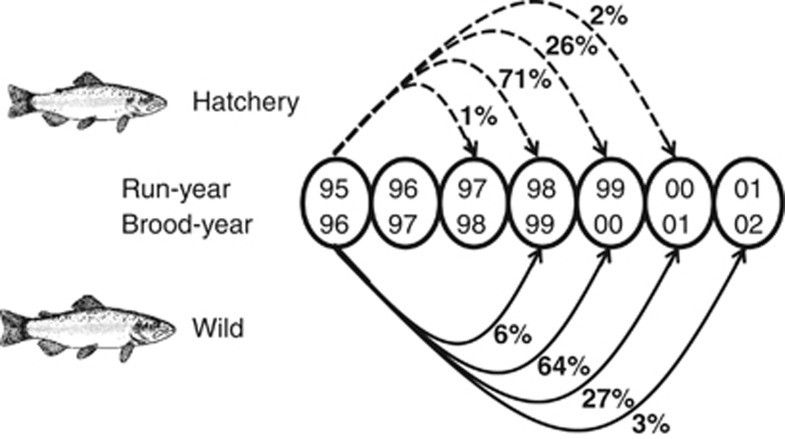
Samples were collected from the Hood River, Oregon, where winter-run steelhead are listed as threatened under the US Endangered Species Act (Busby et al., 1996). Genetic samples for steelhead employed in this study were collected from run-years 1995–2006, which corresponds to fish born in brood-years 1993 through 2003. These run-years also encompass the initiation of the supplementation program (though programs with domesticated, non-local broodstock existed previously; see Olsen, 2003). Winter-run steelhead begin returning to their natal rivers in early December, the year of which designates the run-year, and do not spawn until spring of the next year. Thus a steelhead that spawns in May of 2000 will belong to run-year 1999 (even if it returned in March) and its offspring will belong to brood-year 2000. Because of the accelerated growth rate in hatcheries (that is, smoltification in 1 year vs a typical time of 2 years in the wild), 71% of hatchery-born steelhead return to spawn after 2.5 years, whereas 64% of wild-born steelhead return after 3.5 years (Figure 1; Araki et al., 2007a). Fish from a single run-year come from multiple brood-years. Steelhead that returned to spawning grounds in the Hood River were first passed over the Powerdale dam, which was a complete barrier to migrating fishes. Every fish passed over the dam was individually handled, and samples of scales and fin tissue were collected by staff of the Oregon Department of Fisheries and Wildlife for subsequent aging and genetic analysis. Steelhead returning to the Hood River are easily categorized as hatchery or wild origin because all hatchery fish have their adipose fin removed before release.

Figure 1.

Figure 1

Open in a new tab

Distribution of run-years in which wild and hatchery fish returned. Hatchery fish born in brood-year 1996 (run-year 1995 for their parents) returned predominantly in run-year 1998, while wild fish returned predominately in run-year 1999. Notice that fish in any given run-year come from multiple brood-years.

All wild fish and an approximately equal number of hatchery fish were passed over the dam each year (wild run sizes ranged from 221 to 1027 fish). The winter-run hatchery fish were created using either two wild fish or one wild fish and a first-generation hatchery fish as parents (see Araki et al., 2007a, 2007b). Most fish were spawned with two (or occasionally more) partners, which created returning hatchery fish that were full sibs, half sibs or unrelated. As per Araki et al. (2007a, 2007b), we use ‘wild' to refer to any fish spawned in the river under natural conditions, regardless of whether its parents have hatchery ancestry. Furthermore, fish used as hatchery broodstock were collected randomly from throughout the entire run period and were unlikely to be related. We have DNA samples from all broodstock, and comprehensive records on broodstock pairings in the hatchery. Extensive details on this study system, management practices, steelhead life-history and reproductive success can be found elsewhere (Olsen, 2003; Araki et al., 2007a, 2007b; Kostow, 2009).

The winter-run steelhead samples averaged 907 fish per brood-year for a total of 9977 samples (Table 1). We genotyped all samples at eight highly polymorphic microsatellite loci (Omy 1001, Omy 1011, Omy 1191, Omy77, One108, One2, Ssa407 and Str2), which average 36 alleles per locus (see Araki et al., 2007a, 2007b for details of microsatellite loci, Hardy–Weinberg proportions and molecular methods). These data were previously employed to determine the relative reproductive success of hatchery and wild steelhead (Araki et al., 2007a, 2007b), and of wild-born steelhead having hatchery vs wild parents (Araki et al., 2009). Results from this work documented that hatchery fish created with two wild parents averaged 85% the reproductive success of their wild counterparts and that an additional generation in captivity reduced fitness in the wild by an additional 50% (Araki et al., 2007a).

Table 1. Number of returning adult winter-run steelhead samples.

Brood-year Hatchery
Wild
  Female Male Female Male
1993 107 121 182 120
1994 181 109 135 77
1995 119 79 201 95
1996 93 79 802 436
1997 159 131 598 386
1998 323 319 568 334
1999 309 315 392 255
2000 154 149 323 194
2001 303 250 270 192
2002 79 75 203 153
2003 95 132 219 161
Total 1922 1759 3893 2403
Open in a new tab

Numbers are reported for fish grouped by brood-year (i.e., their year of birth) and separated by sex and hatchery or wild status.

Effective number of broodstock parents

To calculate the effective number of broodstock parents, we first employed parentage analysis to assign hatchery fish back to their broodstock parents. We used genotypes of the known broodstock pairs sorted by the year in which they were spawned as the putative parents. Genotypes of the hatchery fish, sorted and grouped by brood-year, were employed as the putative offspring. Because there can be some error associated with the aging of scales, we also used hatchery fish±1 brood-year as putative offspring. Parentage analysis revealed that very few hatchery fish (<3%) had been assigned via scale ageing to the incorrect brood-year, which is not always the case with wild-born fish (for example, Seamons et al., 2009). We used Mendelian exclusion to assign hatchery fish to their broodstock parents (that is, each allele in an identified offspring matched at least one allele in both parents). To allow for genotyping errors, we allowed an offspring to mismatch to one allele in both parents (Christie, 2010), although 81% of assignments contained no mismatches. No hatchery fish matched to more than one broodstock pair because we had an average of 36 alleles per locus and because we knew the hatchery broodstock pairings, which reduced the required number of pairwise comparisons. Broodstock fish (potential parents) had genotype data at all loci. Hatchery fish that had missing data at more than two loci were not used in this study (<1%), resulting in a total of 74 unassigned fish.

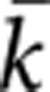After assigning hatchery fish to known broodstock pairs we calculated the mean (Inline graphic) and variance (Vk ) in reproductive success for male and female broodstock from each run-year. We next estimated the inbreeding effective number of breeders (Nb) for each sex as:

graphic file with name hdy201239e2.jpg

where N equals the number of broodstock males or females used in a run-year (Crow and Kimura, 1970; Caballero, 1994). We next combined the estimates for both sexes by setting

graphic file with name hdy201239e3.jpg

Note that under some circumstances it may be necessary to adjust 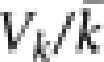Inline graphic to account for errors in parentage assignment and missing parents (Araki et al., 2007c). In our case, however, we had complete genotypes of all putative parents, and using assignments with or without allowing for mismatching loci did not substantially change our estimates (that is, we had very low type a and b errors using the terminology of Araki et al., 2007c). Using records from the Oregon Department of Fish and Wildlife, we compared the effective number of breeders used in each year (as calculated above) to (1) the number of broodstock actually used, (2) the total number of returning offspring that the broodstock produced, and (3) the total number of wild fish passed over the dam each run-year.

Population effects of supplementation

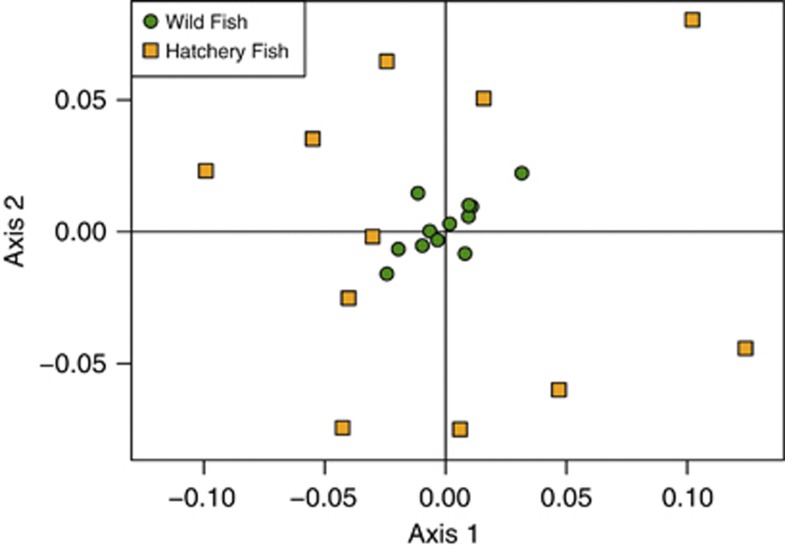
We first calculated FST between the wild and hatchery fish grouped by brood-year using FSTAT 2.9.3 (Goudet, 1995). These results were illustrated with a principal coordinates analysis performed with the package ade4 (Thioulouse et al., 1997) as implemented in R version 2.12 (R Development Core Team, 2011). Correspondence analysis on the genotype data produced a very similar pattern (data not shown). Given the high number of alleles per locus, we also calculated the multi-allele analog, GST, using RECODEDATA (Meirmans, 2006). The numbers of hatchery and wild fish in each group were both large (range: 154–1238) and roughly equal, such that the observed differentiation was not due to differences in sample sizes.

For all 11 years of data, we next calculated the allelic richness and FIS for both wild and hatchery fish using FSTAT. For allelic richness, samples were rarefied to smallest sample size (n=154). Using 5000 permutations in FSTAT, we tested whether differences in allelic richness, within sample gene diversity, and observed heterozygosity were different between hatchery and wild fish. We also calculated the percentage of locus pairs in LD with GENEPOP 4.0 (Raymond and Rousset, 1995) using 10 000 batches and 10 000 iterations per batch. Lastly, we calculated Queller and Goodnight's (1989) pairwise measure of relatedness as implemented in GENALEX 6.41 (Peakall and Smouse, 2006). We performed 999 bootstraps and 999 permutations to determine whether the estimates were different from zero and whether estimates for hatchery and wild fish differed from one another, respectively.

Ryman–Laikre effect

To test for a Ryman–Laikre effect, we first estimated the effective number of breeders per brood-year for wild fish. We used LDNe 1.2 (Waples and Do, 2008) to estimate the effective number of wild breeders (Nw). We used a LD-based method because the presence of resident steelhead (that is, rainbow trout) in the river prevented assignment of a large portion of wild offspring to parents using pedigree methods (see Christie et al., 2011 for a detailed analysis of resident fish). We selected 0.02 as the lowest allele frequency to be used in LDNe, which has been shown to generally provide a good balance between maximizing precision and minimizing bias (Waples and Do, 2008). Selecting smaller values had little effect on our estimates, whereas larger values greatly increased the variance. We calculated confidence intervals by jackknifing over loci. We next calculated the effective number of breeders for hatchery fish (Nc) using LDNe and pedigree-based methods (see the methods described above). Using the equation presented in Ryman and Laikre (1991), we calculated the effective number of breeders for hatchery and wild fish combined as:

graphic file with name hdy201239e5.jpg

where Nc and Nw are the effective number of hatchery and wild breeders, respectively. Because x theoretically equals the contribution of hatchery fish to the next generation (Ryman and Laikre, 1991), we calculated x as:

graphic file with name hdy201239e6.jpg

where NHatchery equals the total number of hatchery fish passed over the dam, RRS equals the reproductive success of hatchery fish relative to wild fish and Ntotal was the total number of fish (wild and hatchery) passed over the dam for a given brood-year. We used an RRS of 0.85, which was the average reproductive success of a hatchery fish created with two wild parents (Araki et al., 2007a). We took the reciprocal of Equation (3) to calculate NeT, the effective number of breeders for the combined hatchery and wild components of the population.

We next calculated NNo Hatchery, which equals the best estimate of what the effective number of breeders would have been in the wild had there been no supplementation program. We calculated this value per brood-year as:

graphic file with name hdy201239e7.jpg

where Nbrood equals the number of fish brought into the hatchery and Ntotal was the total number of fish allowed to spawn in the wild per brood-year. It should be noted that this correction to Nw yielded only slight qualitative differences for the population in this study, but it would be particularly important for hatchery programs that use a larger percentage of the returning fish as broodstock. Lastly, we divided NeT by NNo Hatchery, to measure the Nb of the entire population (hatchery and wild combined) relative to the Nb in the wild had there been no supplementation program. Thus, a ratio =1 indicates that there is no decrease in Nb owing to the hatchery program, whereas a ratio <1 indicates a Ryman–Laikre effect. We next plotted these results as a response to x (the contribution of hatchery fish to the next generation), where RRS=0.85 (see Equation (4)). We also varied RRS from 0 to 1 in the calculation of x (Equation (4)) and divided the harmonic mean of NeT and the harmonic mean of NNo Hatchery (for the 11 brood-years) to illustrate the effect of RRS on the magnitude of the Ryman–Laikre effect.

Results

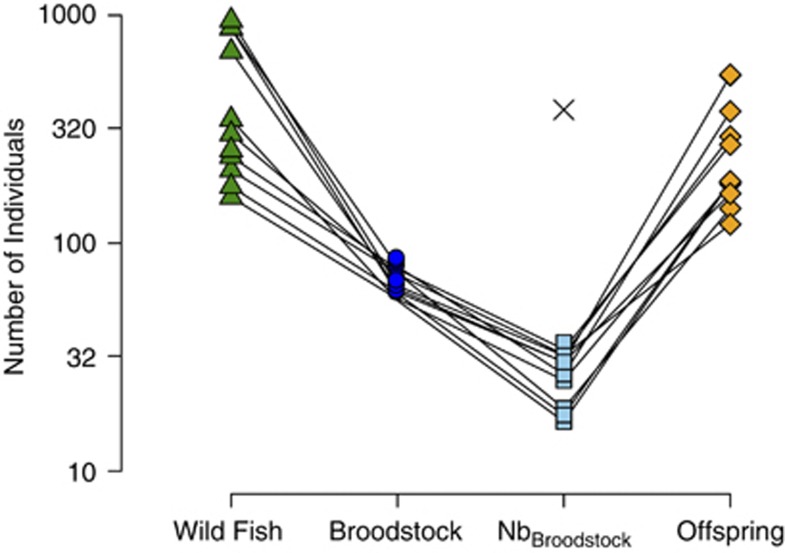
According to hatchery records, a total of 40 to 80 fish were used as broodstock each year. However, the effective number of broodstock parents estimated from their returning offspring ranged from 16.5 to 36.7, with a harmonic mean of 24.9 individuals (Figure 2 and Table 2). The small effective number of breeders was exacerbated by the large variance in family size among broodstock fish (Supplementary Figure S1). In general, there was very good agreement (r2=0.79) between effective number of breeders estimated with pedigree and LD-based methods (Table 2 and Supplementary Figure S2). Although hatchery and wild fish were passed above the dam in approximately equal numbers, all the hatchery fish descended from a handful of breeders, while the wild fish descended from several hundred parents (harmonic mean Nb for wild fish=373, see also Araki et al., 2007c). The low hatchery Nb created many noticeable differences between hatchery and wild fish. The point estimates for FST between hatchery fish brood-years are an order of magnitude greater than between wild fish brood-years (Figure 3). None of the qualitative results differed between FST and GST; however, GST values were approximately an order of magnitude greater than FST (Supplementary Table S1 and Supplementary Table S2).

Figure 2.

Figure 2

Open in a new tab

Genetic bottlenecks created by the supplementation program. Triangles (‘Wild Fish') represent the total number of wild fish passed over the dam for 11 consecutive years. Circles (‘Broodstock') are the total number of wild fish removed from the run and used in the supplementation program. Squares (‘Nb Broodstock') are the effective number of broodstock breeders calculated using pedigree data. The × represents the average effective number of breeders for the wild population as calculated in Araki et al. (2007c). Diamonds (‘Offspring') represent the total number of hatchery offspring assigned to the broodstock from a given run-year. Notice that the ordinate is on a logarithmic scale and that solid lines connect years. A full color version of this figure is available at the Heredity journal online.

Table 2. Point estimates for the effective number of breeders estimated with LDNe and associated 95% confidence intervals (Jackknife CI) for hatchery and wild fish by brood-year (Also presented are the pedigree-based estimates for the effective number of breeders for hatchery fish (Pedigree)).

Brood-year Hatchery fish
Wild fish
  Pedigree LDNe Jackknife CI LDNe Jackknife CI
1993 16.5 23.6 21.7 25.7 222.4 196.9 251.6
1994 32.5 30.3 27.8 32.9 285.5 232.9 362.2
1995 25.0 22.2 20.0 24.6 180.1 157.3 208.2
1996 18.9 21.2 19.2 23.3 250.3 230.5 271.8
1997 34.3 30.7 28.1 33.6 426.6 372.7 491.6
1998 30.2 29.1 27.2 31.1 517.2 452.2 600.1
1999 36.7 38.7 35.3 42.2 588.9 500.1 710.4
2000 17.6 21.6 20.2 23.1 663.6 559.6 808.9
2001 26.6 27.8 25.3 30.5 577.3 492.0 694.4
2002 32.1 33.2 29.3 37.6 650.4 497.0 922.7
2003 30.1 27.7 24.7 30.9 866.1 604.9 1468.9
Open in a new tab

Figure 3.

Figure 3

Open in a new tab

Principal coordinates analysis of pairwise FST between all brood-years of hatchery and wild fish. Circles represent wild fish and squares represent hatchery fish. Notice that the FST between hatchery brood-years is substantially greater than wild brood-years owing to the small effective number of breeders. A full color version of this figure is available at the Heredity journal online.

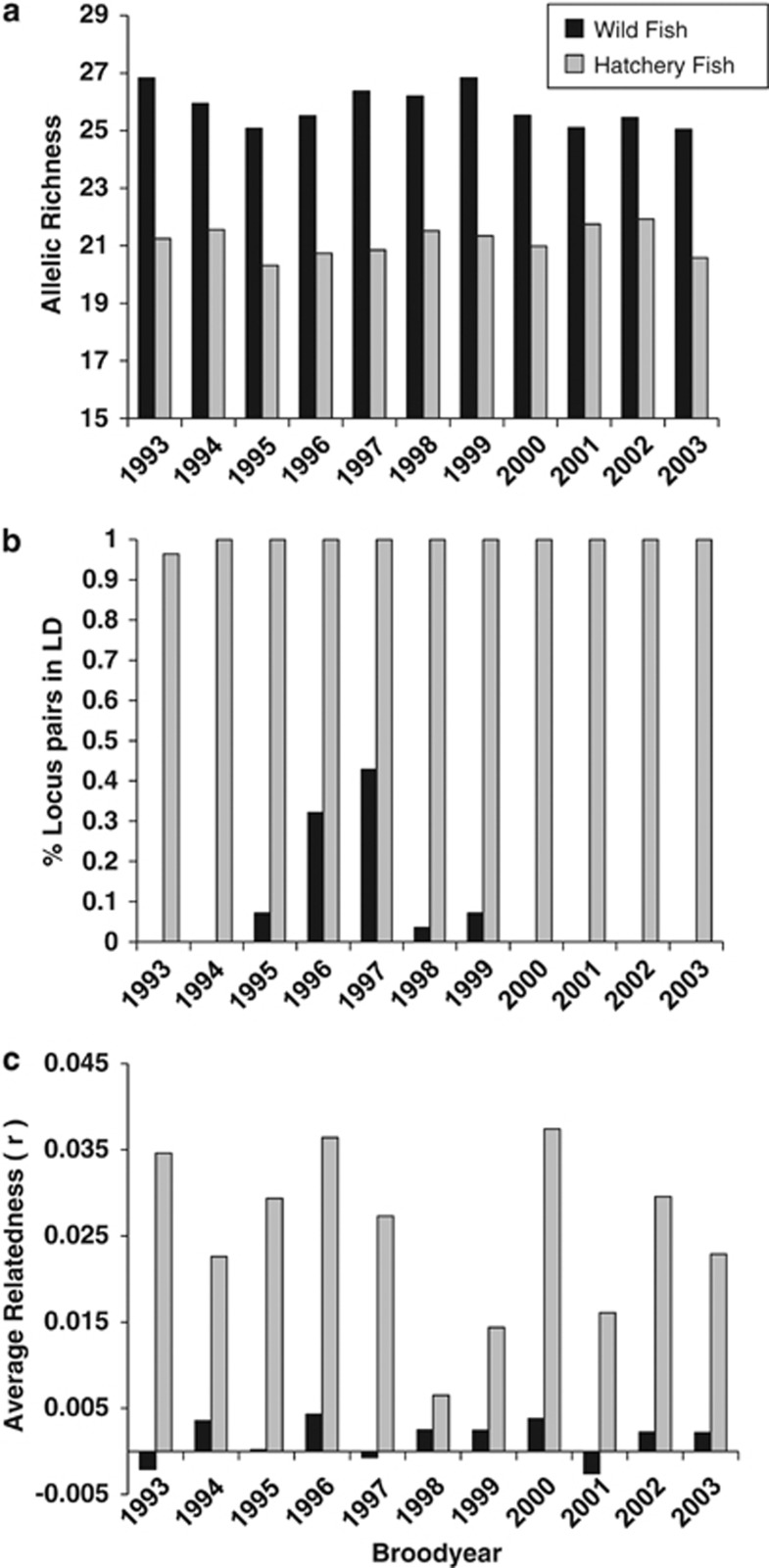
The average allelic richness of hatchery fish was substantially lower than wild fish across all brood-years (Figure 4a). Permutation-based tests revealed that allelic richness (P<0.0002) and within-sample gene diversity (P<0.0004) were significantly lower in hatchery fish than wild fish. Observed heterozygosity was not significantly different between the two groups (P=0.113). Furthermore, out of 11 brood-years examined, 99.9% of loci pairs were in LD for hatchery fish, compared with an average of 8% for wild fish (Figure 4b). In all years, there were slightly more wild fish than hatchery fish, which eliminates a potential bias for statistical tests finding greater numbers of loci pairs in LD for hatchery fish. Importantly, the brood-years for which wild fish had a noticeable percentage of loci pairs in LD corresponded with the return of the first generation of hatchery fish that mated in the wild. The large amount of LD present in hatchery fish is due to low Nb in the returning hatchery fish (Hedgecock et al., 2007) and is further reflected in elevated levels of relatedness in hatchery fish compared with wild fish (Figure 4c). Results from permutation tests revealed that all hatchery estimates of relatedness were significantly greater than wild estimates. The average relatedness of all hatchery fish equaled 0.025, which is equivalent to third-cousins. FIS values were not substantially different between wild and hatchery fish (≈0.01 in both groups).

Figure 4.

Figure 4

Open in a new tab

Differences between wild (black bars) and hatchery (gray bars) fish as a consequence of the low effective number of breeders used to create hatchery fish. (a) Allelic richness (averaged across loci) in hatchery fish was lower than wild fish. Hatchery fish also had a much greater percentage of locus pairs in LD than wild fish (b). (c) illustrates that the average relatedness of hatchery fish was substantially greater than wild fish.

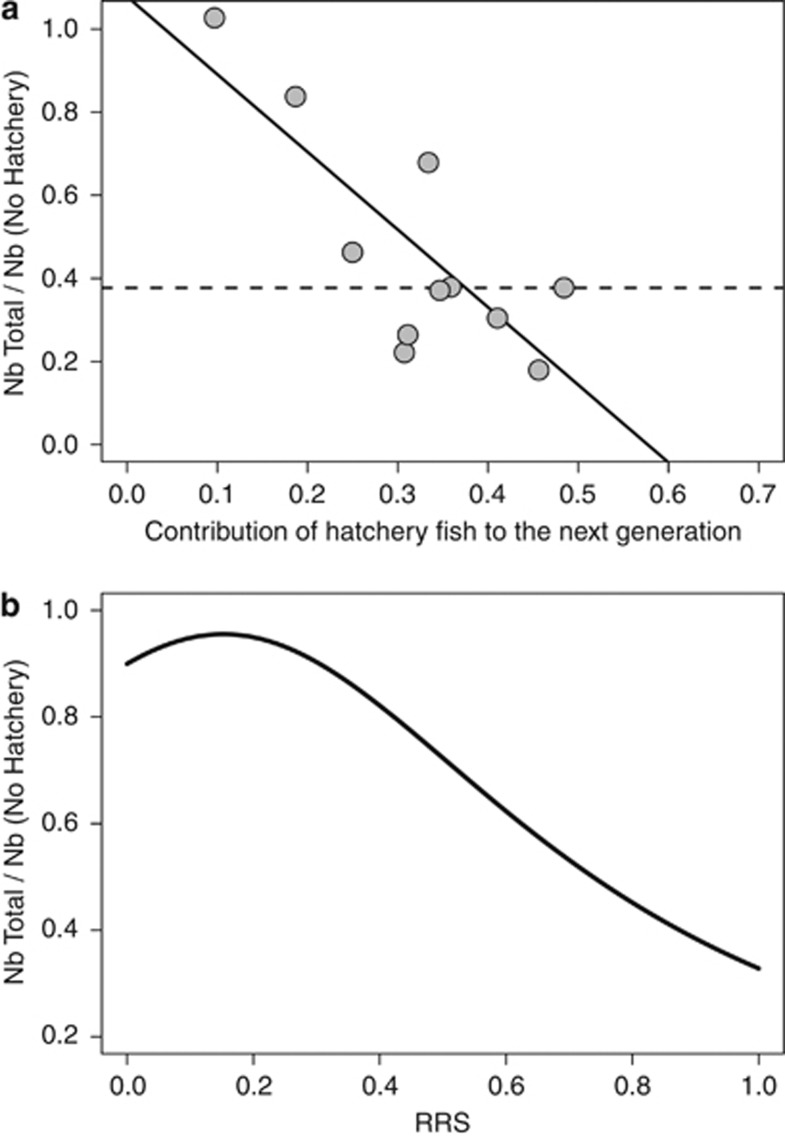
We also documented a Ryman–Laikre effect (Table 3), in which the effective population size of the entire population is reduced due to the hatchery program. On taking the harmonic mean for 11 brood-years and setting the RRS equal to 1, the effective number of breeders for the entire population was 36.5% of the effective number of breeders for wild fish alone despite a near doubling of the total population size. This percentage was reduced to 32.8% when we estimated the effective number of breeders for the wild population had no wild fish been brought into the hatchery (see harmonic means for NeT and NNo Hatchery in Table 3, which were simply divided to obtain these percentages). These percentages changed to 46.3% and 41.6%, respectively, when the population-specific RRS estimate of 0.85 was used (See Table 3 for harmonic means). In brood-year 1996, there was no evidence for a Ryman–Laikre effect, which was the brood-year for which, relative to wild fish, the fewest hatchery fish were allowed onto the spawning grounds. In fact, we found a strong negative relationship (r2=0.65) between the contribution of hatchery fish to the next generation and the reduction in the effective number of breeders for the combined hatchery and wild population (Figure 5a). We also demonstrated, in this population, that a higher reproductive success of hatchery fish resulted in a stronger Ryman–Laikre effect (Figure 5b). Using a wide range of theoretical values for Nc, Nw, RRS, and the proportion of hatchery fish allowed onto spawning grounds, we further illustrate that the Ryman–Laikre effect is most pronounced when (i) the effective number of broodstock breeders is low relative to the wild, (ii) the proportion of hatchery fish allowed onto spawning grounds is high, and (iii) the RRS of hatchery fish is high (Supplementary Figure S3).

Table 3. Estimates of the effective number of breeders with (NeT) and without (NNo Hatchery) a supplementation program.

Brood-year Nc Nw NNo Hatchery XRRS=1 NeTRRS=1 XRRS=0.85 NeTRRS=0.85
1993 16.5 222.4 266.5 0.43 78.9 0.37 100.9
1994 32.5 285.5 318.5 0.58 91.8 0.49 120.1
1995 25.0 180.1 208.9 0.40 118.8 0.34 141.7
1996 18.9 250.3 257.8 0.12 258.5 0.10 264.6
1997 34.3 426.6 456.4 0.23 343.6 0.19 382.1
1998 30.2 517.2 545.0 0.42 156.4 0.35 202.0
1999 36.7 588.9 618.1 0.49 142.7 0.42 187.9
2000 17.6 663.6 717.8 0.37 119.9 0.31 158.6
2001 26.6 577.3 652.9 0.54 86.8 0.46 116.8
2002 32.1 650.4 746.0 0.30 278.9 0.26 345.0
2003 30.1 866.1 973.1 0.37 196.1 0.32 256.8
H Mean 25.4 373.5 415.2 — 136.3 — 172.9
Open in a new tab

NNo Hatchery equals the estimated effective number of breeders had there been no hatchery supplementation program and NeT equals the total effective number of breeders for both wild and hatchery fish considered jointly with relative reproductive success values of 1 and 0.85 (RRS; hatchery relative to wild). Also presented is ‘x', the contribution of hatchery fish to the next generation, and point estimates for the effective number of breeders for the captive (Nc [Pedigree]), and wild fish per brood-year (Nw[LDNe]). Where appropriate, we report the harmonic mean (Mean) for all brood-years.

Figure 5.

Figure 5

Open in a new tab

Illustration of a substantial Ryman–Laikre effect. The ordinate equals the total effective number of breeders (hatchery and wild fish pooled; Nb Total) divided by the effective number of breeders for the population had no hatchery program been implemented (Nb No Hatchery). Thus the ordinate equals the magnitude of the Ryman–Laikre effect (with smaller values equating to a stronger effect). (a) Relationship between the contribution of hatchery fish to the next generation (see Equation (4)) and the Ryman–Laikre effect for 11 brood-years. The dashed line represents the median ordinate value for all years. RRS was fixed at 0.85 such that the contribution of hatchery fish directly reflects the proportion of hatchery fish allowed onto the spawning grounds. (b) Relationship between relative reproductive success of hatchery fish (RRS) and the Ryman–Laikre effect. For visual clarity, we took the harmonic mean of Nb Total and the harmonic mean of Nb No Hatchery across all 11 brood-years to generate a single point estimate for each distinct RRS value.

Discussion

For this Hood River steelhead population, we demonstrate that the effective number of breeders in the supplementation program can be surprisingly low (harmonic mean across years=25 fish). In each cohort of hatchery fish, we also observed lower genetic diversity, higher relatedness, substantial fluctuations in allele frequencies and extensive LD in comparison with wild-born fish. Increased rates of drift could contribute to fitness declines in fish from multi-generation or conventional hatchery programs (for example, owing to random fixation of deleterious alleles). The comparatively low amount of drift among brood-years of wild fish is likely due to the much larger effective number of breeders in the wild and the wild brood-years consisting of offspring from a greater number of run-years.

We also documented a substantial Ryman–Laikre effect in 10 of 11 brood-years. This effect revealed that although the supplementation program doubled the total number of breeding adults in the river each year, it cut the effective population size to roughly one-third of what it would have been had there been no hatchery supplementation program. We further illustrated that allowing more than one hatchery fish for every 10 returning wild fish onto the spawning grounds led to a substantial reduction in the overall effective number of breeders (Table 3). This result is due to the effective number of breeders for hatchery fish equaling about one-tenth of the total effective number of breeders. Clearly, if the goals of supplementation are to bolster the wild population, then allowing only one hatchery fish access to the spawning grounds per 10 wild fish will yield little demographic benefit considering that an equivalent number of wild fish were removed from the population to be used as broodstock. Allowing more hatchery fish onto the spawning grounds, however, would decrease the effective population size, which is also at odds with conservation goals. Although it often occurs, the practice of allowing all returning hatchery fish onto spawning grounds without the careful monitoring of important genetic parameters (for example, Nb) could have large impacts on the long-term conservation of that population (for example, genetic variation important for future adaptation could be rapidly reduced).

In this population, we further documented that the effective size of the total population decreased as the reproductive success of the returning hatchery fish increased, which is due to hatchery fish with higher reproductive success having a greater contribution to subsequent generations (see Equation (3)). This result is also at odds with the goals of some supplementation programs, which aim to create fish that have reproductive success equal to their wild counterparts. Here we show that if supplementation programs meet that goal, then they may be unintentionally decreasing the effective population size. These results make it apparent that any supplementation program will involve some inherent trade-offs. Explicitly accounting for the demographic, genetic and societal costs and benefits of supplementation could pave the way for more prudent management actions.

Our results illustrate in a practical example some of the general outcomes implied by the Ryman–Laikre equation (see Equation (3) and Supplementary Figure S3), which is determined by the effective number of hatchery and wild breeders (Nb) and ‘x', the contribution of hatchery fish to the next generation. Some points to keep in mind about the Ryman–Laikre effect are that: (1) if Nb/N in the hatchery is less than or equal to Nb/N in the wild, then NeT (the combined wild and hatchery effective size) can never be larger than it would be without the program; (2) if Nb/N is higher in the hatchery than in the wild, then it may be possible to actually increase NeT via supplementation. This could be accomplished by equalizing variance in family sizes in the hatchery. However, this benefit would only be realized if the hatchery contribution to the next generation, ‘x', is fairly low; (3) ‘x' should be calculated by taking the relative reproductive success of hatchery fish into account (see Equation (4)), because what matters most is the fraction of genes in the next generation that come from hatchery fish; and (4) the effect of RRS on NeT increases as the proportion of hatchery fish relative to wild fish allowed access to spawning grounds is increased (Supplementary Figure S3). Thus, in order to balance demographic gains with the loss of genetic diversity, supplementation programs may be most useful for a quick demographic boost, when wild returns are very low, and when the programs are only implemented for a short period of time (Waples, 2004).

Our results also suggest several additional management practices that might be considered. Supplementation programs create two large bottlenecks, each corresponding to a reduction in the number of breeders (Figure 2). The first bottleneck occurs simply by choosing a limited number of individuals for broodstock. The second bottleneck is created by the large variance in reproductive success among those hatchery broodstock (Supplementary Figure S1). As mentioned above, deliberately equalizing the variance in reproductive success among broodstock could help to increase the genetic diversity of hatchery fish without taking more breeders from the wild. Equalizing family sizes should also reduce the rate of domestication (Allendorf, 1993; Christie et al., 2012). Of course, any variation in survival that occurs after smolts are released will generally be beyond the control of managers (for example, Reisenbichler et al., 2004). In this study, the 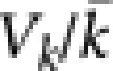Inline graphic was surprisingly large—similar to that observed among breeders in wild populations. Furthermore, broodstock family sizes were not correlated with eggs used per female or any other phenotypic trait of the parents that we could measure (that is, length, weight, age and run-timing; Christie et al., 2012). Thus, determining the cause of the high variance in family size in each brood-year of hatchery fish would be particularly useful. Another practice that could mitigate the Ryman–Laikre effect would be to spread the contribution of a single brood-year over multiple release years. For example, it might be beneficial to exclude the first year of returning hatchery fish onto the spawning grounds (which come from a single brood-year), and there might be merit in allowing a portion of hatchery steelhead take 2 years to smolt in the hatchery (1 year is typical hatchery practice).

In conclusion, we found that a contemporary supplementation program greatly reduced the effective size of a wild population. These results further illustrate that different conservation goals can be at odds with each other in a supplementation program. For example, the small Nb of hatchery fish created in a supplementation program can have unintended genetic consequences, but bringing more wild individuals into the breeding program can also have negative consequences for the population. Furthermore, adding more hatchery fish to the population may temporarily increase the census size, but can drastically decrease the effective population size. Thus, we recommend that (1) programs that release large numbers of captive-born individuals into the wild be rigorously monitored, and that (2) more consideration be given to balancing the competing goals of increasing the census size of the population (while minimizing domestication) and preserving the wild population's genetic diversity.

Data archiving

R scripts for performing parentage analyses are available for download at https://sites.google.com/site/parentagemethods/. Hatchery genotypes and associated scale-ageing data can be found at dryad: doi:10.5061/dryad.2g257.

Acknowledgments

The views and opinions presented here are solely those of the authors and do not necessarily represent those of his/her employers. We thank William Ardren, Becky Cooper, Vindhya Amarasinghe, Jeff Stephenson, and the Oregon State Center for Genome Research and Biotechnology for their advice and help with lab protocols and genotyping efforts. We are especially grateful to all ODFW staff that collected data and acquired tissue samples for this extensive data set. We also thank Hitoshi Araki, Lyle Curtis and two anonymous reviewers for their helpful comments and discussions. This research was funded by grants from the Bonneville Power Administration to Michael Blouin.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Information
Click here for additional data file. (366.5KB, doc)

References

  1. Allendorf FW (1993). Delay of adaptation to captive breeding by equaling family size. Conserv Biol 7: 416–419. [Google Scholar]
  2. Araki H, Ardren WR, Olsen E, Cooper B, Blouin MS (2007b). Reproductive success of captive-bred steelhead trout in the wild: evaluation of three hatchery programs in the Hood River. Conserv Biol 21: 181–190. [DOI] [PubMed] [Google Scholar]
  3. Araki H, Cooper B, Blouin MS (2007a). Genetic effects of captive breeding cause a rapid, cumulative fitness decline in the wild. Science 318: 100–103. [DOI] [PubMed] [Google Scholar]
  4. Araki H, Cooper B, Blouin MS (2009). Carry-over effect of captive breeding reduces reproductive fitness of wild-born descendants in the wild. Biol Lett 5: 621–624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Araki H, Waples RS, Ardren WR, Cooper B, Blouin MS (2007c). Effective population size of steelhead trout: influence of variance in reproductive success, hatchery programs, and genetic compensation between life-history forms. Mol Ecol 16: 953–966. [DOI] [PubMed] [Google Scholar]
  6. Augerot X, Foley DN (2005) Atlas of Pacific salmon: the first map-based status assessment of salmon in the North Pacific. University of California Press: Los Angeles. [Google Scholar]
  7. Berntson EA, Carmichael RW, Flesher MW, Ward EJ, Moran P (2011). Diminished reproductive success of steelhead from a hatchery supplementation program (Little Sheep Creek, Imnaha Basin, Oregon). Trans Am Fish Soc 140: 685–698. [Google Scholar]
  8. Busby PJ, Wainwright TC, Bryant GJ, Lierheimer LJ, Waples RS, Waknitz FW et al (1996). Status review of West Coast steelhead from Washington, Idaho, Oregon, and California. Technical Memorandum NMFS-NWFSC-27. Available at www.nwr.noaa.gov.
  9. Caballero A (1994). Developments in the prediction of effective population size. Heredity 73: 657–679. [DOI] [PubMed] [Google Scholar]
  10. Christie MR (2010). Parentage in natural populations: novel methods to detect parent-offspring pairs in large data sets. Mol Ecol Resour 10: 115–128. [DOI] [PubMed] [Google Scholar]
  11. Christie MR, Marine ML, Blouin MS (2011). Who are the missing parents? Grandparentage analysis identifies multiple sources of gene flow into a wild population. Mol Ecol 20: 1263–1276. [DOI] [PubMed] [Google Scholar]
  12. Christie MR, Marine ML, French RA, Blouin MS (2012). Genetic adaptation to captivity can occur in a single generation. Proc Natl Acad Sci 109: 238–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Crow JF, Kimura M (1970) An Introduction to Population Genetics Theory. Harper & Row: New York. [Google Scholar]
  14. ESA salmon listings (2009) NOAA Endangered Species Act Status of West Coast Salmon & Steelhead. Available at http://www.nwr.noaa.gov/ESA-Salmon-Listings/upload/1-pgr-8-11.pdf.
  15. Goudet J (1995). FSTAT (Version 1.2): A computer program to calculate F-Statistics. J Hered 86: 485–486. [Google Scholar]
  16. Gustafson RG, Waples RS, Myers JM, Weitkam LA, Bryant GJ, Johnson OW et al (2007). Pacific salmon extinctions: quantifying lost and remaining diversity. Conserv Biol 21: 1009–1020. [DOI] [PubMed] [Google Scholar]
  17. Hedgecock D, Launey S, Pudovkin A, Naciri Y, Lapègue S, Bonhomme F (2007). Small effective number of parents (Nb) inferred for a naturally spawned cohort of juvenile European flat oysters, Ostrea edulis. Mar Biol 150: 1173–1182. [Google Scholar]
  18. Kostow K (2009). Factors that contribute to the ecological risks of salmon and steelhead hatchery programs and some mitigating strategies. Rev Fish Biol Fish 19: 9–31. [Google Scholar]
  19. Laikre L, Schwartz MK, Waples RS, Ryman N (2010). Compromising genetic diversity in the wild: unmonitored large-scale release of plants and animals. Trends Ecol Evol 25: 520–529. [DOI] [PubMed] [Google Scholar]
  20. McClure MM, Holmes EE, Sanderson BL, Jordan CE (2003). A large-scale, multispecies status assessment: anadromous salmonids in the Columbia River basin. Ecol Appl 13: 964–989. [Google Scholar]
  21. Meirmans PG (2006). Using the AMOVA framework to estimate a standardized genetic differentiation measure. Evolution 60: 2399–2402. [PubMed] [Google Scholar]
  22. Naish KA, Taylor JE, Levin PS, Quinn TP, Winton JR, Huppert D et al (2008). An evaluation of the effects of conservation and fishery enhancement on wild populations of salmon. In: Sims HW, (ed.). Advances in Marine Biology. Academic Press: The Netherlands. [DOI] [PubMed] [Google Scholar]
  23. Olsen EA (2003) Hood River and Pelton ladder evaluation studies Annual report 2000–2001 of the Oregon Department of Fish and Wildlife Oregon Department of Fish and Wildlife: Portland, OR. [Google Scholar]
  24. Peakall R, Smouse PE (2006). Genalex 6: genetic analysis in Excel. Population genetic software for teaching and research. Mol Ecol Notes 6: 288–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Pemberton JM (2008). Wild pedigrees: the way forward. Proc R Soc Biol Sci 275: 613–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Queller DC, Goodnight KF (1989). Estimating relatedness using genetic markers. Evolution 43: 258–275. [DOI] [PubMed] [Google Scholar]
  27. Quinn TP (2005) The Behavior and Ecology of Pacific Salmon and Trout. University of Washington Press: Seattle. [Google Scholar]
  28. R Development Core Team (2011) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org. [Google Scholar]
  29. Raymond M, Rousset F (1995). GENEPOP (Version 1.2): Population Genetics Software for Exact Tests and Ecumenicism. J Hered 86: 248–249. [Google Scholar]
  30. Reisenbichler RR, Rubin SP, Wetzel L, Phelps SR (2004). Natural selection after release from a hatchery leads to domestication in steelhead, Oncorhynchus mykiss. In: Leber KM, Blankenship HL, Kitada S, Svåsand T, (eds). Stock Enhancement and Sea Ranching: Developments, Pitfalls, and Opportunities 2nd edn. Blackwell Science Ltd.: Oxford. pp 371–383. [Google Scholar]
  31. Ryman N, Jorde PE, Laikre L (1995). Supportive breeding and variance effective population size. Conserv Biol 9: 1619–1628. [Google Scholar]
  32. Ryman N, Laikre L (1991). Effects of supportive breeding on the genetically effective population Size. Conserv Biol 5: 325–329. [Google Scholar]
  33. Seamons TR, Dauer MB, Sneva J, Quinn TP (2009). Use of parentage assignment and DNA genotyping to validate scale analysis for estimating steelhead age and spawning history. N Am J Fisheries Manage 29: 396–403. [Google Scholar]
  34. Theriault V, Moyer GR, Jackson LS, Blouin MS, Banks MA (2011). Reduced reproductive success of hatchery coho salmon in the wild: insights into likely mechanisms. Mol Ecol 20: 1860–1869. [DOI] [PubMed] [Google Scholar]
  35. Thioulouse J, Chessel D, Dole'dec S, Olivier JM (1997). ADE-4: a multivariate analysis and graphical display software. Stat Comput 7: 75–83. [Google Scholar]
  36. Waples RS (1999). Dispelling some myths about hatcheries. Fisheries 24: 12–21. [Google Scholar]
  37. Waples RS (2004). Salmonid insights into effective population size. In: Hendry AP, Stearns SC, (eds). Evolution Illuminated: Salmon and Their Relatives. Oxford University Press: Oxford, UK. pp 295–314. [Google Scholar]
  38. Waples RS, Do C (2008). LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Resour 8: 753–756. [DOI] [PubMed] [Google Scholar]
  39. Waples RS, Teel DJ (1990). Conservation genetics of Pacific salmon I. Temporal changes in allele frequency. Conserv Biol 4: 144–156. [Google Scholar]
  40. Williamson KS, Murdoch AR, Pearsons TN, Ward EJ, Ford MJ (2010). Factors influencing the relative fitness of hatchery and wild spring Chinook salmon (Oncorhynchus tshawytscha) in the Wenatchee river, Washington, USA. Can J Fish Aquat Sci 67: 1840–1851. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (366.5KB, doc)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES