GPU/CPU Algorithm for Generalized Born/Solvent-Accessible Surface Area Implicit Solvent Calculations

Abstract

Molecular dynamics methodologies comprise a vital research tool for structural biology. Molecular dynamics has benefited from technological advances in computing, such as multi-core CPUs and graphics processing units (GPUs), but harnessing the full power of hybrid GPU/CPU computers remains difficult. The generalized Born/solvent-accessible surface area implicit solvent model (GB/SA) stands to benefit from hybrid GPU/CPU computers, employing the GPU for the GB calculation and the CPU for the SA calculation. Here, we explore the computational challenges facing GB/SA calculations on hybrid GPU/CPU computers and demonstrate how NAMD, a parallel molecular dynamics program, is able to efficiently utilize GPUs and CPUs simultaneously for fast GB/SA simulations. The hybrid computation principles demonstrated here are generally applicable to parallel applications employing hybrid GPU/CPU calculations.

Introduction

Laboratory and clinical studies of living cells are increasingly complemented by computational atomic level modeling of cellular processes.^1-8 In fact, modeling has developed today into a computational microscope⁹ used to explore nanoscale structures and processes in structural cell biology^10-12, cellular mechanics,^9,13,14 and nanosensor development.^15,16 Small size and short time scales of many sub-cellular processes challenge experimental methodologies, making the molecular dynamics computational microscope an ideal supporting tool for biological research.

Molecular dynamics (MD) has already enabled, in particular, modeling of health-relevant biomolecular systems and processes, e.g., viral infection,^17,18 interactions between tissues and therapeutics,^1,2 blood coagulation,^13,19-25 and amyloid fibril formation.^26-31 Often, however, simulation time scales are too short to be of value; only by continually adopting the latest computing technologies can simulation speeds increase, and extend the reach of MD to the millisecond scale³² that is necessary to describe many cellular processes.

MD simulations calculate interatomic forces of biopolymer systems and solve the classical equations of motion for each time step,³³ to explore the dynamic behavior of biological systems. The largest computational expense in MD simulations stems from calculating so-called “non-bonded” interactions, forces between atoms which are not covalently bonded, comprising Coulomb and van der Waals forces.

The calculation of non-bonded forces is highly amenable to parallel computing^33,34 because the modeled interaction between two atoms is independent of all other atoms; thus, atom-pair interactions can be calculated independently from one another, then accumulated to determine net atomic forces. Such independent calculations offer a high degree of concurrency, making them ideal for parallel computing.³⁵ Indeed, NAMD successfully conducted recently a 100,000,000-atom MD simulation on 200,000 CPU cores.³⁶ Along with multi-core CPUs, MD programs have also harnessed new computing technologies such as graphics processing units (GPUs).^37,38

Graphics processing units

Though originally developed only for interactive graphics rendering, GPUs are well suited for accelerating general scientific calculations. A single GPU may today contain 16 multiprocessors, each with 32 cores, yielding 512 cores per GPU. Maximizing the use of such highly parallel processors requires meeting strict criteria such as coalescing access to slow memory and issuing 10,000s of independent calculations. Because many molecular biological calculations can meet the strict criteria, GPUs have been used to accelerate biological computing applications such as molecular modeling,³⁹ electrostatic calculations,^37,40 molecular orbital display⁴¹ and simulations of protein diffusion in whole cells.⁴²

The application of GPUs to molecular dynamics⁴³ has already demonstrated significant performance benefits⁴⁴ for both explicit solvent^38,45 and implicit solvent^46,47 models. Each implementation varies in the use of the GPU, ranging from employing the GPUs for calculating forces only³⁸ to using them to integrate the equations of motion^48,49 as well. GPU implementations also vary in regard to how restrictive they are of the MD methodologies they admit; for example, some implementations allow a non-bonded interaction cut-off length³⁷ which is common for large systems, while others do not,⁴⁶ thereby being applicable only to small systems.

The great success already achieved in accelerating full molecular dynamics calculations with GPUs inspires additional work in advancing MD calculations which involve both GPU-accelerated calculations and CPU calculations (those not yet adapted to the GPU) as they arise in, for example, steering⁵⁰ or grid potentials.⁵¹ Prior efforts at GPU-acceleration of MD simulations had adapted almost all of the computation to the GPU, the CPU’s role remaining secondary.^48,49

Hybrid GPU/CPU computing

Each GPU requires a so-called host CPU to send data to and receive data from the GPU as well as instruct the GPU as to which calculations to perform. Therefore, a necessary and difficult component of hybrid GPU/CPU calculations is allowing host CPUs to switch between GPU-hosting responsibilities and performing their own scientific calculations. Because many existing MD methods have not yet been adapted to GPUs, or are not amenable to GPU calculation, it is vital to explore how to efficiently perform hybrid calculations which require full use of both GPUs and CPUs and which, therefore, require coordination between the two.

An ideal application for hybrid computing is the generalized Born (GB) implicit solvent with solvent-accessible surface area (SASA or SA) calculation, commonly abbreviated GB/SA. A GB/SA implicit solvent simulation employs the GB calculation to account for the polar, i.e., hydrophilic, effects of water while the SA calculation models the nonpolar, i.e., hydrophobic, effects.⁵² It is known that the hydrophobic free energy of solvation is approximately equal to the product of the molecular surface area and a surface tension parameter.^53,54 The GB/SA calculation consists of three classes of non-bonded interatomic forces: the classical Coulomb and van der Waals forces, the generalized Born^53,55,56 (GB) force, and the solvent-accessible surface area (SA) force, calculated via the linear combination of pairwise overlaps⁵⁴ (LCPO) algorithm, as in the Amber MD program.⁵⁷ While the Coulomb, van der Waals and GB force calculations are being calculated on the GPU, the LCPO algorithm’s SA calculation is best performed on the CPU, thus making the GB/SA calculation an ideal candidate for hybrid GPU/CPU calculation.

The present work explores a variety of performance and functionality issues relevant to GPU accelerated calculations of the GB/SA implicit solvent model in the context of the NAMD parallel MD program.³³ First, we analyze the necessary non-bonded force calculations and describe why each is best suited for GPUs or CPUs. Second, we outline NAMD’s algorithmic strategy for GB/SA calculations on hybrid GPU/CPU computers. Finally, we explore the effect of the surface tension parameter as well as demonstrate the performance of the hybrid strategy through ~250 benchmark simulations.

Methods

The generalized Born/solvent-accessible surface area (GB/SA) implicit solvent model constitutes a fast representation of a solvent’s polar and nonpolar effects on biomolecules.⁵³ Fast simulation speed can be attained by calculating the Coulomb, van der Waals and generalized Born (GB) forces on the GPU while simultaneously calculating the hydrophobic surface area (SA) force on the CPU. First, we present the equations arising in the Coulomb, van der Waals, GB and SA force calculations which motivate the hybrid GPU/CPU algorithm employed. Then, NAMD’s implementation of the various calculations will be described.

Coulomb and van der Waals forces

The non-bonded forces arising in explicit and implicit solvent simulations are the Coulomb and van der Waals (calculated using the Lennard-Jones description) forces. The total system energy contributed by Coulomb and van der Waals interactions, $E_{\text{T}}^{\text{CW}}$, is

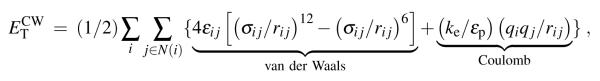(1)

where ε_ij is the well depth and 2^1/6σ_ij equilibrium interaction length parameters of the Lennard-Jones potential, r_ij is the distance between atoms i and j, k_e = 332 kcal Å/e² the Coulomb constant, ε_p = 1 the dielectric constant of the protein interior and q_i the atomic charge; N(i) is the set of all neighbors, j, that are within the interaction cut-off, r_c, from atom i.

The net force, ${\overrightarrow{F}}_i$, on an atom is calculated as

$${\overrightarrow{F}}_i=-\sum _{j\in N\left(i\right)}(d{E}_T∕d{r}_{ij}){\widehat{r}}_{ij};$$ (2)

by applying Eq. (2) to Eq. (1), the net Coulomb and van der Waals forces on an atom, ${\overrightarrow{F}}_i^{\text{CW}}$, is

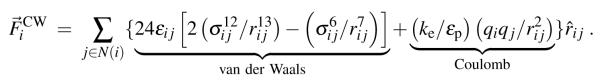(3)

The summation in Eq. (3) requires an MD program to iterate over all pairs of interacting atoms, i and j, where r_ij < r_c; the successful application of GPUs to computing atom-pair interactions, such as Coulomb and van der Waals forces, has previously been demonstrated in NAMD.^37,38

Generalized Born implicit solvent forces

The generalized Born implicit solvent model,^53,56 already implemented in NAMD for the CPU,⁵⁸ describes water as a bulk solvent acting as a dielectric;^53,56 the dielectric solvent screens,^59,60 i.e., reduces, electrostatic interactions between charged atoms. The total GB energy, i.e., hydrophilic energy of solvation, of the atomic system is given by the sum of pair- and self-energies according to

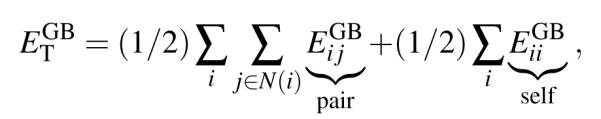(4)

where the pair- and self-GB energies are calculated according to

$$E_{ij}^{GB}=-k_e{D}_{ij}{q}_i{q}_j∕f_{ij}^{GB}.$$ (5)

Here, D_ij is an effective dielectric constant, which depends on the implicit ion concentration,^58,61 between atoms i and j, and $f_{ij}^{\text{GB}}$ is⁵³

$$f_{ij}^{GB}=\sqrt{r_{ij}^2+{\alpha }_i{\alpha }_j\text{exp}(-r_{ij}^2∕4{\alpha }_i{\alpha }_j)}.$$ (6)

The quantities α_i arising in this expression, the so-called atomic Born radii, describe an atom’s exposure to solvent and, thus, characterize the degree to which an atom’s electrostatic interaction is screened; α_i is calculated, according to Onufriev, Bashford and Case’s (OBC) description,⁵⁶ as

$${\alpha }_i={[{({\rho }_i-0.09)}^{-1}-(1∕{\rho }_i)\text{tanh}(\delta {\psi }_i-\beta {\psi }_i^2+\gamma {\psi }_i^3)]}^{-1},$$ (7)

where ρ_i is the atomic radius as parameterized by the OBC model; δ = 1, β = 0.8 and γ = 4.85 are additional dimensionless parameters of the OBC model⁵⁶ which enable calculation of the correct Born radii, i.e., those derived from Poisson-Boltzmann calculations, from the sum, ψ_i, of pairwise atomic descreening, H_ij,

$${\psi }_i=({\rho }_i-0.09)\sum _{j\in N\left(i\right)}{H}_{ij}.$$ (8)

The pairwise descreening, H_ij, between neighboring atoms i and j is given by a distance-dependent piecewise function, defined in four mutually exclusive interaction domains,

$$H_{ij}=\{\begin{array}{cc}0\hfill & (r_{ij}>r_c+{\rho }_j)\hfill \\ f_1(r_{ij},{\rho }_j,r_c)\hfill & (r_{ij}>r_c-{\rho }_j)\hfill \\ f_2(r_{ij},{\rho }_j)\hfill & (r_{ij}>4{\rho }_j)\hfill \\ f_3(r_{ij},{\rho }_j)\hfill & (r_{ij}>{\rho }_i-0.09+{\rho }_j)\hfill \\ f_4(r_{ij},{\rho }_i,{\rho }_j)\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (9)

where f_1–4 are also taken from the OBC model.⁵⁶

Because the GB energy defined in Eq. (4) depends on the interatomic distances directly, through $f_{ij}^{\text{GB}}$, and also indirectly, through α_i, calculating the GB force on an atom, ${\overrightarrow{F}}_i^{GB}$, requires multiple partial derivatives,⁵⁸ namely,

$${\overrightarrow{F}}_i^{GB}=\sum _{j\in N\left(i\right)}[(\partial E_{ij}^{GB}∕\partial f_{ij}^{GB})(d{f}_{ij}^{GB}∕d{r}_{ij})+(\partial E_T^{GB}∕\partial {\alpha }_i)(d{\alpha }_i∕d{r}_{ij})+(\partial E_T^{GB}∕\partial {\alpha }_j)(d{\alpha }_j∕d{r}_{ij})]{\widehat{r}}_{ij}.$$ (10)

Of the various required derivatives, $\partial E_{ij}^{GB}∕\partial f_{ij}^{\text{GB}}$, $\partial E_T^{GB}∕\partial {\alpha }_k$ and $d{\alpha }_k∕d{r}_{ij}$, the most expensive to calculate is $\partial E_T^{GB}∕\partial {\alpha }_k$, as it requires an additional summation over atom-pairs,

$$\partial E_T^{GB}∕\partial {\alpha }_k=(1∕2)\sum _i\sum _{j\in N\left(i\right)}[\partial E_{ik}^{GB}∕\partial {\alpha }_k+\partial E_{kj}^{GB}∕\partial {\alpha }_k]+\sum _i\partial E_{ii}^{GB}∕\partial {\alpha }_k.$$ (11)

The three summations in Eq. (8), Eq. (10) and Eq. (11), known as the three phases of the GB force calculation, require three successive iterations over all pairs of atoms each time step. The three phases compute, in order, the atomic Born radii, α_i, the partial derivatives $\partial E_T^{GB}∕\partial {\alpha }_k$, and, finally, the GB force, ${\overrightarrow{F}}_i^{GB}$.

As in the case of Coulomb and van der Waals forces, iterating over atom-pairs for the three GB phases is amenable to GPU-acceleration. Because calculating the generalized Born force as outlined in Eq. (4)-Eq. (11) is several times more computationally expensive than calculating only the Coulomb and van der Waals forces, and because GPUs are well suited for such arithmetically expensive calculations, the GB calculation stands to benefit strongly from GPU-acceleration as previously demonstrated by other MD programs.^46,47 Even for the case that the computational expense of an implicit solvent simulation is greater than that of an all-atom explicit solvent simulation, because conformational relaxation processes are usually faster in implicit solvent,⁵⁸ such a model can still yield an overall benefit to conformational sampling.

Solvent-accessible surface area forces

The generalized Born model only describes the polar, i.e., hydrophilic, energy of solvation. It is desirable to account also for the nonpolar, i.e., hydrophobic, energy of solvation through a solvent-accessible surface area (SA) calculation, as it is known that the hydrophobic solvation energy is approximately proportional to SA.^53,62 We note here that the hydrophobic energy contributes to every surface element of a protein, even those involving charged side groups; this seemingly counterintuitive issue is discussed below. The linear combination of pairwise overlaps (LCPO) is an approximate method for calculating the SA⁵⁴ and, in particular, the spatial derivatives necessary for hydrophobic force calculation.

The LCPO method,⁵⁴ which considers only non-hydrogen atoms, is founded on calculating the surface area overlap between two spheres representing atoms; for two spheres, centered on atoms i and j, with radii R_i and Rj, separated by a distance r_ij, close enough that their surfaces overlap, i.e., it must hold r_ij < R_i + Rj, the surface area of atom i overlapped by atom j, A_ij⁵⁴

$$A_{ij}=2\pi R_i[(R_i-(r_{ij}∕2)-(R_i^2-R_j^2))∕\left(2r_{ij}\right)],$$ (12)

where the radius, R_i, is the atomic van der Waals radius plus the 1.4 Å solvent probe radius.⁵⁴ According to the LCPO method, the surface area of atom i, SA_i, can be evaluated approximately by multiple overlap summations,

$$S{A}_i=p_{1,i}4\pi R_i^2+P_{2,i}\sum _{j\in N\left(i\right)}{A}_{ij}+P_{3,i}\sum _{j\in N\left(i\right)}{A}_{ij}\sum _{k\in N\left(i\right)\cap N\left(j\right)}{A}_{jk}+P_{4,i}\sum _{j\in N\left(i\right)}\left[A_{ij}\sum _{j\in N\left(i\right)}\sum _{k\in N\left(i\right)\cap N\left(j\right)}{A}_{jk}\right],$$

where k ∈ N(i)∩N(j) represents all atoms k which overlap atoms i and j, thus requiring the LCPO algorithm to iterate over atom triplets, sets of three atoms whose surfaces overlap (i.e., it must hold r_ij < R_i + R_j, r_ik < R_i + R_k, r_jk < R_j + R_k). The total molecular surface area is the sum of atomic surface areas, ${\sum }_i{\text{SA}}_i$. The four atomic parameters P_1–4i were fitted by atom type such that the LCPO algorithm most closely approximates the correct surface area as calculated by numerical methods.⁵⁴ The hydrophobic, surface area force on atom l, ${\overrightarrow{F}}_l^{\text{SA}}$, can then be calculated employing the LCPO algorithm,

$${\overrightarrow{F}}_l^{SA}=-T_S\sum _{i\in N\left(l\right)}(dS{A}_i∕d{r}_l),$$ (13)

where T_S, with units kcal/mol/Ų, is the surface tension parameter. The relatively inexpensive derivatives required for the SA force calculation within the LCPO algorithm were previously described.⁵⁴

For the above three force calculations, approximately 13% of the computational cost is due to Coulomb and van der Waals forces, 70% due to GB forces, and the remaining 17% due to SA forces. Having transferred most of the force calculation (Coulomb, van der Waals, GB) to the GPU, the CPU can perform the relatively inexpensive (17% of total) SA calculation in the same time as the GPU’s expensive (83% of total) force calculations. The SA algorithm requires iterating over all atom triplets, compared to only pairs of atoms as in the case of GB; the summation is feasible due to the low computational cost involved and because the summation over triplets can be performed well by CPUs.

Incorporating the GB/SA calculation into NAMD

To achieve a high performance implementation of the GB/SA model, formulated by Eq. (1)-Eq. (13), we thought to optimize use of hybrid GPU/CPU computers as outlined. Aside from fast performance, an ideal implementation should interfere as little as possible with NAMD’s already highly scalable internal structure.

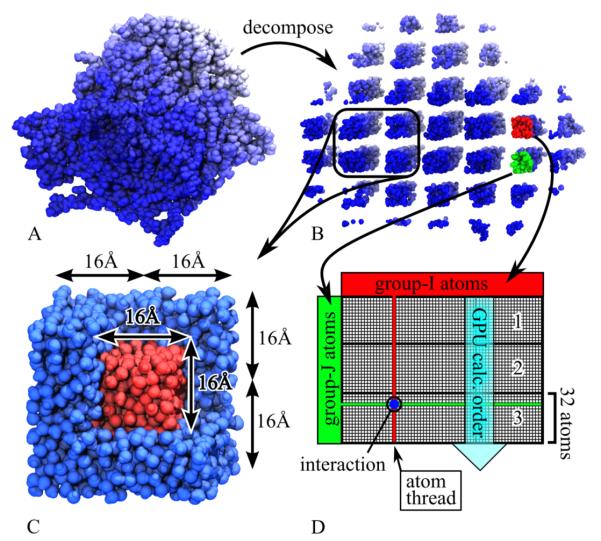
To achieve advanced parallel scaling, NAMD decomposes a simulated system (Figure 1A) into a 3D grid of atom-groups (Figure 1B). In the case of Coulomb, van der Waals and GB forces, atom-groups are defined such that atoms in any atom-group interact only with atoms of the same atom-group and with atoms of adjacent atom-groups. Calculating the atom-pair interactions between two neighboring atom-groups (Figure 1D red and green) constitutes an independent force work unit. To illustrate our GB/SA implementation, we apply NAMD to the 13,340-atom glycogen phosphorylase protein, Protein Data Bank (PDB) ID 1GPB with missing atoms placed by VMD’s⁶³ psfgen tool. The atoms of this protein system can be divided into roughly 100 atom-groups, shown in Figure 1B, and 3,000 force work units which can be assigned across hundreds of CPU cores or GPUs.^37,38

Figure 1.

Hybrid GB/SA decomposition. (A) Simulated protein glycogen phosphorylase. (B) Protein decomposed into a 3D grid of atom-groups. (C) LCPO force work unit involving a 2 × 2 × 2 set of 8 adjacent atom-groups. The force work unit calculates forces for the inner 1/8th core of atoms (red) due to overlap with neighbors (red and blue). (D) Thread block design for GB force calculation on GPU multiprocessor. Each thread (vertical line) calculates the force on one group-I atom (red) due to interactions (blue) with group-J atoms (green); group-J atoms are loaded 32 at a time, in order 1-3, for coalesced and, therefore, accelerated memory access.

GB force calculation on GPUs

NAMD has already achieved a sixfold speed-up on its 92,000-atom ApoA1 benchmark system by calculating Coulomb and van der Waals forces on the GPU using the CUDA language.^37,38 Because of the success of the Coulomb and van der Waals calculations on the GPU and the close algorithmic similarities, NAMD’s GB calculation on the GPU, outlined below, employs a similar GPU implementation as NAMD’s previously reported Coulomb and van der Waals force calculation on the GPU.^37,38

For parallel calculations, each processor core requires a list of instructions to drive computation; for both GPU and CPU processors, a “thread” is the list of instructions detailing what operations a processor core must perform; multi-core CPUs and GPUs both require multiple threads, i.e., multiple lists of instructions, to drive the many processor cores. In CUDA, a thread block is the group of threads which drives one of the GPU’s many 32-core multiprocessors.

In NAMD, a force work unit consists of calculating the atomic interactions between two atom-groups, such as group-I (red) and group-J (green) of Figure 1B and D. The calculation of the force work unit is assigned to a thread block, i.e., is calculated by a single 32-core multiprocessor, as depicted in Figure 1D. Each thread (vertical line) in the thread block calculates the force on a single atom of group-I (red) due to its interactions (blue circle) with atoms of group-J (green). To accelerate memory access, the GPU’s 32-core multiprocessors access group-J atoms 32 at a time, in order 1-3 shown in Figure 1D, and intermediately store the data in “shared” memory, a fast memory shared only by the 32 cores of a multiprocessor.

The above pattern of NAMD’s GPU calculation of Coulomb, van der Waals and GB forces exploits several features of GPU hardware to achieve fast performance. First, because adjacent threads operate on atoms adjacent in memory, reading atomic coordinates from and writing atomic forces to slow memory, is coalesced, giving significant memory speed-up over non-coalesced memory access. Second, because GPUs operate fastest when threads on a multiprocessor perform the same calculation, NAMD pre-sorts atomic coordinates before transferring them to the GPU to reduce the likelihood that threads on a multiprocessor must evaluate differing pairwise functions, f_1–4 of Eq. (9), as doing so dramatically reduces performance. Much work has previously been done exploring implementation patterns for optimal GPU performance of molecular modeling applications.^37-39,64,65

SA force calculation on CPUs

Because Eq. (13) requires iteration over all atom triplets, the LCPO calculation cannot be carried out using the structure of atom-group pairs which NAMD employs for Coulomb, van der Waals and GB force calculation, as it would be possible for a triplet of three overlapping atoms to belong to three neighboring atom-groups, in which case no atom-group pair would evaluate the triplet. Therefore, an LCPO force work unit instead consists of a 2 × 2 × 2 set of 8 adjacent atom-groups as illustrated in Figure 1C. Each LCPO force work unit calculates the surface area and hydrophobic force on the inner 1/8^th fraction of atoms (Figure 1C red) due to surface area overlaps with neighboring atoms (red and blue). LCPO force work units can also be partitioned such that the force work unit in Figure 1C is duplicated with each copy calculating forces for only a fraction of the inner core atoms (red). The ability to partition the SA calculation into many small force work units will be shown to be critical to the efficiency of the hybrid GPU/CPU algorithm.

Balancing the GPU and CPU calculations

With fast algorithms in place to perform the GB force calculation on the GPU and the SA force calculation on the CPU, the remaining obstacle of combining the two into a hybrid GB/SA calculation requires coordination of the GPU and CPU computation. First, the right balance of GPUs and CPU cores will allow the Coulomb, van der Waals and GB calculation on the GPU and the SA calculation on the CPU to be executed in the same amount of time. Second, partitioning the SA calculation into small force work units will allow the host CPU to switch between SA calculations and GPU interaction with high frequency, thereby minimizing the delay of either calculation.

Because GPUs and CPUs possess different computational power and are responsible for calculating workloads of different size, a computationally efficient simulation requires that one must first determine, through benchmarking the particular system to be simulated, an optimal ratio of CPU cores per GPU that balance the durations of GB and SA calculations. While the thorough benchmarking of our implementation provided below (see Table 2) will aid a user in judging performance a priori, the user may want to verify in case of any particular calculation if a chosen ratio of GPUs to CPU cores yields efficient performance, for example by varying the ratio and judging the resulting overall performance. In order to achieve optimal performance, it must also verified that CPU and GPU calculations overlap; the corresponding analysis will be carried out below.

Table 2.

Benchmark simulation speeds, in units seconds/time step, for the four benchmarked protein systems tested on 0-4 GPUs and 1-32 CPU cores. Speeds are reported for three increasingly accurate and expensive simulation types: in vacuo (Vacu), GB, and GB/SA. The small size of system 1YRI, see Figure 2A, prohibited utilization of 32 CPU cores in some cases.

		1YRI			2W5U			1GPB			1IR2
GPU	CPU	Vacu	GB	GB/SA	Vacu	GB	GB/SA	Vacu	GB	GB/SA	Vacu	GB	GB/SA
0	1	8.4E−3	4.9E−2	7.3E−2	4.9E−2	3.5E−1	5.2E−1	3.4E−1	2.4E+0	3.4E+0	2.3E+0	1.6E+1	2.2E+1
	2	5.7E−3	2.7E−2	4.0E−2	2.7E−2	1.8E−1	2.6E−1	1.8E−1	1.2E+0	1.7E+0	1.2E+0	9.5E+0	1.2E+1
	4	3.8E−3	1.5E−2	2.2E−2	1.4E−2	9.3E−2	1.3E−1	9.4E−2	6.2E−1	8.8E−1	5.9E−1	5.1E+0	7.2E+0
	8	2.6E−3	8.7E−3	1.3E−2	8.0E−3	4.7E−2	6.8E−2	4.8E−2	3.2E−1	4.4E−1	3.0E−1	2.1E+0	3.4E+0
	16	2.2E−3	5.6E−3	7.5E−3	4.8E−3	2.6E−2	3.7E−2	2.6E−2	1.6E−1	2.3E−1	1.6E−1	1.1E+0	1.5E+0
	32	1.7E−3	3.7E−3	4.9E−3	3.1E−3	1.4E−2	2.1E−2	1.4E−2	8.3E−2	1.2E−1	8.2E−2	5.4E−1	7.3E−1
1	1	3.6E−3	3.8E−3	3.1E−2	8.1E−3	1.1E−2	1.7E−1	4.3E−2	6.7E−2	1.0E+0	2.3E−1	4.3E−1	6.0E+0
	2	3.2E−3	4.4E−3	1.9E−2	5.0E−3	1.1E−2	8.9E−2	2.3E−2	5.8E−2	5.2E−1	1.1E−1	3.9E−1	3.1E+0
	4	2.1E−3	3.4E−3	1.2E−2	3.6E−3	9.9E−3	4.6E−2	1.4E−2	5.4E−2	2.7E−1	8.1E−2	3.5E−1	1.6E+0
	8	1.8E−3	3.3E−3	6.9E−3	2.8E−3	1.0E−2	2.7E−2	1.3E−2	5.1E−2	1.4E−1	7.5E−2	3.3E−1	8.0E−1
	16	2.1E−3	3.3E−3	4.8E−3	2.7E−3	1.1E−2	1.8E−2	1.3E−2	5.4E−2	8.1E−2	7.1E−2	3.2E−1	4.3E−1
	32				2.8E−3	8.9E−3	1.2E−2	1.2E−2	5.0E−2	6.1E−2	7.0E−2	3.2E−1	3.5E−1
2	2	3.0E−3	3.9E−3	2.0E−2	5.0E−3	9.2E−3	8.9E−2	2.4E−2	4.4E−2	5.2E−1	1.3E−1	2.6E−1	3.1E+0
	4	2.3E−3	3.4E−3	1.1E−2	3.7E−3	9.2E−3	5.0E−2	1.4E−2	3.7E−2	2.7E−1	7.1E−2	2.2E−1	1.6E+0
	8	1.8E−3	3.2E−3	7.9E−3	2.5E−3	8.6E−3	2.9E−2	1.0E−2	3.6E−2	1.4E−1	4.9E−2	2.0E−1	8.1E−1
	16	1.7E−3	3.2E−3	5.8E−3	2.7E−3	8.7E−3	1.9E−2	8.9E−3	3.8E−2	8.1E−2	4.4E−2	1.9E−1	4.0E−1
	32				2.5E−3	7.6E−3	1.3E−2	7.9E−3	3.4E−2	5.3E−2	4.4E−2	2.1E−1	2.7E−1
4	4	2.7E−3	3.4E−3	1.2E−2	3.5E−3	1.0E−2	5.0E−2	1.4E−2	3.0E−2	2.7E−1	7.2E−2	1.6E−1	1.6E+0
	8	1.8E−3	3.1E−3	1.2E−2	2.5E−3	8.1E−3	3.0E−2	8.5E−3	2.6E−2	1.4E−1	3.9E−2	1.2E−1	8.0E−1
	16	2.2E−3	3.2E−3	6.3E−3	2.6E−3	7.9E−3	2.1E−2	7.2E−3	2.8E−2	9.1E−2	2.9E−2	1.1E−1	4.1E−1
	32				2.4E−3	6.7E−3	1.2E−2	6.4E−3	2.3E−2	4.7E−2	2.7E−2	1.2E−1	2.4E−1

Simulations carried out

To analyze the performance of NAMD’s hybrid GB/SA algorithm, four test systems, differing in size, were simulated on 0-4 GPUs and 1-32 CPU cores. Figure 2 depicts the four tested systems and Table 1 lists their SA values; atoms missing in the public PDB structure files were placed by VMD’s⁶³ psfgen tool.

Figure 2.

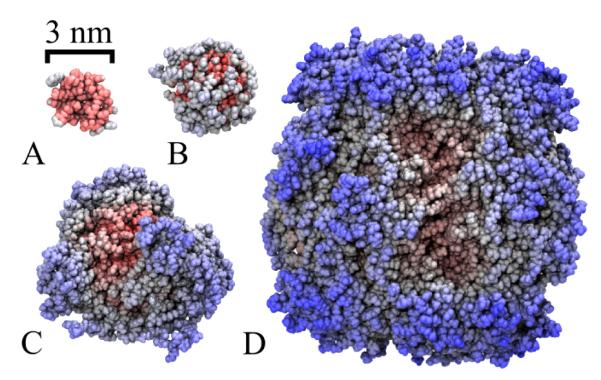
Benchmarked protein systems. (A) Villin headpiece (PDB ID 1YRI) with 582 atoms; (B) flavodoxin (PDB ID 2W5U) with 2,412 atoms; (C) glycogen phosphorylase (PDB ID 1GPB) with 13,340 atoms; (D) RuBisCO (PDB ID 1IR2) with 74,926 atoms.

Table 1.

Benchmarked protein systems. Listed are associated surface areas, in units Ų, as calculated by NAMD’s and Amber’s implementations of the LCPO⁵⁴ algorithm.

Name	PDB ID	# Atoms	NAMD SA	Amber SA
villin headpiece	1YRI	582	2,706.72	2,706.72
flavodoxin	2W5U	2,412	9,988.72	9,988.72
glycogen phosphorylase	1GPB	13,340	46,106.66	46,106.68
RuBisCO	1IR2	74,926	176,335.86	176,335.90

For benchmarking, three types of simulations were performed, each with increasing computational cost and solvent accuracy. In vacuo simulations evaluate only the Coulomb and van der Waals non-bonded forces as defined through Eq. (1)-Eq. (3), GB simulations additionally evaluate the generalized Born forces, determined through Eq. (4)-Eq. (11), and GB/SA simulations further include the SA calculation following the LCPO algorithm as stated through Eq. (12)-Eq. (13).

The following simulation parameters were employed for all simulations. A value of 16 Å was employed for the Coulomb and van der Waals interaction cut-off as well as for the GB phase 2 calculation, c.f. Eq. (11), while the GB phase 1 and 3 calculations, as defined through Eq. (8) and Eq. (10), were cut off at 14 Å. For GB and GB/SA simulations, an implicit ion concentration of 0.3 M was assumed.⁶¹ The GB/SA simulations employed a surface tension of 0.005 kcal/mol/Ų,⁶² unless otherwise specified. A time step of 2 fs was employed, requiring the SHAKE⁶⁶ algorithm to restrain covalent bonds to hydrogen atoms, with all forces being evaluated every time step.

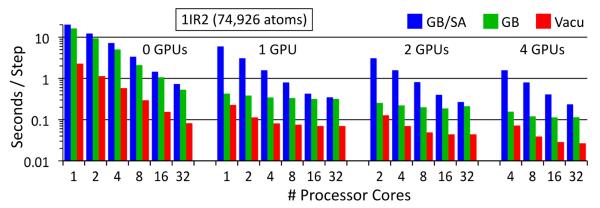
Benchmark simulations were run for 620 time steps on a 2.2 GHz 48-core AMD Opteron 6174 computer accelerated with an NVIDIA S2070 GPU system. The first 20 steps of simulation perform conjugate gradient minimization; the next 500 steps consisted of NAMD load balancing to optimize parallel performance; the simulation speed, in units seconds/time step, was averaged over the final 100 steps. Results of the benchmark simulations are presented in Figure 3 and Figure 4.

Figure 3.

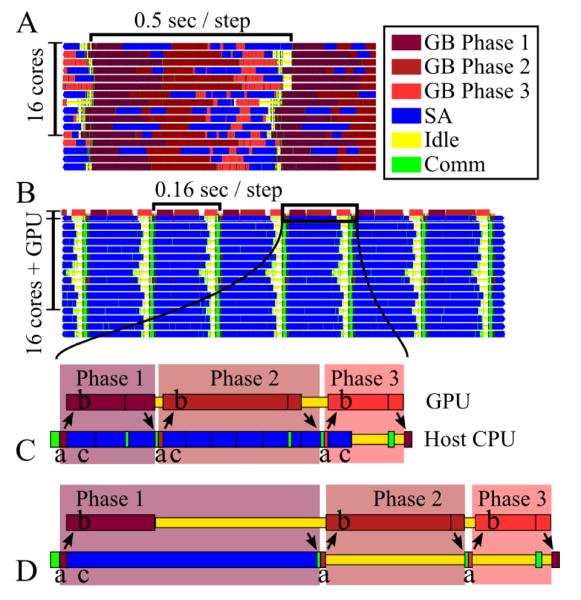
NAMD’s GB/SA calculation for the 1GPB system. (A) Performance on 16 CPUs only. (B) Performance on 16 CPUs with 1 GPU added. Colors represent calculations being performed on the processors: three phases of GB calculation (see text); SA calculation; idle time; communication. (C) Detailed view of host CPU switching between communicating with the GPU and performing the SA calculation; arrows represent the transfer of data between host CPU and GPU; for GB phase 1, 2 and 3 calculations: (a) host CPU initializes the GB calculation on the GPU; (b) GPU calculates a GB phase while (c) host CPU performs SA calculations. (D) Detailed view of how switching without SA partitioning slows performance.

Figure 4.

Simulation speed, in seconds/time step, for the 1IR2 benchmark system on 0-4 GPUs and 1-32 CPU cores; speeds for in vacuo (red), GB (green) and GB/SA (blue) calculations are shown. Both the seconds/step and processor cores axes are logarithmic.

To verify the computational accuracy of NAMD’s new GPU-accelerated GB calculation and multi-core LCPO calculation, energy and surface area calculations were compared to those of prior reference implementations.^57,58 The relative error, (E_ref − E_new)/E_ref, of NAMD’s GB energy calculation, determined through Eq. (4), on the GPU, with NAMD’s CPU implementation⁵⁸ as reference, falls below 5 × 10⁻⁶ for all four benchmark proteins. The relative error, (SA_ref − SA_new)/SA_ref, of NAMD’s surface area calculation, determined through Eq. (13), with the Amber⁵⁷ implementation as reference, falls below 4 × 10⁻⁷ for all four benchmark systems; total molecular surface areas of the four systems, as calculated by the Amber and NAMD implementations of LCPO, are listed in Table 1.

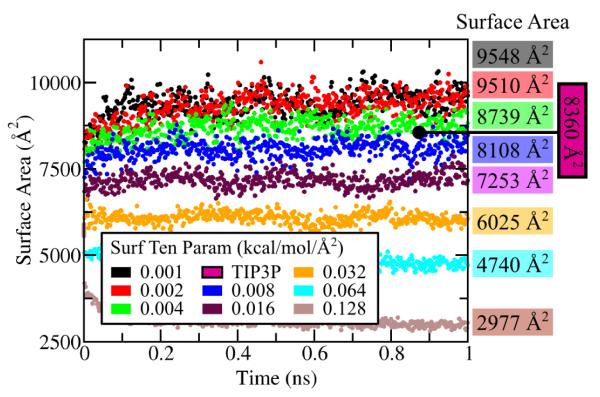
Hydrophobic solvation energy is a significant contributor to solvent behavior,^67,68 necessitating it’s inclusion along with GB calculations. The effect of the hydrophobic energy contributions, accounted for in the SA calculation, was explored by simulating the 2W5U benchmark system using the GB/SA implicit solvent, employing eight different surface tension parameter values. Additionally, the 2W5U system was simulated in TIP3P⁶⁹ explicit solvent to determine which surface tension parameter values most closely reproduce protein behavior in explicit solvent. With the experimentally measured surface tension of hydrocarbons in aqueous solvent being 0.005 kcal/mol/Ų,⁶² surface tension parameter values in the range 0.001-0.128 kcal/mol/Ų were tested. Using otherwise the same simulation parameters previously outlined, the 2W5U system was equilibrated for 1.0 ns, at which time the total surface area, a molecular property closely affected by surface tension, had reached an equilibrium value. The surface areas evaluated during the simulations are plotted in Figure 5; for the TIP3P simulation, only the final protein surface area, as calculated by VMD’s⁶³ high precision solvent-accessible surface area tool, with a solvent probe radius of 1.4 Å, is shown.

Figure 5.

Surface area during eight GB/SA simulations of the 2W5U system employing different surface tension parameter values. The final surface area for each GB/SA simulation is listed at right; shown is also the final surface area resulting from the simulation with explicit (TIP3P) solvent.

Results

The performed simulations examine the hybrid GPU/CPU algorithm by verifying simultaneous overlap of GB and SA force calculations, analyzing the ideal ratio of GPUs to CPU cores which maximizes computing efficiency, benchmarking performance and evaluating appropriate values for the surface tension parameter.

Hybrid GB/SA performance analysis

Central to fast hybrid GPU/CPU algorithms is the simultaneous overlap of calculations on both processor types, brought about by the host CPUs coordinating the GB calculation on the GPU with the SA calculations on the CPU. To demonstrate this coordination, Figure 3 illustrates, using the Projections⁷⁰ tool, the execution process of a GB/SA simulation of the 1GPB system on multiple GPUs and CPU cores.

Figure 3A illustrates the GB/SA calculation executed on 16 CPU cores without GPUs. The three phases of the GB calculation, described by Eq. (8), Eq. (11) and Eq. (10), are carried out with SA calculations interspersed to utilize the CPU when it would otherwise be idle while waiting for other cores to complete the phase; the lack of idle time (shown in yellow) signifies a highly efficient calculation.

Figure 3B demonstrates how the GB/SA calculation executed solely on 16 CPU cores is accelerated through the addition of 1 GPU. Because of its powerful computing capability, the GPU completes all Coulomb, van der Waals and GB calculations in the same time that the 16 CPU cores need to perform the SA calculation, resulting in a three-fold overall performance increase. This performance increase should be judged on the basis of an approximate 1 GPU/16 CPU cores cost ratio of about 1, i.e., by doubling the hardware cost, one triples performance.

A bottleneck for hybrid GPU/CPU calculations is the CPU’s limited ability to switch between performing the SA calculation and GPU-related operations. Figure 3C illustrates the interplay between the GPU execution and the host CPU calculations. For each of the three GB phases, the host CPU initializes the GB calculation on the GPU then, while the GPU calculates the GB phase, the host CPU performs SA calculations. NAMD efficiently overlaps the GB and SA calculations by partitioning the SA calculation into many short, independent force work units, such that at the completion of each SA force work unit, the CPU can engage in GPU-related operations, if needed, then return to the next SA force work unit as highlighted by Figure 3C. Figure 3D illustrates how not partitioning the SA calculation increases GPU idle time during GB phase 1 and CPU idle time during GB phase 2 and 3, thereby decreasing performance.

Because of the performance difference between GPUs and CPUs and the different computational cost of the GB and SA calculations, it was not known what ratio of GPUs to CPUs would be the most efficient. The best ratio would have GPUs and CPUs requiring the same time to perform their respective force calculations. Based on the data in Table 2 and as illustrated in Figure 3, a ratio of 16 CPU cores per GPU allowed highly efficient performance, while deviating from this ratio resulted in either the GB or SA calculation to become rate limiting. For example, Table 2 shows that calculating GB/SA for the 1GPB system on 1 GPU is 1.9 times faster with 16 CPU cores than with 8 CPU cores (adding more cores alleviates the SA calculation bottleneck on the CPU) while 1 GPU with 32 CPU cores is only 1.3 times faster than with 16 CPU cores (GB calculation on GPU begins to be the bottleneck), thereby sharply decreasing computational efficiency. As both GPU and CPU technologies evolve, the ideal ratio of CPU cores per GPU will also evolve, both for our GB/SA algorithm as well as for other hybrid GPU/CPU algorithms.

Performance benchmark results

The performance of the hybrid GB/SA implementation is demonstrated by the benchmarks, which are reported in full in Table 2 and illustrated for the 1IR2 system in Figure 4. The incorporation of GPUs into the MD simulation computation offers dramatic performance increases; for example, for the GB simulations of the 1IR2 system, simulations on 1 GPU are 25% faster than on 32 CPU cores. Additionally, the three largest systems tested were simulated, with the GB model, 30-35 times faster with 1 GPU than on 1 CPU core alone, while even the smallest system, 1YRI, was simulated 13 times faster with 1 GPU than on 1 CPU core alone. The GB/SA simulation of the 1IR2 system executed 50 times faster on 1 GPU with 16 CPU cores than on 1 CPU core and 3.5 times faster than on 16 CPU cores.

In case of larger simulated systems, one can take advantage of more GPU accelerators; because GPUs operate most efficiently when they are issued a lot of concurrent work, for moderately sized systems one achieves the great simulation speeds on relatively few GPUs (see the GB columns of Table 2). The 582-atom villin headpiece is simulated at the same speed on 1 GPU as on 32 CPU cores, but not any faster on 2 GPUs. The larger 2,412-atom flavodoxin is simulated 27% faster on 1 GPU than on 32 CPU cores, and 60% faster on 2 GPUs. The 13,340-atom glycogen phosphorylase is simulated 3.2 times faster on 4 GPUs than on 32 CPU cores while the 74,926-atom RuBisCO is simulated 4.5 times faster for the same comparison.

To enhance performance for large systems, we employed in the present study an interaction cutoff. Because cutoff lengths affect both accuracy and performance, we compare in Table 3 the computational expense of simulating the four benchmark systems as well as the relative error in calculating the total GB energy using a no-cutoff calculation as a reference, $(E_{\text{cutoff}}^{\text{GB}}-E_{\text{no}\text{cutoff}}^{\text{GB}})∕E_{\text{no}\text{cutoff}}^{\text{GB}}$. In case of the 16 Å cutoff, compared to a no-cutoff calculation, computational expense is reduced, the relative error is about 0.5%, and the fraction of computational expense associated with the SA calculation is higher (requiring more CPU cores per GPU).

Table 3.

Computational expense and accuracy for different non-bonded interaction cutoff lengths. Listed for each of the four benchmarked systems and for each cutoff (no cutoff, 30 Å cutoff, and 16 Å cutoff), are the execution time required for one timestep on one CPU core, the percent of computational expense associated with the Coulomb and van der Waals (Vac), GB and SA calculations and the relative error in the total GB energy calculated with cutoff, namely $(E_{\text{cutoff}}^{\text{GB}}-E_{\text{no}\text{cutoff}}^{\text{GB}})∕E_{\text{no}\text{cutoff}}^{\text{GB}}$.

	no cutoff				30 Å cutoff					16 Å cutoff
PDB	Time	Vac	GB	SA	Time	Vac	GB	SA	Err	Time	Vac	GB	SA	Err
1IR2	556s	21%	76%	3%	54.9s	19%	69%	12%	0.04%	22s	10%	62%	28%	0.3%
1GPB	17.8s	19%	74%	7%	6.61s	15%	72%	13%	0.3%	3.4s	10%	60%	30%	0.6%
2W5U	0.61s	15%	75%	10%	0.57s	15%	73%	10%	0.04%	0.52s	10%	57%	33%	0.7%
1YRI	0.05s	15%	60%	25%	0.05s	14%	59%	27%	0.3%	0.07s	8%	59%	33%	0.3%

The impressive speed-ups achieved by utilizing GPU technology demonstrate the benefit which GPUs offer to MD computing. While the benchmarks reported here are only for up to 4 GPUs, the hybrid algorithm also operates on supercomputers built from many GPUs and multi-core CPUs as previously described for GPU-acceleration of NAMD on distributed memory computers.³⁸

Testing surface tension parameters

When employing the SA calculation, the surface tension, in units kcal/mol/Ų, is a parameter of the model, controlling hydrophobic energy of solvation; it is not a physical property measured from the simulation. To explore the effect of the parameter on a protein system, the 2W5U system was equilibrated through a GB/SA implicit solvent simulation employing surface tension parameters ranging from 0.001 to 0.128 kcal/mol/Ų; the system was also equilibrated through a standard all-atom simulation employing explicit TIP3P⁶⁹ solvent. Figure 5 presents protein surface area arising in the GB/SA equilibration simulations as well as the final surface area of each. The protein surface area is expected to diminish with increasing surface tension as the latter imparts an energy penalty for the protein’s surface exposed to solvent. The simulations utilizing surface tension parameter values of 0.004 and 0.008 kcal/mol/Ų returned final surface areas closest to the area of the reference TIP3P equilibrated system, suggesting that employing surface tension parameter values between 0.004 and 0.008 kcal/mol/Ų most closely reproduce protein behavior in explicit solvent. The experimentally measured surface tension of hydrocarbons in aqueous solvent is 0.005 kcal/mol/Å^{2 62} which validates our finding.

Conclusions

The structural biology community has been well served by technological advances of general purpose GPU computing, which have made molecular dynamics more powerful and accurate. Many biological computing programs have already achieved great improvements in performance through GPU acceleration. As it is often neither feasible nor ideal to perform all needed calculations on the GPU, it becomes increasingly important to develop methods for overlapping GPU and CPU calculations. From the present work results an efficient method for performing GB/SA simulations on hybrid GPU/CPU computers, permitting extremely fast and accurate molecular dynamics simulations that can be executed, for example, interactively by researchers.