Abstract
Surveillance systems are often focused on more than one disease within a predefined area. On those occasions when outbreaks of disease are likely to be correlated, the use of multivariate surveillance techniques integrating information from multiple diseases allows us to improve the sensitivity and timeliness of outbreak detection. In this article, we present an extension of the surveillance conditional predictive ordinate to monitor multivariate spatial disease data. The proposed surveillance technique, which is defined for each small area and time period as the conditional predictive distribution of those counts of disease higher than expected given the data observed up to the previous time period, alerts us to both small areas of increased disease incidence and the diseases causing the alarm within each area. We investigate its performance within the framework of Bayesian hierarchical Poisson models using a simulation study. An application to diseases of the respiratory system in South Carolina is finally presented.
Keywords: Disease surveillance, multiple diseases, shared component model, conditional predictive ordinate
1 Introduction
Effective surveillance is essential to protect public health by rapidly detecting and responding to disease outbreaks. Most work on surveillance methodology has evolved in temporal applications, and so numerous methods including process control charts, temporal scan statistics, time-series methodology, and log-linear and other parametric regression models have been proposed to monitor univariate time series of counts of disease.1 Because of the growing threat of bioterrorism and an increase in the emergence and re-emergence of infectious diseases with pandemic potential, numerous studies have recently been conducted to develop new and improved methods for health surveillance. New statistical methods usually use information on both the time and location of events, and so they offer an improved ability to detect localized events that occur in small regions relative to the surveillance of the total count across a larger region. Testing methods are widely used to detect outbreaks of disease in space and time.2,3 Recent developments in the analysis of space-time disease surveillance data use a statistical model to describe the behavior of disease over space and time during endemic periods, that is when the disease occurs at its expected frequency of occurrence, and the emphasis is placed on detection of unusual deviations from predictable patterns based on the estimated model.4–9 These model-based approaches provide a flexible framework for the inclusion of spatial, temporal, space-time interaction, and possible covariate effects.
Multivariate space-time surveillance data also arise naturally in many public health applications. For instance, disease incidence data are often available by age group, gender and race. On some occasions, a range of different diseases are monitored simultaneously to assess the general health status of a region. Some examples are the monitoring of smoking-related cancers, respiratory diseases or gastrointestinal illnesses. In a syndromic surveillance setting, different syndromes associated with disease are monitored simultaneously to detect outbreaks of disease at the earliest possible time, possibly even before definitive disease diagnoses are obtained. Common syndromes are school and work absenteeism, over-the-counter medication sales, emergency department visits, physician telephone calls, etc. On those occasions, the use of surveillance techniques integrating information from the different data sets is important to achieve higher detection power for events that are present simultaneously in more than one data set. One approach to sharing information is to jointly examine the multiple disease incidences. Kulldorff et al.10 proposed an extension of the space-time scan statistic to jointly monitor multiple data sets. The multivariate scan statistic is based on a combined log likelihood which is defined as the sum of the individual log likelihoods for those data sets with more counts than expected in the scanning window. A signal is generated if a cluster is detected in either one or in a combination of data sets. Further extensions, such as the Bayesian multivariate scan statistic,11 have been proposed. Banks et al.12 presented a model-based approach to surveillance of spatial data on multiple diseases. The proposed methodology, which is focused on syndromic surveillance, uses univariate Bayesian hierarchical models to model counts of patients with specific symptoms indicative of the same disease in the absence of an outbreak. Indicator variables modeled as binary Markov random fields are then used to detect disease outbreaks. An increase in the number of cases is assumed for all the symptoms when the disease is present.
In practice, however, the different data sets under study may be influenced by common confounding factors, and so they are likely to be correlated. This suggests that we need to consider multivariate disease models to describe the space-time behavior of diseases. The multivariate conditional autoregressive (MCAR) model13 and the shared component model14,15 are the two main approaches to model disease risk correlations across both spatial units and diseases. The main advantage of the shared component model is that it enables estimation of shared and disease-specific spatial patterns.
In this article, a shared component model is used to describe the behavior of diseases under endemic periods. A novelty of the proposed model formulation is the use of indicator variables, which allow for identification of shared and disease-specific latent spatial fields describing the risk surface for each disease. We show then how the surveillance conditional predictive ordinate (SCPO), which was introduced by Corberán-Vallet and Lawson16 in a univariate model-based surveillance setting to detect areas of unusual disease aggregation, can be straightforwardly extended to incorporate information from multiple diseases. In particular, we define the multivariate surveillance conditional predictive ordinate (MSCPO) for each small area and time period as the conditional predictive distribution of those counts higher than expected given the data collected so far. A parallel surveillance approach across the different areas under surveillance is then carried out, where in each area alarms are sounded if the corresponding MSCPO value is below a specified critical value. This surveillance technique alerts us to both spatial units of increased disease incidence in need of further investigation and the diseases causing the alarm within each area, and consequently it facilitates a timely and informed public health response.
This article is organized as follows. In Section 2, we present our modeling framework. In Section 3, we review the surveillance conditional predictive ordinate and introduce its multivariate extension to multiple disease surveillance. Section 4 shows the results obtained in a simulation study. The surveillance technique is then applied to emergency room discharges for diseases of the respiratory system in South Carolina. Finally, we conclude with a general discussion of the proposed technique and provide directions for future research.
2 Modeling of endemic periods
2.1 The convolution model
Let yit and eit denote, respectively, the observed and expected count of disease in area i and time period t, for i = 1, 2, …, m and t = 1, 2, …, T. We assume here that the observed counts are Poisson distributed
where θit, which is often termed the relative risk, represents the excess risk within area i at time t. This component is usually the focus of interest, and so a wide range of spatiotemporal models have been developed to estimate the true relative risk of a disease of interest across a geographic study region. The most common approach to relative risk modeling is to assume a logarithm link to a linear predictor which is a function of fixed observed covariates and spatial, temporal and space-time interaction random effects.17,18
In a surveillance context, however, the emphasis is placed on detection of changes. To this end, Lawson19 emphasized the need for a relatively simple model capturing the normal historical variation in disease incidence without absorbing changes in the model fit. In a recent study, Corberán-Vallet and Lawson16 have demonstrated that the use of a spatial-only model where the relative risks are assumed to be constant over time may improve outbreak detection capability. Temporal effects would be included in the model only if an overall time trend or seasonal effects were present in the time series data and the emphasis was on detection of unusual outbreaks of disease. Here, we are interested in detecting the start of an outbreak, and so we assume that under endemic conditions θit = θi for all t. Unusual departures from predictable patterns based on the overall spatial risk surface are then attributable to disease outbreaks. To capture spatial correlation in disease maps, we use the convolution model originally proposed by Besag et al.20 This model, denoted here by BYM model, assumes that the logarithm of the relative risk is decomposed as
| (1) |
where ρ is the overall level of the relative risk in the study region, and ui and vi represent, respectively, spatially correlated and uncorrelated random effects. As a prior distribution for the intercept we assume a conventional zero-mean Gaussian distribution with variance . We use an improper conditional autoregressive (CAR) model20 as a prior distribution for the correlated heterogeneity, that is
where u(i) = (u1, u2, …, ui−1, ui+1, …, um)′, ni is the set of spatial neighbors of the ith region, mi is the cardinality of ni, and is the correlated spatial component variance. Here the neighborhood is assumed to consist of spatially adjacent areas, but more general definitions (using, for instance, intercentroidal distances) are also possible. The prior distribution for the uncorrelated heterogeneity is the zero-mean Gaussian distribution with variance .
2.2 The shared component model
In public health it is often appropriate to consider the analysis of spatially aggregated data on multiple diseases. On those occasions, the use of multivariate models accounting for correlations across both diseases and locations may provide a better description of the data and enhance comprehension of disease dynamics. Knorr-Held and Best14 introduced a shared component model for the joint spatial analysis of two related diseases where the underlying risk surface for each disease is separated into a shared and a disease-specific component. These components can be interpreted as surrogates for spatially structured unobserved covariates that are either shared by both diseases or specific to one of the diseases. For the joint analysis of more than two diseases, Held et al.15 proposed a generalized shared component model where latent spatial fields may be shared by some of the diseases or may enter only in one of the diseases. Assume that there are K diseases and a fixed study region common to all the diseases. Let yik and eik be the observed and expected count of disease during a fixed temporal period and θik the relative risk, where i = 1, 2, …, m represents the areal unit and k = 1, 2, …, K the disease. The extended shared component model is defined as
| (2) |
where wj = (wj,1, wj,2, …, wj,m)′ denotes the jth spatial random effect, and the scaling parameter δj,k determines the relative contribution of the spatial random effect to disease k. For each spatial field wj, it is assumed that the terms log(δj,1), log(δj,2), …, log(δj,nwj) follow a multivariate Gaussian distribution with mean zero and marginal variance , but under the restriction that
| (3) |
nwj being the number of relevant diseases for wj. Consequently, this model formulation requires the prespecification of the number of spatial random effects and the diseases relevant for each one of them. In practice, however, this will not always be known in advance. The number of possible shared and disease-specific components increases rapidly with the number of diseases under study, and so numerous model formulations become possible. MacNab21 emphasized the need for a careful and realistic formulation of common risk factors. Because dependencies between disease risks are given a priori in Model (2), an inappropriate formulation of shared and disease-specific components can lead to misspecification of the latent spatial fields, lack of model identifiability and possibly failure of MCMC convergence.
Different variants of the above shared component model have been used to model correlations both between and within areal units. For instance, Ma and Carlin22 replace (2) with
| (4) |
where the term ρk is not included in the model because the expected counts are age-adjusted internally. Similar to the generalized common spatial factor model introduced by Wang and Wall,23 a single spatial random effect is used to model the correlation between diseases and locations. The scaling parameters δk allow different risk gradients for different diseases. To avoid identifiability problems, δK is set equal to 1, while the remaining scaling parameters are assumed to be unconstrained. The disease-specific components ψik are originally assumed to be independent across both areas and diseases, that is , although they can be generalized to independent CAR models.
In our surveillance setting, disease maps which have an associated temporal dimension are analyzed prospectively with the objective of detecting changes in the risk pattern of diseases. Hence, for each area i and time period t there is a vector of K counts of disease. As in the univariate case, we assume constant relative risks during endemic periods, and so at the first level of the hierarchy counts of disease have a Poisson distribution with mean eitkθik. At the second level of the hierarchy the log relative risks are modeled as
| (5) |
where ρk is the disease-specific overall risk; L represents the number of spatial fields wl = (wl,1, wl,2, …, wl,m)′ needed to describe the correlation in the relative risks across both areas and diseases; ϕl,k is a binary indicator variable that takes the value one if the spatial random effect wl has an influence on disease k and the value zero otherwise; δl,k is the scaling parameter that measures the contribution of wl to disease k, and ψik is the uncorrelated term, which is assumed to be zero-mean Gaussian distributed, .
In general, the number of components (L) is not known, and so it must be estimated. There are several different procedures to the estimation of L. A simple approach, which has been successfully implemented in related studies, is to assume a large number of L components a priori. The presence of each latent component is then determined based on the posterior mean of the associated indicator variables.24,25 It is important to emphasize here that a small number of components usually suffices to model the spatial variation in the risk of two or more related diseases. However, larger numbers of components, possibly even larger than K, are also possible. As a prior distribution for ϕl,k, we consider the Bernoulli distribution with probability pl, which can be assumed to be constant or can have a hyperprior distribution. The Beta distribution is then the conventional choice. We assume here that pl ~ Be(a, l), a being a positive constant that controls the rate at which the mean of the distribution tends to zero. This choice is a compromise between allowing for disaggregation of the underlying risk surface for each disease into different latent spatial fields and searching for a parsimonious model. The latent spatial fields are assumed to be independent, with each following a CAR prior distribution, that is
In order to avoid identifiability problems, we set , for l = 1, 2, …, L, so that the variance of δl,k wl,i is determined by δl,k.26 As a prior distribution for the scaling parameters δl,k, which can then be assumed to be unconstrained, we use a non-informative zero-mean Gaussian distribution. Note that this prior distribution differs from the original one (equation (3)).
Similar to the model proposed by Held et al.,15 the proposed shared component model assumes that there may be more than one latent spatial field which can be shared by some of the diseases or may be relevant only to one of them. However, by using indicator variables in the model formulation, it is not necessary to specify the structure of the multivariate model in advance.
3 Detection of outbreaks: The multivariate surveillance conditional predictive ordinate
The conditional predictive ordinate (CPO) was first defined by Geisser and Eddy27 as the posterior predictive distribution of the observation yi when the model is fitted to all data except yi. That is
where y(i) = (y1, y2, …, yi−1, yi+1, …, yn) is the data vector with yi deleted and f(.|φ) represents the model describing the data. Small CPO values, which indicate a poor fit by the model, can be used to detect observations discrepant from the model. The CPO has been widely used in the statistical literature as a Bayesian model assessment tool in different contexts.28 Recently, Corberán-Vallet and Lawson16 adapted the CPO in a surveillance context to detect small areas of unusual disease incidence. Let yt = (y1t, y2t, …, ymt)′ be the vector of disease counts observed at time period t, the vector of all the data observed up to time t − 1, and θ = (θ1, θ2, …, θm)′ the relative risk vector under endemic conditions. The surveillance CPO (SCPO) is defined for each small area i and time period t as
| (6) |
where is a set of relative risks sampled from the posterior distribution that corresponds to the previous time period. The main difference with respect to the CPO is that the SCPO is calculated using only data from previous time points. This is fundamental in a surveillance context, since the inclusion of observations from the new time period may lead to a different model for the relative risk pattern. Hence, if no change in risk takes place at time t, the relative risk in area i and time t, θit, is equal to θi and the observation yit is representative of the data expected under the previously fitted model. Otherwise, SCPO values close to zero are obtained.
In order to detect as early as possible emerging outbreaks of disease, SCPO values are calculated each time new observations become available. An alarm is then generated for the ith small area at time t if the corresponding SCPO value is below a specified critical value α and yit > eitθ̂i, θ̂i being the posterior mean of the relative risk at the previous time period. Since the value of the SCPO depends on the mean of the Poisson distribution, it is necessary to scale the SCPO to use the same critical value for all the areas. A scaled SCPO can be defined as16
so that it takes values close to one if the observation at time t is close to the data expected under the previously fitted model, and values close to zero otherwise.
In the multivariate surveillance setting, spatial data on multiple diseases are observed at each time period, and a decision concerning whether a disease incidence has increased has to be made sequentially based on the data collected so far. We believe that a global increase in the incidence of a disease in all the areas occurring at the same time point is unlikely. Similarly, disease outbreaks need not necessarily occur at the same time for all the diseases under surveillance or affect the same spatial units. So, for each area i and time t, let yit = (yit1, yit2, …, yitK) be the vector of observed counts of disease, eit = (eit1, eit2, …, eitK) the vector of expected counts, θ̂i = (θ̂i1, θ̂i2, …, θ̂iK) the vector of posterior relative risk estimates at the previous time point, and the vector of observed counts higher than expected, that is yitk > eitkθ̂ik. A multivariate extension of the SCPO incorporating information from multiple diseases can be defined as
| (7) |
if it is not null, and MSCPOit equal to one otherwise. Values of the MSCPO close to zero indicate then unusually high disease counts. Note that when , the MSCPOit corresponds to the SCPOit for disease k1. When n ≥ 2, counts of disease higher than expected are looked at in conjunction to improve the outbreak detection capability.
The multiple integral in (7) does not have a closed form solution, and so simulation is required. A Monte-Carlo approximation to the MSCPOit can be obtained from a posterior sampling algorithm as
| (8) |
where is a set of relative risks sampled from the posterior distribution at time t − 1.
As in the univariate surveillance setting, effective measures based on the MSCPO values have to be constructed to assess if there is any outbreak of disease occurring at time period t. To make MSCPO values comparable across areas and time periods, we propose to consider the scaled MSCPO given by
| (9) |
and to perform a parallel surveillance approach across the different areas under surveillance, where an alarm is sounded for the ith small area at time t if the corresponding sMSCPOit is below a specified critical level α. It is important to emphasize here that the proposed surveillance technique alerts us to both small areas of increased disease incidence in need of further investigation and the diseases causing the alarm within each area.
The surveillance technique described herein can be run until the first outbreak is detected and medical intervention takes place. However, it may be of interest to continue the monitoring process to detect either further changes in disease incidences or the end of an outbreak. The first goal can be achieved by sequentially estimating the model describing the normal behavior of diseases using only the last observations. This procedure allows the spatial effects to adapt quickly to changes in the relative risk patterns of diseases, and so it facilitates detection of additional changes in disease risks.16 In order to detect the end of an outbreak, the model describing the behavior of diseases in space and time has to be estimated using only counts of disease corresponding to endemic periods. MSCPO values close to one after consecutive values close to zero are then indicative of the end of the outbreak. Assuming that an outbreak has really occurred when an alarm has been sounded, this goal can be achieved by assuming that observations detected as unusual are missing when they become part of the history.
4 Simulation study
In this section, we present a simulation study to assess the performance of the proposed surveillance technique for outbreak detection. The development of a realistic simulation study is important. Here we used the US state of California, which consists of m = 58 counties, as the base map to generate counts of diseases at county level for T = 20 time periods and K = 3 diseases. Disease 1 corresponds to viral meningitis, which is a relatively common but rarely serious infection of the fluid in the spinal cord and the fluid that surrounds the brain. There is no specific treatment for viral meningitis, which is usually mild and clears up in about a week. It often remains undiagnosed because its symptoms can be similar to those of the common flu. The total number of viral meningitis cases in California in 2010, which is available from the California department of public health (http://www.cdph.ca.gov), was used to calculate monthly expected counts for the study region. Particularly, the expected counts were calculated as
| (10) |
where popi is the population in county i and r1 = 0.5656 is the monthly viral meningitis rate per 100,000 population. Note that constant expected counts over time were assumed. Monthly disease rates for the other two diseases were simulated as r2 = r1 + Ga(3, 1) and r3 = r1 + Ga(1, 1), and the corresponding expected counts were calculated as those in (10).
Two different relative risk models were used to simulate the true background relative risks. In Scenario 1 we assumed that the three diseases shared a common spatial field, while independent diseases were assumed in Scenario 2. Outbreaks of disease of different intensities were then generated using the expected counts of disease and the simulated relative risks as detailed below.
Scenario 1:
| (11) |
where i = 1, 2, …, 58 denotes the county, t = 1, 2, …, 20 the time, and k = 1, 2, 3 the disease; is the disease-specific overall risk; The components w = (w1, w2, …, wm)′ and wk = (wk,1, wk,2, …, wk,m)′ represent spatially correlated random effects, each one of them following a CAR model with variance and , respectively; (ψ1k, ψ2k, …, ψmk)′ is assumed to be a realization of a multivariate Gaussian distribution with zero mean vector and covariance matrix , and each ηik = (ηi1k, ηi2k, …, ηiTk)′ is assumed to follow a random walk independently of all other counties and diseases, that is . The values of the standard deviances were (σρ1, σρ2, σρ3) = (0.01, 0.02, 0.01), (σw, σw1, σw2, σw3) = (0.1, 0.02, 0.05, 0.05), (σψ1, σψ2, σψ3) = (0.2, 0.1, 0.15), and (ση1, ση2, ση3) = (0.01, 0.02, 0.025). Note that the simulated endemic disease risks were allowed to vary slightly over time.
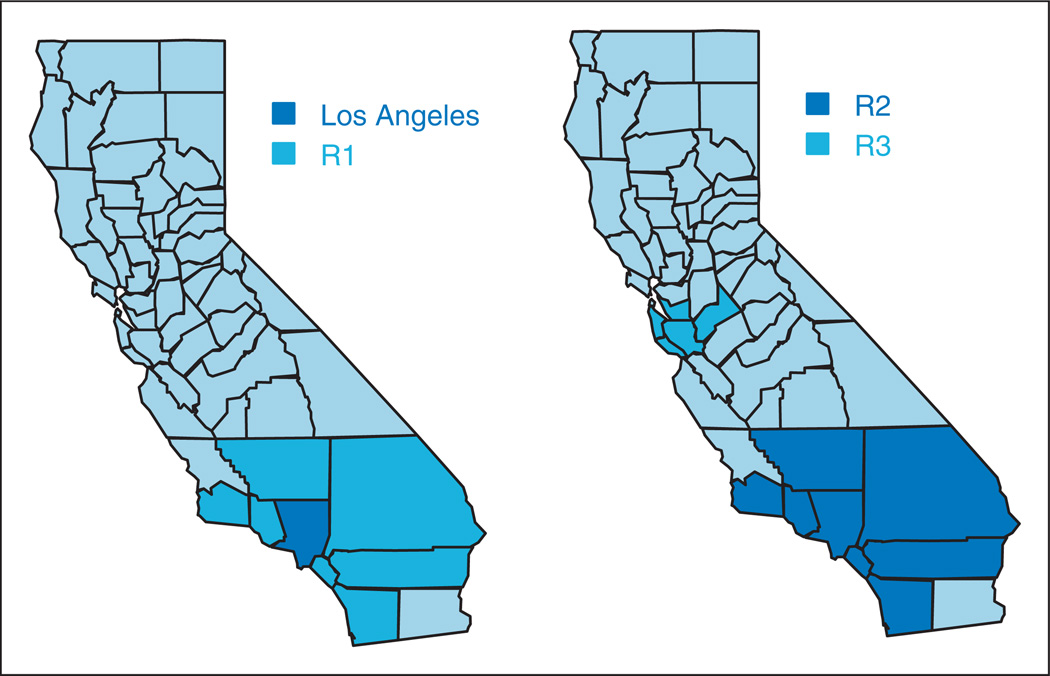
At time t0 = 15, an outbreak was assumed to start in Los Angeles county (i0 = 19) for the three diseases. Initial expected increases in disease counts due to the outbreak were simulated as Ii0t0k = ck ei0t0k θi0t0k, where c1 = 0.3, c2 = 0.1, and c3 = 0.5; that is, at time t0 = 15, a percentage increase in the mean of the Poisson distribution equal to 0.3 was simulated for Disease 1 and so on. At time t1 = 17 the outbreak was assumed to spread to seven neighboring counties (R1, see Figure 1). Increases in disease counts at time t1 for the affected counties were also generated as Iit1k = ck eit1k θit1k, i ∈ R1. Expected increases at subsequent time periods were assumed to be proportional to those observed at the previous time point, that is Iitk = βikIi,t−1,k, for t = 18, 19, 20. For simplicity, we assumed here βi1 = 1.2, βi2 = 1.1, and βi3 = 1.2 for all i ∈ {19, R1}.
Figure 1.
Simulation study. Regions where outbreaks of diseases were simulated.
Left: Scenario 1. Right: Scenario 2.
Scenario 2:
| (12) |
where parameters ρk, ψik and ηitk were defined as those in (11). Spatial correlation in model (12) was introduced by three disjoint sets of neighboring counties of higher risk: A1 = {8, 11, 12, 23, 45, 47, 52, 53}, A2 = {10, 16, 20} and A3 = {2, 3, 5, 9}.
At time t0 = 15, an outbreak was generated for eight counties (R2, see Figure 1) and Diseases 1 and 3. Expected increases in disease counts were simulated as Iit0k = ck eit0k θit0k and Iitk = βik Ii,t−1,k, for t = 16, 17, …, 20. We assumed (c1, c3) = (0.2, 0.5) and (βi1, βi3) = (1.2, 1.3). At time t1 = 17, an outbreak of Disease 2 was simulated in 5 different counties (R3). A percentage increase in the mean of the Poisson distribution of 0.3 was assumed initially. Subsequent increases were defined as Iit2 = 1.25Ii,t−1,2, for i ∈ R3 and t = 18, 19, 20.
Once the values for the expected counts, relative risks, and expected increases in disease counts due to outbreaks were specified, we generated the observed counts in the study region as yitk ~ Po(eitk θitk + Iitk), where Iitk = 0 if no outbreak of disease occurs in county i and time period t. To allow for sampling variability, we simulated 300 data sets for each scenario.
The first step in the analysis of the data is to select the model describing the endemic behavior of diseases. Simulated data for the first 10 time periods were fitted to Model (5) with L = 6 latent spatial fields. Here we accept a latent component in the model if there is at least one associated indicator variable larger than 0.5. Posterior sampling was carried out using MCMC with an initial burn-in period of 50,000 iterations to assess the convergence of MCMC chains. One posterior sample in five iterations was kept after the burn-in period until a set of 5000 iterations was obtained. A range of different hyperprior specifications of parameter pl were experimented with. We found that priors penalizing larger values of the number of latent spatial fields, such as the Be(a, l) distribution for parameter pl or the Exp(a l) distribution for parameter pl/(1 − pl), a being a positive constant, provide more satisfactory results in general. The results presented here correspond to the case where a Be(1, l) prior is used for parameter pl. Hence, E(p1) = 0.5 and, as l increases, the distribution of pl gets more concentrated around its mean, which in turn tends to zero. Following (Ma and Carlin,22 N(0, 100) priors were assumed for the scaling parameters. As a prior distribution for the unknown precision parameters, we used the Ga(2, 0.5), which provides reasonable non-informativeness. Similar results were obtained with alternative non-informative hyperprior distributions, such as the Ga(0.01, 0.01) distribution or the uniform distribution for standard deviation parameters.
In Scenario 1 a large part of the variation in the data comes from disease-specific components, specifically from the uncorrelated terms. This complicates the detection and proper estimation of the shared latent component. Nevertheless, the selected model generally includes four spatial components, one that is shared by the diseases and three disease-specific CAR components. Table 1 shows the mean square error (MSE) of the relative risks estimates obtained, for each disease, with the shared component model and the overall DIC, averaged over the 300 data sets. For comparative purposes, we also include those results obtained when the diseases are modeled separately by using the convolution model. As can be seen, when the diseases of interest share common risk factors, the use of the shared component model provides more accurate risk estimates and a better fit. In Scenario 2, three disease-specific spatial components were selected.
Table 1.
Simulation study. Mean square error of the relative risk estimates obtained, for each disease, with both the shared component model and the convolution model and the overall DIC. The results are averaged over the 300 data sets simulated under Scenario 1.
| Disease 1 | Disease 2 | Disease 3 | DIC | |
|---|---|---|---|---|
| Shared component model | 0.035 | 0.013 | 0.029 | 6068.29 |
| Convolution model | 0.042 | 0.018 | 0.034 | 6084.30 |
We next show the results obtained in the prospective analyses of the data with the proposed surveillance technique. Based on the previous results, we used the shared component model with four spatial components to describe the endemic behavior of diseases in Scenario 1. In Scenario 2 separate convolution models were sequentially fitted to model disease incidences. The relative risk estimates obtained at each time point with the corresponding model were used to calculate the MSCPO values for the new data. Because we are interested in detecting all the areas of increased disease incidence at each time period, we consider the sensitivity, specificity and median time to outbreak detection (MTD) as measures of performance. The sensitivity is defined as the proportion of all the areas undergoing a change in risk that signal an alarm at any time during the outbreak period. The specificity is given by the proportion of in-control areas that are correctly identified as such, that is
where TA, FA, TNA and FNA represent, respectively, true alarms, false alarms, true no alarms, and false no alarms during the outbreak period. Finally, for each small area undergoing an outbreak, let us define the time to outbreak detection as the number of time periods from the beginning of the outbreak until the first alarm is sounded. An infinite time to detection is assigned if no alarm is sounded. The MTD is then defined as the median of the times to detection of those areas of increased disease incidence. It is worthy to emphasize here that a MTD equal to infinity does not mean that no alarm has been sounded, but that the surveillance technique has not detected at least half of the areas of increased disease incidence. The decision rule used in this simulation study was to signal an alarm for the ith county at time t if the sMSCPOit < 0.5 × 10−nit, nit being the number of disease counts higher than expected in area i and time t. So, if there is only one count of disease higher than expected in area i and time t the critical value is equal to 0.05; when two counts of disease are higher than expected the critical value is 0.005, and so on. These values were chosen to assure a specificity around 95% for all the diseases and scenarios. Tables 2 and 3 show the sensitivity and MTD of the proposed surveillance technique. Note that one measure value is obtained for each data set. The results presented here are averaged over the 300 data sets simulated for each scenario. For comparative purposes, we also include the results obtained when the diseases were monitored separately by using the SCPO. In this case, an alarm was sounded for county i at time t if the sSCPOit < 0.05.
Table 2.
Simulation study, Scenario 1. Sensitivity and median time to outbreak detection (both posterior average estimates and 95% credible intervals) of the surveillance conditional predictive ordinate (SCPO) and the multivariate surveillance conditional predictive ordinate (MSCPO).
| SCPO |
MSCPO |
|||
|---|---|---|---|---|
| Sens | MTD | Sens | MTD | |
| Disease 1 | 0.46 | Inf | 0.68 | 2 |
| [0.13,0.75] | [1,Inf) | [0.38,0.94] | [0,Inf) | |
| Disease 2 | 0.28 | Inf | 0.60 | 2.5 |
| [0.13,0.5] | (Inf,Inf) | [0.25,0.88] | [0,Inf) | |
| Disease 3 | 0.78 | 1 | 0.82 | 1 |
| [0.5,1] | [0,Inf) | [0.5,1] | [0,Inf) | |
Table 3.
Simulation study, Scenario 2. Sensitivity and median time to outbreak detection (both posterior average estimates and 95% credible intervals) of the surveillance conditional predictive ordinate (SCPO) and the multivariate surveillance conditional predictive ordinate (MSCPO).
| SCPO |
MSCPO |
|||
|---|---|---|---|---|
| Sens | MTD | Sens | MTD | |
| Disease 1 | 0.42 | Inf | 0.87 | 2.5 |
| [0.13,0.63] | [3,Inf) | [0.63,1] | [1,4] | |
| Disease 2 | 0.67 | 2 | 0.67 | 2 |
| [0.4,1] | [0,Inf) | [0.4,1] | [0,Inf) | |
| Disease 3 | 0.96 | 1 | 0.97 | 1 |
| [0.81,1] | [0,2] | [0.88,1] | [0,2] | |
As expected, the SCPO achieves timely detection when changes in disease risks are substantial enough. For Disease 3, an initial percentage increase in the mean of the Poisson distribution equal to 0.5 was simulated in both scenarios. In this case, the outbreak detection capability of both the SCPO and MSCPO is similar. Both surveillance techniques provide also similar results when an outbreak is present in only one disease. This is the case of Disease 2 in Scenario 2. However, by integrating information from multiple diseases, the MSCPO improves considerably the sensitivity and timeliness of event detection when outbreaks of disease occur simultaneously in more than one disease and the proportional increase in disease counts during the outbreak relative to the endemic level is small. For instance, a percentage increase in the mean of the Poisson distribution equal to 0.1 was simulated for Disease 2 in Scenario 1. Counts of disease before and at the onset of the outbreak were then simulated, respectively, from the Po(eit2 θit2) and Po(eit2 θit2 (1 + 0.1)) distributions, which are not different enough to cause an alert when the disease is monitored separately. Hence, only 28% of the areas undergoing an outbreak are detected based on the SCPO. However, the MSCPO signals an alarm for 60% of those areas of increased disease incidence and reduces the MTD to 2.5 units.
5 Case study
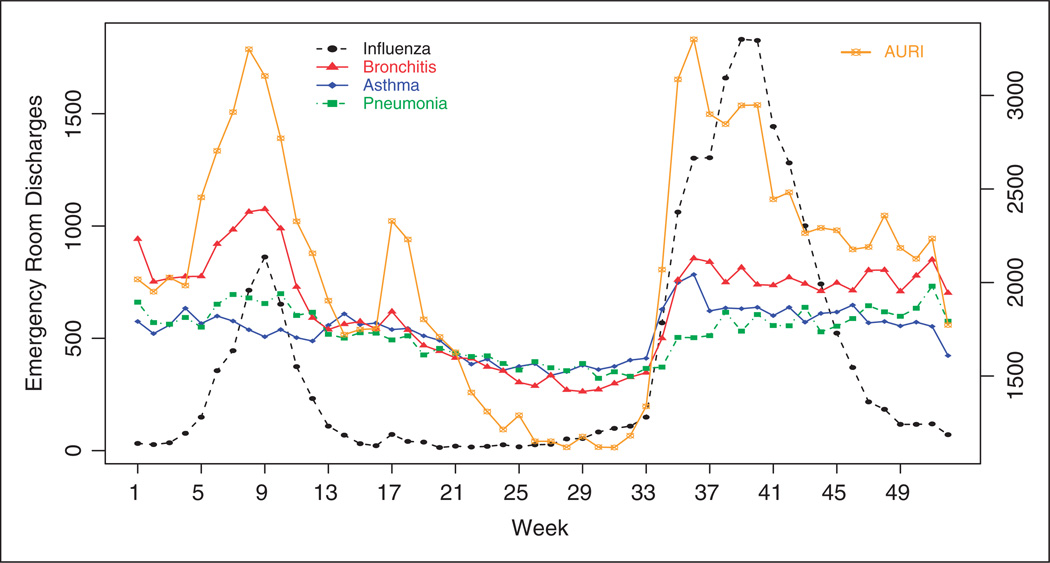
This section applies the MSCPO technique to emergency room discharges (ERD) for diseases of the respiratory system in South Carolina and compares its performance with that of the multivariate space-time scan statistic10 as implemented in the free SaTScan™ software.29 Scan statistics are widely used in the public health arena to detect disease clusters. The multivariate scan statistic incorporates information from multiple data sets to facilitate detection of outbreaks in more than one data set. Specifically, we monitor weekly ERD for acute upper respiratory infections (AURI), influenza, acute bronchitis, asthma and pneumonia in 2009. The data were obtained by county for the 46 counties of South Carolina from the South Carolina Office of Research and Statistics. Total weekly ERD in South Carolina are displayed in Figure 2. The right Y axis corresponds to ERD for AURI, which are considerably larger throughout the year. In the United States, AURI are the most common acute diseases in the general population and one of the most common conditions for visiting a clinician.
Figure 2.
Weekly emergency room discharges for influenza, acute bronchitis, asthma, pneumonia and acute upper respiratory infections (AURI, right Y axis) in South Carolina in 2009.
AURI, influenza, acute bronchitis and pneumonia are closely related acute diseases. Although these diseases can happen at any time, they are most common during the fall and winter months. In the United States, peak flu season months are December, January and February. The unusual behavior shown in Figure 2 is due to the novel H1N1 influenza virus, which arrived in South Carolina in April 2009. Asthma, on the contrary, is a chronic lung disease that inflames and narrows the airways. However, it is known that people with asthma may experience more frequent and severe asthma attacks when they have an upper respiratory infection.
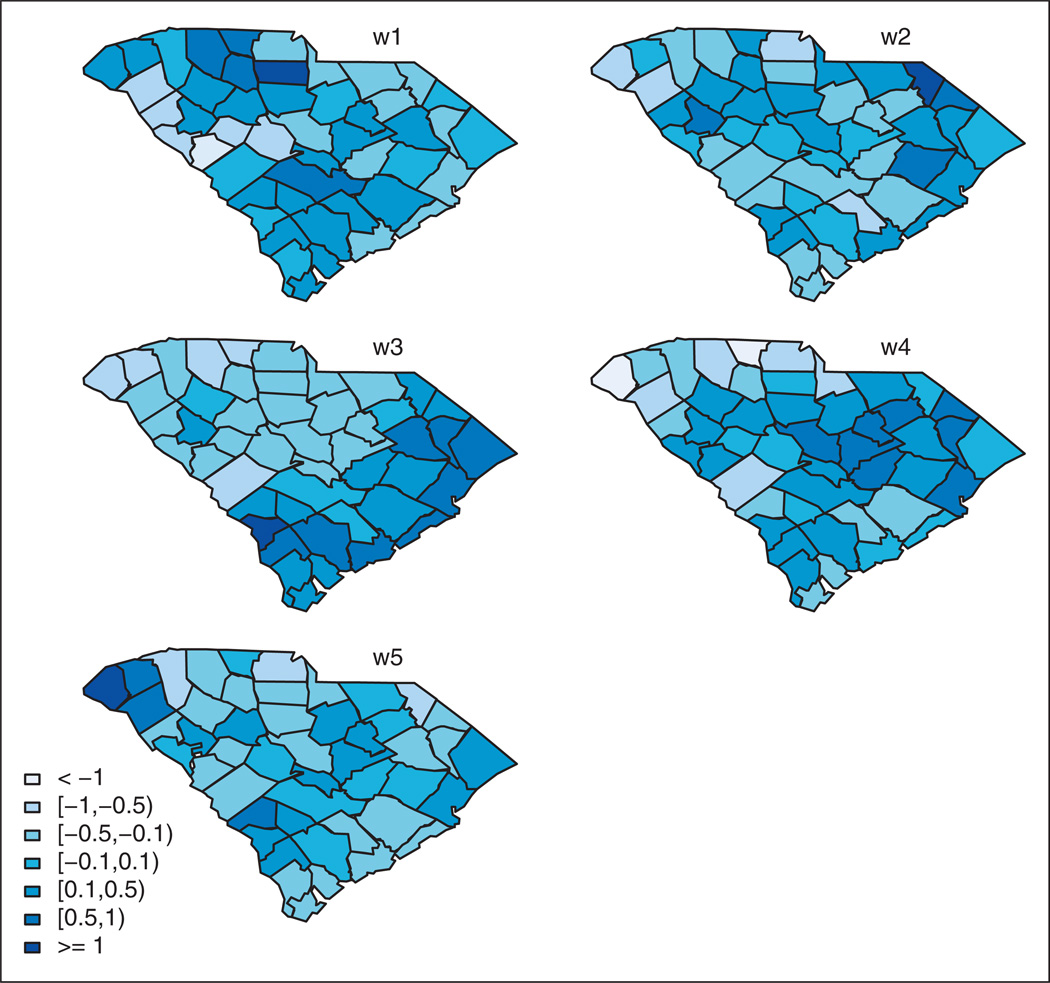
Because we are interested in detecting outbreak onsets, we confine our analysis to data collected from week beginning 28 June (where all the diseases can be assumed to be in an endemic state) to week beginning 27 December (weeks 26–52 in Figure 2). There are 46 counties, 27 time periods (weeks), and five diseases. Expected counts, which are assumed to be constant during the surveillance exercise to properly identify emerging outbreaks, were calculated for each disease and county by internal standardization using the data from the first three weeks. These data were also used to initially estimate the multivariate model describing the endemic behavior of diseases. Model (5) was fitted with L = 10 latent components. The results displayed are computed from 10,000 iterations after a burn-in of 50,000 iterations. Similar to the simulation study, the following prior distributions were assumed: pl ~ Be(1, l), δl,k ~ N(0, 100), and Ga(2, 0.5) for the precision parameters. In this example, five spatial fields are selected. The first one is common to AURI, acute bronchitis, asthma and pneumonia, while the other four spatial fields are only relevant to one disease. Namely, they are relevant to AURI, influenza, asthma and pneumonia, respectively. So, influenza does not share a common spatial field with the other diseases. Figure 3 displays the estimated latent spatial fields.
Figure 3.
Case study. Estimated latent spatial fields from the shared component model. The component w1 is shared by acute upper respiratory infections (AURI), acute bronchitis, asthma and pneumonia. w2, w3, w4 and w5 are only relevant to one disease: AURI, influenza, asthma and pneumonia, respectively.
Table 4 shows the DIC values (together with the pD) for the estimated shared component model. For comparative purposes, we also include the DIC values for the shared component model used by Ma and Carlin22 (Equation (4)) and those obtained when the diseases are modeled separately by using the convolution model. To select the model that best explains the correlation across both locations and diseases, the upper half of the table shows the results obtained with these models when only spatially structured random effects are incorporated into the model. The lower half of the table shows the results when both spatially correlated random effects and disease-specific spatially uncorrelated terms are included in the model. As can be seen, the joint spatial analysis of the data with the proposed shared component model leads to an improved goodness of fit as judged by a lower overall DIC value. The model used by Ma and Carlin22 and our model provide a similar goodness of fit when uncorrelated terms are included in the model. However, by comparing the DIC values in the upper half of the table, we can conclude that a single spatial field cannot explain properly the correlation across both locations and diseases present in the data. This can be further corroborated by examining the uncorrelated components ψik in equation (4). The estimated components (not shown) present a spatial correlation, which violates the independence assumption.
Table 4.
Case study. DIC (pD) values for the shared component model, Ma and Carlin’s model, and individual convolution models. Results obtained when the models only include spatially correlated random effects are shown in the upper half of the table. The lower half shows the results when disease-specific spatially uncorrelated terms are also incorporated into the models.
| Model | AURI | Influ | Bronch | Asthma | Pneum | Total |
|---|---|---|---|---|---|---|
| Shared component model | 810.35 | 268.41 | 583.41 | 659.04 | 651.04 | 2972.26 |
| (38.62) | (20.42) | (27.99) | (30.98) | (26.97) | (144.97) | |
| Ma and Carlin’s model | 828.03 | 312.47 | 645.44 | 719.23 | 732.52 | 3237.69 |
| (29.52) | (2.33) | (9.97) | (6.97) | (4.09) | (52.88) | |
| Convolution model | 815.37 | 271.61 | 590.30 | 663.03 | 659.08 | 2999.39 |
| (41.97) | (17.47) | (34.80) | (32.01) | (29.64) | (155.89) | |
| Shared component model | 808.18 | 268.04 | 578.84 | 657.64 | 652.43 | 2965.13 |
| (39.85) | (20.06) | (32.07) | (33.22) | (32.27) | (157.46) | |
| Ma and Carlin’s model | 808.90 | 266.51 | 580.71 | 657.80 | 653.84 | 2967.75 |
| (39.94) | (18.52) | (31.20) | (31.53) | (31.42) | (152.61) | |
| Convolution model | 810.30 | 268.24 | 584.29 | 659.17 | 656.17 | 2978.16 |
| (40.80) | (19.92) | (33.88) | (33.86) | (32.62) | (161.08) |
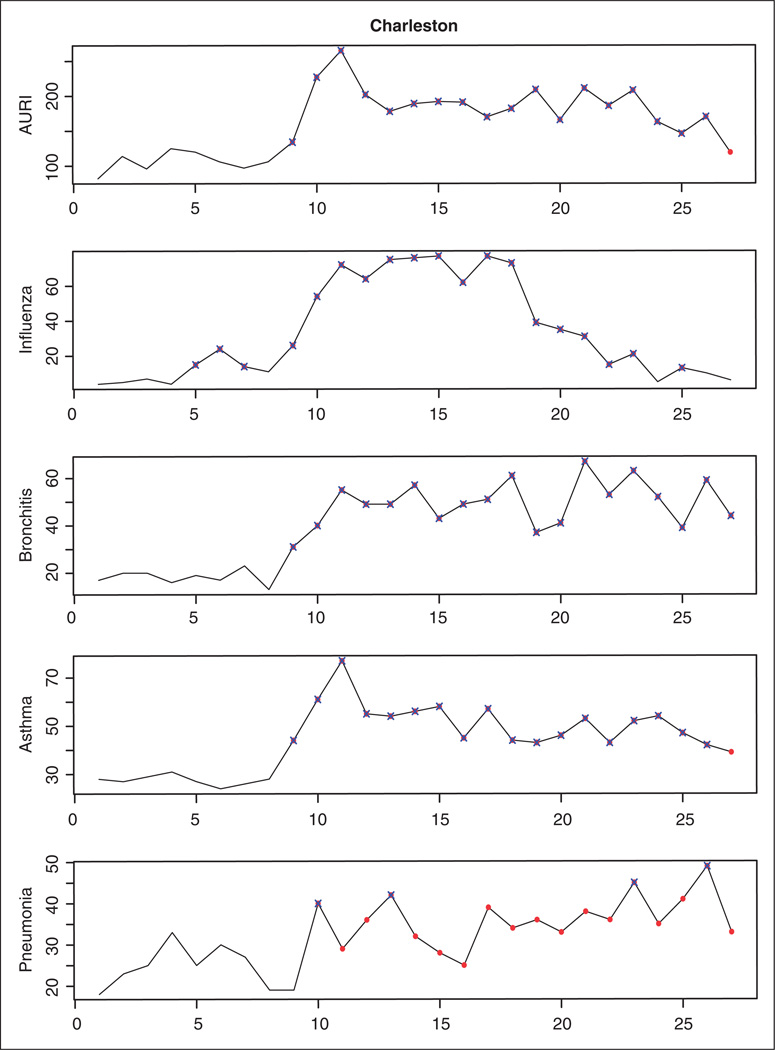
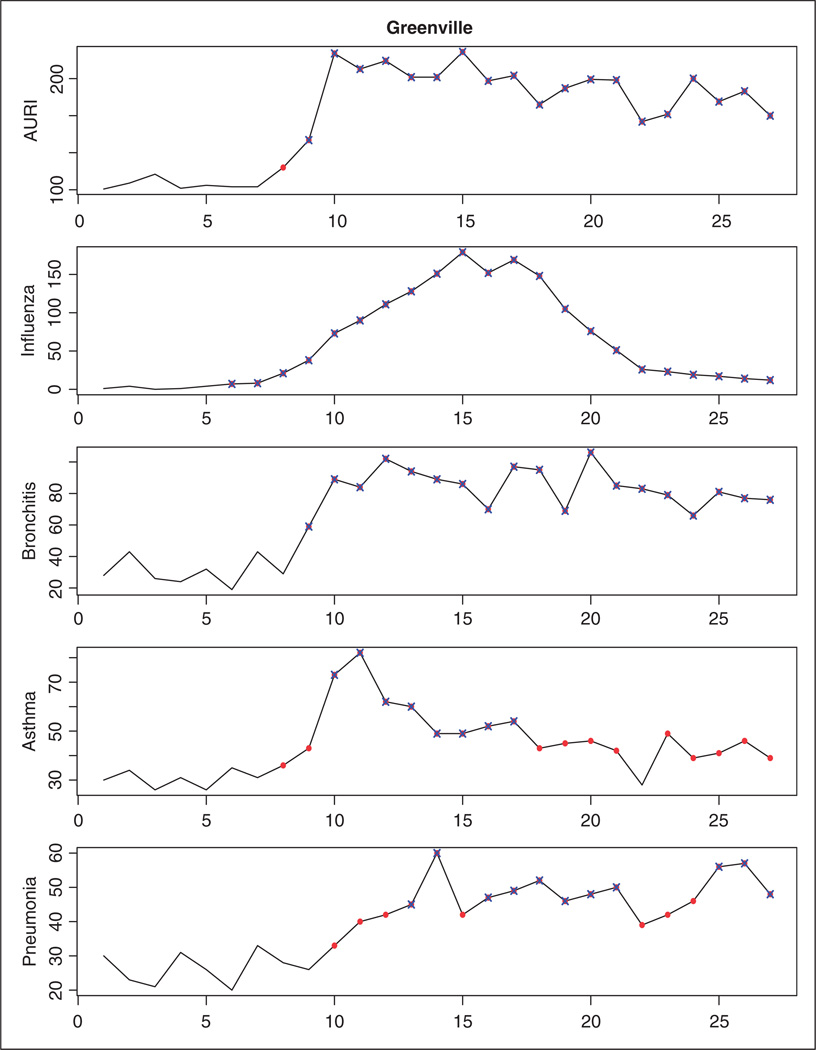
In what follows, we show the results obtained in the prospective analysis of the data using our surveillance technique. At each time point t = 4, 5, …, 27, the shared component model with five spatial fields is estimated using the data observed up to time t − 1, and the MSCPO values associated with the new observations are analyzed to detect emerging outbreaks of diseases. An alarm for the ith county is sounded at time t if the sMSCPOit is below 0.5 × 10−nit, nit being the number of counts higher than expected in county i and time t. In order to detect not only the onset but also the end of an outbreak, counts of disease detected as unusual at time t are assumed to be missing when they become part of the history. This way, the shared component model is sequentially estimated using only data observed during endemic periods. Table 5 shows, for a selection of 28 counties in South Carolina, the time point at which an outbreak is detected for each one of the diseases. Most of these outbreaks of disease are also detected when the diseases are monitored separately by using the univariate SCPO. As an example, Figures 4 and 5 show the temporal profiles for the Charleston and Greenville counties, where highlighted points represent time points corresponding to outbreak periods. As can be seen, when observed counts of disease are unusually high in comparison with the expected counts the univariate and multivariate surveillance techniques signal an alarm at the same time. However, by borrowing information from different diseases, the MSCPO alerts us to unusual counts of disease which are not significant enough to cause an alert on their own. This is the case, for instance, of the AURI, asthma and pneumonia outbreaks in Greenville at the moment of their onsets or the pneumonia outbreak in Charleston, where only some extremely high observations are detected in the separate analysis of the disease.
Table 5.
Case study. A selection of 28 counties of South Carolina: Time point at which an outbreak of disease is detected based on the multivariate surveillance conditional predictive ordinate.
| County | AU | In | Br | As | Pn | County | AU | In | Br | As | Pn |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Calhoun | 9 | 9 | 10 | 9 | 9 | Laurens | 9 | 9 | 9 | 9 | 10 |
| Charleston | 9 | 5 | 9 | 9 | 10 | Lee | 10 | 9 | 10 | 10 | 10 |
| Cherokee | 7 | 8 | 8 | 9 | 12 | Lexington | 8 | 5 | 9 | 9 | 10 |
| Chester | 8 | 10 | 6 | 9 | 10 | Marion | 10 | 10 | 11 | 10 | 10 |
| Chesterfield | 10 | 6 | 9 | 10 | 10 | Marlboro | 8 | 6 | 9 | 5 | 5 |
| Clarendon | 9 | 11 | – | 9 | 13 | Newberry | 9 | 9 | 10 | 11 | 9 |
| Darlington | 10 | 10 | 8 | 10 | 11 | Orangeburg | 9 | 6 | 9 | 9 | 9 |
| Dillon | 11 | 8 | 10 | 10 | 9 | Richland | 9 | 7 | 7 | 9 | 9 |
| Fairfield | 9 | 9 | 10 | 7 | 9 | Saluda | 10 | 10 | 12 | 12 | 12 |
| Florence | 9 | 5 | 10 | 10 | 10 | Spartanburg | 8 | 8 | 7 | 8 | 10 |
| Greenville | 8 | 6 | 9 | 8 | 10 | Sumter | 9 | 5 | 9 | 9 | 9 |
| Greenwood | 5 | 5 | 9 | 9 | 8 | Union | 9 | 9 | 9 | 9 | 11 |
| Kershaw | 9 | 10 | 10 | 10 | 9 | Williamsburg | 10 | 10 | 10 | 10 | 10 |
| Lancaster | 11 | 6 | 11 | 6 | 11 | York | 9 | 9 | 9 | 9 | 10 |
AU: Acute upper respiratory infections; In: Influenza; Br: Acute bronchitis; As: Asthma; Pn: Pneumonia.
Figure 4.
Temporal profile for the Charleston county. Time points corresponding to outbreak periods as detected by the multivariate surveillance conditional predictive ordinate are represented by solid points. Unusual observations based on the univariate surveillance technique are represented by crosses.
Figure 5.
Temporal profile for the Greenville county. Time points corresponding to outbreak periods as detected by the multivariate surveillance conditional predictive ordinate are represented by solid points. Unusual observations based on the univariate surveillance technique are represented by crosses.
Finally, we present the results obtained with the multivariate scan statistic, which is a multivariate extension of the space-time scan statistic3. Similar to the MSCPO, this cluster detection test has the ability to detect outbreaks in either one or in a combination of data sets. A major difference between the two approaches is that, while the MSCPO focuses on detection of individual small areas of increased disease incidence, the multivariate scan statistic uses cylindrical windows with a circular geographic base and with height representing time to detect clusters of cases. Here, the Poisson-based prospective space-time scan statistic is used. We set the maximum spatial cluster size at 50% of the population at risk, which is the default setting, and the maximum temporal window size at 90% of the study period. The non-parametric spatial adjustment provided by the software is used to adjust for purely spatial clusters. In this example, the first alarm is sounded at time period 7. In addition to the most likely cluster, which includes seven counties in the northwest of South Carolina, a statistically significant secondary cluster is detected. The criterion for reporting secondary clusters used here is that no cluster centers are included in other clusters. Table 6 shows a summary of the results provided by the software at this time period.
Table 6.
Case study. Clusters detected by the multivariate space-time scan statistic at time period 7.
| 1. Most likely cluster: Spartanburg, Greenville, Cherokee, Union, Laurens, Pickens, Anderson | |||
|---|---|---|---|
| Time frame: 9 Aug 09 to 15 Aug 09 (week 7 in the analysis) | |||
| p-value: 0.0001 | |||
| Cases | Expected | Relative risk | |
| AURI | 354 | 327.25 | 1.09 |
| Influenza | 16 | 9.50 | 1.72 |
| Bronchitis | 136 | 96.00 | 1.47 |
| Asthma | 100 | 85.50 | 1.18 |
| Pneumonia | 121 | 98.25 | 1.25 |
| 2. Secondary cluster: Clarendon, Sumter, Williamsburg, Calhoun, Lee, Orangeburg, Florence, Berkeley, Dorchester, Darlington, Kershaw, Richland, Georgetown, Bamberg, Marion, Colleton, Lexington, Charleston, Chesterfield, Dillon, Fairfield, Barnwell, Marlboro | |||
|---|---|---|---|
| Time frame: 2 Aug 09 to 15 Aug 09 (weeks 6–7 in the analysis) | |||
| p-value: 0.04 | |||
| Cases | Expected | Relative risk | |
| Influenza | 143 | 108.50 | 1.54 |
| Bronchitis | 236 | 220.50 | 1.09 |
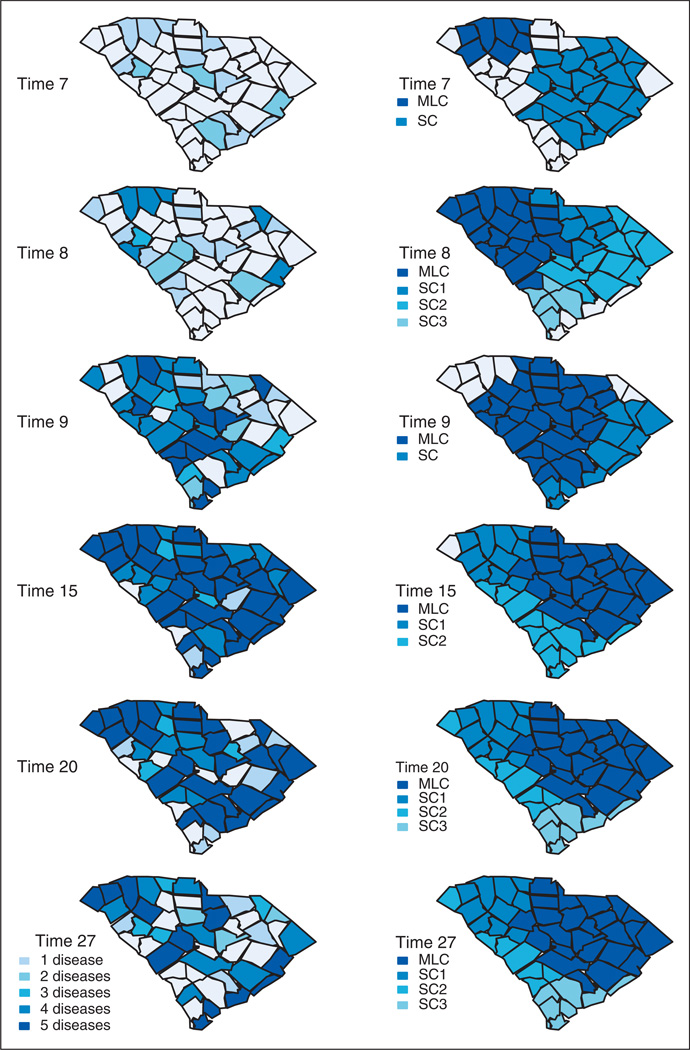
Most of the counties included in these two clusters are also detected with the MSCPO, which signals the first alarm at time 5 (Table 5). However, there are some differences between the results provided by each procedure that are worthy to emphasize. The multivariate space-time scan statistic pinpoints the general time and location of the most likely cluster (and possible significant secondary clusters), and so its exact boundaries remain uncertain. As a consequence, counties with no increase in the number of reported cases can be included in the cluster if their neighbors present an increased disease incidence. This is the case, for instance, of the Union county, where the observed counts of disease at time 7 are similar to those observed at previous time periods. It is also possible that the counties included in the cluster do not undergo an outbreak of disease for all the diseases reported in the cluster. For instance, only the number of ERD for influenza presents an increase in the Greenville county at time 7 (Figure 5). Finally, because the scan statistic focuses on detection of the most likely cluster (secondary clusters), small outbreaks of disease may be missed or reported at later time periods. These conclusions apply to all the time periods during the surveillance exercise. As an example, Figure 6 compares the counties where an outbreak is declared based on the MSCPO and the multivariate scan statistic at six time periods. As can be seen, several large clusters covering practically all the study region are reported by the multivariate scan statistic at each time point. These clusters usually include the five diseases. Our surveillance technique searches, at each time point, for counties of increased disease incidence and the diseases within each county with more counts than expected. As a consequence, it enables a timelier and more accurate outbreak detection. The MSCPO also allows us to report the end of an outbreak, which can be valuable for the planning and reduction of public health interventions.
Figure 6.
Case study. Counties where an outbreak is declared. Left: Areas signaling an alarm based on the multivariate surveillance conditional predictive ordinate. Darker shading indicates a higher number of diseases causing the alarm. Right: Most likely cluster (MLC) and secondary clusters (SC) using the multivariate Poisson-based prospective space-time scan statistic.
6 Discussion
The SCPO was introduced in a univariate surveillance setting to monitor spatially aggregated disease incidence data. The surveillance technique generates an alarm for the ith small area at time period t if the conditional predictive distribution of the new count of disease given the data collected so far is below a critical level α, which controls the trade-off between false alarms and detection delay or detection probability. To assure a low probability of false alarm, a small value of α should be considered. Consequently, small increases in disease incidence may be missed. The results from a simulation study and the subsequent application to ERD for five diseases of the respiratory system demonstrate that, by integrating information from multiple diseases, the proposed multivariate surveillance technique achieves substantial improvements in both detection time and recovery of the true outbreak behavior when changes in disease incidence happen simultaneously for two or more diseases. In the case study, the MSCPO also provides more precise results than the multivariate scan statistic. The MSCPO identifies more accurately the areas affected by disease outbreaks at each time period, reducing so the number of false alarms and enabling a more informed response.
Since the MSCPO does not depend on the model describing the behavior of diseases under endemic periods, it can be applied in any surveillance context where a statistical model is used to describe spatial data on multiple diseases. We have focused here on Bayesian hierarchical Poisson models. In particular, we have proposed a new shared component model formulation that uses binary indicator variables to identify shared and disease-specific spatially correlated latent fields. Joint modeling improves relative risk estimation and goodness of fit when the diseases under study are influenced by common confounding factors. In practice, however, this is not always the case, and so the model includes only disease-specific spatial fields when the diseases of interest are independent. This is equivalent to fitting separate convolution models. A well-known problem with latent structure models is identifiability of the latent components. Empirical evidence of identification is apparent in both the simulated data and the case study. However, additional restrictions such as orthogonality of the latent components may be necessary on some occasions.
As mentioned before, our interest in this article has been to propose a multivariate surveillance technique to jointly monitor multiple diseases in an effort to detect outbreaks at the very moment of their onset. Here the diseases are assumed to be equally important. However, it may be the case that some of the diseases under study have a special relevance. For instance, in the case study, outbreaks of more serious diseases of the respiratory system, such as bronchitis and pneumonia, may be particularly important. As we have shown, these outbreaks are usually preceded by outbreaks of milder diseases such as AURI or influenza. It would be valuable to investigate how this information can be used to predict changes in the relative risk pattern of the diseases of interest. This line of research is particularly useful in a syndromic surveillance setting, where information regarding syndrome-based outbreaks can be used to predict increases in the incidence of the disease of interest.
Acknowledgements
Funding
This research was supported by Grant Number R03CA162029 from the National Cancer Institute. This paper was presented by the author and Prof. Dr. Andrew B. Lawson in an invited talk at GEOMED 2011. The author wishes to express her sincere gratitude to Dr Lawson for his valuable guidance and advice.
References
- 1.Unkel S, Farrington CP, Garthwaite PH, et al. Statistical methods for the prospective detection of infectious disease outbreaks: a review. J Roy Stat Soc Ser A. 2012;175:1–34. [Google Scholar]
- 2.Rogerson PA, Yamada I. Monitoring change in spatial patterns of disease: comparing univariate and multivariate cumulative sum approaches. Stat Med. 2004;23:2195–2214. doi: 10.1002/sim.1806. [DOI] [PubMed] [Google Scholar]
- 3.Kulldorff M. Prospective time-periodic geographical disease surveillance using a scan statistic. J Roy Stat Soc Ser A. 2001;164:61–72. [Google Scholar]
- 4.Kleinman K, Lazarus R, Platt R. A generalized linear mixed models approach for detecting incident clusters of disease in small areas, with an application to biological terrorism. Am J Epidemiol. 2004;159:217–224. doi: 10.1093/aje/kwh029. [DOI] [PubMed] [Google Scholar]
- 5.Diggle P, Rowlingson B, Su T. Point process methodology for on-line spatio-temporal disease surveillance. Environmetrics. 2005;16:423–434. [Google Scholar]
- 6.Vidal Rodeiro CL, Lawson AB. Monitoring changes in spatio-temporal maps of disease. Biometr J. 2006;48:463–480. doi: 10.1002/bimj.200510176. [DOI] [PubMed] [Google Scholar]
- 7.Zhou H, Lawson AB. EWMA smoothing and Bayesian spatial modeling for health surveillance. Stat Med. 2008;27:5907–5928. doi: 10.1002/sim.3409. [DOI] [PubMed] [Google Scholar]
- 8.Watkins RE, Eagleson S, Veenendaal B, et al. Disease surveillance using a hidden Markov model. BMC Medical Informatics and Decision Making. 2009;9:39. doi: 10.1186/1472-6947-9-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Robertson C, Nelson TA, MacNab YC, et al. Review of methods for space-time disease surveillance. Spatial Spatio-temp Epidemiol. 2010;1:105–116. doi: 10.1016/j.sste.2009.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kulldorff M, Mostashari F, Duczmal L, et al. Multivariate scan statistics for disease surveillance. Stat Med. 2007;26:1824–1833. doi: 10.1002/sim.2818. [DOI] [PubMed] [Google Scholar]
- 11.Neill DB, Cooper GF. A multivariate Bayesian scan statistic for early event detection and characterization. Machine Learn. 2010;79:261–282. [Google Scholar]
- 12.Banks D, Datta G, Karr A, et al. Bayesian CAR models for syndromic surveillance on multiple data streams: theory and practice. Inform Fusion. 2010 [Google Scholar]
- 13.Gelfand AE, Vounatsou P. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics. 2003;4:11–25. doi: 10.1093/biostatistics/4.1.11. [DOI] [PubMed] [Google Scholar]
- 14.Knorr-Held L, Best NG. A shared component model for detecting joint and selective clustering of two diseases. J Roy Stat Soc Ser A. 2001;164:73–85. [Google Scholar]
- 15.Held L, Natário I, Fenton SE, et al. Towards joint disease mapping. Stat Meth Med Res. 2005;14:61–82. doi: 10.1191/0962280205sm389oa. [DOI] [PubMed] [Google Scholar]
- 16.Corberán-Vallet A, Lawson AB. Conditional predictive inference for online surveillance of spatial disease incidence. Stat Med. 2011;30:3095–3116. doi: 10.1002/sim.4340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Knorr-Held L. Bayesian modelling of inseparable space-time variation in disease risk. Stat Med. 2000;19:2555–2567. doi: 10.1002/1097-0258(20000915/30)19:17/18<2555::aid-sim587>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 18.Lawson AB. Bayesian disease mapping: hierarchical modeling in spatial epidemiology. Boca Raton: Chapman & Hall; 2009. [Google Scholar]
- 19.Lawson AB. Spatial and spatio-temporal disease analysis. In: Lawson AB, Kleinman K, editors. Spatial and syndromic surveillance for public health. Chichester: Wiley; 2005. pp. 55–76. [Google Scholar]
- 20.Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math. 1991;43:1–59. [Google Scholar]
- 21.MacNab YC. On Bayesian shared component disease mapping and ecological regression with errors in covariates. Stat Med. 2010;29:1239–1249. doi: 10.1002/sim.3875. [DOI] [PubMed] [Google Scholar]
- 22.Ma H, Carlin BP. Bayesian multivariate areal wombling for multiple disease boundary analysis. Bayesian Anal. 2007;2:281–302. [Google Scholar]
- 23.Wang F, Wall MM. Generalized common spatial factor model. Biostatistics. 2003;4:569–582. doi: 10.1093/biostatistics/4.4.569. [DOI] [PubMed] [Google Scholar]
- 24.Lawson AB, Song HR, Cai B, et al. Space-time latent component modeling of geo-referenced health data. Stat Med. 2010;29:2012–2027. doi: 10.1002/sim.3917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Frühwirth-Schnatter S, Lopes HF. Parsimonious Bayesian factor analysis when the number of factors is unknown. Technical Report, University of Chicago Booth School of Business; 2009. [Google Scholar]
- 26.Congdon P. Bayesian statistical modelling. 2nd edn. Chichester: John Wiley & Sons; 2006. pp. 425–455. [Google Scholar]
- 27.Geisser S, Eddy W. A predictive approach to model selection. J Am Stat Assoc. 1979;74:153–160. [Google Scholar]
- 28.Gelfand AE, Dey DK, Chang H. Model determination using predictive distributions with implementation via sampling-based methods. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian statistics 4. Oxford: Oxford University Press; 1992. pp. 147–167. [Google Scholar]
- 29.SaTScan™v9.1.1: Software for the spatial and space-time scan statistics. [accessed 26 October 2011];2009 http://www.satscan.org/