ASSESSMENT OF THE RISK FOR DEVELOPING A SECOND MALIGNANCY FROM SCATTERED AND SECONDARY RADIATION IN RADIATION THERAPY

Abstract

With the average age of radiation therapy patients decreasing and the advent of more complex treatment options comes the concern that the incidences of radiation-induced cancer might increase in the future. The carcinogenic effects of radiation are not well understood for the entire dose range experienced in radiation therapy. Longer epidemiological studies are needed to improve current risk models and reduce uncertainties of current risk model parameters. On the other hand, risk estimations are needed today to judge the risks vs. benefits of modern radiation therapy techniques. This paper describes the current state-of-the-art in risk modeling for radiation-induced malignancies in radiation therapy, distinguishing between two volumes. First, the organs within the main radiation field receiving low or intermediate doses (typically between 0.1 and 50 Gy). Second, the organs far away from the treatment volume receiving low doses mainly due to scattered and secondary radiation (typically below 0.1 Gy). The dosimetry as well as the risk model formalisms are outlined. Furthermore, example calculations and results are presented for intensity-modulated photon therapy vs. proton therapy.

INTRODUCTION

Dose delivered to healthy tissue during radiation therapy can lead to various side effects. Some of the effects can appear immediately (early effects); some of them can occur after a latency period (late effects), as for example causing a second cancer later in life. A radiation-induced tumor has a different histology compared to the original disease. There typically is a latency period of several years for a radiation-associated tumor. Even 30–40 y after initial radiation treatment, cancer survivors remain at an increased risk of developing a second cancer (Chaturvedi et al. 2007). Over a 25 y follow-up the cumulative risk has been estimated to be in the order of 2–11% (Kuttesch et al. 1996; Minniti et al. 2005). The risk might level off after ~10 y for some tumor types (e.g., acute nonlymphocytic leukemia and non-Hodgkin’s lymphoma) while for others it may increase even more than 20 y following treatment (Foss Abrahamsen et al. 2002). Thus, the latency period might not exceed the life expectancy especially for pediatric patients. Consequently, second malignancies are of particular concern for young patients (Neglia et al. 2006; Ron 2006). The Childhood Cancer Survivor Study presents an ongoing multi-institutional retrospective study of over 14,000 cases (Neglia et al. 2001; Kenney et al. 2004; Sigurdson et al. 2005; Bassal et al. 2006; Ronckers et al. 2006; Armstrong et al. 2010, 2011).

The likelihood of developing a second cancer depends on various factors (e.g., the irradiated volume and the dose distribution). Solid cancers are mostly found within or close to the primary cancer treatment field (Doerr and Herrmann 2002; Diallo et al. 2009) (e.g., causing bone and soft tissue sarcoma) (Kuttesch et al. 1996; Rubino et al. 2005). Nevertheless, low doses delivered far outside the main field have also been associated with second malignancies (Ron et al. 1988).

The data on second cancers at medium or high dose levels are quite limited. The number of radiation therapy patients and the variety of treatment sites and modalities (including mixed treatments using radiation and chemotherapy) do not allow a reliable epidemiological analysis of radiation-induced cancer incidences. On the other hand, for low doses one can utilize incidence and cancer mortality data for atomic-bomb survivors (Pierce et al. 1996; Preston et al. 2003; Imaizumi et al. 2006). One needs to note that in these cases the radiation exposure was acute over a very short period of time, unlike in fractionated radiation treatment typically applying doses to the tumor on the order of 2 Gy per daily fraction over several weeks. Furthermore, the radiation field, consisting of neutron, photons, and other particles, was different compared to radiation therapy.

This paper summarizes some of the current approaches towards modeling the radiation-induced cancer risk for patients treated with radiation therapy. As examples, results for risk estimations in intensity modulated photon as well as proton radiation therapy are given.

METHODOLOGY FOR SECOND CANCER RISK MODELING

For cancer risk analysis one might distinguish between two different volumes in the patient. One might exclude the target volume treated with the therapeutic dose because the goal is to kill all cells and therefore, ideally, no mutations should occur in this volume. There are organs in the tumor vicinity that are imaged and considered for treatment planning. These may intersect with the beam path and typically receive low to intermediate doses (typically between 0.1 and 50 Gy). The authors call this volume the in-field volume (IFV). In addition, there is the rest of the patient body, which typically receives very low doses (typically below 0.1 Gy). This area is typically not considered, or even imaged, for treatment planning. The authors call this the out-of-field volume (OFV).

Dosimetry

Epidemiological studies for cancer risk assessment from radiation therapy should not be based on simply characterizing an external radiation field and estimating average organ doses. This might be appropriate for regulatory guidelines and for radiation protection purposes with respect to the general public. Instead, organ and patient specific doses are to be considered.

Organ doses in the IFV are provided by the treatment planning program. Most critical organs are delineated for planning purposes so that organ dose distributions can be extracted. Treatment planning software calculates the dose on a patient computed tomography (CT) dataset using analytical functions based on measured input data. The situation is different for the OFV. Typically, this region is not included in the patient’s CT image used for planning. Even if a whole-body CT is available in rare occasions, the doses in the OFV are typically too low to be deduced to sufficient accuracy from the treatment planning system. Standard algorithms are typically not commissioned for small doses and do not explicitly take into account scattered and secondary radiation far outside of the target.

To estimate the dose in the OFV Monte-Carlo dose calculation can be used. The Monte-Carlo method is the most accurate method of simulating particle interactions within a medium. The simulation outcome is determined from probability distributions describing the underlying physics at each step of a particle being tracked through a geometry. Monte-Carlo simulations offer huge flexibility (e.g., scoring the dose from different particles or interactions separately). Many particles need to be simulated in order to achieve a given uncertainty causing typically long computation times. Whole-body computational phantoms can play an important role when combined with Monte-Carlo dose calculations to simulate scattered or secondary doses (e.g., neutron doses) to organs. Such phantoms provide the geometries to assess adult and pediatric organ doses where whole-body CTs are not available (Zacharatou Jarlskog and Paganetti 2008; Athar and Paganetti 2009, 2011). Many models representing adult male and female as well as children have been developed, mostly from segmented whole-body images (Xu and Eckerman 2009).

Relative Biological Effectiveness

The relative biological effectiveness (RBE) of a radiation is generally defined relative to photon radiation (e.g., ⁶⁰Co). Note that this RBE is defined for a given dose, endpoint, and radiation characteristic. The RBE of protons relative to photons shows only little variation from an average value of ~1.1, except for small volumes in the distal fall-off of a beam and for some biological endpoints with low α/β ratio (Paganetti et al. 2000, 2002). The α and β values are used to parameterize a linear quadratic dose-response curve for cell-line specific endpoints using the form e^{−αDose–βDose2}. In the IFV, the dose delivered to patients by proton beams is scaled by an RBE of 1.1 to cause the same biological effect compared to photon beams. Proton doses are prescribed in the unit Gy(RBE).

The situation is more complex and associated with bigger uncertainties in the OFV. The RBE increases considerably at very small doses. Furthermore, particles generated in nuclear interactions of primary protons can be very short ranged [less than or equal to the range of the primary proton (e.g., secondary protons)] or long-ranged (secondary neutrons). Neutrons can be generated when the primary proton beam interacts with devices in the treatment head but also when interacting inside the patient. When assessing the effectiveness of neutron related doses, not only the absorbed dose but also the neutron energy distribution needs to be considered.

There are very limited data on the RBE of neutron radiation and the impact on potential long-term side effects. It has been estimated that the neutron RBE for carcinogenesis at low doses might be ~25 (Brenner and Hall 2008). Based on the atomic-bomb survivor data, the neutron RBE for tumor induction was estimated to be even 70±50 (Zaider 1991). Others have estimated the low-dose RBE for neutron-induced carcinogenesis in humans to be 100 for solid-cancer mortality (Kellerer et al. 2006) and 63 for overall cancer incidence (Little 1997) based on the atomic-bomb survivors. Values up to 80 have been reported considering several endpoints (Dennis 1987; NCRP 1990; Edwards 1999). Thus, the effectiveness of neutron radiation is subject to significant uncertainties (Kocher et al. 2005; Brenner and Hall 2008; Xu and Paganetti 2010).

While the RBE is defined for a given level of effect, radiation weighting or quality factors are regulatory quantities estimating the maximum RBE (i.e., where the dose approaches infinitesimal values). The equivalent dose is the average absorbed dose in an organ, modified by a radiation weighting factor for the type and energy of the external radiation. For neutrons, the International Commission on Radiological Protection (ICRP) defines an energy dependent bell-shaped curve with a maximum weighting factor of 20 at ~1 MeV (ICRP 1991, 2003, 2007). Most second cancer risk studies in radiation therapy have been done using the weighting factor concept. The average neutron weighting factor in the human body for a proton beam entering the patient is typically found as to be between 2 and 11 (Yan et al. 2002; Jiang et al. 2005; Wroe et al. 2007).

For estimating side effects from low doses in radiation therapy the quality factor concept is more meaningful than the weighting factor concept. The latter causes ambiguities as neutrons deliver most of their dose via secondary protons while both particles are associated with different weighting factors. Using a quality factor, the actual energy deposited is weighted instead of considering particle and energy dependent values. The quality factor is defined as a function of the unrestricted linear energy transfer of charged particles in water. It is independent of the energy-depositing particle and its maximum value is ~30 as defined by the ICRP (2003). This concept allows proper consideration of internal and external radiation (Xu and Paganetti 2010).

Note that the effective dose is the weighted sum of various organ or tissue doses using tissue weighting factors (ICRP 1991, 2003, 2007). It is applicable when estimating effects for the general public. It might even be applicable to patients in order to define regulatory guidelines (e.g., for CT dose exposure). The effective dose is applicable when estimating radiation effects for a group of people, but not for a specific individual (i.e., a patient undergoing radiation therapy). For epidemiological studies or to compare risks for individuals the effective dose should not be used.

Risk models

The dose-response relationships for radiation-induced tumors in the OFV can be assessed based on atomic-bomb survivor data (Pierce et al. 1996; Preston et al. 2004, 2007; Walsh et al. 2004a, 2004b) although these models are associated with considerable uncertainties (NCRP 1997; EPA 1999; Kry et al. 2007). Data on solid tumor mortality among the atomic-bomb survivors are consistent with a linear model up to ~2.5 Sv (Pierce et al. 1996; Preston et al. 2003). This linear dose-response curve seems to be valid also when estimating the relative risk of cancer in patients (Little 2000, 2001). Various dose response relationships for carcinogenesis have been suggested (Brenner et al. 2003; Brenner 2009; Mullenders et al. 2009) and low-dose risk models have been summarized or developed by radiation protection bodies (BEIR 2006; UNSCEAR 2006a, 2006b). The assumption of a linear dose-response curve is not valid for all cancers. An increasing slope has been found as dose-effect relationship for radiation-induced leukemia (Preston et al. 2003) [e.g., a linear-quadratic relationship (BEIR 2006)]. Note also that at very low doses (below ~0.1 Sv), current epidemiological data are insufficient to predict the shape of the dose-response curve (Brenner et al. 2003). Typically, a linear no-threshold model is suggested (ICRP 1991; BEIR 2006). This assumption might at this point be based mainly on the lack of data than on solid scientific facts. The formalism described as follows relies on a linear no-threshold assumption for solid cancers.

Young patients are especially prone to the carcinogenic effects of radiation (Foss Abrahamsen et al. 2002; Bhatia and Landier 2005; Imaizumi et al. 2006). The increasing risk with decreasing patient age is mainly due to a greater radiation effect in humans during the period of rapid cell proliferation (e.g., during development of the thyroid gland).

Risks can be calculated as a function of attained age of the individual (a), age at exposure (e), absorbed dose (D), sex (s), and a parameter denoting population characteristics (Kellerer et al. 2001; BEIR 2006). Low dose models to calculate specific risks of cancer incidence and mortality with organ specific parameters are given, for example, in the report by the Committee on Biological Effects of Ionizing Radiation (BEIR 2006). The excess absolute risk (EAR) can be defined in the form:

$$\mathit{EAR}\left(s,t,a,D\right)=\rho \left(D\right)·{\beta }_s·exp\left(\gamma e\right)·a^{\eta }$$

Slight variations of this formalism apply for specific organs. The model parameters, β, γ, and η, are defined based on fits to cancer incidence or mortality data. The term ρ(D) defines the dose-response relationship and equals D in case of linearity. The formalism is valid for low doses if one assume that the form of the dose response relationship does not change down to infinitesimal doses and if the organ dose is fairly homogeneous.

The formalism presented above is no longer valid in the IFV. At higher doses, dose-volume effects might play a role. Furthermore, mutagenesis is in competition with cell survival causing the dose-response relationship to become nonlinear, as sterilized cells will not mutate (Upton 2001; Sigurdson et al. 2005). The risk might eventually decreases with increasing dose. One also needs to consider that tissues may respond to radiation by accelerated repopulation (Sachs and Brenner 2005).

Nevertheless, a linear increase in risk with dose even beyond 40 Gy was found for meningioma and glioma (Neglia et al. 2006; Meadows et al. 2009), which could be due to cell killing being fully balanced by repopulation. A linear increase to high doses was also suggested for second cancers after Hodgkin lymphoma or cervical cancer (Boice et al. 1987; Gilbert et al. 2003). Some human data do show a leveling off at higher doses (Tucker et al. 1987; Curtis et al. 1997). A slight decrease after ~4 Gy has been observed for leukemia after cervical cancer (Boice et al. 1987; Blettner and Boice 1991; Curtis et al. 1994). For thyroid cancer a bell-shaped response curve with linearity up to ~25 Gy has been seen (Bassal et al. 2006; Meadows et al. 2009) with an eventual decrease of the risk with increasing dose (Sigurdson et al. 2005). A detailed analysis of thyroid cancer in childhood cancer survivors revealed a linear dose-response relationship with an ERR Gy^–1 of ~1.3 for doses below 6 Gy (Ronckers et al. 2006). For higher doses, the authors found a decrease in the ERR Gy⁻¹ of 53% at 20 Gy and 95% at 40 Gy. It is difficult to deduce reliable dose-response curves from radiation therapy due to the inter-patient variability and low frequency of incidence (Suit et al. 2007).

Because simple dose-response parameterizations and data fits as often used in the OFV are not feasible in the IFV a more mechanistic interpretation is necessary when developing risk models. Medium to high dose models do incorporate mechanistic considerations regarding the competing probabilities for DNA mutation and cell survival to guide parameter fits. One such model is based on organ equivalent dose (OED). The OED concept does take into account that IFV organs typically receive inhomogeneous dose distributions. By definition, any dose distribution in an organ is equivalent and corresponds to the same OED if it causes the same radiation-induced cancer incidence. The EAR as a function of D, a, e, and s, can be written as a product of OED and the initial slope (i.e., with a risk factor based on low-dose risk models) like the one given above (Schneider and Kaser-Hotz 2005a, 2005b; Schneider et al. 2005). Parameters for OED are the organ-specific cancer incidence rate at low doses, which can be taken from the data of the atomic-bomb survivors, and an organ-specific cell sterilization at higher doses taking into account cell-killing effects by an exponential function that depends on the dose (Schneider et al. 2005). There are not enough second cancer data to allow accurate parameter fits for the model. Therefore, model parameters to describe the high dose response were estimated by analyzing secondary cancer incidences in patients with Hodgkin’s disease, a patient population with considerable data on second tumors because of genetic susceptibility (Schneider and Walsh 2008).

Several mathematical expressions might describe the dose-response function (e.g., linear, bell-shaped, or plateau-shaped curves). In order to consider not just the average dose but the dose distribution, for a volume N each CT voxel (i) is considered independently:

$$\text{Linear}:\mathit{OED}=\frac{1}{N}\sum _i{V}_i{D}_i$$

$$\text{Bell}-\text{shaped}:\mathit{OED}=\frac{1}{N}\sum _i{V}_i{D}_{i}exp\left(-{\alpha }_{\mathit{organ}}{D}_i\right)$$

$$\text{Plateau}-\text{shaped}:\mathit{OED}=\frac{1}{N}\sum _i{V}_i\frac{\left(1-exp[-{\delta }_{\mathit{organ}}{D}_i]\right)}{{\delta }_{\mathit{organ}}}$$

The parameters are the voxel volume V_i, the voxel dose D_i and parameters describing the shape of the response curve, α_organ and δ_organ.

One might also take into consideration that carcinoma and sarcoma might have different functional dose relationships (Schneider 2009). Carcinoma induction is proportional to the sum of surviving original and repopulated cells and is expected to show a bell-shaped pattern as long as cell repopulation is small.

Uncertainties

Dosimetry in the IFV follows clinical specifications (i.e., the dose is presumably within 2%). Uncertainties in the OFV are considerably bigger. Not only are doses lower, adding statistical uncertainties when simulating them when using Monte-Carlo simulations, but also there might be additional uncertainties due to radiation weighting or quality factors. The biological effectiveness of neutrons is subject to significant uncertainties as has been discussed above. The uncertainty might well be on the order of 10–50%. Risk model parameters are mainly based on atomic-bomb survivor data at low doses and clinical data at higher doses. Furthermore, due to inter-patient variability and the low frequency of second cancers, dose-response relationships from patient data are associated with large uncertainties. To establish a reliable dose-response relationship for second cancers as a function of modality, treatment site, beam characteristics, and patient population, progressively larger epidemiological studies are required. Absolute risk values might thus not be trustworthy. However, comparison of different treatment options (i.e., relative studies) are meaningful (Kry et al. 2007).

STUDIES TO ESTIMATE THE RISK FOR SECOND CANCERS

Risks for radiation-induced cancers in the out-of-field volume

Scattered photon doses in photon therapy have been studied experimentally and theoretically for a long time. In recent years, proton therapy has been the focus of many experimental and theoretical studies as well. Summaries of these studies are given elsewhere (Palm and Johansson 2007; Xu et al. 2008). Although secondary radiation is also generated in the patient itself, treatment head contributions typically dominate.

For photon therapy (at least when using 6 MV beams), the dose in the OFV region is solely due to scattered photons. Increased scattered photon doses can be expected for intensity modulated radiation therapy (IMRT) because of the increased number of monitor units to be delivered as parts of the beam are blocked by the multi-leaf collimator during beam delivery.

In proton therapy, the main concern is for passive scattered proton beam delivery. Here, the OFV dose is mainly caused by secondary neutrons generated when the primary proton beam interacts with objects in the treatment head. Various scatterers, beam-flattening devices, collimators, and energy-modulation devices are in the beam path. Double scattering systems are typically designed to create a homogeneous field with the maximum size commissioned for treatment. For each treatment field, apertures and range compensators are being used. Neutrons are generated in the modulator wheel as well as in collimators and patient specific apertures (Moyers et al. 2008; Perez-Andujar et al. 2009). Depending on the actual required field size for a treatment, a high percentage of primary protons are being stopped in the treatment head. The efficiency of most proton therapy treatment heads is quite low (typically only between 3 and 30% depending on the field size). The neutron dose depends on the ratio of field size to aperture opening and neutron doses from treatment head neutrons typically increase with decreasing field size (Mesoloras et al. 2006; Zacharatou Jarlskog et al. 2008; Hecksel et al. 2010). It has been shown that for a small target volume, the contribution of neutrons from the treatment head can reach ~99 % of the total neutron contribution, while for a large target volume it can go down to ~60 % (Zacharatou Jarlskog et al. 2008). The remainder is due to proton-nuclear interactions in the patient.

Consequently, a treatment head using the passive-scattering technique may show a 10-fold secondary neutron dose disadvantage as compared with the spot-scanning proton delivery technique (Miralbell et al. 2002; Jiang et al. 2005). Proton beam scanning typically does not employ significant scatterers in the treatment head. The efficiency of beam scanning delivery systems is therefore higher and results in less proton interaction in the beam path to the patient, which in turn reduces the neutron production significantly. Proton beam scanning reduces the neutron dose exposure significantly, particularly for small treatment fields (Clasie et al. 2010). It has been shown that the secondary and scattered dose in the OFV is lowest for proton beam scanning when compared with photon therapy and passive scattered proton therapy (Athar et al. 2010).

The majority of the neutron-generated dose is deposited by high-energy neutrons (e.g., about two-thirds of the neutron dose in a typical proton therapy scenario) is deposited via neutrons with energy above 100 MeV (Zheng et al. 2007).

Neutrons, albeit with a much lower fluence, are also generated in the patient. The neutron yield and the neutron dose from neutrons generated in a patient also depend on the beam range, aperture size, snout extension, lateral distance, aperture thickness, and modulation width (Zheng et al. 2007). Thus, in scanning, the main parameter influencing the neutron dose is the treatment volume (Schneider et al. 2002). Neutron doses increase with increasing range and modulation width (Polf and Newhauser 2005; Zacharatou Jarlskog et al. 2008). The greater the penetration of the beam, the greater is the overall likelihood of a nuclear interaction producing neutrons.

Organ doses vary considerably depending on their position relative to the high dose region of the target. Furthermore, they depend on the specific field arrangement, treatment site, modality, etc. This is illustrated in Fig. 1 where the neutron equivalent dose as a function of distance to the target is shown for passive scattered proton therapy. The shaded area shows the range one might expect. The figure also gives the range of published values for scanned proton beams.

Fig. 1.

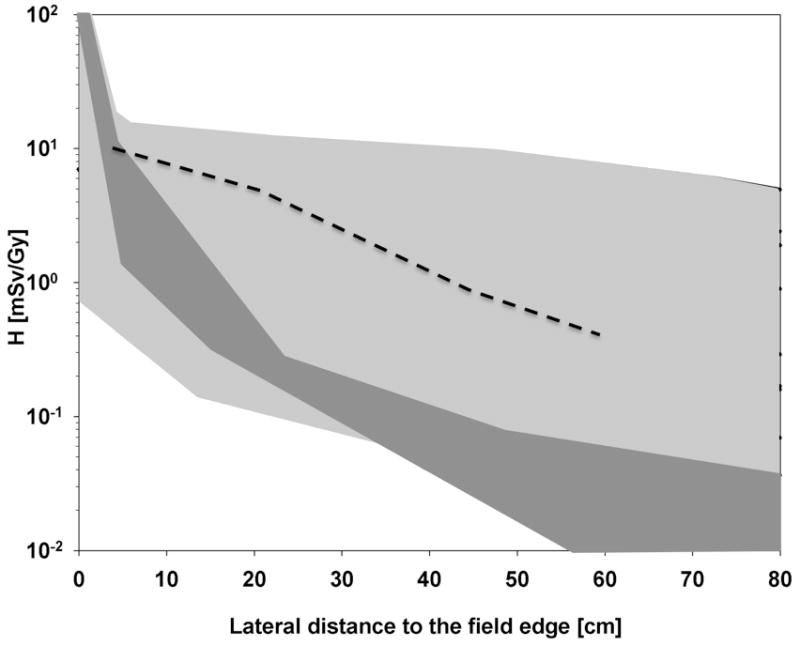
Equivalent dose per treatment dose (mSv Gy⁻¹) as a function of lateral distance to the field. Light grey area: Range of measured (Yan et al. 2002; Mesoloras et al. 2006; Wroe et al. 2007, 2009; Moyers et al. 2008; Yonai et al. 2008; Clasie et al. 2010) and simulated (Polf and Newhauser 2005; Zheng et al. 2007; Moyers et al. 2008; Zacharatou Jarlskog et al. 2008; Clasie et al. 2010) data for a variety of proton beam configurations using passive scattered beam delivery. Dark grey area: Results for scanned proton beams (Schneider et al. 2002; Clasie et al. 2010). Also shown for comparison is the scattered photon dose equivalent for a randomly chosen 10×10 cm² intensity-modulated photon field using a 6 MV beam (dotted line) (Klein et al. 2006).

Various studies have used whole-body patient phantoms and Monte-Carlo simulations to calculate OFV organ doses in radiation therapy (Jiang et al. 2005; Fontenot et al. 2008, 2009; Zacharatou Jarlskog et al. 2008; Athar and Paganetti 2009; Newhauser et al. 2009; Taddei et al. 2009; Athar et al. 2010). Based on such simulations the risks for developing a second malignancy in patients have been estimated (Jiang et al. 2005; Brenner and Hall 2008; Zacharatou Jarlskog and Paganetti 2008; Athar and Paganetti 2009; Newhauser et al. 2009; Taddei et al. 2009; Athar et al. 2010).

The cancer incidence risk from passive scattered proton therapy compared to photon IMRT is shown in Fig. 2 for a treatment site in the spine (close to T12). The figure is based on data that have been published previously (Athar and Paganetti 2011). The treatment fields considered were rather small with an average field diameter of 6 cm. Consequently, there is a slight disadvantage for passively scattered proton therapy, at least for organs relatively close to the target (but in the OFV). As the distance increases, the risk from photon therapy becomes higher compared to proton therapy. If one assumes a linear dose response relationship for second cancer risk estimates for these organs, the relative values protons vs. photons do not change when converting from dose to risk. Most of the calculated lifetime risks in the OFV are below 1% and below the baseline risks (Athar and Paganetti 2009).

Fig. 2.

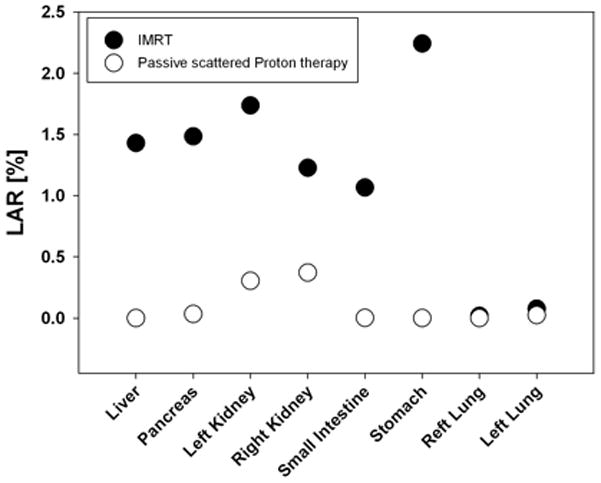
Lifetime attributable risks (LAR) assuming an 8 y old female patient with an expected attained age of 75 y based on EAR for various organs in the OFV. The treatment site was next to the spine, close to T12. The data are averaged over six treatment fields with an average diameter of 6 cm. Risk estimations are based on EAR low-dose risk formalism by BEIR (2006). Close circles: IMRT delivery; open circles: passive scattered proton delivery.

It has been demonstrated that with scanned beam proton therapy there is the potential to reduce the incidence of radiation-induced second cancers by a factor of 2–15 (Miralbell et al. 2002). In another study, cranio-spinal irradiation of a male patient was simulated for passively scattered and scanned-beam proton treatment units and the total lifetime risk of second cancer due exclusively to secondary radiation was 1.5% for the passively scattered treatment vs. 0.8% for a scanned proton treatment (Newhauser et al. 2009).

Risks for radiation-induced cancers in the in-field volume

The risk for developing a second malignancy is typically higher in the IFV compared to the OFV because of the higher doses delivered to organs at risk in-field. Due to the increasing dose conformity, IMRT and proton therapy are expected to decrease the risk for second malignancies compared to conventional photon techniques (Schneider et al. 2008).

In general, one can expect a reduction of the second cancer risk in the IFV when using protons instead of photons. The total energy deposited in the patient for a given treatment volume is always higher with photon irradiation as compared to proton irradiation by a factor of about three considering standard photon techniques and a factor of about two considering IMRT (Lomax et al. 1999). Protons typically allow either a smaller dose to critical structures or a higher dose to the target while maintaining the target dose compared to photon techniques. Reducing dose to critical structures can cause a significant reduction in early and late side effects when using protons in favor of photons (Miralbell et al. 2002; Merchant et al. 2008).

Nevertheless, a direct comparison is not straightforward because for a given organ the risk depends on the actual treatment plan. As doses are inhomogenous for organs in the IFV, treatment planning considerations can influence potential risks for side effects. From a standpoint of reducing the risk for second malignancies it might be beneficial to reduce the overall treatment volume. However, this has to be balanced against other side effects that might deserve higher attention [e.g., radiation-induced reduction in cognitive function (Merchant et al. 2008)].

Using the risk formalism described above, the authors have assessed the risks for a series of organs in the IFV considering a 14 y old male patient with a lesion near the spine (close to T12). The prescribed dose was 52.2 Gy. Treatment plans using passive scattered proton therapy are compared with photon IMRT plans in Fig. 3. The significant advantage of proton therapy is quite obvious for the case considered. Some organs could be spared from radiation entirely by using protons (e.g., liver, stomach, right lung), causing no risk to those organs at all. Overall, the risk reduction can be expected to be roughly proportional to the reduction of energy deposited when using protons. This does not necessarily hold if the dose-response curve is nonlinear.

Fig. 3.

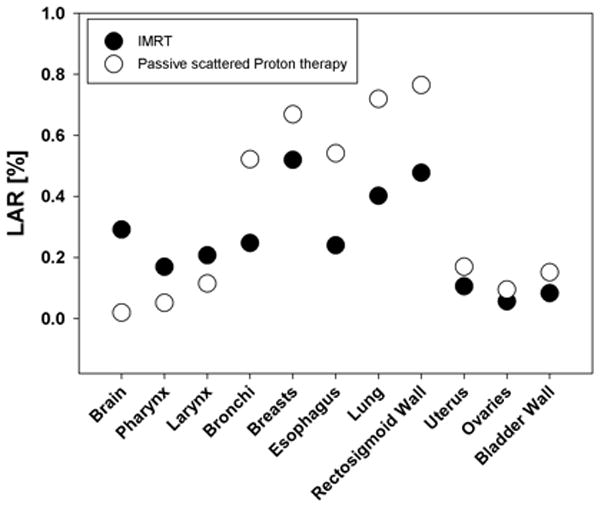
Lifetime attributable risks (LAR) for a 14 y old male patient with an attained age of 75 y based on EAR for various organs in the IFV. Treatment area was the spine, close to T12. Risk estimations are based on the model by Schneider (2009) in combination with the EAR low-dose risk formalism by BEIR (2006). Close circles: IMRT delivery; open circles: passive scattered proton delivery.

CONCLUSION

This paper summarized the methodology to assess the risk for developing a second malignancy caused by low doses of scattered/secondary radiation distant to the target as well as caused by moderate/high doses in the volume considered in treatment planning. Dosimetric considerations as well as risk model formalisms have been presented.

The authors have analyzed the risk for passive scattered proton therapy and photon IMRT treatments. For the treatment fields considered here, there seems to be a clear advantage for proton therapy for organs far away from the target (OFV). However, within approximately 25 cm from the field edge (still OFV), the scattered photon dose in IMRT seems to be lower than the neutron equivalent dose from passive scattered proton therapy (Athar et al. 2010). The results do depend on the patient-specific treatment field. Fields of, on average, 6 cm diameter were applied.

Higher risks are found closer to the target (i.e., in the IFV). In regions where the primary beam delivers the majority of the dose (IFV), there is an overall advantage for proton therapy, as has also been suggested previously (Fontenot et al. 2009; Newhauser et al. 2009; Athar et al. 2010). This can be explained by the reduced total energy deposited in the patient when using protons instead of photons.