Estimating the order of mutations during tumorigenesis from tumor genome sequencing data

Abstract

Motivation: Tumors are thought to develop and evolve through a sequence of genetic and epigenetic somatic alterations to progenitor cells. Early stages of human tumorigenesis are hidden from view. Here, we develop a method for inferring some aspects of the order of mutational events during tumorigenesis based on genome sequencing data for a set of tumors. This method does not assume that the sequence of driver alterations is the same for each tumor, but enables the degree of similarity or difference in the sequence to be evaluated.

Results: To evaluate the new method, we applied it to colon cancer tumor sequencing data and the results are consistent with the multi-step tumorigenesis model previously developed based on comparing stages of cancer. We then applied the new method to DNA sequencing data for a set of lung cancers. The model may be a useful tool for better understanding the process of tumorigenesis.

Availability: The software is available at: http://linus.nci.nih.gov/Data/YounA/OrderMutation.zip

Contact: rsimon@mail.nih.gov

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Human tumors are thought to arise and evolve through a sequence of somatic alterations to DNA but the early stages of oncogenesis occur years before tumor detection and are rarely directly observable. Better understanding the temporal order of mutations is important since the early mutations may represent important therapeutic targets and late mutations may play important roles in metastasis.

Vogelstein et al. (1988) inferred some information about the sequence of genetic alterations associated with the stages of colorectal tumors. By examining the genomes of small colonic adenomas, intermediate-sized adenomas, large adenomas and carcinomas, they discovered that most of the early stage adenomas showed loss of heterozygosity (LOH) in the APC gene. Almost half of intermediate-sized adenomas carried an additional mutation in KRAS. The long arm of Chromosome 18 showed frequent LOH in advanced adenomas and carcinomas. Also frequent LOH on the short arm of Chromosome 17, which later turned out to target TP53, was observed mainly in carcinomas. Although, the loss of APC gene function almost always occurs as an initiating event in colorectal tumors, the precise order of subsequent alterations seemed to vary among tumor samples (Vogelstein et al., 1988; Weinberg, 2006).

Developing evidence for an ordered sequence of mutations driving tumor progression was possible for colorectal tumors due to the accessibility of the colonic epithelium to colonoscopy. For other tumor types, however, such evidence is not well developed. For this reason, there has been interest in indirect computational methods to provide information about the order of mutations (Attolini et al., 2010; Desper et al., 1999; Durinck et al., 2011).

Desper et al. (1999) attempted to estimate the order between gains and losses on chromosomal regions by fitting an oncogenic tree model to CGH data. Attolini et al. (2010) used a population genetics mathematical model describing the evolutionary paths of cells from the unmutated state to the fully mutated state. In their model, the parameters such as rates of mutations, amplification or deletion, and the number of cells per patient at risk of tumorigenesis are assumed constant for all tumor samples. The methods of Desper et al. (1999) and Attolini et al. (2010) are very complex and the number of trees to be searched or the number of parameters to be fit increases exponentially with the number of investigated genes. Consequently, these models are restricted to investigation of a very small number of driver genes. These models address mutational events which co-occur and cannot explain the negative correlation between some pairs of mutations, such as those for genes in the same pathway.

Durinck et al. (2011) estimated the order of mutations in areas of copy-neutral LOH (CN-LOH) as well as the order of occurrence of CN-LOH regions within an individual cancer. They used the idea that if a mutation precedes a regional duplication, its copy number is doubled, whereas mutations following a duplication event appear with haploid copy number. Although this method can provide accurate estimates, it is restricted to CN-LOH regions.

Recent advances in sequencing technologies have made it possible to perform large scale resequencing of tumor genomes. These studies have often identified a large number (dozens) of driver genes (genes causing clonal expansions when mutated). These studies generally define driver genes as those which are more frequently mutated than expected based on the background mutation rate estimated from synonymous mutations. Since the lists of detected driver genes do not generally provide satisfactory insight into the process of oncogenesis, methods which can help to elucidate the order of the mutational events in driver genes and can handle a large number of driver genes would be useful. In this article, we propose a method which can estimate the order of mutations in driver genes from genome sequences of a set of tumors. The method is not restricted to a very small number of driver genes and does not utilize a complex cell level model. By comparing mutation profiles of driver genes in a large number of tumors of a type, the probability distribution for the order of mutations is estimated. This enables the degree of similarity or difference in the order for that set of tumors to be evaluated.

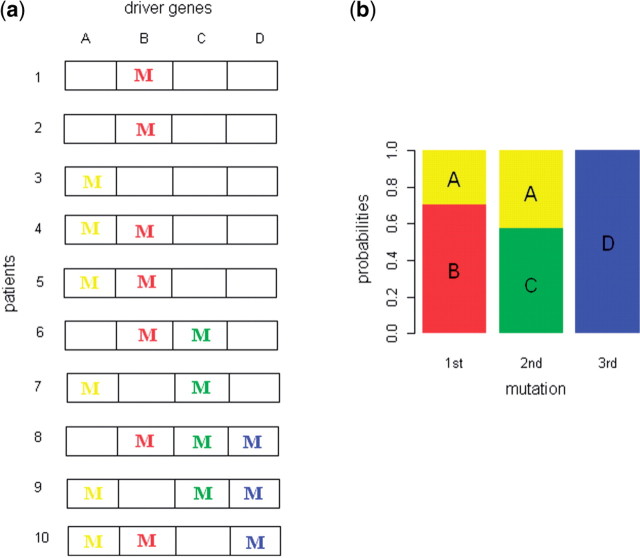
Consider a population of patients at various stages of the same histologic type of cancer in which four tumor driver genes have been identified. For each patient, the colored letter ‘M’ in Figure 1a represents a mutation for the corresponding gene. As tumorigenesis progresses, tumor cells accumulate more mutations in tumor driver genes. Our statistical model estimates P_k,i, the probability that the k-th mutational event involving the four driver genes occurs in gene i. This becomes feasible if we assume that all samples are governed by the same set of P_k,i probabilities. Mutations in gene A, B or C occur in samples having one or two mutations, therefore the probability for the early mutation occurring in gene A, B or C will be high. In contrast, mutations in gene D always occur with mutations in other genes A, B or C. Since other samples support that probability for the early mutation occurring in gene A, B or C will be high, it is likely that gene D occurs as the late event. Figure 1b shows the estimates of P_k,i in which the length of the sub-bar corresponding to gene i at the k-th mutational event is P_k,i.

Fig. 1.

Distribution of mutations in driver genes and estimates of their order (a) Distribution of mutations in four driver genes for ten patients of the same tumor type. For each patient, the colored letter ‘M’ represents a mutation for the corresponding gene. (b) Estimates for P_k,i, the probability that the k-th mutational event involving the four driver genes occurs in gene i. The length of the sub-bar corresponding to gene i at the k-th mutational event is the estimates for P_k,i

We describe the statistical model in Section 2 and present the result obtained by applying this model to lung adenocarcinomas and colorectal tumor sequencing data and simulated data in Section 3.

2 METHODS

An initial step in applying the method we describe is to identify the driver genes based on a study in which a set of tumors have been sequenced. The initial data can consist of either whole exome sequencing or sequencing with regard to a set of candidate genes. For our applications we have identified the driver genes using the method of Youn and Simon (2011). This method finds driver genes based on the frequency of mutations in the genes, and their estimated impact on protein function, and background mutation rate. The background mutation rate is based on the frequency of synonymous mutations and accounts for variation in background mutation rate among tumor samples.

Let G_k^j denote the unknown identity of the driver gene mutated as the k-th event in sample j. These variables take value on the set S of the labels of the driver genes and are defined for k=1,…, m_j where m_j is the number of non-silent mutations in sample j. We assume the probability that G_k^j=i given k≤m_j is the same for all samples and that G_k^j is independent of G_l^j for l≠k and of m_j. We denote this probability by P_k,i.

Let Y_i^j equal the number of times gene i is mutated in sample j. Y_i^j is generally zero or one but in some cases there are more than one mutation in a gene. For each sample we observe all of the Y_i^j-values but do not know the G_k^j-values. For any sample j, there are multiple orders of occurrence of G₁^j, G₂^j,···, G_mj^j that could result in the observed Y_i^j-values. The probability of observing the set of Y_i^j-values for all non-silent mutations for a tumor j can be expressed as

(1)

where the summation is over all sequences of mutations (i₁, i₂,···, i_mj) which are consistent with the observed set of non-silent mutations in sample j. The number of non-silent mutations m_j is represented in this probability to indicate that it is part of the observed data for each sample.

For each order which is consistent with the observed mutations, the probability can be expressed in terms of the random variables G_k^j defined above:

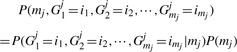(2)

P_k,i was defined as the probability that G_k^j=i given m_j and G_k^j was assumed independent of G_l^j for l≠k and of m_j. Consequently, the probability in (2) can be written as:

(3)

Since the marginal distribution of m_j does not depend on the parameters P_k,i, it can be ignored in the likelihood function. The likelihood function is the product over terms of the form of (1) and can thus be written

(4)

where the summation for the j-th sample is over the same set of mutational sequences as in (1).

We estimate P_k,i by maximizing the log likelihood. Since there is no closed form solution for the maximum-likelihood estimate (MLE) 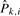, we use a constrained optimization R package ‘alabama’ (Varadhan, 2011) to maximize the log likelihood under the constraint that 0≦P_k,i≦1 and ∑_i∈S P_k,i = 1.

3 RESULTS

3.1 Simulation

First, we checked the validity of our method by applying it to simulated data based on lung tumor sequencing data. Ding et al. (2008) sequenced the coding exons and splice sites of 623 candidate cancer genes in 188 samples from patients with lung adenocarcinomas. We identified 28 tumor driver genes for analysis using the method of Youn and Simon (2011). Table 1 shows the distribution of the number of non-silent mutations in the selected driver genes for each sample. Only samples having any mutations are used in the estimation.

Table 1.

Distribution of number of non-silent mutations in the selected driver genes in samples for non-small-cell lung tumors

Number of mutations	0	1	2	3	4	5	6	7	8
Number of samples	44	42	43	29	9	10	6	0	1

We obtained the MLEs of the 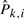as described in Section 2. Since there are few samples which have more than five non-silent mutations, we estimated an averaged distribution for mutations occurring at the n-th step for n>5 by assuming P_n,i=P_5,i for n>5. If we estimate the distribution separately for each n, the estimate would be less accurate. These estimates are shown in Table SB in the Supplementary Materials and will be described below in the section on the lung tumor data but here we regarded those estimates as the true P_k,i for generating simulated data.

1. Sample size effect

To see the effect of the number of samples, we performed the simulation for a quarter, half, equal and double the size of the original number of samples having any mutations in lung tumor data. We generated mutations in samples so that the distribution of the number of mutations in samples was the same as that in lung tumor samples as shown in Table 1. For samples having n mutations, we generated the first mutation according to P₁,., the second mutation according to P₂,., and the n-th mutation according to P_n,.. We performed ten simulations for each size and calculated the MLE 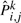for each simulation (k).

Table SA in the Supplementary Materials presents the mean of the MLE 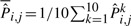for sample size N=144, 288. It shows that the estimates are very close to the true values. We calculated the distance between the MLE and the true value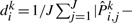 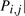for each step i and simulation k and present the mean distance 1/10∑_k=1¹⁰ d_i^k in Table 2. The errors for the original data size are quite small. The distance decreases as the sample size increases. The distance gets smaller for early events, which is because there are more samples that can be used for estimating P_i,., for small i. For example, the samples having any mutations are used for estimating P₁,., whereas only samples having at least five mutations can be used for estimating P₅,..

Table 2.

Distance between the estimate and the true value for each i-th event

No. of samples	i=1	i=2	i=3	i=4	i=5
36	0.019	0.020	0.043	0.043	0.043
72	0.014	0.015	0.033	0.036	0.040
144	0.009	0.011	0.022	0.025	0.030
288	0.005	0.006	0.015	0.013	0.016

The result shows that the estimates obtained from the simulated data with a quarter of the size of the lung data (36 samples) is reasonably close to the true values, especially for early events. However, the accuracy of the estimate depends not only on the size of the data but also on the structure of the data. For example, if the data consist of samples, all of which have five mutations, our method may not give accurate estimates of P_k,i because there are no samples which provide information for early events. In such cases, there may not be a unique MLE and the confidence intervals (CIs) for the estimates will be very wide.

The CI is the best measure for the accuracy and stability of the estimate. In the following section for analysis of the real data, we calculated 90% CI for each estimate of P_k,i. This CI includes the true value of P_k,i 90% of the times that the experiment is repeated when the model is correct. If one applies the method to data with small size or with the structure in which estimation is difficult, the CI will be very wide. Therefore, one can use the CI as the indicator of the reliability of the estimates.

2. Correlation in mutations between genes

Our model assumes independence between k-th event and l-th event when k≠l. Therefore, in a sample having n mutations, the probability that mutations occur in gene i₁, i₂··· i_n in turn is P(G₁=i₁, G₂=i₂,···, G_n=i_n|n)=∏_k=1ⁿP(G_k=i_k|n).

Although we assumed independence between different events, our model can still explain the positive or negative correlations between mutations. For example, if P(G_k=A|n) and P(G_k=B|n) are positive only for k=m, then since both gene A and B mutate only as the m-th event, they cannot mutate together in a sample, showing mutually exclusive mutation patterns. On the other hand, if P(G_k=A|n) is positive only for k=m and P(G_k=B|n) is positive only for k=l and l≠m then since gene A and B mutate only at different steps, they will frequently mutate together in a sample, showing concurrent mutation patterns.

To test whether our model can actually capture the significant interactions existing in the real data, we calculated p-values for positive and negative correlation in mutations between all pairs of genes in real data and those in simulated data generated by our model with P_k,i equal to the MLE estimated from the real data.

For each pair of genes, we calculated the number of samples with concurrent mutations, X₀ and compared this with the null distribution f(x) and used the frequencies of f(x)≧X₀ as p-values for positive correlation and the frequencies of f(x)≦X₀ as p-values for negative correlation. We obtained the null distribution by randomly permuting the observed mutations across samples and genes while keeping the number of mutations in a gene and sample fixed. We repeated permutations for 2000 times and recorded the number of samples with concurrent mutations for each permutation.

For lung data, there is one pair of genes with negative correlation at FDR 0.05: (EGFR, KRAS) and no pair with positive correlation. We simulated data 100 times and calculated the mean p-values between all pairs of 28 driver genes. The mean p-value for negative correlation between EGFR and KRAS is 0.004. No other pairs have p-values for positive or negative correlations <0.05. For colon data, there is no pair with negative correlation and there are five pairs with positive correlations at FDR 0.05: (APC, KRAS), (KRAS, PIK3CA), (KRAS,TP53), (APC,TP53) and (GUCY1A2,RET). For 100 simulated data, the mean p-values for positive correlation for three pairs of genes, (APC, TP53), (APC, KRAS) and (KRAS, TP53) are 0.00009, 0.012 and 0.016, respectively. No other pairs have p-values for positive or negative correlations <0.05. This shows that although our model assumes independence between different mutational events, it can still capture some of the interactions between mutations in genes.

3.2 Lung tumor sequencing data

As described above, we analyzed the data of Ding et al. (2008) on the sequence of exons and splice sites of 623 candidate cancer genes in 188 samples from patients with lung adenocarcinomas. We identified 28 tumor driver genes for analysis using the method of Youn and Simon (2011) and used the profiles of driver mutations to estimate the MLEs of P_1,i, P_2,i, P_3,i, P_4,i, P_5,i. These estimates are shown in Table SB of the Supplementary Materials. Table SB also shows the 90% CIs for the probabilities (CI) computed using the bias-corrected and accelerated bootstrap method (Efron and Tibshirani, 1993).

The result is not affected very much by the stringency criteria used when selecting driver genes. If we loosen the cutoff to FDR level 0.2, 40 driver genes are selected. Table SD in the Supplementary Materials compares the estimates obtained from using 40 driver genes and the estimates obtained from 28 driver genes.

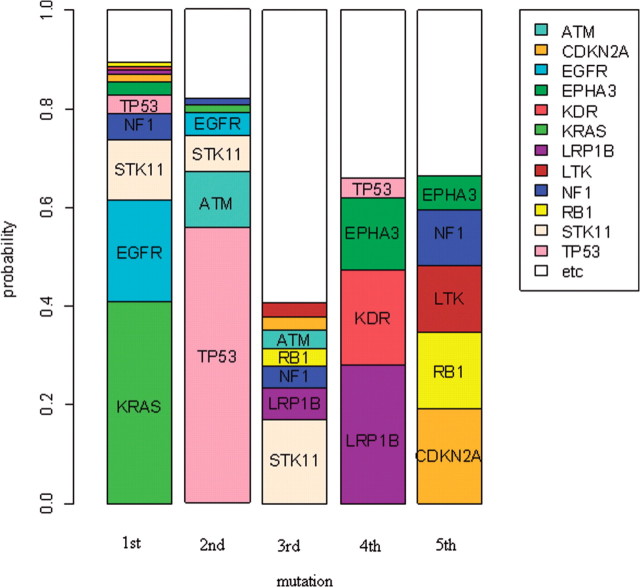
Figure 2 shows a graphical display of the estimates of P_k,i. The length of the sub-bar corresponding to each gene i at the k-th mutational event is the value of P_k,i. It shows that the first mutational event occurs mainly in KRAS, EGFR and STK11. The estimated probability that the first mutation occurs in KRAS is 0.411 with a 90% CI, (0.351,0.476). The probability in EGFR is 0.204 with a 90% CI, (0.157,0.269) and that in STK11 is 0.124 with a 90% CI, (0.05,0.174). For KRAS and EGFR, the estimates of P_k,i for k>1 are almost zero, implying that mutations in EGFR and KRAS occur mainly as the first event. This is consistent with the observation that mutations in EGFR and KRAS occur mutually exclusively. Since mutations in both of these genes occur mostly as the first event, both genes cannot have mutations in the same samples simultaneously. This agrees with the fact that mutations in either gene serves to de-regulate the MAP-kinase pathway.

Fig. 2.

Most frequently mutated genes at each mutational step for non-small-cell lung tumors (Ding et al., 2008). The length of the sub-bar corresponding to gene i at the k-th mutational step is the MLE of P_k,i

EGFR encodes a receptor that binds to epidermal growth factor whose binding leads to cell proliferation. It is known that abnormalities in EGFR is an early event in lung cancer (Kang et al., 2008). KRAS encodes a GTPase which plays an essential role in normal tissue signaling. Its mutation is an essential step in tumorigenesis and there is substantial evidence that KRAS mutation is an early event in lung cancer (Westra et al., 1993).

The second mutational event occurs mainly in TP53 and ATM. Mutations in those genes occur mainly as second events, also explaining the mutually exclusive mutation patterns of these two genes. TP53 encodes a transcription factor with numerous key target genes. There is substantial evidence that TP53 mutates early in lung cancer (Matakidou et al., 2003). ATM protein binds and phosphorylates p53, resulting in its stabilization and activation as a transcription factor. Abnormalities in either ATM or TP53 may have similar consequences in tumorigenesis and therefore, our estimates that mutations in both genes occur at the same step in tumorigenesis is reasonable (Khanna et al., 1998).

The third mutational event occurs most frequently in STK11 although the value of P_3,i is only 0.17. There are many other genes with small values of P_3,i. The fourth mutational event occurs mostly in EPHA3, KDR and LRP1B and the fifth mutational event occurs mainly in CDKN2A, LTK, NF1 and RB1. As k increases (later events), there are more genes with P_k,i>0.1, but no genes have very large values of P_k,i like KRAS or TP53. This may imply that late mutating genes such as EPHA3, KDR, LRP1B, CDKN2A, LTK, NF1 and RB1 are not as essential as initiating events such as EGFR, KRAS, STK11, TP53 and ATM. It is not well known whether mutations in these genes are late events in lung tumorigenesis. For LRP1B, RB1 and CDKN2A, however, there is evidence indicating that they are late mutating genes in other cancer types (Langbein et al., 2002; Macleod, 2010; Sugimoto et al., 1998).

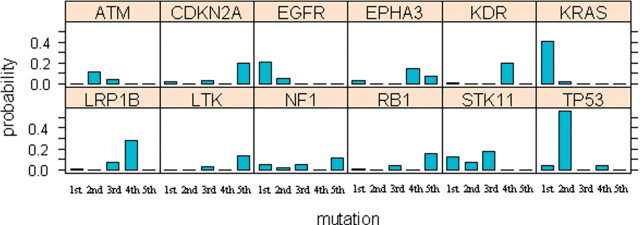
Figure 3 shows another graphical display of the estimates of P_k,i for 12 genes whose P_k,i are >0.1 for at least one event. For each gene, the height of the bar at the k-th mutation is same as the value of P_k,i for that gene i. It shows how the mutation probability of each gene changes over time (mutational events). ATM, EGFR, KRAS, STK11 and TP53 mutate early whereas other genes mutate late. For the genes that were not shown in the figure, the values of P_k,i are small for all k due to their low frequency of mutations and it is hard to tell from these values whether they mutate early or late. A better measure for analyzing such genes is the conditional probability that the gene mutates early (a gene mutates at the k-th event for k≤3) or late (a gene mutates at the k-th event for k>3) given that the gene is mutated in the sample. Table 3 shows these conditional probabilities and their 90% CIs. The conditional probabilities clarify whether a gene mutates early or late especially for the less frequently mutating genes such as EPHA3, ERBB4, RB1 and NRAS. Their probabilities of early or late mutations show substantial differences and their 90% CI for probabilities of early mutations and for probabilities of late mutations do not overlap.

Fig. 3.

Distribution of mutational step for frequently mutated genes in non-small-cell lung tumors (Ding et al., 2008) The height of the bar at the k-th mutational step for gene i is the MLE of P_k,i

Table 3.

Probabilities that observed mutations occur early^a or late^a for non-small-cell lung tumors (Ding et al., 2008)

Gene	Early (90% CI)	Late (90% CI)
APC	0.43 (0.08–1)	0.64 (0–0.97)
ATM	1 (0.57–1)	0 (0-0.51)
CDKN2A	0.08 (0.01–1)	0.97 (0.3–1)
EGFR	1 (0.84–1)	0 (0–0.19)
EPHA3	0.07 (0–0.17)	0.96 (0.87–1)
EPHA5	0.46 (0.07–1)	0.58 (0–0.95)
EPHA7	0.14 (0–1)	0.89 (0–1)
ERBB4	0.12 (0–0.32)	0.9 (0.68–1)
FGFR4	0.11 (0–1)	0.92 (0–1)
INHBA	1 (0–1)	0 (0–1)
KDR	0.04 (0–1)	0.97 (0–1)
KRAS	1 (1–1)	0 (0–0)
LRP1B	0.22 (0.04–1)	0.84 (0–0.97)
LTK	0.06 (0–1)	0.97 (0–1)
MYO3B	0.22 (0–1)	0.8 (0–1)
NF1	0.23 (0.06–1)	0.86 (0.54–0.98)
NRAS	1 (1–1)	0 (0–0.93)
NTRK1	1 (0.14–1)	0 (0–0.9)
NTRK2	0.11 (0–1)	0.93 (0–1)
NTRK3	1 (0–1)	0 (0–1)
PAK3	1 (0–1)	0 (0–1)
PTEN	1 (0.02–1)	0 (0–0.99)
PTPRD	0.44 (0.11–1)	0.6 (0–0.93)
RB1	0.08 (0–0.41)	0.96 (0.52–1)
STK11	1 (0.4–1)	0 (0–0.78)
TFDP1	1 (0.05–1)	0 (0–1)
TP53	0.97 (0.82–1)	0.07 (0–0.4)
ZMYND10	1 (1–1)	0 (0–1)

^aEarly means 1st, 2nd or 3rd event and late means later events.

3.3 Colorectal tumor sequencing data

We also applied our method to colorectal tumor sequencing data since the multi-step process of tumor development has been carefully studied for colorectal tumors. Wood et al. (2007) sequenced 40 selected genes of interest in 133 colorectal tumor samples. Of these 40 genes, we identified 21 tumor driver genes by using the CaMP score of Wood et al. (2007). Table 4 shows the distribution of the number of non-silent mutations in the driver genes for each sample. Since there are few samples which have more than five non-silent mutations, we estimated an averaged distribution for mutations occurring at the n-th step for n>5 by assuming P_n,i=P_5,i for n>5.

Table 4.

Distribution of number of non-silent mutations in the selected driver genes in samples for the data of colorectal tumors (Wood et al., 2007)

Number of mutations	1	2	3	4	5	6	7
Number of samples	14	20	35	37	17	8	2

The MLEs of P_1,i, P_2,i, P_3,i, P_4,i, P_5,i and their 90% CI are shown in Table SC of the Supplementary Materials.

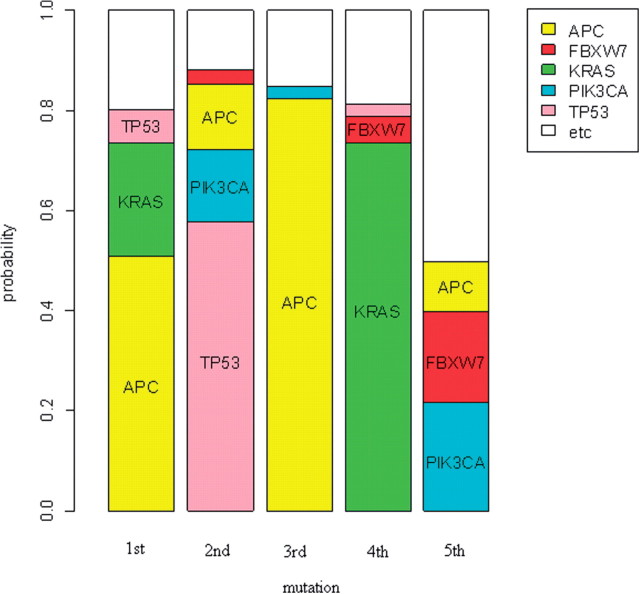
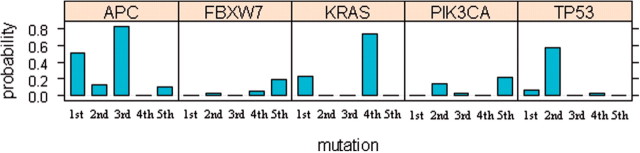
Figures 4 and 5 show graphical displays of the estimates of P_k,i. Based on our analysis, the first mutational event for the genes evaluated occurs most frequently in APC. APC is also frequently the third mutational event. This reflects the fact that APC is a tumor suppressor gene. For the tumorigenesis to occur, both alleles must lose functionality. Although this dataset only reflects a subset of the possible events leading to inactivation of gene function (point mutations, small insertions or deletions), the APC gene contains 2 or 3 mutations for many samples, resulting in high values of both P_1,i and P_3,i.

Fig. 4.

Most frequently mutated genes at each mutational step for colorectal tumors (Wood et al., 2007). The length of the sub-bar corresponding to gene i at the k-th mutational step is the MLE of P_k,i

Fig. 5.

Distribution of mutational step for frequently mutated genes in colorectal tumors (Wood et al., 2007). The height of the bar at the k-th mutational step for gene i is the MLE of P_k,i

The first mutation among these genes also occurs frequently in KRAS. The second mutation occurs most frequently in TP53 and less frequently in PIK3CA and APC. The fourth event occurs most frequently in KRAS and the fifth event occurs mainly in PIK3CA and FBXW7. These results are consistent with information about the sequence of events characterizing colorectal tumor development based on analysis of stages of colon cancer: tumorigenesis begins with the loss of APC function and is followed by mutations activating the KRAS/BRAF pathway. Subsequent mutations in genes controlling the TGF-β, PIK3CA, TP53 and other pathways cause the transition from an adenoma to carcinoma (Jones et al., 2008; Vogelstein et al., 1988).

We calculated the conditional probability that a gene mutates early or late in a tumor sample given the gene mutates in that sample in Table 5. It shows that APC, GUCY1A2 and TP53 are clearly early mutating genes whereas C10orf137, FBXW7, OR51E1, PIK3CA and SEC8L1 are late mutating genes based on the great differences between their probabilities of early and late mutations and short CIs.

Table 5.

Probabilities that observed mutations occur early^a or late^a for colorectal tumors (Wood et al., 2007)

Gene	Early (90% CI)	Late (90% CI)
ADAMTS18	1 (0.21–1)	0 (0–0.8)
ADAMTSL3	0.46 (0–1)	0.57 (0–1)
APC	0.98 (0.95–1)	0.29 (0–0.6)
C10orf137	0 (0–0)	1 (1–1)
EPHA3	0.17 (0–0.8)	0.87 (0.2–1)
EPHB6	1 (0–1)	0 (0–1)
FBXW7	0.06 (0–0.15)	0.97 (0.9–1)
GNAS	1 (1–1)	0 (0–1)
GUCY1A2	1 (1–1)	0 (0–0.9)
KRAS	0.28 (0.17–1)	0.93 (0–0.98)
MAP2K7	1 (0.3–1)	0 (0–0.73)
MMP2	0.08 (0–0.75)	0.93 (0.25–1)
NAV3	0.39 (0.03–1)	0.63 (0–0.98)
OR51E1	0 (0–0.14)	1 (1–1)
PIK3CA	0.28 (0.04–0.53)	0.87 (0.64–0.99)
PTEN	1 (0–1)	0 (0–1)
RET	0.04 (0–1)	0.97 (0–1)
SEC8L1	0 (0–0.03)	1 (1–1)
TCF7L2	0.12 (0–1)	0.91 (0–1)
TNN	0.45 (0–1)	0.56 (0–1)
TP53	0.98 (0.89–1)	0.04 (0–0.24)

^aEarly means 1st, 2nd or 3rd event and late means later events.

There are only five genes identified as driver genes in both datasets: APC, EPHA3, KRAS, PTEN and TP53. The most frequently mutated genes were selected as driver genes for each of the colorectal and lung datasets either by using CaMP score or the method of Youn and Simon (2011) and there was little overlap between those selected genes. This may be due partly to the fact that only 40 genes were investigated in the colorectal study.

APC mutations occur early for colorectal tumors. Loss of function of APC is considered the earliest mutational event in sporadic colon tumorigenesis. Most mutations that occur in the colorectal epithelial cells are soon lost because the cells migrate out of the colonic crypts and die within days by apoptosis. However, loss of APC function results in trapping of the cells within the colonic crypts (Weinberg, 2006). For lung tumors, APC mutations occur early and late with about similar probabilities but there are too few such mutations to estimate the conditional probabilities with precision.

KRAS mutations occur as the first event with high probability for both colorectal and lung tumors. However, for the colorectal dataset, the value of P_4,i is also large whereas for the lung dataset, only the value of P_1,i is large. For TP53, the value of P_k,i is largest for k=2 for both datasets. For PTEN, the probabilities of early mutations are 1 and the probabilities of late mutations are 0 in both datasets (although their CIs are wide), implying PTEN may be a target of early mutations. For EPHA3, the probabilities of early mutations are much smaller than those of late mutations in both datasets, supporting EPHA3 as a late mutating gene.

3.4 Glioblastoma multiforme sequencing data

The result for the analysis of the Glioblastoma multiforme sequencing data downloaded from TCGA data portal is in the Supplementary Material.

4 DISCUSSION

In this article, we have proposed a computational method based on tumor sequencing data for estimating the probability distribution of the relative order of mutational events among tumor driver genes during tumorigenesis. The results obtained from using this method with lung cancer and colorectal tumor sequencing data are consistent with the previous evidence obtained from analyzing various stages of cancer. This provides a degree of validation of the new method. Since the early stages of tumorigenesis are not observable for human tumors, we believe that this method will be a useful tool in understanding the process of tumor development.

Application of the new method to the three datasets described here was somewhat limited by the limited number of genes sequenced in those studies. This will be much less of a limitation in analysis of the large tumor sequencing studies currently underway. These larger datasets may also enable more complex models to be developed.

Our model assumes the number of mutations in driver genes in a sample is independent of the mutated genes. This may not be true in some cases since some genes are known to increase mutation rates when altered (mutator genes). If samples having altered mutator genes tend to have many mutations in driver genes, the probability of late events occurring in mutator genes may be overestimated.

We examined the correlation between mutational status of each driver gene and the number of mutated driver genes in both the lung and colorectal cancer datasets. For the colorectal data, there are no driver genes whose mutational status was strongly correlated with the number of mutations. For lung data, there are several genes which showed some correlation, but it could have resulted from the gene mutating late and the correlation was not strong enough to suggest that they are mutator genes. Even for TP53, the only well known mutator gene in the set of driver genes, the p-value for the correlation was 0.01. Our model estimates that TP53 mutations occur as early events (second event) for both lung and colorectal data. Consequently, the bias caused by our assumption not being strictly true seems to be small. Currently no other computational methods for estimating the order of mutational events account for the increase of the mutation rate by mutator genes.

Our method used all non-silent mutations occurring in driver genes in estimating P_k,i. However, some of the non-silent mutations may be passenger mutations irrelevant to tumorigenesis. Since the purpose of our method is to estimate the order of mutations relevant to tumorigenesis, we may obtain better estimates by restricting to the mutations occurring in well known functional domains within genes.

In this article, we estimated the order of mutations in driver genes. However, it can be used to estimate the order of any events in general. For example, it can be applied to estimate the order of copy number aberrations in a defined chromosomal regions. It can also estimate the order of mutations occurring in different functional domains within a gene if we separate functional domains in a gene when applying our method. If we divide mutations according to different types, such as point mutations, insertions or deletions, we can also capture the order of specific types of mutations occurring within a gene if such order matters and if there are enough data to estimate the order accurately.

As we have indicated previously, the method we have developed does not assume that the sequence of mutations is the same for each tumor. The probability distribution estimated provides information about inter-tumor variability in the order of mutational events. For a given k, the dispersion of P_k,i-values among the genes i indicates the variation among tumors of the k-th event. For a given gene index i, the dispersion of P_k,i-values among the event indices k indicates the degree to which mutations in gene i show an order preference.

Although the sequence of mutations may vary among tumors and late mutations can be clinically important, better understanding the earliest stages of development of individual tumors may be particularly valuable. The earliest mutations are presumably present in all the subsequent sub-clones of the tumor and may therefore represent important therapeutic targets (Simon, 2010). With the further development of rapid single molecule deep sequencing technologies it may become possible to phylogenetically reconstruct the evolution of tumors (Campbell et al., 2008). The current method is a step in using sequencing data and probabilistic modeling to obtain information about the early stages of tumorigenesis.