Comparison of the performance of exact-exchange-based density functional methods

Abstract

How to describe nondynamic electron correlation is still a major challenge to density functional theory (DFT). Recent models designed particularly for this problem, such as Becke'05 (B05) and Perdew-Staroverov-Tao-Scuseria (PSTS) functionals employ the exact-exchange density, the efficient calculation of which is technically quite challenging. We have recently implemented self-consistently the B05 functional based on an efficient resolution-identity (RI) technique. In this study, we report a self-consistent RI implementation of the PSTS functional. In contrast to its original implementation, our version brings no limitation on the choice of the basis set. We have also implemented the Mori-Sanchez-Cohen-Yang-2 (MCY2) functional, another recent DFT method that includes full exact exchange. The performance of PSTS, B05, and MCY2 is validated on thermochemistry, reaction barriers, and dissociation energy curves, with an emphasis on nondynamic correlation effects in the discussion. All three methods perform rather well in general, B05 and MCY2 being on average somewhat better than PSTS. We include also results with other functionals that represent various aspects of the development in this field in recent years, including B3LYP, M06-HF, M06-2X, ωB97X, and TPSSh. The performance of the heavy-parameterized functionals M06-2X and ωB97X is on average better than that of B05, MCY2, and PSTS for standard thermodynamic properties and reactions, while the latter functionals do better in hydrogen abstraction reactions and dissociation processes. In particular, B05 is found to be the only functional that yields qualitatively correct dissociation curves for two-center symmetric radicals like ${\mathrm{He}}_2^{+}$. Finally, we compare the performance of all these functionals on a strongly correlated exemplary case system, the NO dimer. Only PSTS, B05, and MCY2 describe the system qualitatively correctly. Overall, this new type of functionals show good promise of overcoming some of the difficulties DFT encounters for systems with strong nondynamic correlation.

INTRODUCTION

In recent decades, Kohn-Sham density functional theory (DFT)^{1, 2} has become the most efficient theoretical method in a wide range of applications in quantum chemistry. In the Kohn-Sham (KS) scheme, the energy of a system is partitioned into several components, among which only the KS exchange-correlation (XC) functional needs to be approximated. In the past three decades, successive levels of XC functionals have been developed with an increasing complexity. Local spin-density approximation (LSDA) uses spin-resolved electron density as the only functional variable. Generalized gradient approximation (GGA) uses the gradient of the electron density as an additional variable, and meta-GGA functionals use in addition the Laplacian of the electron density and the kinetic energy density. These functionals, when mixed in a hybrid scheme with exact exchange and their parameters optimized, achieve high accuracy for many chemical phenomena, especially concerning properties of stable species at equilibrium.³ However, they have some inherent drawbacks, chief among them is the lack of nondynamic (ND) correlation.^{4, 5, 6, 7, 8} Directly related to this is the failure of describing bond dissociation, mainly due to the lack of left-right correlation in these models. The latter is the dominant part of the nondynamic correlation in polyatomic systems. It is hard to describe theoretically and in general requires a multi-reference (MR) wave function approach. In addition to bond-breaking processes, nondynamic correlation is of crucial importance in charge-transfer states,⁹ and in radical and di-radical systems where these effects are particularly strong¹⁰ (strongly correlated systems). Efforts have been made in recent years to tackle this issue within DFT. Becke has advanced the real-space correlation DFT approach as an alternative to the multi-reference wave function approach. In his B05 functional^{5, 6} the nondynamic correlation is modeled ad hoc via certain real-space correction terms to the exact-exchange hole that compensate the artificial extra-delocalization of the latter. B05 contains only four linear fitting parameters optimized on heats of formation. It showed high accuracy for thermochemistry and reaction barriers.^{5, 6, 11} Perdew et al. have addressed the same problem in a somewhat different manner, based on sophisticated real-space analysis of the exact-exchange hole combined with model DFT exchange-correlation hole.^{12, 13} By extending the Tao-Perdew-Staroverov-Scuseria (TPSS) XC scheme to a new generalized form, they thoroughly explored in their PSTS model, the abnormal regions in real space, where nondynamic correlation effects are locally dominant.¹² Based on this analysis, they proposed a real space correction to the energy functional that takes into account nondynamic correlation effects. The PSTS functional satisfies all known exact scaling constraints that a given functional should obey. It contains five fitting parameters and shows improved results over the TPSS exchange-correlation functional.

Both B05 and PSTS involve the full exact exchange. Also the exact-exchange energy density is incorporated as an extra variable, which is a signature of the hyper-GGA level of the theory.¹² The presence of this variable considerably increases the complexity and the cost of these methods. The calculation of the exact-exchange energy density is prohibitively expensive given that thousands of grid points are used for each atom. However, there are some important benefits of having the full exact exchange in the energy balance instead of a hybrid exchange mixture (or just a pure DFT exchange). It corrects some major drawbacks of previous XC functionals, such as the one electron self-interaction (SI) error, and improves the long-range asymptotic of the Kohn-Sham potential. Mori-Sanchez, Cohen, and Yang¹⁴ have proposed an original approach to the one-electron self-interaction error based on the adiabatic connection formalism involving the full exact exchange from the outset. The MCY functionals, and especially the MCY2 version, show markable improvements with only three extra fitting parameters. MCY2 avoids the use of exact-exchange energy density and is of the same computational efficiency as that of a hyrbid meta-GGA method.

Recently Becke's B05 method was implemented self-consistently (the RI-B05 scheme¹⁵) in the Q-Chem program.¹⁹ The model was modified to make the self-consistency feasible. Resolution-of-identity technique was used to dramatically reduce the cost of the exact-exchange energy density. The four linear B05 parameters were re-optimized within the self-consistent implementation. In this study, we present a self-consistent implementation of the PSTS functional in Q-Chem, applying the same RI technique as for RI-B05. Next, we compare the performance of RI-B05, RI-PSTS, and MCY2 on a diverse set of tests including atomization energies, ionization potentials, electron affinities, reaction barriers, and dissociation curves. The results are also compared with other functionals that represent the current status of functional development at GGA and meta-GGA levels. Among them, B3LYP as the most widely used, M06-2X, a heavily parameterized functional with high accuracy, M06-HF, another heavily parameterized functional with full exact exchange, and ωB97X, a range-separated functional that includes full exact exchange at long range. We also include the Tao-Perdew-Staroverov-Scuseria hybrid functional (TPSSh) in the tests, which is a non-empirical hybrid version of TPSS.

Finally, we compare the performance of the functionals on the strongly correlated case system, the nitric oxide (NO) dimer. It is extremely difficult to describe the electronic structure of this system even qualitatively.^{16, 17} Massive failures at various theoretical levels have been repeatedly reported over the past 25 years or so.^{16, 17, 18}

THEORY AND IMPLEMENTATION DETAILS

In this section we present a brief overview of three DFT methods employing full exact exchange, PSTS, B05, and MCY2, as implemented recently in a development version of the Q-Chem program.¹⁹

PSTS

The PSTS functional is constructed so as to satisfy nearly all known exact constraints for a hyper-GGA functional.¹² It has the following general form:

$$\begin{array}{c}\hfill {\epsilon }_{xc}={\epsilon }_x^{ex}\left(r\right)+[1-a\left(r\right)]\left[{\epsilon }_x^{sl}\left(r\right)-{\epsilon }_x^{ex}\left(r\right)\right]+{\epsilon }_c^{sl}\left(r\right),\end{array}$$ (1)

where ${\epsilon }_x^{sl}\left(r\right)$ and ${\epsilon }_c^{sl}\left(r\right)$ are semilocal DFT exchange and correlation energy densities, respectively, and ${\epsilon }_x^{ex}\left(r\right)$ is the exact-exchange energy density. The TPSS exchange and correlation energy densities are used as semilocal components of Eq. 1.²⁰ They offer the advantage of satisfying certain exact constraints without having empirical parameters. The factor a(r) in Eq. 1 measures the degree of functional nonlocality associated with nondynamic correlation effects, or near degeneracy effects. Its value is used to divide the electron density (in real space) into “normal region” (small a(r)) and “abnormal region” (large a(r)), and has the form

$$\begin{array}{c}\hfill a\left(r\right)=1-(1-a_1\left(r\right))(1-a_2\left(r\right)).\end{array}$$ (2)

In normal regions the semilocal DFT exchange is a good approximation to the exact exchange, and a₁(r) and a₂(r) are close zero. In abnormal regions there are two scenarios: The first scenario of “abnormality” is when the electron density is one-electron-like, rapidly varying over space, or too high. In that case a(r) ≈ a₁(r). The second situation is when the electron density is strongly fluctuating in electron number on the scale of the local Fermi wavelength. Then a(r) ≈ a₂(r). The local coefficient a₁(r) in Eq. 2 has the following form:

$$\begin{array}{c}\hfill a_1=\frac{1}{1+A\ln (1+Bu(r\left)\right)},\end{array}$$ (3)

where A, B are positive empirical parameters. Their values as given in Ref. 13 are: A = 3.74, B = 167. Next, the factor u(r) in Eq. 3 is a theoretically motivated density- and position-dependent function,

$$\begin{array}{c}\hfill u\left(r\right)=\frac{{\epsilon }_c^{\text{GL2TPSS}}}{{\epsilon }_x^{\text{LSD}}},\end{array}$$ (4)

where ${\epsilon }_x^{\text{LSD}}$ is the LSDA exchange energy density, and ${\epsilon }_c^{\text{GL2TPSS}}$ is Görling-Levy second-order or high-density limit of the TPSS correlation energy density at position r.

The local coefficient a₂(r) in Eq. 2 is given by

$$\begin{array}{c}\hfill a_2\left(r\right)=\frac{Dz}{1+Ez\left(r\right)}f\left(\frac{{\epsilon }_x^{ex}\left(r\right)}{{\epsilon }_x^{\mathit{TPSS}}\left(r\right)}\right),\end{array}$$ (5)

with $z\left(r\right)\equiv \frac{{\zeta }^2}{r_s^2}$, where ζ is the spin-polarization parameter

$$\begin{array}{c}\hfill \zeta =\frac{1}{\rho }({\rho }_{\alpha }-{\rho }_{\beta }),\end{array}$$ (6)

r_s is the uniform-gas density parameter defined by $\rho =3/4\pi r_s^3$ and D, E are yet another empirical parameters with values of D = 7.10, E = 9.61. The factor f in Eq. 5 is density- and position-dependent function of the form

$$\begin{array}{c}\hfill f\left(v\right)=\left\{\begin{array}{cc}\hfill 1& \hfill v\le C\\ \hfill \frac{1}{1+\exp \left[1/{(1-v)}^F-1/{(v-C)}^F\right]}& \hfill C<V<1,\\ \hfill 0& \hfill v\ge 1\end{array}\right.\end{array}$$ (7)

where F depends on the empirical parameter C,

$$\begin{array}{c}\hfill F=-\frac{3}{2\ln \left(\right(1-C)/2)}.\end{array}$$ (8)

The optimal value of C is C = 0.909. Overall, there are five empirical parameters in the PSTS functional that are optimized against experimental data.

Compared to the conventional GGA and meta-GGA functionals, the major computational bottleneck in the PSTS method is the spin-summed exact-exchange energy density $e_x^{ex}\left(r\right)$ used as a special functional variable that quantifies the degree of functional nonlocality,

$$\begin{array}{ccc}\hfill e_x^{ex}\left(r\right)& =& -\frac{1}{2}\sum _{\mu ,\lambda ,\nu ,\eta }\left(P_{\mu \lambda }^{\alpha }{P}_{\nu \eta }^{\alpha }+P_{\mu \lambda }^{\beta }{P}_{\nu \eta }^{\beta }\right)\hfill \\ & & \times \int \frac{{\varphi }_{\mu }\left(r\right){\varphi }_{\nu }\left(r\right){\varphi }_{\lambda }\left(r^{\prime }\right){\varphi }_{\eta }\left(r^{\prime }\right)}{|r-r^{\prime }|}d{r}^{\prime },\hfill \end{array}$$ (9)

where ϕ_μ are atomic-orbital (AO) basis functions and P^σ is the spin-resolved density matrix in AO basis. Here and further on we reserve the index notations i,j,k,l for labeling molecular orbitals, while μ,ν,λ,η label atomic orbitals.

Please note that we use here the formalism of PSTS with conventional gauge.¹³ As one can see, the evaluation of $e_x^{ex}\left(r\right)$ by Eq. 9 requires a four-index summation, similar to the computation of the Hartree-Fock (HF) energy for the molecule. While the former involves the integration over the coordinates of one electron only and thus incurs a fraction of the computational cost of the latter, it must be done on thousands of grid points per atom, resulting in the total computing time hundreds of times more than that of a single HF energy calculation. Finding better, cost-effective ways to calculate the exact-exchange energy density is crucial for this type of functionals. In the original PSTS implementation, the integral $\int \frac{{\varphi }_{\nu }\left(r\right){\varphi }_{\lambda }\left(r^{\prime }\right){\varphi }_{\eta }\left(r^{\prime }\right)}{|r-r^{\prime }|}d{r}^{\prime }$ is approximated with resolution of identity using the orbital basis functions as RI auxiliary basis as well,²¹

$$\begin{array}{ccc}& & \int \frac{{\varphi }_{\nu }\left(r\right){\varphi }_{\lambda }\left(r^{\prime }\right){\varphi }_{\eta }\left(r^{\prime }\right)}{|r-r^{\prime }|}d{r}^{\prime }\hfill \\ & & \approx \sum _{p,q}{S}_{p,q}^{-1}{\varphi }_p\left(r\right)\int {\varphi }_q\left(r^{\prime \prime }\right){\varphi }_{\nu }\left(r^{\prime \prime }\right)d{r}^{\prime \prime }\int \frac{{\varphi }_{\lambda }\left(r^{\prime }\right){\varphi }_{\eta }\left(r^{\prime }\right)}{|r^{\prime \prime }-r^{\prime }|}d{r}^{\prime }.\hfill \end{array}$$ (10)

In the above equation, S_μη is the AO overlap matrix. Combining Eqs. 10, 9 one obtains the following formula for the exact-exchange energy density after symmetrization:

$$\begin{array}{ccc}\hfill e_x^{ex}\left(r\right)& \approx & -\frac{1}{2}\sum _{pq\mu \lambda }({\varphi }_p\left(r\right)S_{pq}^{-1}\left(K_{q\lambda }^{\alpha }{P}_{\lambda \mu }^{\alpha }+K_{q\lambda }^{\beta }{P}_{\lambda \mu }^{\beta }\right){\varphi }_{\mu }\left(r\right)\hfill \\ & & +{\varphi }_{\mu }\left(r\right)(P_{\mu \lambda }^{\alpha }{K}_{\lambda q}^{\alpha }+P_{\mu \lambda }^{\beta }{K}_{\lambda q}^{\beta })S_{qp}^{-1}{\varphi }_p\left(r\right)),\hfill \end{array}$$ (11)

with $K_{q\lambda }^{\sigma }$ being the spin-resolved exact-exchange matrix. The computational convenience of Eq. 11 is that the regular Fock matrix can be used in place of the direct calculation of the exchange-energy density on the grid. However, large uncontracted orbital basis sets must be employed with this approach in order to solve Eq. 10 with sufficient accuracy.¹³ In our implementation of PSTS we use a set of auxiliary Gaussian functions to expand the orbital basis function pairs,^{15, 22, 23}

$$\begin{array}{ccc}\hfill {\varphi }_{\mu }\left(r\right){\varphi }_{\nu }\left(r\right)& =& \sum _{pq}{\left({\chi }_p\right|{\chi }_q)}^{-1}\left({\chi }_q\right|{\varphi }_{\mu }{\varphi }_{\nu }){\chi }_p\left(r\right)\hfill \\ & \equiv & \sum _p{C}_{\mu \nu }^p{\chi }_p\left(r\right).\hfill \end{array}$$ (12)

In the above equation, we use the short-handed notation (χ_p|χ_q) for the corresponding Coulomb integral, where χ's are atom-centered Gaussian auxiliary basis functions (index notations p,q,t are reserved for labeling auxiliary functions). This RI technique is widely used for accelerating DFT and second-order Moller-Plesset (MP2) perturbation methods and it has a verified accuracy in calculations of relative energies. Using Eq. 12, the exact-exchange energy density $e_X^{\mathrm{ex}}\left(r\right)$ (Eq. 9) becomes,

$$\begin{array}{ccc}\hfill e_x^{ex}\left(r\right)& \approx & -\frac{1}{2}\sum _{pq\mu \lambda \nu \eta }\left(P_{\mu \lambda }^{\alpha }{P}_{\nu \eta }^{\alpha }+P_{\mu \lambda }^{\beta }{P}_{\nu \eta }^{\beta }\right)C_{\mu \nu }^p{C}_{\lambda \eta }^q{\chi }_p\left(r\right)\hfill \\ & & \times \int \frac{{\chi }_q\left(r^{\prime }\right)}{|r-r^{\prime }|}d{r}^{\prime }.\hfill \end{array}$$ (13)

This equation involves looping over six indices for each grid point. To simplify it for computational efficiency we construct the following intermediate:

$$\begin{array}{c}\hfill C_{ij}^{p,\alpha }=\sum _{\mu }{C}_i^{\mu ,\alpha }\sum _{\nu }{C}_j^{\nu ,\alpha }{C}_{\mu \nu }^p.\end{array}$$ (14)

In the above equation, $C_i^{\mu ,\alpha }$ is the coefficient of the occupied α molecular orbital i. Equation 13 then can be rewritten as

$$\begin{array}{ccc}\hfill e_x^{ex}\left(r\right)& \approx & -\frac{1}{2}\sum _{pq}{\chi }_p\left(r\right)\int \frac{{\chi }_q\left(r^{\prime }\right)}{|r-r^{\prime }|}d{r}^{\prime }\hfill \\ & & \times \sum _{ij}\left(C_{ij}^{p,\alpha }{C}_{ij}^{q,\alpha }+C_{ij}^{p,\beta }{C}_{ij}^{q,\beta }\right).\hfill \end{array}$$ (15)

For the self-consistent-field (SCF) calculation, one needs the PSTS contribution to the Fock matrix. This in turn requires the evaluation of the derivative of $e_X^{\text{HF}}$ with respect to the P density matrix (we follow here the generalized KS approach to the SCF potential¹³),

$$\begin{array}{ccc}\hfill \frac{\partial e_x^{ex}\left(r\right)}{\partial P_{\mu \nu }}& =& -\frac{1}{2}\sum _{pq}{\chi }_p\left(r\right)\int \frac{{\chi }_q\left(r^{\prime }\right)}{|r-r^{\prime }|}d{r}^{\prime }\hfill \\ & & \times \sum _i\left(C_{i\mu }^{p,\alpha }{C}_{i\nu }^{q,\alpha }+C_{i\mu }^{p,\beta }{C}_{i\nu }^{q,\beta }\right),\hfill \end{array}$$ (16)

with

$$\begin{array}{c}\hfill C_{i\mu }^{p,\alpha }=\sum _{\lambda }{C}_i^{\lambda ,\alpha }{C}_{\mu \lambda }^p.\end{array}$$ (17)

Please note the difference between Eqs. 17, 14. Finally, Eqs. 15, 16 need to be symmetrized with respect to the p and q indices. Because the Coulomb potential of (χ_p|χ_q) is a long-range interaction, the computational cost of Eq. 15 at each grid point is O(N) with N being the number of auxiliary basis functions. This makes the total computational cost on the grid scale quadratically with respect to the molecular size. The rest of the cost is essentially the same as for the RI HF calculation.¹⁵

We have recently applied this method for the calculation of the spin-resolved HF exchange energy density in a SCF implementation of the B05 method (the RI-B05 scheme^{15, 22}). We have found that it yields accurate relative energies with a speed-up of hundreds of times compared to the exact implementation of Eq. 9. The advantage of this approach is that it is applicable to any type of orbital basis and is sufficiently accurate when the auxiliary basis set is properly constructed (see Ref. 15 for details). To verify the accuracy of the RI approach, we have calculated the total HF exchange energies of the first- and second-row atoms by summing the RI-approximated exact-exchange energy density over the atomic grids. We found that the average absolute error compared to the exact analytical HF exchange energy is about 3.4 × 10⁻⁶ hartree.²⁴ We denote our implementation of PSTS described above as “RI-PSTS.”

MCY and B05 functionals

MCY is another DFT method that involves full exact exchange. It is based on an original idea of how to simulate well the exact adiabatic connection (AC) formula,¹⁴

$$\begin{array}{c}\hfill E_{\text{XC}}\left[\rho \right]={\int }_0^1{W}_{\lambda }\left[\rho \right]d\lambda ,\end{array}$$ (18)

where W_λ is the λ dependent exchange-correlation energy, λ is the AC interaction-strength parameter. In the MCY scheme W_λ[ρ] is modeled with a Padé form,

$$\begin{array}{c}\hfill W_{\lambda }=a+\frac{\lambda b}{1+\lambda c}\end{array}$$ (19)

with the factors a, b, and c being certain auxiliary functionals that need to be constructed. The corresponding exchange-correlation functional is given as

$$\begin{array}{c}\hfill E_{xc}\left[\rho \right]=a+\frac{b}{c}\left(1-\frac{ln(1+c)}{c}\right).\end{array}$$ (20)

The density dependent factors a, b, and c are determined using the quantities W₀, $W_0^{\prime }$, and $W_{{\lambda }_p}$, where W₀ is the initial point for AC, $W_0^{\prime }$ is its initial slope of the AC integral curve and $W_{{\lambda }_p}$ is a selected point on the AC integral curve. The following known exact constraints of the adiabatic connection are then employed:

• As λ → 0, W_λ → E_x,

• As λ → 0, $\frac{\partial W_{\lambda }}{\partial \lambda }\to 2E_c^{\text{GL}}$.

In the above relations, E_x is the exact-exchange energy, $E_c^{\text{GL}}$ is the second order correlation energy term of the Görling-Levy density functional perturbation expansion.²⁵ Because the computation of $E_c^{\text{GL}}$ is very expensive, the initial slope is alternatively estimated using a pure DFT correlation functional form: when W₀ = E_x, the initial slope $W_0^{\prime }$ for a given functional E_c is,

$$\begin{array}{c}\hfill W_0^{\prime }=2\underset{\lambda \to 0}{\lim }{E}_c\left[{\rho }_{1/\lambda }\right].\end{array}$$ (21)

In MCY the non-empirical TPSS correlation functional is employed as an approximation to E_c in the above expression,

$$\begin{array}{c}\hfill W_0^{\prime }=2\underset{\lambda \to 0}{\lim }{E}_{\text{TPSS}}\left[{\rho }_{1/\lambda }\right].\end{array}$$ (22)

The final piece of information, the form of $W_{{\lambda }_p}$, is determined using certain exact coordinate scaling relations that exchange-correlation functionals should obey

$$\begin{array}{ccc}\hfill W_{{\lambda }_p}\left[\rho \right]& =& \frac{\partial }{\partial \lambda }\left\{{\lambda }^2{E}_{xc}\left[{\rho }_{1/\lambda }\right]\right\}\hfill \\ & =& E_x\left[\rho \right]+2\lambda E_c\left[{\rho }_{1/\lambda }\right]+{\lambda }^2\frac{\partial E_c\left[{\rho }_{1/\lambda }\right]}{\partial \lambda }.\hfill \end{array}$$ (23)

Finally, the density dependent variables a, b, and c are determined as

$$\begin{array}{c}\hfill a=E_x,\end{array}$$ (24)

$$\begin{array}{c}\hfill b=W_0^{\prime },\end{array}$$ (25)

$$\begin{array}{c}\hfill c=\frac{W_{{\lambda }_p}-{\lambda }_{p}b-a}{{\lambda }_p(a-W_{{\lambda }_p})}.\end{array}$$ (26)

There are three empirical parameters in the MCY method that are optimized against experiment. First, $W_0^{\prime }$ is scaled by a numerical factor. Second, a particular λ value is empirically chosen for Eq. 23. Finally, the $W_{{\lambda }_p}\left[\rho \right]$ value is scaled by another factor. In this paper, we use version 2 of those parameters, named as MCY2. Their values are 4.0, 0.69, and 0.9955, respectively. The BLYP exchange-correlation functional is used to evaluate $W_{{\lambda }_p}$ by Eq. 23.

Having presented a gist of the MCY functional, we turn now to a brief description of the B05 method. It is a DFT model that incorporates full exact exchange together with nondynamic correlation effects modeled by certain real-space corrections to the exact-exchange hole. In multi-center systems, the exact-exchange hole alone is artificially too delocalized. In ab-initio multi-reference methods, this extra delocalization is compensated by the corresponding (wave function based) correlation hole.^{4, 6, 12} The resulting ab initio XC hole remains localized within a region of roughly atomic size in finite systems.⁶ When the exact exchange is combined with a model DFT correlation, such a complete cancellation does not occur. In B05, the XC hole is modeled as a sum of exact-exchange hole, ND correlation correction to it in real space and a dynamic correlation remainder. The exact-exchange hole alone is readily given by the occupied KS orbitals and the electron density.^{5, 6} Then, the spherically averaged exact-exchange hole of, say, spin α (${\overline{h}}_{\mathrm{X}\alpha }$) is deepened in a physically motivated fashion by a fraction of the spherically averaged exchange hole of opposite spin β, and by a second order same-spin term.⁶ This results in a real-space ND correlation correction to the XC hole in the following (spherically averaged) form:

$$\begin{array}{cc}& {\displaystyle {\overline{h}}_{\mathrm{XC}\alpha }^{\mathrm{nd}}(\mathbf{r},s)={\overline{h}}_{\mathrm{X}\alpha }^{\mathrm{exact}}(\mathbf{r},s)+\left[f_{\mathrm{c}}\left(\mathbf{r}\right){\overline{h}}_{\mathrm{X}\beta }^{\mathrm{exact}}(\mathbf{r},s)+{\overline{h}}_{\mathrm{C}\alpha \alpha }^{\mathrm{nd}}(\mathbf{r},s)\right],}\\ \\ & {\displaystyle \mathbf{r}={\mathrm{r}}_{1}s=|{\mathrm{r}}_2-{\mathrm{r}}_1|.}\end{array}$$ (27)

The function f_c in Eq. 27 is opposite-spin correlation factor that reflects the strength of the opposite-spin ND correlation at each point of space,⁶

$$\begin{array}{c}\hfill f_{\mathrm{c}}\left(\mathbf{r}\right)=\min (f_{\alpha }\left(\mathbf{r}\right),f_{\beta }\left(\mathbf{r}\right),1),0\le f_{\mathrm{c}}\left(\mathbf{r}\right)\le 1,\end{array}$$ (28)

$$\begin{array}{c}\hfill f_{\alpha }\left(\mathbf{r}\right)=\frac{1-N_{\mathrm{X}\alpha }^{\mathrm{eff}}\left(\mathbf{r}\right)}{N_{\mathrm{X}\beta }^{\mathrm{eff}}\left(\mathbf{r}\right)}.\end{array}$$ (29)

The function $N_{\mathrm{X}\sigma }^{\mathrm{eff}}$ is an effective normalization of the exchange hole within a region of roughly atomic size around the reference point. The closer $N_{\mathrm{X}\sigma }^{\mathrm{eff}}$ to one (from below), the larger the degree of localization of the exact-exchange hole and vice versa. The form of $N_{\mathrm{X}\sigma }^{\mathrm{eff}}\left(\mathbf{r}\right)$ is quite complicated in the B05 model, but it is possible to represent it in a closed analytic form.^{15, 22} The last term of Eq. 27 is a second-order same-spin correction to the XC hole introduced to improve the performance for open-shell systems. The corresponding ND correlation energy is obtained by integrating the respective Coulomb potential of the XC hole, Eq. 27. For example, the opposite-spin component of the ND correlation energy reads,

$$\begin{array}{c}\hfill E_c^{\mathrm{nd}-\mathrm{opp}}=\frac{1}{2}\int f_{\mathrm{c}}\left(\mathbf{r}\right)\left[{\rho }_{\alpha }\left(\mathbf{r}\right)U_{X\beta }^{\mathrm{exact}}\left(\mathbf{r}\right)+{\rho }_{\beta }\left(\mathbf{r}\right)U_{X\alpha }^{\mathrm{exact}}\left(\mathbf{r}\right)\right]d\mathbf{r},\end{array}$$ (30)

where $U_{X\sigma }^{\mathrm{exact}}$ is the spin-resolved Slater potential of exact exchange

$$\begin{array}{c}\hfill U_{X\sigma }^{\mathrm{exact}}\left(\mathbf{r}\right)=4\pi \int sds{\overline{h}}_{X\sigma }^{\mathrm{exact}}(\mathbf{r},s).\end{array}$$ (31)

The second order same-spin ND contribution has a more complicated form. For further details on the SCF implementation of B05 see Ref. 15.

The final form of the B05 energy functional reads

$$\begin{array}{ccc}\hfill E_{\mathrm{XC}}^{\mathrm{B}05}& =& E_{\mathrm{X}}^{\mathrm{HF}}+a_{\mathrm{c}}^{\mathrm{nd}-\mathrm{opp}}{E}_{\mathrm{c}}^{\mathrm{nd}-\mathrm{opp}}+a_{\mathrm{c}}^{\mathrm{nd}-\mathrm{par}}{E}_{\mathrm{c}}^{\mathrm{nd}-\mathrm{par}}\hfill \\ & & +a_{\mathrm{c}}^{\mathrm{D}-\mathrm{opp}}{E}_{\mathrm{c}}^{\mathrm{D}-\mathrm{opp}}+a_{\mathrm{c}}^{\mathrm{D}-\mathrm{par}}{E}_{\mathrm{c}}^{\mathrm{D}-\mathrm{par}},\hfill \end{array}$$ (32)

where $E_{\mathrm{c}}^{\mathrm{D}-\mathrm{opp}}$ and $E_{\mathrm{c}}^{\mathrm{D}-\mathrm{par}}$ are DFT functionals of dynamic correlation. In B05 Becke uses a spin-spin decomposition of his BR94 correlation functional²⁶ for the latter two terms. There are four linear empirical parameters in the B05 functional, $a_{\mathrm{c}}^i$. In our SCF implementation (the RI-B05 version¹⁵), we have re-optimized the four linear parameters with respect to converged SCF solutions, the corresponding values are

$$\begin{array}{cc}\hfill a_{\mathrm{c}}^{\mathrm{nd}-\mathrm{opp}}=0.5260& a_{\mathrm{c}}^{\mathrm{nd}-\mathrm{par}}=0.6467,\hfill \\ \\ \hfill a_{\mathrm{c}}^{\mathrm{D}-\mathrm{opp}}=1.0754& a_{\mathrm{c}}^{\mathrm{D}-\mathrm{par}}=1.130.\hfill \end{array}$$ (33)

Using the same specifically adapted RI technique described above for the RI-PSTS functional, Eqs. 12, 13, 14, 15, 16, 17, is essential for rendering the SCF implementation feasible. In this work we use a converged HF solution as an initial guess to a single-point RI-B05 calculation, which greatly facilitates its convergence.

COMPUTATIONAL DETAILS

A comparison of the relative performance of RI-PSTS, RI-B05, and MCY2 functionals is provided in this work for thermochemistry, chemical reactions, and molecular dissociation. For thermochemistry, we consider enthalpies of formation, ionization potentials, and proton affinities of the molecules from the G2 data set. Barrier heights are calculated for heavy-atom transfer, nucleophilic substitution, unimolecular, association, and hydrogen transfer reactions. The structural data of the transition states, reactants, and products are taken from Minnesota Thermochemistry and Thermochemical Kinetics Databases.²⁷ To assess the methods for nondynamic correlation, we have calculated the dissociation curves of selected diatomic molecules ${\mathrm{H}}_2^{+}$, ${\mathrm{He}}_2^{+}$, H₂, F₂, and N₂, and the energy properties of the NO dimer, a system with strong nondynamic correlation.

The above methods are compared here with other popular functionals, including TPSSh,^{20, 28} B3LYP,^{29, 30} M06-2X,³¹ M06-HF,³² and ωB97X.³³ TPSSh is a non-empirical hybrid version of TPSS. B3LYP is the most-widely used DFT method yielding reliable predictions for many properties. M06-2X is a heavily parameterized hybrid mega-GGA functional that yields accurate predictions in many benchmark studies. M06-HF belongs to the same suite of heavily parameterized functionals as M06-2X but employs the full exact exchange. ωB97X is a multi-parameter long-range corrected functional in which the model DFT potential is replaced at long-range by the exact-exchange potential.

There are two flavors of the B05 method that are included here. The first is the original B05 functional,^{5, 6} which acts in a perturbative (post-LDA) way using converged LDA density. The RI approximated exact-exchange energy density is used with this option as well, and the resulting method is denoted as “PERT-RI-B05.” The second way of employing the B05 functional is in a fully SCF manner, as described in Subsection 2B and named as “SCF-RI-B05.”¹⁵

All calculations in this work were performed with a development version of the Q-Chem package,¹⁹ using G3LARGE basis set³⁴ and a un-pruned ultra-fine grid of 128 radical and 302 angular points per shell within Becke's relative weights integration scheme.³⁵ The RI calculations require an accurate auxiliary Gaussian basis set. We have found that the RI basis used for typical RI Coulomb or RI-MP2 are not sufficiently accurate for calculation of the exact-exchange energy density. We have designed a new set of RI basis using the even-tempered approach. The highest angular momentum is chosen two orders higher than that of the AO basis for each particular element. The largest exponent for each angular type is the double of the largest exponent in the G3LARGE AO basis of the same angular type. The auxiliary basis set for all elements involved in the present calculations is provided in the supplementary material to this work.²⁴ In addition to the DIIS algorithm,³⁶ geometric direct minimization,³⁷ and maximum overlap³⁸ methods were employed for attaining SCF convergence in some difficult cases.

PERFORMANCE FOR THERMOCHEMISTRY

In this section we present comparison results for standard enthalpies of formation, ionization potential, electron affinity, and proton affinity based on the G2 set.^{34, 39} All geometries are optimized at B3LYP/6-31G(d) level of the theory. The zero-point energies (ZPE) are calculated also at B3LYP/6-31G(d) level as well, and the ZPE values are scaled by the recommended factor of 0.96.^{40, 41} The standard enthalpies of formation are computed following the procedure described in Ref. 40. The experimental standard enthalpies of formation and the enthalpies at 0 K for the gaseous atoms involved in the present calculations are taken from Ref. 40 as well. The ionization potentials, electron affinities and proton affinities are calculated at 0 K taking into account the zero-point energy difference between a given ionized and neutral molecule. All deviations (mean error (ME), mean absolute errors (MAE), maximum signed errors MAX(+) and MAX(−)) designated in the tables were computed as “theory minus experiment.”

Table 1 summarizes the performance statistics for the standard enthalpies of formation. Among the three DFT schemes employing full exact exchange, PERT-RI-B05 shows the best performance on this test set (MAE of 2.45 kcal/mol), followed closely by SCF-RI-B05 (MAE of 2.62 kcal/mol) and MCY2 (MAE of 2.77 kcal/mol). The performance of RI-PSTS on this test set is somewhat worse (MAE of 4.75 kcal/mol). All three functionals with full exact exchange perform much better than HF, indicating that these models are capable of recovering the majority of the post-HF correlation effects. MCY2, while containing some aspects of the nonempirical TPSS theory, performs better than the hybrid version of TPSS, i.e., TPSSh. To note also that both RI-B05 versions and MCY2 perform much better than M06-HF, an empirically parameterized functional with full HF exchange. This shows the limitations of the approach of multi-parameter empirical interpolation, as far as functionals with full exact exchange is concerned. Still, all the methods discussed so far are outperformed on this test set by the multi-parameter hybrid functionals ωB97X and M06-2X, which rely to a large extent on cancellation of errors.

Table 1.

Comparison of results for standard enthalpies of formation based on the G2 set. All values are in kcal/mol.

Methods	ME	MAE	Max(+)	Max(−)
RI-PSTS	1.28	4.75	21.59(SiF4)	−19.33(Si2H6)
SCF-RI-B05	−0.29	2.62	7.71(O3)	−14.58(C2F4)
PERT-RI-B05	0.19	2.45	11.55(O3)	−10.21(C2F4)
MCY2	−1.65	2.77	9.22(SiF4)	−10.44(pyridine)
TPSSh	−1.30	4.47	18.75(SiF4)	−19.45(Si2H6)
B3LYP	1.54	3.25	19.71(SiCl4)	−7.99(BeH)
M06-2X	−0.20	2.13	17.18(O3)	−10.33(C2F4)
M06-HF	1.90	4.18	38.93(O3)	−8.89(tri-methylamine)
ωB97X	−0.22	2.02	9.27(Si2)	−9.93(C2F4)
HF	149.38	149.39	344.21(pyridine)	−0.49(BeH)

Table 2 contains the calculated ionization potentials from the G2 set. The three methods with full exact exchange perform much better than the HF method. The performance of MCY2 and RI-PSTS is better than that of both RI-B05 options. In this case, the SCF version of the latter has slightly smaller MAE than the post-LDA version PERT-RI-B05. Among all the XC functionals tested, M06-HF is the least accurate here. The relatively large positive ME and MAE with both PERT-RI-B05 and SCF-RI-B05 shows that RI-B05 tends to somewhat systematically overestimate ionization potentials. Please note that ionization potentials were not included in the training set when the RI-B05 parameters were optimized.

Table 2.

Comparison of results for ionization potential based on the G2 set. All values are in kcal/mol.

Methods	ME	MAE	Max(+)	Max(−)
RI-PSTS	−1.06	3.89	27.08 (CN+)	−15.37 (B2${\mathrm{F}}_4^{+}$)
SCF-RI-B05	3.28	4.64	33.58 (CN+)	−7.27 (B2${\mathrm{F}}_4^{+}$)
PERT-RI-B05	3.24	4.70	33.61 (CN+)	−5.09 (CH2SH+)
MCY2	1.32	3.49	32.88 (CN+)	−9.59 (Si2${\mathrm{H}}_5^{+}$)
TPSSh	−1.53	4.04	32.90 (CN+)	−15.31 (B2${\mathrm{F}}_4^{+}$)
B3LYP	1.32	3.61	36.65 (CN+)	−10.90 (B2${\mathrm{F}}_4^{+}$)
M06-2X	1.25	3.26	40.51 (CN+)	−8.57 (Si2${\mathrm{H}}_4^{+}$)
M06-HF	3.11	6.19	56.20 (CN+)	−11.51 (Si2${\mathrm{H}}_4^{+}$)
ωB97X	0.29	3.15	39.42 (CN+)	−10.49 (Be+)
HF	−20.58	22.21	60.59 (CN+)	−41.88 (Ne+)

Turning to the electron affinity (see Table 3), the performance of the different functionals is relatively more uniform, except for M06-HF. B3LYP and PERT-RI-B05 have here the smallest and the second smallest MAE, respectively. The RI-PSTS functional shows on average a tendency of underestimating the electron affinity while having a relatively small maximum deviation Max(+).

Table 3.

Comparison of results for electron affinity based on G2 set. All values are in kcal/mol.

Methods	ME	MAE	Max(+)	Max(−)
RI-PSTS	−2.66	3.47	8.66 (${\mathrm{C}}_2^{-}$)	−10.33 (${\mathrm{CH}}_2^{-}$)
SCF-RI-B05	2.73	3.36	44.18 (${\mathrm{C}}_2^{-}$)	−4.84 (${\mathrm{CH}}_2^{-}$)
PERT-RI-B05	1.72	2.82	22.80 (${\mathrm{C}}_2^{-}$)	−3.76 (${\mathrm{CH}}_2^{-}$)
MCY2	−1.28	3.13	19.89 (${\mathrm{C}}_2^{-}$)	−6.98 (S2O−)
TPSSh	−2.00	3.91	21.69 (${\mathrm{C}}_2^{-}$)	−9.24 (HOO−)
B3LYP	1.08	2.79	25.32 (${\mathrm{C}}_2^{-}$)	−5.00 (CH3CO−)
M06-2X	−0.93	3.46	24.28 (${\mathrm{C}}_2^{-}$)	−7.79 (${\mathrm{CH}}_2^{-}$)
M06-HF	1.51	4.66	41.87 (${\mathrm{C}}_2^{-}$)	−7.45 (${\mathrm{CH}}_2^{-}$)
ωB97X	−1.00	3.83	42.42 (${\mathrm{C}}_2^{-}$)	−17.67 (LiH−)
HF	−25.15	26.26	17.25 (${\mathrm{C}}_2^{-}$)	−50.80 (F−)

Finally, with respect to proton affinity, all the functionals tested, except RI-PSTS, perform reasonably well (Table 4). B3LYP and MCY2 have here the smallest and the second smallest MAE, respectively. The majority of MAE values are below 2.0 kcal/mol, except with RI-PSTS, TPSSh, and M06-HF. Both PERT-RI-B05 and SCF-RI-B05 tend to somewhat underestimate proton affinities, which may be related to their trend of overestimating ionization potentials.

Table 4.

Comparison of results for proton affinity based on G2 set. All values are in kcal/mol.

Methods	ME	MAE	Max(+)	Max(−)
RI-PSTS	−0.33	2.78	4.62 (C2${\mathrm{H}}_3^{+}$)	−4.31 (H2Cl+)
SCF-RI-B05	−1.74	1.74	…	−3.45 (${\mathrm{H}}_3^{+}$)
PERT-RI-B05	−1.89	1.89	…	−3.25 (${\mathrm{H}}_3^{+}$)
MCY2	0.26	1.10	2.86 (C2${\mathrm{H}}_3^{+}$)	−1.59 (${\mathrm{H}}_3^{+}$)
TPSSh	2.38	2.38	5.32 (C2${\mathrm{H}}_3^{+}$)	…
B3LYP	−0.19	0.90	2.02 (C2${\mathrm{H}}_3^{+}$)	−1.77 (${\mathrm{H}}_3^4$)
M06-2X	−0.56	1.60	3.08 (${\mathrm{H}}_3^{+}$)	−2.35 (H2Cl+)
M06-HF	−0.05	2.16	5.10 (Si${\mathrm{H}}_5^{+}$)	−3.64 (H2Cl+)
ωB97X	1.12	1.44	4.71 (C2${\mathrm{H}}_3^{+}$)	−1.12 (Si${\mathrm{H}}_5^{+}$)
HF	2.44	3.50	7.79 (P${\mathrm{H}}_4^{+}$)	−2.05 (${\mathrm{H}}_3^{+}$)

REACTION BARRIERS

It is well known that traditional semilocal functionals tend to underestimate reaction barriers due to some intrinsic errors, such as self-interaction error, delocalization error, poor account of left-right correlation, and other errors.⁸ These errors become particularly large in systems with stretched bonds, such as in the transition states of many reactions. In this section we analyze the functional performance on reaction barriers. We use the HTBH38/04 set of forward and reverse reaction barriers,²⁷ as well as 18 reactions of hydrogen transfer that are known to be among the most difficult to describe theoretically.

The HTBH38/04 set consists of six heavy-atom transfer reactions, eight nucleophilic substitution reactions, and five unimolecular and association reactions (see Table 5). We used the fixed geometries provided by the authors of this test set²⁷ optimized at the quadratic configuration interaction with singles and doubles (QCISD) level of theory. All single-point calculations of the reactants, products, and transition states are done with the Q-Chem program following the same computational setup as described in Sec. 3. Energy differences are in kcal/mol, and mean errors are computed as theory minus experiment.

Table 5.

Reactions from the HTBH38/04 database.

Type	Index	Reaction
Heavy-atom transfer	TS1	H + N2O → OH + N2
	TS2	H + FH → HF + H
	TS3	H + ClH → HCl + H
	TS4	H + FCH3 → HF + CH3
	TS5	H + F2 → HF + F
	TS6	CH3 + FCl → CH3F + Cl
Nucleophilic substitution	TS7	F− + CH3F → FCH3 + F−
	TS8	F−⋅⋅⋅CH3F → FCH3⋅⋅⋅F−
	TS9	Cl− + CH3Cl → ClCH3 + Cl−
	TS10	Cl−⋅⋅⋅CH3Cl → ClCH3⋅⋅⋅Cl−
	TS11	F− + CH3Cl → FCH3 + Cl−
	TS12	F−⋅⋅⋅CH3Cl → FCH3⋅⋅⋅Cl−
	TS13	OH− + CH3F → HOCH3 + F−
	TS14	OH−⋅⋅⋅CH3F → HOCH3⋅⋅⋅F−
Unimolecular and	TS15	H + N2 → HN2
association	TS16	H + CO → HCO
	TS17	H + C2H4 → CH3CH2
	TS18	CH3 + C2H4 → CH3CH2CH2
	TS19	HCN → HNC

Table 6 contains the ME and mean absolute errors (MAE) for the six heavy-atom transfer reactions from the HTBH38/04 set. It is seen that many functionals tend to underestimate these reaction barriers. Among the schemes with full exact exchange, MCY2 performs the best here with MAE of 2.06 kcal/mol, followed closely by PERT-RI-B05 with MAE of 2.22 kcal/mol. The SCF-RI-B05 estimates (MAE of 3.44 kcal/mol) are less accurate than those of PERT-RI-B05 here. RI-PSTS yields better results than TPSS and TPSSh, but still it has a strong tendency to underestimate these reaction barriers (MAE of 5.19 kcal/mol). Among the functionals tested, M06-2X has the lowest MAE of 1.46 kcal/mol on this test set. ωB97X and MCY2 have the second best MAE of 2.05 kcal/mol and 2.06 kcal/mol, respectively, PERT-RI-B05 is close behind with MAE of 2.22 kcal/mol. The performance of the above four functionals is far better than that of B3LYP (MAE of 8.7 kcal/mol) and M06-HF (MAE of 4.69 kcal/mol).

Table 6.

Reaction barriers of heavy-atom transfer reactions.

Methods	Type	ME	MAE	Max(+)	Max(−)
RI-PSTS	Vf	−4.00	4.00	…	−5.86 (TS6 )
	Vr	−6.37	6.37	…	−10.03 (TS1 )
	Average	−5.19	5.19	…	−10.03 (TS1 )
SCF-RI-B05	Vf	−2.71	2.71	…	−5.44 (TS6 )
	Vr	−4.17	4.17	…	−6.93 (TS1 )
	Average	−3.44	3.44	0.00 (…)	−6.93 (TS1 )
PERT-RI-B05	Vf	−1.09	1.86	2.15 (TS5 )	−4.72 (TS6 )
	Vr	−1.69	2.58	2.69 (TS5 )	−4.32 (TS6 )
	Average	−1.39	2.22	2.69 (TS5 )	−4.72 (TS6 )
MCY2	Vf	−0.84	1.51	2.00 (TS1 )	−4.99 (TS2 )
	Vr	−2.61	2.61	…	−4.99 (TS2 )
	Average	−1.73	2.06	2.00 (TS1 )	−4.99 (TS2 )
TPSSh	Vf	−10.20	10.20	…	−12.88 (TS2 )
	Vr	−13.18	13.18	…	−16.96 (TS1 )
	Average	−11.69	11.69	…	−16.96 (TS1 )
B3LYP	Vf	−8.23	8.23	…	−10.94 (TS2 )
	Vr	−9.18	9.18	…	−11.00 (TS5 )
	Average	−8.70	8.70	…	−11.00 (TS5 )
M06-2X	Vf	−0.98	1.24	0.58 (TS4 )	−3.36 (TS2 )
	Vr	−1.07	1.69	1.65 (TS5 )	−3.36 (TS2 )
	Average	−1.03	1.46	1.65 (TS5 )	−3.36 (TS2 )
M06-HF	Vf	0.14	2.80	4.08 (TS5 )	−6.72 (TS2 )
	Vr	2.39	6.57	11.84 (TS1 )	−6.72 (TS2 )
	Average	1.26	4.69	11.84 (TS1 )	−6.72 (TS2 )
ωB97X	Vf	0.48	1.96	3.00 (TS3 )	−3.29 (TS6 )
	Vr	−0.78	2.13	3.00 (TS3 )	−2.88 (TS5 )
	Average	−0.15	2.05	3.00 (TS3 )	−3.29 (TS6 )
HF	Vf	8.75	12.79	16.98 (TS4 )	−12.11 (TS5)
	Vr	20.50	20.50	40.60 (TS1 )	…
	Average	14.62	16.64	40.60 (TS1 )	−12.11 (TS5)

Turning to the nucleophilic substitution reactions as listed in Table 7, most functionals tend again to underestimate on average these reaction barriers, except for ωB97X and M06-2X. The latter two have the smallest and second smallest MAE of 1.18 kcal/mol and 1.34 kcal/mol, respectively. Among the schemes with full exact exchange (including M06-HF), M06-HF and MCY2 are the most accurate on this test set with MAE of 1.64 kcal/mol and 1.65 kcal/mol, respectively, followed by PERT-RI-B05 with MAE of 2.88 kcal/mol. RI-PSTS has the largest MAE (4.39 kcal/mol) among the considered methods with full exact exchange, even though there is slight improvement in the results over TPSS and TPSSh.

Table 7.

Reaction barriers of nucleophilic substitution reactions.

Methods	Type	ME	MAE	Max(+)	Max(−)
RI-PSTS	Vf	−4.50	4.50	…	−6.37 (TS10)
	Vr	−4.29	4.29	…	−6.37 (TS10)
	Average	−4.39	4.39	…	−6.37 (TS10)
SCF-RI-B05	Vf	−3.28	3.28	…	−4.39 (TS10)
	Vr	−3.40	3.40	…	−4.39 (TS10)
	Average	−3.34	3.34	…	−4.39 (TS10)
PERT-RI-B05	Vf	−2.84	2.84	…	−3.96 (TS10)
	Vr	−2.88	2.88	…	−3.96 (TS10)
	Average	−2.86	2.86	…	−3.96 (TS10)
MCY2	Vf	−1.70	1.70	…	−3.20 (TS10)
	Vr	−1.63	1.65	0.06 (TS11)	−3.20 (TS10)
	Average	−1.67	1.67	0.06 (TS11)	−3.20 (TS10)
TPSSh	Vf	−5.67	5.67	…	−6.64 (TS11)
	Vr	−5.61	5.61	…	−6.39 (TS10)
	Average	−5.64	5.64	…	−6.64 (TS11)
B3LYP	Vf	−3.32	3.32	…	−4.45 (TS10)
	Vr	−3.31	3.31	…	−4.45 (TS10)
	Average	−3.31	3.31	…	−4.45 (TS10)
M06-2X	Vf	0.37	1.16	3.56 (TS14)	−2.19 (TS11)
	Vr	1.30	1.52	3.94 (TS12)	−0.85 (TS9 )
	Average	0.83	1.34	3.94 (TS12)	−2.19 (TS11)
M06-HF	Vf	−1.00	1.65	1.90 (TS14)	−2.65 (TS13)
	Vr	−0.56	1.64	2.54 (TS12)	−2.99 (TS13)
	Average	−0.78	1.64	2.54 (TS12)	−2.99 (TS13)
ωB97X	Vf	0.43	1.34	2.25 (TS10)	−1.93 (TS7 )
	Vr	0.49	1.02	2.25 (TS10)	−1.93 (TS7 )
	Average	0.46	1.18	2.25 (TS10)	−1.93 (TS7 )
HF	Vf	9.71	9.71	42.75 (TS14)	…
	Vr	3.73	10.82	13.56 (TS11)	−28.37 (TS14)
	Average	6.72	10.27	42.75 (TS14)	−28.37 (TS14)

Next we present in Table 8 our results for the unimolecular and association reactions from the HTBH38/04 set (see Table 5). Unlike the heavy-atom transfer reactions and nucleophilic substitution reactions, here the errors spread more evenly between the positive and negative signs. The best prediction for this test sets comes again from M06-2X functional (MAE of 0.90 kcal/mol), followed closely by SCF-RI-B05 (MAE of 1.12 kcal/mol) and PERT-RI-B05 (MAE of 1.39 kcal/mol). Among the schemes with full exact exchange PERT-RI-B05 and SCF-RI-B05 outperform on this test set M06-HF (MAE of 1.48 kcal/mol), as well as RI-PSTS (MAE of 1.70 kcal/mol) and MCY2 (MAE of 2.05 kcal/mol). The B05 and PSTS models incorporate ND correlation effects explicitly in real space, which for this type of reactions seems to matter more.

Table 8.

Reaction barriers of unimolecular and association reactions.

Methods	Type	ME	MAE	Max(+)	Max(−)
RI-PSTS	Vf	−1.51	1.96	1.12 (TS18)	−4.22 (TS15)
	Vr	0.58	1.43	3.49 (TS17)	−1.41 (TS18)
	Average	−0.46	1.70	3.49 (TS17)	−4.22 (TS15)
SCF-RI-B05	Vf	−0.50	0.65	0.38 (TS18)	−1.44 (TS15)
	Vr	−0.87	1.58	1.26 (TS19)	−3.54 (TS18)
	Average	−0.69	1.12	1.26 (TS19)	−3.54 (TS18)
PERT-RI-B05	Vf	0.68	0.80	1.80 (TS16)	−0.31 (TS15)
	Vr	0.20	1.97	2.53 (TS16)	−3.25 (TS18)
	Average	0.44	1.39	2.53 (TS16)	−3.25 (TS18)
MCY2	Vf	1.56	2.36	3.83 (TS17)	−1.56 (TS15)
	Vr	1.03	1.74	3.45 (TS16)	−1.77 (TS18)
	Average	1.30	2.05	3.83 (TS17)	−1.77 (TS18)
TPSSh	Vf	−5.26	5.26	…	−10.35 (TS15)
	Vr	−0.67	1.25	1.45 (TS16)	−3.09 (TS18)
	Average	−2.96	3.25	1.45 (TS16)	−10.35 (TS15)
B3LYP	Vf	−2.76	2.76	…	−7.00 (TS15)
	Vr	−0.16	1.26	1.94 (TS16)	−3.55 (TS18)
	Average	−1.46	2.01	1.94 (TS16)	−7.00 (TS15)
M06-2X	Vf	−0.39	1.03	1.21 (TS17)	−1.99 (TS19)
	Vr	0.78	0.78	1.81 (TS17)	…
	Average	0.20	0.90	1.81 (TS17)	−1.99 (TS19)
M06-HF	Vf	0.83	1.87	2.91 (TS15)	−2.03 (TS19)
	Vr	0.22	1.09	2.14 (TS15)	−1.19 (TS16)
	Average	0.53	1.48	2.91 (TS15)	−2.03 (TS19)
ωB97X	Vf	0.02	1.52	2.45 (TS17)	−1.77 (TS18)
	Vr	3.20	3.20	5.30 (TS17)	…
	Average	1.61	2.36	5.30 (TS17)	−1.77 (TS18)
HF	Vf	4.34	4.45	8.40 (TS15)	−0.29 (TS19)
	Vr	1.01	3.12	4.96 (TS19)	−5.21 (TS16)
	Average	2.67	3.79	8.40 (TS15)	−5.21 (TS16)

Finally, in Tables 9, 10 we present results for hydrogen abstraction. This type of reactions has been in the focus of the DFT studies for a long time. Earlier semilocal and hybrid functionals suffered a massive failure in accurately reproducing these reaction barriers, especially concerning the “very simple” hydrogen abstraction (reaction TS5 in Table 10).^{42, 43} The transition state for this reaction is the linear three-center doublet radical H₃. Strong ND correlation and delocalization effects have been shown to be pertinent for this structure, which makes it very difficult to achieve an accurate estimate of this and other similar barrier heights.⁴³ Among the results listed in Table 10, PERT-RI-B05 (MAE of 1.26 kcal/mol) and M06-2X (MAE of 1.33 kcal/mol) have the smallest and the second smallest MAE, respectively, followed closely by SCF-RI-B05 with MAE of 1.73 kcal/mol. The rest of the functionals have MAE ranging from 2.16 kcal/mol (with wB97X) to 10.15 kcal/mol (with TPSSh). Among the schemes with full exact exchange, the B05 based options outperform the rest, with M06-HF giving the largest MAE within this group of functionals.

Table 9.

Reactions of hydrogen abstraction.

Index	Reaction
TS1	H + HCl → H2 + Cl
TS2	H + HCl → HCl + H
TS3	H + OH → H2 + O
TS4	H2 + F → HF + H
TS5	H2 + H → H2 + H
TS6	OH + H2 → H + H2O
TS7	OH + NH3 → H2O + NH2
TS8	H + H2S → H2 + HS
TS9	O + HCl → Cl + OH
TS10	H + CH3OH → H2 + CH2OH

Table 10.

Reaction barriers of hydrogen abstraction reactions.

Methods	Type	ME	MAE	Max(+)	Max(−)
RI-PSTS	Vf	−0.83	1.66	3.06 (TS6)	−5.64 (TS1)
	Vr	−0.27	2.69	4.65 (TS3)	−7.55 (TS4)
	Average	−0.55	2.18	4.65 (TS3)	−7.55 (TS4)
SCF-RI-B05	Vf	−1.66	1.82	0.80 (TS10)	−4.10 (TS3)
	Vr	−1.63	1.63	…	−3.40 (TS9)
	Average	−1.64	1.73	0.80 (TS10)	−4.10 (TS3)
PERT-RI-B05	Vf	0.75	1.47	6.00 (TS9)	−2.90 (TS3)
	Vr	0.93	1.05	3.80 (TS9)	−0.30 (TS2)
	Average	0.84	1.26	6.00 (TS9)	−2.90 (TS3)
MCY2	Vf	−1.42	2.28	2.68 (TS10)	−4.56 (TS3)
	Vr	−2.47	2.57	0.48 (TS10)	−4.94 (TS4)
	Average	−1.95	2.42	2.68 (TS10)	−4.94 (TS4)
TPSSh	Vf	−10.16	10.16	…	−13.25 (TS9)
	Vr	−10.13	10.13	…	−15.12 (TS4)
	Average	−10.15	10.15	…	−15.12 (TS4)
B3LYP	Vf	−5.68	5.68	…	−8.34 (TS9)
	Vr	−5.36	5.36	…	−10.19 (TS4)
	Average	−5.52	5.52	…	−10.19 (TS4)
M06-2X	Vf	−0.03	1.22	2.72 (TS10)	−2.49 (TS9)
	Vr	−0.43	1.44	2.03 (TS5)	−2.83 (TS9)
	Average	−0.23	1.33	2.72 (TS10)	−2.83 (TS9)
M06-HF	Vf	2.26	2.70	6.60 (TS5)	−1.58 (TS1)
	Vr	2.29	2.64	6.60 (TS5)	−1.72 (TS9)
	Average	2.28	2.67	6.60 (TS5)	−1.72 (TS9)
ωB97X	Vf	−0.35	2.12	3.00 (TS2)	−5.28 (TS4)
	Vr	−1.14	2.21	3.00 (TS2)	−4.72 (TS4)
	Average	−0.75	2.16	3.00 (TS2)	−5.28 (TS4)
HF	Vf	13.33	13.33	24.81 (TS7)	…
	Vr	10.34	11.75	19.55 (TS3)	−7.04 (TS4)
	Average	11.83	12.54	24.81 (TS7)	−7.04 (TS4)

THE DISSOCIATION AS A PROBE OF NONDYNAMIC CORRELATION

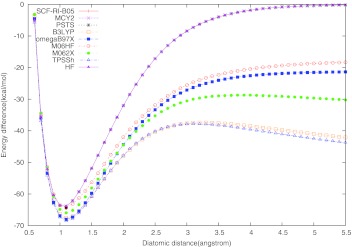
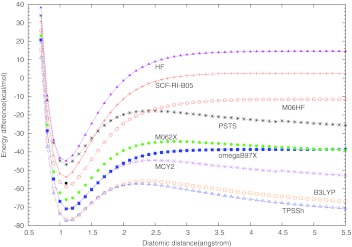
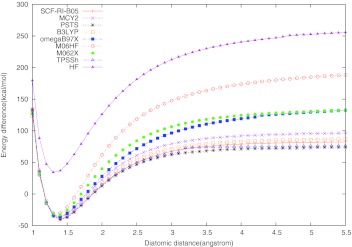
The correct description of dissociation energy curves is still a great challenge for approximate DFT methods.^{8, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52} Particularly large dissociation errors may occur for symmetric radicals with odd number of electrons. The “simplest” such cases are ${\mathrm{H}}_2^{+}$ and ${\mathrm{He}}_2^{+}$. Their dissociation curves are shown in Figs. 12 calculated here with different functionals. All curves were scanned with 0.1 Å step size and the plotted binding energy was calculated as $E_{X_2}-2E_X$.

Figure 1.

Dissociation curve for ${\mathrm{H}}_2^{+}$ cation. The experimental equilibrium bond length is 1.057 Å, and the experimental bond dissociation energy D_e is −64.4 kcal/mol⁵⁷ (noted with a black dot in the figure).

Figure 2.

Dissociation curve for ${\mathrm{He}}_2^{+}$ cation. The experimental equilibrium bond length is 1.081 Å, and the experimental bond dissociation energy D_e is −57.0 kcal/mol⁵⁸ (noted with a black dot in the figure).

The dissociation state of ${\mathrm{He}}_2^{+}$, Fig. 2, can be described with a symmetric two-reference, three-electron wave function of the form:

$$\begin{array}{c}\hfill {\Psi }^{{\mathrm{He}}_2^{+}}(1,2,3)\approx \frac{1}{2}\left[\right|{\mathrm{He}}_A^{+},{\mathrm{He}}_B⟩+|{\mathrm{He}}_B^{+},{\mathrm{He}}_A⟩].\end{array}$$ (34)

At large He–He distance, all three states, the asymmetric $|{\mathrm{He}}_A^{+},{\mathrm{He}}_B⟩$, $|{\mathrm{He}}_B^{+},{\mathrm{He}}_A⟩$, and the symmetric ${\Psi }^{{\mathrm{He}}_2^{+}}$, become degenerate.⁴⁵ In the context of wave function 34, the charge on each He center is an ensemble average of the two pure He states with integer charge 0 and 1^{45, 52, 53} and the resulting average positive charge in ${\mathrm{He}}_2^{+}$ is distributed evenly by a fraction of +0.5 on each center.

Similar is the situation with the ${\mathrm{H}}_2^{+}$ symmetric radical as far as the appearance of fractional charge on each H center concern. Single-reference methods such as Hartree-Fock or Kohn-Sham SCF would normally converge (at any He–He distance) to the symmetric state with a fractional charge of +0.5 on each center, unless symmetry breaking is enforced from the outset. Most approximate functionals show a large SI error in symmetric distribution of the radical charge. This leads to an artificial lowering of the dissociation energy after certain critical distance (delocalization error⁸). In contrast, the Hartree-Fock energy dependence on the fractional charge results in a spurious concave curve which leads to the observed shift of the HF dissociation curve of ${\mathrm{He}}_2^{+}$ above the zero line at large distances (a localization error). All this is clearly illustrated with our results shown in Figs. 12. In the exact quantum-mechanical description, the symmetric and asymmetric solutions for such systems become degenerate in the dissociation limit.^{45, 52} This is not the case with most approximate DFT methods. Hartree-Fock reproduces this exact feature for ${\mathrm{H}}_2^{+}$ but not for ${\mathrm{He}}_2^{+}$, as it can be seen on Figs. 12. The symmetric dissociation curves of ${\mathrm{H}}_2^{+}$ and ${\mathrm{He}}_2^{+}$ obtained with LSD, GGA, meta-GGA, and hybrid functionals have the typical spurious maximum at certain critical distance, after which the curves gradually fall downward, instead of correctly approaching the zero line upward. Our calculations confirm this delocalization error for TPSSh, B3LYP, and M06-2X functionals, for both ${\mathrm{H}}_2^{+}$ and ${\mathrm{He}}_2^{+}$. Considering the functionals with full exact exchange, all of them except M06-HF yield the exact (HF) dissociation curve for the one-electron ${\mathrm{H}}_2^{+}$ system. However, RI-PSTS and MCY2 show a noticeable delocalization error for ${\mathrm{He}}_2^{+}$, albeit smaller than the B3LYP and TPSSh errors. The long-range corrected functional ωB97X and the full exact-exchange scheme M06-HF give symmetric dissociation curves without a spurious maximum, tending asymptotically to the right direction for both ${\mathrm{He}}_2^{+}$ and ${\mathrm{H}}_2^{+}$ , but still quite below the zero line (Figs. 12). The only functional among those tested here that gives a reasonably accurate dissociation curve for ${\mathrm{He}}_2^{+}$ is SCF-RI-B05. We have tried to analyze the reason why SCF-RI-B05 is the only accurate option for the ${\mathrm{He}}_2^{+}$ dissociation. The HF symmetric dissociation curve alone is about 14 kcal/mol above the zero line in the asymptotic region. The SCF-RI-B05 curve is only about 1.5 kcal/mol above the zero line (no delocalization error, but a slight localization error), which means that the localization error pertinent to the 100% HF (or exact exchange in the case of B05) is largely suppressed in SCF-RI-B05 by its four other energy components: two nondynamic and two dynamic correlation terms. We conducted a numerical experiment by calculating the ${\mathrm{He}}_2^{+}$ dissociation curve in the asymptotic region with a “truncated” SCF-RI-B05 scheme in which all ND terms are omitted. This leads to only a slight shift of the dissociation curve upward by about 0.6 kcal/mol. Therefore, the opposite-spin and the same-spin components of the (re-scaled) dynamic correlation functional BR94²⁶ that is involved in the B05 scheme⁶ is responsible for the remaining lowering of the localization error of HF on stand alone. This shows that ${\mathrm{He}}_2^{+}$ system contains no ND correlation. The reason is that in neutral He₂, both alpha and beta exchange holes are completely localized. When a beta electron is removed, it will only cause the other beta electron delocalized, but not the alpha electrons. Thus, no nondynamic correlation of opposite spin should occur according to B05 theory. The reason for the zero ND correlation of parallel spin was explained in the B05 paper.⁶ The overall result also indicates that BR94 gives quite accurate count of the dynamic correlation for this system.

The other two hyper-GGA functionals, RI-PSTS and MCY2 show large delocalization error by about 29 kcal/mol and 56 kcal/mol, respectively. A large delocalization error is mostly caused by a large self-interaction error, as analyzed previously.^{45, 52} In the case of RI-PSTS and MCY2, the dominant contribution to the self-interaction error comes from the model pure-DFT exchange terms.^{8, 45} B05 does not involve such terms, while RI-PSTS and MCY do have GGA and meta-GGA model exchange components. In MCY2, the GGA exchange functional Becke'88 is involved in a sophisticated nonlinear fashion, which may explain the larger delocalization error of MCY2 compared to RI-PSTS. Having functionals with diminished delocalization or localization errors is important in studying various ion-radical organic processes.⁴⁴

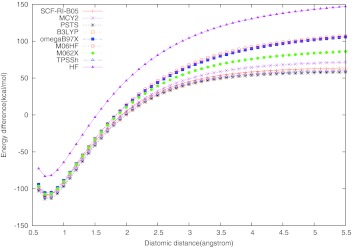
Next, we consider the dissociation of singlet molecules such as H₂, N₂ and F₂. The dissociation of H₂, Fig. 3, is a case example illustrating the essence of the left-right ND correlation and why most approximate functionals fail to describe it correctly.^{4, 5, 6, 12} Real-space analysis of the exact-exchange hole vs. approximate XC holes has revealed the deficiency of common functionals in this vein and has lead to the development of new functionals (B05,⁶ RI-PSTS¹²) with explicit ND correlation corrections. A complementary approach to this problem is the analysis of the fractional-spin error that approximate functionals show in describing such dissociation processes.^{8, 52} The dissociation state of H₂ can be described by a symmetric two-reference, two-electron wave function of the form

$$\begin{array}{ccc}\hfill {\Psi }^{{\mathrm{H}}_2}(1,2)& \approx & \frac{1}{2}\left[\right|{\mathrm{H}}_A(\alpha ,0),{\mathrm{H}}_B\left(0,\beta \right)⟩\hfill \\ & & +|{\mathrm{H}}_A(0,\beta ),{\mathrm{H}}_B(\alpha ,0)⟩],\hfill \end{array}$$ (35)

where α, β ≠ α show the direction and the magnitude of the spin that localizes asymptotically on each H atom. At large H–H distance, all three states |H_A(α, 0), H_B(0, β)⟩, |H_A(0, β), H_B(α, 0)⟩, and ${\Psi }^{{\mathrm{H}}_2}$ become degenerate for any fractional values of α and β.⁵² In the context of the two-reference state 35, the observable spin localized on each H center is an ensemble average of the two integer-spin states^{8, 53} leading to effective fractional spin occupancy as in H(0.5,−0.5) on each center. In a formally exact DFT (spin-restricted) treatment, the energy of the H₂ dissociation state remains the same for any fractional values of α and β^{8, 52} as dictated also by the exact multi-reference treatment. Approximate functionals violate this condition. The approximate spin-restricted DFT dissociation energy changes in a concave manner with variation of the fractional atomic spin, reaching a spurious maximum at the observable state of H(0.5,−0.5). It has been shown that inaccurate/incomplete treatment of ND correlation is responsible for this spurious maximum.⁸ The dissociation energy at the maximum is equal to the difference between the energy curve asymptote and the zero line. This energy difference reflects the magnitude of the “fractional-spin” error of a given functional.⁸ From this perspective, the close-packed (spin-restricted) dissociation curves with B3LYP, TPSSh, SCF-RI-B05, and RI-PSTS (Fig. 3) have the lowest fractional-spin error in the H₂ case, RI-PSTS being the front-runner. MCY2 has a slightly larger error compared to the above close-packed group, while the error is somewhat more significant for M06-2X. The ωB97X and M06-HF functionals have the largest fractional-spin error here. Still, the smallest error (with RI-PSTS) is about 40 kcal/mol above the exact zero line.

Figure 3.

Dissociation curve for H₂. The experimental equilibrium bond length is 0.741 Å, and the experimental bond dissociation energy D_e is −109.4 kcal/mol.⁵⁹

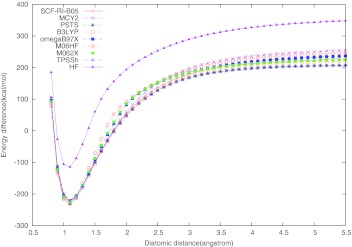
Turning to the dissociation of N₂, Fig. 4, we have the same close-packed group of curves with B3LYP, TPSSh, SCF-RI-B05, and RI-PSTS being the closest to the zero line. The front-runner (the RI-PSTS curve) is still about 150 kcal/mol above the zero line. Next are the MCY2, M06-2X, and ωB97X curves, the latter reaching about 310 kcal/mol above the zero line. The largest fractional-spin error in the N₂ case shows again M06-HF.

Figure 4.

Dissociation curve for N₂. The experimental equilibrium bond length is 1.098 Å,⁶⁰ and the experimental bond dissociation energy D_e is −228.4 kcal/mol.⁶¹

Finally, considering the dissociation of F₂, Fig. 5, the same group of four curves are the closest to the zero line, with RI-PSTS being again the front runner with about 50 kcal/mol above the zero line. M06-HF shows the largest fractional-spin error in this case as well.

Figure 5.

Dissociation curve for F₂. The experimental equilibrium bond length is 1.412 Å,⁶⁰ and the experimental bond dissociation energy D_e is −37.5 kcal/mol.⁶²

The above examples show that the multi-parameter functionals such as M06-2X and ωB97X have large errors under bond stretching even though they perform well at equilibrium. The RI-PSTS, B05, and MCY methods perform relatively better here but still need further improvement with respect to taking properly into account the fractional-spin problem.

THE STRONGLY CORRELATED NO DIMER TEST

The cis-NO dimer (ONNO) is a good test case system of ND correlation because the correlation effects are very strong and difficult to describe.^{16, 17, 22} Massive failures of LSD, various GGA, meta-GGA, and hybrid functionals have been repeatedly reported over the past 25 years in describing the subtle energetics and structure of this dimer.^{16, 17, 18, 23, 54, 55} The usual covalent picture of each monomer sharing a single electron to form a covalent N–N bond pair is not qualitatively correct here. The experiment indicates a very weak binding energy (D_e) of about 2.9 kcal/mol–3.3 kcal/mol.⁵⁴ The latter value has been confirmed by MR studies^{18, 55, 56} showing that the cis-NO dimer bonding has a strong multi-reference character in its ¹A₁ singlet ground state. The closest triplet state, ³B₁, is about 6.3 kcal/mol higher.⁵⁶ Single-reference methods such as MP2 and coupled-cluster with singles, doubles and perturbative triples (CCSD(T)) fail to predict the correct energy ordering of these dimer states. The early DFT studies reported in literature¹⁶ yielded a triplet ground state in contradiction to experiment.

Table 11 contains our results for the binding energy and the singlet-triplet split of cis-ONNO obtained with various methods. The singlet-triplet split is calculated at the respective optimized geometries of both states. We note first that B3LYP, TPSSh, and M06-HF fail to predict the correct ground-state multiplicity, giving a triplet state as the lowest (negative △_TS split). In regard to the binding energy, we confirm the failure of most methods to yield any real binding of the NO dimer, the M06-HF result being the worst in this respect. Only SCF-RI-B05, MCY2, and RI-PSTS yield a positive binding here. The RI-PSTS values of +11.2 kcal/mol for D_e and +11.8 kcal/mol for △_TS are too large compared to the MRCI benchmarks. The SCF-RI-B05 and MCY2 functionals both yield a rather good estimate of △_TS and quite reasonable D_e value, given the fact that no other option gives any positive binding here. The SCF-RI-B05 result for D_e is about 2.0 kcal/mol larger the multi-reference configuration interaction method (MRCI) benchmark of 3.3 kcal/mol, while the MCY2 estimate is about 1.9 kcal/mol smaller than the MRCI result. The good agreement between the energy estimates by B05 and MCY2 here may be related to the reported similarity of these two functionals as far as their energy dependence on the fractional-spin value is concerned.⁵²

Table 11.

Singlet-triplet split energy △_TS (kcal/mol), dimerization energy De (kcal/mol, BSSE corrected) of cis-NO dimer. Both singlet and triplet states are optimized. The geometries reported in the table (in Å) correspond to the singlet state.

Methods	△TS	De	RN − N	RN − O	ANNO
Experimental54	…	2.9–3.3	2.26	1.15	97.17
MRCI18, 56	6.30	3.30	2.28	1.15	96.10
RI-PSTS	11.81	11.20	2.00	1.15	100.60
SCF-RI-B05	6.60	5.30	2.00	1.15	101.30
MCY2	6.72	1.39	1.93	1.14	102.30
TPSSh	−3.96	−1.44	1.99	1.15	100.49
B3LYP	−2.25	−3.11	1.97	1.15	101.53
M06-2X	3.90	−6.74	1.83	1.14	104.24
M06-HF	−18.38	−18.02	1.64	1.14	109.00
ωB97X	2.09	−7.05	1.84	1.15	103.74
HF	−49.20	−49.68	1.61	1.13	110.12

Concerning the difficult to reproduce N–N bond length, SCF-RI-B05 and PSTS yield the best N–N bond of 2.0 Å, which is still shorter by about 0.26 Å than the experimental value. The MCY2 optimized N–N distance of 1.93 Å is too short. The geometries obtained with the rest of the methods are only informative because these methods do not yield any positive binding of the NO dimer.

The present results confirm the previous findings^{15, 17, 22, 23, 56} that the subtle structure of the NO dimer cannot be even remotely described properly without including explicitly ND correlation corrections in the method. Methods with full exact exchange and only a few fitting parameters, such as the functionals MCY2 and SCF-RI-B05 show some very good promise in describing the energetics of the NO dimer, while its geometry characteristics still remain elusive.

CONCLUSION

In this paper we report a SCF implementation of PSTS functional based on RI approximation for the exchange energy density. The new implementation allows the use of general Gaussian basis functions with the PSTS method. The RI-PSTS method is then compared with RI-B05, a method that also estimates the nondynamic correlation in real space using the exchange-energy density, and with MCY2, a functional that employs full exact exchange. The comparisons are made on a variety of properties, including thermochemistry, reaction barriers, dissociation energy curves, and the NO dimer. Those methods are also compared to a selection of representative hybrid GGA and meta functionals, and range-corrected functionals, namely M06-HF, TPSSh, B3LYP, M06-2X, and ωB97X.

The three hyper-GGA methods, MCY2, RI-B05, and RI-PSTS perform very well for most tested properties, considering the small numbers of empirical parameters built-in. In particular, these methods almost systematically outperform the M06-HF, a heavily parameterized meta-GGA functional with full exact exchange. The only exception are the nucleophilic substitution reactions. Among the three methods, MCY2 performs the best for the thermochemistry embodied in the G2 database, with RI-B05 being a close second. RI-B05 on the other hand is shown to be best among the three functionals for reaction barriers, except for heavy-atom transfer reactions where MCY2 performs slightly better. We find that as a group, these three methods do not perform as well as the heavily parameterized meta-GGA and range-corrected GGA functionals such as M06-2X and ωB97X for most of the thermodynamic properties and reaction barriers, except for hydrogen-transfer reactions. The picture is different, however, under bond-stretching, with neutral and cationic diatomics. Here M06-2X and ωB97X deteriorate at a faster pace than the group of three functionals with full exact exchange. RI-B05, in particular, dissociates ${\mathrm{He}}_2^{+}$ almost perfectly. The rest of the functionals show large delocalization error in the dissociation limit of this system. Still none of these functionals dissociate correctly in general at large bond separations.

Finally, we subjected all the functionals to the stringent NO dimer test, a well-known system of strong nondynamic correlation. In this case, all the hybrid GGA and meta-GGA functionals fail to predict qualitatively either the correct ground state or the binding energy or both. In contrast, the three hyper-GGA functionals with full exact exchange do so, showing that these models incorporate new important effects that are missing from the rest of the functionals.