Genetic composition of yield heterosis in an elite rice hybrid

Abstract

Heterosis refers to the superior performance of hybrids relative to the parents. Utilization of heterosis has contributed tremendously to the increased productivity in many crops for decades. Although there have been a range of studies on various aspects of heterosis, the key to understanding the biological mechanisms of heterotic performance in crop hybrids is the genetic basis, much of which is still uncharacterized. In this study, we dissected the genetic composition of yield and yield component traits using data of replicated field trials of an “immortalized F₂” population derived from an elite rice hybrid. On the basis of an ultrahigh-density SNP bin map constructed with population sequencing, we calculated single-locus and epistatic genetic effects in the whole genome and identified components pertaining to heterosis of the hybrid. The results showed that the relative contributions of the genetic components varied with traits. Overdominance/pseudo-overdominance is the most important contributor to heterosis of yield, number of grains per panicle, and grain weight. Dominance × dominance interaction is important for heterosis of tillers per plant and grain weight and has roles in yield and grain number. Single-locus dominance has relatively small contributions in all of the traits. The results suggest that cumulative effects of these components may adequately explain the genetic basis of heterosis in the hybrid.

Heterosis, or hybrid vigor, refers to the superior performance of the hybrids relative to the parents (1). Utilization of heterosis has tremendously increased productivity of many crops globally. However, the understanding of the underpinning biological mechanism is still fragmentary after a century of debate and quest. Although there have been a range of studies on various aspects of heterosis (2–5), the key to understanding the biological mechanisms of heterotic performance in crop hybrids is the genetic basis (6), much of which is still uncharacterized (7).

Three classic genetic hypotheses—dominance (8–11), overdominance (12–15), and epistasis (16, 17)—were proposed as explanations for the genetic basis of heterosis. Although there have been a large number of genetic analyses in plants with results favoring one hypothesis or another (18–31), genetic composition pertaining to heterotic performance of crop hybrids has not been fully characterized in an experimental population. There has been no assessment about the relative contributions of these genetic components to heterosis in a crop hybrid.

The following conditions should be met for complete genetic characterization of heterosis relevant to crop production: (i) the genetic materials are based on elite hybrids that have shown time-honored superiority in crop production; (ii) the targets are key traits of agronomic performance; (iii) the experimental population allows identification of all of the genetic components concerned, including dominance (d/a ≤1, where d is the dominant effect and a is the additive effect, and d/a is referred to as the degree of dominance), overdominance (d/a >1), and epistasis (nonadditive interactions between loci); and (v) there is a full set of markers that could detect the genetic effects of any region in the entire genome.

Shanyou 63 is an elite indica rice hybrid that has been grown in a large area in the past 3 decades, mostly in China. We previously constructed an “immortalized F₂” (IMF2) population by intercrossing recombinant inbred lines (RILs) derived from a cross between Zhenshan 97 and Minghui 63, the parents of Shanyou 63 (24, 25). The entire population was field tested for yield traits, resulting in data that were particularly useful for studying the genetics of heterosis by mapping heterotic effects and identifying genetic components contributing to heterosis. More recently we resequenced the RILs and developed an algorithm for constructing an ultrahigh-density bin map, which provided more precise information for genetic mapping (32, 33).

In this study, we analyzed the genetic effects of all of the bins in the IMF2 population, including additive, dominance, and epistasis, and assessed their relative contributions to heterosis in the F₁ hybrid. The analyses displayed a picture that accumulation of small advantages genome-wide could explain the genetic basis of heterosis in this elite rice hybrid.

Results

Bin Map for the IMF2 Population.

The experimental population was obtained by three rounds of paired crosses of 240 RILs derived by single-seed descent from a cross between Zhenshan 97 and Minghui 63. The details of the mating scheme, genetic characteristics of the population, and field experiment were described previously (24). We obtained genomic sequence data for 210 of the RILs using new sequencing technology and constructed an ultrahigh-density SNP map consisting of 1,619 bins using an algorithm we developed (32, 33). Data for 278 crosses were obtained on the basis of the 210 RILs, and genotype for each cross was deduced according to the RILs that were used as the parents for crossing, on the basis of which a bin map for the 278 crosses was constructed (Dataset S1). There were three genotypes in each bin, a homozygote for each parental genotype (A and B), and a heterozygote (H), with frequencies equivalent to those in an F₂ population. Similarly, genotypic frequencies of multilocus combinations should also be similar to those in an F₂ population. This population was thus referred to as an IMF2 population, which has distinct advantages in heterosis study (24, 25).

The accuracy of the ultrahigh-density bin map of the RILs was previously evaluated with two known genes, which precisely resolved GS3 (33, 34) and GW5/qSW5 (35, 36) to their known locations. However, for the IMF2, we did not have data for grain length or width. We thus assessed the quality of the IMF2 bin map using related traits [grain weight for GS3 and GW5/qSW5 and grain number for Ghd7 (37)]. These quantitative trait loci (QTLs) were successfully mapped to their known locations, showing the accuracy of the bin map (Fig. S1 A–F).

Landscape of Heterotic Effects by Analyzing Effects of the Bins in the Entire Genome.

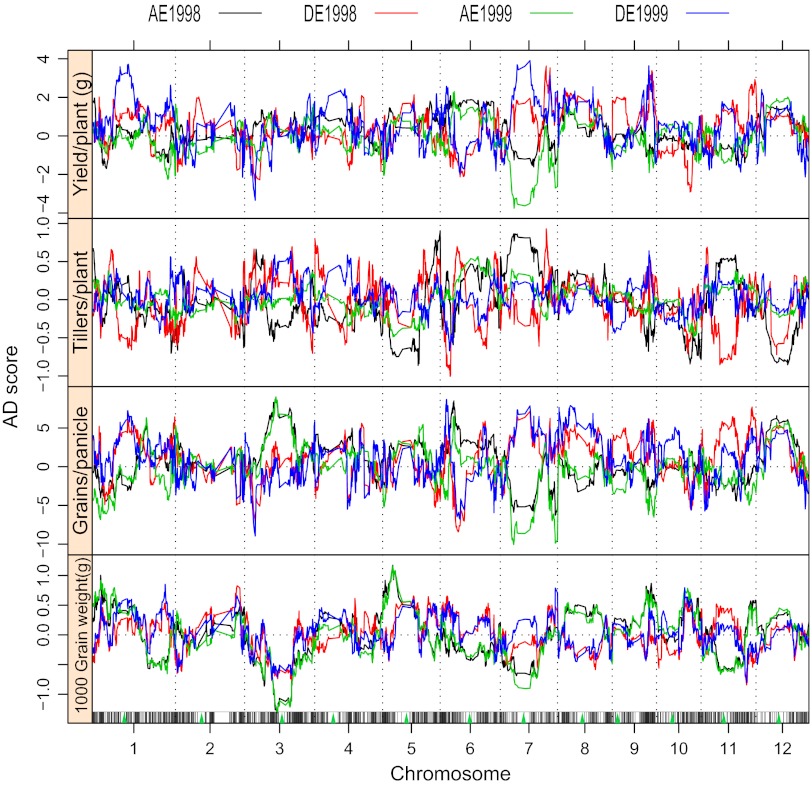
We estimated the additive and dominance effects in each of the 1,619 bins for the four traits, according to the SNP bin map using the IMF2 data collected in 2 y (Fig. 1 and Dataset S2). Percentage of bins showing positive dominance (including overdominance) ranged from a low of 52.1% (844 of 1,619) in grain weight in 1999 to a high of 65.8% (1,066) in yield per plant in 1998 (Table S1). Conversely, negative dominance varied from 34.1% (553) in yield in 1998 to 50.2% (814) in tillers per plant in 1998. In general, the data were consistent in 2 y that positive dominance was detected in much larger numbers of bins than negative dominance for all four traits in both years. The only exception occurred in tillers per plant in 1998, in which the number of bins (805) showing positive dominance was slightly lower than those (814) exhibiting negative dominance. Also of note, greater numbers of bins showed positive dominance in yield and grains per panicle than the other two traits, whereas more bins showed negative dominance in tillers per plant and grain weight than the other two traits.

Fig. 1.

Profiles of additive and dominance effects in the entire genome for yield and yield component traits. AE1998, DE1999, etc. indicate additive and dominance effects detected in the data of 1998 and 1999, respectively. AD score refers to the absolute amounts of additive and dominance effects of the trait. Green triangles indicate the centromere positions on the chromosomes.

A locus is regarded as exhibiting overdominance if the ratio of the estimated dominance to the absolute value of additive effect (d/a, degree of dominance) is larger than unity, and partial dominance if the ratio was between 0 and 1. Degrees of dominance in the entire genome varied from partial dominance, to full dominance, to overdominance, in both positive and negative directions (Dataset S2). For yield, 41.2% (667) and 39.4% (639) of the 1,619 bins showed positive overdominance in 1998 and 1999, respectively (Table S1), whereas the proportions of bins with overdominance for other traits were lower, ranging from 20.7% in grain weight in 1998 to 35.4% in grains per panicle in 1998. Negative overdominance was also observed in 12.7–25.4% of the bins for the four traits. Again, bins showing positive overdominance occurred more frequently than those exhibiting negative overdominance for all four traits in both years, with the only exception being tillers per plant in 1998. The values of net dominance calculated by summing up the dominance effects over the bins, as well as the sums of the dominance values in each category, were also similar in both years (Table S1).

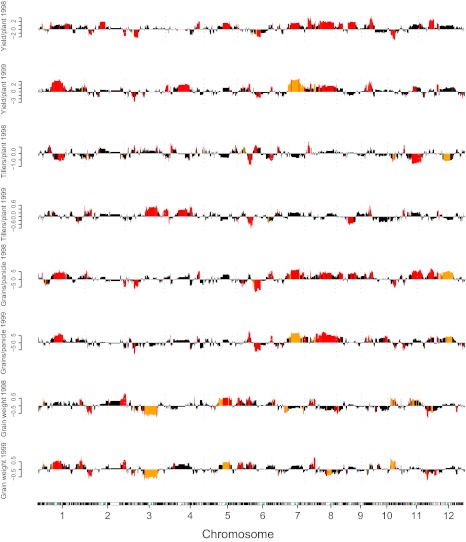
We used an h statistic to identify bins that have statistically significant (P < 0.05) dominant effects on the trait, or heterotic bins, and the ones showing significant effects (P < 0.05) were subjected to permutation tests. The results of both years consistently showed that much greater numbers of bins demonstrated positive dominance than showed negative dominance (Fig. 2, Table S1, and Dataset S2).

Fig. 2.

Dominance and overdominance in the entire genome for yield and yield component traits. The effects were identified using an h test confirmed by permutation. The adjacent bins that are clustered are separated by columns. The height of the columns shows the dominance values. Red indicates overdominance, and orange indicates partial to full dominance. Black represents statistically insignificant effects. Green triangles indicate the centromere positions on the chromosomes.

It is certain that the effects detected in many adjacent bins using the above procedure might result from the same bins, leading to possible overestimation of the number as well as the effects of the heterotic bins. We thus attempted to merge the heterotic bins into clusters according to their physical positions, which were distinguished by recombinations between adjacent bins in RILs wherever possible (Fig. 2 and Dataset S2). However, this merge process might eliminate some of the adjacent bins that show similar effects, resulting in underestimation of the number and effects of heterotic bins. Thus, the numbers so identified may represent the minimum of heterotic loci (Table S1). Given all those technological limitations, it is nonetheless clear that much greater numbers of bins exhibited positive dominance than showed negative dominance.

Dominance Detected in Digenic Interactions.

Interactions of all possible two-locus combinations were calculated using two-way ANOVA at P ≤ 0.001. Only two-locus datasets with all of the marker genotypic classes containing three or more crosses in the IMF2 were included in the calculation. The total numbers of tests were 1,248,255 for 1998 and 1,259,379 for 1999, and the numbers of significant interactions detected are given in Table S2.

The large numbers of interactions detected in this search might be inflated in two ways: false positive by chance, and redundancy resulting from adjacent two-locus combinations. We conducted a permutation test to reduce false positives, followed by merging of interactions detected from adjacent two-locus combinations. These processes greatly reduced the number of significant interactions detected for each trait (Table S2), and interactions that survived may therefore be regarded as the minimum number of significant interactions for this trait at P ≤ 0.001.

We partitioned each of the significant interactions into four components using the orthogonal contrast test, according to the modes of gene actions at the two loci: additive (first locus) × additive (second locus), additive × dominance, dominance × additive, and dominance × dominance. It was shown that additive × additive interactions occurred at the highest frequencies, making up more than 50% of total significant interactions, followed by additive × dominance (dominance × additive); dominance × dominance interactions occurred least frequently in both years (Table S2).

Because the real hybrid (Shanyou 63) would be heterozygous at all of the polymorphic loci detected by the analysis, only dominance × dominance interactions, in which heterozygote at one locus would affect the performance of the heterozygote at the other locus, would contribute to heterosis in F₁, whereas all other genetic components would have no role. We thus calculated the digenic dominance (DD = dh − mp, where dh is the performance of the double heterozygote, and mp is the mean of the two parental homozygotes) of two-locus genotypes that showed significant dominance × dominance interactions (Fig. S2 and Dataset S3). Both positive and negative DD effects were detected in various two-locus combinations. In general the net DD effects were positive and large on yield, positive and small on grain weight, trivial on grain number, and inconsistent between years on tiller number.

Relative Contributions of Dominance, Overdominance, and Epistasis to Heterosis of the Hybrid.

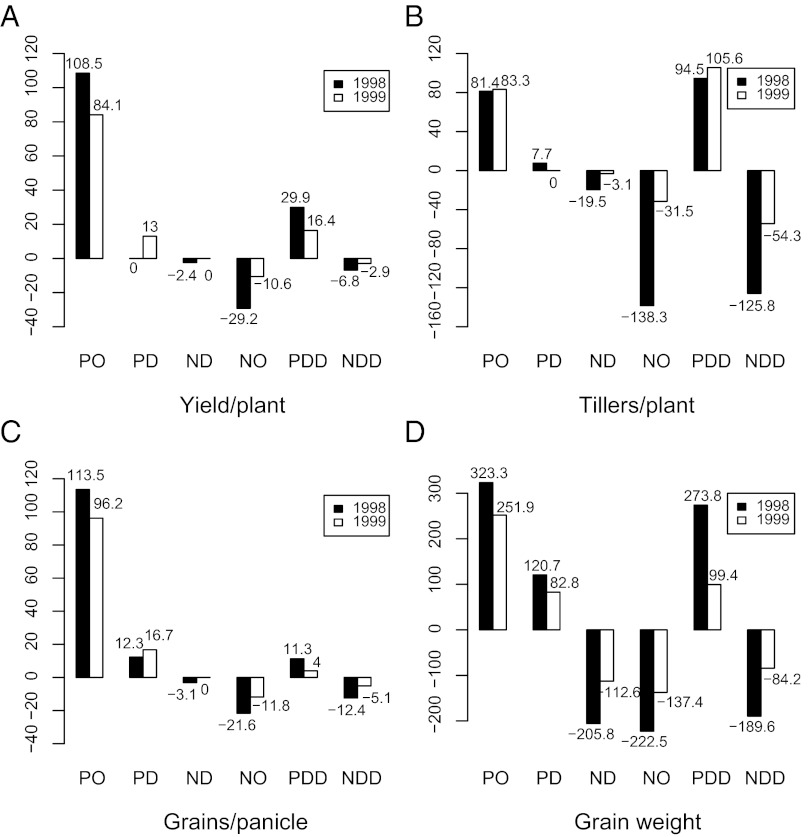
To assess the relative contributions of the three types of genetic effects to heterosis in the F₁ hybrid, the heterotic bins were grouped according to the genetic effects: single-locus dominance, single-locus overdominance, and digenic heterotic effects. We calculated the total effect of each group (Table 1) and the relative importance of these components (Fig. 3). For yield, overdominance is the most important contributor, followed by DD. Overdominance also contributed the most to grains per panicle. DD effects were higher than overdominance for tillers per plant, but the heterotic effects of this trait were not consistent between years. For grain weight, the contribution of overdominance was also higher than DD and dominance, although the total amount of heterotic effect was relatively small.

Table 1.

Amounts of single-locus dominance, overdominance, and digenic dominance in the IMF2 population identified in the entire genome on the basis of clusters

Trait	Year	Positive overdominance	Positive dominance	Negative dominance	Negative overdominance	Positive digenic dominance	Negative digenic dominance	Sum
Yield/plant	1998	4.509	0	−0.099	−1.214	1.242	−0.283	4.155
	1999	6.931	1.069	0	−0.875	1.352	−0.238	8.239
Tillers/plant	1998	1.308	0.123	−0.313	−2.222	1.519	−2.022	−1.607
	1999	2.021	0	−0.076	−0.763	2.561	−1.317	2.426
Grains/panicle	1998	4.241	0.458	−0.117	−0.806	0.423	−0.464	3.735
	1999	3.764	0.652	0	−0.460	0.157	−0.200	3.913
Grain weight	1998	1.122	0.419	−0.714	−0.772	0.950	−0.658	0.347
	1999	1.335	0.439	−0.597	−0.728	0.527	−0.446	0.530

The value presented for each component is the summation over loci divided by the trait mean. The single-locus effects were not included in the calculation if they are involved in dominance × dominance interactions.

Fig. 3.

(A–D) Relative contributions of dominance, overdominance, and epistasis to heterosis. Numbers indicated the percentage contribution of each effect. ND, negative dominance; NDD, negative digenic dominance; NO, negative overdominance; PD, positive dominance; PDD, positive digenic dominance; PO, positive overdominance.

Genic Nature of Overdominance.

The cause of overdominance is still a controversial issue in the literature; it was argued that the apparent overdominance may result from genes with opposite additive effects linked in repulsion, a phenomenon termed pseudo-overdominance (7, 38). In this study a bin is a DNA fragment of ∼250 kb on average, encompassing dozens of genes. Thus, the effects detected for each bin represent the collective effects of all of the genes.

We investigated gene expression patterns for a number of bins showing high overdominance (d/a >>1) in grains per panicle using microarray analysis of young panicle at secondary branch differentiation stage (Dataset S4). Higher expression levels in Zhenshan 97 than Minghui 63 were observed for many genes, whereas the reverse was observed for many other genes. We also compared the available genome sequences between the parents (32), which showed that insertion/deletions (InDels) occurred in many regions in Zhenshan 97 relative to Minghui 63, whereas the reverse was the case in many other regions (Dataset S5). Such complementarities in gene expression and genomic sequences seemed to support the pseudo-overdominance hypothesis.

Discussion

We performed a complete dissection of the heterotic effects of yield traits exhibited by the elite rice hybrid Shanyou 63, based on the ultrahigh-density SNP map of the rice genome using an IMF2 population. The advantage of the IMF2 design in QTL identification and heterosis study was previously discussed in detail (24, 25). A similar experimental design referred to as RIX (recombinant inbred intercrosses) was reported in a genetic study of mice (39). The analysis revealed that varying amounts of heterotic effects, in the forms of dominance, overdominance, and epistasis in both positive and negative directions, occurred in almost all of the bins in the entire genome. Although large proportions of the minor effects could not be detected if a preset statistical threshold was applied, and it may be difficult to separate the linked effects of adjacent bins, an overall picture has emerged that heterosis of these yield traits observed in the F₁ hybrid is the result of cumulative effects of net-positive heterotic effects after cancelation of negative ones. The cumulative effects of these components could adequately explain the genetic basis of heterosis in the hybrid. This picture may have generality as the genetic basis of heterosis in other organisms.

The causal mechanisms of such heterotic effects may be glimpsed with the cloned genes. For example, Xue et al. (37) showed that the near isogenic line heterozygous for Ghd7 produced 198.8 spikelets, which was 25.2 (14.5%) more than the average of the two homozygotes. Ghd7 is fully functional in Minghui 63 but completely lacking in Zhenshan 97. Thus, heterotic effect contributed by this locus results from a typical presence/absence type of genetic variation between the parents. Although a complete molecular illustration of heterosis has to await the cloning and characterization of the underlying genes, it is almost certain that the mechanism of heterotic effect may vary from one locus to another depending on the biochemical nature of the genes.

An important outcome from this analysis is the relative importance of various genetic components in heterosis of the F₁ hybrid, a controversial issue that has concerned the community for more than a century. The results showed that the relative contribution of the various genetic components to heterosis is trait dependent. Overdominance/pseudo-overdominance is the most important contributor to heterosis of yield, grain number, and grain weight. Dominance × dominance interaction is important for heterosis of tillers per plant and grain weight and has roles in yield and grain number. Dominance has relatively small contributions in all of the traits. It should be noted that overdominance (also other genetic effects) detected in a bin represents the collective effects of all of the genes in this region. Although overdominance effects seemed to be prevalent in traits of this study, there has not been evidence for overdominance in any of the genes cloned in rice to date (40), unlike the case reported for fruit number in tomato (41). It is therefore possible that overdominance detected in many of the bins may be pseudo-overdominance resulting from genes linked in repulsing phase, such that the genes have opposite additive effects, each of which shows partial dominance but not overdominance, as previously discussed (7, 38). Again, characterization of the genetic effects and molecular mechanisms of the contributing genes is essential for resolving these issues. Furthermore, advanced statistical methods that are able to include and assess the magnitudes of all of the effects in a single model (42, 43) would help quantitative understanding of the relative contributions of the various genetic components to heterosis.

Methods

Plant Materials and SNP Bin Map.

The IMF2 population was previously described in detail (24, 25). It consisted of 360 crosses made by random permutations of the 240 RILs derived by single-seed descent from a cross between Zhenshan 97 and Minghui 63, the parents of Shanyou 63. Field data of yield, number of tillers per plant, number of grains per panicle, and grain weight were collected in the 1998 and 1999 rice-growing seasons from replicated field trials on the experimental farm of Huazhong Agricultural University, Wuhan, China (24).

The ultrahigh-density bin map was constructed by genotyping the RILs with population sequencing (32, 33).

Analysis of One-Locus Effects.

Additive effect of each locus was half of the difference between the two homozygotes. Significant dominance effects were identified by an h test (44), 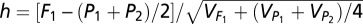, which is similar to the t test, at P ≤ 0.05. The results were confirmed with a permutation test, in which the positions of the phenotype scores in the dataset were randomized, and the h statistic was recalculated. This process was repeated 10,000 times. If no more than 5% of the random h values was larger than the h statistic from the real data, it was regarded to be significant at P ≤ 0.05. We grouped the bins showing significant dominance into clusters using the following steps. Adjacent bins in a sliding window of 1,000 kb with dominance effects of the same sign (+ or −) were grouped. Within each group, the most significant bin was selected as the seed, and dominance effect of the bin next to the seed was calculated sequentially using information from the recombinants between the two bins. Bins and seed were merged to the same cluster if the dominance effects based on the recombinants were not significant; otherwise they were placed in different clusters. The process was repeated until all of the bins were grouped into clusters. We used the dominance effect of the bin showing the lowest P value to represent the cluster.

Analysis of Two-Locus Interactions.

For identifying epistatic interactions, bins in the entire genome were searched pairwise for two-locus interactions using two-way ANOVA. The calculation was based on unweighted cell means, and the sums of squares were multiplied by the harmonic means of the cell sizes to form the test criteria. Those that showed significant interactions at P ≤ 0.001 were subjected to permutation tests, in which the positions of the phenotype scores in the dataset were randomized to perform the two-way ANOVA again. This process was repeated 10,000 times. If no more than 0.1% of the random F values was larger than the F from the real data, it was regarded to be significant at P ≤ 0.001. To resolve the significant interactions detected by adjacent bins, the nearby bins in the two genomic regions (e.g., A and B) in the 2D space were scanned in pairs. For illustration, we denoted the two bins from the two regions as A_x and B_y, and the resulting F score from the two-way ANOVA as 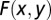. We used a 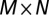matrix F to represent all of the two-locus combinations with M bins from region A centered around A_x and N bins from region B centered around B_y:

in which both M and N are no less than 10, and the distances between A₁ and A_m and between B₁ and B_n are no less than 1,000 kb.

The two-locus combination with the largest F(x, y) was chosen as the starting point to perform a merging process. We first fixed bin A_x and searched bins in region B (B_j, 1 ≤ j ≤ n) to check whether F(x, j) was significant. The bins were merged using a threshold 1.5 -Lg₁₀P-drop support interval, in which P is the probability obtained from the two-way ANOVA, resulting in an expanded combination 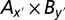in which y′ denoted all of the bins in region B in the 1.5 -Lg₁₀P-drop support interval. Similarly, by fixing B_y we obtained an expanded combination of 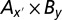in which x′ denoted all of the bins in region A in the 1.5 -Lg₁₀P-drop support interval. Finally, the combination 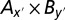consisting of two groups of bins from regions A and B were regarded as one epistatic pair, and the one F(x, y) with the largest F score was used for subsequent estimation of genetic effects.

A significant interaction was partitioned into four components, each specified by a single degree of freedom: additive × additive, additive × dominance, dominance × additive, and dominance × dominance. Statistical significance for each term was assessed using an orthogonal contrast test performed using a Perl script. Digenic dominance effect was calculated by subtracting the mean of the two parental homozygotes from the performance of double heterozygote.