Similarities of artificial photosystems by ruthenium oxo complexes and native water splitting systems

Abstract

The nature of chemical bonds of ruthenium(Ru)–quinine(Q) complexes, mononuclear [Ru(trpy)(3,5-t-Bu₂Q)(OH₂)](ClO₄)₂ (trpy = 2,2^′:6^′,2^′′-terpyridine, 3,5-di-tert-butyl-1,2-benzoquinone) (1), and binuclear [Ru₂(btpyan)(3,6-di-Bu₂Q)₂(OH₂)]²⁺ (btpyan = 1,8-bis(2,2^′:6^′,2^′′-terpyrid-4^′-yl)anthracene, 3,6-t-Bu₂Q = 3,6-di-tert-butyl-1,2-benzoquinone) (2), has been investigated by broken-symmetry (BS) hybrid density functional (DFT) methods. BS DFT computations for the Ru complexes have elucidated that the closed-shell structure (2b) Ru(II)–Q complex is less stable than the open-shell structure (2bb) consisting of Ru(III) and semiquinone (SQ) radical fragments. These computations have also elucidated eight different electronic and spin structures of tetraradical intermediates that may be generated in the course of water splitting reaction. The Heisenberg spin Hamiltonian model for these species has been derived to elucidate six different effective exchange interactions (J) for four spin systems. Six J values have been determined using total energies of the eight (or seven) BS solutions for different spin configurations. The natural orbital analyses of these BS DFT solutions have also been performed in order to obtain natural orbitals and their occupation numbers, which are useful for the lucid understanding of the nature of chemical bonds of the Ru complexes. Implications of the computational results are discussed in relation to the proposed reaction mechanisms of water splitting reaction in artificial photosynthesis systems and the similarity between artificial and native water splitting systems.

Photosynthesis is one of the most important chemical processes on our planet. Extensive experimental studies (1–6) on the process have revealed that oxygenic photosynthesis involves several protein-cofactor complexes embedded in the photosynthetic thylakoid membranes of plants, green algae, and cyanobacteria. Among these complexes, photosystem II (PSII) has a prominent role because it catalyzes the oxidation of water (2H₂O → O₂ + 4H⁺ + 4e^-), which is the prerequisite for all aerobic life. The main cyclic process to catalyze the water-oxidation consists of successive four steps, which is referred to as the Kok cycle (6). During this process, the oxygen-evolving complex (OEC), the catalyst of the water oxidation reaction, takes five oxidation states (S₀–S₄). The OEC in PSII contains an inorganic cluster consisting of four manganese ions and one calcium ion that are bridged by at least five oxygens; the active site is therefore expressed with the CaMn₄O₅ cluster (3) (5). Very recently, the electronic structure and reactivity of 3 (7–10) have been elucidated based on the new high-resolution X-ray structure (5).

In the past decades, a number of experimental and theoretical studies (11–29) have been performed to design artificial photosynthetic systems that mimic native PSII systems. Many binuclear transition-metal catalysts such as L(H₂O)M-O-M(OH₂)L or L(H₂O)M-BL-M(OH₂) (where L and BL are nonbridging and bridging organic ligands, respectively) were prepared and characterized for their catalytic properties toward water oxidation (11–21). By combining structural and kinetic studies, impressive progress has been achieved in unraveling the molecular mechanism of the catalytic action of the so-called blue dimmer (12), [cis,cis-(bpy)₂(H₂O)Ru-O-Ru(OH₂)(bpy)₂](bpy = 2,2^′-bipyridine); however, the detailed mechanism of the final stage of the O─O bond formation and O₂ evolution remains unsettled despite several theoretical investigations (22–24, 26, 28). Radical coupling and acid-base mechanisms for the oxygen–oxygen (O─O) bond formations are still competitive.

On the other hand, Tanaka and coworkers (16–21) have reported water oxidation catalytic activity of Ru-quinone complexes: Mononuclear [Ru(trpy)(3,5-t-Bu₂Q)(OH₂)](ClO₄)₂ (trpy = 2,2^′:6^′,2^′′-terpyridine, 3,5-t-Bu₂Q = 3.5-di-tert-butyl-1,2-benzoquinone) (1) and binuclear [Ru₂(btpyan)(3,6-di-Bu₂Q)₂(OH₂)](SbF₆)₂ (btpyan = 1,8-bis (2,2′:6′,2′′-terpyrid-4′-yl) anthracene, 3,6-di-Bu₂Q = 3,6-t-Bu₂Q₂ (3,6-di-tert-butyl-1,2- benzoquinone) (2). Recently Muckerman et al. (25) and Ghosh and Baik (27) have performed density functional (DFT) calculations of these Tanaka catalysts. However, computational results by these groups are different on the relative stability between the closed-shell and open-shell structures of 1 and 2 (SI Text).

Here, we perform broken-symmetry (BS) DFT computations of the above mononuclear (1) and binuclear (2) Tanaka catalysts. Eight different electronic and spin structures are calculated for tetraradical intermediates generated in the course of water splitting reaction by 2. The Heisenberg spin Hamiltonian model for the species is derived to elucidate six different effective exchange interactions (J) for four spin systems (7–10). Six J values are determined using total energies of the eight (or seven) BS solutions for different spin configurations. The natural orbital analyses of these BS DFT solutions are also performed to elucidate natural orbitals and their occupation numbers that are utilized for MO-theoretical explanation of the nature of chemical bonds of 2. Implications of the computational results are discussed in relation to reaction mechanisms proposed for the water splitting reaction in artificial photosynthesis systems and the similarity between artificial and native water splitting systems.

Results

Possible Electronic and Spin States of Mononuclear and Binuclear Ruthenium Quinone Complexes.

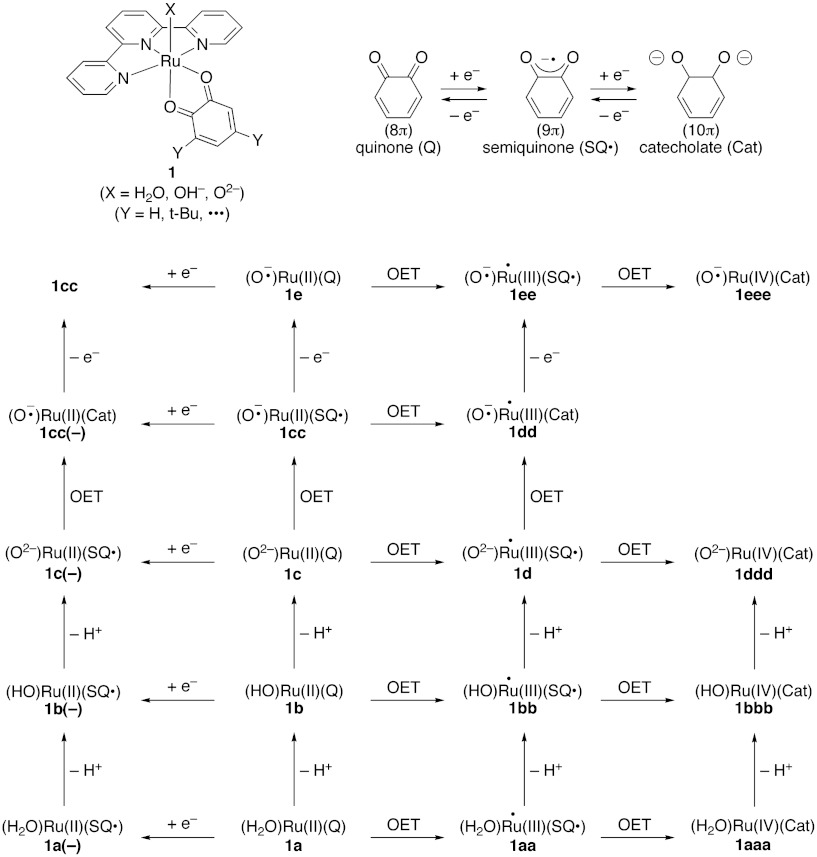
Dioxolene, dithiolene, and benzoquinodiimine have been accepted as non-innocent ligands in transition-metal complexes that often exhibit catalytic activity. The notable point in the catalysts reported by Tanaka and coworkers (16–21) is that quinone is used as a redox-active ligand. In fact, various mixed-valence structures have been proposed for active valence states of the mononuclear Ru complex (1), [Ru(II)(3,5-tertially-butyl quinone; t-BuQ)(terpyridyl; tpy)X] (X = H₂O, OH^- and O^2-), as illustrated in Fig. 1. Although the Ru complex (1) synthesized by Tanaka and coworkers (16–21) is formally regarded as a closed-shell species, Ru(II)(t-BuQ)(tpy)(H₂O) (1a) (Fig. 1), thermal one-ET from the HOMO(D) of Ru(II) to the LUMO(A) of t-BuQ is theoretically conceivable, providing the •Ru(III)(t-BuSQ•)(tpy)(H₂O) diradical structure (1aa). On the other hand, contribution of the double ET (DET) structure Ru(IV)(t-BuCat)(tpy)(H₂O) (1aaa) is usually neglected. Relative contributions of 1a and 1aa are highly dependent on substituents introduced into the quinone skeleton and environmental conditions employed because the HOMO(D)-LUMO(A) gaps are sensitive to them. The situation is the same even for the deprotonated structures, Ru(II)(tBuQ)(tpy)(OH^-) (1b), and one- and double-ET from Ru(II) to tBuQ afford •Ru(III)(tBuSQ•)(tpy)(OH^-) (1bb) and Ru(IV)(tBuCat)(tpy)(OH^-) (1bbb), respectively. Further deprotonation of 1b provides a formal closed-shell structure, Ru(II)(tBuQ)(tpy)(O^2-) (1c). One ET from the HOMO(D) of oxygen dianion (O^2-) to the LUMO(A) of quinone is feasible to generate the triplet diradical structure, Ru(II)(tBuSQ-•)(tpy)(O^-•)(1cc). The closed-shell configuration of 1c (Fig. 1) becomes more unstable than the open-shell ET configuration of 1cc (Fig. 1), indicating that the ET diradical state becomes the ground state (Fig. S1C).

Fig. 1.

Possible active intermediates generated by deprotonation (-H⁺), oxidation (-e^-) and intramolecular one electron-transfer (OET) of mononuclear ruthenium complex (1).

The effective exchange integral (J) between t-BuQ-• and O^-• radicals is positive (ferromagnetic) because of the orbital orthogonality. Tanaka and coworkers (18) have indeed concluded that the observed species by the ESR spectroscopy can be assigned to be the triplet state of 1cc, and a visible absorption band at 870 nm is assigned as MLCT of 1cc (Fig. S2B). On the other hand, deprotonation of 1bb provides an open-shell structure, •Ru(III)(tBuSQ•)(tpy)(O^2-) (1d). One ET from the HOMO(D) of oxygen dianion (O^2-) to the LUMO(A) of SQ of 1d provides another mixed-valence triplet structure •Ru(III)(tBuCat)(tpy)(O^-•) (1dd). The effective exchange integral (J) between Ru(III)• and O^-• radicals is also positive because of the orbital orthogonality (Hund rule). One electron oxidation of 1cc provides a free radical doublet structure, Ru(II)(tBuQ) (tpy)(O^-•↑) (1e) in Fig. 1. One ET (OET) from HOMO(D) of Ru(II) to LUMO(A) of quinone of 1e provides 1ee. One electron oxidation of 1d and 1dd also affords the same triradical species, ↑•Ru(III)(tBuSQ•↓)(tpy)(O^-•↑) (1ee). The high-valent free radical species, Ru(IV)(tBuCat)(tpy)(O^-•) (1eee), is also conceivable via one more OET, though it may be too unstable. The radical coupling for the O─O bond formation may be feasible for radical species with an oxyl-radical site, 1cc, 1dd, 1e, and 1ee in Fig. 1. Indeed, Tanaka et al. (30) have demonstrated experimentally that 1ee can abstract the hydrogen atom of organic substrates, but 1cc does not have such activity.

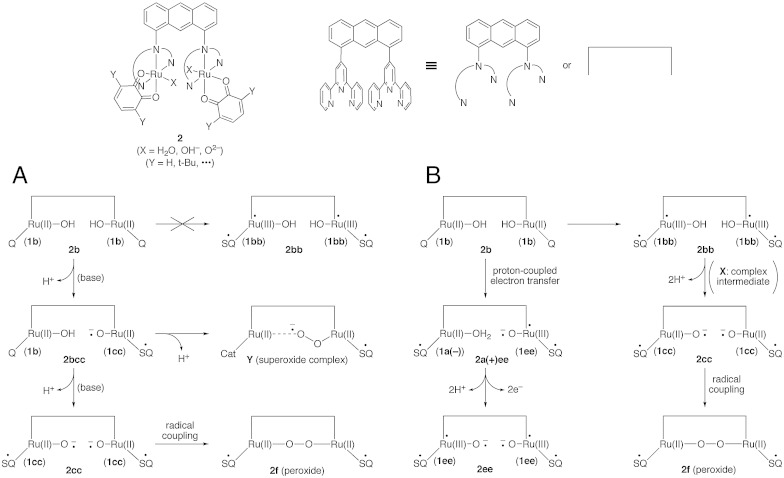
Tanaka and coworkers (20, 21) have synthesized a dimer (2) of the mononuclear Ru complex (1), [Ru(II)₂(3,6-t-BuQ)₂(btpyan)X₂]ⁿ⁺ (btpyan = 1,8-bis(2,2^′:6^′,2^′′-terpyridyl anthracene, X = H₂O, OH^- and O^2-), which can electrocatalytically oxidize water to produce molecular oxygen. On the basis of various experimental results such as CV and UV–visible spectra, Tanaka and coworkers (21) have proposed simple reaction pathways for the O─O bond formation that is a crucial step for water splitting reaction: 2b → 2bcc → 2cc → 2f (peroxide) in methanol and 2b → 2cc → 2f (peroxide) in water as shown in Fig. 2A. The stepwise deprotonation of 2b by base (tBuOK) entails an intermediacy of an unsymmetrical mixed structure 2bcc = [(1b)(1cc)] in methanol, while spontaneous deprotonation of 2b in water directly afford 2cc. The radical coupling between oxyl-radicals has been assumed for the O─O bond formation in 2f (peroxide).

Fig. 2.

Possible mechanisms for the oxygen–oxygen (O─O) bond formation by binuclear ruthenium complex (2) proposed by Tanaka, Muckerman, Fujita and collaborators (A) and by Ghosh and Baik (B). Muckerman, Fujita, and collaborators assume that the divalent Ru(II) ion remains intact throughout the reactions. The radical-coupling and superoxide mechanisms have been proposed for water splitting reaction. Ghosh and Baik assume that the trivalent Ru(III)-semiquinone (SQ) configuration (2bb) plays an important role for water splitting reaction in methanol, while in water solution, an unsymmetrical structure 2a(+)ee is formed.

On the other hand, Ghosh and Baik (27) have presented a different pathway involving electron-transfer configurations: 2b → 2bb → X → 2cc → 2f (peroxide) in methanol as shown in Fig. 2B. They have emphasized an important role of 2bb (double OET structure) and a mixed valence intermediate (X) based on the DFT computational results. However, the radical-coupling step by their model is the same with that of Tanaka reaction path model in Fig. 2A. They have also proposed a possible role of the unsymmetrical polar structure 2a(+)ee in water: 2b → 2a(+)ee → 2ee. Thus the proposed mechanisms by Tanaka and coworkers (21) and Ghosh and Baik (27) are the radical-coupling type instead of the polar ionic mechanism, even in water.

DFT computations by Muckerman et al. (25) have indicated that the possible contribution of one ET configuration 2bb = [(1b)(1b)] is scarce, in accord with their experimental results, though early papers by the Tanaka group have proposed one ET structure 2bb on the basis of the X-ray diffraction and spectroscopic observations (16). However, Muckerman et al. (25) have noticed that contribution of 2bb increases with introduction of electron-withdrawing substituents like chlorine into quinone skeletons. Muckerman et al. (25) have proposed a possible reaction pathway involving intermediacy of the Ru-superoxide anion complex for water splitting reaction: 2b → 2bcc → Y shown in Fig. 2A. The intermediate consists of 1b and 1cc, namely 2bcc = [(1b)(1cc)], and the O─O bond formation between the hydroxy anion (-HO-Ru(II)-Q: 1b) and the oxyl radical (-•O-Ru(II)-SQ•: 1cc) has been assumed at this step. The superoxide complex Y[SQ•-Ru(II)-(-•O-O)-Ru(II)-Cat] is formed via deprotonation at the O─O bond formation step because quinone (Q) accepts an excess of two electrons, forming chatecholate (Cat) as illustrated in Fig. 2A. The valence of the Ru ion remains to be divalent throughout water activation processes for the O─O bond formation.

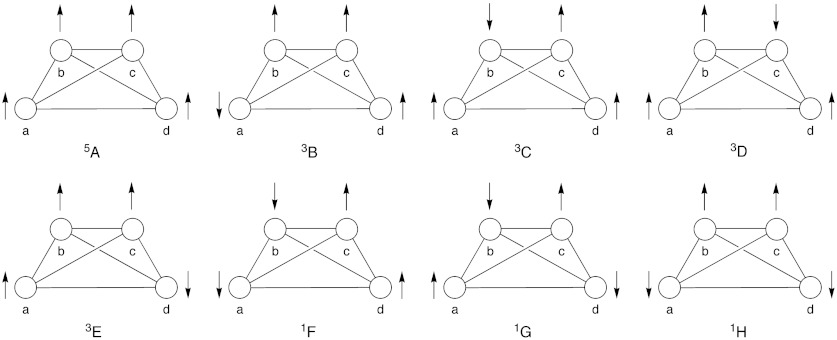
In the proposed mechanisms mentioned above (21, 25, 27), 2bb and 2a(+)ee are assumed to be key redox intermediates during catalysis leading to the O─O bond formation. Notably, these four-site four-spin systems are analogous to the CaMn₄O₅ (3) cluster in OEC of PSII (7–10). Therefore we have investigated in detail electronic and spin structures and magnetic interactions of the binuclear ruthenium quinone complexes 2bb and 2a(+)ee (X = H) by assuming the geometries optimized by Ghosh and Baik (27). There are eight different spin configurations for the four-site spin systems, as illustrated in Fig. 3, where the notations (abcd) or (4321) mean the sites (SQ₂)(Ru₂)(Ru₁)(SQ₁) for 2bb and (SQ₂)(O₁)(Ru₁)(SQ₁) for 2a(+)ee, in conformity with the notation of OEC, Ca(Mn_a(4))(Mn_b(3))(Mn_c(2))(Mn_d(1)). We have constructed eight broken-symmetry (BS) solutions by the B3LYP method with the double-ζ LANL2DZ(Ru)/6-31G*(C,H,O,N) basis set implemented in Gaussian 09 (31). Table 1 summarizes relative energies of the open-shell configurations (2bb and 2a(+)ee) with reference to the closed-shell (CS) configuration (2b); Mulliken spin densities of 2bb and 2a(+)ee are given in Tables S1 and S2.

Fig. 3.

Possible eight spin structures for four spin-site systems: (abcd) denotes (SQ₂,Ru₂,Ru₁,SQ₁) (2bb) or (SQ₂,O₁,Ru₁,SQ₁) (2a(+)ee) in accord with the notation for CaMn₄O₅ cluster CaMn_a(4)Mn_b(3)Mn_c(2)Mn_d(1) (3). The same spin Hamiltonian model has been derived to elucidate similarity between artificial (2bb) and native (3) catalysts for water splitting reaction.

Table 1.

Relative energies of 2b, 2bb, and 2a(+)ee at the B3LYP level

Species	Spin state	Relative energy *
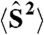		Before AP	After AP
2b	CS	0.0 (0.0) †	0.0	0.00
2bb	5A	−6.4	−6.4	6.03
	3B	−10.2	−12.2	2.72
	3C	−10.1	−12.1	2.72
	3D	−8.3	−9.6	2.86
	3E	−8.3	−9.7	2.86
	1F	−6.4	−6.4	2.03
	1G	−12.0	−15.4	1.56
	1H	−12.1 (−12.1) †	−15.4	1.56
2a(+)ee	5A	−3.1	−3.1	6.03
	3B	−3.1	−3.1	3.03
	3C	3.7	10.1	3.00
	3D	1.0	5.1	2.83
	3E	−5.0	−6.3	2.88
	1F	3.7	10.1	2.00
	1G	1.0	5.2	1.83
	1H	−5.0 (−4.0) †	−6.3	1.88

^*Relative energies without zero-point correction are given in kcal mol^-1.

^†Results by Ghosh and Baik (27) are given in parentheses.

As for 2bb, the antiferromagnetic (AF) configuration (↓•SQ₂)(↑•Ru₂)(↑•Ru₁) (↓•SQ₁) (¹H) is the most stable among the eight BS states. But the other AF configuration (↑•SQ₂)(↓•Ru₂)(↑•Ru₁)(↓•SQ₁) (¹G) is almost degenerated in energy: The energy gap of this group is about -12 kcal/mol. The next stable group is given by the triplet configurations (↓•SQ₂)(↑•Ru₂)(↑•Ru₁)(↑•SQ₁) (³B) and (↑•SQ₂)(↓•Ru₂)(↑•Ru₁) (↑•SQ₁) (³C). The energy gap is about -10 kcal/mol. The other triplet group is (↑•SQ₂)(↑•Ru₂)(↑•Ru₁)(↓•SQ₁) (³E) and (↑•SQ₂)(↑•Ru₂)(↓•Ru₁)(↑•SQ₁) (³D) and provides the energy gap = -8.3 kcal/mol. The gap is about -6.4 kcal/mol for the group of unstable tetraradical species, (↑•SQ₂)(↑•Ru₂)(↑•Ru₁)(↑•SQ₁) (⁵A) and (↓•SQ₂)(↓•Ru₂)(↑•Ru₁) (↑•SQ₁) (¹F). Thus the energy gaps for the eight BS configurations of 2bb are not so large, indicating labile electronic chemical bonds of Tanaka catalysts (16–21).

Concerning the polar structure 2a(+)ee, the antiferromagnetic (AF) configuration (↓•SQ₂)(↑•O₁)(↑•Ru₁)(↓•SQ₁) (¹H) is the most stable among the eight BS states. But the triplet configuration (↑•SQ₂)(↑•O₁)(↑•Ru₁)(↓•SQ₁) (³E) is almost degenerated in energy: The energy gap of this group is about -5 kcal/mol. The next stable group is given by the configurations (↑•SQ₂)(↑•O₁)(↑•Ru₁)(↑•SQ₁) (⁵A) and (↓•SQ₂)(↑•O₁)(↑•Ru₁)(↑•SQ₁) (³B); the energy gap = -3.1 kcal/mol. The unstable group (↑•SQ₂)(↑•O₁)(↓•Ru₁)(↑•SQ₁) (³D) and (↑•SQ₂)(↓•O₁)(↑•Ru₁)(↓•SQ₁) (¹G) provide the positive energy gap = 1.0 kcal/mol. The gap becomes about 3.7 kcal/mol for the group of further unstable tetraradical species, (↓•SQ₂)(↓•O₁)(↑•Ru₁)(↑•SQ₁) (¹F) and (↑•SQ₂)(↓•O₁)(↑•Ru₁)(↑•SQ₁) (³C). Thus the energy gaps for the eight BS configurations of 2a(+)ee are not so large, indicating labile electronic chemical bonds of Tanaka catalysts.

Heisenberg Spin Hamiltonian Model and Spin Vector Model.

Magnetic measurements have been performed for a number of exchange-coupled systems. The Heisenberg spin Hamiltonian model has been employed for analysis of the experimental results available. In order to elucidate similarity between the Tanaka catalyst (2) and CaMn₄O₅ (3), we here consider the Hamiltonian model for four-site four-spin systems like 2bb and 2a(+)ee examined above. The Heisenberg spin Hamiltonian for the systems is given by Eqs. S16 and S17. Therefore the expectation value for the spin Hamiltonian is given on the quantum mechanics in Eq. S18. The expectation values of the Heisenberg spin Hamiltonian are often approximated on the assumption that local spins are regarded as classical (axial) spin (vector). Here the up- and down-spin vectors are considered in accord with BS calculations of the different-orbitals-for-different-spins (DODS) type. Then the expectation values of the classical Heisenberg model are given by (7–10)

[1]

where S_i and S_ij are spin quantum numbers of quantum spin i and spin pair (ij) in Eq. S17, respectively. J_ab denotes the effective exchange integral between sites a and b as shown in Fig. 3. J_ab values can be determined by electron spin resonance (ESR) (18) and other magnetic measurements.

We can construct simultaneous equations for J values from the total energies of eight BS solutions examined previously, as shown in Eqs. S21. By solving these equations, we can obtain all J values, as summarized in Table 2. As expected, energy levels in the previous section, J_ab and J_cd for 2bb (-3.77 and -1.88 kcal/mol, respectively) are negative in sign, indicating the greater stability of the singlet pairs. However, the magnitude is considerably different in accord with the unsymmetrical electronic state as shown below. As for 2a(+)ee, J_bc is largely positive in sign, indicating the greater stability of the triplet pair (↑•O₁)(↑•Ru₁). The singlet-triplet gap for this pair is about J = 6.4 kcal/mol under the BS approximation. However, spins in molecules are the angular momentums described by quantum mechanics. Therefore the above classical approximation in Eq. 1 is a drastic approximation. We can determine the quantum corrections using the (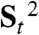) values by the UB3LYP calculations as shown in SI Text. Table 2 summarizes the quantum-corrected J values after the approximate spin projection (AP) that eliminates the spin contamination in the BS solution (7–10). The AP correction is not negligible for the AF exchange integrals, J_ab and J_cd, because the size of local spin is 1/2 in 2bb and 2a(+)ee.

Table 2.

Effective exchange integrals (J) for the intermediates (2bb and 2a(+)ee)^*

J	2bb		2a(+)ee
	Before AP	After AP	Before AP	After AP
Jab	−3.77	−2.89	0.00	0.00
Jac	0.00	0.00	−0.01	−0.01
Jad	−0.01	−0.01	0.00	0.00
Jbc	0.03	0.03	6.36	6.13
Jbd	−0.01	−0.01	0.42	0.43
Jcd	−1.88	−1.61	−2.33	−2.02

^*J values are given in kcal mol^-1.

The energy gaps for key species after AP correction are summarized in Table 1. The energy gaps between closed-shell 2b and open-shell 2bb before and after AP are 12.0 and 15.4 kcal/mol, indicating a non-negligible correction (3.4 kcal/mol). On the other hand, the energy gaps between 2b and 2a(+)ee before and after AP are 5.0 and 6.3 kcal/mol. The very large corrections are necessary for ³C, ³D, ¹F and ¹G states of 2a(+)ee. This is attributable to the large J_bc value (= 6.4 kcal/mol). For lucid understanding of AP correction, let us consider the •O-R(III)• biradical (1dd in Fig. 1) as shown in Fig. S3. The singlet–triplet (S–T) energy gap for 1dd is about 6.4 (= J_bc) kcal/mol by the BS UB3LYP calculation but it becomes about 12.3 (= 2J_bc) kcal/mol after AP correction. The gap after AP is smaller than the isoelectronic molecular oxygen (22.4 kcal/mol; note that the BS energy gap is 11 kcal/mol) (32) and that of the iron-oxo species (about 14 kcal/mol) (33), although the latter value for the three-spin system is regarded as the energy of the equal mixture of local singlet and triplet states (34). On the other hand, the S-T gaps for OH-Ru(III)•-SQ• biradical (1aa and 1bb in Fig. 1) becomes about 4 and 6 kcal/mol before and after AP as shown in Fig. S3. The ground state of •O-Ru(II)-SQ• biradical (1cc in Fig. 1) is triplet (J_bd > 0) in accord with the ESR experiment by Tanaka and coworkers (16, 18).

The J values in Table 2 are applicable to estimate energy gaps for a triradical species, the •O-Ru(III)•-SQ• radical (1ee in Fig. 1). There are four spin alignments for 1ee: A(↑•O-Ru(III)•↑-SQ•↓), B(↑↑↑), C(↑↓↑), and D(↓↑↑). The relative energies for A(↑↑↓), C(↑↓↑), and D(↓↑↑), setting the ferromagnetic state B(↑↑↑) as the reference are, respectively, -1.91, 4.03, and 6.78 (kcal/mol) under the BS approximation. On the other hand, they become -7.63, 8.24 and 13.12, (kcal/mol) after quantum correction by AP. The significant correction energies are attributable to the large J_bc value (= 6.4 kcal/mol) as in the case of 2a(+)ee in Table 1. These energy gaps for 1ee are used to estimate the energy gaps for hexaradical species: dimmer of 1ee in Fig. 1 (•SQ-Ru(III)•-O• •O-Ru(III)•-SQ•). Fig. S4 illustrates possible spin alignments for the hexaradical species 1ee-1ee. The ground spin configurations ³A(↓↑↑↑↑↓) and ¹A(↓↑↑↓↓↑) are nearly degenerated in energy because the effective exchange coupling between the oxygen radicals (O• •O) is weak. The first excited configurations ⁷B(↑↑↑↑↑↑) and ¹B(↑↑↑↓↓↓) consist of the ferromagnetic spin alignment of the monomer (1ee). The energy gap between the ground and the first excited states are about 3.8 and 6.4 (kcal/mol) before and after AP as illustrated in Fig. S4. The energy diagram in Fig. S4 can be applicable for examination of the possible reaction pathways for water splitting reactions.

Discussion

Natural Orbital Analysis of BS Solutions.

Present UB3LYP calculations have elucidated that one electron transfer (OET) configuration from HOMO of Ru(II) to the LUMO of quinone plays an important role to generate four spin sites denoted as (SQ₂,Ru₂,Ru₁,SQ₁) (2bb). Therefore, eight spin structures are feasible as shown in Fig. 3, where (SQ₂,Ru₂,Ru₁,SQ₁) (2bb) is expressed by (abcd) as in the case of native water splitting enzyme CaMn_a(4) Mn_b(3)Mn_c(2)Mn_d(1) (3) in photosystem II (7–10). The same spin Hamiltonian model has been derived to elucidate similarity between artificial (2bb) and native (3) catalysts for the water splitting reaction, though the size of local spin is different between 2bb (size of each spin = 1/2) and 3 [size of each spin = 4/2 for Mn(III)]. However, as shown in the previous natural orbital analysis of BS solutions for 3, the magnetic local spins in three t_2g orbitals of each Mn(X) (X = III, IV) ions are almost intact for the O─O bond formation. This means that local spin (s = 1/2) in the e_g orbital of the Mn ion plays an important role for formation of the labile Mn-O bond (7–10), indicating the similarity between 2bb and 3.

The natural orbital analysis of the BS solution is useful for elucidation of effective exchange interactions of active electrons in 2bb. Fig. S5 shows natural orbitals (NO) and their occupation numbers for the antiferromagnetic spin configuration (↓•SQ₂)(↑•Ru₂)(↑•Ru₁)(↓•SQ₁) (¹H in Fig. 3) of 2bb. The HONO and LUNO are delocalized orbitals, and their mixing provides more or less localized (diradicaloid) orbitals. The orbital overlaps for diradicaloid (frontier) orbitals for (↑•Ru₁)(↓•SQ₁) and (↓•SQ₂)(↑•Ru₂) are 0.40 and 0.55, respectively, as shown in Fig. S5. Therefore the effective exchange interaction between the former pair is about one-half of the latter pair because the magnitude of J is roughly parallel to the square of the orbital overlap: (0.4)²/(0.55)² = J_cd/J_ab = 0.16/0.30 = 1.88(1.61)/3.77(2.89). Thus the left and right pairs of 2bb are not equivalent, namely breaking of cluster symmetry in the electronic state.

The proton-coupled electron transfer may be feasible for 2bb to afford the unsymmetrical structure 2a(+)ee. Fig. S6 illustrates NOs and their occupation numbers for the antiferromagnetic spin configuration (↓•SQ₂)(↑•O₁)(↑•Ru₁)(↓•SQ₁) (¹H in Fig. 3) of 2a(+)ee. The complete mixing of HONO and LUNO affords localized orbitals for the former pair. In fact, the orbital overlaps for the active orbitals for (↓•SQ₂)(↑•O₁) and (↑•Ru₁)(↓•SQ₁) are 0.00 and 0.38, respectively. The effective exchange interaction for the (↓•SQ₂)(↑•O₁) pair is essentially zero (complete diradical) because of zero orbital overlap. The local spin on the O₁ site is expected to show high radical reactivity. On the other hand, the orbital overlap (0.38) for the (↑•Ru₁)(↓•SQ₁) pair is almost the same (0.40) as that of 2bb. Thus the natural orbital analysis provides a lucid MO-theoretical explanation of exchange-coupled electrons in Tanaka catalysts.

Radical Coupling and Nonradical Mechanisms for the O─O Bond Formation.

Accumulated experimental and theoretical studies (11–29) on artificial photosynthesis systems have elucidated dual possible mechanisms of the water splitting reaction: (i) the radical coupling (RC) mechanism and (ii) the acid-base mechanism. Tanaka and coworkers have proposed the former mechanism for the water splitting reaction by their Ru-quinone complexes as illustrated in Fig. 2A, where the Ru(II) ion is intact throughout the reaction (25). Similarly, Ghosh and Baik (27) have proposed the radical coupling mechanism (i) for the O─O bond formation, though they have considered the contribution of the one-electron transfer from Ru(II) to quinone (2bb) as illustrated in Fig. 2B. On the other hand, Muckerman et al. (25) have considered the superoxide mechanism for the water splitting reaction that may be regarded as one of the acid-base (B) mechanism as illustrated in Fig. 2A. However, newly obtained experimental results by Tanaka group (30), together with present DFT computational results, may indicate a refined radical coupling mechanism for water splitting reaction as shown in Fig. S7.

The deprotonation of waters in ¹1 in Fig. S7 affords the key tetraradical intermediate ¹3(¹2bb) via one-electron transfer (OET) in ¹2. However, the oxygen-radical pair in ¹3 is local triplet diradical (LTD), suppressing facile O─O bond formation by the radical coupling (RC) mechanism. The two-electron removal from ¹3 provides the hexaradical species ³4 in Fig. 2 proposed by Ghosh and Baik (27). The oxygen radical pair (see ³A in Fig. S7) is still LTD-type, indicating the necessity of spin inversion (SI) for generation of local singlet diradical (LSD) pair in ¹5 (see ¹A in Fig. S4). The RC mechanism in ¹5 is facile, giving the peroxide species ¹6. The next step for generation of the oxygen dianion may become the rate-determining step in the Tanaka catalyst as shown in ¹7. The β-spin at the terminal oxygen anion in ¹7 is moved to the Ru₂(III) site with the α-spin to form the singlet pair as shown in ¹8. The spin exchange (SE) between ↓•Ru₁(III) and SQ₁•↑ to generate ↑•Ru₁(III) and SQ₁•↓ is necessary for one more OET from superoxide anion to •Ru₁(III) to afford triplet molecular oxygen in ¹9. The SE process is easy because the exchange coupling for the •O-O-Ru(III)• is weak. Thus the SQ₁• radical plays an important role for spin catalysis. The two-electron removal from ¹9 is necessary for reproduction of ¹1. Thus the BS computational results provide the orbital and spin correlation diagram for the water splitting reaction in Fig. S7.

Similarity Between Artificial and Native Water Splitting Systems.

Very recently Umena, Kawakami, Shen, and Kamiya (5) have determined the XRD structure of the OEC of PSII refined to the 1.9 Å resolution, which corresponds to the dark-stable S₁-state of the catalytic cycle [the S₀–S₄ states of the Kok cycle (6)]. Their XRD result (5) has elucidated the Mn–Mn, Ca-Mn, and Mn-O distances of the CaMn₄O₅ cluster and the positions of a number of waters in PSII. Very recently, possible electronic and spin structures of the CaMn₄O₅ cluster (3) have been elucidated by the hybrid DFT calculations on the basis of the new X-ray structure (7–10). The DFT computational results provide fundamental information to inspire artificial photosynthesis systems. Thus accumulated experimental and theoretical results (35–44) for OEC of PSII indicated a dual possibility for water splitting reaction: (i) the radical-coupling mechanism and (ii) nucleophilic attack of hydroxide anion (water) to the electrophilic metal-oxo species.

The nature of high-valent metal-oxo species is labile as shown in our early paper (45). The high-valent Mn(V)═O bond formally has a triple bond in the sense of the simple MO theory. However, the one ET from HOMO of oxygen dianion to Mn(V) occurs to afford the •Mn(IV)═O•. Moreover, BS solutions for Mn(V)═O indicate continuous variation from the nucleophilic Mn(V)═O^2- oxygen to electrophilic oxygen Mn(III)═O⁰ through •Mn(IV)═O•, depending on electron donating ability of coordination ligands. In fact, oxyl radical character is computationally detected even in the prophyrine Mn(V)═O complex (44). We have thoroughly examined the radical-coupling (RC) mechanism for the O─O bond formation process for the CaMn₄O₅ cluster (3) in hydrophobic conditions (gas phase) like in the case of the Tanaka catalysts (Fig. S7). However, the UB3LYP computations have elucidated that the metal diradical character •Mn(IV)═O• of the manganese-oxo bond of 3 has been reduced by clustering of waters to the active site (46, 47). Therefore we have proposed a water-assisted acid-base mechanism in hydrophilic conditions (46, 47).

Very recent DFT calculations (7–10) also indicated that the orbital overlap for the Mn(IV)-oxyl radical pair of 3 is about 0.5, predicting non-negligible •Mn═O• radical character. This means the oxygen activation by the high-valent Mn ion. However, the orbital overlap at the transition structure (TS) for the O─O bond formation is about 1.0, indicating that the radical character is lost at the TS. Therefore the O─O bond formation between OH and Mn═O is essentially ionic (essentially acid-base type) in nature in accord with the mechanism (ii). Recent DFT computations for blue dimmer (22–24, 28) also supported the acid-base mechanism under the hydrophilic condition. Fig. S8 illustrates possible analogy between the artificial Ru-quinone complex and the native CaMn₄O₅ cluster in OEC of PSII in detail.